СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
 |
|
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Задания
Версия для печати и копирования в MS Word
Тип 2 № 275869 
Найдите расстояние между вершинами C и 
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Спрятать решение
Решение.
Рассмотрим прямоугольный треугольник 
По теореме Пифагора
Ответ: 33.
Аналоги к заданию № 245372: 275869 276367 275871 275875 275877 275879 275881 275883 275885 275887 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Спрятать решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Тренировочный вариант №26 пробник решу ЕГЭ 2023 по математике 11 класс профильный уровень от 8 марта 2023 года с ответами и решением по новой демоверсии ЕГЭ 2023 года для подготовки на 100 баллов, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
▶Скачать вариант с ответами
▶Решение заданий с 1 по 18
▶Распечатай и реши вариант
вариант_26_егэ2023_профиль_математика
Ответы и решения
решение_варианта_26_профиль
1. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, sin 𝐴 = 0,8. Найдите sin 𝐵.
2. Дана правильная треугольная призма 𝐴𝐵𝐶𝐴1𝐵1𝐶1, площадь основания которой равна 9, а боковое ребро равно 4. Найдите объём многогранника, вершинами которого являются точки 𝐴, 𝐴1, 𝐵1, 𝐶1.
3. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что произведение выпавших очков делится на 5, но не делится на 30.
4. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,98. Вероятность того, что масса окажется больше 790 г, равна 0,83. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
7. На рисунке изображён график дифференцируемой функции 𝑦 = 𝑓(𝑥), определённой на интервале (−3; 8). Найдите точку из отрезка [−2; 5], в которой производная функции 𝑓(𝑥) равна 0.
8. Два тела, массой 𝑚 = 2 кг каждое, движутся с одинаковой скоростью 𝑣 = 8 м/с под углом 2𝛼 друг к другу. Энергия (в Дж), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле 𝑄 = 𝑚𝑣 2 sin2𝛼, где 𝑚 − масса (в кг), 𝑣 − скорость (в м/с). Найдите, под каким углом 2𝛼 должны двигаться тела, чтобы в результате соударения выделилась энергия, равная 32 Дж. Ответ дайте в градусах.
9. Смешали некоторое количество 19-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
10. На рисунке изображён график функции вида 𝑓(𝑥) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐. Найдите значение 𝑓(−2).
11. Найдите точку максимума функции 𝑦 = ln(𝑥 + 9) − 10𝑥 + 7.
12. а) Решите уравнение 3 ∙ 9 𝑥+1 − 5 ∙ 6 𝑥+1 + 8 ∙ 2 2𝑥 = 0. б) Найдите все корни этого уравнения, принадлежащие отрезку.
13. В правильной треугольной призме 𝐴𝐵𝐶𝐴1𝐵1𝐶1 все рёбра равны 2. Точка 𝑀 − середина ребра 𝐴𝐴1. а) Докажите, что прямые 𝑀𝐵 и 𝐵1𝐶 перпендикулярны. б) Найдите расстояние между прямыми 𝑀𝐵 и 𝐵1𝐶.
15. В июле 2016 года планируется взять кредит в банке на три года в размере 𝑆 млн рублей, где 𝑆 − целое число. Условия его возврата таковы: – каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года; – с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; – в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей. Найдите наибольшее значение 𝑆, при котором разница между наибольшей и наименьшей выплатами будет меньше 1 млн рублей.
16. В трапеции 𝐴𝐵𝐶𝐷 боковая сторона 𝐴𝐵 перпендикулярна основаниям. Из точки 𝐴 на сторону 𝐶𝐷 опустили перпендикуляр 𝐴𝐻. На стороне 𝐴𝐵 отмечена точка 𝐸 так, что прямые 𝐶𝐷 и 𝐶𝐸 перпендикулярны. а) Докажите, что прямые 𝐵𝐻 и 𝐸𝐷 параллельны. б) Найдите отношение 𝐵𝐻 к 𝐸𝐷, если ∠𝐵𝐶𝐷 = 135°.
18. В течение 𝑛 дней каждый день на доску записывают натуральные числа, каждое из которых меньше 6. При этом каждый день (кроме первого) сумма чисел, записанных на доску в этот день, больше, а количество меньше, чем в предыдущий день. а) Может ли 𝑛 быть больше 5? б) Может ли среднее арифметическое чисел, записанных в первый день, быть меньше 3, а среднее арифметическое всех чисел, записанных за все дни, быть больше 4? в) Известно, что сумма чисел, записанных в первый день, равна 6. Какое наибольшее значение может принимать сумма всех чисел, записанных за все дни?
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
ЕГЭ профильный уровень. №7 Первообразная. Задача 4
Задача 4. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = {x^3} + 30{x^2} + 302x — frac{{15}}{8}) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры.
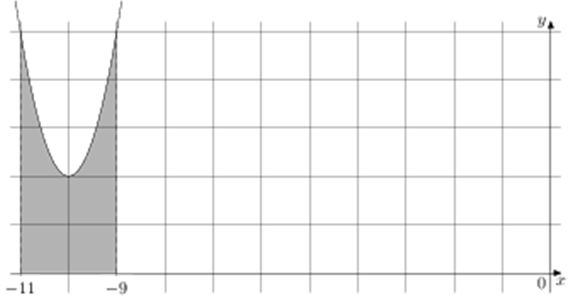
ОТВЕТ: 6.
Площадь закрашенной фигуры равна интегралу (intlimits_{ — 11}^{ — 9} {left( x right)dx} = Fleft( { — 9} right) — Fleft( { — 11} right).) Найдём значение первообразной в точках – 9 и – 11:
(Fleft( { — 9} right) = {left( { — 9} right)^3} + 30 cdot {left( { — 9} right)^2} + 302 cdot left( { — 9} right) — frac{{15}}{8} = — 729 + 2430 — 2718 — frac{{15}}{8} = — 1017 — frac{{15}}{8})
(Fleft( { — 11} right) = {left( { — 11} right)^3} + 30 cdot {left( { — 11} right)^2} + 302 cdot left( { — 11} right) — frac{{15}}{8} = — 1331 + 3630 — 3322 — frac{{15}}{8} = — 1023 — frac{{15}}{8})
Тогда площадь закрашенной фигуры:
(S = Fleft( { — 9} right) — Fleft( { — 11} right) = — 1017 — frac{{15}}{8} — left( { — 1023 — frac{{15}}{8}} right) = 6)
Ответ: 6.
Комментарии для сайта Cackle
| 3554 | Решите уравнение (7x)/(3x^2-26)=1. Если уравнение имеет более одного корня, в ответе запишите меньший из корней Решение  График |
Решите уравнение 7x / 3×2 — 26 =1 ! 36 вариантов ФИПИ Ященко 2023 Вариант 14 Задание 5 | |
| 3551 | а) Решите уравнение 25^(x-0.5)-13*10^(x-1)+4^(x+0.5)=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [-pi/2; pi].Решение График |
а) Решите уравнение 25^ x-0,5 — 13 10^ x-1 +4^ x+0,5 =0! 36 вариантов ФИПИ Ященко 2023 Вариант 14 Задание 12 | |
| 3550 | Решите неравенство: 8^(lg(-1-x))<=(x^2-1)^(lg2)Решение График |
Решите неравенство: 8 lg(-1-x)<=(x2 — 1) lg2 ! 36 вариантов ФИПИ Ященко 2023 Вариант 14 Задание 14 | |
| 3536 | а) Решите уравнение 2cos(x)*sin(2x)=2sin(x)+cos(2x) б) Найдите все корни этого уравнения, принадлежащие отрезку [3pi; (9pi)/2].Решение График |
а) Решите уравнение 2cos x sin 2x =2sinx +cos2x ! 36 вариантов ФИПИ Ященко 2023 Вариант 9 Задание 12 | |
| 3533 | Решите неравенство: 4log_{0.25}(1-4x) -log_{sqrt(2)}(-1-x)+. 4log_{4}(x^2-1) <= log_{2}(x^2).Решение График |
Решите неравенство: 4log 0,25 (1-4x) — log sqrt2 (-1-x) +4log4 (x2 -1) <= log2 x2 ! 36 вариантов ФИПИ Ященко 2023 Вариант 9 Задание 14 | |
| 3528 | а) Решите уравнение (log_{2}(8x^2))^2-log_{4}(2x)-1=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [0,4; 0,8]Решение График |
а) Решите уравнение log2 2(8×2) -log4 (2x) -1 =0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 8 Задание 12 | |
| 3526 | Решите неравенство (sqrt(x-2)(4-3^(x-1)))/(2^(1-x^2)-3)>= 0Решение График |
Решите неравенство (sqrt(x -2)(4 -3 x-1)/ 2^1-x2 -3 >= 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 8 Задание 14 |
|
| 3517 | а) Решите уравнение (log_{2}(4x^2))^2+3*log_{0.5}(8x)=1 б) Найдите все корни этого уравнения, принадлежащие отрезку [0,15; 1,5]Решение График |
а) Решите уравнение log2 2 (4×2) + 3log 0.5 (8x) = 1 ! 36 вариантов ФИПИ Ященко 2023 Вариант 7 Задание 12 | |
| 3515 | Решите неравенство (sqrt(x+4)(8-3^(2+x^2)))/(4^(x-1)-3)<= 0Решение |
Решите неравенство sqrt(x+4)(8 -3^ 2+x2) / 4^x-1 -3 <= 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 7 Задание 14 |
|
| 3510 | Решите уравнение log_{4}(2^(8x+20))=8Решение График |
Решите уравнение log 4 2^(8x+20 =8 ! 36 вариантов ФИПИ Ященко 2023 Вариант 5 Задание 5 | |
Показать ещё…
Показана страница 2 из 5
|
Contains([ Условие задачи], ‘решите’) | Clear |
9 марта 2023
В закладки
Обсудить
Жалоба
Теория и практика.
Содержание
1) Прямые
2) Параболы
3) Как искать пересечение параболы и прямой, двух парабол
4) Гипербола. Асимптотические точки гиперболы
5) Пересечение гиперболы и прямой
6) Иррациональные функции
7) Пересечение корня и прямой
Тригонометрические функции
9) Показательные функции
10) Логарифмические функции
10_zadacha.pdf
Источник: vk.com/profimatika
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
|
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
||||
|
|
||||
|
|
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
| |
||||
|
|
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
| |
||||
|
|
||||
|
|
||||
| Показать сообщения за: Сортировать по: |
Добавлено: Вчера, 09:59 
