Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Спрятать решение
Решение.
Вероятность того, что батарейка исправна, равна 0,94. Вероятность произведения независимых событий (обе батарейки окажутся исправными) равна произведению вероятностей этих событий: 0,94·0,94 = 0,8836.
Ответ: 0,8836.
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Гость 15.08.2014 12:42
Откуда взяли цифру 0,94?Но ведь в задаче не написана эта цифра.
Александр Иванов
Батарейка либо бракованная, либо исправная. Вероятность того, что она бракованная по условию 0,06. Во всех остальных случаях она исправна. Вероятность того, что батарейка исправна равна 1-0,06=0,94
Ilya Khmelev 25.03.2015 14:13
Можете ли объяснить, почему если умножить 0,06 на 0,06 — вероятность того, что обе батарейки бракованные, а после отнимаю её от единицы не получается тоже самое? Спасибо.
Служба поддержки
Умножая вероятности того, что батарейки неисправны, вы находите вероятность купить две неисправные батарейки. Вычитая из единицы найденную величину, вы получите вероятность противоположного события — покупки не двух неисправных батареек одновременно, а любой другой возможности: покупки двух исправных батареек или покупку одной исправной и одной неисправной батарейки.
Artur Mikhilovsky 09.06.2020 07:14
Формулировка задания неверная. В первом предложении задачи говорится о бракованных батарейках. Во втором предложении говорят, что ТАКИХ батареек взято 2 штуки. Каких это таких? Должно быть объяснено слово ТАКИХ.
Татьяна Кравченко
Таких — это таких батареек, которые могут быть бракованными с вероятностью 0,06. (А не других батареек, выпущенных на другом заводе и неисправных с вероятностью 0,1, например.)
Вероятность того, что батарейка
Дата: 2015-03-04
5078
Категория: Вероятность
Метка: ЕГЭ-№3
320210. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Вероятность того, что батарейка исправна, равна 1 – 0,06 = 0,94.
Первая батарейка исправна и вторая батарейка исправна – это два независимые события.
Вероятность совершения независимых событий (обе батарейки окажутся исправными) равна произведению вероятностей этих событий:
Ответ: 0,8836
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
1. Задание 4 № 1001
На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный вопрос.
Ответ: 0,95
2. Задание 4 № 1011
В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.
Ответ: 0,4
3. Задание 4 № 1024
На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Ответ: 0,25
4. Задание 4 № 282853
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Ответ: 0,14
5. Задание 4 № 282854
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Ответ: 0,5
6. Задание 4 № 282855
В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Ответ: 0,25
7. Задание 4 № 282856
При производстве в среднем на каждые 2982 исправных насоса приходится 18 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
Ответ: 0,006
8. Задание 4 № 282857
Фабрика выпускает сумки. В среднем 8 сумок из 100 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов.
Ответ: 0,92
9. Задание 4 № 282858
В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Ответ: 0,36
10. Задание 4 № 283651
Фабрика выпускает сумки. В среднем 11 сумок из 160 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов. Результат округлите до сотых.
Ответ: 0,93
11. Задание 4 № 285922
Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Ответ: 0,16
12. Задание 4 № 285923
Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление исполнителя из России состоится в третий день конкурса?
Ответ: 0,225
13. Задание 4 № 285924
На конференцию приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Ответ: 0,3
14. Задание 4 № 285925
Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 спортсменов из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России.
Ответ: 0,36
15. Задание 4 № 285926
В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по теме «Ботаника». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Ботаника».
Ответ: 0,2
16. Задание 4 № 285927
В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по теме «Неравенства». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме «Неравенства».
Ответ: 0,6
17. Задание 4 № 285928
На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 8 прыгунов из России и 9 прыгунов из Парагвая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что шестым будет выступать прыгун из Парагвая.
Ответ: 0,36
18. Задание 4 № 320169
Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
Ответ: 0,25
19. Задание 4 № 320170
В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Ответ: 0,25
20. Задание 4 № 320178
На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?
Ответ: 0,5
21. Задание 4 № 320179
Из множества натуральных чисел от 10 до 19 наудачу выбирают одно число. Какова вероятность того, что оно делится на 3?
Ответ: 0,3
22. Задание 4 № 320181
В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?
Ответ: 0,4
23. Задание 4 № 320183
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
Ответ: 0,375
24. Задание 4 № 320184
Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «А = сумма очков равна 5»?
Ответ: 4
25. Задание 4 № 320185
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что наступит исход ОР (в первый раз выпадает орёл, во второй — решка).
Ответ: 0,25
26. Задание 4 № 320186
На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
Ответ: 0,33
27. Задание 4 № 320189
В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных.
Ответ: 0,498
28. Задание 4 № 320190
На борту самолёта 12 кресел расположены рядом с запасными выходами и 18 — за перегородками, разделяющими салоны. Все эти места удобны для пассажира высокого роста. Остальные места неудобны. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.
Ответ: 0,1
29. Задание 4 № 320191
На олимпиаде по русскому языку 250 участников разместили в трёх аудиториях. В первых двух удалось разместить по 120 человек, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Ответ: 0,04
30. Задание 4 № 320192
В классе 26 учащихся, среди них два друга — Андрей и Сергей. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
Ответ: 0,48
31. Задание 4 № 320193
В фирме такси в наличии 50 легковых автомобилей; 27 из них чёрного цвета с жёлтыми надписями на бортах, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
Ответ: 0,46
32. Задание 4 № 320194
В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
Ответ: 0,2
33. Задание 4 № 320195
Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Ответ: 0,006
34. Задание 4 № 320208
В кармане у Миши было четыре конфеты — «Грильяж», «Белочка», «Коровка» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».
Ответ: 0,25
35. Задание 4 № 320209
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 10, но не дойдя до отметки 1.
Ответ: 0,25
36. Задание 4 № 325904
За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
Ответ: 0,25
37. Задание 4 № 325905
За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки будут сидеть рядом.
Ответ: 0,5
38. Задание 4 № 325907
За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки не будут сидеть рядом.
Ответ: 0,5
39. Задание 4 № 325909
За круглый стол на 201 стул в случайном порядке рассаживаются 199 мальчиков и 2 девочки. Найдите вероятность того, что между девочками будет сидеть один мальчик.
Ответ: 0,01
40. Задание 4 № 325913
За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что девочки не будут сидеть рядом.
Ответ: 0,75
41. Задание 4 № 325917
За круглый стол на 17 стульев в случайном порядке рассаживаются 15 мальчиков и 2 девочки. Найдите вероятность того, что девочки будут сидеть рядом.
Ответ: 0,125
42. Задание 4 № 500037
Проводится жеребьёвка Лиги Чемпионов. На первом этапе жеребьёвки восемь команд, среди которых команда «Барселона», распределились случайным образом по восьми игровым группам — по одной команде в группу. Затем по этим же группам случайным образом распределяются еще восемь команд, среди которых команда «Зенит». Найдите вероятность того, что команды «Барселона» и «Зенит» окажутся в одной игровой группе.
Ответ: 0,125
43. Задание 4 № 501210
В соревновании по биатлону участвуют спортсмены из 25 стран, одна из которых ― Россия. Всего на старт вышло 60 участников, из которых 6 ― из России. Порядок старта определяется жребием, стартуют спортсмены друг за другом. Какова вероятность того, что десятым стартовал спортсмен из России?
Ответ: 0,1
44. Задание 4 № 509081
У Вити в копилке лежит 12 рублёвых, 6 двухрублёвых, 4 пятирублёвых и 3 десятирублёвых монеты. Витя наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей.
Ответ: 0,72
45. Задание 4 № 509110
У Дины в копилке лежит 7 рублёвых, 5 двухрублёвых, 6 пятирублёвых и 2 десятирублёвых монеты. Дина наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит менее 60 рублей.
Ответ: 0,1
46. Задание 4 № 510333
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что выпадет хотя бы две решки.
Ответ: 0,5
47. Задание 4 № 510381
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 4, но не дойдя до отметки 7 часов.
Ответ: 0,25
48. Задание 4 № 510400
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 8, но не дойдя до отметки 11 часов.
Ответ: 0,25
49. Задание 4 № 510419
Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 16 спортсменов из России, в том числе Игорь Чаев. Какова вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
Ответ: 0,2
50. Задание 4 № 510838
В среднем из 2000 садовых насосов, поступивших в продажу, 6 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает?
Ответ: 0,997
51. Задание 4 № 514685
В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Ответ: 0,995
1. Задание 4 № 510061
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Ответ: 0,15
2. Задание 4 № 319355
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Ответ: 0,156
3. Задание 4 № 320212
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу
Ответ: 0,0625
4. Задание 4 № 320210
Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Ответ: 0,8836
5. Задание 4 № 509011
Какова вероятность того, что случайно выбранный телефонный номер оканчивается двумя чётными цифрами?
Ответ: 0,25
6. Задание 4 № 509569
Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Ответ: 0,06
7. Задание 4 № 509916
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0,82. Вероятность того, что окажется меньше 10 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 10 до 17.
Ответ: 0,31
8. Задание 4 № 320201
В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).
Ответ: 0,027
9. Задание 4 № 510117
В торговом центре два одинаковых автомата продают кофе. Обслуживание автоматов происходит по вечерам после закрытия центра. Известно, что вероятность события «К вечеру в первом автомате закончится кофе» равна 0,25. Такая же вероятность события «К вечеру во втором автомате закончится кофе». Вероятность того, что кофе к вечеру закончится в обоих автоматах, равна 0,15. Найдите вероятность того, что к вечеру дня кофе останется в обоих автоматах.
Ответ: 0,65
10. Задание 4 № 320197
Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °С, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °С или выше.
Ответ: 0,19
11. Задание 4 № 320176
Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Ответ: 0,08
12. Задание 4 № 320196
При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.
Ответ: 0,035
13. Задание 4 № 320173
Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Ответ: 0,02
14. Задание 4 № 320175
Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Ответ: 0,91
15. Задание 4 № 320187
При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
В ответе укажите наименьшее необходимое количество выстрелов.
Ответ: 5
16. Задание 4 № 320171
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос по теме «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Ответ: 0,35
17. Задание 4 № 320188
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Ответ: 0,32
18. Задание 4 № 320206
В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Ответ: 0,392
19. Задание 4 № 320174
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Ответ: 0,9975
20. Задание 4 № 320172
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Ответ: 0,52
21. Задание 4 № 319353
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Ответ: 0,019
22. Задание 4 № 320180
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Ответ: 0,52
23. Задание 4 № 320177
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Ответ: 0,75
24. Задание 4 № 320199
Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Ответ: 0,408
25. Задание 4 № 320203
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.
Ответ: 0,38
26. Задание 4 № 320200
На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.
Ответ: 0,98
27. Задание 4 № 320198
Вероятность того, что на тестировании по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.
Ответ: 0,07
28. Задание 4 № 320202
По отзывам покупателей Иван Иванович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Ответ: 0,02
29. Задание 4 № 320205
Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры.
Ответ: 0,125
30. Задание 4 № 320207
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Ответ: 0,0545
31. Задание 4 № 320211
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.
Ответ: 0,0296
32. Задание 4 № 500998
В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Ответ: 0,6
33. Задание 4 № 501061
Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).
Ответ: 0,91
34. Задание 4 № 526004
Перед началом волейбольного матча капитаны команд тянут жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Мотор» по очереди играет с командами «Статор», «Стартер» и «Ротор». Найдите вероятность того, что «Мотор» будет начинать с мячом только вторую игру.
Ответ: 0,125
B10 № 320176. Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Решение.
Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», тогда A + B = «чайник прослужит больше года».
События A и В совместные, вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения. Вероятность произведения этих событий, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду — равна нулю. Тогда:
P(A + B) = P(A) + P(B) − P(A·B) = P(A) + P(B),
откуда, используя данные из условия, получаем
0,97 = P(A) + 0,89.
Тем самым, для искомой вероятности имеем:
P(A) = 0,97 − 0,89 = 0,08.
Ответ: 0,08.
B10 № 319353. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение.
Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,45 · 0,03 = 0,0135.
Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,55 · 0,01 = 0,0055.
Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна 0,0135 + 0,0055 = 0,019.
Ответ: 0,019.
B10 № 319355. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение.
Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,52 · 0,3 = 0,156.
Ответ: 0,156
B10 № 320169. Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
Решение.
Жребий начать игру может выпасть каждому из четырех мальчиков. Вероятность того, что это будет именно Петя, равна одной четвертой.
Ответ: 0,25.
B10 № 320170. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение.
Вероятность того, что команда России окажется во второй группе, равна отношению количества карточек с номером 2, к общему числу карточек. Тем самым, она равна
Ответ: 0,25.
B10 № 320171. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 0,2 + 0,15 = 0,35.
Ответ: 0,35.
B10 № 320172. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение.
Рассмотрим события
А = кофе закончится в первом автомате,
В = кофе закончится во втором автомате.
Тогда
A·B = кофе закончится в обоих автоматах,
A + B = кофе закончится хотя бы в одном автомате.
По условию P(A) = P(B) = 0,3; P(A·B) = 0,12.
События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48.
Следовательно, вероятность противоположного события, состоящего в том, что хотя бы кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52.
Ответ: 0,52.
Приведем другое решение.
Вероятность того, что кофе останется в первом автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется во втором автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,12 = 0,88. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − х, откуда искомая вероятость х = 0,52. Примечание.
Заметим, что события А и В не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий: P(A·B) = 0,3·0,3 = 0,09, однако по условию эта вероятность равна 0,12.
B10 № 320173. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Решение.
Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 − 0,8 = 0,2. Cобытия попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся» равна
Ответ: 0,02
B10 № 320174. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение.
Найдем вероятность того, что неисправны оба автомата. Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,05 · 0,05 = 0,0025.
Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна 1 − 0,0025 = 0,9975.
Ответ: 0,9975.
Приведем другое решение.
Вероятность того, что исправен первый автомат (событие А) равна 0,95. Вероятность того, что исправен второй автомат (событие В) равна 0,95. Это совместные независимые события. Вероятность их произведения равна произведению вероятностей этих событий, а вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения. Имеем:
P(A + B) = P(A) + P(B) − P(A·B) = P(A) + P(B) − P(A)P(B) = 0,95 + 0,95 − 0,95·0,95 = 0,9975.
B10 № 320175. Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение.
Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равно произведению вероятностей этих событий: 0,3·0,3 = 0,09.
Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное. Следовательно, его вероятность равна 1 − 0,09 = 0,91.
Ответ: 0,91.
B10 № 320177. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Решение.
Пусть событие состоит в том, что яйцо имеет высшую категорию, события
и
состоят в том, что яйцо произведено в первом и втором хозяйствах соответственно. Тогда события
и
— события, состоящие в том, что яйцо высшей категории произведено в первом и втором хозяйстве соответственно. По формуле полной вероятности, вероятность того, что будет куплено яйцо высшей категории, равна:
Поскольку по условию эта вероятнсть равна 0,35, имеем:
Ответ: 0,75.
B10 № 320178. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?
Решение.
На клавиатуре телефона 10 цифр, из них 5 четных: 0, 2, 4, 6, 8. Поэтому вероятность того, что случайно будет нажата четная цифра равна 5 : 10 = 0,5.
Ответ: 0,5.
B10 № 320179. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?
Решение.
Натуральных чисел от 10 до 19 десять, из них на три делятся три числа: 12, 15, 18. Следовательно, искомая вероятность равна 3:10 = 0,3.
Ответ: 0,3.
B10 № 320180. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Решение.
Джон промахнется, если схватит пристрелянный револьвер и промахнется из него, или если схватит непристрелянный револьвер и промахнется из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0,4·(1 − 0,9) = 0,04 и 0,6·(1 − 0,2) = 0,48. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,04 + 0,48 = 0,52.
Ответ: 0,52.
Приведем другое решение.
Джон попадает в муху, если схватит пристрелянный револьвер и попадет из него, или если схватит непристрелянный револьвер и попадает из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0,4·0,9 = 0,36 и 0,6·0,2 = 0,12. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,36 + 0,12 = 0,48. Событие, состоящее в том, что Джон промахнется, противоположное. Его вероятность равна 1 − 0,48 = 0,52.
B10 № 320181. В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин?
Решение.
Всего туристов пять, случайным образом из них выбирают двоих. Вероятность быть выбранным равна 2 : 5 = 0,4.
Ответ: 0,4.
B10 № 320183. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
Решение.
Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Физиком», другую сторону монеты обозначим «0». Тогда благоприятных комбинаций три: 110, 101, 011, а всего комбинаций 23 = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, искомая вероятность равна:
Ответ: 0,375.
B10 № 320184. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «А = сумма очков равна 5»?
Решение.
Сумма очков может быть равна 5 в четырех случаях: «3 + 2», «2 + 3», «1 + 4», «4 + 1».
Ответ: 4.
B10 № 320185. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что в первый раз выпадает орёл, а во второй — решка.
Решение.
Всего возможных исходов — четыре: орел-орел, орел-решка, решка-орел, решка-решка. Благоприятным является один: орел-решка. Следовательно, искомая вероятность равна 1 : 4 = 0,25.
Ответ: 0,25.
B10 № 320186. На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
Решение.
Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих (Д — Дания, Ш — Швеция, Н — Норвегия):
…Д…Ш…Н…, …Д…Н…Ш…, …Ш…Н…Д…, …Ш…Д…Н…, …Н…Д…Ш…, …Н…Ш…Д…
Дания находится после Швеции и Норвегии в двух случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна
Ответ: 0,33.
Замечание.
Пусть требуется найти вероятность того, что датские музыканты окажутся последними среди выступающих от разных государств групп. Поставим команду Дании на последнее место и найдем количество перестановок без повторений из
предыдущих групп: оно равно
Общее количество перестановок из всех
групп равно
Поэтому искомая вероятность равна
B10 № 320187. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Решение.
Найдем вероятность противоположного события, состоящего в том, что цель не будет уничтожена за n выстрелов. Вероятность промахнуться при первом выстреле равна 0,6, а при каждом следующем — 0,4. Эти события независимые, вероятность их произведения равна произведению вероятности этих событий. Поэтому вероятность промахнуться при n выстрелах равна:
Осталось найти наименьшее натуральное решение неравенства
Последовательно проверяя значения
, равные 1, 2, 3 и т. д. находим, что искомым решением является
. Следовательно, необходимо сделать 5 выстрелов.
Ответ: 5.
Примечание.
Можно решать задачу «по действиям», вычисляя вероятность уцелеть после ряда последовательных промахов:
Р(1) = 0,6.
Р(2) = Р(1)·0,4 = 0,24.
Р(3) = Р(2)·0,4 = 0,096.
Р(4) = Р(3)·0,4 = 0,0384;
Р(5) = Р(4)·0,4 = 0,015536.
Последняя вероятность меньше 0,02, поэтому достаточно пяти выстрелов по мишени.
Приведем другое решение.
Вероятность поразить мишень равна сумме вероятностей поразить ее при первом, втором, третьем и т. д. выстрелах. Поэтому задача сводится к нахождению наименьшего натурального решения неравенства
В нашем случае неравенство решается подбором, в общем случае понадобится формула суммы геометрической прогрессии, использование которой сведет задачу к простейшему логарифмическому неравенству.
B10 № 320188. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Решение.
Команда может получить не меньше 4 очков в двух играх тремя способами: 3+1, 1+3, 3+3. Эти события несовместны, вероятность их суммы равна сумме их вероятностей. Каждое из этих событий представляет собой произведение двух независимых событий — результата в первой и во второй игре. Отсюда имеем:
Ответ: 0,32.
B10 № 320189. В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных.
Решение.
Из 5000 тысяч новорожденных 5000 − 2512 = 2488 девочек. Поэтому частота рождения девочек равна
Ответ: 0,498.
B10 № 320190. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.
Решение.
В самолете 12 + 18 = 30 мест удобны пассажиру В., а всего в самолете 300 мест. Поэтому вероятность того, что пассажиру В. достанется удобное место равна 30 : 300 = 0,1.
Ответ: 0,1.
B10 № 320191. На олимпиаде в вузе участников рассаживают по трём аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 250 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Решение.
Всего в запасную аудиторию направили 250 − 120 − 120 = 10 человек. Поэтому вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории, равна 10 : 250 = 0,04.
Ответ: 0,04.
B10 № 320192. В классе 26 человек, среди них два близнеца — Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
Решение.
Пусть один из близнецов находится в некоторой группе. Вместе с ним в группе может оказаться 12 человек из 25 оставшихся одноклассников. Вероятность этого события равна 12 : 25 = 0,48.
B10 № 320193. В фирме такси в наличии 50 легковых автомобилей; 27 из них чёрные с жёлтыми надписями на бортах, остальные — жёлтые с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
Решение.
Машин желтого цвета с черными надписями 23, всего машин 50. Поэтому вероятность того, что на случайный вызов приедет машина желтого цвета с черными надписями, равна:
Ответ: 0,46.
B10 № 320194. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
Решение.
На первом рейсе 6 мест, всего мест 30. Тогда вероятность того, что турист П. полетит первым рейсом вертолёта, равна:
Ответ: 0,2.
B10 № 320195. Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение.
Частота (относительная частота) события «гарантийный ремонт» равна 51 : 1000 = 0,051. Она отличается от предсказанной вероятности на 0,006.
Ответ: 0,006.
B10 № 320196. При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного меньше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.
Решение.
По условию, диаметр подшипника будет лежать в пределах от 66,99 до 67,01 мм с вероятностью 0,965. Поэтому искомая вероятность противоположного события равна 1 − 0,965 = 0,035.
Ответ: 0,035.
B10 № 320198. Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.
Решение.
Рассмотрим события A = «учащийся решит 11 задач» и В = «учащийся решит больше 11 задач». Их сумма — событие A + B = «учащийся решит больше 10 задач». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем: 0,74 = P(A) + 0,67, откуда P(A) = 0,74 − 0,67 = 0,07.
Ответ: 0,07.
B10 № 320199. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решение.
Для того, чтобы поступить хоть куда-нибудь, З. нужно сдать и русский, и математику как минимум на 70 баллов, а помимо этого еще сдать иностранный язык или обществознание не менее, чем на 70 баллов. Пусть A, B, C и D — это события, в которых З. сдает соответственно математику, русский, иностранный и обществознание не менее, чем на 70 баллов. Тогда поскольку
для вероятности поступления имеем:
Ответ: 0,408.
B10 № 320200. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до тысячных.
Решение.
Пусть завод произвел тарелок. В продажу поступят все качественные тарелки и 20% невыявленных дефектных тарелок:
тарелок. Поскольку качественных из них
, вероятность купить качественную тарелку равна
B10 № 320201. В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).
Решение.
Вероятность произведения независимых событий равна произведению вероятностей этих событий. Поэтому вероятность того, что все три продавца заняты равна
Ответ: 0,027.
B10 № 320202. По отзывам покупателей Иван Иванович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Решение.
Вероятность того, что первый магазин не доставит товар равна 1 − 0,9 = 0,1. Вероятность того, что второй магазин не доставит товар равна 1 − 0,8 = 0,2. Поскольку эти события независимы, вероятность их произведения (оба магазина не доставят товар) равна произведению вероятностей этих событий: 0,1 · 0,2 = 0,02.
Ответ: 0,02.
B10 № 320203. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятость того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.
Решение.
Рассмотрим события A = «в автобусе меньше 15 пассажиров» и В = «в автобусе от 15 до 19 пассажиров». Их сумма — событие A + B = «в автобусе меньше 20 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем: 0,94 = 0,56 + P(В), откуда P(В) = 0,94 − 0,56 = 0,38.
Ответ: 0,38.
B10 № 320205. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры.
Решение.
Требуется найти вероятность произведения трех событий: «Статор» начинает первую игру, не начинает вторую игру, начинает третью игру. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда находим: 0,5·0,5·0,5 = 0,125.
Ответ: 0,125.
B10 № 320206. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Решение.
Для погоды на 4, 5 и 6 июля есть 4 варианта: ХХО, ХОО, ОХО, ООО (здесь Х — хорошая, О — отличная погода). Найдем вероятности наступления такой погоды:
P(XXO) = 0,8·0,8·0,2 = 0,128;
P(XOO) = 0,8·0,2·0,8 = 0,128;
P(OXO) = 0,2·0,2·0,2 = 0,008;
P(OOO) = 0,2·0,8·0,8 = 0,128.
Указанные события несовместные, вероятность их сумы равна сумме вероятностей этих событий:
P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392.
Ответ: 0,392
B10 № 320207. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Решение.
Анализ пациента может быть положительным по двум причинам: А) пациент болеет гепатитом, его анализ верен; B) пациент не болеет гепатитом, его анализ ложен. Это несовместные события, вероятность их суммы равна сумме вероятностей этих событий. Имеем:
Ответ: 0,0545.
B10 № 320208. В кармане у Миши было четыре конфеты — «Грильяж», «Белочка», «Коровка» и «Ласточка», а так же ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».
Решение.
В кармане было 4 конфета, а выпала одна конфета. Поэтому вероятность этого события равна одной четвертой.
Ответ: 0,25.
B10 № 320209. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 1 час.
Решение.
На циферблате между десятью часами и одним часом три часовых деления. Всего на циферблате 12 часовых делений. Поэтому искомая вероятность равна:
Ответ: 0,25.
B10 № 320210. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Решение.
Вероятность того, что батарейка исправна, равна 0,94. Вероятность произведения независимых событий (обе батарейки окажутся исправными) равна произведению вероятностей этих событий: 0,94·0,94 = 0,8836.
Ответ: 0,8836.
B10 № 320211. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная из упаковки батарейка будет забракована.
Решение.
Ситуация, при которой батарейка будет забракована, может сложиться в результате событий: A = батарейка действительно неисправна и забракована справедливо или В = батарейка исправна, но по ошибке забракована. Это несовместные события, вероятность их суммы равна сумме вероятностей эти событий. Имеем:
Ответ: 0,0296.
B10 № 320212. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу .
Решение.
На каждой из четырех отмеченных развилок паук с вероятностью 0,5 может выбрать или путь, ведущий к выходу D, или другой путь. Это независимые события, вероятность их произведения (паук дойдет до выхода D) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу D равна (0,5)4 = 0,0625.
Ответ: 0,0625.
Введите заголовок для поиска…
Кол-во строк:
|
Вопросы периодической проверки охранника для Андроид |
|---|
|
Охранникам |
|
Экзамен охранника. |
ЕГЭ профильный уровень. №7 Первообразная. Задача 4
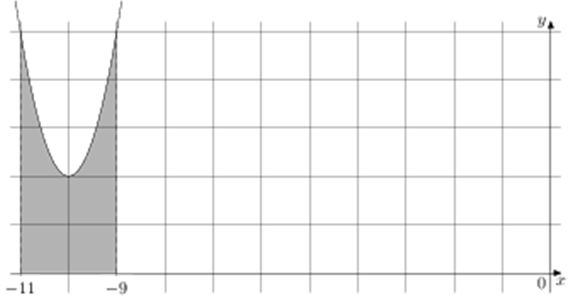
ОТВЕТ: 6.
Площадь закрашенной фигуры равна интегралу (intlimits_{ — 11}^{ — 9} {left( x right)dx} = Fleft( { — 9} right) — Fleft( { — 11} right).) Найдём значение первообразной в точках – 9 и – 11:
(Fleft( { — 9} right) = {left( { — 9} right)^3} + 30 cdot {left( { — 9} right)^2} + 302 cdot left( { — 9} right) — frac{{15}}{8} = — 729 + 2430 — 2718 — frac{{15}}{8} = — 1017 — frac{{15}}{8})
(Fleft( { — 11} right) = {left( { — 11} right)^3} + 30 cdot {left( { — 11} right)^2} + 302 cdot left( { — 11} right) — frac{{15}}{8} = — 1331 + 3630 — 3322 — frac{{15}}{8} = — 1023 — frac{{15}}{8})
Тогда площадь закрашенной фигуры:
(S = Fleft( { — 9} right) — Fleft( { — 11} right) = — 1017 — frac{{15}}{8} — left( { — 1023 — frac{{15}}{8}} right) = 6)
Ответ: 6.
Комментарии для сайта Cackle
Тренировочный вариант №26 пробник решу ЕГЭ 2023 по математике 11 класс профильный уровень от 8 марта 2023 года с ответами и решением по новой демоверсии ЕГЭ 2023 года для подготовки на 100 баллов, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
▶Скачать вариант с ответами
▶Решение заданий с 1 по 18
▶Распечатай и реши вариант
вариант_26_егэ2023_профиль_математика
Ответы и решения
решение_варианта_26_профиль
1. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, sin 𝐴 = 0,8. Найдите sin 𝐵.
2. Дана правильная треугольная призма 𝐴𝐵𝐶𝐴1𝐵1𝐶1, площадь основания которой равна 9, а боковое ребро равно 4. Найдите объём многогранника, вершинами которого являются точки 𝐴, 𝐴1, 𝐵1, 𝐶1.
3. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что произведение выпавших очков делится на 5, но не делится на 30.
4. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,98. Вероятность того, что масса окажется больше 790 г, равна 0,83. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
7. На рисунке изображён график дифференцируемой функции 𝑦 = 𝑓(𝑥), определённой на интервале (−3; 8). Найдите точку из отрезка [−2; 5], в которой производная функции 𝑓(𝑥) равна 0.
8. Два тела, массой 𝑚 = 2 кг каждое, движутся с одинаковой скоростью 𝑣 = 8 м/с под углом 2𝛼 друг к другу. Энергия (в Дж), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле 𝑄 = 𝑚𝑣 2 sin2𝛼, где 𝑚 − масса (в кг), 𝑣 − скорость (в м/с). Найдите, под каким углом 2𝛼 должны двигаться тела, чтобы в результате соударения выделилась энергия, равная 32 Дж. Ответ дайте в градусах.
9. Смешали некоторое количество 19-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
10. На рисунке изображён график функции вида 𝑓(𝑥) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐. Найдите значение 𝑓(−2).
11. Найдите точку максимума функции 𝑦 = ln(𝑥 + 9) − 10𝑥 + 7.
12. а) Решите уравнение 3 ∙ 9 𝑥+1 − 5 ∙ 6 𝑥+1 + 8 ∙ 2 2𝑥 = 0. б) Найдите все корни этого уравнения, принадлежащие отрезку.
13. В правильной треугольной призме 𝐴𝐵𝐶𝐴1𝐵1𝐶1 все рёбра равны 2. Точка 𝑀 − середина ребра 𝐴𝐴1. а) Докажите, что прямые 𝑀𝐵 и 𝐵1𝐶 перпендикулярны. б) Найдите расстояние между прямыми 𝑀𝐵 и 𝐵1𝐶.
15. В июле 2016 года планируется взять кредит в банке на три года в размере 𝑆 млн рублей, где 𝑆 − целое число. Условия его возврата таковы: – каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года; – с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; – в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей. Найдите наибольшее значение 𝑆, при котором разница между наибольшей и наименьшей выплатами будет меньше 1 млн рублей.
16. В трапеции 𝐴𝐵𝐶𝐷 боковая сторона 𝐴𝐵 перпендикулярна основаниям. Из точки 𝐴 на сторону 𝐶𝐷 опустили перпендикуляр 𝐴𝐻. На стороне 𝐴𝐵 отмечена точка 𝐸 так, что прямые 𝐶𝐷 и 𝐶𝐸 перпендикулярны. а) Докажите, что прямые 𝐵𝐻 и 𝐸𝐷 параллельны. б) Найдите отношение 𝐵𝐻 к 𝐸𝐷, если ∠𝐵𝐶𝐷 = 135°.
18. В течение 𝑛 дней каждый день на доску записывают натуральные числа, каждое из которых меньше 6. При этом каждый день (кроме первого) сумма чисел, записанных на доску в этот день, больше, а количество меньше, чем в предыдущий день. а) Может ли 𝑛 быть больше 5? б) Может ли среднее арифметическое чисел, записанных в первый день, быть меньше 3, а среднее арифметическое всех чисел, записанных за все дни, быть больше 4? в) Известно, что сумма чисел, записанных в первый день, равна 6. Какое наибольшее значение может принимать сумма всех чисел, записанных за все дни?




