В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Спрятать решение
Решение.
Чтобы пятирублевые монеты оказались в разных карманах, Петя должен взять из кармана одну пятирублевую и две десятирублевые монеты. Это можно сделать тремя способами: 5, 10, 10; 10, 5, 10 или 10, 10, 5. Эти события несовместные, вероятность их суммы равна сумме вероятностей этих событий:
Другое рассуждение.
Вероятность того, что Петя взял пятирублевую монету, затем десятирублевую, и затем еще одну десятирублевую (в указанном порядке) равна
Поскольку Петя мог достать пятирублевую монету не только первой, но и второй или третьей, вероятность достать набор из одной пятирублевой и двух десятирублевых монет в 3 раза больше. Тем самым, она равна 0,6.
Ответ: 0,6.
Приведем другое решение.
Количество способов взять 3 монеты из 6, чтобы переложить их в другой карман, равно Количество способов выбрать 1 пятирублевую монету из 2 пятирублевых монет и взять вместе с ней еще 2 десятирублевых монеты из имеющихся 4 десятирублевых монет по правилу произведения равно
Поэтому искомая вероятность того, что пятирублевые монеты лежат в разных карманах, равна
Дата: 2015-06-19
23984
Категория: Вероятность
Метка: ЕГЭ-№4
500998. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Чтобы пятирублевые монеты оказались в разных карманах, Петя должен взять из кармана одну пятирублевую и две десятирублевые монеты. Наборы монет, которые получаются:
5, 10, 10
10, 5, 10
10, 10, 5
По условию пятирублёвых монет две, десятирублёвых четыре.
Определим число всевозможных исходов. Это число всех вариантов, какими можно выбрать три монеты из шести. Используем формулу сочетания (она позволяет узнать сколькими способами можно выбрать N объектов из М):
Значит
Теперь определим число благоприятных исходов.
Одну пятирублёвую монету из двух можно выбрать двумя способами. Найдём сколькими способами можно выбрать две десятирублёвые монеты из четырёх. Используем формулу сочетания:
Выбор пятирублёвой монеты и двух десятирублёвых события независимые. но так как они происходят одновременно, то количество благоприятных исходов будет равно произведению, то есть 2∙6 = 12.
Таким образом, вероятность того, что пятирублёвые монеты лежат в разных карманах равна 12 к 20 или 12/20 = 0,6
Второй способ:
Чтобы пятирублевые монеты оказались в разных карманах, Петя должен взять из кармана одну пятирублевую и две десятирублевые монеты. Это можно сделать тремя способами: 5, 10, 10; 10, 5, 10 или 10, 10, 5. Эти события несовместные, вероятность их суммы равна сумме вероятностей этих событий.
Итак!
Вероятность того, что Петя взял пятирублевую монету, затем десятирублевую, и затем еще одну десятирублевую (в указанном порядке) равна
Вероятность того, что Петя взял десятирублевую монету, затем пятирублёвую, и затем снова десятирублевую (в указанном порядке) равна
Вероятность того, что Петя взял десятирублевую монету, затем ещё одну десятирублевую, и затем пятирублёвую (в указанном порядке) равна
Таким образом, искомая вероятность равна:
Ответ: 0,6
Новый тренировочный вариант №41054180 решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
скачать вариант ЕГЭ 2022
скачать ответы и решения
Решу ЕГЭ 2022 по математике профиль тренировочный вариант №41054180
Ответы и решения для варианта:
Задание 2 решу ЕГЭ №320189 В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных.
Правильный ответ: 0,498
Задание 3 решу ЕГЭ № 27900 Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
Правильный ответ: 2
Задание 6 решу ЕГЭ № 525688 На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0 . Найдите значение производной функции g(x) = 6f(x) − 3x в точке x0.
Правильный ответ: -7
Задание 8 решу ЕГЭ № 99590 Расстояние между городами и равно 435 км. Из города в город со скоростью 60 км ч выехал первый автомобиль, а через час после этого навстречу ему из города выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города автомобили встретятся? Ответ дайте в километрах.
Правильный ответ: 240
Задание 10 решу ЕГЭ № 500998 В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Правильный ответ: 0,6
Задание 13 решу ЕГЭ № 508233 В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP. а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC. б) Найдите площадь сечения.
Правильный ответ: 3 корень из 3
Задание 15 решу ЕГЭ № 506956 Два брокера купили акции одного достоинства на сумму 3640 р. Когда цена на эти акции возросла, они продали часть акций на сумму 3927 р. Первый брокер продал 75% своих акций, а второй 80% своих. При этом сумма от продажи акций, полученная вторым брокером, на 140% превысила сумму, полученную первым брокером. На сколько процентов возросла цена одной акции?
Правильный ответ: 37,5
Задание 16 решу ЕГЭ № 514717 На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD. а) Докажите, что треугольник DCL равнобедренный. б) Известно, что В каком отношении прямая DL делит сторону AB?
Задание 18 решу ЕГЭ № 526295 В ящике лежат 73 овоща, масса каждого из которых выражается целым числом граммов. В ящике есть хотя бы два овоща различной массы, а средняя масса всех овощей равна 1000 г. Средняя масса овощей , масса каждого из которых меньше 1000 г, равна 988 г. Средняя масса овощей, масса каждого из которых больше 1000 г, равна 1030 г. а) Могло ли в ящике оказаться поровну овощей массой меньше 1000 г и овощей массой больше 1000 г? б) Могло ли в ящике оказаться ровно 11 овощей, масса каждого из которых равна 1000 г? в) Какую наименьшую массу может иметь овощ в этом ящике?
Правильный ответ: а) Нет; б) Нет; в) 449.
Другие тренировочные варианты ЕГЭ 2022 по математике:
28.09.2021 Математика 11 класс МА2110101-МА2110112 ЕГЭ 2022 работа статград ответы и задания
Тренировочный вариант №145 ЕГЭ 2022 по математике 11 класс профильный уровень с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
ЕГЭ профильный уровень. №7 Первообразная. Задача 4
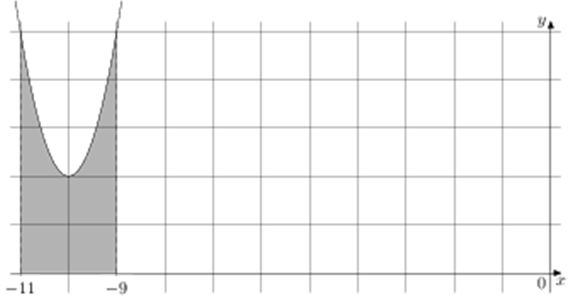
ОТВЕТ: 6.
Площадь закрашенной фигуры равна интегралу (intlimits_{ — 11}^{ — 9} {left( x right)dx} = Fleft( { — 9} right) — Fleft( { — 11} right).) Найдём значение первообразной в точках – 9 и – 11:
(Fleft( { — 9} right) = {left( { — 9} right)^3} + 30 cdot {left( { — 9} right)^2} + 302 cdot left( { — 9} right) — frac{{15}}{8} = — 729 + 2430 — 2718 — frac{{15}}{8} = — 1017 — frac{{15}}{8})
(Fleft( { — 11} right) = {left( { — 11} right)^3} + 30 cdot {left( { — 11} right)^2} + 302 cdot left( { — 11} right) — frac{{15}}{8} = — 1331 + 3630 — 3322 — frac{{15}}{8} = — 1023 — frac{{15}}{8})
Тогда площадь закрашенной фигуры:
(S = Fleft( { — 9} right) — Fleft( { — 11} right) = — 1017 — frac{{15}}{8} — left( { — 1023 — frac{{15}}{8}} right) = 6)
Ответ: 6.
Комментарии для сайта Cackle
9 марта 2023
В закладки
Обсудить
Жалоба
Теория и практика.
Содержание
1) Прямые
2) Параболы
3) Как искать пересечение параболы и прямой, двух парабол
4) Гипербола. Асимптотические точки гиперболы
5) Пересечение гиперболы и прямой
6) Иррациональные функции
7) Пересечение корня и прямой

9) Показательные функции
10) Логарифмические функции
10_zadacha.pdf
Источник: vk.com/profimatika
WEB-DL
- Год выхода: 2019
- Страна: Россия
- Жанр: Комедия
- Режиссер: Константин Смирнов, Константин Колесов
- Актёры: Вячеслав Чепурченко, Павел Комаров, Вадим Дубровин, Максим Лагашкин, Екатерина Стулова
- Сезоны: 1-3 сезон
- Серии: 1-16 серия
- Время: 00:30
Никита, Дэн и Артемий разработали уникальное приложение для смартфонов, вот-вот продадут его и осуществят все свои мечты. Но в последний момент многомиллионная сделка срывается и парней забирают в армию. Чтобы не ставить под угрозу успех своего стартапа, они выбирают альтернативную службу в глухой деревне Жуки, где будут пытаться довести свой проект до конца. Только не так просто разрабатывать приложение там, где нет даже интернета…
Смотреть онлайн Жуки (2019) в хорошем качестве HD
Плеер 1
Плеер 2
В закладки
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
|
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
|
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
  |
||||
| Показать сообщения за: Сортировать по: |









