Решите неравенство:
Спрятать решение
Решение.
Заменим на
перенесем полученное выражение в правую часть и применим на области определения формулу суммы логарифмов. Получим:
Тогда исходное уравнение равносильно системам:
Ответ:
Примечание.
Выше мы воспользовались тем, что число, большее положительного, положительно:
Запомните этот прием, он позволяет уменьшать количество неравенств в системах без потери равносильности.
Примечание 2.
Чтобы не решать кубическое неравенство, можно подобрать подходящую группировку:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек,
ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Тренировочный вариант №26 пробник решу ЕГЭ 2023 по математике 11 класс профильный уровень от 8 марта 2023 года с ответами и решением по новой демоверсии ЕГЭ 2023 года для подготовки на 100 баллов, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
▶Скачать вариант с ответами
▶Решение заданий с 1 по 18
▶Распечатай и реши вариант
вариант_26_егэ2023_профиль_математика
Ответы и решения
решение_варианта_26_профиль
1. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, sin 𝐴 = 0,8. Найдите sin 𝐵.
2. Дана правильная треугольная призма 𝐴𝐵𝐶𝐴1𝐵1𝐶1, площадь основания которой равна 9, а боковое ребро равно 4. Найдите объём многогранника, вершинами которого являются точки 𝐴, 𝐴1, 𝐵1, 𝐶1.
3. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что произведение выпавших очков делится на 5, но не делится на 30.
4. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,98. Вероятность того, что масса окажется больше 790 г, равна 0,83. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
7. На рисунке изображён график дифференцируемой функции 𝑦 = 𝑓(𝑥), определённой на интервале (−3; 8). Найдите точку из отрезка [−2; 5], в которой производная функции 𝑓(𝑥) равна 0.
8. Два тела, массой 𝑚 = 2 кг каждое, движутся с одинаковой скоростью 𝑣 = 8 м/с под углом 2𝛼 друг к другу. Энергия (в Дж), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле 𝑄 = 𝑚𝑣 2 sin2𝛼, где 𝑚 − масса (в кг), 𝑣 − скорость (в м/с). Найдите, под каким углом 2𝛼 должны двигаться тела, чтобы в результате соударения выделилась энергия, равная 32 Дж. Ответ дайте в градусах.
9. Смешали некоторое количество 19-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
10. На рисунке изображён график функции вида 𝑓(𝑥) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐. Найдите значение 𝑓(−2).
11. Найдите точку максимума функции 𝑦 = ln(𝑥 + 9) − 10𝑥 + 7.
12. а) Решите уравнение 3 ∙ 9 𝑥+1 − 5 ∙ 6 𝑥+1 + 8 ∙ 2 2𝑥 = 0. б) Найдите все корни этого уравнения, принадлежащие отрезку.
13. В правильной треугольной призме 𝐴𝐵𝐶𝐴1𝐵1𝐶1 все рёбра равны 2. Точка 𝑀 − середина ребра 𝐴𝐴1. а) Докажите, что прямые 𝑀𝐵 и 𝐵1𝐶 перпендикулярны. б) Найдите расстояние между прямыми 𝑀𝐵 и 𝐵1𝐶.
15. В июле 2016 года планируется взять кредит в банке на три года в размере 𝑆 млн рублей, где 𝑆 − целое число. Условия его возврата таковы: – каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года; – с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; – в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей. Найдите наибольшее значение 𝑆, при котором разница между наибольшей и наименьшей выплатами будет меньше 1 млн рублей.
16. В трапеции 𝐴𝐵𝐶𝐷 боковая сторона 𝐴𝐵 перпендикулярна основаниям. Из точки 𝐴 на сторону 𝐶𝐷 опустили перпендикуляр 𝐴𝐻. На стороне 𝐴𝐵 отмечена точка 𝐸 так, что прямые 𝐶𝐷 и 𝐶𝐸 перпендикулярны. а) Докажите, что прямые 𝐵𝐻 и 𝐸𝐷 параллельны. б) Найдите отношение 𝐵𝐻 к 𝐸𝐷, если ∠𝐵𝐶𝐷 = 135°.
18. В течение 𝑛 дней каждый день на доску записывают натуральные числа, каждое из которых меньше 6. При этом каждый день (кроме первого) сумма чисел, записанных на доску в этот день, больше, а количество меньше, чем в предыдущий день. а) Может ли 𝑛 быть больше 5? б) Может ли среднее арифметическое чисел, записанных в первый день, быть меньше 3, а среднее арифметическое всех чисел, записанных за все дни, быть больше 4? в) Известно, что сумма чисел, записанных в первый день, равна 6. Какое наибольшее значение может принимать сумма всех чисел, записанных за все дни?
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
ЕГЭ профильный уровень. №7 Первообразная. Задача 4
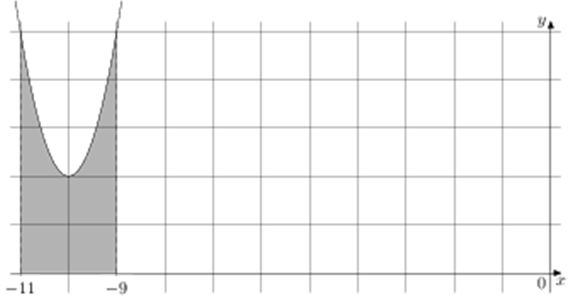
ОТВЕТ: 6.
Площадь закрашенной фигуры равна интегралу (intlimits_{ — 11}^{ — 9} {left( x right)dx} = Fleft( { — 9} right) — Fleft( { — 11} right).) Найдём значение первообразной в точках – 9 и – 11:
(Fleft( { — 9} right) = {left( { — 9} right)^3} + 30 cdot {left( { — 9} right)^2} + 302 cdot left( { — 9} right) — frac{{15}}{8} = — 729 + 2430 — 2718 — frac{{15}}{8} = — 1017 — frac{{15}}{8})
(Fleft( { — 11} right) = {left( { — 11} right)^3} + 30 cdot {left( { — 11} right)^2} + 302 cdot left( { — 11} right) — frac{{15}}{8} = — 1331 + 3630 — 3322 — frac{{15}}{8} = — 1023 — frac{{15}}{8})
Тогда площадь закрашенной фигуры:
(S = Fleft( { — 9} right) — Fleft( { — 11} right) = — 1017 — frac{{15}}{8} — left( { — 1023 — frac{{15}}{8}} right) = 6)
Ответ: 6.
Комментарии для сайта Cackle
Задание 507254 егэ математика
—>
Задание 14 № 507254
Чтобы не решать кубическое неравенство, можно подобрать подходящую группировку:
Почему в решении проигнорировано ОДЗ на третий логарифм? (аргумент >0)? В данном случае это не привело к искажению решения, но вполне могло привести!
Задание 14 № 507254
—>
Почему в решении проигнорировано ОДЗ на третий логарифм.
Math-ege. sdamgia. ru
05.02.2020 20:10:37
2020-02-05 20:10:37
Источники:
Https://math-ege. sdamgia. ru/problem? id=507254
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Задание 507254 егэ математика
Задание 507254 егэ математика
Задание 507254 егэ математика
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Бегун пробежал 50 м за 5 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв слов или цифр.
Ege. sdamgia. ru
13.11.2020 7:07:49
2020-11-13 07:07:49
Источники:
Https://ege. sdamgia. ru/test? id=39764873
Решу ЕГЭ 2022 тренировочный вариант №41054184 по математике профиль 11 класс с ответами — Математика и Английский » /> » /> .keyword { color: red; } Задание 507254 егэ математика
Решу ЕГЭ 2022 тренировочный вариант №41054184 по математике профиль 11 класс с ответами
Решу ЕГЭ 2022 тренировочный вариант №41054184 по математике профиль 11 класс с ответами
Новый тренировочный вариант №41054184 решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
Решу ЕГЭ 2022 по математике профиль тренировочный вариант №41054184
Ответы и решения для варианта:
Задание 2 решу ЕГЭ № 320179 Из множества натуральных чисел от 10 до 19 наудачу выбирают одно число. Какова вероятность того, что оно делится на 3?
Ответ: 0,3
Задание 3 решу ЕГЭ № 27938 Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Ответ: 2
Задание 5 решу ЕГЭ № 27062 Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, а боковое ребро призмы равно 10.
Ответ: 248
Задание 6 решу ЕГЭ № 27491 На рисунке изображён график — производной функции определенной на интервале (−8; 3). В какой точке отрезка [−3; 2] функция принимает наибольшее значение?
Ответ: -3
Задание 8 решу ЕГЭ № 99575 Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Ответ: 100
Задание 10 решу ЕГЭ № 320206 В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Ответ: 0,392
Задание 13 решу ЕГЭ № 515801 Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости. б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
Задание 15 решу ЕГЭ № 512441 Баржа грузоподъемностью 134 тонны перевозит контейнеры типов А и В. Количество загруженных на баржу контейнеров типа В не менее чем на 25% превосходит количество загруженных контейнеров типа А. Вес и стоимость одного контейнера типа А составляет 2 тонны и 5 млн. руб., контейнера типа В – 5 тонн и 7 млн. руб. соответственно. Определите наибольшую возможную суммарную стоимость (в млн. руб.) всех контейнеров, перевозимых баржей при данных условиях.
Ответ: 220 млн. руб.
Задание 16 решу ЕГЭ № 514482 В трапеции ABCD точка E — середина основания AD, точка M — середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O. а) Докажите, что площади четырёхугольника AMOE и треугольника COD равны. б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD = 4.
Ответ: б) 2/9
Задание 18 № 514485 На доске написано 10 неотрицательных чисел. За один ход стираются два числа, а вместо них записывается сумма, округлённая до целого числа (например, вместо 5,5 и 3 записывается 9, а вместо 3,3 и 5 записывается 8). а) Приведите пример 10 нецелых чисел и последовательности 9 ходов, после которых на доске будет записано число, равное сумме исходных чисел. б) Может ли после 9 ходов на доске быть написано число, отличающееся от суммы исходных чисел на 7? в) На какое наибольшее число могут отличаться числа, записанные на доске после 9 ходов, выполненных с одним и тем же набором исходных чисел в различном порядке?
Ответ: а) например, числа 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; 0,99; 0,01 и любая последовательность ходов; б) нет; в) 5.
Решу ЕГЭ 2022 тренировочный вариант №41054184 по математике профиль 11 класс с ответами
Новый тренировочный вариант №41054184 решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
Задание 2 решу ЕГЭ № 320179 Из множества натуральных чисел от 10 до 19 наудачу выбирают одно число. Какова вероятность того, что оно делится на 3?
Ответ: 0,3
Задание 3 решу ЕГЭ № 27938 Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Ответ: 2
Задание 5 решу ЕГЭ № 27062 Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, а боковое ребро призмы равно 10.
Ответ: 248
Задание 6 решу ЕГЭ № 27491 На рисунке изображён график — производной функции определенной на интервале (−8; 3). В какой точке отрезка [−3; 2] функция принимает наибольшее значение?
Ответ: -3
Задание 8 решу ЕГЭ № 99575 Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Ответ: 100
Задание 10 решу ЕГЭ № 320206 В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Ответ: 0,392
Задание 13 решу ЕГЭ № 515801 Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости. б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
Задание 15 решу ЕГЭ № 512441 Баржа грузоподъемностью 134 тонны перевозит контейнеры типов А и В. Количество загруженных на баржу контейнеров типа В не менее чем на 25% превосходит количество загруженных контейнеров типа А. Вес и стоимость одного контейнера типа А составляет 2 тонны и 5 млн. руб., контейнера типа В – 5 тонн и 7 млн. руб. соответственно. Определите наибольшую возможную суммарную стоимость (в млн. руб.) всех контейнеров, перевозимых баржей при данных условиях.
Ответ: 220 млн. руб.
Задание 16 решу ЕГЭ № 514482 В трапеции ABCD точка E — середина основания AD, точка M — середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O. а) Докажите, что площади четырёхугольника AMOE и треугольника COD равны. б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD = 4.
Ответ: б) 2/9
Задание 18 № 514485 На доске написано 10 неотрицательных чисел. За один ход стираются два числа, а вместо них записывается сумма, округлённая до целого числа (например, вместо 5,5 и 3 записывается 9, а вместо 3,3 и 5 записывается 8). а) Приведите пример 10 нецелых чисел и последовательности 9 ходов, после которых на доске будет записано число, равное сумме исходных чисел. б) Может ли после 9 ходов на доске быть написано число, отличающееся от суммы исходных чисел на 7? в) На какое наибольшее число могут отличаться числа, записанные на доске после 9 ходов, выполненных с одним и тем же набором исходных чисел в различном порядке?
Ответ: а) например, числа 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; 0,99; 0,01 и любая последовательность ходов; б) нет; в) 5.
Найдите радиус окружности.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword Вариант 42789571 решу егэ математика профиль
Вариант 42789571 решу егэ математика профиль
Вариант 42789571 решу егэ математика профиль
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
За пи сы вай тесь на бес плат ное за ня тие.
Источники:
Решу Егэ Математика Профиль 2022 — Новости, справки, информация, советы » /> » /> .keyword Вариант 42789571 решу егэ математика профиль
Решу Егэ Математика Профиль 2022
Решу Егэ Математика Профиль 2022
Решу ЕГЭ 2022 математика, профильный уровень, задания, ответы
Ну что, давайте вместе решать ЕГЭ 2022 года по математике! А что бы выпускные экзамены удалось вам решить легко на 5 баллов, тогда нужно немного подготовиться к ним! Здесь можно бесплатно скачать демоверсии заданий и вопросов с ответами, которые будут на едином государственном экзамене в школе для учеников 11 класса. Все варианты для решения ЕГЭ были взяты с официального сайта ФИПИ. После домашнего изучения КИМ и тестовых вариантов, вы смело сможете сказать себе, что я РЕШУ ЕГЭ!
Официальный сайт. Единый Государственный Экзамен. Открытый банк заданий ЕГЭ-22. ФИПИ ШКОЛЕ. ФГОС. ОРКСЭ. МЦКО. Школа России. 21 век. . Решебник. Перспектива. Школа 2100. Планета знаний. Россия. Беларусь.
Скачать бесплатно новые задания, тесты, тренировочные варианты, ответы и решения Решу ЕГЭ-2022
Демонстрационный вариант реальных заданий контрольных измерительных материалов единого государственного экзамена 2022 года по Математике. Профильный уровень. Формат PDF
Скачать бесплатно
Кодификатор элементов содержания по Математике. База для составления контрольных измерительных материалов для проведения единого государственного экзамена
Скачать бесплатно
Кодификатор требований к уровню подготовки выпускников образовательных организаций для проведения единого государственного экзамена по математике
Скачать бесплатно
Спецификация контрольных измерительных материалов для проведения в 2022 году единого государственного экзамена по Математике Профиль.
Скачать бесплатно
Правильные ответы и решения заданий ЕГЭ-2022
Скачать бесплатно
Решу егэ математика профиль 2022
С вопросами, мнением об экзаменах обращайтесь через форму для письма, рисунок конверта кликабелен.
И, пожалуйста, напишите об ошибке, если обнаружите таковую в моих решениях.
Узнайте, как можно поддержать сайт и помочь его развитию.
Внимание: в обсуждаемом варианте еще могут быть изменения.
Предлагаемый вариант профильного ЕГЭ по математике в следующем году заметно отличается от вариантов прошлых лет, как в части заданий с кратким ответом, так и в части заданий с развёрнутым ответом.
Основные отличия варианта 2022 от ЕГЭ 2021:
Из варианта удалены первые три задания по темам: простейшие текстовые задачи, задания на анализ статистических графиков и диаграмм, задачи по геометрии на клетчатой бумаге. В первую часть добавлены задания на график функции, на решение обратных задач теории вероятностей, на комплексные числа. Последние два задания вызывают вопросы у педагогов и еще подлежат общественно-профессиональному обсуждению. Соответственно изменён порядок следования оставшихся заданий первой части. К некоторым заданиям добавлены иные образцы формулировок задачи, у некоторых число образцов уменьшено. При этом сохранилось правило – задания 1–7 имеют базовый уровень сложности.
Во второй части изменения менее явные.
Интерактивные страницы с Демо-версиями для экзамена 2022 Будут обновляться осенью, когда окончательно утвердят контрольно-измерительные материалы ЕГЭ по математике. Здесь рассматриваются только предлагаемые новые задания и их решения.
Задания, которых не было в прошлом году
Задание 3.
Задача.
На рисунке изображён график функции вида (f(x)= ax^2 + bx + c,) где числа (a, b; и ;c) — целые. Найдите значение (f(-12)).
Формула функции – квадратный трёхчлен, график функции – парабола. Требуется определить значение функции в точке, которая не видна на графике, поэтому нужно воспользоваться формулой. Для этого сначала нужно определить неизвестные коэффициенты квадратного трёхчлена.
Три неизвестных коэффициента можно найти путём решения системы трёх линейных уравнений. Чтобы составить такую систему уравнений, берём на графике три «удобные» точки и подставляем их координаты в формулу функции.
Точки «удобны», если их координаты хорошо считываются, например, находятся в узлах сетки, или мы о них что-то знаем из теории. Для параболы очень хорошими точками являются вершина и точка пересечения с осью ординат. К сожалению, последняя на заданном участке графика также не видна.
На рисунке показаны выбранные мною точки, которые задают следующие соотношения
[x_в=-4;Rightarrow;-frac = -4; f(-3)=-2; Rightarrow;a(-3)^2 + b(-3) + c = -2; f(-2)=1;Rightarrow;a(-2)^2 + b(-2) + c = 1.]
Получили ситему уравнений [ begin — dfrac = -4, 9a -3b + c = -2, 4a -2b + c = 1. end]
Решаем её [begin b = 8a,9a -24a + c = -2,4a -16a + c = 1; end;
Begin b = 8a,c = 15a-2,c = 12a+1; end; begin b = 8a, = 3a-3,c = 12a+1; end;
Begin b = 8,a = 1,c = 13. end]
Таким образом, уравнение функции имеет вид (f(x)= x^2 + 8x + 13), чтобы найти её значение в заданной точке, подставляем −12 в формулу [f(-12)= (-12)^2 + 8cdot(-12) +13 = 144-96+13 = 61.]
Замечание: Внимательные пользователи заметили, что полезность точки «Вершина параболы» в представленном решении использована не на все сто процентов. Постарайтесь вспомнить, что еще вы знаете о вершине параболы, и подумать о том, как сократить объём вычислений. Затем перейдите по ссылке, чтобы посмотреть второй вариант решения этой задачи.
Ответ:
Задание 7с.
Дополнительный образец формулировки задания на геометрический смысл производной.
Задача.
На рисунке изображён график (y = f'(x)) — производной функции (f(x)),
Определённой на интервале (−9;12). В какой точке отрезка [−8;11] функция (f(x)) принимает наибольшее значение?
Задачу лучше решать, делая отметки на чертеже.
Выделим на чертеже отрезок, на котором требуется найти искомое значение. Наибольшее значение непрерывной функции может быть достигнуто в одной из крайних точек отрезка, либо в одной из точек максимума функции внутри отрезка.
Крайние точки отрезка x = −8 и x = 11.
Внутренние точки отрезка, в которых функция имеет экстремальные значения, совпадают с точками, в которых её производная равна нулю. Эти точки также отмечаем на чертеже (здесь красными кружками).
Чтобы определиться, в каких точках экстремум является максимумом, нам нужно определить знак производной в окрестности каждой из этих точек. Знаки производной хорошо видны по её графику. Делаем соответствующие отметки на интервалах. Интервалу, где производная положительна соответствует интервал возрастания функции, интервалу, где производная отрицательна соответствует интервал убывания функции. Отмечаем свои наблюдения стрелочками. Обратите внимание, стрелочки относятся не к тому графику, который мы видим на чертеже, не к графику производной, а к графику исходной функции. Максимум функции может быть только в тех точках, левее которых функция возрастала, а правее стала убывать. Таким образом, кандидаты на ответ – точки максимума внутри отрезка: x = −7, x = 0, x = 7, x = 10.
Вернёмся к крайним точкам. Точка x = −8 находится на участке возрастания функции, поэтому во внутренних точках отрезка, расположенных правее её, значения функции будут больше. Точка x = 11 находится на участке убывания функции, и соответственно во внутренних точках отрезка, расположенных левее её, значения функции будут больше. Т. е. в крайних точках отрезка, наибольшего значения функция не достигает.
Итак, наибольшее значение функции может быть в одной из четырёх точек, но для однозначного ответа (ведь у нас I-я часть ЕГЭ) требуется выбрать одну из них. Для этого нужно вспомнить, что функция связана со своей производной через первообразную (неопределённый интеграл) (f(x) = intdx + C), а она, в свою очередь, связана с площадью под кривой через определённый интеграл. Например, площадь под кривой на отрезке [2;7], отмеченную на рисунке светлозелёным цветом, можно вычислить по формуле (S = intlimits_2^7dx = f(7) — f(2).)
Оценивая по клеточкам площади криволинейных трапеций между кривой и осью абсцисс на интервалах между точками экстремумов, мы можем прикинуть сколько единиц «теряет» функция на этом интервале, если участок отмечен знаком минус, и сколько «приобретает» там, где участок отмечен знаком «+».
Предположим, что наибольшее значение функции f(−7). Далее прибавляем и вычитаем примерные значения площадей, двигаясь к следующим точкам предполагаемого ответа слева направо. Как видно из рисунка, покрашенный участок имеет наибольшую площадь и соответственно добавит к значению функции больше, чем остальные, тем более, что часть из них с плюсом, другая с минусом, и они друг друга компенсируют. Таким образом, наибольшее значение функции будет достигнуто в точке x = 7.
Ответ:
Всё понятно? Остались ли у вас вопросы по этому заданию? А у меня остался вопрос к разработчикам из ФИПИ:
ПОЧЕМУ ЭТА ЗАДАЧА ОТНОСИТСЯ К БАЗОВОМУ УРОВНЮ СЛОЖНОСТИ?
Если я ошибаюсь, и есть решение проще представленного, напишите мне об этом на почту. (Жми конвертик!)
Задание 10.
Следующие задания, в которых требуется определить вероятность некого события при условии, что другое связанное с ним событие уже произошло, и мы об этом знаем, в теории вероятностей решаются с использованием теоремы Байеса (или формулы Байеса). Не уверена, что все школьники знают, а тем более понимают эту теорему, поэтому привожу альтернативные способы решения этих задач. Такие более «школьные» способы существуют для случаев, когда взаимосвязанных событий, упоминаемых в условии задачи немного.
Задача.
Симметричную игральную кость бросили три раза. Известно, что в сумме
Выпало 6 очков. Какова вероятность события «хотя бы раз выпало три очка»?
Постараемся решить, используя лишь классическое определение вероятности (P =dfrac,) где (n -) общее число исходов, (m -) число исходов, благоприятствующих запрашиваемому событию.
Для этого рассмотрим, из каких трёх слагаемых может состоять число 6.
1) 6 = 1+2+3;
2) 6 = 2+2+2;
3) 6 = 4+1+1.
При трёхкратном бросании игральной кости вариант 1 может реализоваться 6-ю способами, т. к. очки могут выпадать в любом порядке: перестановки из 3-ёх элементов 3! = 6.
Вариант 2 может реализоваться только одним способом.
Вариант 3 реализуется 3-мя способами: 4 очка могут выпасть при первом, или при втором, или при третьем бросании.
Итого (n = 6+1+3 = 10.)
В первом варианте тройка присутствует по одному разу в каждом из 6-ти способов. Во втором и третьем вариантах тройки вообще нет.
Итого (m = 6.) [P =frac = frac = 0,6.]
Ответ: 0,6
Задача.
В городе 48% взрослого населения мужчины. Пенсионеры составляют 12,6% взрослого населения, причем доля пенсионеров среди женщин равна 15%. Для проведения исследования социологи случайным образом выбрали взрослого мужчину, проживающего в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
Эту задачу постараемся решить, используя лишь И/ИЛИ-правила (правила умножения/сложения вероятностей).
От долей населения в процентах перейдём к соответствующим вероятностям в десятичных дробях. (Это можно сделать, опираясь на такое доказа если в городе живёт N взрослых человек и 48% из них мужчины, то мужчин в городе живёт (dfrac,) тогда вероятность встретить взрослого мужчину составляет (dfrac = dfrac = 0,48).)
Неизвестную вероятность события «выбранный мужчина является пенсионером» обозначим X. А находить будем вероятность другого, более общего события «выбранный взрослый житель города является пенсионером». Это событие можно записать так:
«Житель города является пенсионером, если он мужчина И при этом пенсионер ИЛИ она женщина И при этом пенсионер».
Учитывая независимость и несовместимость событий (один человек не может быть одновременно женщиной и мужчиной, быть и не быть персионером), к «И» применяем правило умножения вероятностей, к «ИЛИ» — правило сложения вероятностей. Получим формулу для вероятностей
В этой формуле введены такие обозначения
- Событие П — «Житель города является пенсионером». Вероятность этого события P(П) = 0,126 находим в условии задачи (пенсионеры составляют 12,6% взрослого населения).
Получаем уравнение 0,126 = 0,48·X + 0,52·0,15,
Из которого находим 0,48X = 0,126 − 0,52·0,15 = 0,048;
X = 0,048/0,48 = 0,1.
Ответ: 0,1.
Задание 11.
Задание по теме «Комплексные числа» вызывает больше всего вопросов у школьников и учителей, так как эта тема слабо представлена в действующих учебниках. Тем не менее, рассмотрим решение задачи из перспективного демонстрационного варианта.
Задача.
Про комплексное число (z) известно, что (|z — 4 — 7i| = | z + 4 — i|). Найдите наименьшее значение (|z|).
Пусть (z = a+ib), тогда [|z| = sqrt; z-4 — 7i = (a-4) +(b-7)i; ;; |z-4 — 7i| = sqrt;
Z+4 — i = (a+4) +(b-1)i; ;; |z+4 — i| = sqrt;
|z — 4 — 7i| = | z + 4 — i| ;; Leftrightarrow ;; sqrt = sqrt.]
Из последнего равенства следует ((a-4)^2 +(b-7)^2 = (a+4)^2 +(b-1)^2.)
Преобразуем это уравнение, чтобы выразить одну из неизвестных переменных через другую
[(a-4)^2 — (a+4)^2 = (b-1)^2 — (b-7)^2 ; (a-4 — a-4)(a-4 +a+4) = (b-1-b+7)(b-1+b-7); -8cdot2a = 6cdot(2b-8);
A = — frac.] Теперь можем записать (|z|) как функцию одной переменной [|z| = sqrt = sqrt = sqrt.> ]
Теперь видно, что наименьшее значение (|z|) будет достигнуто при таких значениях (b), при которых выражение (9(b-4)^2 + 16b^2) минимально. Ищем минимум этого выражения через производную.
[(9(b-4)^2 + 16b^2)’ = 9cdot2(b-4)+16cdot2b = 18b — 72 + 32b = 0; 50b = 72; ;; b = 1,44; |z| = sqrt > = sqrt> = 2,4.]
Ответ: 2,4
Моё мнение по этому заданию – требует существенных затрат времени на вычисление и проверку. Для I-ой части с учётом того, что нужно решить ещё 8 больших заданий, это может оказаться проблемой многих школьников. Если есть более простые подходы, напишите мне о них. (Жми на конвертик!)
Спасибо посетителям сайта, которые откликнулись и присылают мне свои варианты решения. Чтобы ознакомиться с вариантом геометрического решения этой задачи перейдите по ссылке.
Что касается первой части в целом, то, на мой взгляд, она стала сложнее, трудозатратнее, требует больше времени на выполнение. Действительно базовый уровень ушел.
Задание 15.
Примеры решения заданий второй части представлены непосредственно в демонстрационном варианте. Но для неравенств и их систем имеет большое значение прорисовка множеств на числовой оси, поэтому привожу здесь решение этого задания с рисунками. Другие типы неравенств можно найти здесь по ссылкам на этот номер.
A) Решаем систему неравенств [begin8x^2+7>0; ;;(1)x^2+x+1>0; ;;(2)dfrac+7>0; ;;(3)
Log_> ge log_ , ;;(4)end]
Где первые 3 неравенства следуют из ограниченности области определения логарифма, т. е. это ОДЗ выражения, а 4-е неравенство уже частично преобразованно с использованием свойства разности логарифмов с одинаковым основанием.
(1) (8x^2+7>0 ; Leftrightarrow ; x in (-infty;infty),) т. к. состоит из положительных слагаемых;
(3) Решаем методом интервалов [ frac+ ^7>0; frac>0;]
(4) Так как основание логарифма 11>1, то переходим от логарифмического наравенства к рациональному («отбраcываем логарифм») с сохранением знака неравенства [frac ge frac +7].
Преобразуем и также решаем методом интервалов
[frac — frac-7 ge 0; frac ge 0;
Frac ge 0; frac ge 0;]
[ x in (-infty;-12]cup(-5;0].]
Чтобы завершить решение системы пересекаем все полученные множества. Фактически, это потребуется только для пунктов (3) и (4), потому что в (1) и (2) вся числовая ось.
Итак, ответ на задание пункта a) виден из рисунка
Ответ a) ( x in ( — infty ; — 12];left( — dfrac ;0 right]. ).
Б) Квадратный корень имеет ограниченную область определения, поэтому иррациональное уравнение надо начинать решать с ОДЗ, т. е. с анализа подкоренных выражений. В данном случае замечаем, что оба квадратных трёхчлена образуют полные квадраты, поэтому область допустимых значений выражения (x in R).
Преобразуем уравнение [sqrt+sqrt =10, sqrt + 14^2>+sqrt + 4^2> =10, sqrt+sqrt =10, |x+14|+|x+4| =10.]
Уравнение свелось к сумме модулей по определению арифметического квадратного корня. Нужно определить знаки постоянства подмодульных выражений, чтобы упростить уравнение дальше.[|x+14|+|x+4| ; Leftrightarrow ;; left[ begin
-(x+14)-(x+4),text X le -14; (x+14)-(x+4),text -14 X ge -4. end right.] Таким образом, наше уравнение будет равносильно совокупности
[ left[ begin -2x-18 = 10,text X le -14; 10 = 10,text -14 X ge -4.end right.] Корни первого и третьего уравнений (x= -14) и (x = -4) являются границами интервала, на котором уравнение выродилось в тождество. Таким образом, оно верно для всех точек отрезка [−14;−4].
Ответ б) ( x in [-14;-4]).
В) Чтобы решить систему, представленную в последнем пункте задания достаточно пересечь множества из предыдущих двух ответов.
Как видно из рисунка, решением этой системы будут промежутки [−14;−12] и (left( — dfrac;-4 right].)
Ответ в) ( x in [-14;-12]cup left( — dfrac;-4 right]).
Вывод по варианту в целом: изменения делают вариант более интересным и насыщенным, но распределение заданий не соответствует заявленному уровню сложности, а главное, все представленные новые задания времяёмкие.
- Событие П — «Житель города является пенсионером». Вероятность этого события P(П) = 0,126 находим в условии задачи (пенсионеры составляют 12,6% взрослого населения).
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword Вариант 42789571 решу егэ математика профиль
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
За пи сы вай тесь на бес плат ное за ня тие.
Следующие задания, в которых требуется определить вероятность некого события при условии, что другое связанное с ним событие уже произошло, и мы об этом знаем, в теории вероятностей решаются с использованием теоремы Байеса или формулы Байеса.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Я решу егэ математика профиль
Я решу егэ математика профиль
Я решу егэ математика профиль
Задание 14 № 507254
Чтобы не решать кубическое неравенство, можно подобрать подходящую группировку:
Почему в решении проигнорировано ОДЗ на третий логарифм? (аргумент >0)? В данном случае это не привело к искажению решения, но вполне могло привести!
Задание 14 № 507472
Найдём значения X, при которых определены обе части неравенства:
Для таких X получаем:
Тогда исходное неравенство примет вид: Учитывая, что неравенство определено на множестве имеем:
Мы ведь могли (в последней строчке) сделать множителем логарифма сразу 10, тогда бы и не было икса x=9. Исходя из каких волшебных выводов, вы часто поступаете нетривиально, нелогично непросто, и попадаете в яблочко?! Меня сильно волнует это. Так как(уверен) многие бы вынесли именно «10, а не «5*2» и упустили бы корень 9. Заранее спасибо! Надеюсь, откроете тайну вселенной!
Никакой тайны вселенной тут нет. Нужно следить за тем, чтобы преобразования были эквивалентными. То, о чем пишете Вы таковым не является, а является очень грубой ошибкой.
Просьба, проверить данный ответ, комментарий был по делу, а Вы ссылаетесь на эквивалентность, которая противоречит свойству.
По свойству: , а не так как рассуждал автор вопроса. И тогда никакие «корни» не теряются. Если любите работать с модулями, можете решать, используя это свойство. А можно как в решении вынести 5 и оставить под логарифмом квадрат и тогда никаких модулей.
Задание 14 № 507254
Я решу егэ математика профиль.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Я решу егэ математика профиль
Я решу егэ математика профиль
Я решу егэ математика профиль
Задание 14 № 505567
Областью определения неравенства являются положительные числа, отличные от 0,25 и 1. Выражение либо равно нулю при при этом неравенство верно; либо положительно, и тогда на него можно разделить, не меняя знака неравенства. Имеем:
Учитывая, что получаем ответ:
Ладно 2 исчезла, но куда исчез x?
На него поделили, учитывая, что всё это в системе, в которой есть условие х>0
Задание 14 № 507258
Решим неравенство методом рационализации:
Задание 14 № 507635
Левая часть неравенства имеет смысл при и то есть при и При этих условиях получаем:
Сделаем замену тогда
Откуда или Из полученного набора нужно ещё исключить точку 8. Получаем
А изменение ОДЗ не происходит, когда мы к разным основаниям логарифма переходим? Точнее, я уверен, что оно изменяется, но как это отражается на решении? Я ничего не нашел, что как-то касалось бы этого в решении.
Я правильно понимаю, мы допускаем переход к новому основанию только потому, что новые приобретенные корни мы потом можем отсечь проверкой на ОДЗ?
А как быть, если корни теряются? Как в таком случае переходить к новому основанию?
Формула перехода к новому (положительному и не равному единице) основанию, верна всегда.
Поэтому в задачах удобно переходить к десятичным логарифмам, натуральным логарифмам, логарифмам по основанию 2.
А вот переход к новому переменному основанию требует дополнительных рассуждений, и его лучше избегать
- Событие П — «Житель города является пенсионером». Вероятность этого события P(П) = 0,126 находим в условии задачи (пенсионеры составляют 12,6% взрослого населения).
Источники:
Решу Егэ Математика Профиль 2022 — Новости, справки, информация, советы » /> » /> .keyword Вариант 42789571 решу егэ математика профиль
Решу ЕГЭ 2022 математика, профильный уровень, задания, ответы
Ну что, давайте вместе решать ЕГЭ 2022 года по математике! А что бы выпускные экзамены удалось вам решить легко на 5 баллов, тогда нужно немного подготовиться к ним! Здесь можно бесплатно скачать демоверсии заданий и вопросов с ответами, которые будут на едином государственном экзамене в школе для учеников 11 класса. Все варианты для решения ЕГЭ были взяты с официального сайта ФИПИ. После домашнего изучения КИМ и тестовых вариантов, вы смело сможете сказать себе, что я РЕШУ ЕГЭ!
Официальный сайт. Единый Государственный Экзамен. Открытый банк заданий ЕГЭ-22. ФИПИ ШКОЛЕ. ФГОС. ОРКСЭ. МЦКО. Школа России. 21 век. . Решебник. Перспектива. Школа 2100. Планета знаний. Россия. Беларусь.
Скачать бесплатно новые задания, тесты, тренировочные варианты, ответы и решения Решу ЕГЭ-2022
Демонстрационный вариант реальных заданий контрольных измерительных материалов единого государственного экзамена 2022 года по Математике. Профильный уровень. Формат PDF
Скачать бесплатно
Кодификатор элементов содержания по Математике. База для составления контрольных измерительных материалов для проведения единого государственного экзамена
Скачать бесплатно
Кодификатор требований к уровню подготовки выпускников образовательных организаций для проведения единого государственного экзамена по математике
Скачать бесплатно
Спецификация контрольных измерительных материалов для проведения в 2022 году единого государственного экзамена по Математике Профиль.
Скачать бесплатно
Правильные ответы и решения заданий ЕГЭ-2022
Скачать бесплатно
А Приведите пример 10 нецелых чисел и последовательности 9 ходов, после которых на доске будет записано число, равное сумме исходных чисел.
Dankonoy. com
18.07.2018 3:59:43
2018-07-18 03:59:43
Источники:
Https://dankonoy. com/ege/ege13/archives/22267
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
|
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
|
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
  |
||||
| Показать сообщения за: Сортировать по: |















