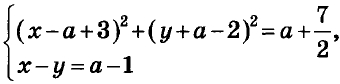Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень даётся не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно пять мишеней» больше вероятности события «стрелок поразит ровно четыре мишени»?
Спрятать решение
Решение.
Сначала найдём вероятность попасть в мишень с первого или второго выстрела: Соответственно, вероятность противоположного события, состоящего в том, что стрелок не попадёт в мишень с двух выстрелов, равна 1 − 0,84 = 0,16.
Вероятность события «стрелок поразит ровно пять мишеней» равна P5(5) = 0,845. Для нахождения вероятности события «стрелок поразит ровно четыре мишени» воспользуемся формулой Бернулли:
Теперь найдём искомое отношение вероятностей:
Ответ: 1,05.
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-14

Александр
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Отзывов (2)
-
Максим
2016-07-18 в 02:03
Потеряли знак минуса при вычислении синуса.
Ответить
-
Александр
2016-07-19 в 22:34
Спасибо!
Ответить
-
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Новые тренировочные варианты в формате решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки к экзамену, каждый вариант составлен по новой демоверсии ФИПИ ЕГЭ 2022 года, к тренировочным заданиям прилагаются правильные ответы и пояснения.
-
Тренировочный вариант №41054170 с ответами
-
Тренировочный вариант №41054171 с ответами
-
Тренировочный вариант №41054172 с ответами
-
Тренировочный вариант №41054173 с ответами
-
Тренировочный вариант №41054174 с ответами
-
Тренировочный вариант №41054175 с ответами
-
Тренировочный вариант №41054176 с ответами
-
Тренировочный вариант №41054177 с ответами
-
Тренировочный вариант №41054178 с ответами
-
Тренировочный вариант №41054179 с ответами
-
Тренировочный вариант №41054180 с ответами
-
Тренировочный вариант №41054181 с ответами
-
Тренировочный вариант №41054182 с ответами
-
Тренировочный вариант №41054183 с ответами
-
Тренировочный вариант №41054184 с ответами
Другие тренировочные варианты ЕГЭ 2022 по математике:
Тренировочные варианты ЕГЭ по математике 11 класс задания с ответами
Пробный вариант ЕГЭ 2022 №211004 по математике 11 класс с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.
Тренировочные варианты ЕГЭ 2022 по математике (профиль)
| egemath.ru | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| variant 8 | скачать |
| variant 9 | скачать |
| variant 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 19 | скачать |
| variant 20 | скачать |
| yagubov.ru | |
| вариант 21 | ege2022-yagubov-prof-var21 |
| вариант 22 | ege2022-yagubov-prof-var22 |
| вариант 23 | ege2022-yagubov-prof-var23 |
| вариант 24 | ege2022-yagubov-prof-var24 |
| вариант 25 | ege2022-yagubov-prof-var25 |
| вариант 26 | ege2022-yagubov-prof-var26 |
| вариант 27 | ege2022-yagubov-prof-var27 |
| вариант 28 | ege2022-yagubov-prof-var28 |
| Досрочный Москва 28.03.2022 | скачать |
| egemathschool.ru | |
| вариант 1 | ответ |
| вариант 2 | ответ |
| вариант 3 | ответ |
| вариант 4 | ответ |
| ЕГЭ 100 баллов (с решениями) | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| Вариант 8 | скачать |
| Вариант 9 | скачать |
| Вариант 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 20 | скачать |
| variant 21 | скачать |
| variant 23 | скачать |
| variant 24 | скачать |
| variant 25 | скачать |
| variant 26 | скачать |
| variant 29 | скачать |
| variant 30 | скачать |
| math100.ru (с ответами) | |
| Вариант 140 | скачать |
| Вариант 141 | скачать |
| Вариант 142 | скачать |
| Вариант 143 | math100-ege22-v143 |
| Вариант 144 | math100-ege22-v144 |
| Вариант 145 | math100-ege22-v145 |
| Вариант 146 | math100-ege22-v146 |
| variant 147 | math100-ege22-v147 |
| variant 148 | math100-ege22-v148 |
| variant 149 | math100-ege22-v149 |
| variant 150 | math100-ege22-v150 |
| variant 151 | math100-ege22-v151 |
| variant 152 | math100-ege22-v152 |
| variant 153 | math100-ege22-v153 |
| variant 154 | math100-ege22-v154 |
| variant 155 | math100-ege22-v155 |
| variant 156 | math100-ege22-v156 |
| variant 157 | math100-ege22-v157 |
| variant 158 | math100-ege22-v158 |
| variant 159 | math100-ege22-v159 |
| variant 160 | math100-ege22-v160 |
| variant 161 | math100-ege22-v161 |
| variant 162 | math100-ege22-v162 |
| variant 163 | math100-ege22-v163 |
| variant 164 | math100-ege22-v164 |
| variant 165 | math100-ege22-v165 |
| variant 166 | math100-ege22-v166 |
| variant 167 | math100-ege22-v167 |
| variant 168 | math100-ege22-v168 |
| variant 169 | math100-ege22-v169 |
| variant 170 | math100-ege22-v170 |
| variant 171 | math100-ege22-v171 |
| variant 172 | math100-ege22-v172 |
| variant 173 | math100-ege22-v173 |
| variant 174 | math100-ege22-v174 |
| alexlarin.net | |
| Вариант 358 |
скачать |
| Вариант 359 | скачать |
| Вариант 360 | скачать |
| Вариант 361 | скачать |
| Вариант 362 | проверить ответы |
| Вариант 363 | проверить ответы |
| Вариант 364 | проверить ответы |
| Вариант 365 | проверить ответы |
| Вариант 366 | проверить ответы |
| Вариант 367 | проверить ответы |
| Вариант 368 | проверить ответы |
| Вариант 369 | проверить ответы |
| Вариант 370 | проверить ответы |
| Вариант 371 | проверить ответы |
| Вариант 372 | проверить ответы |
| Вариант 373 | проверить ответы |
| Вариант 374 | проверить ответы |
| Вариант 375 | проверить ответы |
| Вариант 376 | проверить ответы |
| Вариант 377 | проверить ответы |
| Вариант 378 | проверить ответы |
| Вариант 379 | проверить ответы |
| Вариант 380 | проверить ответы |
| Вариант 381 | проверить ответы |
| Вариант 382 | проверить ответы |
| Вариант 383 | проверить ответы |
| Вариант 384 | проверить ответы |
| Вариант 385 | проверить ответы |
| Вариант 386 | проверить ответы |
| Вариант 387 | проверить ответы |
| Вариант 388 | проверить ответы |
| vk.com/ekaterina_chekmareva (задания 1-12) | |
| Вариант 1 | ответы |
| Вариант 2 | |
| Вариант 3 | |
| Вариант 4 | |
| Вариант 5 | |
| Вариант 6 | |
| Вариант 7 | ответы |
| Вариант 8 | |
| Вариант 9 | |
| Вариант 10 | |
| vk.com/matematicalate | |
| Вариант 1 | matematikaLite-prof-ege22-var1 |
| Вариант 2 | matematikaLite-prof-ege22-var2 |
| Вариант 3 | matematikaLite-prof-ege22-var3 |
| Вариант 4 | matematikaLite-prof-ege22-var4 |
| Вариант 5 | matematikaLite-prof-ege22-var5 |
| Вариант 6 | matematikaLite-prof-ege22-var6 |
| Вариант 7 | matematikaLite-prof-ege22-var7 |
| Вариант 8 | matematikaLite-prof-ege22-var8 |
| vk.com/pro_matem | |
| variant 1 | pro_matem-prof-ege22-var1 |
| variant 2 | pro_matem-prof-ege22-var2 |
| variant 3 | pro_matem-prof-ege22-var3 |
| variant 4 | разбор |
| variant 5 | разбор |
| vk.com/murmurmash | |
| variant 1 | otvet |
| variant 2 | otvet |
| → Купить сборники тренировочных вариантов ЕГЭ 2022 по математике |
Структура варианта КИМ ЕГЭ
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Связанные страницы:
Средний балл ЕГЭ 2021 по математике
Решение задач с параметром при подготовке к ЕГЭ
Изменения в КИМ ЕГЭ 2022 года по математике
Купить сборники типовых вариантов ЕГЭ по математике
Как решать экономические задачи ЕГЭ по математике профильного уровня?
- ЕГЭ по математике профиль
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.
Тренировочные варианты ЕГЭ 2022 по математике (профиль)
Структура варианта КИМ ЕГЭ
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Связанные страницы:
Решение и ответы заданий Варианта №8 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса. Полный разбор.
Задание 1.
Найдите корень уравнения log4 25x+7 = 3.
Задание 2.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 шахматистов, среди которых 4 спортсмена из России, в том числе Фёдор Волков. Найдите вероятность того, что в первом туре Фёдор Волков будет играть с каким-либо шахматистом из России.
Задание 3.
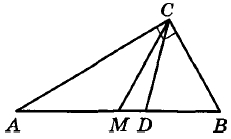
Угол между биссектрисой CD и медианой СМ проведёнными из вершины прямого угла С треугольника АВС, равен 10°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Задание 4.
Найдите значение выражения frac{a^{3,33}}{ a^{2,11}cdot a^{2,22}} при а = frac{2}{7}.
Задание 5.
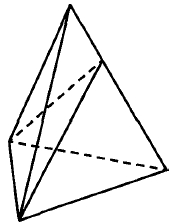
Объём треугольной пирамиды равен 14. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 2:5, считая от вершины пирамиды. Найдите больший из объёмов пирамид, на которые плоскость разбивает исходную пирамиду.
Задание 6.
Прямая у = 9х + 6 является касательной к графику функции у = ах2 – 19х + 13. Найдите а.
Ответ задания: 28.
Задание 7.
Расстояние от наблюдателя, находящегося на высоте h м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле l=sqrt{frac{Rh}{500}}, где 𝑅 = 6400 км – радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4 километра. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 24 км?
Ответ задания: 43,75.
Задание 8.
Первый садовый насос перекачивает 10 литров воды за 5 минут, второй насос перекачивает тот же объём воды за 7 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 72 литра воды?
Ответ задания: 21.
Задание 9.
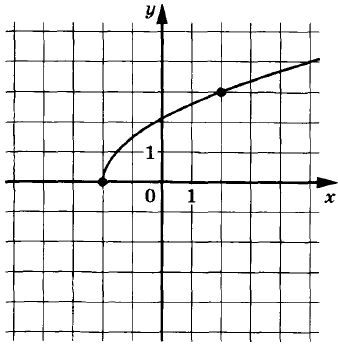
На рисунке изображён график функции f(x) = ksqrt{x+p}. Найдите f(0,25).
Задание 10.
Игральный кубик бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых.
Задание 11.
Найдите наибольшее значение функции у = 2х2 – 12х + 8lnх – 5 на отрезке [frac{12}{13};frac{14}{13}].
Задание 12.
а) Решите уравнение 7cosx – 4cos3x = 2√3sin2x.
б) Найдите все корни этого уравнения, принадлежащие отрезку [–4π; –3π].
Ответ задания: a)frac{pi}{2}+pi k,k in Z;frac{pi}{3}+2pi n,n in Z;frac{2pi}{3}+2pi m,m in Z;б)-frac{11pi}{3};-frac{7pi}{2};-frac{10pi}{3}.
Задание 13.
Основание пирамиды SABC — прямоугольный треугольник АВС с прямым углом при вершине С. Высота пирамиды проходит через точку В.
а) Докажите, что середина ребра SA равноудалена от вершин В и С.
б) Найдите угол между плоскостью SBC и прямой, проходящей через середины рёбер ВС и SA, если известно, что BS = 2AC.
Задание 14.
Решите неравенство log52(x4) – 28log0,04 (x2) ≤ 8.
Ответ задания: [–sqrt[4]{5}; –0,04]; [0,04; sqrt[4]{5}].
Задание 15.
Производство х тыс. единиц продукции обходится в q = 3х2 + 6х + 13 млн рублей в год. При цене р тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет рх – q. При каком наименьшем значении р через пять лет суммарная прибыль может составить не менее 70 млн рублей при некотором значении х?
Ответ задания: 24.
Задание 16.
Точки A1, B1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС.
а) Докажите, что окружности, описанные около треугольников А1СВ1, А1ВС1 и В1АС1 пересекаются в одной точке.
б) Известно, что АВ = АС = 17 и ВС = 16. Найдите радиус окружности, вписанной в треугольник, вершины которого – центры окружностей, описанных около треугольников А1СВ1, А1ВС1 и В1АС1.
Задание 17.
Найдите все значения а, при каждом из которых система уравнений
имеет единственное решение.
Задание 18.
Для действительного числа х обозначим через [х] наибольшее целое число, не превосходящее х. Например, [frac{11}{4}] = 2, так как 2≤frac{11}{4}<2
а) Существует ли такое натуральное число n, что [frac{n}{2}]+[frac{n}{3}]+[frac{n}{9}]=n?
б) Существует ли такое натуральное число n, что [frac{n}{2}]+[frac{n}{3}]+[frac{n}{5}]=n+2?
в) Сколько существует различных натуральных n, для которых [frac{n}{2}]+[frac{n}{3}]+[frac{n}{8}]+[frac{n}{23}]=n+2021?
Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
ЕГЭ по математике – одно из основных испытаний для выпускников школ, прежде чем, получить аттестат и поступить в высшее учебное заведение. Такой вариант контроля знаний применяется с целью оценки знаний по дисциплинам, полученным в процессе школьного обучения. Единый государственный экзамен проходит в форме тестирования, подготовка заданий для финального испытания осуществляется Рособрнадзором и другими уполномоченными органами в сфере образования. Проходной балл по математике зависит от индивидуальных требований ВУЗа, в который поступает выпускник. Успешная сдача экзамена на высокую оценку – важный фактор успеха при поступлении.
Тренировочные варианты (2020 год)
Тренировочные варианты (2019 год)
Тренировочные варианты (2018 год)
Ресурс носит неофициальный информационно-справочный характер, персональные данные не собирает и не обрабатывает, на интеллектуальные права третьих лиц не претендует.
Все ссылки ведут напрямую на официальные сайты описываемых услуг.
Карта сайта
Если вы хотите приобрести доступ на Экзамер для группы из 10 и более учеников,
мы будем рады сделать вам скидку.
Пожалуйста, расскажите нам подробности:
Необходимо заполнить все поля, кроме телефона
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 2 .
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами