Спрятать решение
Решение.
По графику, g(−2) = −1, g(−1) = −3, g(2) = 3. Тогда
Решая полученную систему, получаем: a = 1, b = 1, из g(2) = 3 получим c = −3. Найдём абсциссу точки B:
Таким образом, абсцисса точки B — 6. Теперь найдём ординату точки B:
Ответ: 39.
Решать все задания №13 ЕГЭ 2022 по профильной математике 11 класс, которые могут попасться на реальном экзамене ЕГЭ 2022 кто сдаёт профиль, более 100 практических заданий с ответами.
Задание 13 Профильного ЕГЭ (Стереометрия) многие считают самой сложной геометрической задачей в варианте ЕГЭ, решаем и готовимся к экзамену!
Задание 13 на вычисление отношений отрезков
Задание 13 на расстояние от точки до прямой и плоскости
Задание 13 на углы между прямыми
Задание 13 площадь сечения
Задание 13 расстояние между скрещивающимися прямыми
Задание 13 угол между плоскостями
Задание 13 угол между прямой и плоскостью
Задание 13 фигуры вращения цилиндр, конус, шар
Задание 13 объём многогранника
Некоторые задания и ответы:
1)Дана четырѐхугольная призма ABCDA1B1C1D1. Постройте прямую пересечения плоскостей AA1C1 и BB1D1.
2)Дан параллелепипед ABCDA1B1C1D1. Постройте прямую пересечения плоскостей BB1D1 и ABC1.
3)Дана треугольная призма ABCA1B1C1, M — точка пересечения медиан основания ABC. Постройте прямую пересечения плоскостей ABC и A1MC1.
4)Четырѐхугольник ABCD — основание пирамиды SABCD. Постройте прямую пересечения плоскостей ASB и CSD, если: а) прямые AB и CD пересекаются; б) прямые AB и CD параллельны.
5)Основание пирамиды SABCD — трапеция ABCD с основаниями AD и BC. Точка M лежит на ребре SB. Постройте прямую пересечения плоскостей ADM и SBC.
6)Дана треугольная пирамида ABCD, M — точка пересечения медиан грани ABC. Постройте прямую пересечения плоскости ADC с плоскостью, проходящей через точку M параллельно прямым AC и BD.
7)Дана треугольная призма ABCA1B1C1, M — точка, лежащая на ребре CC1. Постройте прямую пересечения плоскостей ABC и BMA1.
8)Дан параллелепипед ABCDA1B1C1D1. Точки K, L и M лежат на рѐбрах AD, CD и BB1 соответственно. Постройте прямую пересечения плоскостей KLM и BB1D1D.
9)Основание пирамиды SABCDEF — шестиугольник ABCDEF, противоположные стороны которого попарно равны и параллельны. Постройте прямую пересечения плоскостей ASD и CSF.
10)Дана шестиугольная призма ABCDEFA1B1C1D1E1F1, основания которой — правильные шестиугольники. Точка O — центр основания ABCDEF, M — середина бокового ребра DD1. Постройте прямую пересечения плоскости A1B1C1 с плоскостью, проходящей через точки O и M параллельно прямой AE.
11)Дана треугольная пирамида ABCD. Точка M лежит на ребре BC, причѐм BM : MC = 1 : 2. Постройте точку пересечения прямой, проходящей через точку M и середину ребра CD, с плоскостью ABD.
12)Дан параллелепипед ABCDA1B1C1D1. Точка M лежит на ребре AA1. Постройте точку пересечения прямой DM с плоскостью A1B1C1.
13)Дана треугольная призма ABCA1B1C1, M — точка пересечения медиан грани ABC, точка N лежит на боковом ребре CC1. Постройте точку пересечения прямой MN с плоскостью A1B1C1.
14)Дана четырѐхугольная пирамида SABCD, основание которой — параллелограмм ABCD. Точка M лежит на боковом ребре SC. Постройте точку пересечения прямой BM с плоскостью ASD.
15)Дан параллелепипед ABCDA1B1C1D1. Точка M лежит на ребре AA1. Постройте точку пересечения прямой CM с плоскостью A1B1C1.
16)Дана треугольная пирамида ABCD, M — точка пересечения медиан грани ABC. Постройте точку пересечения прямой, проходящей через точку B и середину отрезка DM, с плоскостью ACD.
17)Дана треугольная пирамида ABCD. Точки K, L и M лежат на рѐбрах AB, BC и CD соответственно. Постройте точку пересечения прямой KM с плоскостью ALD.
18)Дана четырѐхугольная пирамида SABCD с вершиной S. Точка M лежит на боковом ребре SD. Постройте точку пересечения прямой BM с плоскостью ASC.
19)Дан параллелепипед ABCDA1B1C1D1. Точка M лежит на ребре DD1. Постройте точку пересечения прямой DB1 с плоскостью AMC.
20)Точка M лежит на ребре AB треугольной пирамиды ABCD, причѐм AM : MB = 1 : 2. а) Постройте сечение пирамиды плоскостью, проходящей через точку M и середины рѐбер BC и AD. б) В каком отношении плоскость сечения делит ребро CD?
21)Точка M — середина ребра AD треугольной пирамиды ABCD. Точки K и L лежат на прямых AB и AC соответственно, причём B — середина отрезка AK, а C — середина отрезка AL. а) Постройте сечение пирамиды плоскостью, проходящей через точки M, K и L. б) В каком отношении плоскость сечения делит ребро BD?
22)Точки M и N — середины рёбер соответственно AB и BC параллелепипеда ABCDA1B1C1D1. а) Постройте сечение параллелепипеда плоскостью, проходящей через точки M, N и D1. б) В каком отношении плоскость сечения делит ребро AA1?
23)Точка M — середина ребра CD параллелепипеда ABCDA1B1C1D1. а) Постройте сечение параллелепипеда плоскостью, проходящей через точки M, A1 и C1. б) Пусть секущая плоскость пересекает прямую DD1 в точке P. Найдите отношение PD : PD1.
24)Основание пирамиды SABCD — параллелограмм ABCD с центром O. Точка M лежит на отрезке SO, причём OM : MS = 1 : 2. а) Постройте сечение пирамиды плоскостью, проходящей через прямую AM параллельно прямой BD. б) В каком отношении плоскость сечения делит ребро SC?
25)Основание пирамиды SABCD — параллелограмм ABCD с центром O. Точка M — середина отрезка AO. а) Постройте сечение пирамиды плоскостью, проходящей через точку M параллельно прямым SA и BD. б) В каком отношении плоскость сечения делит ребро SC?
26)В кубе ABCDA1B1C1D1 на ребре ВВ1 взята точка Е так, что 1 В Е ЕВ : 2:3 . а) Постройте сечение куба плоскостью, проходящей через точки E и С1 параллельно прямой BD1. б) В каком отношении плоскость сечения делит ребро A1B1?
27)Боковые рѐбра пирамиды SABC с вершиной S попарно перпендикулярны, M — произвольная точка на ребре BC. а) Докажите, что плоскости AMS и BSC перпендикулярны. б) Высота SH пирамиды равна 12. Прямая AH пересекает ребро BC в точке K. Найдите расстояние от точки K до прямой AS, если AS = 20.
28)Основание пирамиды SABCD — параллелограмм ABCD. Боковые рѐбра SA и SD равны. Точка M лежит на боковом ребре SC и не совпадает с его концами. Плоскость α проходит через точку M параллельно прямым BC и SA. а) Докажите, что сечение пирамиды плоскостью α — равнобедренная трапеция. б) Найдите расстояние от точки A до плоскости α, если боковая сторона этой трапеции равна меньшему основанию, а все рѐбра пирамиды равны 1.
29)Точка K лежит на стороне AB основания ABCD правильной четырѐхугольной пирамиды SABCD, все рѐбра которой равны. Плоскость α проходит через точку K параллельно плоскости ASD. Сечение пирамиды плоскостью α — четырѐхугольник, в который можно вписать окружность. а) Докажите, что BK = 2AK. б) Найдите расстояние от вершины S до плоскости α, если все рѐбра пирамиды равны 1.
30)В правильной четырѐхугольной пирамиде SABCD сторона основания AB равна 16, а высота пирамиды равна 4. На рѐбрах AB, CD и AS отмечены точки M, N и K соответственно, причѐм AM = DN = 4 и AK = 3. а) Докажите, что плоскости MNK и SBC параллельны. б) Найдите расстояние от точки K до плоскости SBC.
11 задание ЕГЭ 2022 математика профиль 11 класс прототипы с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
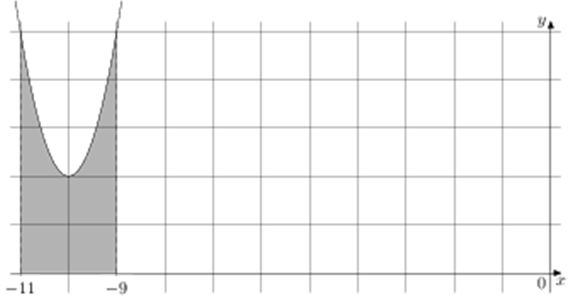
ЕГЭ профильный уровень. №7 Первообразная. Задача 4
ОТВЕТ: 6.
Площадь закрашенной фигуры равна интегралу (intlimits_{ — 11}^{ — 9} {left( x right)dx} = Fleft( { — 9} right) — Fleft( { — 11} right).) Найдём значение первообразной в точках – 9 и – 11:
(Fleft( { — 9} right) = {left( { — 9} right)^3} + 30 cdot {left( { — 9} right)^2} + 302 cdot left( { — 9} right) — frac{{15}}{8} = — 729 + 2430 — 2718 — frac{{15}}{8} = — 1017 — frac{{15}}{8})
(Fleft( { — 11} right) = {left( { — 11} right)^3} + 30 cdot {left( { — 11} right)^2} + 302 cdot left( { — 11} right) — frac{{15}}{8} = — 1331 + 3630 — 3322 — frac{{15}}{8} = — 1023 — frac{{15}}{8})
Тогда площадь закрашенной фигуры:
(S = Fleft( { — 9} right) — Fleft( { — 11} right) = — 1017 — frac{{15}}{8} — left( { — 1023 — frac{{15}}{8}} right) = 6)
Ответ: 6.
Комментарии для сайта Cackle
Решу егэ математика профиль 509158
Задание 9 № 509158
На рисунке изображены графики функций и которые пересекаются в точках A и B. Найдите ординату точки B.
По графику, G(−2) = −1, G(−1) = −3, G(2) = 3. Тогда
Решая полученную систему, получаем: A = 1, B = 1, из G(2) = 3 получим C = −3. Найдём абсциссу точки B:
Таким образом, абсцисса точки B — 6. Теперь найдём ординату точки B:
Задание 9 № 509158
На рисунке изображены графики функций и которые пересекаются в точках A и B.
Ege. sdamgia. ru
14.02.2018 16:39:30
2018-02-14 16:39:30
Источники:
Https://ege. sdamgia. ru/test? pid=509158
Решу егэ математика профиль 509158 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ математика профиль 509158
Решу егэ математика профиль 509158
Решу егэ математика профиль 509158
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 9 № 509182
На рисунке изображены графики функций и которые пересекаются в точках A и B. Найдите ординату точки B.
По графику, F(2) = 1, тогда Значит, гипербола имеет вид
Заметим, что A — тангенс угла наклона прямой по отношению к оси абсцисс, тогда По графику, G(2) = 1, тогда Значит, функция прямой имеет вид
Теперь найдём абсциссу точки B:
Таким образом, абсцисса точки B — −0,2. Тогда ордината точки B равна
Задание 9 № 509182
Таким образом, абсцисса точки B 0,2.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ математика профиль 509158
Решу егэ математика профиль 509158
Решу егэ математика профиль 509158
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 9 № 509158
На рисунке изображены графики функций и которые пересекаются в точках A и B. Найдите ординату точки B.
По графику, G(−2) = −1, G(−1) = −3, G(2) = 3. Тогда
Решая полученную систему, получаем: A = 1, B = 1, из G(2) = 3 получим C = −3. Найдём абсциссу точки B:
Таким образом, абсцисса точки B — 6. Теперь найдём ординату точки B:
Задание 9 № 509158
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ математика профиль 509158
Решу егэ математика профиль 509158
Решу егэ математика профиль 509158
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 9 № 509150
На рисунке изображены графики функций и которые пересекаются в точках A и B. Найдите абсциссу точки B.
По графику, G(−2) = −1, G(1) = 5, G(−3) = 1. Тогда
Решая полученную систему, получаем: A = 1, B = 3, из G(1) = 5 получим C = 1. Теперь найдём абсциссу точки B:
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ математика профиль 509158
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 9 № 509158
На рисунке изображены графики функций и которые пересекаются в точках A и B. Найдите ординату точки B.
По графику, G(−2) = −1, G(−1) = −3, G(2) = 3. Тогда
Решая полученную систему, получаем: A = 1, B = 1, из G(2) = 3 получим C = −3. Найдём абсциссу точки B:
Таким образом, абсцисса точки B — 6. Теперь найдём ординату точки B:
Задание 9 № 509158
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Dankonoy. com
18.02.2017 0:05:23
2017-02-18 00:05:23
Источники:
Https://dankonoy. com/ege/ege12/archives/4545
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
|
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
|
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
  |
||||
| Показать сообщения за: Сортировать по: |


