Алексей вышел из дома на прогулку со скоростью υ км/ч. После того, как он прошел 6 км, из дома следом за ним выбежала собака Жучка, скорость которой была на 9 км/ч больше скорости Алексея. Когда Жучка догнала хозяина, они повернули назад и вместе возвратились домой со скоростью 4 км/ч. Найдите значение υ, при котором время прогулки Алексея окажется наименьшим. Сколько при этом составит время его прогулки?
Спрятать решение
Решение.
Скорость сближения Алексея и Жучки (разность скоростей) Δυ = 9 км/ч. Первоначальная разность расстояний между хозяином и собакой составляет ΔS = 6 км. Найдем разностное отношение часа. Это и есть время, которое потребовалось Жучке, чтобы догнать Алексея.
С того времени, как Жучка бежала за хозяином, Алексей прошел расстояние, равное км. В соответствии с условием задачи Алексей прошел еще 6 км пока Жучка была дома. Значит, в направлении от дома Алексей, будучи на прогулке, прошел
км. Такой же путь Алексей прошел после того, как Жучка догнала его, но в обратном направлении. На преодоление этого пути (со скоростью 4 км/ч) потребовалось
часа. Итак, вся прогулка Алексея продлилась
часа.
Эта сумма будет наименьшей, когда сумма двух взаимно обратных положительных выражений и
примет наименьшее значение. И эта наименьшая сумма заведомо известна, она равна 2 (классическое неравенство
— наименьшее значение достигается при a = 1). Следовательно, в нашем случае должно выполняться равенство
то есть
= 6 км/ч. Время всей прогулки Алексея составляет
часа.
Ответ: 6 км/ч, часа.
Приведем решение Андрея Анатольевича.
Пусть v — скорость Алексея, и S — расстояние,на котором он находился в тот момент, когда его догнала Жучка. Время движения Алексея до того момента, когда из дому выбежала Жучка, равно время движения от этого момента до встречи с Жучкой равно
время движения до возвращения домой
тогда общее время составит
С другой стороны, время движения Жучки до встречи с Алексеем составит Тогда
Подставив данное выражение для S в первое уравнение, получим
Для нахождения минимального времени исследуем функцию f(v) на максимум и минимум с помощью производной:
Учитывая, что v > 0, найдем, что производная обращается в 0 при v = 6.
При v = 6 км/ч функция f(v) принимает наименьшее значение, равное часа, или 4 часа 10 минут.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Источник: А. Ларин: Тренировочный вариант № 116.
ЕГЭ профильный уровень. №7 Первообразная. Задача 4
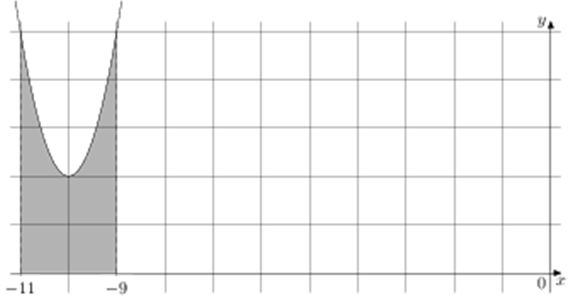
ОТВЕТ: 6.
Площадь закрашенной фигуры равна интегралу (intlimits_{ — 11}^{ — 9} {left( x right)dx} = Fleft( { — 9} right) — Fleft( { — 11} right).) Найдём значение первообразной в точках – 9 и – 11:
(Fleft( { — 9} right) = {left( { — 9} right)^3} + 30 cdot {left( { — 9} right)^2} + 302 cdot left( { — 9} right) — frac{{15}}{8} = — 729 + 2430 — 2718 — frac{{15}}{8} = — 1017 — frac{{15}}{8})
(Fleft( { — 11} right) = {left( { — 11} right)^3} + 30 cdot {left( { — 11} right)^2} + 302 cdot left( { — 11} right) — frac{{15}}{8} = — 1331 + 3630 — 3322 — frac{{15}}{8} = — 1023 — frac{{15}}{8})
Тогда площадь закрашенной фигуры:
(S = Fleft( { — 9} right) — Fleft( { — 11} right) = — 1017 — frac{{15}}{8} — left( { — 1023 — frac{{15}}{8}} right) = 6)
Ответ: 6.
Комментарии для сайта Cackle
Видеоуроки, тесты, практика и консультации репетитора онлайн. Экстренная подготовка накануне экзамена
About this course
Онлайн-курс посвящён задаче №18 (элементы теории чисел) в профильном ЕГЭ. Эта задача – последняя в экзамене и самая дорогая по баллам. Тема базируется на знаниях из средней школы: натуральные числа, делимость, уравнения.
Курс рассчитан на быструю подготовку: его можно полностью освоить за неделю до экзамена. Вы повысите свой балл и сэкономите время, потому что:
- Обучение идёт от простого к сложному.
- Репетитор разберёт типичные сценарии, которые встречаются в экзамене, а не все задачи подряд.
- Выдержана сложность и не даётся лишнего. Вы будете решать задачи с реальных ЕГЭ прошлых лет.
- Видеоуроки смонтированы без «воды».
- Все темы доступны сразу. Можете пропускать то, что уже хорошо знаете
Этот курс — всего лишь один раздел из моего большого курса «Задачи с оформлением».
Другие бесплатные разделы:
Задание 12: уравнение
Задание 14: неравенство
Задание 17: параметр
Whom this course is for
Ученики 11 класса, абитуриенты
Meet the Instructors
Course content
Share this course
https://stepik.org/course/97260/promo
WEB-DL
- Год выхода: 2019
- Страна: Россия
- Жанр: Комедия
- Режиссер: Константин Смирнов, Константин Колесов
- Актёры: Вячеслав Чепурченко, Павел Комаров, Вадим Дубровин, Максим Лагашкин, Екатерина Стулова
- Сезоны: 1-3 сезон
- Серии: 1-16 серия
- Время: 00:30
Никита, Дэн и Артемий разработали уникальное приложение для смартфонов, вот-вот продадут его и осуществят все свои мечты. Но в последний момент многомиллионная сделка срывается и парней забирают в армию. Чтобы не ставить под угрозу успех своего стартапа, они выбирают альтернативную службу в глухой деревне Жуки, где будут пытаться довести свой проект до конца. Только не так просто разрабатывать приложение там, где нет даже интернета…
Смотреть онлайн Жуки (2019) в хорошем качестве HD
Плеер 1
Плеер 2
В закладки
Тренировочный вариант №17 и вариант №18 в формате решу ЕГЭ 2023 по математике 11 класс профильный уровень от 19 января 2023 года с ответами и решением по новой демоверсии ЕГЭ 2023 года для подготовки на 100 баллов, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
- Скачать вариант №17 с ответами
- Скачать вариант №18 с ответами
- Скачать решение варианта №17
- Скачать решение варианта №18
вариант17-егэ2023-профиль
1. Острый угол 𝐵 прямоугольного треугольника равен 66°. Найдите угол между биссектрисой 𝐶𝐷 и медианой 𝐶𝑀, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Ответ: 21
2. Шар, объем которого равен 35𝜋, вписан в куб. Найдите объём куба.
Ответ: 210
3. Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 теннисистов, среди которых 7 спортсменов из России, в том числе Анатолий Москвин. Найдите вероятность того, что в первом туре Анатолий Москвин будет играть с каким-либо теннисистом из России.
Ответ: 0, 08
4. В городе 46% взрослого населения – мужчины. Пенсионеры составляют 7,7% взрослого населения, причём доля пенсионеров среди женщин равна 10%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
Ответ: 0, 05
5. Найдите корень уравнения (𝑥 + 3) 9 = 512.
Ответ: -1
7. На рисунке изображены график функции 𝑦 = 𝑓(𝑥) и касательная к нему в точке с абсциссой 𝑥0. Найдите значение производной функции 𝑓(𝑥) в точке 𝑥0.
Ответ: 0,25
8. Груз массой 0,16 кг колеблется на пружине. Его скорость 𝑣 (в м/с) меняется по закону 𝜈 = 𝜈0 cos 2𝜋𝑡 𝑇 , где 𝑡 − время с момента начала наблюдения в секундах, 𝑇 = 2 с – период колебаний, 𝜈0 = 1,5 м/с. Кинетическая энергия 𝐸(в Дж) груза вычисляется по формуле 𝐸 = 𝑚𝜈 2 2 , где 𝑚 − масса груза (в кг), 𝜈 − скорость груза (в м/с). Найдите кинетическую энергию груза через 20 секунд после начала наблюдения. Ответ дайте в джоулях.
Ответ: 0, 18
9. Два человека отправляются из одного дома на прогулку до опушки леса, находящейся в 1,5 км от дома. Один идёт со скоростью 2,2 км/ч, а другой — со скоростью 4,4 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча? Ответ дайте в километрах.
Ответ: 1
10. На рисунке изображён график функции вида 𝑓(𝑥) = log𝑎 𝑥. Найдите значение 𝑓(16).
Ответ: -4
12. а) Решите уравнение 4 ∙ 16𝑥− 1 2 − 5 ∙ 12𝑥 + 2 ∙ 9 𝑥+ 1 2 = 0. б) Найдите все корни этого уравнения, принадлежащие отрезку [2; 3].
13. На рёбрах 𝐶𝐷 и 𝐵𝐵1 куба 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 с ребром 12 отмечены точки 𝑃 и 𝑄 соответственно, причём 𝐷𝑃 = 4, а 𝐵1𝑄 = 3. Плоскость 𝐴𝑃𝑄 пересекает ребро 𝐶𝐶1 в точке 𝑀. а) Докажите, что точка 𝑀 является серединой ребра 𝐶𝐶1. б) Найдите расстояние от точки 𝐶 до плоскости 𝐴𝑃𝑄.
14. Решите неравенство log2 2 (16 + 6𝑥 − 𝑥 2) + 10 log0,5 (16 + 6𝑥 − 𝑥 2) + 24 > 0.
15. Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на 𝑥 млн рублей, где 𝑥 − целое число. Найдите наименьшее значение 𝑥, при котором банк за четыре года начислит на вклад больше 7 млн рублей.
Ответ: 5
16. В окружность вписана трапеция 𝐴𝐵𝐶𝐷, 𝐴𝐷 − большее основание, проведена высота 𝐵𝐻, вторично пересекающая окружность в точке 𝐾. а) Докажите, что 𝐴𝐶 перпендикулярна 𝐴𝐾. б) Найдите 𝐴𝐷, если радиус описанной окружности равен 12, ∠𝐵𝐴𝐶 = 30°, 𝐶𝐾 пересекает основание 𝐴𝐷 в точке 𝑁. Площадь четырёхугольника 𝐵𝐻𝑁𝐶 в 8 раз больше, чем площадь треугольника 𝐾𝐻𝑁.
Ответ: 4√33
18. В нескольких одинаковых бочках налито некоторое количество литров воды (необязательно одинаковое). За один раз можно перелить любое количество воды из одной бочки в другую. а) Пусть есть четыре бочки, в которых 29, 32, 40, 91 литров. Можно ли не более чем за четыре переливания уравнять количество воды в бочках? б) Пусть есть семь бочек. Всегда ли можно уравнять количество воды во всех бочках не более чем за пять переливаний? в) За какое наименьшее количество переливаний можно заведомо уравнять количество воды в 26 бочках?
Ответ: а) да б) нет в) 25
Вариант №18 ЕГЭ 2023 профильный уровень
вариант18-егэ2023-профиль
1. Основания трапеции равны 2 и 4. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Ответ: 2
2. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Образующая конуса равна 50√2. Найдите радиус сферы.
Ответ: 50
3. В группе туристов 300 человек. Их вертолётом доставляют в труднодоступный район, перевозя по 15 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист В. полетит первым рейсом вертолёта.
Ответ: 0,05
4. Вероятность того, что новый сканер прослужит больше года, равна 0,94. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Ответ: 0,07
5. Решите уравнение √40 + 3𝑥 = 𝑥. Если уравнение имеет более одного корня, укажите меньший из них.
Ответ: 8
7. На рисунке изображён график функции 𝑦 = 𝑓(𝑥). На оси абсцисс отмечены точки −2, −1, 3, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Ответ: -1
8. На рисунке изображена схема моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами. Введём систему координат: ось 𝑂𝑦 направим вертикально вверх вдоль одного из пилонов, а ось 𝑂𝑥 направим вдоль полотна моста, как показано на рисунке. В этой системе координат линия, по которой провисает цепь моста, задаётся формулой 𝑦 = 0,0043𝑥 2 − 0,74𝑥 + 35, где 𝑥 и 𝑦 измеряются в метрах. Найдите длину ванты, расположенной в 70 метрах от пилона. Ответ дайте в метрах.
Ответ: 4,27
9. Теплоход проходит по течению реки до пункта назначения 775 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 28 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 61 час. Ответ дайте в км/ч.
Ответ: 3
10. На рисунке изображены графики функций видов 𝑓(𝑥) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 и 𝑔(𝑥) = 𝑘𝑥, пересекающиеся в точках 𝐴 и 𝐵. Найдите абсциссу точки 𝐵.
Ответ: 5
11. Найдите наибольшее значение функции 𝑦 = (𝑥 + 10) 2𝑥 + 2 на отрезке [−11; −4].
Ответ: 2
13. В основании прямой треугольной призмы 𝐴𝐵𝐶𝐴1𝐵1𝐶1 лежит равнобедренный (𝐴𝐵 = 𝐵𝐶) треугольник 𝐴𝐵𝐶. Точка 𝐾 − середина ребра 𝐴1𝐵1, а точка 𝑀 делит ребро 𝐴𝐶 в отношении 𝐴𝑀: 𝑀𝐶 = 1: 3. а) Докажите, что 𝐾𝑀 ⊥ 𝐴𝐶. б) Найдите угол между прямой 𝐾𝑀 и плоскостью 𝐴𝐵𝐵1, если 𝐴𝐵 = 6, 𝐴𝐶 = 8 и 𝐴𝐴1 = 3.
15. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно 𝑡 2 часов в неделю, то за эту неделю они производят 3𝑡 единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно 𝑡 2 часов в неделю, то за эту неделю они производят 4𝑡 единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Ответ: 500
16. В равнобедренном треугольнике 𝐴𝐵𝐶 с углом 120° при вершине 𝐴 проведена биссектриса 𝐵𝐷. В треугольник 𝐴𝐵𝐶 вписан прямоугольник 𝐷𝐸𝐹𝐻 так, что сторона 𝐻𝐹 лежит на отрезке 𝐵𝐶, а вершина 𝐸 − на отрезке 𝐴𝐵. а) Докажите, что 𝐹𝐻 = 2𝐷𝐻. б) Найдите площадь прямоугольника 𝐷𝐸𝐹𝐻, если 𝐴𝐵 = 4.
Ответ: 24 − 12√3
17. Найдите все значения 𝑎, при каждом из которых уравнение log1−𝑥 (𝑎 − 𝑥 + 2) = 2 имеет хотя бы один корень, принадлежащий промежутку [−1; 1).
18. Рассмотрим частное трёхзначного числа, в записи которого нет нулей, и произведения его цифр. а) Приведите пример числа, для которого это частное равно 113 27 . б) Может ли это частное равняться 125 27 ? в) Какое наибольшее значение может принимать это частное, если оно равно несократимой дроби со знаменателем 27?
Ответ: а) 339 б) нет в) 931/27
Пробный вариант состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий с кратким ответом базового и повышенного уровней сложности.
Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Решу ЕГЭ 2023 профиль по математике 11 класс
Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
9 марта 2023
В закладки
Обсудить
Жалоба
Теория и практика.
Содержание
1) Прямые
2) Параболы
3) Как искать пересечение параболы и прямой, двух парабол
4) Гипербола. Асимптотические точки гиперболы
5) Пересечение гиперболы и прямой
6) Иррациональные функции
7) Пересечение корня и прямой

9) Показательные функции
10) Логарифмические функции
10_zadacha.pdf
Источник: vk.com/profimatika

