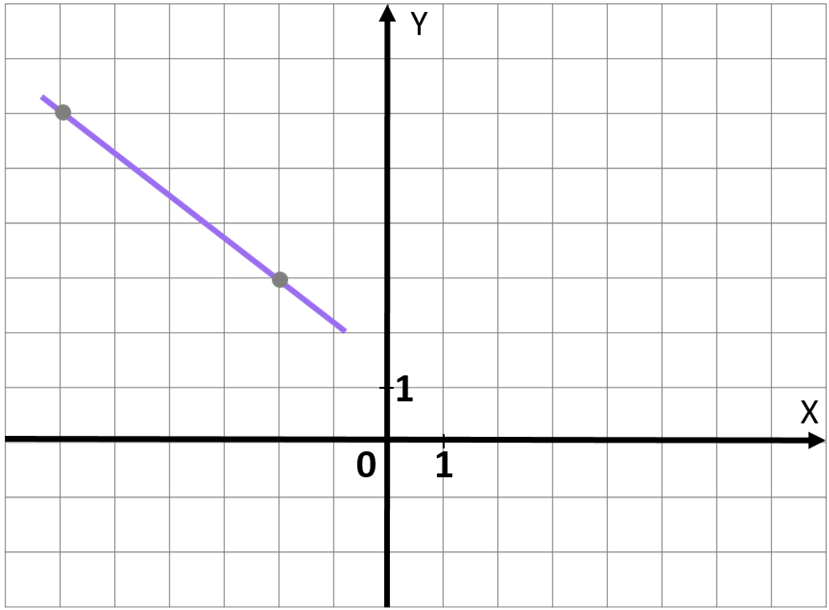
Найдите все значения а, при каждом из которых система уравнений
имеет ровно четыре различных решения.
Спрятать решение
Решение.
Изобразим на координатной плоскости множество точек, координаты которых удовлетворяют первому уравнению системы.
Рассмотрим три случая.
1) Если то получаем уравнение
Полученное уравнение задаёт параболу
2) Если то координаты любой точки прямой
удовлетворяют уравнению
3) Если то получаем уравнение
Полученное уравнение задаёт параболу
Таким образом, в первом случае мы получаем дугу параболы
c концом в точке
во втором — прямую l, задаваемую уравнением х = 2, в третьем — дугу
параболы
с концом в точке А (см. рис.).
Рассмотрим второе уравнение системы. При каждом значении а оно задаёт прямую m, параллельную прямой или совпадающую с ней. Прямая m проходит через точку А при a = −2.
Касательная к параболе имеет с ней единственную общую точку. Запишем уравнения и
как квадратные относительно x и найдем, при каких значениях параметра их дискриминанты обращаются в нуль. Тем самым, при
и
прямые m касаются дуг
и
соответственно.
Таким образом, прямая m пересекает прямую l при любом значении а, имеет одну общую точку с дугой при
и
имеет две общие точки с дугой
при
имеет одну общую точку с дугой
при
и
имеет две общие точки с дугой
при
Число решений исходной системы равно числу точек пересечения прямой l и дуг и
с прямой m. Таким образом, исходная система имеет ровно четыре решения при
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| C помощью верного рассуждения получено множество значений a, отличащееся от искомого только включением/исключением точки а = −2 | 3 |
| C помощью верного рассуждения получен один из промежутков множества значений a: |
2 |
| Задача верно сведена к исследованию взаимного расположения дуг окружностей и прямых (аналитически и графически)
ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл: | 4 |
Источник: ЕГЭ по математике 06.06.2016. Основная волна. Вариант 601 (C часть).
Тренировочный вариант №26 пробник решу ЕГЭ 2023 по математике 11 класс профильный уровень от 8 марта 2023 года с ответами и решением по новой демоверсии ЕГЭ 2023 года для подготовки на 100 баллов, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
▶Скачать вариант с ответами
▶Решение заданий с 1 по 18
▶Распечатай и реши вариант
вариант_26_егэ2023_профиль_математика
Ответы и решения
решение_варианта_26_профиль
1. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, sin 𝐴 = 0,8. Найдите sin 𝐵.
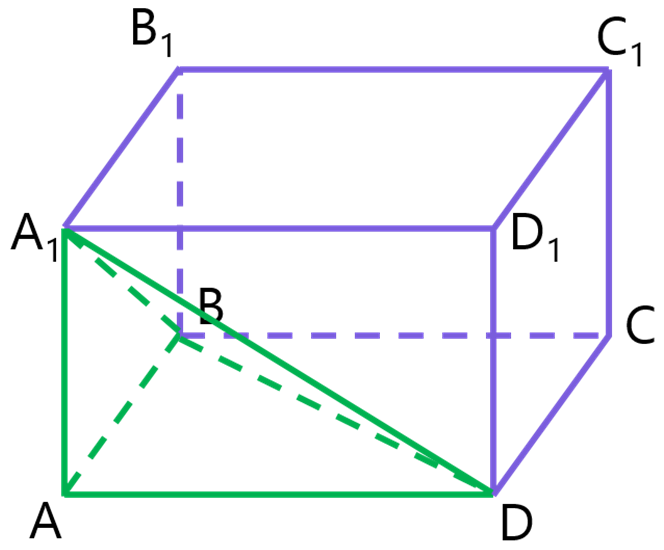
2. Дана правильная треугольная призма 𝐴𝐵𝐶𝐴1𝐵1𝐶1, площадь основания которой равна 9, а боковое ребро равно 4. Найдите объём многогранника, вершинами которого являются точки 𝐴, 𝐴1, 𝐵1, 𝐶1.
3. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что произведение выпавших очков делится на 5, но не делится на 30.
4. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,98. Вероятность того, что масса окажется больше 790 г, равна 0,83. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
7. На рисунке изображён график дифференцируемой функции 𝑦 = 𝑓(𝑥), определённой на интервале (−3; 8). Найдите точку из отрезка [−2; 5], в которой производная функции 𝑓(𝑥) равна 0.
8. Два тела, массой 𝑚 = 2 кг каждое, движутся с одинаковой скоростью 𝑣 = 8 м/с под углом 2𝛼 друг к другу. Энергия (в Дж), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле 𝑄 = 𝑚𝑣 2 sin2𝛼, где 𝑚 − масса (в кг), 𝑣 − скорость (в м/с). Найдите, под каким углом 2𝛼 должны двигаться тела, чтобы в результате соударения выделилась энергия, равная 32 Дж. Ответ дайте в градусах.
9. Смешали некоторое количество 19-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
10. На рисунке изображён график функции вида 𝑓(𝑥) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐. Найдите значение 𝑓(−2).
11. Найдите точку максимума функции 𝑦 = ln(𝑥 + 9) − 10𝑥 + 7.
12. а) Решите уравнение 3 ∙ 9 𝑥+1 − 5 ∙ 6 𝑥+1 + 8 ∙ 2 2𝑥 = 0. б) Найдите все корни этого уравнения, принадлежащие отрезку.
13. В правильной треугольной призме 𝐴𝐵𝐶𝐴1𝐵1𝐶1 все рёбра равны 2. Точка 𝑀 − середина ребра 𝐴𝐴1. а) Докажите, что прямые 𝑀𝐵 и 𝐵1𝐶 перпендикулярны. б) Найдите расстояние между прямыми 𝑀𝐵 и 𝐵1𝐶.
15. В июле 2016 года планируется взять кредит в банке на три года в размере 𝑆 млн рублей, где 𝑆 − целое число. Условия его возврата таковы: – каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года; – с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; – в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей. Найдите наибольшее значение 𝑆, при котором разница между наибольшей и наименьшей выплатами будет меньше 1 млн рублей.
16. В трапеции 𝐴𝐵𝐶𝐷 боковая сторона 𝐴𝐵 перпендикулярна основаниям. Из точки 𝐴 на сторону 𝐶𝐷 опустили перпендикуляр 𝐴𝐻. На стороне 𝐴𝐵 отмечена точка 𝐸 так, что прямые 𝐶𝐷 и 𝐶𝐸 перпендикулярны. а) Докажите, что прямые 𝐵𝐻 и 𝐸𝐷 параллельны. б) Найдите отношение 𝐵𝐻 к 𝐸𝐷, если ∠𝐵𝐶𝐷 = 135°.
18. В течение 𝑛 дней каждый день на доску записывают натуральные числа, каждое из которых меньше 6. При этом каждый день (кроме первого) сумма чисел, записанных на доску в этот день, больше, а количество меньше, чем в предыдущий день. а) Может ли 𝑛 быть больше 5? б) Может ли среднее арифметическое чисел, записанных в первый день, быть меньше 3, а среднее арифметическое всех чисел, записанных за все дни, быть больше 4? в) Известно, что сумма чисел, записанных в первый день, равна 6. Какое наибольшее значение может принимать сумма всех чисел, записанных за все дни?
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
ЕГЭ профильный уровень. №7 Первообразная. Задача 4
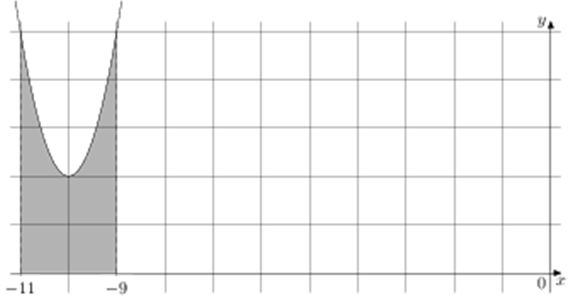
ОТВЕТ: 6.
Площадь закрашенной фигуры равна интегралу (intlimits_{ — 11}^{ — 9} {left( x right)dx} = Fleft( { — 9} right) — Fleft( { — 11} right).) Найдём значение первообразной в точках – 9 и – 11:
(Fleft( { — 9} right) = {left( { — 9} right)^3} + 30 cdot {left( { — 9} right)^2} + 302 cdot left( { — 9} right) — frac{{15}}{8} = — 729 + 2430 — 2718 — frac{{15}}{8} = — 1017 — frac{{15}}{8})
(Fleft( { — 11} right) = {left( { — 11} right)^3} + 30 cdot {left( { — 11} right)^2} + 302 cdot left( { — 11} right) — frac{{15}}{8} = — 1331 + 3630 — 3322 — frac{{15}}{8} = — 1023 — frac{{15}}{8})
Тогда площадь закрашенной фигуры:
(S = Fleft( { — 9} right) — Fleft( { — 11} right) = — 1017 — frac{{15}}{8} — left( { — 1023 — frac{{15}}{8}} right) = 6)
Ответ: 6.
Комментарии для сайта Cackle
Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.
Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.
Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.
Задачи из сборников Ященко, 2021 год
Квадратные уравнения
Показательные уравнения
Логарифмические уравнения
Модуль числа
Уравнения с модулем
Тригонометрический круг
Формулы тригонометрии
Формулы приведения
Простейшие тригонометрические уравнения 1
Простейшие тригонометрические уравнения 2
Тригонометрические уравнения
Что необходимо помнить при решении уравнений?
1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если
2) Стараемся записывать решение в виде цепочки равносильных переходов.
3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.
4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.
5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где
— целое, а найти надо корни на отрезке
На указанном промежутке лежит точка
. От нее и будем отсчитывать. Получим:
6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!
Давайте потренируемся.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Упростим левую часть по формуле приведения.
Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Видим, что указанному отрезку принадлежат решения
Ответ:
Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где
— целое, а найти надо корни на отрезке
На указанном промежутке лежит точка
От нее и отсчитываем.
Получим:
2. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.
а)
Степени равны, их основания равны. Значит, равны и показатели.
Это ответ в пункте (а).
б) Отберем корни, принадлежащие отрезку
Отметим на тригонометрическом круге отрезок и найденные серии решений.
Видим, что указанному отрезку принадлежат точки и
из серии
Точки серии не входят в указанный отрезок.
А из серии в указанный отрезок входит точка
Ответ в пункте (б):
3. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а)
Применим формулу косинуса двойного угла:
Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.
Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.
б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.
Сначала серия
Теперь серия
Ответ: .
Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».
Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.
Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке
Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.
4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие
появляется, поскольку в уравнении есть
ОДЗ:
Уравнение равносильно системе:
Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси
.
Ответ в пункте а)
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки
и
5. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Это значит, что уравнение равносильно системе:
Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или
. Заметим, что среди них находятся и углы, для которых
Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие
. Остальные серии решений нас устраивают.
Тогда в ответ в пункте (а) войдут серии решений:
б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.
На отрезке нам подходит корень
.
На отрезке нам подходят корни
.
На отрезке — корни
Ответ в пункте б):
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
| 3069 | а) Решите уравнение 2sin^3(pi+x)=1/2cos(x-(3pi)/2) б) Найдите все корни уравнения, принадлежащие отрезку [-(7pi)/2; -(5pi)/2]. |
а) Решите уравнение 2sin 3 (pi +x) =1/2 cos(x — 3/2 pi) ! 36 вариантов ФИПИ Ященко 2022 Вариант 1 Задание 12 | |
| 3068 | Решите неравенство (4^x-5*2^x)^2-20(4^x-5*2^x) <= 96 |
Решите неравенство (4 x -5 2 x) 2 -20(4 x-5 2 x) <= 96 ! 36 вариантов ФИПИ Ященко 2022 Вариант 1 Задание 14 | |
| 2859 | Решите неравенство (25^x-4*5^x)^2+8*5^x < 2*25^x+15 |
Решите неравенство (25 x -4 5 x) 2 + 8 5 x < 2 25 x + 15 ! ЕГЭ по математике профильного уровня 07-06-2021 основная волна Задание 15 (15.3) # Математика 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 2 Задание 14 | |
| 2549 | а) Решите уравнение sin^4(x/4)-cos^4(x/4)=cos(x-pi/2) б) Найдите все корни этого уравнения, принадлежащие отрезку [-(3pi)/2; pi]. |
Решите уравнение sin^4(x/4) -cos^4(x/4) = cos(x-pi/2) ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 12 #36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 13 | |
| 2548 | Решите неравенство (2*0.5^(x+2)-0.5*2^(x+2)). (2log_{0.5)^2(x+2)-0.5log_{2}(x+2)) <= 0. |
Решите неравенство (2*0.5^(x+2)- 0.5*2^(x+ 2)) (2log^2_{0.5)(x+2)- 0.5log_{2}(x+ 2)) <= 0 ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 14 #36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 15 | |
| 2543 | Решите неравенство lg^4(x^2-26)^4-4lg^2(x^2-26)^2 <= 240. |
Решите неравенство lg^4(x^2 -26)^4 -4lg^2(x^2 -26)^2 <= 240 ! 36 вариантов ФИПИ Ященко 2022 Вариант 14 Задание 14 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 4 Задание 15 | |
| 2532 | а) Решите уравнение (x^2+2x-1)(log_{2}(x^2-3)+log_{0.5}(sqrt(3)-x))=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [-2.5; -1.5] |
Решите уравнение (x^2+ 2x -1)(log_{2}(x^2 -3)+ log_{0.5}(sqrt(3) -x))=0 ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 3 Задание 13 | |
| 2531 | Решите неравенство (4^(x-0.5)+1)/(9*4^x-16^(x+0.5)-2) <= 0.5 |
Решите неравенство (4^(x-0,5)+ 1)/ (9*4^x-16^(x+0,5) -2) <= 0,5 ! 36 вариантов ФИПИ Ященко 2022 Вариант 13 Задание 14 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 3 Задание 15 | |
| 2524 | Решите неравенство x^2*log_{243}(-x-3) >= log_{3}(x^2+6x+9) |
Решите неравенство x^2* log_{243}(-x- 3) >= log_{3}(x^2+ 6x+9) ! 36 вариантов ФИПИ Ященко 2022 Вариант 12 Задание 14 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 2 Задание 15 # Задача-Аналог 2367 | |
Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного , отсекает треугольник, периметр которого равен
. Найдите периметр трапеции.
Объём параллелепипеда равен
. Найдите объём треугольной пирамиды
3
Задание 3. Классическое определение вероятности
4
Задание 4. Вероятности сложных событий
Элина и Алмаз(физик) решили поиграть в боулинг. Элина справедливо прикинула, что в среднем она выбивает страйк один раз в десять бросков. Алмаз справедливо прикинул, что в среднем он выбивает страйк один раз в восемь бросков. Элина и Алмаз делают ровно по одному броску (независимо от результата). Какова вероятность того, что среди них не будет страйков?
5
Задание 5. Тригонометрические уравнения
Найдите наименьший положительный корень уравнения: .
6
Задание 6. Преобразование буквенных иррациональных выражений
Найдите значение выражения: при
.
7
Задание 7. Первообразная
8
Задание 8. Тригонометрические уравнения и неравенства
9
Задание 9. Задачи на движение по воде
10
Задание 10. Кусочно-линейная функция
На рисунке изображены часть графика функции Найдите
11
Задание 11. Сложные функции
Найдите наибольшее значение функции на отрезке
12
Задание 12. Тригонометрические уравнения
а)Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
13
Задание 13. Расстояние от точки до плоскости
14
Задание 14. Смешаные неравенства
Решите неравенство:
Сбербанк в течение трёх лет в конце каждого года увеличивает сумму, имеющуюся на вкладе, на А банк Тинькофф увеличивает эту сумму на
в течение каждого из первых двух лет. Найдите наименьшее целое число процентов за третий год по вкладу в Тинькофф банке, при котором за все три года этот вклад всё ещё останется выгоднее вклада в Сбербанке.
16
Задание 16. Многоугольники и их свойства
17
Задание 17. Системы с параметром
Найдите все значения , при каждом из которых система уравнений имеет ровно три различных решения:
18
Задание 18. Числа и их свойства
В каждой клетке квадратной таблицы стоит натуральное число, меньшее
. Вася в каждом столбце находит сумму чисел и из полученных сумм выбирает наименьшую. Петя в каждой строке находит сумму чисел и из полученных сумм выбирает наименьшую.
а) Может ли число у Пети получиться в три раза больше, чем число у Васи?
б) Может ли число у Пети получиться в пять раз больше, чем число у Васи?
в) В какое наибольшее число раз число у Пети может быть больше, чем число у Васи?
Отличная работа!
Так держать!
Если остались вопросы, напиши своему куратору.
Нужно авторизоваться
Нужно авторизоваться
Введите больше 6 символов
На почту 12345@mail.ru отправлена ссылка для сброса пароля.
Пожалуйста, подтвердите ваш номер телефона
Пополнение
счёта
Курс заблокирован
К сожалению, данный курс заблокирован. Необходимо внести доплату
Вывод
средств
Ваше задание
подтверждено!
успешно
Теперь вы можете приступить
к следующему уроку
курса по математике
Перейти к уроку
Подтверждение
замены
Для смены номера телефона
мы отправили Вам код по СМС,
введите его в поле ниже.
Подтвердить
Ты включаешь автопродление — 25-го числа каждого месяца доступ к купленным курсам будет автоматически продлеваться. Деньги будут списываться с одной из привязанных к учетной записи банковских карт. Управлять автопродлением можно из раздела «Финансы»
Для активации регулярного платежа мы спишем небольшую сумму с карты и сразу её вернем
Вы дествительно хотите отменить автопродление?
Благодарим за покупку!
В ближайшее время курс будет доступен в разделе Моё обучение
Материалы будут доступны за сутки до начала урока
Чат будет доступен после выдачи домашнего задания
Укажите вашу электронную почту
Мы используем cookie. Это позволяет нам анализировать взаимодействие посетителей с сайтом и делать его лучше. Продолжая пользоваться сайтом, вы соглашаетесь с использованием файлов cookie. Для лучшей работоспособности сайта просим вас отключить AdBlock.
OK