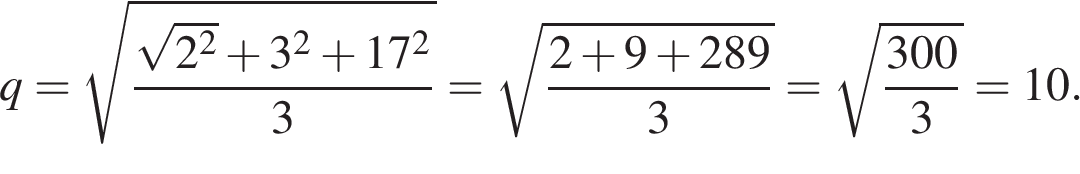Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
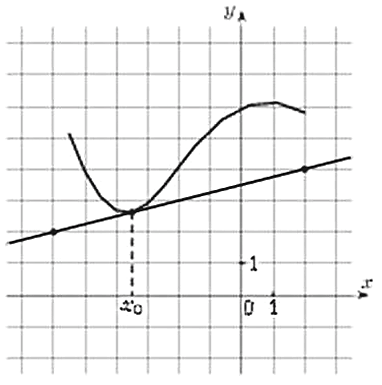
На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 6x или совпадает с ней.
Спрятать решение
Решение.
Поскольку касательная параллельна прямой y = 6x или совпадает с ней, она имеет угловой коэффициент равный 6. Значение производной в точке касания равно угловому коэффициенту касательной. Осталось найти, в какой точке x производная принимает значение 6: искомая точка x = 5.
Ответ: 5.
Тренировочные варианты профильного ЕГЭ 2022 по математике с ответами.admin2022-04-17T20:59:36+03:00
Варият ЕГЭ 2016г. Базовы.
Учитель математики Магометова Х. Н.
1. Задание 1 Вычислите:
Пояснение.
Найдём значение выражения:
Ответ: 2,65.
2. Задание 2 .
Найдите значение выражения .
Пояснение.
Выполним преобразования:
Ответ: 80.
3. Задание 3 В начале года число абонентов телефонной компании «Восток» составляло 400 тыс. человек, а в конце года их стало 480 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
Пояснение.
Число абонентов компании «Восток» к концу года увеличилось на 480 − 400 = 80 тыс. человек. Значит, число абонентов компании увеличилось на 80 : 400 · 100% = 20%.
Ответ: 20
4. Задание 4 № 506737. Среднее квадратическое трёх чисел и
вычисляется по формуле
. Найдите среднее квадратичное чисел
и
.
Пояснение.
Найдём среднее квадратичное число:
Ответ: 10.
5. Задание 5 . Найдите , если
.
Пояснение.
Выполним преобразования:
.
Ответ: -14.
6. Задание 6 Баночка йогурта стоит 14 рублей 60 копеек. Какое наибольшее количество баночек йогурта можно купить на 100 рублей?
Пояснение.
Разделим 100 на 14,6:
Следовательно, на 100 рублей можно приобрести 6 баночек йогурта.
Ответ: 6.
7. Задание 7 . Найдите корень уравнения .
Пояснение.
Перейдем к одному основанию степени:
Ответ: −1.
8. Задание 8
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
Пояснение.
Участок, изображенный на плане, представляет собой прямоугольник, площадь которого равна произведению длин его сторон. Таким образом площадь участка: 3 · 3 − 1= 8.
Ответ: 8.
9. Задание 9 . Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
|
ВЕЛИЧИНЫ |
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
|
|
А) площадь территории России Б) площадь поверхности тумбочки В) площадь почтовой марки Г) площадь баскетбольной площадки |
1) 364 кв. м 2) 0,2 кв. м 3) 17,1 млн. кв. км 4) 6,8 кв. см |
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Пояснение.
Площадь России колоссальна и составляет 17,1 млн. кв. км, площадь баскетбольной площадки ориентировочно 364 кв. м., площадь поверхности тумбочки 0,2 кв. м = 2000 кв. см., а площадь почтовой марки навскидку 6,8 кв. см. Получили соответствие А — 3, Г — 1, Б — 2 и В — 4. Окончательно получим 3241.
Ответ: 3241.
10. Задание 10 . В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно один раз
Пояснение.
Равновозможны 8 исходов эксперимента: орел-орел-орёл, орел-орёл-решка, орёл-решка-орел, орёл-решка-решка решка-орёл-решка, решка-орёл-орёл, решка-решка-орёл, решка-решка-решка. Орел выпадает ровно один раз в трёх случаях: решка-решка-орёл, решка-орел-решка, орёл-решка-решка. Поэтому вероятность того, что орел выпадет ровно 1 раз, равна
.
Ответ: 0,375.
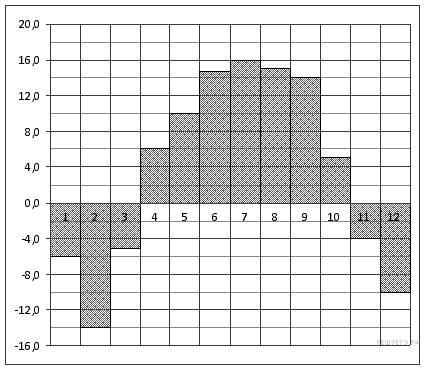
11. Задание 11 . На диаграмме показана среднемесячная температура в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году. Ответ дайте в градусах Цельсия.
Пояснение.
Из диаграммы видно, что наименьшая среднемесячная температура составляет −14 °C (см. рисунок).
Ответ: −14.
12. Задание 12 . В таблице указаны средние цены (в рублях) на некоторые основные продукты питания в трех городах России (по данным на начало 2010 года).
|
Наименование продукта |
Тверь |
Липецк |
Барнаул |
|
Пшеничный хлеб (батон) |
11 |
12 |
14 |
|
Молоко (1 литр) |
26 |
23 |
25 |
|
Картофель (1 кг) |
9 |
13 |
16 |
|
Сыр (1 кг) |
240 |
215 |
260 |
|
Мясо (говядина) (1 кг) |
260 |
280 |
300 |
|
Подсолнечное масло (1 литр) |
38 |
44 |
50 |
Определите, в каком из этих городов окажется самым дешевым следующий набор продуктов: 2 батона пшеничного хлеба, 3 кг картофеля, 1,5 кг говядины, 1 л подсолнечного масла. В ответ запишите стоимость данного набора продуктов в этом городе (в рублях).
Пояснение.
В Твери стоимость 2 батонов пшеничного хлеба, 3 кг картофеля, 1,5 кг говядины, 1 л подсолнечного масла составит 11 2 + 9
3 + 1,5
260 + 1
38 = 477 руб.
В Липецке стоимость 2 батонов пшеничного хлеба, 3 кг картофеля, 1,5 кг говядины, 1 л подсолнечного масла составит 12 2 + 13
3 + 1,5
280 + 1
44 = 527 руб.
В Барнауле стоимость 2 батонов пшеничного хлеба, 3 кг картофеля, 1,5 кг говядины, 1 л подсолнечного масла составит 14 2 + 16
3 + 1,5
300 + 1
50 = 576 руб.
Самый дешёвый набор продуктов можно купить в Твери по цене 477 руб.
13. Задание 13 .
Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
Пояснение.
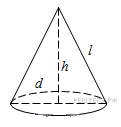
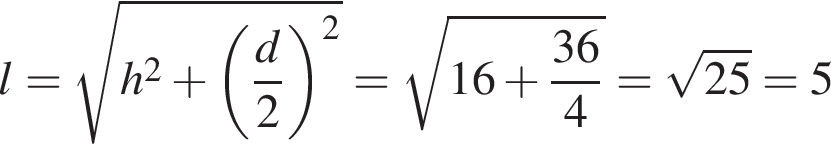
Ответ: 5.
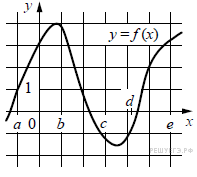
14. Задание 14 На рисунке изображён график функции y = f(x) . Точки a, b, c, d и e задают на оси Ox интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции или её производной.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения автомобиля на этом интервале.
|
ИНТЕРВАЛЫ ВРЕМЕНИ |
ХАРАКТЕРИСТИКИ |
|
|
А) ( a; b) Б) (b; c ) В) (c; d ) Г) ( d ; e) |
1) Значения функции положительны в каждой точке интервала. 2) Значения производной функции положительны в каждой точке интервала. 3) Значения функции отрицательны в каждой точке интервала. 4) Значения производной функции отрицательны в каждой точке интервала. |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Пояснение.
Если функция возрастает, то производная положительна и наоборот.
На интервале (a;b) значения функции положительны в каждой точке интервала.
На интервале (b;c) значения производной функции отрицательны в каждой точке интервала.
На интервале (c;d) значения функции отрицательны в каждой точке интервала.
На интервале (d;e) значения производной функции положительны в каждой точке интервала.
Таким образом, получаем соответствие А — 1, Б — 4, В — 3 и Г — 2.
Ответ: 1432.
15. Задание 15
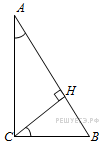
,
. Найдите высоту CH.
Пояснение.
Последовательно получаем:
.
Ответ: 25,2.
6. Задание 16 . 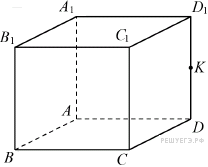
ребро CC1 = 2. Точка K — середина ребра DD1. Найдите площадь сечения, проходящего через точки C1, B1 и К
Пояснение.
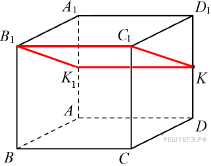
— параллелограмм. Кроме того, ребро
перпендикулярно граням
и
, поэтому углы
и
— прямые. Следовательно, сечение
— прямоугольник.
Из прямоугольного треугольника по теореме Пифагора найдем
Тогда площадь прямоугольника равна:
Ответ:5.
17. Задание 17 На координатной прямой отмечены числа и
:
Расположите числа в порядке возрастания:
Пояснение.
Заметим, что , тогда
, а
Ответ: 4132.
18. Задание 18 Школа приобрела стол, доску, магнитофон и принтер. Известно, что принтер дороже магнитофона, а доска дешевле магнитофона и дешевле стола. Выберите утверждения, которые следуют из приведённых данных.
1) Магнитофон дешевле стола.
2) Принтер дороже доски.
3) Доска — самая дешёвая из покупок.
4) Принтер и стол точно не стоят одинаково.
В ответе запишите номера выбранных утверждений без пробелов, запятых и
других дополнительных символов.
Пояснение.
П М Д
1) И магнитофон, и стол дороже доски. Больше про зависимость между ними ничего не сказано.
2) Принтер дороже магнитофона, а магнитофон дороже доски. Значит, принтер дороже доски.
3) Да, так как все остальные вещи дороже неё.
4) Они могут стоить одинаково.
19. Задание 19 . Приведите пример трёхзначного натурального числа, большего 600, которое при делении на 4, на 5 и на 6 даёт в остатке 3 и цифры которого расположены в порядке убывания слева направо. В ответе укажите ровно одно такое число.
Пояснение.
Так как число даёт одинаковый остаток по модулям 4, 5 и 6, то оно также даёт такой же остаток и по модулю 60. То есть число имеет вид Все такие числа: 603, 663, 723, 783, 843, 903, 963. Из них подходят под последнее условие только 843 и 963.
20. Задание 20 Хозяин договорился с рабочими, что они копают колодец на следующих условиях: за первый метр он заплатит им 3500 рублей, а за каждый следующий метр — на 1600 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 9 метров?
Пояснение.
Последовательность цен за метр — арифметическая прогрессия с первым элементом и разностью
Сумма первых
элементов арифметической прогрессии —
То есть в нашем случае имеем
Ответ: 89100
Новый тренировочный вариант №41054182 решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
скачать вариант ЕГЭ 2022
скачать ответы и решения
Решу ЕГЭ 2022 по математике профиль тренировочный вариант №41054182
Ответы и решения для варианта:
Задание 2 решу ЕГЭ № 1001 На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный вопрос.
Ответ: 0,95
Задание 3 решу ЕГЭ № 27913 Сторона ромба равна 1, острый угол равен 30 градусов. Найдите радиус вписанной окружности этого ромба.
Ответ: 0,25
Задание 6 решу ЕГЭ № 515183 На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 6x или совпадает с ней.
Ответ: 5
Задание 8 решу ЕГЭ № 99595 Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?
Ответ: 12
Задание 10 решу ЕГЭ № 320177 Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства— яйца высшей категории, а из второго хозяйства— 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Ответ: 0,75
Задание 13 решу ЕГЭ № 514655 В основании прямой треугольной призмы ABCA1B1C1 лежит прямоугольный треугольник ABC с прямым углом C, AC = 4, BC = 16, Точка Q — середина ребра A1B1 , а точка P делит ребро B1C1 в отношении 1:2, считая от вершины C1 . Плоскость APQ пересекает ребро CC1 в точке M. а) Докажите, что точка M является серединой ребра CC1 . б) Найдите расстояние от точки A1 до плоскости APQ.
Задание 15 решу ЕГЭ № 513923 В июле 2016 года планируется взять кредит в размере 4,2 млн. руб. Условия возврата таковы: — каждый январь долг возрастает на r% по сравнению с концом предыдущего года. — с февраля по июнь необходимо выплатить часть долга. — в июле 2017, 2018 и 2019 годов долг остается равным 4,2 млн. руб. — суммы выплат 2020 и 2021 годов равны. Найдите r, если в 2021 году долг будет выплачен полностью и общие выплаты составят 6,1 млн. рублей.
Ответ: 10
Задание 16 решу ЕГЭ № 509467 В прямоугольном треугольнике ABC с прямым углом C известны стороны AC = 12, BC = 5. Окружность радиуса с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности. а) Докажите, что радиус второй окружности меньше, чем длины катета AC. б) Найдите радиус второй окружности.
Ответ: 2
Задание 18 решу ЕГЭ № 505503 а) Можно ли число 2014 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр? б) Можно ли число 199 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр? в) Найдите наименьшее натуральное число, которое можно представить в виде суммы пяти различных натуральных чисел с одинаковой суммой цифр.
Ответ: а) да; б) нет; в) 110.
Другие тренировочные варианты ЕГЭ 2022 по математике:
Тренировочные варианты ЕГЭ по математике 11 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Задания
Версия для печати и копирования в MS Word
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Спрятать решение
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; 4), B (2; 2), С (−6; 2). Угол наклона касательной к оси абсцисс будет равен углу ABC. Поэтому
Ответ: 0,25.
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Гость 11.05.2012 21:01
Разве не должно быть -0,25?
Служба поддержки
Проверяйте знак так: угол наклона острый, значит, его тангенс положительный.
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-20

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Дата: 2015-07-28
516
Категория: Производная
Метка: ЕГЭ-№7
27504. На рисунке изображены график функции у=f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках
A(2; 4), B(2; 2), C(–6; 2)
Углом наклона касательной к оси абсцисс будет угол АВС. Поэтому
Ответ: 0,25
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
Подборка по базе: Творческие задания социальная педагогика (3).pdf, Письменные задания для практических занятий.pdf, 11кл Олимпиадные задания по биологии.doc, 10 класс сайты для подготовки по АЛГЕБРЕ.docx, Письменные задания (1).docx, Практические задания к теме 3 (доработанное).docx, Учебные задания проверяемые вручную.docx, Пример 6 задания.docx, Практические задания.docx, Практическое занятие 11. Задания 2-4, 6-7_ просмотр попытки.pdf
1. Тип 7 № 119975
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
2. Тип 7 №
119976
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
3. Тип 7 №
119977
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени
с.
4. Тип 7 №
119978
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
5. Тип 7 №
119979
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?
6. Тип 7 №
501059

Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).
1. Тип 7 №
27489

2. Тип 7 №
27501

3. Тип 7 №
27503

4. Тип 7 №
510384

5. Тип 7 №
510403

6. Тип 7 №
510938

7. Тип 7 №
27504
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
8. Тип 7 №
27505
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
9. Тип 7 №
27506
На рисунке изображён график функции и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
10. Тип 7 №
40129
На рисунке изображен график функции y = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите
11. Тип 7 №
40130
На рисунке изображен график производной функции Найдите абсциссу точки, в которой касательная к графику
параллельна прямой
или совпадает с ней.
12. Тип 7 №
40131
На рисунке изображен график производной функции Найдите абсциссу точки, в которой касательная к графику
параллельна оси абсцисс или совпадает с ней.
13. Тип 7 №
27485
Прямая параллельна касательной к графику функции
Найдите абсциссу точки касания.
14. Тип 7 №
27486
Прямая является касательной к графику функции
Найдите абсциссу точки касания.
15. Тип 7 №
119972
Прямая y = 3x + 1 является касательной к графику функции ax2 + 2x + 3. Найдите a.
16. Тип 7 №
119974
Прямая является касательной к графику функции
Найдите
17. Тип 7 №
119973
Прямая является касательной к графику функции
Найдите b, учитывая, что абсцисса точки касания больше 0.
18. Тип 7 №
515183
На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 6x или совпадает с ней.
19. Тип 7 №
525688
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Найдите значение производной функции g(x) = 6f(x) − 3x в точке x0.
20. Тип 7 №
525689
На рисунке изображены график функции и касательная к этому графику, проведённая в точке
Найдите значение производной функции
в точке x0.
21. Тип 7 №
525690

На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение производной функции
в точке x0.
22. Тип 7 №
525691
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение функции
в точке x0.
23. Тип 7 №
525698
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение производной функции
в точке x0.
24. Тип 7 №
525699
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Найдите значение производной функции
в точке x0.
Тема 1.
Исключение двух терминов (любой блок)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
исключение двух терминов (любой блок)
1.01Политика
1.02Право
1.03Социология
1.04Человек и общество
1.05Экономика
Решаем задачу:
Ниже приведён перечень терминов. Все они, за исключением двух, относятся к отличительным признакам научного знания.
1) объективность; 2) проверяемость знаний; 3) образность; 4) системность; 5) логичность; 6) опора на религиозные верования.
Найдите два примера, “выпадающих” из общего ряда, и запишите цифры, под которыми они указаны.
Показать ответ и решение
Для выполнения данного задания повторите тему “Наука”.
Наука — форма духовной деятельности людей, направленная на производство знаний о природе, человеке и обществе, на постижение истины и открытия объективных законов.
Особенности научного познания: рациональность, объективность, использование специальных способов и методов, специального языка, доказательность, проверяемость, системность, универсальность.
Вернемся к тексту задания: образность и опора на религиозные верования не являются отличительными признаками научного знания. Образность характерна для художественного познания, а опора на религиозные верования для религиозного познания.
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
Зарегистрирован: 10 июн 2010, 15:00 |
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
Зарегистрирован: 06 май 2012, 21:09 |
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
Зарегистрирован: 18 ноя 2015, 07:49 |
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
Skip to content
ЕГЭ профильный уровень. №7 Геометрический смысл производной, касательная. Задача 2
ЕГЭ профильный уровень. №7 Геометрический смысл производной, касательная. Задача 2admin2023-03-11T19:34:48+03:00
Задача 2. Прямая (y = — 2x + 6) является касательной к графику функции (y = {x^3} — 3{x^2} + x + 5). Найдите абсциссу точки касания.
Чтобы прямая (y = — 2x + 6) была касательной (в какой-либо точке) к графику функции (y = {x^3} — 3{x^2} + x + 5), производная от неё должна быть равна угловому коэффициенту касательной, то есть, ( — 2) (коэффициент перед x):
(y’ = {left( {{x^3} — 3{x^2} + x + 5} right)^prime } = 3{x^2} — 6x + 1)
(3{x^2} — 6x + 1 = — 2,,,,,, Leftrightarrow ,,,,,3{x^2} — 6x + 3 = 0,,,,, Leftrightarrow ,,,,,x = 1.)
Проверим, является ли найденная точка действительно точкой касания. Для этого найдём значение прямой (y = — 2x + 6) и функции (y = {x^3} — 3{x^2} + x + 5) в точке (x = 1:)
(yleft( 1 right) = — 2 cdot 1 + 6 = 4)
(yleft( 1 right) = {1^3} — 3 cdot {1^2} + 1 + 5 = 4)
Так как найденные значения равны, то (x = 1) является искомой точкой касания.
Ответ: 1.
ЕГЭ профильный уровень. №7 Первообразная. Задача 4
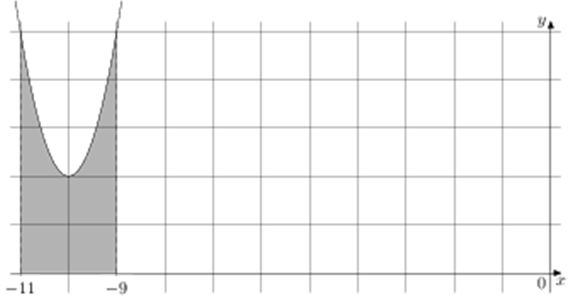
ОТВЕТ: 6.
Площадь закрашенной фигуры равна интегралу (intlimits_{ — 11}^{ — 9} {left( x right)dx} = Fleft( { — 9} right) — Fleft( { — 11} right).) Найдём значение первообразной в точках – 9 и – 11:
(Fleft( { — 9} right) = {left( { — 9} right)^3} + 30 cdot {left( { — 9} right)^2} + 302 cdot left( { — 9} right) — frac{{15}}{8} = — 729 + 2430 — 2718 — frac{{15}}{8} = — 1017 — frac{{15}}{8})
(Fleft( { — 11} right) = {left( { — 11} right)^3} + 30 cdot {left( { — 11} right)^2} + 302 cdot left( { — 11} right) — frac{{15}}{8} = — 1331 + 3630 — 3322 — frac{{15}}{8} = — 1023 — frac{{15}}{8})
Тогда площадь закрашенной фигуры:
(S = Fleft( { — 9} right) — Fleft( { — 11} right) = — 1017 — frac{{15}}{8} — left( { — 1023 — frac{{15}}{8}} right) = 6)
Ответ: 6.
Комментарии для сайта Cackle
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
|
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
|
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
Решу егэ профиль математика 517739
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Задание 12 № 517747
Ответ а 3 и 27; б 3.
Ege. sdamgia. ru
12.01.2020 13:48:01
2020-01-12 13:48:01
Источники:
Https://ege. sdamgia. ru/test? likes=517739
Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Б Заметим, что Значит, указанному отрезку принадлежит корень 3.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Dankonoy. com
16.06.2020 6:45:22
2020-06-16 06:45:22
Источники:
Https://dankonoy. com/ege/ege11/archives/10087
Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Материал для подготовки к экзамену по математике 1 курс
Материал для подготовки к экзамену по математике 1 курс.
Материал для подготовки к экзамену по математике для 1 курса СПО.
Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»
Логарифмические уравнения
1. Задание 5 № 26646
Найдите корень уравнения
2. Задание 5 № 26647
Найдите корень уравнения
3. Задание 5 № 26648
Найдите корень уравнения
4. Задание 5 № 26649
Найдите корень уравнения
5. Задание 5 № 26657
Найдите корень уравнения
6. Задание 5 № 26658
Найдите корень уравнения
7. Задание 5 № 26659
Найдите корень уравнения
8. Задание 5 № 77380
Решите уравнение
9. Задание 5 № 77381
Решите уравнение
10. Задание 5 № 77382
Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11. Задание 5 № 315120
Найдите корень уравнения
12. Задание 5 № 315535
Найдите корень уравнения
13. Задание 5 № 525399
Решите уравнение
Тригонометрические уравнения
1. Задание 5 № 26669
Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.

Значениям соответствуют положительные корни.
Если, то и
Если, то и
Значениям соответствуют меньшие значения корней.
Следовательно, наибольшим отрицательным корнем является число
2. Задание 5 № 77376
Решите уравнение В ответе напишите наибольший отрицательный корень.
Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.
3. Задание 5 № 77377
Решите уравнение В ответе напишите наименьший положительный корень.
Значениям соответствуют отрицательные корни.
Если, то и
Если, то и
Значениям соответствуют большие положительные корни.
Наименьшим положительным решением является 0,5.
Преобразования числовых логарифмических выражений
1. Задание 9 № 26843
Найдите значение выражения
2. Задание 9 № 26844
Найдите значение выражения
3. Задание 9 № 26845
Найдите значение выражения
4. Задание 9 № 26846
Найдите значение выражения
5. Задание 9 № 26847
Найдите значение выражения
6. Задание 9 № 26848
Найдите значение выражения
7. Задание 9 № 26849
Найдите значение выражения
8. Задание 9 № 26850
Найдите значение выражения
9. Задание 9 № 26851
Найдите значение выражения
10. Задание 9 № 26852
Найдите значение выражения
11. Задание 9 № 26853
Найдите значение выражения
12. Задание 9 № 26854
Найдите значение выражения
13. Задание 9 № 26855
Найдите значение выражения
14. Задание 9 № 26856
Найдите значение выражения
15. Задание 9 № 26857
Найдите значение выражения
16. Задание 9 № 26858
Найдите значение выражения
17. Задание 9 № 26859
Найдите значение выражения
18. Задание 9 № 26860
Найдите значение выражения
19. Задание 9 № 26861
Найдите значение выражения
20. Задание 9 № 26862
Найдите значение выражения
21. Задание 9 № 26882
Найдите значение выражения
22. Задание 9 № 26883
Найдите значение выражения
23. Задание 9 № 26885
Найдите значение выражения
24. Задание 9 № 26889
Найдите значение выражения
25. Задание 9 № 26892
Найдите значение выражения
26. Задание 9 № 26893
Найдите значение выражения
27. Задание 9 № 26894
Найдите значение выражения
28. Задание 9 № 26896
Найдите значение выражения
29. Задание 9 № 77418
Вычислите значение выражения:
30. Задание 9 № 505097
Найдите значение выражения
31. Задание 9 № 509086
Найдите значение выражения
32. Задание 9 № 510939
Найдите значение выражения
33. Задание 9 № 525403
Найдите значение выражения
Вычисление значений тригонометрических выражений
1. Задание 9 № 26775
Найдите, если и
2. Задание 9 № 26776
Найдите, если и
3. Задание 9 № 26777
Найдите, если и
4. Задание 9 № 26778
Найдите, если и
5. Задание 9 № 26779
Найдите, если
6. Задание 9 № 26780
Найдите, если
7. Задание 9 № 26783
Найдите значение выражения, если
8. Задание 9 № 26784
Найдите, если и
9. Задание 9 № 26785
Найдите, если и
10. Задание 9 № 26786
Найдите, если
11. Задание 9 № 26787
Найдите, если
12. Задание 9 № 26788
Найдите, если
13. Задание 9 № 26789
Найдите, если
14. Задание 9 № 26790
Найдите, если
15. Задание 9 № 26791
Найдите, если
16. Задание 9 № 26792
Найдите значение выражения, если
17. Задание 9 № 26793
Найдите значение выражения, если
18. Задание 9 № 26794
Найдите, если
19. Задание 9 № 316350
Найдите, если
20. Задание 9 № 501598
Найдите значение выражения
21. Задание 9 № 502014
Найдите значение выражения
22. Задание 9 № 502045
Найдите значение выражения
23. Задание 9 № 502106
Найдите значение выражения
24. Задание 9 № 502285
Найдите значение выражения
25. Задание 9 № 502305
Найдите значение выражения если и
26. Задание 9 № 504410
Найдите значение выражения:
27. Задание 9 № 504824
Найдите значение выражения
28. Задание 9 № 508966
Найдите если
29. Задание 9 № 510424
Найдите если и
30. Задание 9 № 549336
Найдите если и
Преобразования числовых тригонометрических выражений
1. Задание 9 № 26755
Найдите значение выражения
2. Задание 9 № 26756
Найдите значение выражения
3. Задание 9 № 26757
Найдите значение выражения
4. Задание 9 № 26758
Найдите значение выражения
5. Задание 9 № 26759
Найдите значение выражения
6. Задание 9 № 26760
Найдите значение выражения
7. Задание 9 № 26761
Найдите значение выражения
8. Задание 9 № 26762
Найдите значение выражения
9. Задание 9 № 26763
Найдите значение выражения
10. Задание 9 № 26764
Найдите значение выражения
11. Задание 9 № 26765
Найдите значение выражения
12. Задание 9 № 26766
Найдите значение выражения
13. Задание 9 № 26767
Найдите значение выражения
14. Задание 9 № 26769
Найдите значение выражения
15. Задание 9 № 26770
Найдите значение выражения
16. Задание 9 № 26771
Найдите значение выражения
17. Задание 9 № 26772
Найдите значение выражения
18. Задание 9 № 26773
Найдите значение выражения
19. Задание 9 № 26774
Найдите значение выражения
20. Задание 9 № 77412
Найдите значение выражения
21. Задание 9 № 77413
Найдите значение выражения
22. Задание 9 № 77414
Найдите значение выражения:
23. Задание 9 № 245169
Найдите значение выражения
24. Задание 9 № 245170
Найдите значение выражения
25. Задание 9 № 245171
Найдите значение выражения
26. Задание 9 № 245172
Найдите значение выражения
27. Задание 9 № 501701
Найдите значение выражения
28. Задание 9 № 502994
Найдите значение выражения
29. Задание 9 № 503310
Найдите значения выражения
30. Задание 9 № 510013
Найдите если и
31. Задание 9 № 510312
Найдите значение выражения
32. Задание 9 № 510386
Найдите значение выражения
33. Задание 9 № 510405
Найдите значение выражения
34. Задание 9 № 510824
Найдите значение выражения
35. Задание 9 № 510843
Найдите значение выражения
36. Задание 9 № 525113
Найдите значение выражения
37. Задание 9 № 526009
Найдите значение выражения
Логарифмические и показательные уравнения
1. Задание 13 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
2. Задание 13 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
3. Задание 13 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
4. Задание 13 № 516760
А) Решите уравнение:
Б) Определите, какие из его корней принадлежат отрезку
5. Задание 13 № 514623
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
6. Задание 13 № 502053
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
7. Задание 13 № 525377
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
8. Задание 13 № 513605
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
9. Задание 13 № 503127
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
10. Задание 13 № 514081
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащего отрезку
11. Задание 13 № 502999
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].
12. Задание 13 № 528517
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
13. Задание 13 № 550261
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие промежутку
14. Задание 13 № 555265
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
15. Задание 13 № 555583
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
16. Задание 13 № 561853
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].
17. Задание 13 № 562032
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].
18. Задание 13 № 562757
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
б) Укажите корни этого уравнения, принадлежащие отрезку
Решите уравнение В ответе напишите наименьший положительный корень.
Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»
Б Укажите корни этого уравнения, принадлежащие отрезку.
Multiurok. ru
06.02.2020 18:29:01
2020-02-06 18:29:01
Источники:
Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html