Задания
Версия для печати и копирования в MS Word
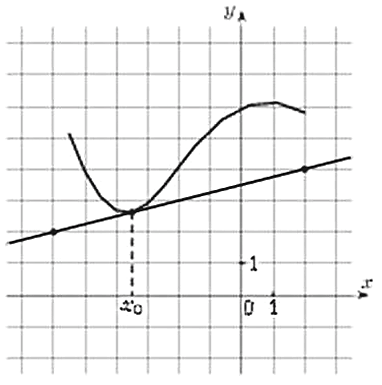
На рисунке изображены график функции
и касательная к этому графику, проведённая в точке x0. Найдите значение производной функции g(x) = 6f(x) − 3x в точке x0.
Спрятать решение
Решение.
Найдём производную функции g(x):
По рисунку найдём значение Значение производной в точке касания равно угловому коэффициенту касательной, который, в свою очередь, равен тангенсу угла наклона данной касательной к оси абсцисс. Поэтому
Тогда для искомого значения получаем
Ответ: −7.
Новый тренировочный вариант №41054180 решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
скачать вариант ЕГЭ 2022
скачать ответы и решения
Решу ЕГЭ 2022 по математике профиль тренировочный вариант №41054180
Ответы и решения для варианта:
Задание 2 решу ЕГЭ №320189 В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных.
Правильный ответ: 0,498
Задание 3 решу ЕГЭ № 27900 Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
Правильный ответ: 2
Задание 6 решу ЕГЭ № 525688 На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0 . Найдите значение производной функции g(x) = 6f(x) − 3x в точке x0.
Правильный ответ: -7
Задание 8 решу ЕГЭ № 99590 Расстояние между городами и равно 435 км. Из города в город со скоростью 60 км ч выехал первый автомобиль, а через час после этого навстречу ему из города выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города автомобили встретятся? Ответ дайте в километрах.
Правильный ответ: 240
Задание 10 решу ЕГЭ № 500998 В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Правильный ответ: 0,6
Задание 13 решу ЕГЭ № 508233 В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP. а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC. б) Найдите площадь сечения.
Правильный ответ: 3 корень из 3
Задание 15 решу ЕГЭ № 506956 Два брокера купили акции одного достоинства на сумму 3640 р. Когда цена на эти акции возросла, они продали часть акций на сумму 3927 р. Первый брокер продал 75% своих акций, а второй 80% своих. При этом сумма от продажи акций, полученная вторым брокером, на 140% превысила сумму, полученную первым брокером. На сколько процентов возросла цена одной акции?
Правильный ответ: 37,5
Задание 16 решу ЕГЭ № 514717 На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD. а) Докажите, что треугольник DCL равнобедренный. б) Известно, что В каком отношении прямая DL делит сторону AB?
Задание 18 решу ЕГЭ № 526295 В ящике лежат 73 овоща, масса каждого из которых выражается целым числом граммов. В ящике есть хотя бы два овоща различной массы, а средняя масса всех овощей равна 1000 г. Средняя масса овощей , масса каждого из которых меньше 1000 г, равна 988 г. Средняя масса овощей, масса каждого из которых больше 1000 г, равна 1030 г. а) Могло ли в ящике оказаться поровну овощей массой меньше 1000 г и овощей массой больше 1000 г? б) Могло ли в ящике оказаться ровно 11 овощей, масса каждого из которых равна 1000 г? в) Какую наименьшую массу может иметь овощ в этом ящике?
Правильный ответ: а) Нет; б) Нет; в) 449.
Другие тренировочные варианты ЕГЭ 2022 по математике:
28.09.2021 Математика 11 класс МА2110101-МА2110112 ЕГЭ 2022 работа статград ответы и задания
Тренировочный вариант №145 ЕГЭ 2022 по математике 11 класс профильный уровень с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Задания
Версия для печати и копирования в MS Word
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Спрятать решение
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; 4), B (2; 2), С (−6; 2). Угол наклона касательной к оси абсцисс будет равен углу ABC. Поэтому
Ответ: 0,25.
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Гость 11.05.2012 21:01
Разве не должно быть -0,25?
Служба поддержки
Проверяйте знак так: угол наклона острый, значит, его тангенс положительный.
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-20

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Дата: 2015-07-28
516
Категория: Производная
Метка: ЕГЭ-№7
27504. На рисунке изображены график функции у=f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках
A(2; 4), B(2; 2), C(–6; 2)
Углом наклона касательной к оси абсцисс будет угол АВС. Поэтому
Ответ: 0,25
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
Подборка по базе: Творческие задания социальная педагогика (3).pdf, Письменные задания для практических занятий.pdf, 11кл Олимпиадные задания по биологии.doc, 10 класс сайты для подготовки по АЛГЕБРЕ.docx, Письменные задания (1).docx, Практические задания к теме 3 (доработанное).docx, Учебные задания проверяемые вручную.docx, Пример 6 задания.docx, Практические задания.docx, Практическое занятие 11. Задания 2-4, 6-7_ просмотр попытки.pdf
1. Тип 7 № 119975
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
2. Тип 7 №
119976
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
3. Тип 7 №
119977
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени
с.
4. Тип 7 №
119978
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
5. Тип 7 №
119979
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?
6. Тип 7 №
501059

Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).
1. Тип 7 №
27489

2. Тип 7 №
27501

3. Тип 7 №
27503

4. Тип 7 №
510384

5. Тип 7 №
510403

6. Тип 7 №
510938

7. Тип 7 №
27504
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
8. Тип 7 №
27505
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
9. Тип 7 №
27506
На рисунке изображён график функции и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
10. Тип 7 №
40129
На рисунке изображен график функции y = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите
11. Тип 7 №
40130
На рисунке изображен график производной функции Найдите абсциссу точки, в которой касательная к графику
параллельна прямой
или совпадает с ней.
12. Тип 7 №
40131
На рисунке изображен график производной функции Найдите абсциссу точки, в которой касательная к графику
параллельна оси абсцисс или совпадает с ней.
13. Тип 7 №
27485
Прямая параллельна касательной к графику функции
Найдите абсциссу точки касания.
14. Тип 7 №
27486
Прямая является касательной к графику функции
Найдите абсциссу точки касания.
15. Тип 7 №
119972
Прямая y = 3x + 1 является касательной к графику функции ax2 + 2x + 3. Найдите a.
16. Тип 7 №
119974
Прямая является касательной к графику функции
Найдите
17. Тип 7 №
119973
Прямая является касательной к графику функции
Найдите b, учитывая, что абсцисса точки касания больше 0.
18. Тип 7 №
515183
На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 6x или совпадает с ней.
19. Тип 7 №
525688
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Найдите значение производной функции g(x) = 6f(x) − 3x в точке x0.
20. Тип 7 №
525689
На рисунке изображены график функции и касательная к этому графику, проведённая в точке
Найдите значение производной функции
в точке x0.
21. Тип 7 №
525690

На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение производной функции
в точке x0.
22. Тип 7 №
525691
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение функции
в точке x0.
23. Тип 7 №
525698
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение производной функции
в точке x0.
24. Тип 7 №
525699
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Найдите значение производной функции
в точке x0.
Тема 1.
Исключение двух терминов (любой блок)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
исключение двух терминов (любой блок)
1.01Политика
1.02Право
1.03Социология
1.04Человек и общество
1.05Экономика
Решаем задачу:
Ниже приведён перечень терминов. Все они, за исключением двух, относятся к отличительным признакам научного знания.
1) объективность; 2) проверяемость знаний; 3) образность; 4) системность; 5) логичность; 6) опора на религиозные верования.
Найдите два примера, “выпадающих” из общего ряда, и запишите цифры, под которыми они указаны.
Показать ответ и решение
Для выполнения данного задания повторите тему “Наука”.
Наука — форма духовной деятельности людей, направленная на производство знаний о природе, человеке и обществе, на постижение истины и открытия объективных законов.
Особенности научного познания: рациональность, объективность, использование специальных способов и методов, специального языка, доказательность, проверяемость, системность, универсальность.
Вернемся к тексту задания: образность и опора на религиозные верования не являются отличительными признаками научного знания. Образность характерна для художественного познания, а опора на религиозные верования для религиозного познания.
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
Зарегистрирован: 10 июн 2010, 15:00 |
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
Зарегистрирован: 06 май 2012, 21:09 |
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
Зарегистрирован: 18 ноя 2015, 07:49 |
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
Skip to content
ЕГЭ профильный уровень. №7 Геометрический смысл производной, касательная. Задача 2
ЕГЭ профильный уровень. №7 Геометрический смысл производной, касательная. Задача 2admin2023-03-11T19:34:48+03:00
Задача 2. Прямая (y = — 2x + 6) является касательной к графику функции (y = {x^3} — 3{x^2} + x + 5). Найдите абсциссу точки касания.
Чтобы прямая (y = — 2x + 6) была касательной (в какой-либо точке) к графику функции (y = {x^3} — 3{x^2} + x + 5), производная от неё должна быть равна угловому коэффициенту касательной, то есть, ( — 2) (коэффициент перед x):
(y’ = {left( {{x^3} — 3{x^2} + x + 5} right)^prime } = 3{x^2} — 6x + 1)
(3{x^2} — 6x + 1 = — 2,,,,,, Leftrightarrow ,,,,,3{x^2} — 6x + 3 = 0,,,,, Leftrightarrow ,,,,,x = 1.)
Проверим, является ли найденная точка действительно точкой касания. Для этого найдём значение прямой (y = — 2x + 6) и функции (y = {x^3} — 3{x^2} + x + 5) в точке (x = 1:)
(yleft( 1 right) = — 2 cdot 1 + 6 = 4)
(yleft( 1 right) = {1^3} — 3 cdot {1^2} + 1 + 5 = 4)
Так как найденные значения равны, то (x = 1) является искомой точкой касания.
Ответ: 1.
ЕГЭ профильный уровень. №7 Первообразная. Задача 4
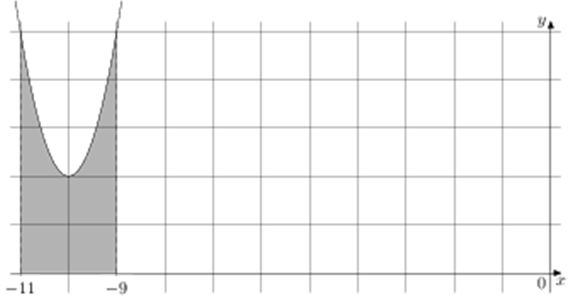
ОТВЕТ: 6.
Площадь закрашенной фигуры равна интегралу (intlimits_{ — 11}^{ — 9} {left( x right)dx} = Fleft( { — 9} right) — Fleft( { — 11} right).) Найдём значение первообразной в точках – 9 и – 11:
(Fleft( { — 9} right) = {left( { — 9} right)^3} + 30 cdot {left( { — 9} right)^2} + 302 cdot left( { — 9} right) — frac{{15}}{8} = — 729 + 2430 — 2718 — frac{{15}}{8} = — 1017 — frac{{15}}{8})
(Fleft( { — 11} right) = {left( { — 11} right)^3} + 30 cdot {left( { — 11} right)^2} + 302 cdot left( { — 11} right) — frac{{15}}{8} = — 1331 + 3630 — 3322 — frac{{15}}{8} = — 1023 — frac{{15}}{8})
Тогда площадь закрашенной фигуры:
(S = Fleft( { — 9} right) — Fleft( { — 11} right) = — 1017 — frac{{15}}{8} — left( { — 1023 — frac{{15}}{8}} right) = 6)
Ответ: 6.
Комментарии для сайта Cackle
Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.
Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.
Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.
Задачи из сборников Ященко, 2021 год
Квадратные уравнения
Показательные уравнения
Логарифмические уравнения
Модуль числа
Уравнения с модулем
Тригонометрический круг
Формулы тригонометрии
Формулы приведения
Простейшие тригонометрические уравнения 1
Простейшие тригонометрические уравнения 2
Тригонометрические уравнения
Что необходимо помнить при решении уравнений?
1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если
2) Стараемся записывать решение в виде цепочки равносильных переходов.
3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.
4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.
5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где
— целое, а найти надо корни на отрезке
На указанном промежутке лежит точка
. От нее и будем отсчитывать. Получим:
6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!
Давайте потренируемся.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Упростим левую часть по формуле приведения.
Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Видим, что указанному отрезку принадлежат решения
Ответ:
Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где
— целое, а найти надо корни на отрезке
На указанном промежутке лежит точка
От нее и отсчитываем.
Получим:
2. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.
а)
Степени равны, их основания равны. Значит, равны и показатели.
Это ответ в пункте (а).
б) Отберем корни, принадлежащие отрезку
Отметим на тригонометрическом круге отрезок и найденные серии решений.
Видим, что указанному отрезку принадлежат точки и
из серии
Точки серии не входят в указанный отрезок.
А из серии в указанный отрезок входит точка
Ответ в пункте (б):
3. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а)
Применим формулу косинуса двойного угла:
Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.
Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.
б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.
Сначала серия
Теперь серия
Ответ: .
Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».
Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.
Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке
Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.
4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие
появляется, поскольку в уравнении есть
ОДЗ:
Уравнение равносильно системе:
Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси
.
Ответ в пункте а)
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки
и
5. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Это значит, что уравнение равносильно системе:
Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или
. Заметим, что среди них находятся и углы, для которых
Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие
. Остальные серии решений нас устраивают.
Тогда в ответ в пункте (а) войдут серии решений:
б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.
На отрезке нам подходит корень
.
На отрезке нам подходят корни
.
На отрезке — корни
Ответ в пункте б):
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Подборка по базе: Творческие задания социальная педагогика (3).pdf, Письменные задания для практических занятий.pdf, 11кл Олимпиадные задания по биологии.doc, 10 класс сайты для подготовки по АЛГЕБРЕ.docx, Письменные задания (1).docx, Практические задания к теме 3 (доработанное).docx, Учебные задания проверяемые вручную.docx, Пример 6 задания.docx, Практические задания.docx, Практическое занятие 11. Задания 2-4, 6-7_ просмотр попытки.pdf
1. Тип 7 № 119975
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
2. Тип 7 №
119976
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
3. Тип 7 №
119977
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени
с.
4. Тип 7 №
119978
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
5. Тип 7 №
119979
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?
6. Тип 7 №
501059

Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).
1. Тип 7 №
27489

2. Тип 7 №
27501

3. Тип 7 №
27503

4. Тип 7 №
510384

5. Тип 7 №
510403

6. Тип 7 №
510938

7. Тип 7 №
27504
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
8. Тип 7 №
27505
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
9. Тип 7 №
27506
На рисунке изображён график функции и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
10. Тип 7 №
40129
На рисунке изображен график функции y = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите
11. Тип 7 №
40130
На рисунке изображен график производной функции Найдите абсциссу точки, в которой касательная к графику
параллельна прямой
или совпадает с ней.
12. Тип 7 №
40131
На рисунке изображен график производной функции Найдите абсциссу точки, в которой касательная к графику
параллельна оси абсцисс или совпадает с ней.
13. Тип 7 №
27485
Прямая параллельна касательной к графику функции
Найдите абсциссу точки касания.
14. Тип 7 №
27486
Прямая является касательной к графику функции
Найдите абсциссу точки касания.
15. Тип 7 №
119972
Прямая y = 3x + 1 является касательной к графику функции ax2 + 2x + 3. Найдите a.
16. Тип 7 №
119974
Прямая является касательной к графику функции
Найдите
17. Тип 7 №
119973
Прямая является касательной к графику функции
Найдите b, учитывая, что абсцисса точки касания больше 0.
18. Тип 7 №
515183
На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 6x или совпадает с ней.
19. Тип 7 №
525688
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Найдите значение производной функции g(x) = 6f(x) − 3x в точке x0.
20. Тип 7 №
525689
На рисунке изображены график функции и касательная к этому графику, проведённая в точке
Найдите значение производной функции
в точке x0.
21. Тип 7 №
525690

На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение производной функции
в точке x0.
22. Тип 7 №
525691
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение функции
в точке x0.
23. Тип 7 №
525698
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение производной функции
в точке x0.
24. Тип 7 №
525699
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Найдите значение производной функции
в точке x0.