Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие отрезку 
Спрятать решение
Решение.
а) Запишем в исходное уравнение в виде:
Значит, 
откуда 
или 
Уравнение 
корней не имеет.
б) С помощью числовой окружности отберём корни, принадлежащие отрезку 
Получим числа: 
Ответ: а) 
б)
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а),
ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Источник: Задания 13 (С1) ЕГЭ 2019
Тренировочный вариант №26 пробник решу ЕГЭ 2023 по математике 11 класс профильный уровень от 8 марта 2023 года с ответами и решением по новой демоверсии ЕГЭ 2023 года для подготовки на 100 баллов, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
▶Скачать вариант с ответами
▶Решение заданий с 1 по 18
▶Распечатай и реши вариант
вариант_26_егэ2023_профиль_математика
Ответы и решения
решение_варианта_26_профиль
1. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, sin 𝐴 = 0,8. Найдите sin 𝐵.
2. Дана правильная треугольная призма 𝐴𝐵𝐶𝐴1𝐵1𝐶1, площадь основания которой равна 9, а боковое ребро равно 4. Найдите объём многогранника, вершинами которого являются точки 𝐴, 𝐴1, 𝐵1, 𝐶1.
3. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что произведение выпавших очков делится на 5, но не делится на 30.
4. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,98. Вероятность того, что масса окажется больше 790 г, равна 0,83. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
7. На рисунке изображён график дифференцируемой функции 𝑦 = 𝑓(𝑥), определённой на интервале (−3; 8). Найдите точку из отрезка [−2; 5], в которой производная функции 𝑓(𝑥) равна 0.
8. Два тела, массой 𝑚 = 2 кг каждое, движутся с одинаковой скоростью 𝑣 = 8 м/с под углом 2𝛼 друг к другу. Энергия (в Дж), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле 𝑄 = 𝑚𝑣 2 sin2𝛼, где 𝑚 − масса (в кг), 𝑣 − скорость (в м/с). Найдите, под каким углом 2𝛼 должны двигаться тела, чтобы в результате соударения выделилась энергия, равная 32 Дж. Ответ дайте в градусах.
9. Смешали некоторое количество 19-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
10. На рисунке изображён график функции вида 𝑓(𝑥) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐. Найдите значение 𝑓(−2).
11. Найдите точку максимума функции 𝑦 = ln(𝑥 + 9) − 10𝑥 + 7.
12. а) Решите уравнение 3 ∙ 9 𝑥+1 − 5 ∙ 6 𝑥+1 + 8 ∙ 2 2𝑥 = 0. б) Найдите все корни этого уравнения, принадлежащие отрезку.
13. В правильной треугольной призме 𝐴𝐵𝐶𝐴1𝐵1𝐶1 все рёбра равны 2. Точка 𝑀 − середина ребра 𝐴𝐴1. а) Докажите, что прямые 𝑀𝐵 и 𝐵1𝐶 перпендикулярны. б) Найдите расстояние между прямыми 𝑀𝐵 и 𝐵1𝐶.
15. В июле 2016 года планируется взять кредит в банке на три года в размере 𝑆 млн рублей, где 𝑆 − целое число. Условия его возврата таковы: – каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года; – с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; – в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей. Найдите наибольшее значение 𝑆, при котором разница между наибольшей и наименьшей выплатами будет меньше 1 млн рублей.
16. В трапеции 𝐴𝐵𝐶𝐷 боковая сторона 𝐴𝐵 перпендикулярна основаниям. Из точки 𝐴 на сторону 𝐶𝐷 опустили перпендикуляр 𝐴𝐻. На стороне 𝐴𝐵 отмечена точка 𝐸 так, что прямые 𝐶𝐷 и 𝐶𝐸 перпендикулярны. а) Докажите, что прямые 𝐵𝐻 и 𝐸𝐷 параллельны. б) Найдите отношение 𝐵𝐻 к 𝐸𝐷, если ∠𝐵𝐶𝐷 = 135°.
18. В течение 𝑛 дней каждый день на доску записывают натуральные числа, каждое из которых меньше 6. При этом каждый день (кроме первого) сумма чисел, записанных на доску в этот день, больше, а количество меньше, чем в предыдущий день. а) Может ли 𝑛 быть больше 5? б) Может ли среднее арифметическое чисел, записанных в первый день, быть меньше 3, а среднее арифметическое всех чисел, записанных за все дни, быть больше 4? в) Известно, что сумма чисел, записанных в первый день, равна 6. Какое наибольшее значение может принимать сумма всех чисел, записанных за все дни?
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
ЕГЭ профильный уровень. №7 Первообразная. Задача 4
Задача 4. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = {x^3} + 30{x^2} + 302x — frac{{15}}{8}) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры.
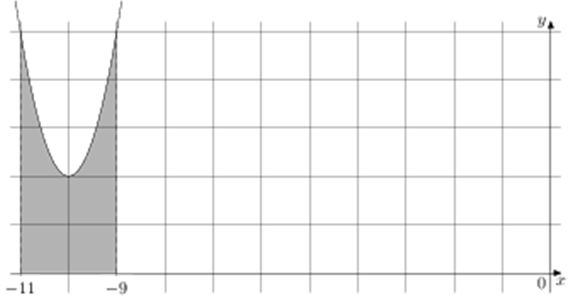
ОТВЕТ: 6.
Площадь закрашенной фигуры равна интегралу (intlimits_{ — 11}^{ — 9} {left( x right)dx} = Fleft( { — 9} right) — Fleft( { — 11} right).) Найдём значение первообразной в точках – 9 и – 11:
(Fleft( { — 9} right) = {left( { — 9} right)^3} + 30 cdot {left( { — 9} right)^2} + 302 cdot left( { — 9} right) — frac{{15}}{8} = — 729 + 2430 — 2718 — frac{{15}}{8} = — 1017 — frac{{15}}{8})
(Fleft( { — 11} right) = {left( { — 11} right)^3} + 30 cdot {left( { — 11} right)^2} + 302 cdot left( { — 11} right) — frac{{15}}{8} = — 1331 + 3630 — 3322 — frac{{15}}{8} = — 1023 — frac{{15}}{8})
Тогда площадь закрашенной фигуры:
(S = Fleft( { — 9} right) — Fleft( { — 11} right) = — 1017 — frac{{15}}{8} — left( { — 1023 — frac{{15}}{8}} right) = 6)
Ответ: 6.
Комментарии для сайта Cackle
| 3069 | а) Решите уравнение 2sin^3(pi+x)=1/2cos(x-(3pi)/2) б) Найдите все корни уравнения, принадлежащие отрезку [-(7pi)/2; -(5pi)/2]. Решение  График |
а) Решите уравнение 2sin 3 (pi +x) =1/2 cos(x — 3/2 pi) ! 36 вариантов ФИПИ Ященко 2022 Вариант 1 Задание 12 | |
| 3068 | Решите неравенство (4^x-5*2^x)^2-20(4^x-5*2^x) <= 96Решение График |
Решите неравенство (4 x -5 2 x) 2 -20(4 x-5 2 x) <= 96 ! 36 вариантов ФИПИ Ященко 2022 Вариант 1 Задание 14 | |
| 2859 | Решите неравенство (25^x-4*5^x)^2+8*5^x < 2*25^x+15Решение График |
Решите неравенство (25 x -4 5 x) 2 + 8 5 x < 2 25 x + 15 ! ЕГЭ по математике профильного уровня 07-06-2021 основная волна Задание 15 (15.3) # Математика 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 2 Задание 14 | |
| 2549 | а) Решите уравнение sin^4(x/4)-cos^4(x/4)=cos(x-pi/2) б) Найдите все корни этого уравнения, принадлежащие отрезку [-(3pi)/2; pi].Решение График |
Решите уравнение sin^4(x/4) -cos^4(x/4) = cos(x-pi/2) ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 12 #36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 13 | |
| 2548 | Решите неравенство (2*0.5^(x+2)-0.5*2^(x+2)). (2log_{0.5)^2(x+2)-0.5log_{2}(x+2)) <= 0.Решение График |
Решите неравенство (2*0.5^(x+2)- 0.5*2^(x+ 2)) (2log^2_{0.5)(x+2)- 0.5log_{2}(x+ 2)) <= 0 ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 14 #36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 15 | |
| 2543 | Решите неравенство lg^4(x^2-26)^4-4lg^2(x^2-26)^2 <= 240.Решение График |
Решите неравенство lg^4(x^2 -26)^4 -4lg^2(x^2 -26)^2 <= 240 ! 36 вариантов ФИПИ Ященко 2022 Вариант 14 Задание 14 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 4 Задание 15 | |
| 2532 | а) Решите уравнение (x^2+2x-1)(log_{2}(x^2-3)+log_{0.5}(sqrt(3)-x))=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [-2.5; -1.5]Решение График |
Решите уравнение (x^2+ 2x -1)(log_{2}(x^2 -3)+ log_{0.5}(sqrt(3) -x))=0 ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 3 Задание 13 | |
| 2531 | Решите неравенство (4^(x-0.5)+1)/(9*4^x-16^(x+0.5)-2) <= 0.5Решение График |
Решите неравенство (4^(x-0,5)+ 1)/ (9*4^x-16^(x+0,5) -2) <= 0,5 ! 36 вариантов ФИПИ Ященко 2022 Вариант 13 Задание 14 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 3 Задание 15 | |
| 2524 | Решите неравенство x^2*log_{243}(-x-3) >= log_{3}(x^2+6x+9)Решение График |
Решите неравенство x^2* log_{243}(-x- 3) >= log_{3}(x^2+ 6x+9) ! 36 вариантов ФИПИ Ященко 2022 Вариант 12 Задание 14 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 2 Задание 15 # Задача-Аналог 2367 | |
Информация о числах
Свойства и характеристики одного числа
Все делители числа, сумма и произведение цифр, двоичный вид, разложение на простые множители…
Свойства пары чисел
Наименьшее общее кратное, наибольший общий делитель, сумма, разность и произведение чисел…
Тринадцать
и
пятьсот двадцать семь тысяч сто пятьдесят семь
| Сумма | 527170 |
| Разность | -527144 |
| Частное | 0.000024660584987015254 |
| Остаток от деления | 13 |
| Произведение | 6853041 |
| Наибольший общий делитель (НОД) | 1 |
| Наименьшее общее кратное (НОК) | 6853041 |
| Среднее арифметическое | 263585 |
| Среднее геометрическое | 2617.8313543847703 |
| Гипотенуза | 527157.0001602938 |
|
Простые числа-близнецы? |
Нет |
|
Расстояние Левенштейна |
5 |
| Общие делители | 1 |
|
Взаимнопростые числа? |
Да |
| Общие цифры | 1 |
Описание
Два числа 13 и 527157 дают в сумме 527170 и имеют разность -527144.
Если поделить 13 на 527157, то получится 0.000025. При делении 13 на 527157 образуется остаток 13. При произведении чисел получается 6853041.
Наибольший общий делитель (НОД) 1 . Наименьшее общее кратное (НОК) 6853041.
Для 13 и 527157 общий делитель это 1.
Среднее арифметическое для 13 и 527157 — 263585 . Среднее геометрическое для этой пары — 2617.831354.
Числа 13 и 527157 – взаимнопростые. 1 — это общая цифра.
Видеоуроки, тесты, практика и консультации репетитора онлайн. Экстренная подготовка накануне экзамена
About this course
Онлайн-курс посвящён задаче №18 (элементы теории чисел) в профильном ЕГЭ. Эта задача – последняя в экзамене и самая дорогая по баллам. Тема базируется на знаниях из средней школы: натуральные числа, делимость, уравнения.
Курс рассчитан на быструю подготовку: его можно полностью освоить за неделю до экзамена. Вы повысите свой балл и сэкономите время, потому что:
- Обучение идёт от простого к сложному.
- Репетитор разберёт типичные сценарии, которые встречаются в экзамене, а не все задачи подряд.
- Выдержана сложность и не даётся лишнего. Вы будете решать задачи с реальных ЕГЭ прошлых лет.
- Видеоуроки смонтированы без «воды».
- Все темы доступны сразу. Можете пропускать то, что уже хорошо знаете
Этот курс — всего лишь один раздел из моего большого курса «Задачи с оформлением».
Другие бесплатные разделы:
Задание 12: уравнение
Задание 14: неравенство
Задание 17: параметр
Whom this course is for
Ученики 11 класса, абитуриенты
Meet the Instructors
Course content
Share this course
https://stepik.org/course/97260/promo