Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Спрятать решение
Решение.
а) Преобразуем уравнение:
б) С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа:
Ответ: а) б)
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах | 2 |
| Обоснованно получен верный ответ в пункте а),
ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б) |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Разные задачи, Задания 13 ЕГЭ–2021
Критерии
Оценивание
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.
Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.
Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.
Задачи из сборников Ященко, 2021 год
Квадратные уравнения
Показательные уравнения
Логарифмические уравнения
Модуль числа
Уравнения с модулем
Тригонометрический круг
Формулы тригонометрии
Формулы приведения
Простейшие тригонометрические уравнения 1
Простейшие тригонометрические уравнения 2
Тригонометрические уравнения
Что необходимо помнить при решении уравнений?
1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если
2) Стараемся записывать решение в виде цепочки равносильных переходов.
3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.
4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.
5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где
— целое, а найти надо корни на отрезке
На указанном промежутке лежит точка
. От нее и будем отсчитывать. Получим:
6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!
Давайте потренируемся.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Упростим левую часть по формуле приведения.
Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Видим, что указанному отрезку принадлежат решения
Ответ:
Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где
— целое, а найти надо корни на отрезке
На указанном промежутке лежит точка
От нее и отсчитываем.
Получим:
2. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.
а)
Степени равны, их основания равны. Значит, равны и показатели.
Это ответ в пункте (а).
б) Отберем корни, принадлежащие отрезку
Отметим на тригонометрическом круге отрезок и найденные серии решений.
Видим, что указанному отрезку принадлежат точки и
из серии
Точки серии не входят в указанный отрезок.
А из серии в указанный отрезок входит точка
Ответ в пункте (б):
3. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а)
Применим формулу косинуса двойного угла:
Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.
Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.
б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.
Сначала серия
Теперь серия
Ответ: .
Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».
Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.
Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке
Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.
4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие
появляется, поскольку в уравнении есть
ОДЗ:
Уравнение равносильно системе:
Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси
.
Ответ в пункте а)
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки
и
5. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Это значит, что уравнение равносильно системе:
Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или
. Заметим, что среди них находятся и углы, для которых
Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие
. Остальные серии решений нас устраивают.
Тогда в ответ в пункте (а) войдут серии решений:
б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.
На отрезке нам подходит корень
.
На отрезке нам подходят корни
.
На отрезке — корни
Ответ в пункте б):
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
ЕГЭ профильный уровень. №7 Первообразная. Задача 4
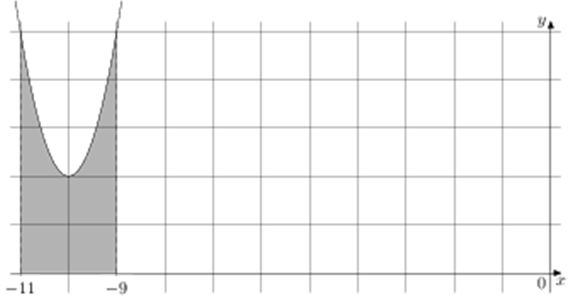
ОТВЕТ: 6.
Площадь закрашенной фигуры равна интегралу (intlimits_{ — 11}^{ — 9} {left( x right)dx} = Fleft( { — 9} right) — Fleft( { — 11} right).) Найдём значение первообразной в точках – 9 и – 11:
(Fleft( { — 9} right) = {left( { — 9} right)^3} + 30 cdot {left( { — 9} right)^2} + 302 cdot left( { — 9} right) — frac{{15}}{8} = — 729 + 2430 — 2718 — frac{{15}}{8} = — 1017 — frac{{15}}{8})
(Fleft( { — 11} right) = {left( { — 11} right)^3} + 30 cdot {left( { — 11} right)^2} + 302 cdot left( { — 11} right) — frac{{15}}{8} = — 1331 + 3630 — 3322 — frac{{15}}{8} = — 1023 — frac{{15}}{8})
Тогда площадь закрашенной фигуры:
(S = Fleft( { — 9} right) — Fleft( { — 11} right) = — 1017 — frac{{15}}{8} — left( { — 1023 — frac{{15}}{8}} right) = 6)
Ответ: 6.
Комментарии для сайта Cackle
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:
На какие числа делится число онлайн калькулятор. Посчитать делители числа.
Какие числа делятся на 563717?
На число 563717 без остатка (нацело) делятся следующие числа: 563717, 1127434, 1691151, 2254868, 2818585, 3382302, 3946019, 4509736, 5073453, 5637170, 6200887, 6764604 и многие другие.
Какие четные числа делятся на 563717?
На число 563717 делятся следующие четные числа: 1127434, 2254868, 3382302, 4509736, 5637170, 6764604, 7892038, 9019472, 10146906, 11274340, 12401774, 13529208 и многие други.
Какие нечетные числа делятся на 563717?
На число 563717 делятся следующие нечетные числа: 563717, 1691151, 2818585, 3946019, 5073453, 6200887, 7328321, 8455755, 9583189, 10710623, 11838057, 12965491 и многие другие.
На какое наибольшее число делится число 563717 без остатка?
Наибольшее число на которое делится число 563717 есть само число 563717. т.е делиться на само себя без остатка.
На какое наибольшее число делится число 563717 без остатка, не считая числа 563717 и 1?
Наибольшим делителем числа 563717 не считая самого числа 563717 является число 80531.
Какое наименьшее натуральное число делится на 563717?
Наименьшее натуральное число которое делиться на число 563717 является само число 563717.
На какое наименьшее натуральное число делится число 563717?
Наименьшее натуральное число на которое можно разделить число 563717 — это число 1.
Делители числа 563717.
(что бы не забыть запишите все делители числа 563717 в блокнот.)На какие целые и(или) натуральные числа делится число 563717?
Число 563717 делится на следующие целые, натуральные числа (все делители числа 563717): 1, 7, 11, 77, 7321, 51247, 80531, 563717
На какие четные числа делится число 563717?
Таких чисел нет.
На какие нечетные числа делится число 563717?
Число 563717 делится на следующие нечетные числа (нечетные делители числа): 1, 7, 11, 77, 7321, 51247, 80531, 563717
Сколько делителей имеет число 563717?
Число 563717 имеет 8 делителей
Сколько четных делителей имеет число 563717?
Число 563717 имеет 0 четных делителей
Сколько нечетных делителей имеет число 563717?
Число 563717 имеет 8 нечетных делителей
Число 563717 прописью, словами.
— пятьсот шестьдесят три тысячи семьсот семнадцать
(что бы не забыть запишите число 563717 прописью в блокнот.)
Числа кратные 563717.
— кратные числа, числу 563717 : 1127434, 1691151, 2254868, 2818585, 3382302, 3946019, 4509736, 5073453, 5637170, 6200887, 6764604 и многие другие.
Простые множители числа 563717.
Простые множители числа 563717 = 7, 11, 7321 (единица также является простым множителем числа 563717)
Сумма цифр числа 563717.
Сумма цифр числа 563717 равна 29
Произведение цифр числа 563717.
Произведение цифр числа 563717 равна 4410
Квадрат числа 563717.
Квадрат числа 563717 равен 317776856089
Куб числа 563717.
Куб числа 563717 равен 179136215983922813
Квадратный корень числа 563717.
Квадратный корень числа 563717 равен 750.8108.
Число 563717 в двоичной системе счисления.
Запись числа 563717 в двоичной системе счисления выглядит так: 10001001101000000101
Количество значащих нулей в двоичной записи числа 563717 = 13
Количество едениц в двоичной записи числа 563717 = 7
(что бы не забыть запишите число 563717 в двоичной системе счисления в блокнот.)Число 563717 в шестнадцатеричной системе счисления.
Запись числа 563717 в шестнадцатеричной системе счисления выглядит так: 89a05
(что бы не забыть запишите число 563717 в шестнадцатеричной системе счисления в блокнот.)Число 563717 в восьмеричной системе счисления.
Запись числа 563717 в восьмеричной системе счисления выглядит так: 2115005
(что бы не забыть запишите число 563717 в восьмеричной системе счисления в блокнот.)Число 563717 не является простым!
Корни числа 563717.
Корень 3 степени из 563717.
Корень 3 (третьей) степени из 563717 равен 82.607670865283
Корень 4 степени из 563717.
Корень 4 (четвертой) степени из 563717 равен 27.40092872452
Корень 5 степени из 563717.
Корень 5 (пятой) степени из 563717 равен 14.132279771192
Корень 6 степени из 563717.
Корень 6 (шестой) степени из 563717 равен 9.0888762157531
Корень 7 степени из 563717.
Корень 7 (седьмой) степени из 563717 равен 6.6310173114731
Корень 8 степени из 563717.
Корень 8 (восьмой) степени из 563717 равен 5.234589642419
Корень 9 степени из 563717.
Корень 9 (девятой) степени из 563717 равен 4.355186852264
Корень 10 степени из 563717.
Корень 10 (десятой) степени из 563717 равен 3.7592924561933
Корень 11 степени из 563717.
Корень 11 (одиннадцатой) степени из 563717 равен 3.332911173376
Корень 12 степени из 563717.
Корень 12 (двенадцатой) степени из 563717 равен 3.0147763127226
Корень 13 степени из 563717.
Корень 13 (тринадцатой) степени из 563717 равен 2.7694231476793
Корень 14 степени из 563717.
Корень 14 (четырнадцатой) степени из 563717 равен 2.5750761758583
Корень 15 степени из 563717.
Корень 15 (пятнадцатой) степени из 563717 равен 2.4177092688757
Степени числа 563717.
563717 в 3 степени.
563717 в 3 степени равно 179136215983922813.
563717 в 4 степени.
563717 в 4 степени равно 1.0098213026581E+23.
563717 в 5 степени.
563717 в 5 степени равно 5.6925343527051E+28.
563717 в 6 степени.
563717 в 6 степени равно 3.2089783877039E+34.
563717 в 7 степени.
563717 в 7 степени равно 1.8089556697813E+40.
563717 в 8 степени.
563717 в 8 степени равно 1.0197390633021E+46.
563717 в 9 степени.
563717 в 9 степени равно 5.7484424554746E+51.
563717 в 10 степени.
563717 в 10 степени равно 3.2404947356728E+57.
563717 в 11 степени.
563717 в 11 степени равно 1.8267219709092E+63.
563717 в 12 степени.
563717 в 12 степени равно 1.029754229275E+69.
563717 в 13 степени.
563717 в 13 степени равно 5.8048996486424E+74.
563717 в 14 степени.
563717 в 14 степени равно 3.2723206152338E+80.
563717 в 15 степени.
563717 в 15 степени равно 1.8446627602577E+86.
Какое число имеет такую же сумму цифр как и число 563717?Математика. Найти сумму цифр числа 563717.
Число 563717 состоит из следующих цифр — 5, 6, 3, 7, 1, 7.
Определить сумму цифр числа 563717 не так уж и сложно.
Сумма цифр шестизначного числа 563717 равна 5 + 6 + 3 + 7 + 1 + 7 = 29.
Числа сумма цифр которых равна 29.
Следующие числа имеют такую же сумму цифр как и число 563717 — 2999, 3899, 3989, 3998, 4799, 4889, 4898, 4979, 4988, 4997, 5699, 5789, 5798, 5879, 5888, 5897, 5969, 5978, 5987, 5996.
Четырехзначные числа сумма цифр которых равна 29 — 2999, 3899, 3989, 3998, 4799, 4889, 4898, 4979, 4988, 4997.
Пятизначные числа сумма цифр которых равна 29 — 11999, 12899, 12989, 12998, 13799, 13889, 13898, 13979, 13988, 13997.
Шестизначные числа сумма цифр которых равна 29 — 101999, 102899, 102989, 102998, 103799, 103889, 103898, 103979, 103988, 103997.
Квадрат суммы цифр числа 563717.
Квадрат суммы цифр шестизначного числа 563717 равен 5 + 6 + 3 + 7 + 1 + 7 = 29² = 841.
Сумма квадратов цифр шестизначного числа 563717.
Сумма квадратов цифр числа 563717 равна 5² + 6² + 3² + 7² + 1² + 7² = 25 + 36 + 9 + 49 + 1 + 49 = 169.
Сумма четных цифр числа 563717.
Сумма четных цифр шестизначного числа 563717 равна 6 = 6.
Квадрат суммы четных цифр шестизначного числа 563717.
Квадрат суммы четных цифр числа 563717 равна 6 = 6² = 36.
Сумма квадратов четных цифр шестизначного числа 563717.
Сумма квадратов четных цифр числа 563717 равна 6² = 36 = 36.
Сумма нечетных цифр числа 563717.
Сумма нечетных цифр шестизначного числа 563717 равна 5 + 3 + 7 + 1 + 7 = 23.
Квадрат суммы нечетных цифр шестизначного числа 563717.
Квадрат суммы нечетных цифр числа 563717 равна 5 + 3 + 7 + 1 + 7 = 23² = 529.
Сумма квадратов нечетных цифр шестизначного числа 563717.
Сумма квадратов нечетных цифр числа 563717 равна 5² + 3² + 7² + 1² + 7² = 25 + 9 + 49 + 1 + 49 = 133.
Произведение цифр числа 563717.
Какое число имеет такое же произведение цифр как и число 563717?Математика. Найти произведение цифр числа 563717.
Число 563717 состоит из следующих цифр — 5, 6, 3, 7, 1, 7.
Найти сумму цифр числа 563717 просто.
Решение:
Произведение цифр числа 563717 равно 5 * 6 * 3 * 7 * 1 * 7 = 4410.
Числа произведение цифр которых равно 4410.
Следующие числа имеют такое же произведение цифр как и число 563717 — 25779, 25797, 25977, 27579, 27597, 27759, 27795, 27957, 27975, 29577, 29757, 29775, 35677, 35767, 35776, 36577, 36757, 36775, 37567, 37576.
Пятизначные числа произведение цифр которых равно 4410 — 25779, 25797, 25977, 27579, 27597, 27759, 27795, 27957, 27975, 29577.
Шестизначные числа произведение цифр которых равно 4410 — 125779, 125797, 125977, 127579, 127597, 127759, 127795, 127957, 127975, 129577.
Квадрат произведения цифр числа 563717.
Квадрат произведения цифр шестизначного числа 563717 равен 5 * 6 * 3 * 7 * 1 * 7 = 4410² = 19448100.
Произведение квадратов цифр шестизначного числа 563717.
Произведение квадратов цифр числа 563717 равна 5² * 6² * 3² * 7² * 1² * 7² = 25 * 36 * 9 * 49 * 1 * 49 = 19448100.
Произведение четных цифр числа 563717.
Произведение четных цифр шестизначного числа 563717 равно 6 = 6.
Квадрат произведения четных цифр шестизначного числа 563717.
Квадрат произведения четных цифр числа 563717 равен 6 = 6² = 36.
Произведение квадратов четных цифр шестизначного числа 563717.
Произведение квадратов четных цифр числа 563717 равно 6² = 36 = 36.
Произведение нечетных цифр числа 563717.
Произведение нечетных цифр шестизначного числа 563717 равно 5 * 3 * 7 * 1 * 7 = 735.
Квадрат произведения нечетных цифр шестизначного числа 563717.
Квадрат произведения нечетных цифр числа 563717 равен 5 * 3 * 7 * 1 * 7 = 735² = 540225.
Произведение квадратов нечетных цифр шестизначного числа 563717.
Произведение квадратов нечетных цифр числа 563717 равно 5² * 3² * 7² * 1² * 7² = 25 * 9 * 49 * 1 * 49 = 540225.
Запишите числа которые в сумме дают число 563717.
Задача: Данно число 563717.Какие 2(два) числа дают в сумме число 563717?Решение:
1) 4693 + 559024 = 563717
2) 187756 + 375961 = 563717
3) 11733 + 551984 = 563717
4) 179943 + 383774 = 563717
5) 62876 + 500841 = 563717
Какие 3(три) числа дают в сумме число 563717?Решение:
1) 99136 + 60041 + 404540 = 563717
2) 52905 + 222 + 510590 = 563717
3) 63445 + 165056 + 335216 = 563717
4) 142262 + 55792 + 365663 = 563717
5) 24196 + 159090 + 380431 = 563717
Какие 4(четыре) числа дают в сумме число 563717?Решение:
1) 79367 + 5456 + 203206 + 275688 = 563717
2) 5471 + 56193 + 201076 + 300977 = 563717
3) 113555 + 107653 + 112576 + 229933 = 563717
4) 83307 + 69037 + 70193 + 341180 = 563717
5) 62610 + 84949 + 98348 + 317810 = 563717
Какие 5(пять) чисел дают в сумме число 563717?Решение:
1) 45573 + 60120 + 135847 + 30757 + 291420 = 563717
2) 3156 + 89729 + 65023 + 120744 + 285065 = 563717
3) 100353 + 32279 + 133401 + 37061 + 260623 = 563717
4) 104020 + 49974 + 23209 + 54571 + 331943 = 563717
5) 98343 + 106592 + 148811 + 33564 + 176407 = 563717
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
|
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
|
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
















