Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
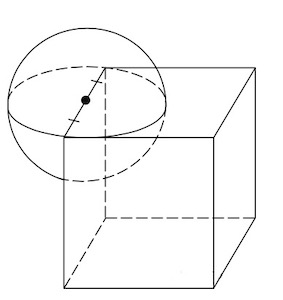
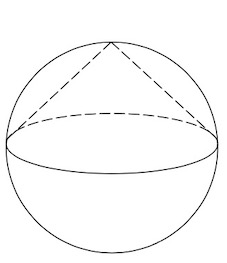
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
2
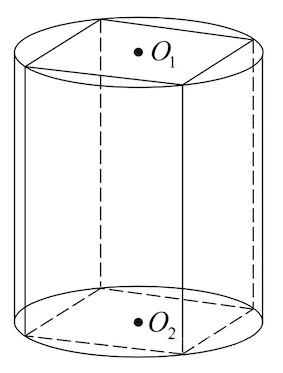
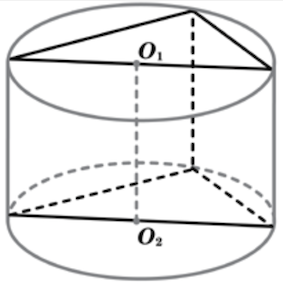
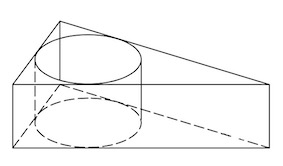
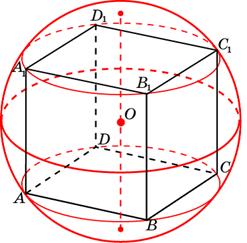
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
3
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
4
В куб вписан шар радиуса 1. Найдите объем куба.
5
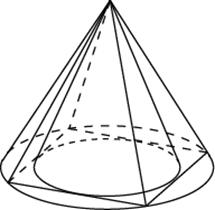
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны
Найдите объем цилиндра, описанного около этой призмы.
Пройти тестирование по этим заданиям
ЕГЭ Профиль №5. Комбинация тел
Скачать файл в формате pdf.
ЕГЭ Профиль №5. Комбинация тел
| Задача 1. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Ответ
ОТВЕТ: 4. |
 |
| Задача 2. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
Ответ
ОТВЕТ: 0,25. |
 |
| Задача 3. Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем.
Ответ
ОТВЕТ: 8. |
 |
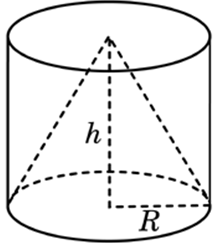
| Задача 4. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны (frac{5}{pi }). Найдите объем цилиндра, описанного около этой призмы.
Ответ
ОТВЕТ: 125. |
 |
| Задача 5. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны (frac{2}{pi }). Найдите объем цилиндра, описанного около этой призмы.
Ответ
ОТВЕТ: 4. |
 |
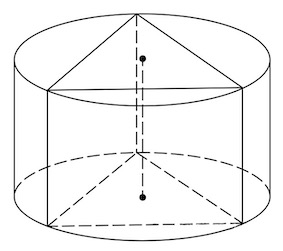
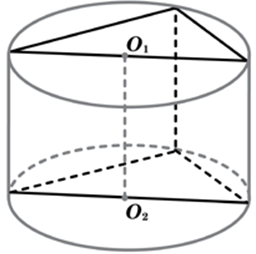
| Задача 6. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25.
Ответ
ОТВЕТ: 75. |
 |
| Задача 7. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Ответ
ОТВЕТ: 8. |
|
| Задача 8. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен (sqrt 3 ), а высота равна 2.
Ответ
ОТВЕТ: 36. |
|
| Задача 9. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен (sqrt 3 ), а высота равна 2.
Ответ
ОТВЕТ: 24. |
 |
| Задача 10. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
Ответ
ОТВЕТ: 12. |
|
| Задача 11. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
Ответ
ОТВЕТ: 7,5. |
 |
| Задача 12. Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.
Ответ
ОТВЕТ: 50. |
 |
| Задача 13. Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.
Ответ
ОТВЕТ: 3. |
|
| Задача 14. Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на (pi ).
Ответ
ОТВЕТ: 16. |
|
| Задача 15. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Ответ
ОТВЕТ: 2. |
 |
| Задача 16. В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на (pi ).
Ответ
ОТВЕТ: 4,5. |
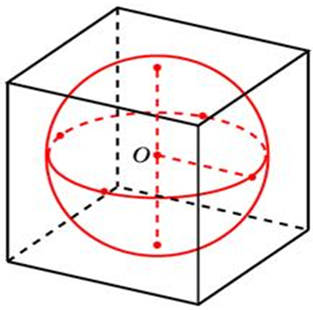 |
| Задача17 . Около куба с ребром (sqrt 3 ) описан шар. Найдите объем этого шара, деленный на (pi ).
Ответ
ОТВЕТ: 4,5. |
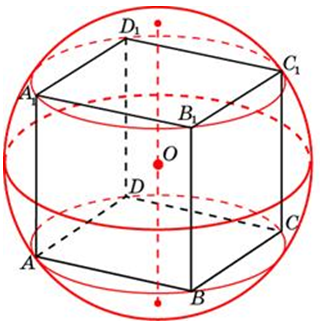 |
| Задача 18. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен (2sqrt 3 ), а высота равна 2.
Ответ
ОТВЕТ: 36. |
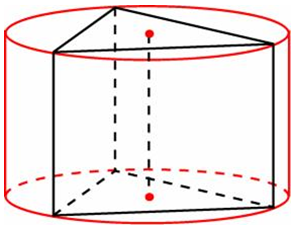 |
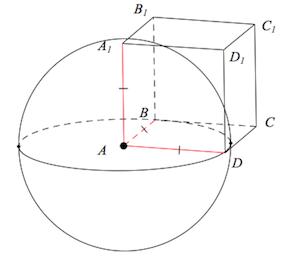
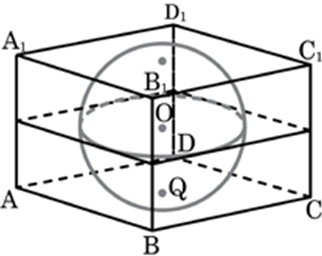
| Задача 19. Вершина A куба ABCDA1B1C1D1 со стороной 1,6 является центром сферы, проходящей через точку A1. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину (frac{S}{pi }).
Ответ
ОТВЕТ: 1,28. |
|
| Задача 20. Середина ребра куба со стороной 1,9 является центром шара радиуса 0,95. Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите (frac{S}{pi }).
Ответ
ОТВЕТ: 0,9025. |
|
| Задача 21. Объем тетраэдра равен 1,9. Найдите объем многогранника, вершинами которого являются середины ребер данного тетраэдра.
Ответ
ОТВЕТ: 0,95. |
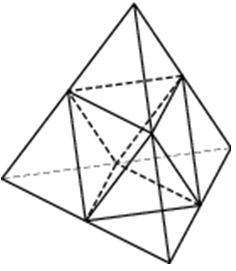 |
| Задача 22. Площадь поверхности тетраэдра равна 1,2. Найдите площадь поверхности многогранника, вершинами которого являются середины ребер данного тетраэдра.
Ответ
ОТВЕТ: 0,6. |
 |
| Задача 23. Цилиндр описан около шара. Объем цилиндра равен 9. Найдите объем шара.
Ответ
ОТВЕТ: 6. |
|
| Задача 24. Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
Ответ
ОТВЕТ: 36. |
|
| Задача 25. Конус вписан в цилиндр. Объем конуса равен 16. Найдите объем цилиндра.
Ответ
ОТВЕТ: 48. |
|
| Задача 26. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
Ответ
ОТВЕТ: 7. |
|
| Задача 27. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 27. Найдите объем шара.
Ответ
ОТВЕТ: 108. |
|
| Задача 28. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
Ответ
ОТВЕТ: 3. |
|
| Задача 29. Куб вписан в шар радиуса (5sqrt 3 ). Найдите объем куба.
Ответ
ОТВЕТ: 1000. |
|
| Задача 30. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна (7sqrt 2 ). Найдите радиус сферы.
Ответ
ОТВЕТ: 7. |
|
| Задача 31. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен (28sqrt 2 ). Найдите образующую конуса.
Ответ
ОТВЕТ: 56. |
|
| Задача 32. Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
Ответ
ОТВЕТ: 166,5. |
|
| Задача 33. Шар, объем которого равен (6pi ), вписан в куб. Найдите объем куба.
Ответ
ОТВЕТ: 36. |
Задача 1. Объем прямоугольного параллелепипеда, описанного около сферы, равен Найдите радиус сферы.
Решение: + показать
Задача 2. В куб вписан шар радиуса Найдите объем куба.
Решение: + показать
Задача 3. Шар, объём которого равен вписан в куб. Найдите объём куба.
Решение: + показать
Задача 4. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен Объем параллелепипеда равен
Найдите высоту цилиндра.
Решение: + показать
Задача 5. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны Найдите объем параллелепипеда.
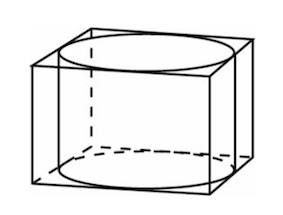
Задача 6. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны Найдите площадь боковой поверхности призмы.
Решение: + показать
Задача 7. В основании прямой призмы лежит квадрат со стороной . Боковые ребра равны
Найдите объем цилиндра, описанного около этой призмы.
Решение: + показать
Задача 8. Около шара описан цилиндр, площадь поверхности которого равна Найдите площадь поверхности шара.
Решение: + показать
Задача 9. Цилиндр описан около шара. Объем цилиндра равен Найдите объем шара.
Решение: + показать
Задача 10. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен Найдите объем конуса.
Решение: + показать
Задача 11. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен Найдите объем шара.
Решение: + показать
Задача 12. Середина ребра куба со стороной является центром шара радиуса
Найдите площадь
части поверхности шара, лежащей внутри куба. В ответе запишите
Решение: + показать
Задача 13. Вершина куба
со стороной
является центром сферы, проходящей через точку
. Найдите площадь
части сферы, содержащейся внутри куба. В ответе запишите величину
.
Решение: + показать
Задача 14. Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен
Решение: + показать
Задача 15. Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса.
Решение: + показать
Задача 16. Конус описан около правильной четырехугольной пирамиды со стороной основания и высотой
Найдите его объем, деленный на
.
Решение: + показать
Задача 17. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Решение: + показать
Задача 18. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен Найдите объем конуса.
Решение: + показать
Задача 19. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен Найдите образующую конуса.
Решение: + показать
Задача 20. В основании прямой призмы лежит прямоугольный треугольник с катетами и
Боковые ребра равны
. Найдите объем цилиндра, описанного около этой призмы.
Решение: + показать
Задача 21. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна
Решение: + показать
Задача 22. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен а высота равна
Решение: + показать
Задача 23. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен
Решение: + показать
Задача 24. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна
Решение: + показать
Задача 25. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна
Решение: + показать
Задача 26. Около куба с ребром описан шар. Найдите объем этого шара, деленный на
Решение: + показать
Задача 27. Куб вписан в шар радиуса Найдите объем куба.
Решение: + показать

Решу ЕГЭ задание №5 по математике 11 класс профильный уровень с ответами и решением для практики и подготовки, задание 5 профильного ЕГЭ по математике – это основы стереометрии.
- Скачать задания куб, прямоугольный параллелепипед
- Скачать задания составные многогранники
- Скачать задания площадь поверхности многогранника
- Скачать задания призма
- Скачать задания пирамида
- Скачать задания цилиндр, конус шар
- Скачать задания комбинация тел
Куб, прямоугольный параллелепипед решу задания и ответы:
Составные многогранники решу задания и ответы:
Площадь поверхности многогранника решу задания и ответы:
Призма решу задания и ответы:
Пирамида задания и ответы:
Цилиндр и конус шар задания и ответы:
Комбинация тел задания и ответы:
Задания и ответы:
1)Площадь поверхности куба равна 18. Найдите его диагональ.
Правильный ответ: 3
2)Объем куба равен 8. Найдите площадь его поверхности.
Правильный ответ: 24
3)Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Правильный ответ: 4
4)Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?
Правильный ответ: 27
5)Диагональ куба равна 12 . Найдите его объем.
Правильный ответ: 8
6)Объем куба равен 24 3 . Найдите его диагональ.
Правильный ответ: 6
7)Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
Правильный ответ: 2
8)Диагональ куба равна 1. Найдите площадь его поверхности.
Правильный ответ: 2
9)Площадь поверхности куба равна 24. Найдите его объем.
Правильный ответ: 8
10)Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Правильный ответ: 4
11)В кубе ABCDA1B1C1D1 точка K — середина ребра AA1, точка L — середина ребра A1B1, точка M — середина ребра A1D1. Найдите угол MLK. Ответ дайте в градусах.
Правильный ответ: 60
12)В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и B1D1. Ответ дайте в градусах.
Правильный ответ: 60
13)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Правильный ответ: 5
14)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
Правильный ответ: 3
15)Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Правильный ответ: 24
16)Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Правильный ответ: 48
17)Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Правильный ответ: 8
18)Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Правильный ответ: 5
19)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Правильный ответ: 4
20)Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
Правильный ответ: 6
21)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Правильный ответ: 32
22)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
Правильный ответ: 7
23)Одна из граней прямоугольного параллелепипеда – квадрат. Диагональ параллелепипеда равна 8 и образует с плоскостью этой грани угол 45o . Найдите объем параллелепипеда.
Правильный ответ: 4
24)Диагональ прямоугольного параллелепипеда равна 8 и образует углы 30o , 30o и 45o с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
Правильный ответ: 4
25)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
Правильный ответ: 64
26)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.
Правильный ответ: 22
27)Объем параллелепипеда ABCDA1B1C1D1 равен 4,5. Найдите объем треугольной пирамиды AD1CB1.
Правильный ответ: 1,5
28)Найдите объем многогранника, вершинами которого являются точки A, D, A1, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 3, AD = 4, AA1 = 5.
Правильный ответ: 30
29)Найдите объем многогранника, вершинами которого являются точки A, B, C, D1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 4, AD = 3, AA1 = 4.
Правильный ответ: 8
30)Найдите объем многогранника, вершинами которого являются точки A1, B, C, C1, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 4, AD = 3, AA1 = 4.
Правильный ответ: 16
31)Найдите объем многогранника, вершинами которого являются точки A, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 3, AD = 3, AA1 = 4.
Правильный ответ: 3
32)Найдите объем многогранника, вершинами которого являются точки A, B, B1, C1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 5, AD = 3, AA1 = 4.
Правильный ответ: 10
33)Найдите угол ABD1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3. Ответ дайте в градусах.
Правильный ответ: 45
34)Найдите угол C1BC прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 4. Ответ дайте в градусах.
Правильный ответ: 45
35)Найдите угол DBD1 прямоугольного параллелепипеда, для которого AB = 4, AD = 3, AA1 = 5. Ответ дайте в градусах.
Правильный ответ: 45
36)В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AC1 = 13, C1D1 = 3, B1C1 = 12. Найдите длину ребра AA1.
Правильный ответ: 4
37)В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1 = 11, C1D1 = 16, B1C1 = 8. Найдите длину диагонали DB1.
Правильный ответ: 21
38)В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро AB 2 , ребро AD 5 , ребро 1 AA 2 . Точка K — середина ребра BB1. Найдите площадь сечения, проходящего через точки A1, D1 и K.
Правильный ответ: 5
39)В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра AB = 24, AD = 10, AA1 =22. Найдите площадь сечения, проходящего через точки A, A1 и С.
Правильный ответ: 572
40)В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра AB = 8, AD = 6, AA1 =21. Найдите синус угла между прямыми CD и A1C1.
Правильный ответ: 0,6
41)Найдите расстояние между вершинами A и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 3
42)Найдите квадрат расстояния между вершинами D и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 5
43)Найдите расстояние между вершинами B1 и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 3
44)Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Правильный ответ: 60
45)Найдите угол ABD многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Правильный ответ: 45
46)Найдите тангенс угла B2A2C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 2
47)Найдите квадрат расстояния между вершинами B2 и D3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 11
48)Найдите квадрат расстояния между вершинами B и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 14
49)Найдите квадрат расстояния между вершинами A и C3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 17
50)Найдите тангенс угла C2C3B2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 3
51)Найдите тангенс угла ABB3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 2
52)Найдите тангенс угла C3D3B3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 3
53)Найдите квадрат расстояния между вершинами E и B2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 53
54)Найдите угол D2EF многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Правильный ответ: 45
55)Найдите угол EAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Правильный ответ: 60
56)Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Правильный ответ: 18
57)Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Правильный ответ: 76
58)Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Правильный ответ: 92
59)В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в cм3 .
Правильный ответ: 184
60)В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
Правильный ответ: 5
61)Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
Правильный ответ: 300
62)Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Правильный ответ: 248
63)Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 5, а площадь поверхности равна 190.
Правильный ответ: 7
64)Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Правильный ответ: 12
65)Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
Правильный ответ: 4
66)Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны 3 .
Правильный ответ: 4,5
67)Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Правильный ответ: 8
68)Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Правильный ответ: 20
69)Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны 2 3 и наклонены к плоскости основания под углом 30o .
Правильный ответ: 18
70)От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
Правильный ответ: 4
71)Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Правильный ответ: 288
72)В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
Правильный ответ: 10
73)В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
Правильный ответ: 240
74)Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
Правильный ответ: 10
75)Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
Правильный ответ: 16
76)Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.
Правильный ответ: 1,5
77)Найдите объем многогранника, вершинами которого являются точки A, B, C, A1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 2, а боковое ребро равно 3.
Правильный ответ: 2
78)Найдите объем многогранника, вершинами которого являются точки A, B, C, A1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 3, а боковое ребро равно 2.
Правильный ответ: 4
79)Найдите объем многогранника, вершинами которого являются точки A1, B1, B, C правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 4, а боковое ребро равно 3.
Правильный ответ: 4
80)Найдите объем многогранника, вершинами которого являются точки A, B, C, D, E, F, A1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 4, а боковое ребро равно 3.
Правильный ответ: 4
81)Найдите объем многогранника, вершинами которого являются точки A, B, C, A1, B1, C1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 3.
Правильный ответ: 3
82)Найдите объем многогранника, вершинами которого являются точки A, B, D, E, A1, B1, D1, E1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.
Правильный ответ: 8
83)Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.
Правильный ответ: 6
84)Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Правильный ответ: 340
85)Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Правильный ответ: 360
86)Объем параллелепипеда ABCDA1B1C1D1 равен 9. Найдите объем треугольной пирамиды ABCA1.
Правильный ответ: 1,5
87)Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
Правильный ответ: 8
88)Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
Правильный ответ: 4
89)Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна 3 .
Правильный ответ: 0,25
90)Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен 3 .
Правильный ответ: 3
91)Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?
Правильный ответ: 4
92)В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
Правильный ответ: 256
93)Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60o . Высота пирамиды равна 6. Найдите объем пирамиды.
Правильный ответ: 48
94)Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
Правильный ответ: 4,5
95)Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.
Правильный ответ: 6
96)Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
Правильный ответ: 3
97)От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Правильный ответ: 3
98)Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1:2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.
Правильный ответ: 10
99)Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?
Правильный ответ: 4
100)Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
Правильный ответ: 96
101)Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
Правильный ответ: 9
102)Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 6 и высота равна 4.
Правильный ответ: 60
103)Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?
Правильный ответ: 4
104)Ребра правильного тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.
Правильный ответ: 0,25
105)Найдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4.
Правильный ответ: 24
106)В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
Правильный ответ: 13
107)Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
Правильный ответ: 12
108)Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
Правильный ответ: 7
109)Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45o . Найдите объем пирамиды.
Правильный ответ: 48
110)Объем параллелепипеда ABCDA1B1C1D1 равен 12. Найдите объем треугольной пирамиды B1ABC.
Правильный ответ: 2
Тренировочные варианты ЕГЭ 2022 по математике профиль
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Задание 1176
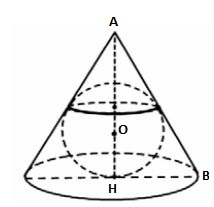
В равносторонний конус (диаметр основания конуса равен длине его образующей) вписан шар. Найдите отношение объема конуса к объему шара.
Ответ: 2.25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Объем конуса вычисляется по формуле:
$$V_{1}=frac{1}{3}S*h=frac{1}{3}pi HB^{2}*AH$$
Объем шара вычисляется по формуле:
$$V_{2}=frac{4}{3}pi R^{3}=frac{4}{3}pi OH^{3}$$
Дан равносторонний конус, то есть в осевом сечении будет равносторонний треугольник. Пусть AB = x, тогда HB = 0,5x и по теореме Пифагора из треугольника AHB: $$AH = frac{sqrt{3}}{2}x$$. OH — радиус вписанной в правильный треугольник окружности, и он равен 1/3 от высоты: $$OH = frac{1}{3}AH = frac{sqrt{3}}{6}x$$
Значит объем конуса равен:
$$V_{1}=frac{1}{3}S*h=frac{1}{3}pi (0.5x)^{2}* frac{sqrt{3}}{2}x$$
Объем шара равен:
$$V_{2}=frac{4}{3}pi R^{3}=frac{4}{3}pi (frac{sqrt{3}}{6}x)^{3}$$
Тогда:
$$frac{V_{1}}{V_{2}}=frac{frac{1}{3}pi (0.5x)^{2}* frac{sqrt{3}}{2}x}{frac{4}{3}pi (frac{sqrt{3}}{6}x)^{3}}$$
$$frac{V_{1}}{V_{2}}=frac{0.25x^{3}* frac{sqrt{3}}{2}}{ 4(frac{sqrt{3}}{6}x)^{3}}=2.25$$
Задание 3867
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Ответ: 4
Задание 3868
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
Ответ: 0,25
Задание 3869
В куб вписан шар радиуса 1. Найдите объем куба.
Ответ: 8
Задание 3870
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны $$frac{5}{pi}$$. Найдите объем цилиндра, описанного около этой призмы.
Ответ: 125
Задание 3871
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны $$frac{2}{pi}$$. Найдите объем цилиндра, описанного около этой призмы.
Ответ: 4
Задание 3872
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
Ответ: 12
Задание 3873
Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
Ответ: 7,5
Задание 3874
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Ответ: 75
Задание 3875
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.
Ответ: 50
Задание 3876
Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
Ответ: 3
Задание 3877
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на $$pi$$.
Ответ: 16
Задание 3878
Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Ответ: 2
Задание 3879
В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на $$pi$$.
Ответ: 4,5
Задание 3880
Около куба с ребром $$sqrt{3}$$ описан шар. Найдите объем этого шара, деленный на $$pi$$.
Ответ: 4,5

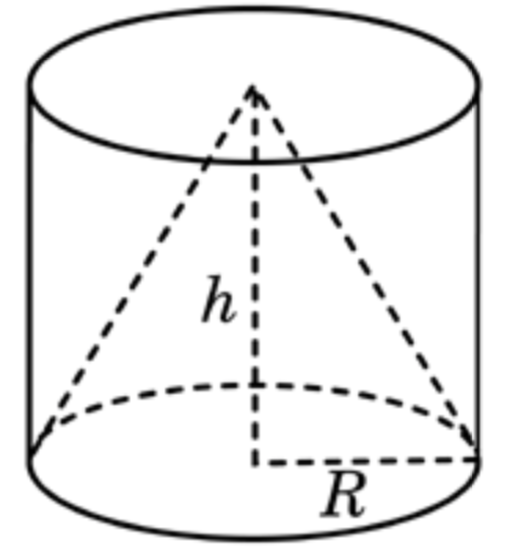
Задача 1. Цилиндр и конус имеют общее основание и общую высоту (см. рис. 1). Вычислите объём цилиндра, если объём конуса равен 16.
Рис. 1.
Решение.
Объём конуса равен , а объём цилиндра —
, где
— площадь их общего основания,
— общая высота. Видно, что объём цилиндра в 3 раза больше объёма конуса и равен
.
Ответ: 48.
Задача 2. Прямоугольный параллелепипед описан около цилиндра (см. рис. 2), радиус основания которого равен 5. Объём параллелепипеда равен 600. Найдите высоту цилиндра.
Решение.
Каждая сторона прямоугольника в основании параллелепипеда равна диаметру цилиндра, то есть . Площадь основания параллелепипеда равна
.
Рис. 2.
Высоту параллелепипеда находим из формулы объёма параллелепипеда:
. Найденная высота параллелепипеда одновременно является и высотой цилиндра.
Ответ: 6.
Задача 3. Объём куба равен 30 (см. рис. 3). Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Рис. 3.
Решение.
Рассмотрим куб как четырёхугольную призму. Его объём равен . Основание пирамиды совпадает с основанием призмы, а высота вдвое меньше высоты призмы. Поэтому
Ответ: 5.
Задача 4. Объём правильной шестиугольной пирамиды равен 60 (см. рис. 4). Найдите объём треугольной пирамиды
.
Рис. 4.
Решение.
Обозначим сторону шестиугольника в основании пирамиды через . Правильный шестиугольник можно разбить на 6 правильных треугольников, поэтому площадь шестиугольника равна
Найдём площадь треугольника
.
Таким образом, площадь основания пирамиды в 6 раз меньше площади основания шестиугольной пирамиды, а их высоты совпадают. Поэтому объёмы этих пирамид находятся в том же соотношении, что и площади их оснований.
Ответ: 10.
В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.
Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.
1 способ – находим формулу по точкам
Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.
Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

Алгоритм:
1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:
2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

3. Решаем эту систему и получаем готовую формулу.

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

2 способ – преобразование графиков функций
Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).
Вот как выглядит применение этого способа:

Для использования этого способа надо знать, как выглядят изначальные функции:

И понимать, как меняются функции от преобразований:




Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

Пример:

3 способ – гибридный
Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая — через точку ((1;0)).

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).
Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.


Как отвечать на вопросы в задаче, когда уже определили функцию
— Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:
— Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой — то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:
— Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

— Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

— Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример: