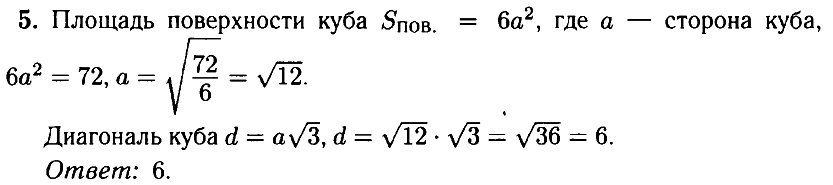Каталог заданий.
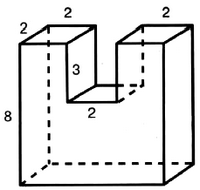
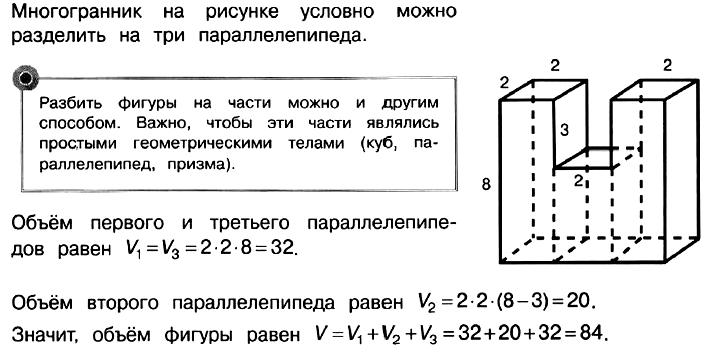
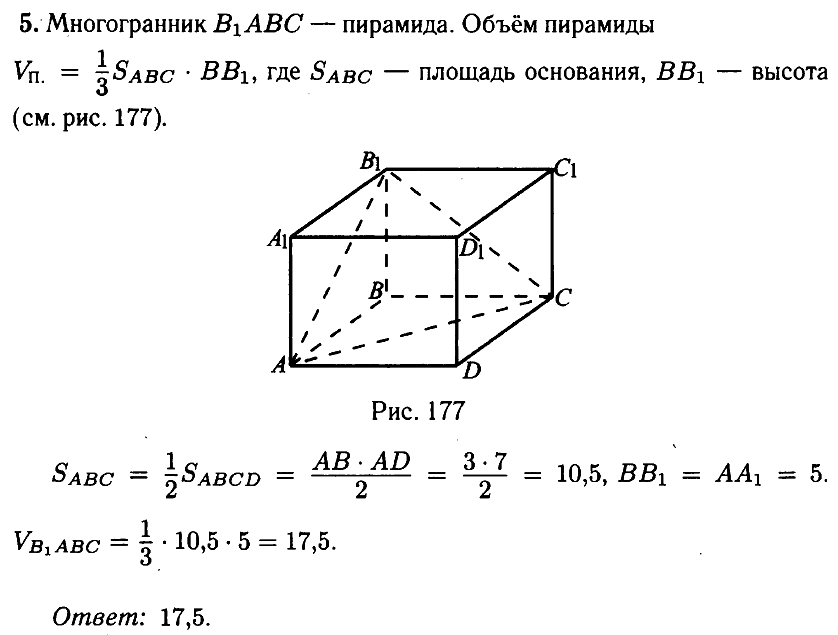
Объем составного многогранника
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
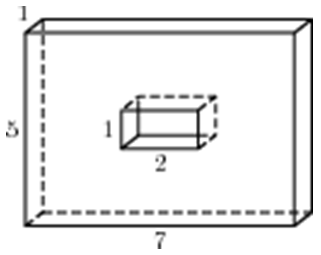
1
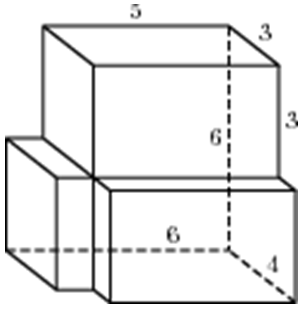
Тип 2 № 27044
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Аналоги к заданию № 27044: 4893 4903 4895 4897 4899 4901 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
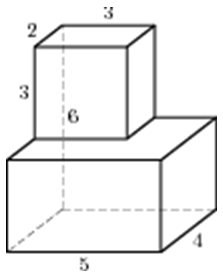
2
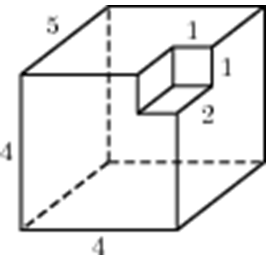
Тип 2 № 27117
Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
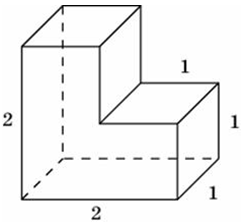
3
Тип 2 № 27187
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 27187: 25531 25539 25533 25535 25537 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
4
Тип 2 № 27188
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 27188: 25551 25559 25553 25555 25557 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
5
Тип 2 № 27189
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 27189: 25571 25579 25573 25575 25577 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 218 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …
Добавить в вариант
Источник: Пробный ЕГЭ по математике, Санкт-Петербург, 04.03.2018. Вариант 1.
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Источник: ЕГЭ по математике 10.06.2013. Вторая волна. Центр. Вариант 601.
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Всего: 218 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …
Решу ЕГЭ задание №5 по математике 11 класс профильный уровень с ответами и решением для практики и подготовки, задание 5 профильного ЕГЭ по математике – это основы стереометрии.
- Скачать задания куб, прямоугольный параллелепипед
- Скачать задания составные многогранники
- Скачать задания площадь поверхности многогранника
- Скачать задания призма
- Скачать задания пирамида
- Скачать задания цилиндр, конус шар
- Скачать задания комбинация тел
Куб, прямоугольный параллелепипед решу задания и ответы:
Составные многогранники решу задания и ответы:
Площадь поверхности многогранника решу задания и ответы:
Призма решу задания и ответы:
Пирамида задания и ответы:
Цилиндр и конус шар задания и ответы:
Комбинация тел задания и ответы:
Задания и ответы:
1)Площадь поверхности куба равна 18. Найдите его диагональ.
Правильный ответ: 3
2)Объем куба равен 8. Найдите площадь его поверхности.
Правильный ответ: 24
3)Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Правильный ответ: 4
4)Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?
Правильный ответ: 27
5)Диагональ куба равна 12 . Найдите его объем.
Правильный ответ: 8
6)Объем куба равен 24 3 . Найдите его диагональ.
Правильный ответ: 6
7)Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
Правильный ответ: 2
8)Диагональ куба равна 1. Найдите площадь его поверхности.
Правильный ответ: 2
9)Площадь поверхности куба равна 24. Найдите его объем.
Правильный ответ: 8
10)Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Правильный ответ: 4
11)В кубе ABCDA1B1C1D1 точка K — середина ребра AA1, точка L — середина ребра A1B1, точка M — середина ребра A1D1. Найдите угол MLK. Ответ дайте в градусах.
Правильный ответ: 60
12)В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и B1D1. Ответ дайте в градусах.
Правильный ответ: 60
13)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Правильный ответ: 5
14)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
Правильный ответ: 3
15)Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Правильный ответ: 24
16)Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Правильный ответ: 48
17)Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Правильный ответ: 8
18)Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Правильный ответ: 5
19)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Правильный ответ: 4
20)Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
Правильный ответ: 6
21)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Правильный ответ: 32
22)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
Правильный ответ: 7
23)Одна из граней прямоугольного параллелепипеда – квадрат. Диагональ параллелепипеда равна 8 и образует с плоскостью этой грани угол 45o . Найдите объем параллелепипеда.
Правильный ответ: 4
24)Диагональ прямоугольного параллелепипеда равна 8 и образует углы 30o , 30o и 45o с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
Правильный ответ: 4
25)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
Правильный ответ: 64
26)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.
Правильный ответ: 22
27)Объем параллелепипеда ABCDA1B1C1D1 равен 4,5. Найдите объем треугольной пирамиды AD1CB1.
Правильный ответ: 1,5
28)Найдите объем многогранника, вершинами которого являются точки A, D, A1, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 3, AD = 4, AA1 = 5.
Правильный ответ: 30
29)Найдите объем многогранника, вершинами которого являются точки A, B, C, D1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 4, AD = 3, AA1 = 4.
Правильный ответ: 8
30)Найдите объем многогранника, вершинами которого являются точки A1, B, C, C1, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 4, AD = 3, AA1 = 4.
Правильный ответ: 16
31)Найдите объем многогранника, вершинами которого являются точки A, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 3, AD = 3, AA1 = 4.
Правильный ответ: 3
32)Найдите объем многогранника, вершинами которого являются точки A, B, B1, C1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 5, AD = 3, AA1 = 4.
Правильный ответ: 10
33)Найдите угол ABD1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3. Ответ дайте в градусах.
Правильный ответ: 45
34)Найдите угол C1BC прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 4. Ответ дайте в градусах.
Правильный ответ: 45
35)Найдите угол DBD1 прямоугольного параллелепипеда, для которого AB = 4, AD = 3, AA1 = 5. Ответ дайте в градусах.
Правильный ответ: 45
36)В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AC1 = 13, C1D1 = 3, B1C1 = 12. Найдите длину ребра AA1.
Правильный ответ: 4
37)В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1 = 11, C1D1 = 16, B1C1 = 8. Найдите длину диагонали DB1.
Правильный ответ: 21
38)В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро AB 2 , ребро AD 5 , ребро 1 AA 2 . Точка K — середина ребра BB1. Найдите площадь сечения, проходящего через точки A1, D1 и K.
Правильный ответ: 5
39)В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра AB = 24, AD = 10, AA1 =22. Найдите площадь сечения, проходящего через точки A, A1 и С.
Правильный ответ: 572
40)В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра AB = 8, AD = 6, AA1 =21. Найдите синус угла между прямыми CD и A1C1.
Правильный ответ: 0,6
41)Найдите расстояние между вершинами A и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 3
42)Найдите квадрат расстояния между вершинами D и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 5
43)Найдите расстояние между вершинами B1 и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 3
44)Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Правильный ответ: 60
45)Найдите угол ABD многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Правильный ответ: 45
46)Найдите тангенс угла B2A2C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 2
47)Найдите квадрат расстояния между вершинами B2 и D3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 11
48)Найдите квадрат расстояния между вершинами B и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 14
49)Найдите квадрат расстояния между вершинами A и C3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 17
50)Найдите тангенс угла C2C3B2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 3
51)Найдите тангенс угла ABB3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 2
52)Найдите тангенс угла C3D3B3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 3
53)Найдите квадрат расстояния между вершинами E и B2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Правильный ответ: 53
54)Найдите угол D2EF многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Правильный ответ: 45
55)Найдите угол EAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Правильный ответ: 60
56)Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Правильный ответ: 18
57)Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Правильный ответ: 76
58)Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Правильный ответ: 92
59)В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в cм3 .
Правильный ответ: 184
60)В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
Правильный ответ: 5
61)Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
Правильный ответ: 300
62)Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Правильный ответ: 248
63)Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 5, а площадь поверхности равна 190.
Правильный ответ: 7
64)Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Правильный ответ: 12
65)Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
Правильный ответ: 4
66)Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны 3 .
Правильный ответ: 4,5
67)Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Правильный ответ: 8
68)Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Правильный ответ: 20
69)Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны 2 3 и наклонены к плоскости основания под углом 30o .
Правильный ответ: 18
70)От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
Правильный ответ: 4
71)Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Правильный ответ: 288
72)В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
Правильный ответ: 10
73)В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
Правильный ответ: 240
74)Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
Правильный ответ: 10
75)Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
Правильный ответ: 16
76)Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.
Правильный ответ: 1,5
77)Найдите объем многогранника, вершинами которого являются точки A, B, C, A1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 2, а боковое ребро равно 3.
Правильный ответ: 2
78)Найдите объем многогранника, вершинами которого являются точки A, B, C, A1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 3, а боковое ребро равно 2.
Правильный ответ: 4
79)Найдите объем многогранника, вершинами которого являются точки A1, B1, B, C правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 4, а боковое ребро равно 3.
Правильный ответ: 4
80)Найдите объем многогранника, вершинами которого являются точки A, B, C, D, E, F, A1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 4, а боковое ребро равно 3.
Правильный ответ: 4
81)Найдите объем многогранника, вершинами которого являются точки A, B, C, A1, B1, C1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 3.
Правильный ответ: 3
82)Найдите объем многогранника, вершинами которого являются точки A, B, D, E, A1, B1, D1, E1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.
Правильный ответ: 8
83)Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.
Правильный ответ: 6
84)Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Правильный ответ: 340
85)Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Правильный ответ: 360
86)Объем параллелепипеда ABCDA1B1C1D1 равен 9. Найдите объем треугольной пирамиды ABCA1.
Правильный ответ: 1,5
87)Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
Правильный ответ: 8
88)Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
Правильный ответ: 4
89)Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна 3 .
Правильный ответ: 0,25
90)Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен 3 .
Правильный ответ: 3
91)Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?
Правильный ответ: 4
92)В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
Правильный ответ: 256
93)Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60o . Высота пирамиды равна 6. Найдите объем пирамиды.
Правильный ответ: 48
94)Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
Правильный ответ: 4,5
95)Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.
Правильный ответ: 6
96)Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
Правильный ответ: 3
97)От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Правильный ответ: 3
98)Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1:2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.
Правильный ответ: 10
99)Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?
Правильный ответ: 4
100)Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
Правильный ответ: 96
101)Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
Правильный ответ: 9
102)Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 6 и высота равна 4.
Правильный ответ: 60
103)Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?
Правильный ответ: 4
104)Ребра правильного тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.
Правильный ответ: 0,25
105)Найдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4.
Правильный ответ: 24
106)В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
Правильный ответ: 13
107)Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
Правильный ответ: 12
108)Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
Правильный ответ: 7
109)Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45o . Найдите объем пирамиды.
Правильный ответ: 48
110)Объем параллелепипеда ABCDA1B1C1D1 равен 12. Найдите объем треугольной пирамиды B1ABC.
Правильный ответ: 2
Тренировочные варианты ЕГЭ 2022 по математике профиль
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Многогранники
Многогранник – это поверхность, составленная из многоугольников, ограничивающая некоторое геометрическое тело.
В данной теме мы рассмотрим составные многогранники (многогранники, состоящие обычно из нескольких параллелепипедов).
Объемы различных многогранников:
- Призма $V=S_{осн}·h$
- Пирамида $V={1}/{3}S_{осн}·h$
- Параллелепипед $V=a·b·c$, где $a, b$ и $c$ — длина, ширина и высота.
- Куб $V=а^3$, где $а$ — сторона куба
Задачи на нахождение объема составного многогранника:
- Первый способ.
- Составной многогранник надо достроить до полного параллелепипеда или куба.
- Найти объем параллелепипеда.
- Найти объем лишней части фигуры.
- Вычесть из объема параллелепипеда объем лишней части.
Пример:
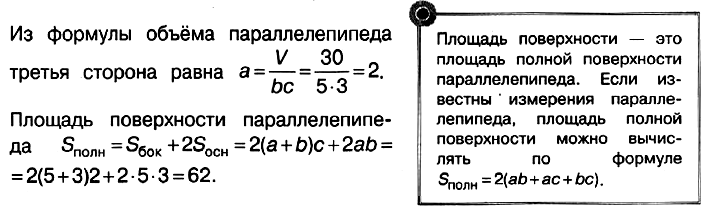
Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
Решение:
1. Достроим составной многогранник до параллелепипеда.
Найдем его объем. Для этого перемножим все три измерения параллелепипеда:
$V=10·9·4=360$
2. Найдем объем лишнего маленького параллелепипеда:
Его длина равна $9-4=5$
Ширина равна $4$
Высота равна $7$
$V=7·4·5=140$
3. Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:
$V=360-140=220$
Ответ: $220$
- Второй способ
- Разделить составной многогранник на несколько параллелепипедов.
- Найти объем каждого параллелепипеда.
- Сложить объемы.
Задачи на нахождение площади поверхности составного многогранника.
— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:
$S_{полн.пов.}=P_{осн}·h+2S_{осн}$
Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.
Пример:
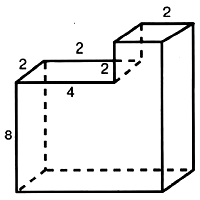
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Представим данный многогранник как прямую призму с высотой равной $12$.
$S_{полн.пов.}=P_{осн}·h+2S_{осн}$
$P_{осн}=8+6+6+2+2+4=28$
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
$S_1=6·6=36$
$S_2=2·4=8$
$S_осн=36+8=44$
Далее подставим все данные в формулу и найдем площадь поверхности многогранника
$S_{полн.пов.}=28·12+2·44=336+88=424$
Ответ: $424$
— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.
Задачи на нахождение расстояния между точками составного многогранника.
В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.
Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Задачи на рассмотрение подобия фигур.
При увеличении всех линейных размеров многогранника в $k$ раз, площадь его поверхности увеличится в $k^2$ раз.
При увеличении всех линейных размеров многогранника в $k$ раз, его объём увеличится в $k^3$ раз.
ЕГЭ Профиль №2. Площадь поверхности и объем составного многогранника
Скачать файл в формате pdf.
ЕГЭ Профиль №2. Площадь поверхности и объем составного многогранника
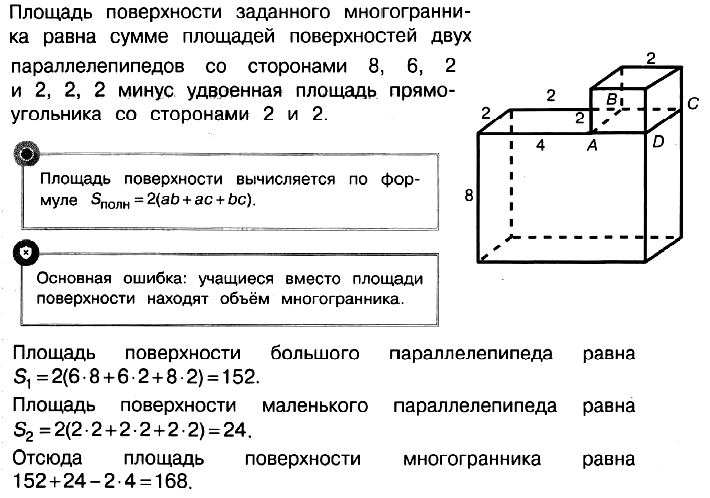
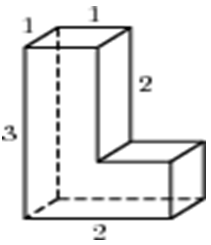
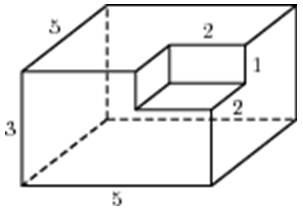
| Задача 1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 18. |
 |
| Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 76. |
 |
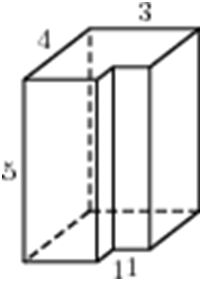
| Задача 3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 92. |
 |
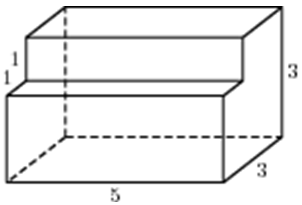
| Задача 4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 110. |
 |
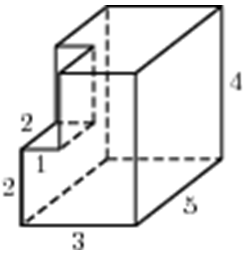
| Задача 5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 94. |
 |
| Задача 6. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 132. |
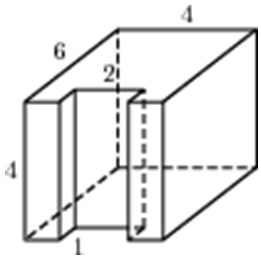 |
| Задача 7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 114. |
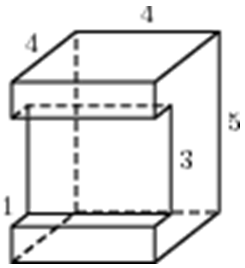 |
| Задача 8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 48. |
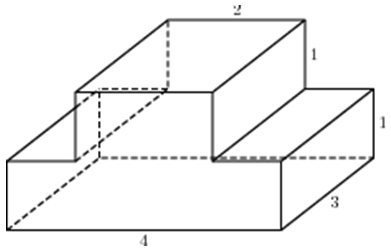 |
| Задача 9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 84. |
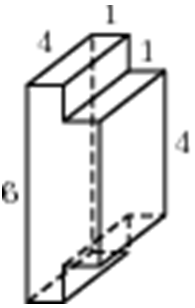 |
| Задача 10. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 96. |
 |
| Задача 11. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 124. |
 |
| Задача 12. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ
ОТВЕТ: 14. |
 |
| Задача 13. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Ответ
ОТВЕТ: 30. |
 |
| Задача 14. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
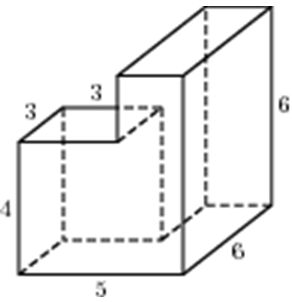
Ответ
ОТВЕТ: 162. |
 |
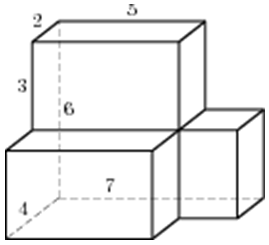
| Задача 15. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 156. |
 |
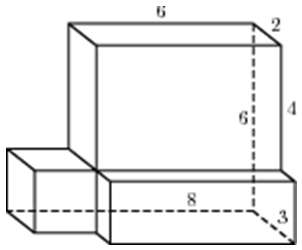
| Задача 16. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 152. |
 |
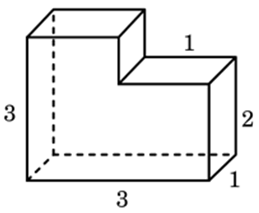
| Задача 17. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Ответ
ОТВЕТ: 8. |
 |
| Задача 18. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 56. |
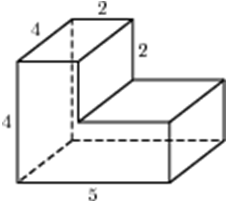 |
| Задача 19. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 7. |
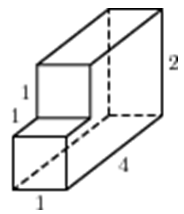 |
| Задача 20. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 40. |
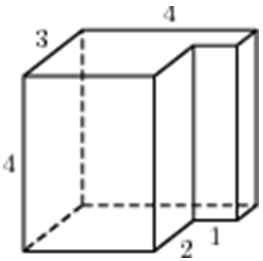 |
| Задача 21. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 34. |
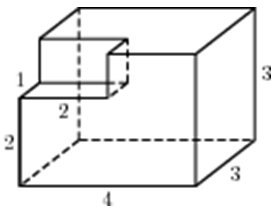 |
| Задача 22. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 36. |
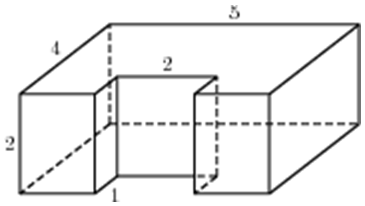 |
| Задача 23. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 90. |
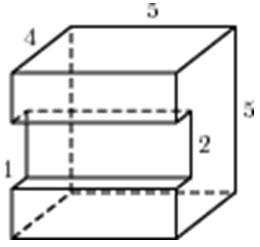 |
| Задача 24. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 18. |
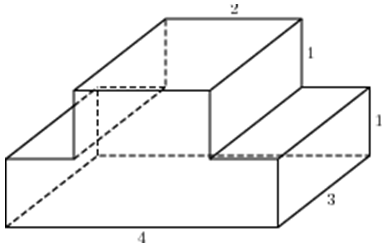 |
| Задача 25. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 24. |
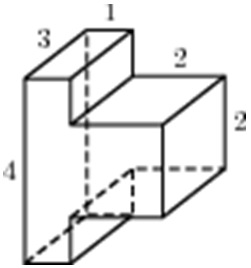 |
| Задача 26. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 45. |
 |
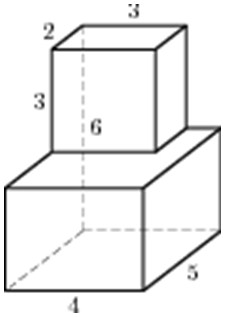
| Задача 27. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 78. |
 |
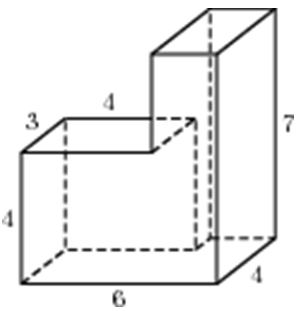
| Задача 28. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 104. |
 |
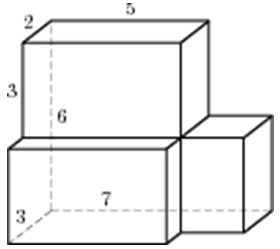
| Задача 29. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 87. |
 |
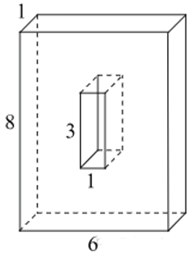
| Задача 30. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 114. |
 |
| Задача 31. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 78. |
 |
ЕГЭ по математике Профиль. Задание 5: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
ЕГЭ Профиль. Задание № 5
АЛГОРИТМ ВЫПОЛНЕНИЯ
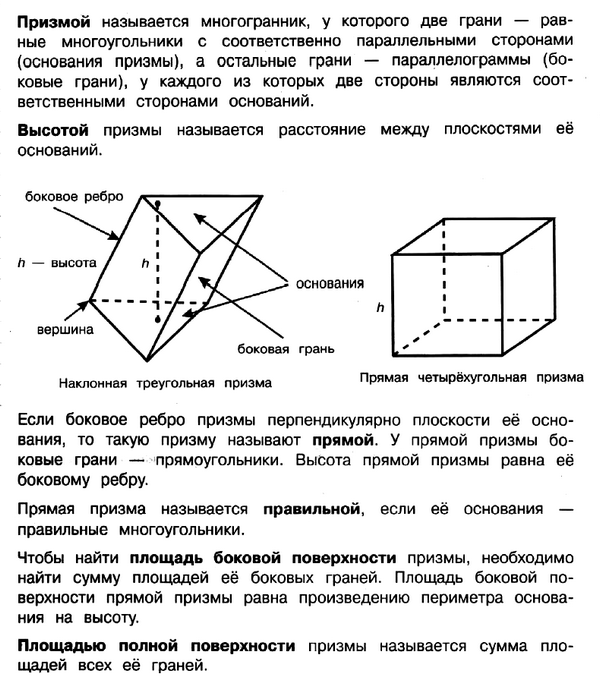
Задание № 5 рассчитано на умение решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов), использовать при выполнении знание свойств основных пространственных тел, применять планиметрические факты и методы.
Задание состоит из текстовой задачи и рисунка. Рассматриваются простые пространственные тела: куб, прямоугольный параллелепипед, правильная пирамида, правильная призма. Ответом является конечная десятичная дробь или целое число.
План выполнения:
- Внимательно прочитайте задачу.
- При необходимости выполните на черновике чертёж и дополнительные построения.
- Сделайте на черновике необходимые вычисления.
- Запишите полученное число в поле ответа КИМ и бланк ответов № 1.
Задачи на Прямоугольный параллепипед
Для решения подобных задач необходимо повторить свойства куба и прямоугольного параллелепипеда, формулы для вычисления площади поверхности, объёма этих тел.
Задача № 5 (1). Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 5. Объём параллелепипеда равен 30. Найдите площадь его поверхности.
Решение:
Ответ: 62.
Задачи на Составные многогранники
Задача № 5 (2). Найдите объём многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.
Решение:
Ответ: 84.
Задача № 5 (3). Найдите площадь поверхности многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.
Решение:
Ответ: 168.
Задачи на Призмы
Для решения задач этого типа необходимо повторить свойства призмы, формулы для вычисления площади поверхности и объёма призмы.
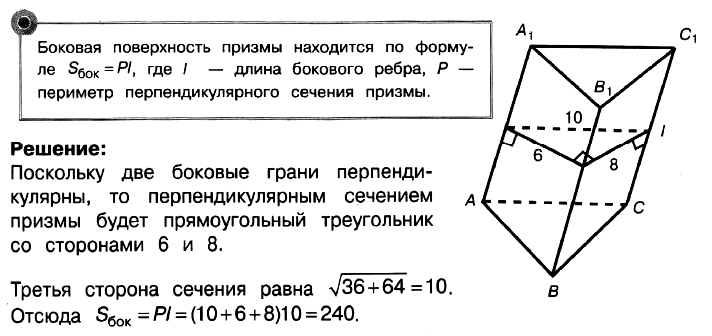
Задача № 5 (4). В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых рёбер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
Решение:
Ответ: 240.
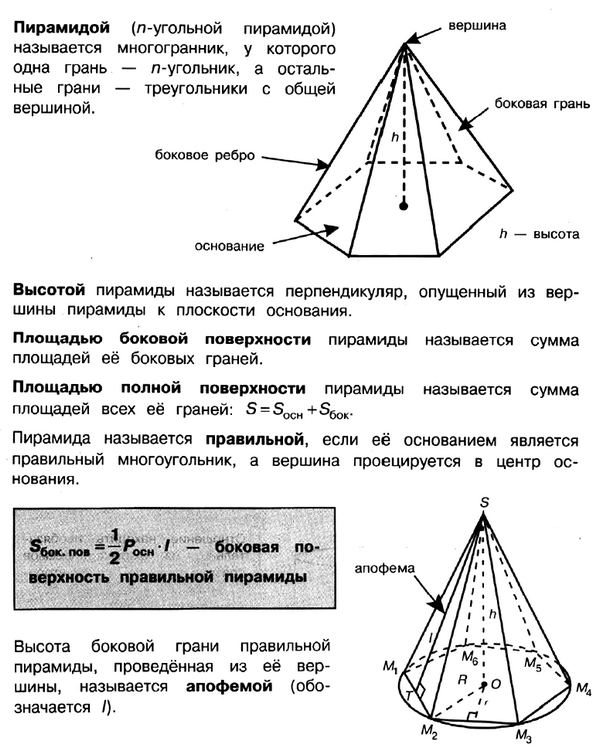
Задачи на Пирамиды
При подготовке нужно повторить основные свойства пирамиды, формулы для вычисления площади поверхности и объёма пирамиды.
Задача № 5 (5). Основание пирамиды — треугольник, у которого длины двух сторон равны 2 и 6, а угол между этими сторонами составляет 30°. Вычислите объём пирамиды, если её высота равна 3.
Решение:
Ответ: 3.
Задачи на Цилиндры
Для решения задач этого типа необходимо повторить формулы вычисления площади круга, длины окружности, площади поверхности цилиндра, объёма цилиндра.
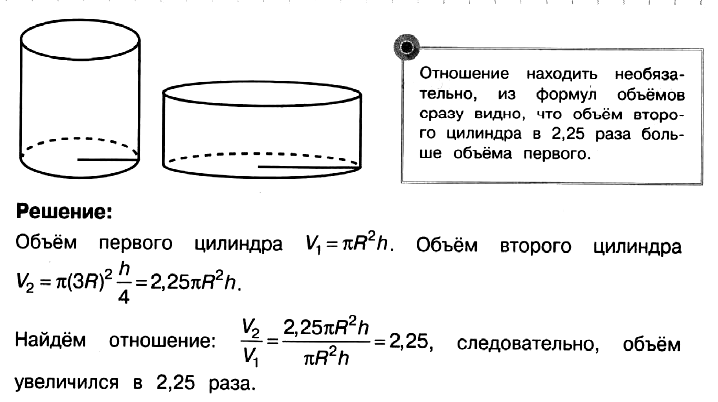
Задача № 5 (6). Радиус основания цилиндра увеличили в 3 раза, а его высоту уменьшили в 4 раза. Во сколько раз увеличится объём цилиндра?
Решение:
Ответ: 2,25.
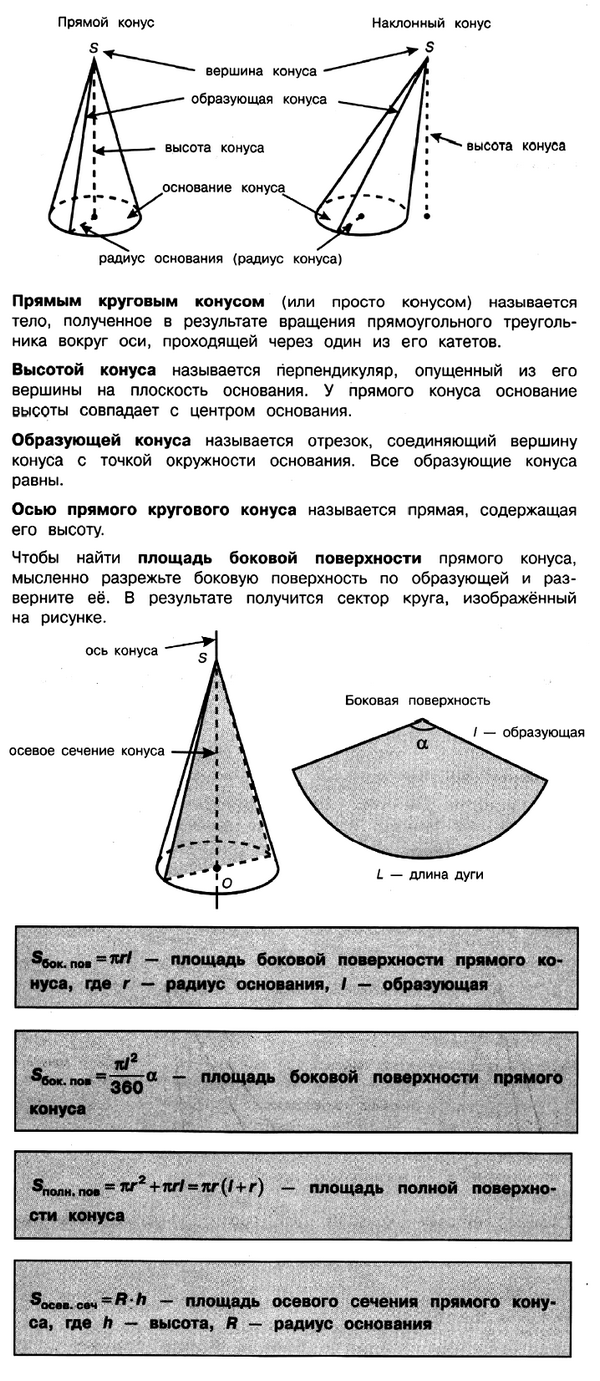
Задачи на Конусы
При подготовке необходимо повторить свойства конуса, формулы для вычисления площади поверхности и объёма конуса, площади круга и длины окружности.
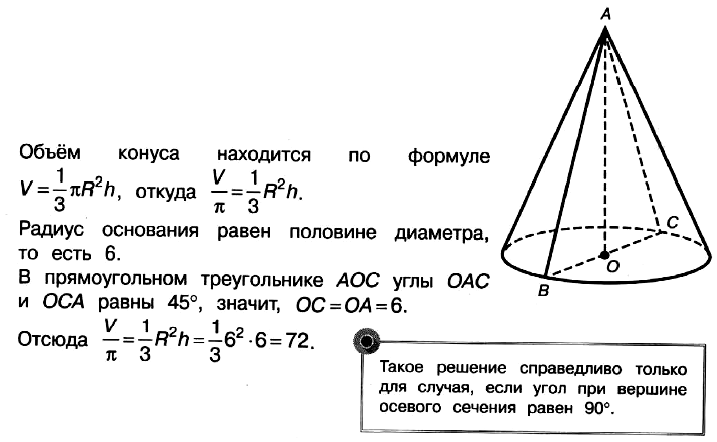
Задача № 5 (7). Диаметр основания конуса равен 12, угол при вершине осевого сечения равен 90°. Вычислите объём конуса, делённый на π.
Решение:
Ответ: 72.
Задачи на Шары
Для решения задач этого типа необходимо повторить формулы для вычисления площади круга, длины окружности, площади поверхности шара, объёма шара.
Задача № 5 (8). Площадь сечения шара плоскостью равна 36π см2. Найдите радиус шара, если плоскость находится на расстоянии 8 см от центра шара.
Решение:
Ответ: 10.
Задачи на Комбинации многогранников
и тел вращения
Задача № 5 (9). В основании прямой призмы лежит прямоугольный треугольник с катетами 3 и 4. Боковые рёбра призмы равны 4/π. Найдите объём цилиндра, описанного около этой призмы.
Решение:
Ответ: 25.
Задача № 5 (10). Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 15. Найдите площадь поверхности шара.
Решение:
Ответ: 10.
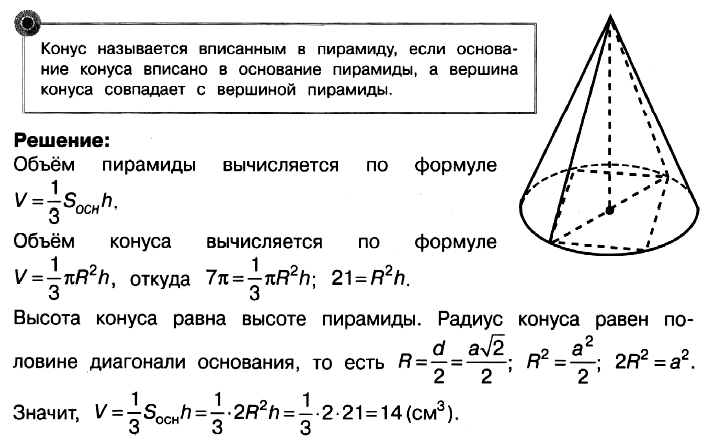
Задача № 5 (11). Объём конуса равен 7π см3. Найдите объём правильной четырёхугольной пирамиды, вписанной в конус.
Решение:
Ответ: 14.
Задача № 5 (12). Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 20. Найдите объём конуса.
Решение:
Ответ: 5.
Тренировочные задания с самопроверкой
№ 5.1. Площадь поверхности куба равна 72 (см. рис.). Найдите его диагональ.
Открыть ОТВЕТ
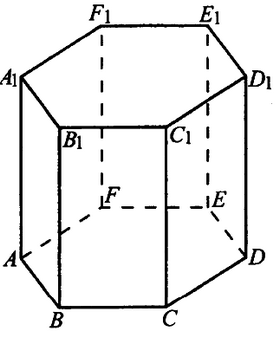
№ 5.2. Найдите объём многогранника, вершинами которого являются точки А, В, D, Е, А1, В1, D1, E1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1 (см. рис.). Площадь основания призмы равна 15, а боковое ребро равно 4.
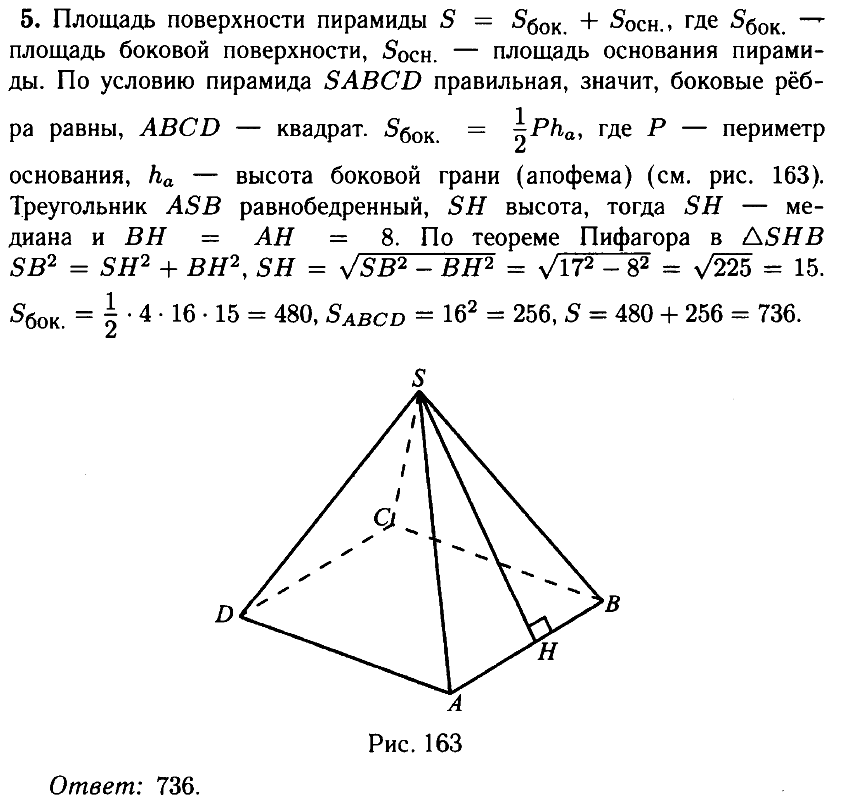
Открыть ОТВЕТ
№ 5.3. Стороны основания правильной четырёхугольной пирамиды равны 16, боковые рёбра равны 17 (см. рис.). Найдите площадь поверхности этой пирамиды.
Открыть ОТВЕТ
№ 5.4. В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты (см. рис.). Объём жидкости равен 60 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Открыть ОТВЕТ
№ 5.5. Найдите объём многогранника, вершинами которого являются точки А, В, С, В прямоугольного параллелепипеда ABCDA1B1C1D1, у которого АВ = 3, AD = 7, АА1 = 5 (см. рис.).
Открыть ОТВЕТ
Вы смотрели: ЕГЭ по математике Профиль. Задание 5: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
Просмотров:
13 610
Дидактический материал
Задачи ЕГЭ по теме «Многогранники»
-
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 1, а боковые рёбра равны 2. Точка N принадлежит ребру MC, причём MN: NC = 2:1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки B и N параллельно прямой AC.
Решение
Отрезок NK параллелен AC (точка K принадлежит ребру MA).
Пусть NK пересекает MO в точке P(O — центр основания пирамиды), причём тогда точка P является точкой пересечения медиан треугольника MBD. Прямая BP пересекает ребро MD в точке E. Четырёхугольник BNEK — искомое сечение.
Отрезок BE — медиана треугольника MBD, значит, ;
Поскольку прямая BD перпендикулярна плоскости MAC, диагонали BE и NK четырёхугольника BNEK перпендикулярны, следовательно, .
Ответ: .
2. Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD равна 108, а площадь полной поверхности этой пирамиды равна 144. Найдите площадь сечения, проходящего через вершину S этой пирамиды и через диагональ её основания.
Решение
Площадь основания пирамиды равна 144 − 108 = 36, поэтому AB = 6. Площадь боковой грани равна Пусть SM — высота грани SAB. Тогда поэтому SM = 9. Пусть SH — высота пирамиды. Имеем
Тогда
Ответ: 36.
3. Точка E — середина ребра CC1 куба ABCDA1B1C1D1. Найдите площадь сечения куба плоскостью A1BE, если ребра куба равны 2.
Решение
Прямая пересекает прямую в точке Прямая пересекает ребро в его середине — точке . — сечение куба плоскостью .
Равнобедренный треугольник подобен треугольнику и высота
Поскольку — средняя линия треугольника получаем:
Ответ: 4,5.
4. В правильной треугольной призме ABCA1B1C1 стороны основания равны 8, боковые рёбра равны . Изобразите сечение, проходящее через вершины A, C и середину ребра A1B1. Найдите его площадь.
Решение
Обозначим через и средины ребер и соответственно.
По теореме о средней линии треугольника так что прямые и лежат в одной плоскости. Сечение про которое спрашивается в условии, − это сечение призмы этой плоскостью. Оно представляет собой равнобокую трапецию Основания трапеции по теореме Пифагора найдем боковую сторону:
Проведем в трапеции высоту . Отрезок равен полуразности оснований трапеции:
Следовательно, высота трапеции Зная её, находим площадь трапеции:
Ответ: 30.
5. Дан куб c ребром, равным 4. Пусть точка лежит на стороне так, что Найдите расстояние от точки до плоскости , где — середина .
Решение
Введем декартову систему координат. В выбранной системе координат: Уравнение плоскости имеет вид: Пусть Найдем значения при
Искомое уравнение имеет вид: или
Расстояние от точки до указанной плоскости будем находить по формуле:
,где — координаты точки
.
Ответ: .
-
В основании прямой призмы лежит прямоугольный равнобедренный треугольник с прямым углом и гипотенузой . Найти расстояние от точки до прямой если точка — середина ребра , которое равно
Решение
По теореме Пифагора имеем:
Очевидно, что
Для получения искомого расстояния воспользуемся методом площадей. Найдем площадь равнобедренного треугольника Для этого вычислим высоту этого треугольника h, опущенную на основание
.
Это с одной стороны. Но с другой же стороны .
Следовательно,
Ответ: 6.
-
К диагонали куба провели перпендикуляры из середин ребер AB и AD. Найдите угол между этими перпендикулярами.
Решение
Пусть ребро куба равно О — центр куба, точки К и N — середины рёбер AD и AВ соответственно.
Заметим, что A1N = NC = , треугольник A1NC равнобедренный, его медиана NO является высотой, поэтому NО — перпендикуляр к AС. Аналогично KO перпендикуляр к АС.
Найдём угол KON. Введем систему координат как показано на рисунке. В этой системе координат:
Найдём угол между векторами из их скалярного произведения:
Следовательно, .
Ответ: 60°.
-
Точки — середины ребер и соответственно куба . Найти угол между прямой и плоскостью, проходящей через точку перпендикулярно прямой .
Решение
Координатно-векторный способ.
Пусть ребро куба равно 2.
Введем декартову систему координат, как показано на рис.
Найдем координаты необходимых точек:
Если — искомый угол, то:
Элементарно-геометрический подход.
Угол между заданной плоскостью и ребром будет равен углу между прямой , перпендикулярной к плоскости, и прямой PE, перпендикулярной к ребру
Треугольник — прямоугольный, к тому же равнобедренный. Следовательно, .
Ответ: .
9. Площадь треугольника, образованного диагональным сечением правильной четырёхугольной пирамиды SABCD с вершиной S, вдвое больше площади её основания.
а) Постройте это сечение;
б) Найдите косинус плоского угла при вершине пирамиды.
Решение
а) Соединим точки B и D отрезком. Проведем плоскость через точки S, B и D, не лежащие на одной прямой. Сечение построено. Это — треугольник BSD. Но таких сечений будет два: можно было бы построить также сечение, проходящие через АС — диагональ основания. Поскольку диагонали квадрата (основания) равны, боковые ребра правильной пирамиды также равны, то получим два равных решения. Для нашего случая достаточно взять одно решение: треугольник BSD
б) Проведем высоту пирамиды SO, O — точка пересечения АС и BD.
Для удобства дальнейших вычислений пусть сторона квадрата ABCD будет равна .Тогда
В по теореме косинусов будем иметь:
Ответ:
-
В треугольной пирамиде два ребра, исходящие из одной вершины, равны по а все остальные ребра равны по 2. Найдите объем пирамиды.
Решение
Пусть ребра пирамиды таковы, как показано на рисунке с точностью до обозначений вершин. (В основании пирамиды равносторонний треугольник со стороной 2). Пусть О — центр основания пирамиды.
Пусть K — середина отрезка AB. Проведем отрезки SK и CK.
Ясно, что
Рассмотрим треугольник SKC. Он равнобедренный, поскольку SK = SC = 2. SO — высота этого треугольника. Очевидно, что этот же отрезок будет служить высотой заданной пирамиды, так как наклонные SA = SB, BO = AO, поскольку KC — серединный перпендикуляр к отрезку AB. Значит, О — ортогональная проекция вершины пирамиды на плоскость (ABC).
.
Итак, .
Ответ: .