Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Каталог заданий.
Первообразная
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 4].
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2.
2
На рисунке изображён график некоторой функции
(два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 1., Пробный экзамен по математике Санкт-Петербург 2014. Вариант 1.
3
На рисунке изображён график функции y = f(x). Функция
— одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
4
На рисунке изображён график некоторой функции y = f(x). Функция
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Пройти тестирование по этим заданиям
Версия для печати и копирования в MS Word
1
На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 4].
Ответ:
2
На рисунке изображён график некоторой функции
(два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
Ответ:
3
На рисунке изображён график функции y = f(x). Функция
— одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
Ответ:
4
На рисунке изображён график некоторой функции y = f(x). Функция
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Ответ:
5
Завершить тестирование, свериться с ответами, увидеть решения.
Поиск
Всего: 29 1–20 | 21–29
Добавить в вариант
На рисунке изображён график некоторой функции
(два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 1., Пробный экзамен по математике Санкт-Петербург 2014. Вариант 1.
На рисунке изображён график функции y = f(x). Функция
— одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 4].
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2.
Источник: Пробный экзамен по математике Санкт-Петербург 2014. Вариант 2.
На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 4). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 3].
На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−4; 3). Найдите количество решений уравнения f(x) = 0 на отрезке [−3; 1].
На рисунке изображён график функции и одной из первообразных некоторой функции
определённой на интервале
Пользуясь рисунком, определите количество решений уравнения
на отрезке
Всего: 29 1–20 | 21–29
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Первообразная функции»
Открытый банк заданий по теме первообразная функции. Задания B7 из ЕГЭ по математике (профильный уровень)
Геометрические фигуры на плоскости: вычисление величин с использованием углов
Геометрические фигуры в пространстве: нахождение длины, площади, объема
Задание №1164
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(9)-F(5), где F(x) — одна из первообразных функции f(x).
Показать решение
Решение
По формуле Ньютона-Лейбница разность F(9)-F(5), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=9 и x=5. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 4 и 3 и высотой 3.
Её площадь равна frac{4+3}{2}cdot 3=10,5.
Ответ
10,5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1158
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-3; 4].
Показать решение
Решение
Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 4], в которых производная функции F(x) равна нулю. Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 7 (четыре точки минимума и три точки максимума).
Ответ
7
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1155
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(5)-F(0), где F(x) — одна из первообразных функции f(x).
Показать решение
Решение
По формуле Ньютона-Лейбница разность F(5)-F(0), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=5 и x=0. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 5 и 3 и высотой 3.
Её площадь равна frac{5+3}{2}cdot 3=12.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1149
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 4). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке (-3; 3].
Показать решение
Решение
Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 3], в которых производная функции F(x) равна нулю.
Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 5 (две точки минимума и три точки максимума).
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1146
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображен график некоторой функции y=f(x). Функция F(x)=-x^3+4,5x^2-7 — одна из первообразных функции f(x).
Найдите площадь заштрихованной фигуры.
Показать решение
Решение
Заштрихованная фигура является криволинейной трапецией, ограниченной сверху графиком функции y=f(x), прямыми y=0, x=1 и x=3. По формуле Ньютона-Лейбница её площадь S равна разности F(3)-F(1), где F(x) — указанная в условии первообразная функции f(x). Поэтому S= F(3)-F(1)= -3^3 +(4,5)cdot 3^2 -7-(-1^3 +(4,5)cdot 1^2 -7)= 6,5-(-3,5)= 10.
Ответ
10
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №907
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график некоторой функции y=f(x). Функция F(x)=x^3+6x^2+13x-5 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.
Показать решение
Решение
Заштрихованная фигура является криволинейной трапецией, ограниченной графиком функции y=f(x) и прямыми y=0, x=-4 и x=-1. По формуле Ньютона-Лейбница её площадь S равна разности F(-1)-F(-4), где F(x) — указанная в условии первообразная функции f(x).
Поэтому S= F(-1)-F(-4)= (-1)^3+6(-1)^2+13(-1)-5-((-4)^3+6(-4)^2+13(-4)-5)= -13-(-25)=12.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №307
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображен график некоторой функции y=f(x). Функция F(x)=x^3+18x^2+221x-frac12 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.
Показать решение
Решение
По формуле Ньютона-Лейбница S=F(-1)-F(-5).
F(-1)= (-1)^3+18cdot(-1)^2+221cdot(-1)-frac12= -204-frac12.
F(-5)= (-5)^3+18cdot(-5)^2+221cdot(-5)-frac12= -125+450-1105-frac12= -780-frac12.
F(-1)-F(-5)= -204-frac12-left (-780-frac12right)= 576.
Ответ
576
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №306
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображен график некоторой функции y=f(x).Пользуясь рисунком, вычислите F(9)-F(3), где F(x) — одна из первообразных функции f(x).
Показать решение
Решение
F(9)-F(3)=S, где S — площадь фигуры, ограниченной графиком функции y=f(x), прямыми y=0 и x=3,:x=9. Рассмотрим рисунок ниже.
Данная фигура — трапеция с основаниями 6 и 1 и высотой 2. Ее площадь равна frac{6+1}{2}cdot2=7.
Ответ
7
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №104
Тип задания: 7
Тема:
Первообразная функции
Условие
На координатной плоскости изображен график функции y=f(x). Одна из первообразных этой функции имеет вид: F(x)=-frac13x^3-frac52x^2-4x+2. Найдите площадь заштрихованной фигуры.
Показать решение
Решение
На рисунке видно, что заштрихованная фигура ограничена по оси абсцисс точками −4, −1, а по оси ординат графиком функции: f(x). Значит площадь фигуры мы можем найти с помощью разности значений первообразных в точках −4 и −1, по формуле определенного интеграла:
intlimits_{-4}^{-1}f(x)dx=F(-1)-F(-4)
Подставим значение первообразной из условия и получим площадь фигуры:
F(-1)-F(-4)=
=frac13-frac52+4+2-frac{64}{3}+frac{80}{2}-16-2=
=-frac{63}{3}+frac{75}{2}-12=-21+37,5-12=4,5
Ответ
4,5
Задание №103
Тип задания: 7
Тема:
Первообразная функции
Условие
Первообразная y=F(x) некоторой функции y=f(x) определена на интервале (−16; −2). Определите сколько решений имеет уравнение f(x) = 0 на отрезке [−10; −5].
Показать решение
Решение
Формула первообразной имеет следующий вид:
f(x) = F'(x)
По условию задачи нужно найти точки, в которых функция f(x) равна нулю. Принимая во внимание формулу первообразной, это значит, что, нужно найти точки, в которых F'(x) = 0, то есть те точки, в которых производная от первообразной равна нулю.
Мы знаем, что производная равна нулю в точках локального экстремума, т.е. функция имеет решения в тех точках, в которых возрастание F(x) сменяется убыванием и наоборот.
На отрезке [−10; −5] видно что это точки: −9; −7; −6. Значит уравнение f(x) = 0 имеет 3 решения.
Ответ
3
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
ЕГЭ Профиль №6. Первообразная
Скачать файл в формате pdf.
ЕГЭ Профиль №6. Первообразная
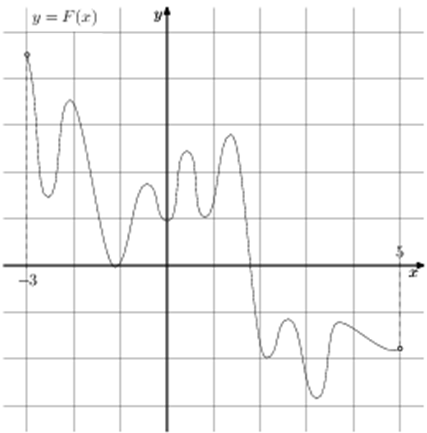
| Задача 1. На рисунке изображён график функции (y = Fleft( x right)) — одной из первообразных некоторой функции (fleft( x right)), определённой на интервале (left( { — 3;;5} right)). Пользуясь рисунком, определите количество решений уравнения (fleft( x right) = 0) на отрезке (left[ { — 2;;4} right]).
Ответ
ОТВЕТ: 10. |
 |
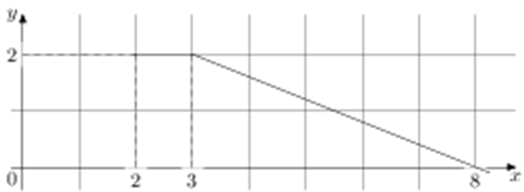
| Задача 2. На рисунке изображён график некоторой функции (y = fleft( x right)) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите (Fleft( 8 right) — Fleft( 2 right)), где (Fleft( x right))— одна из первообразных функции (fleft( x right)).
Ответ
ОТВЕТ: 7. |
 |
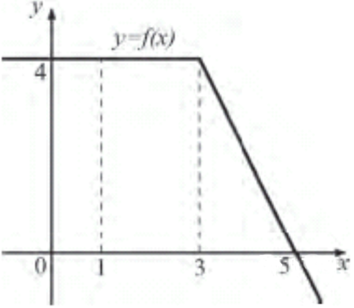
| Задача 3. На рисунке изображен график некоторой функции (y = fleft( x right)). Пользуясь рисунком, вычислите определенный интеграл (intlimits_1^5 {fleft( x right)} ,dx)
Ответ
ОТВЕТ: 12. |
 |
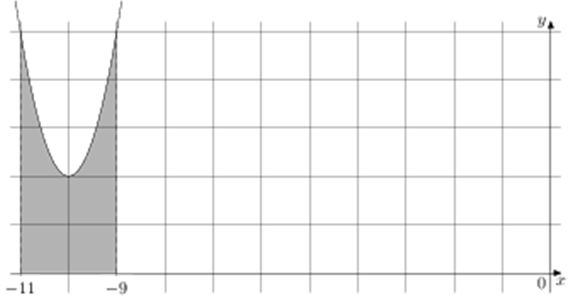
| Задача 4. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = {x^3} + 30{x^2} + 302x — frac{{15}}{8}) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры.
Ответ
ОТВЕТ: 6. |
 |
Задача 5. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = — {x^3} — 27{x^2} — 240x —  — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры. — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры.
Ответ
ОТВЕТ: 4. |
 |
| Задача6 . На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = frac{1}{2}{x^3} — frac{9}{2}{x^2} + 14x — 12) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры.
Ответ
ОТВЕТ: 6. |
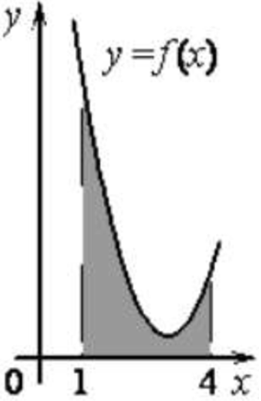 |
| Задача 7. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = — {x^3} — frac{9}{2}{x^2} — 6x — frac{{123}}{7}) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры.
Ответ
ОТВЕТ: 0,5. |
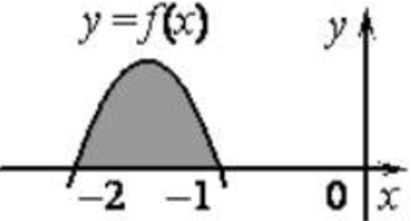 |
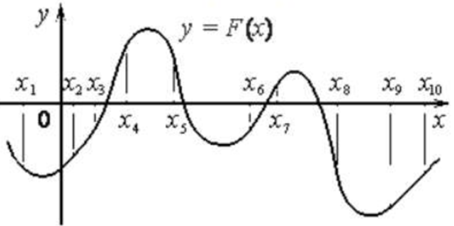
| Задача 8. На рисунке изображён график функции (y = Fleft( x right)) — одной из первообразных некоторой функции (fleft( x right)) и отмечены десять точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10. В скольки из этих точек функция (fleft( x right)) положительна?
Ответ
ОТВЕТ: 7. |
 |
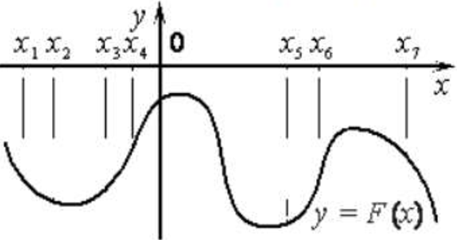
| Задача 9. На рисунке изображён график функции (y = Fleft( x right)) — одной из первообразных некоторой функции (fleft( x right)) и отмечены семь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7. В скольки из этих точек функция (fleft( x right)) отрицательна?
Ответ
ОТВЕТ: 3. |
 |
Блок 1. Физический смысл производной
| 1 | Материальная точка движется прямолинейно по закону x(t) = t^3 — 9t^2 + 2t +30 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени её скорость была равна 50 м/с? | Смотреть видеоразбор |
| 2 | Материальная точка движется прямолинейно по закону x(t)=−t^4+6t^3+5t+23, где x−расстояние от точки отсчета в метрах, t−время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3 с. | Смотреть видеоразбор |
Блок 2. Анализ графика функции, касательные
| 3 | На графике дифференцируемой функции у=f(x) отмечены семь точек: х1 ,…, х7. Найдите все отмеченные точки, в которых производная функции f(x) равна нулю. В ответе укажите количество этих точек. |
Смотреть видеоразбор |
| 4 | На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек x1, x2, …, x9. Среди этих точек найдите все точки, в которых производная функции f(x) отрицательна. В ответе укажите количество найденных точек.  |
Смотреть видеоразбор |
| 5 | На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой X0. Найдите значение производной функции f(x) в точке X0.  |
Смотреть видеоразбор |
| 6 | На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой X0. Найдите значение производной функции f(x) в точке X0.  |
Смотреть видеоразбор |
| 7 | На рисунке изображен график функции y = f(x) и отмечены точки -7, -3, 1, 5. В какой из этих точек значение производной этой функции наибольшее? В ответе укажите эту точку.  |
Смотреть видеоразбор |
| 8 | На рисунке изображен график функции y = f(x), одна из первообразных которой равна F(x). Найдите разность F(4) — F(-1). |
Смотреть видеоразбор |
| 9 | На рисунке изображен график функции y = f(x), определенной на интервале (-2; 12). Найдите сумму точек экстремума функции f(x). |
Смотреть видеоразбор |
| 10 | На рисунке изображен график функции y = f(x), определенной на интервале (-5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней. |
Смотреть видеоразбор |
| 11 | На рисунке изображен график функции y = f(x). Касательная к этому графику, проведенная в точке с абсциссой -1, проходит через начало координат. Найдите значение производной функции f(x) в точке -1.  |
Смотреть видеоразбор |
| 12 | На рисунке изображен график функции y=f(x) и касательная к этому графику, проведенная в точке x0. Уравнение касательной y=-2x-7. Найдите значение производной функции y=-frac{1}{4}f(x)+5x-3 в точке x0. |
Смотреть видеоразбор |
| 13 | На рисунке изображен график функции y=f(x), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции f(x) отрицательна. |
Смотреть видеоразбор |
| 14 | На рисунке изображен график функции y=f(x), определенной на интервале (-6;8). Определите количество целых точек, в которых производная функции положительна. |
Смотреть видеоразбор |
| 15 | На рисунке изображен график функции и шесть точек на оси абсцисс: x_1, x_2, x_3, x_4, x_5, x_6. В скольких из этих точек производная функции отрицательна? |
Смотреть видеоразбор |
| 16 | Функция f(x) определена на интервале (-4; 6). На рисунке изображен ее график. В скольких целых точках ее производная положительна? |
Смотреть видеоразбор |
Блок 3. Анализ графика производной
| 17 | На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-18; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-13;1]. |
Смотреть видеоразбор |
| 18 | На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6;9]. |
Смотреть видеоразбор |
| 19 | На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 3). В какой точке отрезка [-3; 2] функция f(x) принимает наибольшее значение? |
Смотреть видеоразбор |
| 20 | На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 4). В какой точке отрезка [-7; -3] функция f(x) принимает наименьшее значение? |
Смотреть видеоразбор |
| 21 | На рисунке изображён график y = f′(x) производной функции f(x) и шесть точек на оси абсцисс: x1 , x2 , . . . , x6. В скольких из этих точек функция f(x) возрастает? |
Смотреть видеоразбор |
| 22 | На рисунке изображен график y=f'(x) — производной функции f(x), определенной на интервале (-3; 19). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-2; 15]. |
Смотреть видеоразбор |
| 23 | На рисунке изображен график производной функции f(x) и отмечены одиннадцать точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11. В скольких из этих точек функция f(x) возрастает?  |
Смотреть видеоразбор |
| 24 | На рисунке изображен график производной функции f(x), определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=-2x-11 или совпадает с ней.  |
Смотреть видеоразбор |
| 25 | На рисунке изображен график производной функции f(x), определенной на интервале (-17; 2). Найдите число точек минимума функции y=f(x).  |
Смотреть видеоразбор |
| 26 | На рисунке изображен график производной функции f(x), определенной на интервале (-4; 4). Найдите абсциссу точки, в которой касательная к графику функции f(x) параллельна прямой y=-3x-11 или совпадает с ней. |
Смотреть видеоразбор |
| 27 | На рисунке изображен график производной функции f(x), определенной на интервале (-6; 8). Найдите количество таких чисел x, что касательная к графику функции f(x) в точке x параллельна прямой y=2x-5 или совпадает с ней. |
Смотреть видеоразбор |
| 28 | На рисунке изображен график производной функции f(x), определенной на интервале (-8; 4). В какой точке отрезка [-7; -2] функция f(x) принимает наибольшее значение?  |
Смотреть видеоразбор |
| 29 | Функция f(x) определена на отрезке [-6; 6]. На рисунке изображен график ее производной. Найдите наибольшую длину промежутка возрастания функции f(x). |
Смотреть видеоразбор |
| 30 | Функция y = f(x) определена и непрерывна на отрезке [-5; 5]. На рисунке изображен график её производной. Найдите точку x, в которой функция принимает наименьшее значение, если f(-5) больше либо равна f(5).  |
Смотреть видеоразбор |
Блок 4. Задачи на производную без готовых графиков
| 31 | Прямая y=-4x-11 является касательной к графику функции y=x^3+7x^2+7x-6. Найдите абсциссу точки касания. | Смотреть видеоразбор |
| 32 | Прямая y=7x-5 параллельна касательной к графику функции y=x^2+6x-8. Найдите абсциссу точки касания. | Смотреть видеоразбор |
Блок 5. Первообразная, интеграл
| 33 | На рисунке изображен график функции y=f(x). Функция F(x)=-x^3-21x^2-144x-frac{11}{4} — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры. |
Смотреть видеоразбор |
| 34 | На рисунке изображен график y=F(x) одной из первообразных некоторой функции f(x), определенной на интервале (-8; 7). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-5; 5].  |
Смотреть видеоразбор |
| 35 | На рисунке изображен график некоторой функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислить F(8)-F(2), где F(x) — одна из первообразных функции f(x). |
Смотреть видеоразбор |
| 36 | На рисунке изображен график некоторой функции y=f(x). Пользуясь рисунком, вычислите intlimits_{-7}^{-1} f(x)dx |
Смотреть видеоразбор |
| 37 | На рисунке изображен график некоторой функции y=f(x). Функция F(x) = x^3+30x^2+302x-frac{15}{8} — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры. |
Смотреть видеоразбор |
| 38 | На рисунке изображен график одной из первообразных некоторой функции, определенной на интервале (-3;5). Пользуясь рисунком, определите число корней уравнения на отрезке [-2;4]  |
Смотреть видеоразбор |
| 39 | На рисунке изображен график функции y = f(x). Пользуясь рисунком, вычислите F(8) — F(2), где F(x) — одна из первообразных функции f(x). |
Смотреть видеоразбор |
| 40 | На рисунке изображен график функции y=F(x) — одной из первообразных некоторой функции f(x), определенной на интервале (-3; 5). Пользуясь графиком, определите число корней уравнения f(x)=0 на отрезке [-2; 4]. |
Смотреть видеоразбор |
| 41 | На рисунке изображен график функции y=F(x) одной из первообразных некоторой функции f(x), определенной на интервале (-3; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [1; 4].  |
Смотреть видеоразбор |
| 42 | Значение первообразной F(x) функции f(x)=frac{7}{x} в точке 1 равно -11. Найдите F(e^2) | Смотреть видеоразбор |
Блок 6. Нестандартные задачи
- ЕГЭ по математике профиль
Прототипы задания №6 ЕГЭ по математике профильного уровня — производная и первообразная. Практический материал для подготовки к экзамену в 11 классе.
Для успешного выполнения задания №6 необходимо уметь выполнять действия с функциями.
Практика
Примеры заданий:
Коды проверяемых элементов содержания (по кодификатору) — 4.1–4.3
Уровень сложности задания — базовый.
Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 4
Связанные страницы:













.png)

.png)