Решу егэ математика профиль планиметрия

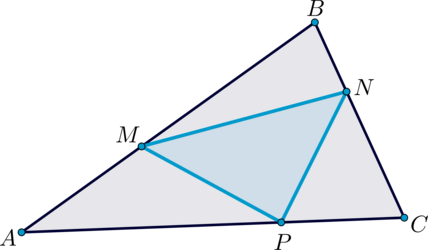
Точки (M, N, P) лежат на сторонах (AB, BC, CA) соответственно треугольника (ABC), причем (AM:AB=BN:BC=CP:CA=1:3). Площадь треугольника (MNP) равна (15). Найдите площадь треугольника (ABC).

Т.к. площади треугольников, имеющих общих угол, относятся как произведения сторон, образующих этот угол, то

[dfrac{S_{MBN}}{S_{ABC}}=dfrac{frac23BAcdot frac13BC}{BAcdot BC}=
dfrac29 quad Rightarrow quad S_{MBN}=dfrac29S_{ABC}]

Аналогично рассуждая, получаем, что

[S_{MAP}=S_{PCN}=dfrac29S_{ABC}]

Следовательно, [15+3cdot dfrac29S_{ABC}=S_{ABC} quad Rightarrow
quad S_{ABC}=3cdot 15=45.]

Ответ: 45

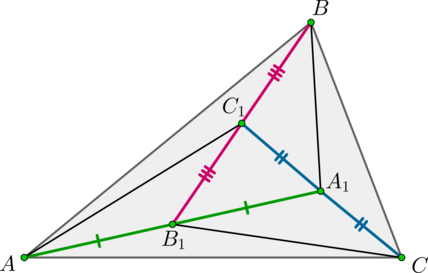
Внутри треугольника (ABC) взяты точки (A_1, B_1, C_1) так, что (B_1) – середина (AA_1), (C_1) – середина (BB_1), (A_1) – середина (CC_1). Найдите отношение площадей треугольников (A_1B_1C_1) и (ABC).

Т.к. медиана делит треугольник на два равновеликих треугольника, то

[S_{triangle AB_1C}=S_{triangle A_1B_1C}=S_{triangle A_1B_1C_1}.]

Аналогично,

[S_{triangle CA_1B}=S_{triangle C_1A_1B}=S_{triangle AC_1B}=S_{triangle
AC_1B_1}.]

Таким образом, все семь образовавшихся треугольников имеют одинаковые площади. Значит,

[S_{triangle A_1B_1C_1}:S_{triangle ABC}=1:7.]

Ответ:

(1:7)

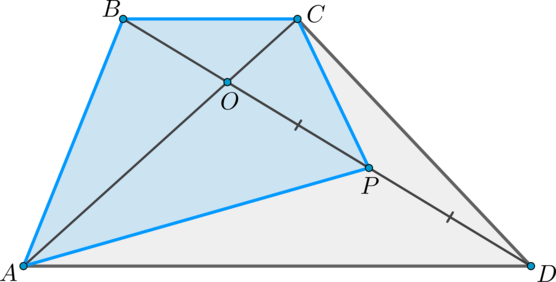
Дана трапеция (ABCD), ее основания (BC) и (AD) равны (2) и (6) соответственно. Диагонали (BD) и (AC) пересекаются в точке (O). Точка (P) – середина (OD). (S_{bigtriangleup ABO}=9). Найдите площадь четырехугольника (ABCP).

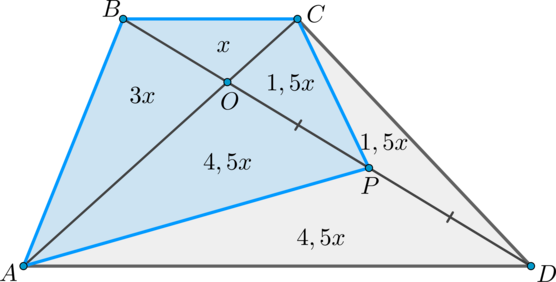
Пусть (S_{bigtriangleup BOC}=x). Заметим, что (bigtriangleup BCO
sim bigtriangleup AOD) по двум углам, так как (BCparallel AD), (angle BCA = angle CAD) как накрест лежащие и (angle BOC = angle
AOD) как вертикальные.

Следовательно, [dfrac{BC}{AD} =dfrac{BO}{OD} =dfrac{CO}{OA}
=dfrac{2}{6} =dfrac{1}{3}.]

(dfrac{S_{bigtriangleup ABO}}{S_{bigtriangleup BCO}}
=dfrac{AO}{OC} =dfrac{3}{1} Rightarrow S_{bigtriangleup
ABO}=3x), аналогично, (S_{bigtriangleup CDO}=3x).
 

(dfrac{S_{bigtriangleup COP}}{S_{bigtriangleup CPD}}
=dfrac{OP}{PD} =dfrac{1}{1} Rightarrow S_{bigtriangleup
COP}=S_{bigtriangleup CPD}=1,5x).
 

Площади подобных треугольников относятся как коэффициент подобия в квадрате, следовательно, [dfrac{S_{bigtriangleup BOC}}{S_{bigtriangleup AOD}} =left(
dfrac{1}{3} right)^2 =dfrac{1}{9} Rightarrow
S_{bigtriangleup ADO}=9x Rightarrow S_{bigtriangleup APO}=4,5x
Rightarrowqquad S_{ABCP}=10x.] Так как (3x=9), то (x=3) и, следовательно, (S_{ABCP}=30).

Ответ: 30

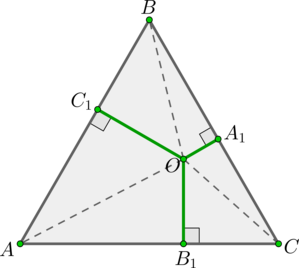
Внутри равностороннего треугольника со стороной (m) движется точка. Докажите, что сумма расстояний от этой точки до сторон треугольника не меняется, и найдите эту сумму.

Рассмотрим (triangle AOB, triangle BOC, triangle COA). Их площади равны (0,5mcdot OC_1; 0,5mcdot OA_1; 0,5mcdot OB_1) соответственно. Тогда сумма их площадей равна площади всего (triangle ABC), следовательно:

[0,5mcdot (OC_1+OA_1+OB_1)=S_{triangle ABC}=dfrac{sqrt3}4m^2 quad
Leftrightarrow quad OC_1+OA_1+OB_1=dfrac{sqrt3}2m.]

Таким образом, мы доказали, что для фиксированного равностороннего треугольника сумма постоянна, а также нашли ее.

Ответ:

(dfrac{sqrt3}2m)

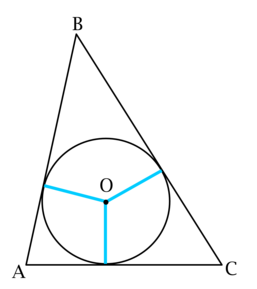
Радиус вписанной в треугольник (ABC) окружности равен трети одной из его высот.

а) Докажите, что одна из сторон треугольника (ABC) равна среднему арифметическому двух других его сторон.

б) Найдите наибольшее возможное значение периметра такого треугольника, если одна из его сторон равна (4), а две другие имеют целые длины.

а) (S_{ABC} = pcdot r), где (p) – полупериметр, а (r) – радиус вписанной в (ABC) окружности.

Пусть (h) – длина той высоты, которая равна (3r), (a) – длина стороны, высота к которой имеет длину (h), (P) – периметр треугольника (ABC).

В итоге имеем: [dfrac{1}{2}hcdot a = S_{ABC} = pcdot r = pcdotdfrac{h}{3},] откуда (a = dfrac{P}{3}), тогда (b + c = dfrac{2P}{3} = 2a), где (b) и (c) длины других сторон треугольника.

б) Длины сторон треугольника (ABC) образуют арифметическую прогрессию: если обозначить (a — c = d), то (a = c + d), (b = c + 2d).

Пусть (d > 0). Тогда (b) наибольшая сторона треугольника (ABC) и существование треугольника (ABC) с длинами сторон (a), (b) и (c) равносильно выполнению неравенства [b < a + cqquadLeftrightarrowqquad c + 2d < 2c + dqquadLeftrightarrowqquad d < c.] Так как длины всех сторон треугольника (ABC) – целые числа, то (d) – целое, следовательно, (dleq c — 1).

Так как (c) – меньшая из сторон, то (cleq 4), тогда (dleq 3), откуда (aleq 7), (bleq 10), тогда [P_{triangle ABC}leq 4 + 7 + 10 = 21.] При этом случай (c = 4), (a = 7), (b = 10) подходит, следовательно, при (d > 0) максимально возможный периметр равен 21.

При (d = 0) треугольник (ABC) равносторонний и (P_{triangle ABC} = 12 < 21).

Случай (d < 0) рассматривается аналогично (меняется только то, что (c > a > b), следовательно, достаточно в рассуждении из случая (d > 0) всюду поменять местами (b) и (c)).

Таким образом, наибольший возможный периметр треугольника (ABC) равен 21.

Ответ:

б) (21).

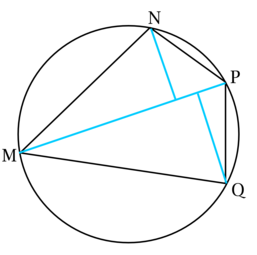
Четырёхугольник (MNPQ) вписан в окружность, причём (dfrac{MN}{PQ} = dfrac{QM}{PN}).

а) Докажите, что точки (N) и (Q) равноудалены от прямой, содержащей (MP).

б) Найдите расстояние от точки (P) до прямой, содержащей (MQ), если (MP = 4), расстояние от (N) до прямой, содержащей (MP) равно (1,5), (MQ = 3).

Так как (MNPQ) вписанный, то (angle MNP = 180^circ — angle MQP), следовательно, (sinangle MNP = sinangle MQP).

В итоге [S_{triangle MNP} = 0,5cdot MNcdot PNcdotsinangle MNP = 0,5cdot QMcdot PQcdotsinangle MQP = S_{triangle MQP}.]

С другой стороны, у треугольников (MNP) и (MQP) общее основание, следовательно, их площади относятся как высоты, проведённые к этому основанию, тогда эти высоты равны, значит, точки (N) и (Q) равноудалены от прямой, содержащей (MP).

б) В данном случае (S_{triangle MNP} = 0,5cdot 4cdot 1,5 = 3), но (S_{triangle MNP} = S_{triangle MQP}). Обозначим расстояние от точки (P) до прямой, содержащей (MQ) через (h), тогда [S_{triangle MQP} = 3 = 0,5cdot 3cdot h,] следовательно, (h = 2).

Ответ:

б) (2).

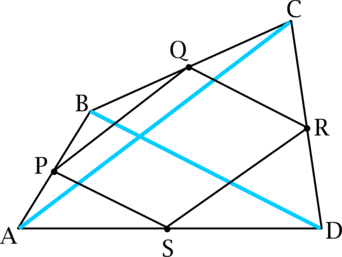
(ABCD) – выпуклый четырёхугольник, точки (P), (Q), (R) и (S) середины его сторон, причём (PQRS) тоже выпуклый четырёхугольник. (A_1B_1C_1D_1) другой выпуклый четырёхугольник с серединами сторон в точках (P), (Q), (R) и (S).

а) Докажите, что диагонали (PQRS) точкой пересечения делятся пополам.

б) Найдите максимально возможное значение величины (dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}}).

Рассмотрим треугольники (APS) и (ABD): (PS) – средняя линия в треугольнике (ABD), тогда треугольники (APS) и (ABD) подобны, причём (dfrac{PS}{BD} = dfrac{1}{2}).

Аналогично (dfrac{QR}{BD} = dfrac{1}{2}), следовательно, (PS = QR).

Аналогично доказывается равенство (PQ = RS). В итоге в выпуклом четырёхугольнике (PQRS) противоположные стороны равны, тогда (PQRS) – параллелограмм, следовательно, его диагонали точкой пересечения делятся пополам.

б) Докажем, что по взаимному расположению середин сторон выпуклого четырёхугольника его площадь восстанавливается однозначно.

Из подобия (APS) и (ABD) получаем: [dfrac{S_{APS}}{S_{ABD}} = left(dfrac{1}{2}right)^2 = dfrac{1}{4}.]

Аналогично (4S_{QCR} = S_{CBD}), (4S_{PBQ} = S_{ABC}), (4S_{SDR} = S_{ACD}). Тогда [S_{ABCD} = S_{ABD} + S_{CBD} = 4S_{APS} + 4S_{QCR}.] С другой стороны, [S_{ABCD} = S_{ABC} + S_{ACD} = 4S_{PBQ} + 4S_{SDR},] тогда [S_{ABCD} + S_{ABCD} = 4S_{APS} + 4S_{QCR} + 4S_{PBQ} + 4S_{SDR} qquadLeftrightarrow] [S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} = dfrac{1}{2}S_{ABCD}.] Но (S_{ABCD} = S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} + S_{PQRS}), откуда окончательно [S_{PQRS} = dfrac{1}{2}S_{ABCD}.]

Таким образом, по взаимному расположению точек (P), (Q), (R), (S) однозначно восстанавливается площадь параллелограмма (PQRS), а значит и площадь любого выпуклого четырёхугольника с серединами сторон в точках (P), (Q), (R) и (S).

В итоге [dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}} = 1.]

Ответ:

б) (1).