А. Ларин: Тренировочный вариант № 8.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Дано уравнение
а) Решите уравнение.
б) Найдите все корни на промежутке
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Ребро куба ABCDA1B1C1D1 равно 1. Найдите расстояние между прямыми AD1 и A1C1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите систему
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Четырехугольник KLMN вписан в окружность, его диагонали KM и LN пересекаются в точке F, причем KL = 8, MN = 4, периметр треугольника MNF равен 9, площадь треугольника KLF равна Найдите радиус окружности, описанной около треугольника KNF.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Найдите наименьшее значение a, при котором имеет решение система
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Лужков и Батурина поворачивают с Рублевки на МКАД в разные стороны — Лужков — налево, Батурина — направо. За сколько минут каждый из них проезжает полный круг по МКАД, если известно, что Лужков тратит на 12 минут меньше Батуриной, при этом проезжая круг не быстрее 31 минуты. Время проезда одного круга измеряется целым числом минут и их седьмая встреча произошла снова на Рублёвке.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Тренировочный вариант №8 решу ЕГЭ 2023 по математике профильный уровень с ответами и решением по новой демоверсии ЕГЭ 2023 года от ФИПИ для подготовки на 100 баллов в новом формате, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет.
Скачать вариант с ответами
Скачать решение каждого задания
Решу ЕГЭ 2023 математика профиль 8 вариант
вариант8-решу-егэ2023-профиль-математика
Задания и ответы с варианта
Задание 1. Острые углы прямоугольного треугольника равны 84° и 6°. Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Ответ: 78
Задание 2. В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 известно, что 𝐴𝐵 = 5, 𝐵𝐶 = 4, 𝐴𝐴1 = 3. Найдите объём многогранника, вершинами которого являются точки 𝐴, 𝐵, 𝐶, 𝐷, 𝐴1, 𝐵1.
Ответ: 30
Задание 3. В фирме такси в наличии 60 легковых автомобилей; 27 из них чёрного цвета с жёлтыми надписями на боках, остальные – жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
Ответ: 0, 55
Задание 4. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Протор», «Ротор» и «Мотор». Найдите вероятность того, что «Стартер» будет начинать только вторую и последнюю игры.
Ответ: 0, 125
Задание 5. Найдите корень уравнения √28 − 2𝑥 = 2.
Ответ: 12
Задание 7. На рисунке изображён график 𝑦 = 𝑓 ′(𝑥) − производной функции 𝑓(𝑥). На оси абсцисс отмечены шесть точек: 𝑥1, 𝑥2, 𝑥3, 𝑥4, 𝑥5, 𝑥6. Сколько из этих точек лежит на промежутках возрастания функции 𝑓(𝑥)?
Ответ: 3
Задание 8. Для сматывания кабеля на заводе используют лебёдку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону 𝜑 = 𝜔𝑡 + 𝛽𝑡 2 2 , где 𝑡 — время в минутах, прошедшее после начала работы лебёдки, 𝜔 = 50 град./мин — начальная угловая скорость вращения катушки, а 𝛽 = 4 град./мин2 — угловое ускорение, с которым наматывается кабель. Определите время, прошедшее после начала работы лебёдки, если известно, что за это время угол намотки 𝜑 достиг 2500°. Ответ дайте в минутах.
Ответ: 25
Задание 9. Семья состоит из мужа, жены и их дочери-студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Ответ: 27
Задание 10. На рисунке изображены графики функций видов 𝑓(𝑥) = 𝑎√𝑥 и 𝑔(𝑥) = 𝑘𝑥, пересекающиеся в точках 𝐴 и 𝐵. Найдите абсциссу точки 𝐵.
Ответ: 16
Задание 11. Найдите наибольшее значение функции 𝑦 = (𝑥 + 10) 2𝑥 + 7 на отрезке [−12; −6].
Ответ: 7
Задание 13. Точка 𝐸 лежит на высоте 𝑆𝑂, а точка 𝐹 − на боковом ребре 𝑆𝐶 правильной четырёхугольной пирамиды 𝑆𝐴𝐵𝐶𝐷, причём 𝑆𝐸: 𝐸𝑂 = 𝑆𝐹: 𝐹𝐶 = 2: 1. а) Докажите, что плоскость 𝐵𝐸𝐹 пересекает ребро 𝑆𝐷 в его середине. б) Найдите площадь сечения пирамиды плоскостью 𝐵𝐸𝐹, если 𝐴𝐵 = 8, 𝑆𝑂 = 14.
Задание 15. В июле 2016 года планируется взять кредит в банке на три года в размере 𝑆 млн рублей, где 𝑆 − целое число. Условия его возврата таковы: – каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года; – с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; – в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Задание 16. Диагонали 𝐴𝐶 и 𝐵𝐷 четырёхугольника 𝐴𝐵𝐶𝐷, вписанного в окружность, пересекаются в точке 𝑃, причём 𝐵𝐶 = 𝐶𝐷. а) Докажите, что 𝐴𝐵:𝐵𝐶 = 𝐴𝑃: 𝑃𝐷. б) Найдите площадь треугольника 𝐶𝑂𝐷, где 𝑂 − центр окружности, вписанной в треугольник 𝐴𝐵𝐷, если дополнительно известно, что 𝐵𝐷 − диаметр описанной около четырёхугольника 𝐴𝐵𝐶𝐷 окружности, 𝐴𝐵 = 6, а 𝐵𝐶 = 6√2.
Задание 18. Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более 2 11 от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более 2 5 от общего числа учащихся группы, посетивших кино.
- а) Могло ли быть в группе 9 мальчиков, если дополнительно известно, что всего в группе было 20 учащихся?
- б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 20 учащихся?
- в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а и б?
Смотрите также на нашем сайте:
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 варианты и ответы
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Тренировочный вариант №8 профильного ЕГЭ

Пробный вариант составлен на основе официальной демоверсии от ФИПИ за 2022 год.
В конце варианта приведены правильные ответы ко всем заданиям. Вы можете свериться с ними и найти у себя ошибки.
Скачать тренировочный вариант ЕГЭ: Скачать
Решать работу: Онлайн
Интересные задания
2. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Протор», «Ротор» и «Мотор». Найдите вероятность того, что «Стартер» будет начинать только вторую и последнюю игры.
5. В сосуде, имеющем форму конуса, уровень жидкости достигает 2/3 высоты. Объём жидкости равен 144 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
8. Два велосипедиста одновременно отправились в 160-километровый пробег. Первый ехал со скоростью, на 6 км/ч большей, чем скорость второго, и прибыл к финишу на 6 часов раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
10. Помещение освещается фонарём с двумя лампами. Вероятность перегорания
одной лампы в течение года равна 0,18. Найдите вероятность того, что в
течение года хотя бы одна лампа не перегорит.
13. В основании пирамиды 𝑆𝐴𝐵𝐶𝐷 лежит прямоугольник 𝐴𝐵𝐶𝐷 со стороной 𝐴𝐵 = 5 и диагональю 𝐵𝐷 = 9. Все боковые рёбра пирамиды равны 5. На диагонали 𝐵𝐷 основания 𝐴𝐵𝐶𝐷 отмечена точка 𝐸, а на ребре 𝐴𝑆 − точка 𝐹 так, что 𝑆𝐹 = 𝐵𝐸 = 4.
а) Докажите, что плоскость 𝐶𝐸𝐹 параллельна ребру 𝑆𝐵.
б) Плоскость 𝐶𝐸𝐹 пересекает ребро 𝑆𝐷 в точке 𝑄. Найдите расстояние от точки 𝑄 до плоскости 𝐴𝐵𝐶.
15. Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно 𝑡2 часов в неделю, то за эту неделю они производят 2𝑡 единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно 𝑡2 часов в неделю, то за эту неделю они производят 5𝑡 единиц товара. За каждый час работы (на каждом из заводов) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 580 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?
Вам будет интересно:
ЕГЭ по математике (профиль) 11 класс 2022. Новый тренировочный вариант №7 — №211018 (задания и ответы)
* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР
Поделиться:
В треугольнике ABC известно, что AC=BC, высота AH=8, BH=20. Найдите tg∠BAC.
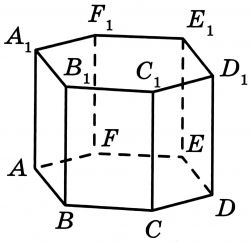
Найдите объём многогранника, вершинами которого являются вершины A₁,B₁,F₁,E правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 10, а боковое ребро равно 9.
В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвертым рейсом вертолёта.
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Найдите корень уравнения (left(dfrac19right)^{x+4}=729)
Найдите значение выражения (log_61{,}25cdotlog_{0{,}8}6)
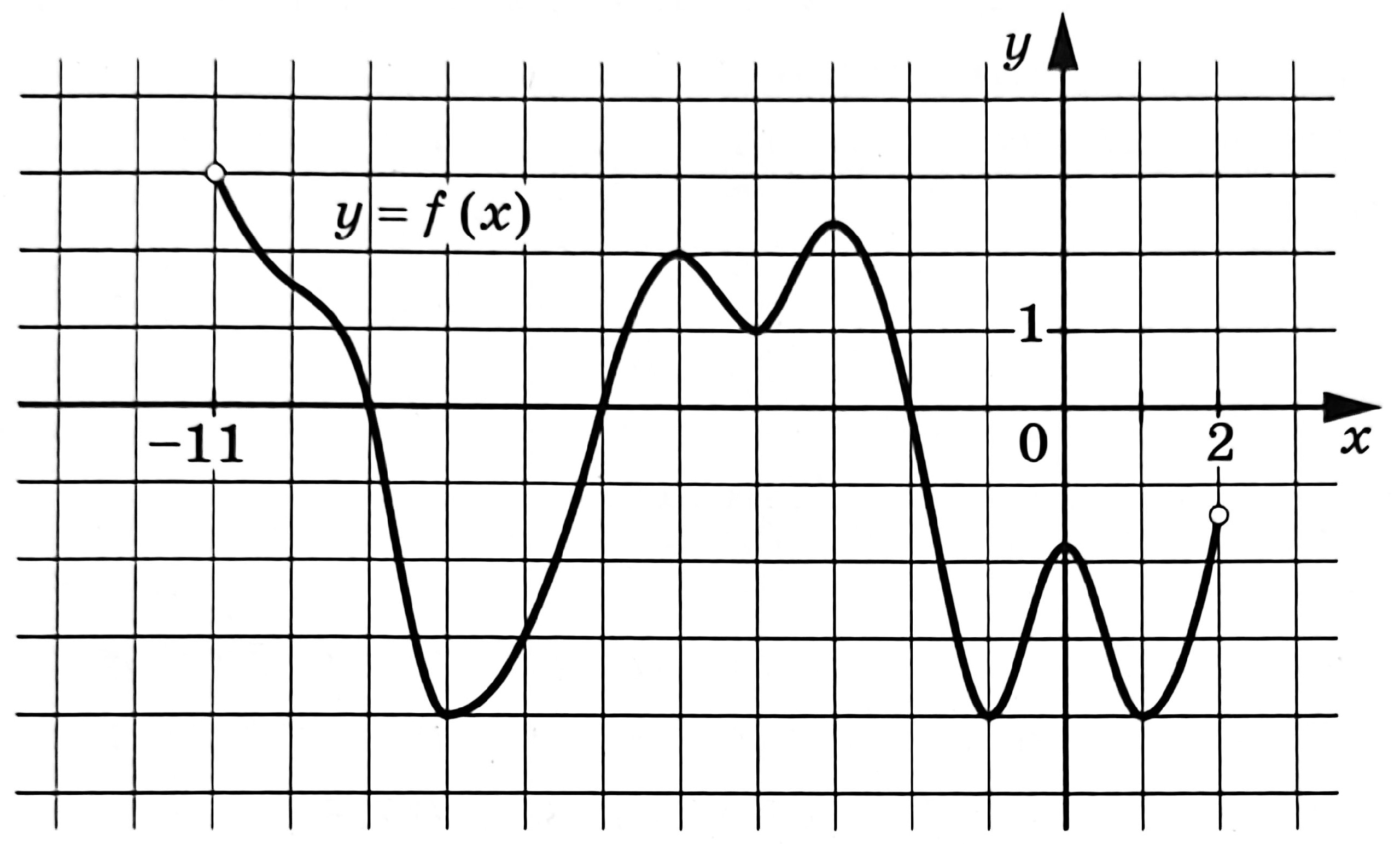
На рисунке изображен график функции y=f(x), определенной на интервале (-11;2). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна или совпадает с прямой y=-4.
Высота над землей подброшенного вверх мяча меняется по закону (h(t)=1+11t-5t^2), где (h) – высота в метрах, (t) – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Имеется два сосуда. Первый содержит 25 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
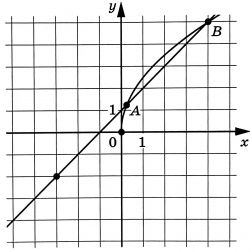
На рисунке изображены графики функций (f(x)=asqrt{x}) и (g(x)=kx+b), которые пересекаются в точках A и B. Найдите абсциссу точки A.
Найдите наименьшее значение функции (y=6x-6sin x+17) на отрезке (left[0;dfrac{pi}{2}right])
а) Решите уравнение (log^2_2(8x^2)-log_4(2x)-1=0)
б) Найдите все корни этого уравнения, принадлежащие отрезку ([0{,}4;0{,}8])
Сторона основания правильной четырехугольной пирамиды SABCD относится к боковому ребру как 1:√2. Через вершину D проведена плоскость α, перпендикулярная боковому ребру SB и пересекающая его в точке M.
а) Докажите, что сечение пирамиды SABCD плоскостью α – это четырехугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.
Решите неравенство (dfrac{sqrt{x-2}left(4-3^{x-1}right)}{2^{1-x^2}-3}geqslant0)
15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
– в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года;
– в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
– в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей. В ответ запишите количество миллионов.
Окружность с центром в точке C касается гипотенузы AB прямоугольного треугольника ABC и пересекает его катеты AC и BC в точках E и F. Точка D – основание высоты, опущенной на AB. I и J – центры окружностей, вписанных в треугольники BCD и ACD.
а) Докажите, что E и F лежат на прямой IJ.
б) Найдите расстояние от точки C до прямой IJ, если AC=2√3, BC=2.
Найдите все значения (a), при каждом из которых оба уравнения (a+dfrac{x}3=|x|) и (2a+x=sqrt{2a^2+4ax-x^2+12}) имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число n.
а) Может ли n равняться 64?
б) Может ли n равняться 78?
в) Какое наибольшее значение может принимать n, если все цифры ненулевые?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.

Пробный вариант № 8 ЕГЭ по математике профильного уровня на 2021 год составлен в соответствии с кодификатором ФИПИ и официальными демоверсиями.
Файл в формате pdf содержит задания, решения и ответы.
Скачать вариант в формате pdf — СКАЧАТЬ.
Вариант составлен авторами: Школа Пифагора.
Смотрите также:
- ЕГЭ по математике
- Расписание ЕГЭ 2021
- Шкала перевода баллов ЕГЭ
Одноклассники
Вконтакте
Мой мир