При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
В обменном пункте 1 гривна стоит 3 рубля 70 копеек. Отдыхающие обменяли рубли на гривны и купили 3 кг помидоров по цене 4 гривны за 1 кг. Во сколько рублей обошлась им эта покупка? Ответ округлите до целого числа.
Ответ:
2
На рисунке жирными точками показан курс евро, установленный Центробанком РФ, во все рабочие дни с 22 сентября по 22 октября 2010 года. По горизонтали указываются числа месяца, по вертикали — цена евро в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько рабочих дней из данного периода курс евро был ровно 41,4 рубля.
Ответ:
3
На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведённой к гипотенузе.
Ответ:
4
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Ответ:
5
Решите уравнение
Ответ:
6
7
На рисунке изображен график производной функции f(x), определенной на интервале (−8; 4). В какой точке отрезка [−7; −3] f(x) принимает наименьшее значение?
Ответ:
8
Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Ответ:
9
Найдите значение выражения
Ответ:
10
11
Расстояние между городами A и B равно 435 км. Из города A в город B со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах.
Ответ:
12
Найдите точку максимума функции
Ответ:
13
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
14
В пирамиде SABC в основании лежит правильный треугольник ABC со стороной
Точка O — основание высоты пирамиды, проведённой из вершины S.
а) Докажите, что точка O лежит вне треугольника ABC.
б) Найдите объём четырёхугольной пирамиды SABCO.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
15
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
16
17
На рисунке изображены графики функций вида $fleft(xright)=kx+b$, которые пересекаются в точке $A$. Найдите абсциссу точки $A$.
Ответ:
18
Найдите все значения a, при каждом из которых уравнение
имеет ровно один корень на отрезке [4; 8].
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
19
Возрастающие арифметические прогрессии и
состоят из натуральных чисел.
а) Существуют ли такие прогрессии, для которых ?
б) Существуют ли такие прогрессии, для которых ?
в) Какое наибольшее значение может принимать произведение если
?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Решать новый тренировочный вариант ЕГЭ № 33006758 по математике 11 класс профильный уровень, в данном варианте содержится 19 новых типовых заданий ЕГЭ.
Ссылка для скачивания варианта (заданий): скачать
Ссылка для скачивания ответов (решений) к варианту: скачать
Решать ЕГЭ новый вариант 33006758 по математике 11 класс онлайн:
Задания и ответы для с варианта 33006758:
Задание 1 №77334)В обменном пункте 1 гривна стоит 3 рубля 70 копеек. Отдыхающие обменяли рубли на гривны и купили 3 кг помидоров по цене 4 гривны за 1 кг. Во сколько рублей обошлась им эта покупка? Ответ округлите до целого числа.
Ответ: 44
Задание 2 №263631)На рисунке жирными точками показан курс евро, установленный Центробанком РФ, во все рабочие дни с 22 сентября по 22 октября 2010 года. По горизонтали указываются числа месяца, по вертикали — цена евро в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько рабочих дней из данного периода курс евро был ровно 41,4 рубля.
Ответ: 2
Задание 4 №320174)В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Ответ: 0, 9975
Задание 5 №77368)Решите уравнение (2x+7)2=(2x-1)2.
Ответ: -1,5
Задание 6 №27327)В треугольнике ABC AC=BC=27, AH-высота, sinBAC=2/3. Найдите BH.
Ответ: 30
Задание 7 №27492)На рисунке изображен график производной функции f(x), определенной на интервале (−8; 4). В какой точке отрезка [−7; −3] f(x) принимает наименьшее значение?
Ответ: -7
Задание 8 №27125)Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Ответ: 12
Задание 9 №27125)Найдите значение выражения log 0,8 3* log3 1,25.
Ответ: -1
Задание 10 №27969)Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому , где — мощность излучения звезды (в Ваттах), — постоянная, м — площадь поверхности звезды (в квадратных метрах), а — температура (в кельвинах). Известно, что площадь поверхности некоторой звезды равна м, а мощность её излучения равна Вт. Найдите температуру этой звезды в Кельвинах.
Ответ: 4000
Задание 11 №99590)Расстояние между городами и равно 435 км. Из города в город со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города автомобили встретятся? Ответ дайте в километрах.
Ответ: 240
Задание 12 №26725)Найдите точку максимума функции y=(x2-10x+10)e5-x.
Ответ: 10
Задание 13 №512335) а)Решите уравнение (tg2x-1) корень из 13cosx=0. б) Найдите все корни этого уравнения, принадлежащие отрезку [-3п;-3п/2].
Задание 14 №513253) В пирамиде SABC в основании лежит правильный треугольник ABC со стороной 2 корень из 3, SA=SC=корень из 33, SB=7. Точка O — основание высоты пирамиды, проведённой из вершины S. а) Докажите, что точка O лежит вне треугольника ABC. б) Найдите объём четырёхугольной пирамиды SABCO.
Задание 16 №509161) В прямоугольном треугольнике ABC с прямым углом C известны стороны AC = 12, BC = 5. Окружность радиуса 1/2 с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности. а) Докажите, что радиус второй окружности меньше, чем 1/5 длины катета AC. б) Найдите радиус второй окружности.
Ответ: 2
Задание 17 №509205) Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Ответ: 500 единиц товара
Задание 19 №516337)Возрастающие арифметические прогрессии a1 a2 an и b1, b2, bn состоят из натуральных чисел.
а)Существуют ли такие прогрессии, для которых a1b1+a3b3=3a2b2?
б)Существуют ли такие прогрессии, для которых a1b1+2a4b4=3a3b3?
в)Какое наибольшее значение может принимать произведение a3b3, если a1b1+2a4b4< 300?
Смотрите также другие варианты:
Новые тренировочные варианты ЕГЭ 2020 с ответами по математике профильный уровень
Архив работ
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Тренировочный вариант 33006758 ЕГЭ по математике профильный уровень с ответами
ПОДЕЛИТЬСЯ
Решать новый тренировочный вариант ЕГЭ № 33006758 по математике 11 класс профильный уровень, в данном варианте содержится 19 новых типовых заданий ЕГЭ.
Ссылка для скачивания варианта (заданий): скачать
Ссылка для скачивания ответов (решений) к варианту: скачать
Решать ЕГЭ новый вариант 33006758 по математике 11 класс онлайн:
Задания и ответы для с варианта 33006758:
Задание 1 №77334)В обменном пункте 1 гривна стоит 3 рубля 70 копеек. Отдыхающие обменяли рубли на гривны и купили 3 кг помидоров по цене 4 гривны за 1 кг. Во сколько рублей обошлась им эта покупка? Ответ округлите до целого числа.
Ответ: 44
Задание 2 №263631)На рисунке жирными точками показан курс евро, установленный Центробанком РФ, во все рабочие дни с 22 сентября по 22 октября 2010 года. По горизонтали указываются числа месяца, по вертикали — цена евро в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько рабочих дней из данного периода курс евро был ровно 41,4 рубля.
Ответ: 2
Задание 4 №320174)В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Ответ: 0, 9975
Задание 5 №77368)Решите уравнение (2x+7)2=(2x-1)2.
Ответ: -1,5
Задание 6 №27327)В треугольнике ABC AC=BC=27, AH-высота, sinBAC=2/3. Найдите BH.
Ответ: 30
Задание 7 №27492)На рисунке изображен график производной функции f(x), определенной на интервале (−8; 4). В какой точке отрезка [−7; −3] f(x) принимает наименьшее значение?
Ответ: -7
Задание 8 №27125)Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Ответ: 12
Задание 9 №27125)Найдите значение выражения log 0,8 3* log3 1,25.
Ответ: -1
Задание 10 №27969)Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому , где — мощность излучения звезды (в Ваттах), — постоянная, м — площадь поверхности звезды (в квадратных метрах), а — температура (в кельвинах). Известно, что площадь поверхности некоторой звезды равна м, а мощность её излучения равна Вт. Найдите температуру этой звезды в Кельвинах.
Ответ: 4000
Задание 11 №99590)Расстояние между городами и равно 435 км. Из города в город со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города автомобили встретятся? Ответ дайте в километрах.
Ответ: 240
Задание 12 №26725)Найдите точку максимума функции y=(x2-10x+10)e5-x.
Ответ: 10
Задание 13 №512335) а)Решите уравнение (tg2x-1) корень из 13cosx=0. б) Найдите все корни этого уравнения, принадлежащие отрезку [-3п;-3п/2].
Задание 14 №513253) В пирамиде SABC в основании лежит правильный треугольник ABC со стороной 2 корень из 3, SA=SC=корень из 33, SB=7. Точка O — основание высоты пирамиды, проведённой из вершины S. а) Докажите, что точка O лежит вне треугольника ABC. б) Найдите объём четырёхугольной пирамиды SABCO.
Задание 16 №509161) В прямоугольном треугольнике ABC с прямым углом C известны стороны AC = 12, BC = 5. Окружность радиуса 1/2 с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности. а) Докажите, что радиус второй окружности меньше, чем 1/5 длины катета AC. б) Найдите радиус второй окружности.
Ответ: 2
Задание 17 №509205) Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Ответ: 500 единиц товара
Задание 19 №516337)Возрастающие арифметические прогрессии a1 a2 an и b1, b2, bn состоят из натуральных чисел.
а)Существуют ли такие прогрессии, для которых a1b1+a3b3=3a2b2?
б)Существуют ли такие прогрессии, для которых a1b1+2a4b4=3a3b3?
в)Какое наибольшее значение может принимать произведение a3b3, если a1b1+2a4b4
13. Уравнения
Демонстрационный вариант ЕГЭ 2019 г. – задание №13. Найдите корни этого уравнения, принадлежащие отрезку.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение:
a) Запишем исходное уравнение в виде:
Значит, sinx = 0, откуда x = πk , k ∈ Ζ, или , откуда
б) С помощью числовой окружности отберём корни, принадлежащие отрезку
Ответ: а)
б)
Демонстрационный вариант ЕГЭ 2017, 2018 г. – задание №13. Найдите все корни этого уравнения, принадлежащие промежутку.
а) Решите уравнение cos2x=1-cos( -x)
б) Найдите все корни этого уравнения, принадлежащие промежутку
Решение:
Преобразуем обе части уравнения:
1− 2sin 2 x =1− sin x ; 2sin 2 x − sin x = 0 ; sin x( 2sin x −1) = 0 ,
откуда sin x = 0 или sin x = .
Из уравнения sin x = 0 находим: x = πn , где n∈Ζ.
Из уравнения sin x = находим: , где k∈Ζ.
б) С помощью числовой окружности отберём корни уравнения, принадлежащие промежутку
Ответ: а) , k∈Ζ.
б) .
Досрочный вариант ЕГЭ по математике 2017 профильный уровень задание №13.
а) Решите уравнение
8 x − 9⋅ 2 x +1 + 2 5−x = 0.
б) Укажите корни этого уравнения, принадлежащие отрезку [log5 2; log5 20].
Решение:
Умножим обе части на t:
Ответ: a)
Ответ: б)
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение:
а) Преобразуем уравнение:
Ответ: a)
б) С помощью числовой окружности отберём корни уравнения, принадлежащие промежутку
Ответ: б)
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение:
а) Преобразуем уравнение:
Пусть 2 x = t, тогда уравнение приметвид:
Ответ: а) 5;2+log29
5 не принадлежит
log235 Ответ: б) 2+log29
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение:
а) Преобразуем уравнение:
x1=-1 (не подходит по ОДЗ) ; x2=2 (подходит по ОДЗ) ; x3=-3 (подходит по ОДЗ)
Ответ: 2;-3
3) x 3 -2x 2 -5x-5>0
-3 -1 = -log34 не принадлежит
-1 Ответ: 2
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащего отрезку [2; 3].
Решение:
а) Преобразуем уравнение:
(t-3).(t-4)=0 => t=3 или t=4.
Ответ: ;
(frac<3><2>)^3″ align=»absmiddle» /> => не подходит
Ответ:
а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение:
а) Преобразуем уравнение:
т.к. степени одинаковые, основания можно опустить:
Ответ: 2;
2 не входит в заданный промежуток
Ответ: б)
а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение:
( только в том случае, если их степени равны 1)
Делаем обратную замену:
(возводим во вторую степень обе части ур-я)
Ответ: а) ;
Ответ: б) 3
Материалы для экспертов ЕГЭ 2016
а) Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие промежутку
Решение:
Ответ: а)
б) принадлежащие промежутку
Ответ:
ЕГЭ по математике 19.06.2014. Основная волна, резервный день. Запад. Вариант 1.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение:
Ответ:
б) принадлежащие отрезку
Ответ:
ЕГЭ — 2016 по математике. Основная волна 06.06.2016. Вариант 3 (C часть)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение:
Ответ:
б) принадлежащие отрезку
Ответ:
Примеры заданий №13 ЕГЭ 2017 Профиль.
Примеры заданий №13 с решениями ЕГЭ 2016 Профиль.
Подготовка к ЕГЭ, ОГЭ, ВПР и КДР
Подготовка к ЕГЭ, ОГЭ, ВПР и КДР по всем предметам с возможностью прохождения онлайн.
Более 100 вариантов и тысячи заданий с решениями.
Видео уроки.
ВАЖНО! Никаких реальных вариантов ЕГЭ ни до экзамена, ни во время его проведения на сайте нет, не было и не будет.
Задание 13 512335 а решите уравнение б найдите все корни этого уравнения принадлежащие отрезку

Задание. а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку [-3п/4; -п/4].
Решение:
Задание. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку [-5п/2; -п].
Решение:
Задание. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку [-2π; 3π/2].
Решение:
Задание. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку [-3π; π].
Решение:
Задание. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку [-3П/2; П].
Задания по теме «Тригонометрические уравнения»
Открытый банк заданий по теме тригонометрические уравнения. Задания C1 из ЕГЭ по математике (профильный уровень)
Задание №1179
Условие
а) Решите уравнение 2(sin x-cos x)=tgx-1.
б) Укажите корни этого уравнения, принадлежащие промежутку left[ frac<3pi >2;,3pi right].
Решение
а) Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 sin x-2 cos x-tg x=0. Учитывая, что cos x neq 0, слагаемое 2 sin x можно заменить на 2 tg x cos x, получим уравнение 1+2 tg x cos x-2 cos x-tg x=0, которое способом группировки можно привести к виду (1-tg x)(1-2 cos x)=0.
1) 1-tg x=0, tg x=1, x=fracpi 4+pi n, n in mathbb Z;
2) 1-2 cos x=0, cos x=frac12, x=pm fracpi 3+2pi n, n in mathbb Z.
б) С помощью числовой окружности отберём корни, принадлежащие промежутку left[ frac<3pi >2;, 3pi right].
x_1=fracpi 4+2pi =frac<9pi >4,
x_2=fracpi 3+2pi =frac<7pi >3,
x_3=-fracpi 3+2pi =frac<5pi >3.
Ответ
а) fracpi 4+pi n, pmfracpi 3+2pi n, n in mathbb Z;
б) frac<5pi >3, frac<7pi >3, frac<9pi >4.
Задание №1178
Условие
а) Решите уравнение (2sin ^24x-3cos 4x)cdot sqrt =0.
б) Укажите корни этого уравнения, принадлежащие промежутку left( 0;,frac<3pi >2right] ;
Решение
а) ОДЗ: begin tgxgeqslant 0\xneq fracpi 2+pi k,k in mathbb Z. end
Исходное уравнение на ОДЗ равносильно совокупности уравнений
left[!!begin 2 sin ^2 4x-3 cos 4x=0,\tg x=0. endright.
Решим первое уравнение. Для этого сделаем замену cos 4x=t, t in [-1; 1]. Тогда sin^24x=1-t^2. Получим:
t_1=frac12, t_2=-2, t_2notin [-1; 1].
4x=pm fracpi 3+2pi n,
x=pm fracpi <12>+frac<pi n>2, n in mathbb Z.
Решим второе уравнение.
tg x=0,, x=pi k, k in mathbb Z.
При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.
Знаком «+» отмечены 1 -я и 3 -я четверти, в которых tg x>0.
Получим: x=pi k, k in mathbb Z; x=fracpi <12>+pi n, n in mathbb Z; x=frac<5pi ><12>+pi m, m in mathbb Z.
б) Найдём корни, принадлежащие промежутку left( 0;,frac<3pi >2right].
Ответ
а) pi k, k in mathbb Z; fracpi <12>+pi n, n in mathbb Z; frac<5pi ><12>+pi m, m in mathbb Z.
Задание №1177
Условие
а) Решите уравнение: cos ^2x+cos ^2fracpi 6=cos ^22x+sin ^2fracpi 3;
б) Укажите все корни, принадлежащие промежутку left( frac<7pi >2;,frac<9pi >2right].
Решение
а) Так как sin fracpi 3=cos fracpi 6, то sin ^2fracpi 3=cos ^2fracpi 6, значит, заданное уравнение равносильно уравнению cos^2x=cos ^22x, которое, в свою очередь, равносильно уравнению cos^2x-cos ^2 2x=0.
Но cos ^2x-cos ^22x= (cos x-cos 2x)cdot (cos x+cos 2x) и
cos 2x=2 cos ^2 x-1, поэтому уравнение примет вид
(cos x-(2 cos ^2 x-1)),cdot (cos x+(2 cos ^2 x-1))=0,
(2 cos ^2 x-cos x-1),cdot (2 cos ^2 x+cos x-1)=0.
Тогда либо 2 cos ^2 x-cos x-1=0, либо 2 cos ^2 x+cos x-1=0.
Решая первое уравнение как квадратное уравнение относительно cos x, получаем:
(cos x)_<1,2>=frac<1pmsqrt 9>4=frac<1pm3>4. Поэтому либо cos x=1, либо cos x=-frac12. Если cos x=1, то x=2kpi , k in mathbb Z. Если cos x=-frac12, то x=pm frac<2pi >3+2spi , s in mathbb Z.
Аналогично, решая второе уравнение, получаем либо cos x=-1, либо cos x=frac12. Если cos x=-1, то корни x=pi +2mpi , m in mathbb Z. Если cos x=frac12, то x=pm fracpi 3+2npi , n in mathbb Z.
Объединим полученные решения:
x=mpi , m in mathbb Z; x=pm fracpi 3 +spi , s in mathbb Z.
б) Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.
Получим: x_1 =frac<11pi >3, x_2=4pi , x_3 =frac<13pi >3.
Ответ
а) mpi, m in mathbb Z; pm fracpi 3 +spi , s in mathbb Z;
б) frac<11pi >3, 4pi , frac<13pi >3.
Задание №1176
Условие
а) Решите уравнение 10cos ^2frac x2=frac<11+5ctgleft( dfrac<3pi >2-xright) ><1+tgx>.
б) Укажите корни этого уравнения, принадлежащие интервалу left( -2pi ; -frac<3pi >2right).
Решение
а) 1. Согласно формуле приведения, ctgleft( frac<3pi >2-xright) =tgx. Областью определения уравнения будут такие значения x , что cos x neq 0 и tg x neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 cos ^2 frac x2=1+cos x. Получим уравнение: 5(1+cos x) =frac<11+5tgx><1+tgx>.
Заметим, что frac<11+5tgx><1+tgx>= frac<5(1+tgx)+6><1+tgx>= 5+frac<6><1+tgx>, поэтому уравнение принимает вид: 5+5 cos x=5 +frac<6><1+tgx>. Отсюда cos x =frac<dfrac65><1+tgx>, cos x+sin x =frac65.
2. Преобразуем sin x+cos x по формуле приведения и формуле суммы косинусов: sin x=cos left(fracpi 2-xright), cos x+sin x= cos x+cos left(fracpi 2-xright)= 2cos fracpi 4cos left(x-fracpi 4right)= sqrt 2cos left( x-fracpi 4right) = frac65.
Отсюда cos left(x-fracpi 4right) =frac<3sqrt 2>5. Значит, x-fracpi 4= arccos frac<3sqrt 2>5+2pi k, k in mathbb Z,
или x-fracpi 4= -arccos frac<3sqrt 2>5+2pi t, t in mathbb Z.
Поэтому x=fracpi 4+arccos frac<3sqrt 2>5+2pi k,k in mathbb Z,
или x =fracpi 4-arccos frac<3sqrt 2>5+2pi t,t in mathbb Z.
Найденные значения x принадлежат области определения.
б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=fracpi 4+arccos frac<3sqrt 2>5 и b=fracpi 4-arccos frac<3sqrt 2>5.
1. Докажем вспомогательное неравенство:
Заметим также, что left( frac<3sqrt 2>5right) ^2=frac<18> <25>значит frac<3sqrt 2>5
2. Из неравенств (1) по свойству арккосинуса получаем:
Отсюда fracpi 4+0
Аналогично, -fracpi 4
0=fracpi 4-fracpi 4 fracpi 4
При k=-1 и t=-1 получаем корни уравнения a-2pi и b-2pi.
Bigg( a-2pi =-frac74pi +arccos frac<3sqrt 2>5,, b-2pi =-frac74pi -arccos frac<3sqrt 2>5Bigg). При этом -2pi
-2pi Значит, эти корни принадлежат заданному промежутку left( -2pi , -frac<3pi >2right).
При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.
Действительно, если kgeqslant 1 и tgeqslant 1, то корни больше 2pi. Если kleqslant -2 и tleqslant -2, то корни меньше -frac<7pi >2.
Ответ
а) fracpi4pm arccosfrac<3sqrt2>5+2pi k, kinmathbb Z;
б) -frac<7pi>4pm arccosfrac<3sqrt2>5.
Задание №1175
Условие
а) Решите уравнение sin left( fracpi 2+xright) =sin (-2x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [0; pi ];
Решение
а) Преобразуем уравнение:
cos x+2 sin x cos x=0,
x =fracpi 2+pi n, n in mathbb Z;
x=(-1)^cdot fracpi 6+pi k, k in mathbb Z.
б) Корни, принадлежащие отрезку [0; pi ], найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число fracpi 2.
Ответ
а) fracpi 2+pi n, n in mathbb Z; (-1)^cdot fracpi 6+pi k, k in mathbb Z;
б) fracpi 2.
Задание №1174
Условие
б) Найдите все корни этого уравнения, принадлежащие отрезку left[ -frac<3pi ><2>; -frac<pi >2 right].
Решение
а) Найдём ОДЗ уравнения: cos 2x neq -1, cos (pi +x) neq -1; Отсюда ОДЗ: x neq frac pi 2+pi k,
k in mathbb Z, x neq 2pi n, n in mathbb Z. Заметим, что при sin x=1, x=frac pi 2+2pi k, k in mathbb Z.
Полученное множество значений x не входит в ОДЗ.
Значит, sin x neq 1.
Разделим обе части уравнения на множитель (sin x-1), отличный от нуля. Получим уравнение frac 1<1+cos 2x>=frac 1<1+cos (pi +x)>, или уравнение 1+cos 2x=1+cos (pi +x). Применяя в левой части формулу понижения степени, а в правой — формулу приведения, получим уравнение 2 cos ^2 x=1-cos x. Это уравнение с помощью замены cos x=t, где -1 leqslant t leqslant 1 сводим к квадратному: 2t^2+t-1=0, корни которого t_1=-1 и t_2=frac12. Возвращаясь к переменной x , получим cos x = frac12 или cos x=-1, откуда x=frac pi 3+2pi m, m in mathbb Z, x=-frac pi 3+2pi n, n in mathbb Z, x=pi +2pi k, k in mathbb Z.
б) Решим неравенства
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 ,
2) -frac<3pi >2 leqslant -frac pi 3+2pi n leqslant -frac pi
3) -frac<3pi >2 leqslant pi+2pi k leqslant -frac pi 2 , m, n, k in mathbb Z.
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 , -frac32 leqslant frac13+2m leqslant -frac12 -frac<11>6 leqslant 2m leqslant -frac56 , -frac<11> <12>leqslant m leqslant -frac5<12>.
Нет целых чисел, принадлежащих промежутку left [-frac<11><12>;-frac5<12>right] .
2) -frac <3pi>2 leqslant -frac<pi >3+2pi n leqslant -frac<pi ><2>, -frac32 leqslant -frac13 +2n leqslant -frac12 , -frac76 leqslant 2n leqslant -frac1<6>, -frac7 <12>leqslant n leqslant -frac1<12>.
Нет целых чисел, принадлежащих промежутку left[ -frac7 <12>; -frac1 <12>right].
3) -frac<3pi >2 leqslant pi +2pi kleqslant -frac<pi >2, -frac32 leqslant 1+2kleqslant -frac12, -frac52 leqslant 2k leqslant -frac32, -frac54 leqslant k leqslant -frac34.
Этому неравенству удовлетворяет k=-1, тогда x=-pi.
Ответ
а) frac pi 3+2pi m; -frac pi 3+2pi n; pi +2pi k, m, n, k in mathbb Z;
источники:
http://onlyege.ru/uravneniya/
http://bezikev.ru/matege/zadanie-13/
http://academyege.ru/theme/trigonometricheskie-uravneniya-3.html
Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.
Тренировочные варианты ЕГЭ 2022 по математике (профиль)
| egemath.ru | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| variant 8 | скачать |
| variant 9 | скачать |
| variant 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 19 | скачать |
| variant 20 | скачать |
| yagubov.ru | |
| вариант 21 | ege2022-yagubov-prof-var21 |
| вариант 22 | ege2022-yagubov-prof-var22 |
| вариант 23 | ege2022-yagubov-prof-var23 |
| вариант 24 | ege2022-yagubov-prof-var24 |
| вариант 25 | ege2022-yagubov-prof-var25 |
| вариант 26 | ege2022-yagubov-prof-var26 |
| вариант 27 | ege2022-yagubov-prof-var27 |
| вариант 28 | ege2022-yagubov-prof-var28 |
| Досрочный Москва 28.03.2022 | скачать |
| egemathschool.ru | |
| вариант 1 | ответ |
| вариант 2 | ответ |
| вариант 3 | ответ |
| вариант 4 | ответ |
| ЕГЭ 100 баллов (с решениями) | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| Вариант 8 | скачать |
| Вариант 9 | скачать |
| Вариант 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 20 | скачать |
| variant 21 | скачать |
| variant 23 | скачать |
| variant 24 | скачать |
| variant 25 | скачать |
| variant 26 | скачать |
| variant 29 | скачать |
| variant 30 | скачать |
| math100.ru (с ответами) | |
| Вариант 140 | скачать |
| Вариант 141 | скачать |
| Вариант 142 | скачать |
| Вариант 143 | math100-ege22-v143 |
| Вариант 144 | math100-ege22-v144 |
| Вариант 145 | math100-ege22-v145 |
| Вариант 146 | math100-ege22-v146 |
| variant 147 | math100-ege22-v147 |
| variant 148 | math100-ege22-v148 |
| variant 149 | math100-ege22-v149 |
| variant 150 | math100-ege22-v150 |
| variant 151 | math100-ege22-v151 |
| variant 152 | math100-ege22-v152 |
| variant 153 | math100-ege22-v153 |
| variant 154 | math100-ege22-v154 |
| variant 155 | math100-ege22-v155 |
| variant 156 | math100-ege22-v156 |
| variant 157 | math100-ege22-v157 |
| variant 158 | math100-ege22-v158 |
| variant 159 | math100-ege22-v159 |
| variant 160 | math100-ege22-v160 |
| variant 161 | math100-ege22-v161 |
| variant 162 | math100-ege22-v162 |
| variant 163 | math100-ege22-v163 |
| variant 164 | math100-ege22-v164 |
| variant 165 | math100-ege22-v165 |
| variant 166 | math100-ege22-v166 |
| variant 167 | math100-ege22-v167 |
| variant 168 | math100-ege22-v168 |
| variant 169 | math100-ege22-v169 |
| variant 170 | math100-ege22-v170 |
| variant 171 | math100-ege22-v171 |
| variant 172 | math100-ege22-v172 |
| variant 173 | math100-ege22-v173 |
| variant 174 | math100-ege22-v174 |
| alexlarin.net | |
| Вариант 358 |
скачать |
| Вариант 359 | скачать |
| Вариант 360 | скачать |
| Вариант 361 | скачать |
| Вариант 362 | проверить ответы |
| Вариант 363 | проверить ответы |
| Вариант 364 | проверить ответы |
| Вариант 365 | проверить ответы |
| Вариант 366 | проверить ответы |
| Вариант 367 | проверить ответы |
| Вариант 368 | проверить ответы |
| Вариант 369 | проверить ответы |
| Вариант 370 | проверить ответы |
| Вариант 371 | проверить ответы |
| Вариант 372 | проверить ответы |
| Вариант 373 | проверить ответы |
| Вариант 374 | проверить ответы |
| Вариант 375 | проверить ответы |
| Вариант 376 | проверить ответы |
| Вариант 377 | проверить ответы |
| Вариант 378 | проверить ответы |
| Вариант 379 | проверить ответы |
| Вариант 380 | проверить ответы |
| Вариант 381 | проверить ответы |
| Вариант 382 | проверить ответы |
| Вариант 383 | проверить ответы |
| Вариант 384 | проверить ответы |
| Вариант 385 | проверить ответы |
| Вариант 386 | проверить ответы |
| Вариант 387 | проверить ответы |
| Вариант 388 | проверить ответы |
| vk.com/ekaterina_chekmareva (задания 1-12) | |
| Вариант 1 | ответы |
| Вариант 2 | |
| Вариант 3 | |
| Вариант 4 | |
| Вариант 5 | |
| Вариант 6 | |
| Вариант 7 | ответы |
| Вариант 8 | |
| Вариант 9 | |
| Вариант 10 | |
| vk.com/matematicalate | |
| Вариант 1 | matematikaLite-prof-ege22-var1 |
| Вариант 2 | matematikaLite-prof-ege22-var2 |
| Вариант 3 | matematikaLite-prof-ege22-var3 |
| Вариант 4 | matematikaLite-prof-ege22-var4 |
| Вариант 5 | matematikaLite-prof-ege22-var5 |
| Вариант 6 | matematikaLite-prof-ege22-var6 |
| Вариант 7 | matematikaLite-prof-ege22-var7 |
| Вариант 8 | matematikaLite-prof-ege22-var8 |
| vk.com/pro_matem | |
| variant 1 | pro_matem-prof-ege22-var1 |
| variant 2 | pro_matem-prof-ege22-var2 |
| variant 3 | pro_matem-prof-ege22-var3 |
| variant 4 | разбор |
| variant 5 | разбор |
| vk.com/murmurmash | |
| variant 1 | otvet |
| variant 2 | otvet |
| → Купить сборники тренировочных вариантов ЕГЭ 2022 по математике |
Структура варианта КИМ ЕГЭ
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Связанные страницы:
Средний балл ЕГЭ 2021 по математике
Решение задач с параметром при подготовке к ЕГЭ
Изменения в КИМ ЕГЭ 2022 года по математике
Купить сборники типовых вариантов ЕГЭ по математике
Как решать экономические задачи ЕГЭ по математике профильного уровня?
В треугольнике ABC известно, что AC=BC, высота AH=8, BH=20. Найдите tg∠BAC.
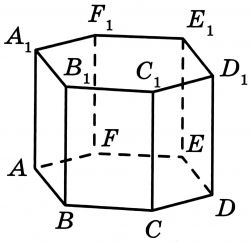
Найдите объём многогранника, вершинами которого являются вершины A₁,B₁,F₁,E правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 10, а боковое ребро равно 9.
В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвертым рейсом вертолёта.
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Найдите корень уравнения (left(dfrac19right)^{x+4}=729)
Найдите значение выражения (log_61{,}25cdotlog_{0{,}8}6)
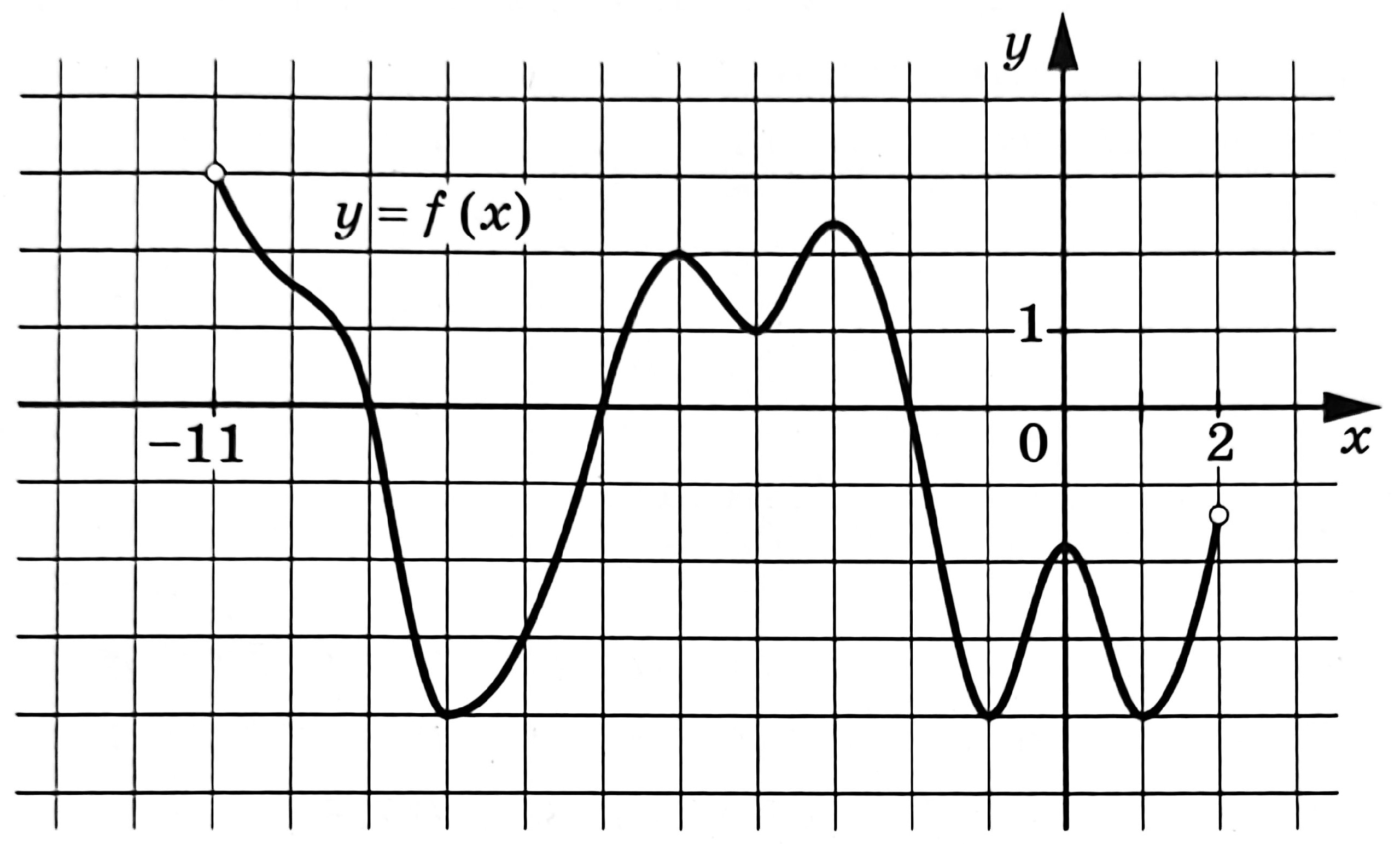
На рисунке изображен график функции y=f(x), определенной на интервале (-11;2). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна или совпадает с прямой y=-4.
Высота над землей подброшенного вверх мяча меняется по закону (h(t)=1+11t-5t^2), где (h) – высота в метрах, (t) – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Имеется два сосуда. Первый содержит 25 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
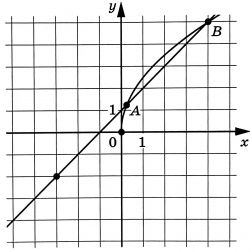
На рисунке изображены графики функций (f(x)=asqrt{x}) и (g(x)=kx+b), которые пересекаются в точках A и B. Найдите абсциссу точки A.
Найдите наименьшее значение функции (y=6x-6sin x+17) на отрезке (left[0;dfrac{pi}{2}right])
а) Решите уравнение (log^2_2(8x^2)-log_4(2x)-1=0)
б) Найдите все корни этого уравнения, принадлежащие отрезку ([0{,}4;0{,}8])
Сторона основания правильной четырехугольной пирамиды SABCD относится к боковому ребру как 1:√2. Через вершину D проведена плоскость α, перпендикулярная боковому ребру SB и пересекающая его в точке M.
а) Докажите, что сечение пирамиды SABCD плоскостью α – это четырехугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.
Решите неравенство (dfrac{sqrt{x-2}left(4-3^{x-1}right)}{2^{1-x^2}-3}geqslant0)
15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
– в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года;
– в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
– в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей. В ответ запишите количество миллионов.
Окружность с центром в точке C касается гипотенузы AB прямоугольного треугольника ABC и пересекает его катеты AC и BC в точках E и F. Точка D – основание высоты, опущенной на AB. I и J – центры окружностей, вписанных в треугольники BCD и ACD.
а) Докажите, что E и F лежат на прямой IJ.
б) Найдите расстояние от точки C до прямой IJ, если AC=2√3, BC=2.
Найдите все значения (a), при каждом из которых оба уравнения (a+dfrac{x}3=|x|) и (2a+x=sqrt{2a^2+4ax-x^2+12}) имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число n.
а) Может ли n равняться 64?
б) Может ли n равняться 78?
в) Какое наибольшее значение может принимать n, если все цифры ненулевые?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Информация о генераторе вариантов:

Источники заданий:
1) Прототипы из fipi.ru;
2) Прототипы из os.fipi.ru;
3) Прототипы с реальных ЕГЭ всех лет;
4) Прототипы с mathege.ru.
На каждую позицию рандомно выпадает случайное задание из базы заданий.
Описание каждой из позиций №1–18:





• Задание 6. Вычисления и преобразования – на данный момент 10 прототипов.




Условия прототипов заданий первой части взяты у Евгения Пифагора из его видеокурса: «1–11 задания ЕГЭ профиль (первая часть с нуля)».
• Задание 12. Уравнения – на данный момент 10 прототипов.
• Задание 13. Стереометрическая задача – на данный момент 4 прототипа.
• Задание 14. Неравенства – на данный момент 10 прототипов.
• Задание 15. Финансовая математика – на данный момент 9 прототипов.
• Задание 16. Планиметрическая задача – на данный момент 4 прототипа.
• Задание 17. Задача с параметром – на данный момент 7 прототипов.
• Задание 18. Числа и их свойства – на данный момент 9 прототипов.


Примеры заданий, развёрнутая часть.

Время выполнения варианта.



Теги: тренировочные варианты, 11 класс, 2021, с ответами, новый вариант, профиль, пробный егэ.









.png)