Задания
Версия для печати и копирования в MS Word
а) Решите уравнение
б) Найдите решения уравнения, принадлежащие отрезку
Спрятать решение
Решение.
а) Сделаем замену переменной: Получаем
или
Тогда:
Заметим, что и поэтому,
получаем:
Равенство верно только для неположительных значений a. Поэтому
откуда
б) В силу цепочки неравенств
из всех решений уравнения на отрезке лежат только решения
Ответ: а) б)
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а),
ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Наиль Фаттахов 13.12.2016 22:23
Почему написано решить уравнение, а в решении рассматривается неравенство. решая уравнение х=8. при проверке он удовлетворяет исходному равенству. непонятно, почему в ответе интервал.
Кирилл Колокольцев
Решением уравнения могут быть не только дискретные значения, но и целые множества, как в данном случае. Аналогично с неравенствами: решением может быть не интервал, а точка.
Решу егэ математика 507572
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 12 № 507577
A) Решите уравнение
Б) Определите, являются ли решениями уравнения числа 1,5 и
А) Сделаем замену переменной Получаем:
Учитывая, что и поэтому преобразуем уравнение:
Равенство верно только для неположительных значений A. Поэтому
Ответ к пункту а):
Б) Число 1,5 лежит в найденном отрезке, поэтому является решением уравнения. Число не является решением уравнения, поскольку
—>
Задание 12 № 507577
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Ege. sdamgia. ru
07.07.2017 0:55:59
2017-07-07 00:55:59
Источники:
Https://ege. sdamgia. ru/test? likes=507572
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика 507572
Решу егэ математика 507572
Решу егэ математика 507572
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 12 № 507572
А) Решите уравнение
Б) Найдите решения уравнения, принадлежащие отрезку
А) Сделаем замену переменной: Получаем или Тогда:
Заметим, что и поэтому, получаем:
Равенство верно только для неположительных значений A. Поэтому откуда
Б) В силу цепочки неравенств из всех решений уравнения на отрезке лежат только решения
—>
Задание 12 № 507572
А Сделаем замену переменной Получаем или Тогда.
Ege. sdamgia. ru
13.09.2019 21:24:40
2019-09-13 21:24:40
Источники:
Https://ege. sdamgia. ru/problem? id=507572
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика 507572
Решу егэ математика 507572
Решу егэ математика 507572
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 12 № 507572
А) Решите уравнение
Б) Найдите решения уравнения, принадлежащие отрезку
А) Сделаем замену переменной: Получаем или Тогда:
Заметим, что и поэтому, получаем:
Равенство верно только для неположительных значений A. Поэтому откуда
Б) В силу цепочки неравенств из всех решений уравнения на отрезке лежат только решения
Почему написано решить уравнение, а в решении рассматривается неравенство. решая уравнение х=8. при проверке он удовлетворяет исходному равенству. непонятно, почему в ответе интервал.
Решением уравнения могут быть не только дискретные значения, но и целые множества, как в данном случае. Аналогично с неравенствами: решением может быть не интервал, а точка.
Задание 12 № 507572
—>
Задание 12 507572.
Ege. sdamgia. ru
21.06.2020 8:21:52
2020-06-21 08:21:52
Источники:
Https://ege. sdamgia. ru/test? pid=507572
Тренировочный вариант №26 пробник решу ЕГЭ 2023 по математике 11 класс профильный уровень от 8 марта 2023 года с ответами и решением по новой демоверсии ЕГЭ 2023 года для подготовки на 100 баллов, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
▶Скачать вариант с ответами
▶Решение заданий с 1 по 18
▶Распечатай и реши вариант
вариант_26_егэ2023_профиль_математика
Ответы и решения
решение_варианта_26_профиль
1. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, sin 𝐴 = 0,8. Найдите sin 𝐵.
2. Дана правильная треугольная призма 𝐴𝐵𝐶𝐴1𝐵1𝐶1, площадь основания которой равна 9, а боковое ребро равно 4. Найдите объём многогранника, вершинами которого являются точки 𝐴, 𝐴1, 𝐵1, 𝐶1.
3. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что произведение выпавших очков делится на 5, но не делится на 30.
4. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,98. Вероятность того, что масса окажется больше 790 г, равна 0,83. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
7. На рисунке изображён график дифференцируемой функции 𝑦 = 𝑓(𝑥), определённой на интервале (−3; 8). Найдите точку из отрезка [−2; 5], в которой производная функции 𝑓(𝑥) равна 0.
8. Два тела, массой 𝑚 = 2 кг каждое, движутся с одинаковой скоростью 𝑣 = 8 м/с под углом 2𝛼 друг к другу. Энергия (в Дж), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле 𝑄 = 𝑚𝑣 2 sin2𝛼, где 𝑚 − масса (в кг), 𝑣 − скорость (в м/с). Найдите, под каким углом 2𝛼 должны двигаться тела, чтобы в результате соударения выделилась энергия, равная 32 Дж. Ответ дайте в градусах.
9. Смешали некоторое количество 19-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
10. На рисунке изображён график функции вида 𝑓(𝑥) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐. Найдите значение 𝑓(−2).
11. Найдите точку максимума функции 𝑦 = ln(𝑥 + 9) − 10𝑥 + 7.
12. а) Решите уравнение 3 ∙ 9 𝑥+1 − 5 ∙ 6 𝑥+1 + 8 ∙ 2 2𝑥 = 0. б) Найдите все корни этого уравнения, принадлежащие отрезку.
13. В правильной треугольной призме 𝐴𝐵𝐶𝐴1𝐵1𝐶1 все рёбра равны 2. Точка 𝑀 − середина ребра 𝐴𝐴1. а) Докажите, что прямые 𝑀𝐵 и 𝐵1𝐶 перпендикулярны. б) Найдите расстояние между прямыми 𝑀𝐵 и 𝐵1𝐶.
15. В июле 2016 года планируется взять кредит в банке на три года в размере 𝑆 млн рублей, где 𝑆 − целое число. Условия его возврата таковы: – каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года; – с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; – в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей. Найдите наибольшее значение 𝑆, при котором разница между наибольшей и наименьшей выплатами будет меньше 1 млн рублей.
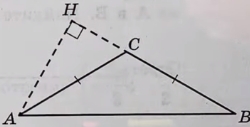
16. В трапеции 𝐴𝐵𝐶𝐷 боковая сторона 𝐴𝐵 перпендикулярна основаниям. Из точки 𝐴 на сторону 𝐶𝐷 опустили перпендикуляр 𝐴𝐻. На стороне 𝐴𝐵 отмечена точка 𝐸 так, что прямые 𝐶𝐷 и 𝐶𝐸 перпендикулярны. а) Докажите, что прямые 𝐵𝐻 и 𝐸𝐷 параллельны. б) Найдите отношение 𝐵𝐻 к 𝐸𝐷, если ∠𝐵𝐶𝐷 = 135°.
18. В течение 𝑛 дней каждый день на доску записывают натуральные числа, каждое из которых меньше 6. При этом каждый день (кроме первого) сумма чисел, записанных на доску в этот день, больше, а количество меньше, чем в предыдущий день. а) Может ли 𝑛 быть больше 5? б) Может ли среднее арифметическое чисел, записанных в первый день, быть меньше 3, а среднее арифметическое всех чисел, записанных за все дни, быть больше 4? в) Известно, что сумма чисел, записанных в первый день, равна 6. Какое наибольшее значение может принимать сумма всех чисел, записанных за все дни?
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
- ЕГЭ по математике профиль
Сколько первичных баллов дает каждое задание ЕГЭ 2022 по профильной математике можно узнать в демоверсии текущего года.
Распределение баллов ЕГЭ 2022 по заданиям — математика профиль
| № задания | Первичные баллы |
| 1 | 1 |
| 2 | 1 |
| 3 | 1 |
| 4 | 1 |
| 5 | 1 |
| 6 | 1 |
| 7 | 1 |
| 8 | 1 |
| 9 | 1 |
| 10 | 1 |
| 11 | 1 |
| 12 | 2 |
| 13 | 3 |
| 14 | 2 |
| 15 | 2 |
| 16 | 3 |
| 17 | 4 |
| 18 | 4 |
| Всего | 31 |
Система оценивания выполнения отдельных заданий и экзаменационной работы в целом
Оценивание правильности выполнения заданий, предусматривающих краткий ответ, осуществляется с использованием специальных аппаратно-программных средств.
Правильное решение каждого из заданий 1–11 оценивается 1 баллом. Задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа или конечной десятичной дроби.
Решения заданий с развёрнутым ответом оцениваются от 0 до 4 баллов.
Полное правильное решение каждого из заданий 12, 14 и 15 оценивается 2 баллами; каждого из заданий 13 и 16 – 3 баллами; каждого из заданий 17 и 18 – 4 баллами.
Проверка выполнения заданий 12–18 проводится экспертами на основе разработанной системы критериев оценивания.
Максимальный первичный балл за всю работу – 31.
Связанные страницы:
ЕГЭ по математике 2019, реальный вариант, основная волна, 29 мая, 29.05.2019
29 декабря 2021
В закладки
Обсудить
Жалоба
В версии ЕГЭ-2022 по математике появилось новое 9 задание, в котором требуется работа с функциями.
Эта тема пока вызывает затруднения у учащихся в связи со своей новизной. В презентации представлены решения задач с использованием линейной и квадратичной функций. Некоторые задачи решены 3 способами, чтобы учащиеся смогли выбрать наиболее понятный для себя.
ege9new.pptx
ege9new.pdf
Автор: Лесных Марина Владимировна.
Тест «Витамины»
Проверочная работа по биологии в 8 классе.
Консультация по физике
Онлайн-трансляция по вопросам подготовки к ЕГЭ по физике.
Ресурс носит неофициальный информационно-справочный характер, персональные данные не собирает и не обрабатывает, на интеллектуальные права третьих лиц не претендует.
Все ссылки ведут напрямую на официальные сайты описываемых услуг.
Карта сайта
Решение и ответы заданий Варианта №2 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко. ГДЗ Решебник профиль для 11 класса. Полный разбор. Ответы с решением.
Задание 1.
Найдите корень уравнения 92х+5 = 3,24·52х+5.
Задание 2.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,25. Вероятность того, что это вопрос по теме «Площадь», равна 0,3. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Задание 3.
В тупоугольном треугольнике ABC известно, что AC = BC, высота AH равна 3, СН = √7. Найдите синус угла ACB.
Задание 4.
Найдите значение выражения .
Задание 5.
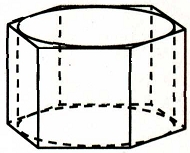
Цилиндр вписан в правильную шестиугольную призму. Радиус основания цилиндра равен √3, а высота равна 2. Найдите площадь боковой поверхности призмы.
Задание 6.
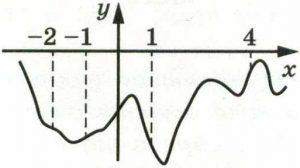
На рисунке изображён график функции 𝑦 = 𝑓(𝑥). На оси абсцисс отмечены точки −2, –1, 1, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Задание 7.
При температуре 0°С рельс имеет длину 𝑙0 = 15 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону 𝑙(𝑡°) = 𝑙0(1 + 𝛼∙𝑡°), где 𝛼 = 1,2∙10−5(°С )−1 – коэффициент теплового расширения, 𝑡° – температура (в градусах Цельсия). При какой температуре рельс удлинится на 7,2 мм? Ответ дайте в градусах Цельсия.
Задание 8.
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 135 км. На следующий день он отправился обратно в А со скоростью на 9 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в B. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Задание 9.
На рисунке изображён график функции вида f(x) = ax2 + bx + c, где числа a, b и c – целые. Найдите значение f(−9).
Задание 10.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 25% этих стекол, вторая – 75%. Первая фабрика выпускает 5% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Задание 11.
Найдите точку минимума функции y = x√x – 5x + 4.
Задание 12.
а) Решите уравнение 2cos3(x – π) = sin( + x).
б) Найдите все корни уравнения, принадлежащие отрезку .
Задание 13.
В правильной четырёхугольной пирамиде SABCD сторона основания AD равна 10, высота SH равна 12. Точка К – середина бокового ребра SD. Плоскость АКВ пересекает боковое ребро SC в точке Р.
а) Докажите, что площадь четырёхугольника CDKP составляет площади треугольника SCD.
б) Найдите объем пирамиды ACDKP.
Задание 14.
Решите неравенство (25х – 4·5х)2 + 8·5х < 2·25x + 15.
Задание 15.
В июле 2023 года планируется взять кредит на 10 лет. Условия его возврата таковы:
– каждый январь с 2024 по 2028 год долг возрастает на 18% по сравнению с концом предыдущего года;
– каждый январь с 2029 по 2033 год долг возрастает на 16% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2033 года долг должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат по кредиту должна составить 1470 тысяч рублей?
Задание 16.
Точки A, B, C, D и E лежат на окружности в указанном порядке, причем BC = CD = DE, а AC⊥BE. Точка K – пересечение прямых BE и AD.
а) Докажите, что прямая EC делит отрезок KD пополам.
б) Найдите площадь треугольника ABK, если AD = 4, DC = √3.
Задание 17.
Найдите все значения 𝑎, при каждом из которых уравнение
|x2 – a2| = |x + a|·
имеет ровно два различных корня.
Задание 18.
На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго.
а) Может ли сумма этих чисел быть равна 3456?
б) Может ли сумма этих чисел быть равна 2345?
в) В тройке чисел первое число трёхзначное, а третье равно 5. Сколько существует таких троек?
Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.2 / 5. Количество оценок: 6
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Видеоуроки, тесты, практика и консультации репетитора онлайн. Экстренная подготовка накануне экзамена
About this course
Онлайн-курс посвящён задаче №18 (элементы теории чисел) в профильном ЕГЭ. Эта задача – последняя в экзамене и самая дорогая по баллам. Тема базируется на знаниях из средней школы: натуральные числа, делимость, уравнения.
Курс рассчитан на быструю подготовку: его можно полностью освоить за неделю до экзамена. Вы повысите свой балл и сэкономите время, потому что:
- Обучение идёт от простого к сложному.
- Репетитор разберёт типичные сценарии, которые встречаются в экзамене, а не все задачи подряд.
- Выдержана сложность и не даётся лишнего. Вы будете решать задачи с реальных ЕГЭ прошлых лет.
- Видеоуроки смонтированы без «воды».
- Все темы доступны сразу. Можете пропускать то, что уже хорошо знаете
Этот курс — всего лишь один раздел из моего большого курса «Задачи с оформлением».
Другие бесплатные разделы:
Задание 12: уравнение
Задание 14: неравенство
Задание 17: параметр
Whom this course is for
Ученики 11 класса, абитуриенты
Meet the Instructors
Course content
Share this course
https://stepik.org/course/97260/promo
| 5 | В правильной четырёхугольной пирамиде MABCT боковое ребро в два раза больше стороны основания. Найти угол между прямыми AM и BK, где K — точка пересечения медиан грани CTM |
Задача 14 на четырёхугольную пирамиду векторным способом | |
| 4 | Сторона основания правильной треугольной призмы 8, высота 6. найти угол между CA1 и AB1 |
Задача 14 ЕГЭ на правильную треугольную призму и вектор | |
| 3 | В правильной треугольной призме ABCA1B1C1 все рёбра равны 1. a) Постройте прямую пересечения плоскости ABB1 и плоскости, проходящей через точки C, C1 перпендикулярно плоскости ACC1. б) Найдите косинус угла между прямыми AB1 и BC1 |
В правильной треугольной призме ABCA1B1C1 все рёбра равны 1 ! Диагностическая работа 16 Ященко 20 вариантов Тематическая рабочая тетрадь 2019 и 2018 # Решение задачи 14 на призму векторным способом # Ошибка в ответе пособия (в ответах пособий перепутаны номера задач) | |
| 2 | В правильной четырёхугольной пирамиде SABCD сторона основания 4, L — середина [SC]. Тангенс угла между прямыми BL и SA равен 2sqrt(2/17). a) Пусть О — центр основания пирамиды. Докажите, что прямые BO и LO перпендикулярны. б) Найти площадь поверхности пирамиды |
20 вариантов тестов ЕГЭ 2019 Ященко Тематическая рабочая тетрадь Диагностическая работа 10 Задача 14 # Аналоги 876 819 |
|
| 1 | При каких значениях параметра a система уравнений {(a^(3-x-2*y)=x-y-2),(2x+y-5=0) :} имеет два решения |
Графическое решение системы уравнений егэ по математике | |