Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Номер в банке ФИПИ: B1C5FD
2
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
РЕШЕНИЯ
Номер в банке ФИПИ: 59750B
3
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
РЕШЕНИЯ
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Номер в банке ФИПИ: 7D2DBE
4
Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и множествами их решениями.
РЕШЕНИЯ
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 166214., ЕГЭ по базовой математике 26.03.2015. Досрочная волна
5
Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и множествами их решениями.
РЕШЕНИЯ
Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 166212.
Пройти тестирование по этим заданиям
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Решение неравенств
Задание
1
#2500
Уровень задания: Легче ЕГЭ
Решите неравенство [x+10<3x^2]
Перенесем слагаемые в левую часть: [-3x^2+x+10<0] Разложим на множители выражение (-3x^2+x+10): [-3x^2+x+10=0 quad Rightarrow quad x_1=2quadtext{и}quad x_2=-dfrac53] Следовательно, (-3x^2+x+10=-3(x-2)left(x-frac53right)=-(x-2)(3x+5)).
Тогда неравенство примет вид [-(x-2)(3x+5)< 0quad Rightarrow
quad (x-2)(3x+5)>0] Решим его методом интервалов:
Таким образом, подходят (xin
left(-infty;-frac53right)cup(2;+infty)).
Ответ:
(left(-infty;-frac53right)cup(2;+infty))
Задание
2
#2501
Уровень задания: Легче ЕГЭ
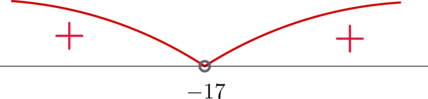
Решите неравенство [x^2+34x+289>0]
Заметим, что по формуле квадрата суммы (x^2+34x+289=(x+17)^2), следовательно, неравенство принимает вид: [(x+17)^2>0] Решим его методом интервалов:
Таким образом, нам подходят (xin(-infty;-17)cup(-17;+infty)).
Ответ:
((-infty;-17)cup(-17;+infty))
Задание
3
#2502
Уровень задания: Легче ЕГЭ
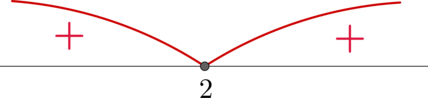
Решите неравенство [x^2-4x+4leqslant 0]
Заметим, что по формуле квадрата разности (x^2-4x+4=(x-2)^2), следовательно, неравенство принимает вид: [(x-2)^2leqslant 0] Решим его методом интервалов:
Таким образом, нам подходят (xin{2}).
Ответ:
({2})
Задание
4
#2503
Уровень задания: Легче ЕГЭ
Решите неравенство [x^2+3x+3geqslant 0]
Разложим на множители выражение (x^2+3x+3), для этого решим уравнение (x^2+3x+3=0). Оно имеет отрицательный дискриминант, следовательно, не разлагается на множители и принимает значения одного знака: либо положительно, либо отрицательно при всех (x). Проверить его знак можно, подставив вместо (x) любое число, например, (x=0): получим (3), следовательно, выражение всегда (>0).
Таким образом, нам подходят (xin mathbb{R}).
Ответ:
(mathbb{R})
Задание
5
#2412
Уровень задания: Легче ЕГЭ
Решите неравенство
[begin{aligned}
dfrac{(x — 1)(x + 2)}{(x — 3)(x + 4)}leqslant 0
end{aligned}]
ОДЗ:
[begin{aligned}
(x — 3)(x + 4)neq 0
end{aligned}]
Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.
1) Нули числителя находятся из уравнения [(x — 1)(x + 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = 1,qquadqquad x = -2]
2) Найдём нули знаменателя: [(x — 3)(x + 4) = 0qquadLeftrightarrowqquad
left[
begin{gathered}
x = 3\
x = -4
end{gathered}
right.]
По методу интервалов:
откуда [xin(-4; -2]cup[1; 3),.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).
Ответ:
((-4; -2]cup[1; 3))
Задание
6
#3762
Уровень задания: Легче ЕГЭ
Решить неравенство [dfrac 6{xsqrt3-3}+dfrac{xsqrt3-6}{xsqrt3-9}geqslant 2]
(Задача от подписчиков)
Пусть (xsqrt3-3=t). Тогда [dfrac 6t+dfrac{t-3}{t-6}geqslant 2quadLeftrightarrowquad
dfrac{t^2-15t+36}{t(t-6)}leqslant 0quadLeftrightarrowquad
dfrac{(t-3)(t-12)}{t(t-6)}leqslant 0] Решая данное неравенство методом интервалов, получим (0<tleqslant 3) или (6<tleqslant 12). Следовательно, [left[begin{gathered}begin{aligned}
&0<xsqrt3-3leqslant 3\
&6<xsqrt3-3leqslant
12end{aligned}end{gathered}right.quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&sqrt3<xleqslant 2sqrt3\
&3sqrt3<xleqslant 5sqrt3
end{aligned}end{gathered}right.]
Ответ:
((sqrt3;2sqrt3]cup(3sqrt3;5sqrt3])
Задание
7
#2413
Уровень задания: Легче ЕГЭ
Решите неравенство
[begin{aligned}
dfrac{(x + 1)(x — 2)}{(x + 3)(x^2 + 4)}leqslant 0
end{aligned}]
ОДЗ:
[begin{aligned}
(x — 3)(x^2 + 4)neq 0
end{aligned}]
Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.
1) Нули числителя находятся из уравнения [(x + 1)(x — 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = -1,qquadqquad x = 2]
2) Найдём нули знаменателя: [(x + 3)(x^2 + 4) = 0] так как (x^2geqslant 0), то (x^2 + 4geqslant 4), следовательно, нули знаменателя: [x = -3]
По методу интервалов:
откуда [xin(-infty; -3)cup[-1; 2],.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).
Ответ:
((-infty; -3)cup[-1; 2])

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Неравенства»
Открытый банк заданий по теме неравенства. Задания C3 из ЕГЭ по математике (профильный уровень)
Стереометрия. Расстояния и углы в пространстве
Задание №1198
Условие
Для xgeqslant 0 решите систему неравенств
begin{cases} x^4-3x^3-3x^2+5x+12geqslant 0,\ x^4-4x^3+x^2+4x+6leqslant 0. end{cases}
Показать решение
Решение
1. Заметим, что x=0 решением системы не является, так как второе неравенство системы при x=0 не является верным (6 leqslant 0). Пусть x>0.
Вычитая из первого неравенства второе, получаем
x^3-4x^2+x+6 geqslant 0.
А вычитая из второго неравенства системы последнее неравенство, получаем
x^4-5x^3+5x^2+3x leqslant 0,
x(x^3-5x^2+5x+3) leqslant 0.
Так как x>0, то из последнего неравенства получаем:
x^3-5x^2+5x+3 leqslant 0.
Таким образом система неравенств
begin{cases} x^3-4x^2+x+6 geqslant 0, \ x^3-5x^2+5x+3 leqslant 0 end{cases}
является следствием исходной.
Вычитая из первого неравенства последней системы второе, умноженное на 2, и деля полученное неравенство на -x (причём снова обращаем внимание на известное нам ограничение x>0), получаем x^2-6x+9 leqslant 0.
Последнее неравенство (следствие исходной системы) имеет единственное решение x=3. Простой подстановкой убеждаемся, что x=3 является решением системы.
Ответ
3
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1197
Условие
Решите неравенство frac1{log_x 0,5}+6geqslant 16log_{4x}2.
Показать решение
Решение
ОДЗ неравенства: begin{cases} x>0, \ xneq 1, \ xneq frac14. end{cases}
Т.к. frac1{log_x 0,5}= -frac1{log_x 2}= -log_2 x, а log_{4x} 2 =frac1{log_2 x+2}, то неравенство примет вид: -log_2 x+6 geqslant frac{16}{log_2 x+2}. Пусть log_2 x=t, тогда frac{16}{t+2}+ t-6 leqslant 0, frac{(t-2)^2}{t+2}leqslant 0, t=2 или t<-2. log_2 x=2, откуда x=4 или log_2 x<-2, откуда x<frac14. Учитывая ОДЗ, получим 0 < x < frac14, x=4.
Ответ
left( 0;,frac14right) , 4.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1196
Условие
Решите неравенство log_x2+2log_{2x}2geqslant 2.
Показать решение
Решение
Заметим, что x>0, x neq frac12, x neq 1.
Используя свойства логарифмов, преобразуем неравенство:
frac1{log_2x}+frac2{log_22x}geqslant 2,
frac1{log_2x}+frac2{log_22+log_2x}geqslant 2,
frac1{log_2x}+frac2{1+log_2x}geqslant 2.
Пусть log_2x=t, тогда получим неравенство, которое удобно решить методом интервалов:
frac1t+frac2{1+t}geqslant 2,
frac{(1+t)+2t-2t(1+t)}{t(1+t)}geqslant 0,
frac{2t^3-t-1}{t(1+t)}leqslant 0,
frac{(2t+1)(t-1)}{t(t+1)}leqslant 0.
Получим два двойных неравенства, решим их, возвращаясь к переменной x:
1. -1< t leqslant -frac12,
log_2frac12<log_2xleqslant log_2frac1{sqrt 2},
frac12<xleqslant frac1{sqrt 2}.
2. 0<tleqslant 1,
log_21<log_2xleqslant log_22,
1<xleqslant 2.
Так как найденные значения переменной удовлетворяют ОДЗ, то решение неравенства — left( frac12; frac1{sqrt 2}right] cup (1; 2].
Ответ
left( frac12; frac1{sqrt 2}right] cup (1; 2].
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1195
Условие
Решите неравенство log_{tfrac{sqrt 2+sqrt 3}3}5geqslant log_{tfrac{sqrt 2+sqrt 3}3}(7-x^2).
Показать решение
Решение
ОДЗ: 7-2^x>0, x<log_27.
Заметим, что sqrt 2>1,4, a sqrt 3>1,7. Тогда frac{sqrt 2+sqrt 3}3>1.
Получаем неравенство 5geqslant 7-2^x, 2^xgeqslant 2, xgeqslant 1.
С учетом ОДЗ имеем xin[1; log_27).
Ответ
[1; log_27).
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1194
Условие
Решите неравенство frac{3^x-5^{x+1}}{4^x-2^{x+log_25}+4}leqslant 0.
Показать решение
Решение
План решения.
1. Отдельно преобразуем числитель и знаменатель.
1.1. В числителе вынесем за скобки 5^x, чтобы в скобке осталась разность некоторого числа в степени x и константы (вместо этого можно вынести за скобки 3^x, а потом дополнительно преобразовать, или сразу вынести за скобки 3^{x+1}).
1.2. В знаменателе «избавимся» от log_2 5 в показателе степени (преобразуем его в множитель). После этого получим квадратичное выражение от 2^x (если сделать замену t=2^x, то получим квадратичное выражение от t). Квадратичное выражение разложим на множители.
2. Все множители в числителе и знаменателе заменим более простыми, совпадающими по знаку (в том числе равными нулю одновременно с исходными — таким образом, не надо будет дополнительно думать об ОДЗ).
3. Решим неравенство, полученное на предыдущем шаге, методом интервалов.
Решение.
1. frac{3^x-5^{x+1}}{4^x-2^{x+log_25}+4}leqslant 0,
frac{left( left( dfrac35right) ^x-5right)cdot 5^x}{2^{2x}-5cdot 2^x+4}leqslant 0,
frac{left( dfrac35right) ^x-5}{(2^x-4)(2^x-1)}leqslant 0.
2. frac{left( dfrac35right) ^x-left( dfrac35right) ^{log_tfrac355}}{(2^x-2^2)(2^x-2^0)}leqslant 0.
Выражения left( frac35right) ^x-5, 2^x-2^2, 2^x-2^0 совпадают по знаку с выражениями left( frac35-1right)cdot {x-log_{tfrac35}5}, (2-1)cdot (x-2) и (2-1)cdot (x-0) соответственно.
frac{left( dfrac35-1right)cdot (x-log_{tfrac35}5)}{(2-1)cdot (x-2)cdot (2-1)cdot (x-0)}leqslant 0.
3. frac{x-log_{tfrac35}5}{(x-2)cdot x}geqslant 0.
xin[log_{tfrac35}5; 0)cup (2; +infty ).
Ответ
[log_{tfrac35}5; 0)cup(2; +infty ).
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1193
Условие
Решите неравенство 3^{2x^2+7}+3^{(x+3)(x+1)}-4cdot 3^{8x}geqslant 0.
Показать решение
Решение
3^{2x^2+7}+3^{x^2+4x+3}-4cdot 3^{8x}geqslant 0, разделим обе части неравенства на 3^{8x}neq 0, 3^{8x}>0; неравенство примет вид 3^{2x^2-8x+7}+3^{x^2-4x+3}geqslant 0, введем обозначение 3^{x^2-4x+3}=t, t>0, получим: 3t^2+t-4geqslant 0. Найдем корни уравнения 3t^2+t-4=0, t_1=-frac43, t_2=1. Решением неравенства 3t^2+t-4geqslant0 являются промежутки left( -infty ; -frac43right] и left[ 1; +infty right). Так как t>0, то 3^{x^2-4x+3}geqslant 1, 3^{x^2-4x+3}geqslant 3^0, x^2-4x+3geqslant 0, xleqslant 1 и xgeqslant 3. То есть решениями этого неравенства являются xin(-infty ; 1]cup [3;+infty ).
Ответ
(-infty ; 1]cup [3;+infty ).
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1192
Условие
Решите неравенство 3^{3x}-3^{x+1}cdot 2^{2x}+18^x-3cdot 8^xgeqslant 0.
Показать решение
Решение
3^{3x}-3^xcdot 2^{2x}cdot 3+3^{2x}cdot 2^x-3cdot 2^{3x} geqslant 0.
Разделим обе части неравенства на 2^{3x}, 2^{3x} neq 0, 2^{3x}>0, неравенство примет вид frac{3^{3x}}{2^{3x}}-frac{3^xcdot 2^{2x}cdot 3}{2^{3x}},,,+ frac{3^{2x}cdot 2^x}{2^{3x}}-frac{3cdot 2^{3x}}{2^{3x}}geqslant 0,
left( frac32right) ^{3x}-3cdot left( frac32right) ^x+left( frac32right) ^{2x}-3geqslant 0, введем обозначение left( frac32right) ^x=t, t>0.
t^3+t^2-3t-3geqslant 0,
t^2(t+1)-3(t+1)geqslant 0,
(t+1)(t^2-3)geqslant 0,
tin[-sqrt 3;-1]cup [sqrt 3;+infty ), но t>0, следовательно, решением неравенства t^3+t^2-3t-3geqslant 0 является tin[sqrt 3;+infty ).
left( frac32right) ^x=t, тогда left( frac32right) ^xgeqslant sqrt 3.
xgeqslant log_{tfrac32}sqrt 3=frac{dfrac12log_33}{log_33-log_32},
xgeqslant frac1{2(1-log_32)}.
x inleft[ frac1{2(1-log_32) }; +infty right).
Ответ
left[ frac1{2(1-log_32) }; +infty right).
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1191
Условие
Решите неравенство frac1{log_{x^2+x}0,5},,,+ frac1{log_{x^2+x}0,25},,,+ frac1{log_{x^2+x}4}geqslant 1.
Показать решение
Решение
ОДЗ неравенства является множество всех решений системы
begin{cases} x^2+x>0,\ x^2+xneq 1; end{cases} begin{cases} x^2+x>0,\ x^2+x-1neq 0.end{cases}
x in left( -infty ; frac{-1-sqrt 5}{2}right),, cup left( frac{-1-sqrt 5}{2}; -1right) ,,cup left( 0;frac{-1+sqrt 5}{2}right) ,,cup left( frac{-1+sqrt 5}{2};+infty right).
Перейдём в неравенстве к логарифмам по основанию 2.
frac1{dfrac{log_2 0,5}{log_2(x^2+x)}},,+ frac1{dfrac{log_2 0,25}{log_2(x^2+x)}},,+ frac1{ dfrac{log_2 4}{log_2(x^2+x)}}geqslant 1,
frac{log_2(x^2+x)}{-1},,+ frac{log_2(x^2+x)}{-2},,+ frac{log_2(x^2+x)}{2}geqslant 1,
log_2(x^2+x)cdot left( -1-frac12+frac12right) geqslant 1,
-log_2(x^2+x)geqslant 1,
log_2(x^2+x)leqslant 1.
log_2(x^2+x)leqslant log_2 0,5,
x^2+xleqslant 0,5,
x^2+x-0,5leqslant 0.
Находим корни квадратного трёхчлена x^2+x-0,5:
x_{1,2}=frac{-1pmsqrt 3}2, поэтому множеством решений неравенства x^2+x-0,5 leqslant 0 будет множество left[ frac{-1-sqrt 3}{2}; frac{-1+sqrt 3}{2}right].
Так как frac{-1-sqrt 5}2<frac{-1-sqrt 3}2<-1 и 0<frac{-1+sqrt 3}2<frac{-1+sqrt 5}2, то множеством решений неравенства будет множество left[ frac{-1-sqrt 3}2; -1right) cup left( 0;frac{-1+sqrt 3}2right].
Ответ
left[ frac{-1-sqrt 3}2; -1right) cup left( 0;frac{-1+sqrt 3}2right].
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1190
Условие
Решите неравенство frac{4log_2(x+0,5)}{5^{1-sqrt x}-1}leqslant 5^{sqrt x}log_2(x+0,5).
Показать решение
Решение
ОДЗ: begin{cases} x+0,5>0,\5^{1-sqrt x}-1neq 0,\xgeqslant 0; end{cases} begin{cases} xgeqslant 0,\xneq 1. end{cases}
xin[0; 1) cup (1; +infty).
frac{4 log_2(x+0,5)-5^{sqrt x} log_2(x+0,5)cdot (5^{1-sqrt x}-1)}{5^{1-sqrt x}-1}leqslant 0,
frac{log_2(x+0,5)(4-5^{sqrt {x}+1-sqrt x}+5^{sqrt x})}{5^{1-sqrt x}-1}leqslant 0.
frac{log_2(x+0,5)(5^{sqrt x}-5^0)}{5^{1-sqrt x}-5^0}leqslant 0.
Применим метод замены множителя, учитывая, что:
а) log_{h(x)}f(x)rightarrow (h(x)-1)(f(x)-1), тогда log_2(x+0,5)rightarrow (2-1)(x+0,5-1)=x-0,5.
б) h(x)^{p(x)}-h(x)^{q(x)}rightarrow (h(x)-1)(p(x)-q(x)),
тогда 5^{sqrt x}-5^0=(5-1)(sqrt x-0)=4sqrt x,
5^{1-sqrt x}-5^0= (5-1)(1-sqrt x-0)= 4(1-sqrt x).
Неравенство примет вид frac{(x-0,5)cdot sqrt x}{1-sqrt x}leqslant 0.
На ОДЗ имеем 0 leqslant x leqslant 0,5; x>1.
Ответ
[0; 0,5] cup (1; +infty ).
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №995
Условие
Решите неравенство frac{log_{25}(2-x)+log_{35}dfrac{1}{2-x}}{log_{35}x^3-3log_{49}x}leq log_{49}25.
Показать решение
Решение
Найдём ОДЗ неравенства.
begin{cases} 2-x > 0, \ x > 0, \ log_{35}x^3-3log_{49}x neq 0;end{cases}
begin{cases}x < 2, \ x > 0, \ frac{3 ln x}{ln 35} -frac{3 ln x}{ln 49} neq 0;end{cases}
begin{cases} x < 2, \ x > 0, \ ln x left ( frac{1}{ ln 35}-frac{1}{ln 49}right ) neq 0;end{cases}
begin{cases}x < 2, \ x > 0, \ ln x neq 0; end{cases}
begin{cases}x < 2, \ x > 0, \ x neq 1; end{cases}
(0;1) cup (1;2).
Исследуем знак левой части неравенства.
При 0 < x < 1:
log_{35}x^3-3log_{49}x= 3log_{35}x-3log_{49}x= frac{3}{log_{x}35}-frac{3}{log_{x}49} < 0
(так как log_{x}49 < log_{x}35 < 0).
log_{25}(2-x)+log_{35}left ( frac{1}{2-x}right )= log_{25}(2-x)-log_{35}(2-x)= frac{1}{log_{2-x}25}-frac{1}{log_{2-x}35} > 0 (так как 2-x > 1, и значит, 0 < log_{2-x}25 < log_{2-x}35).
При 1 < x < 2:
log_{35}x^{3}-3 log_{49}x= 3 log_{35}x-3 log_{49}x= frac{3}{log_{x}35}-frac{3}{log_{x}49} > 0
(так как 0 < log_{x}35 < log_{x}49);
log_{25}(2-x)+log_{35}left ( frac{1}{2-x}right )= log_{25}(2-x)-log_{35}(2-x)= frac{1}{log_{2-x}25}-frac{1}{log_{2-x}35} < 0 (так как 2-x < 1, и значит, log_{2-x}35 < log_{2-x}25 < 0).
Таким образом, левая часть исходного неравенства отрицательна при всех значениях x из ОДЗ. С другой стороны, log_{49}25 > 0. Значит, левая часть исходного неравенства не превосходит log_{49}25 при любом значении x из ОДЗ.
Следовательно, решение данного неравенства: (0;1) cup (1;2).
Ответ
(0;1) cup (1;2).
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 22 № 52
Найдите сумму целых решений неравенства
Источник: Централизованное тестирование по математике, 2011
2
Найдите наибольшее целое решение неравенства
Источник: Централизованное тестирование по математике, 2013
3
Найдите наибольшее целое решение неравенства
Источник: Централизованное тестирование по математике, 2015
4
Решите неравенство В ответе запишите сумму целых решений, принадлежащих промежутку [−20; −2].
Источник: Централизованное тестирование по математике, 2017
5
Найдите произведение наибольшего целого отрицательного и наибольшего целого положительного решений неравенства
Источник: Централизованное тестирование по математике, 2020
Пройти тестирование по этим заданиям





.png)


