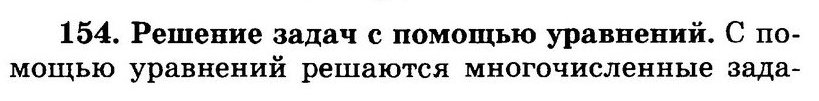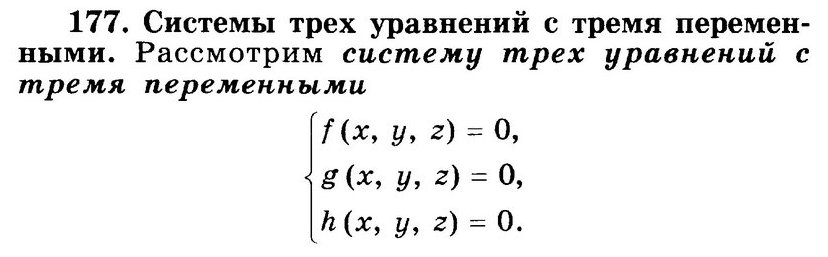Решу егэ математика системы уравнений

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 94    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 94    1–20 | 21–40 | 41–60 | 61–80 …

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 580    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 580    1–20 | 21–40 | 41–60 | 61–80 …

Часть 1. УРАВНЕНИЯ

1. Целые рациональные уравнения

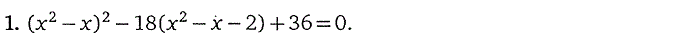
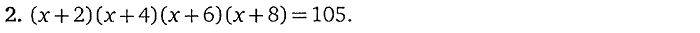
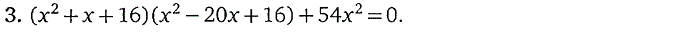
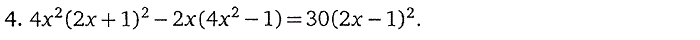
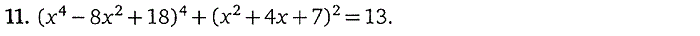
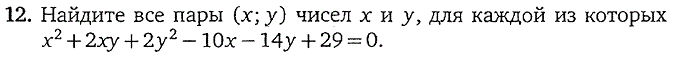
2. Уравнения, содержащие переменную
под знаком абсолютной величины (модуля)

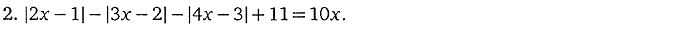
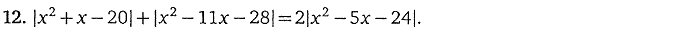
3. Дробно-рациональные уравнения

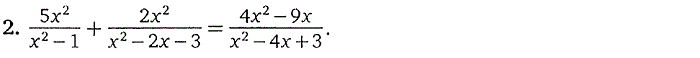
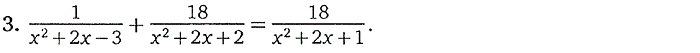
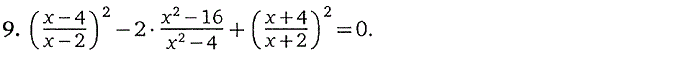
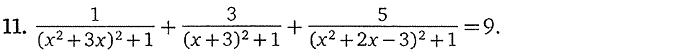
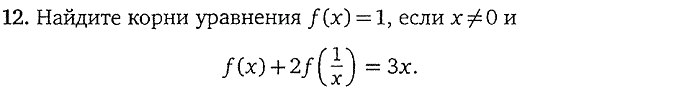
4. Иррациональные уравнения

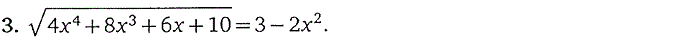
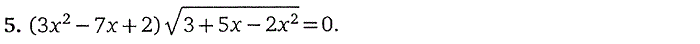
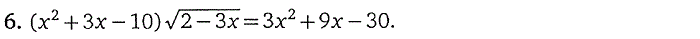
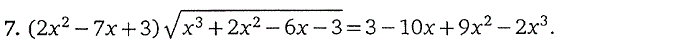
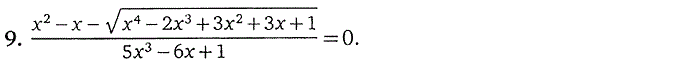
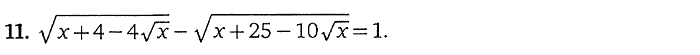
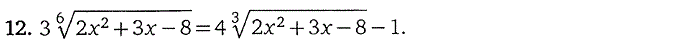
5. Тригонометрические уравнения

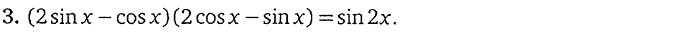
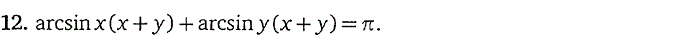
6. Показательные уравнения

7. Логарифмические уравнения

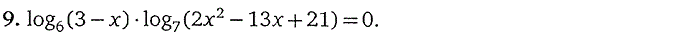
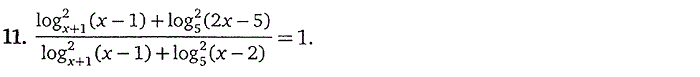
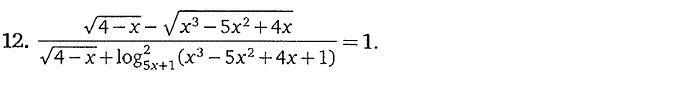
Часть 2. СИСТЕМЫ УРАВНЕНИЙ

1. Системы целых алгебраических уравнений

2. Системы, содержащие
дробно-рациональные уравнения

3. Системы, содержащие
иррациональные уравнения

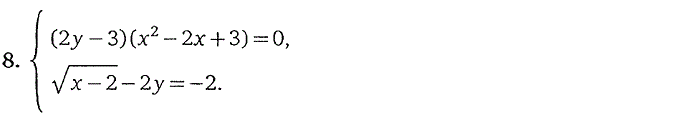
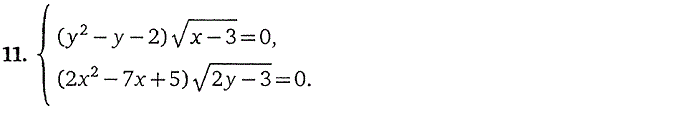
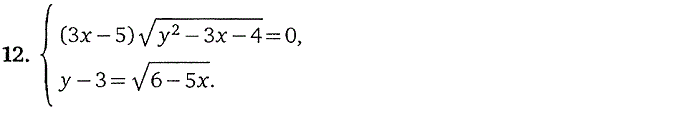
4. Системы, содержащие
тригонометрические уравнения

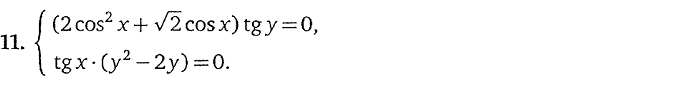
5. Системы, содержащие
показательные уравнения

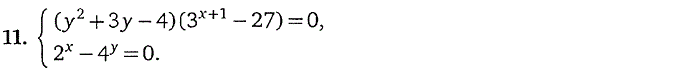
6. Системы, содержащие
логарифмические уравнения

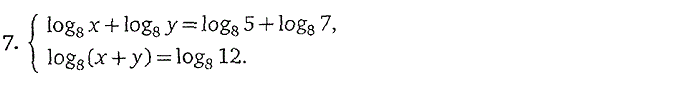
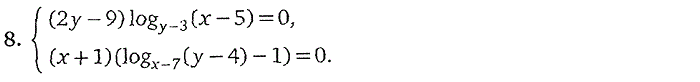
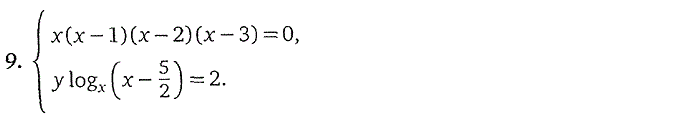
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Системы алгебраических уравнений

Систему уравнений можно решать методом подстановки – выражать переменную из одного уравнения и подставлять в другое.

Уравнения в системе можно также складывать друг с другом и вычитать одно из другого. Например, левую часть одного уравнения складываем с левой частью другого, правую – с правой.

Можно умножать и даже делить одно уравнение на другое! Конечно, при этом надо следить, чтобы не умножить или не поделить на ноль.

Обратите внимание – когда мы решаем систему уравнений, она не распадается на «кусочки», на отдельные уравнения. Каждый раз мы переходим от системы уравнений к равносильной ей системе.

1. Решите систему уравнений:

Раскроем скобки в каждом уравнении:

Вычтем из первого уравнения системы второе: . И подставим во второе уравнение.

2. Решите систему уравнений:

Мы разложили левую часть первого уравнения на множители по формуле суммы кубов.

Поделим первое уравнение системы на второе

Подставим в уравнение

3. Решите систему уравнений:

Дальше – цепочка равносильных переходов.

Решения первой системы:

Решим квадратное уравнение . Его корни:
и .

Это полезно

Узнаете, чем отличаются официально-деловой, публицистический, научный, художественный и разговорный стили.

Системы уравнений

СОДЕРЖАНИЕ

1. Метод последовательного исключения неизвестных
2. Простейшие нелинейные системы из двух алгебраических уравнений с двумя неизвестными
3. Системы, сводящиеся к однородным уравнениям
4. Системы из трех уравнений с тремя неизвестными
5. Линейные системы, содержащие параметр. Число решений системы в зависимости от параметра
6. Системы, содержащие логарифмы
7. Системы, содержащие показательные функции

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Скачать пособие «Системы уравнений» (формат pdf, 247кб)

С необходимыми теоретическими сведениями, используемыми при решении задач, можно ознакомиться в разделе «Алгебра» нашего «Справочника по математике для школьников».

Рекомендуем также ознакомиться с методами и примерами решения систем уравнений, представленных в разделах нашего справочника «Системы линейных уравнений», «Системы с нелинейными уравнениями».

Со свойствами логарифмов можно ознакомиться в разделе «Логарифмы» нашего справочника.

С понятиями степени с целочисленным показателем и арифметического корня можно также ознакомиться в разделе «Степень с целочисленным показателем и арифметический корень» нашего справочника.

С понятием степени с рациональным показателем и свойствами степеней можно ознакомиться в разделе «Степень с рациональным показателем» нашего справочника.

Графики логарифмических функций представлены в разделе «Графики степенных, показательных и логарифмических функций» нашего справочника.

Как решать систему уравнений

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Основные понятия

Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.

Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.

Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.

Линейное уравнение с двумя переменными

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.

Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.

Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:

Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.

Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.

Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).

Провести прямую через эти две точки и вуаля — график готов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Система двух линейных уравнений с двумя переменными

Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.

Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:

Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.

Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.

Можно записать систему иначе:

Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.

Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.

Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.

Метод подстановки

Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:

Выразить одну переменную через другую из более простого уравнения системы.

Подставить то, что получилось на место этой переменной в другое уравнение системы.

Решить полученное уравнение, найти одну из переменных.

Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.

Записать ответ. Ответ принято записывать в виде пар значений (x; y).

Потренируемся решать системы линейных уравнений методом подстановки.

Пример 1

Решите систему уравнений:

x − y = 4
x + 2y = 10

Выразим x из первого уравнения:

x − y = 4
x = 4 + y

Подставим получившееся выражение во второе уравнение вместо x:

x + 2y = 10
4 + y + 2y = 10

Решим второе уравнение относительно переменной y:

4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2

Полученное значение подставим в первое уравнение вместо y и решим уравнение:

x − y = 4
x − 2 = 4
x = 4 + 2
x = 6

Ответ: (6; 2).

Пример 2

Решите систему линейных уравнений:

x + 5y = 7
3x = 4 + 2y

Сначала выразим переменную x из первого уравнения:

x + 5y = 7
x = 7 − 5y

Выражение 7 − 5y подставим вместо переменной x во второе уравнение:

3x = 4 + 2y
3 (7 − 5y) = 4 + 2y

Решим второе линейное уравнение в системе:

3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1

Подставим значение y в первое уравнение и найдем значение x:

x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2

Ответ: (2; 1).

Пример 3

Решите систему линейных уравнений:

x − 2y = 3
5x + y = 4

Из первого уравнения выразим x:

x − 2y = 3
x = 3 + 2y

Подставим 3 + 2y во второе уравнение системы и решим его:

5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1

Подставим получившееся значение в первое уравнение и решим его:

x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1

Ответ: (1; −1).

Метод сложения

Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:

При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.

Складываем почленно левые и правые части уравнений системы.

Решаем получившееся уравнение с одной переменной.

Находим соответствующие значения второй переменной.

Запишем ответ в в виде пар значений (x; y).

Система линейных уравнений с тремя переменными

Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:

Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).

Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.

Решение задач

Разберем примеры решения систем уравнений.

Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?

5x − 8y = 4x − 9y + 3

5x − 8y = 4x − 9y + 3

5x − 8y − 4x + 9y = 3

Задание 2. Как решать систему уравнений способом подстановки

Выразить у из первого уравнения:

Подставить полученное выражение во второе уравнение:

Найти соответствующие значения у:

Задание 3. Как решать систему уравнений методом сложения

1. Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:

1. Решаем полученное квадратное уравнение любым способом. Находим его корни:

1. Найти у, подставив найденное значение в любое уравнение:

1. Ответ: (1; 1), (1; -1).

Задание 4. Решить систему уравнений

Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.

Задание 5. Как решить систему уравнений с двумя неизвестными

При у = -2 первое уравнение не имеет решений, при у = 2 получается:

Материалы для подготовки к ЕГЭ. Онлайн-Справочник по математике.
Раздел 4 «Уравнения и системы уравнений» (§§ 14-16). Уравнения с одной переменной. Уравнения с двумя переменными. Система уравнений.

ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА

Раздел IV. Уравнения и системы уравнений

ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА

§ 14. Уравнения с одной переменной.

138. Определение уравнения. Корни уравнения.

139. Равносильность уравнений.

140. Линейные уравнения.

141. Квадратные уравнения.

142. Неполные квадратные уравнения.

143. Теорема Виета.

144. Системы и совокупности уравнений.

145. Уравнения, содержащие переменную под знаком модуля.

146. Понятие следствия уравнения. Посторонние корни.

147. Уравнения с переменной в знаменателе.

148. Область определения уравнения.

149. Рациональные уравнения.

150. Решение уравнения р(х) = 0 методом разложения его левой части на множители.

151. Решение уравнений методом введения новой переменной.

152. Биквадратные уравнения.

153. Уравнения высших степеней.

154. Решение задач с помощью уравнений.

155. Иррациональные уравнения.

156. Показательные уравнения.

157. Логарифмические уравнения.

158. Показательно-логарифмические уравнения.

159. Простейшие тригонометрические уравнения.

160. Решение тригонометрических уравнений методом разложения на множители.

161. Решение тригонометрических уравнений методом введения новой переменной.

162. Однородные тригонометрические уравнения.

163. Универсальная подстановка.

164. Метод введения вспомогательного аргумента.

165. Графическое решение уравнений.

166. Уравнения с параметром.

§ 15. Уравнения с двумя переменными.

167. Решение уравнения с двумя переменными.

168. График уравнения с двумя переменными.

169. Линейное уравнение с двумя переменными и его график.

§ 16. Системы уравнений.

170. Системы двух уравнений с двумя переменными. Равносильные системы.

171. Решение систем двух уравнений с двумя переменными методом подстановки.

172. Решение систем двух уравнений с двумя переменными методом сложения.

173. Решение систем двух уравнений с двумя переменными методом введения новых переменных.

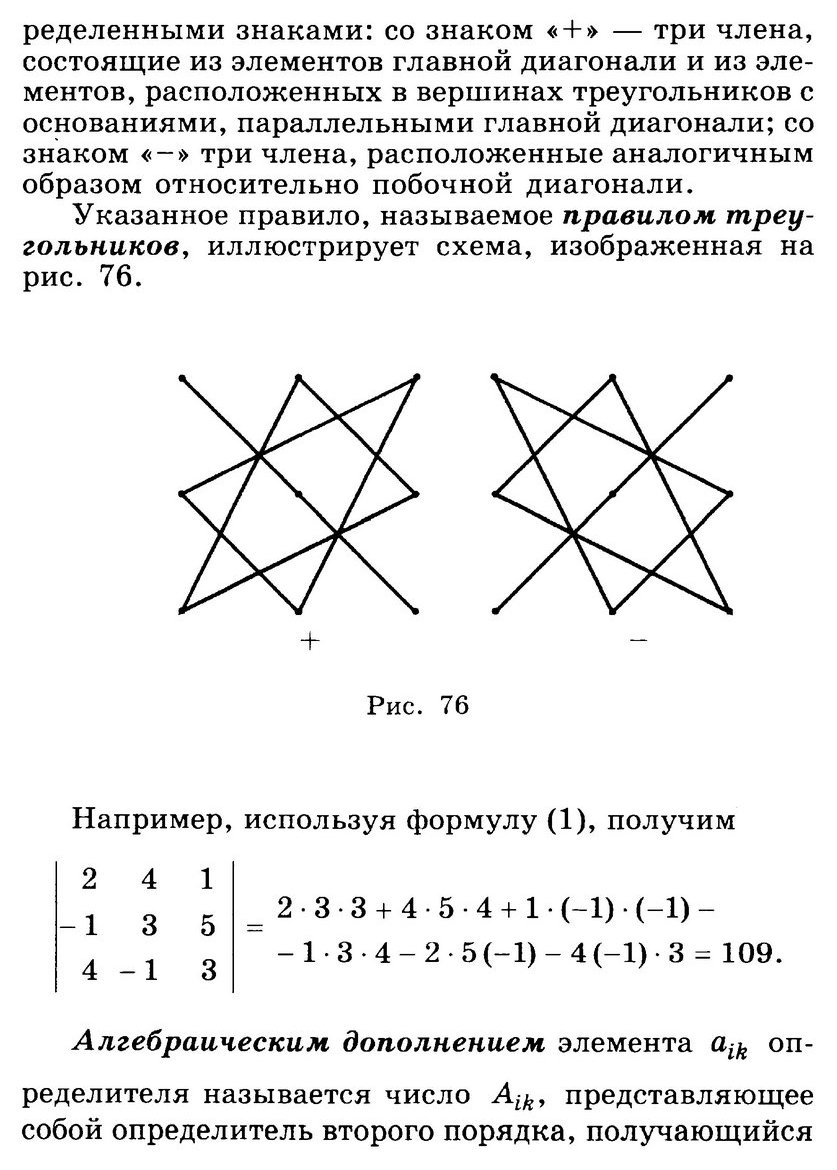
174. Определители второго порядка. Исследование систем двух линейных уравнений с двумя переменными.

175. Симметрические системы.

176. Графическое решение систем двух уравнений с двумя переменными.

177. Системы трех уравнений с тремя переменными.

178. Определители третьего порядка. Исследование систем трех линейных уравнений с тремя переменными.

179. Системы показательных и логарифмических уравнений.

180. Системы тригонометрических уравнений.

 

---

ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА

Материалы для подготовки к ЕГЭ. Онлайн справочник по математике.
Раздел 4 «Уравнения и системы уравнений» (§§ 14-16). Уравнения с одной переменной. Уравнения с двумя переменными. Система уравнений.

Просмотров:
4 595