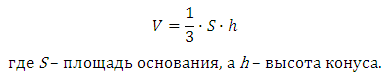Дата: 2019-04-13
2368
Категория: Стерео Цилиндр Конус
Метка: ЕГЭ-№2
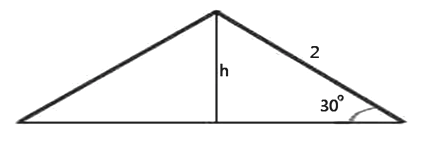
27093. Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30°. В ответе укажите V/Пи.
Объем конуса равен одной трети произведения площади основания и высоты:
Для наглядности рассмотрим проекцию конуса с боку. Высоту конуса можем найти из прямоугольного треугольника. Известно, что в прямоугольном треугольнике катет лежащий напротив угла в 30° равен половине гипотенузы. В данном случае гипотенуза это образующая конуса. Значит h = 1.
Для нахождения площади основания необходимо знать его радиус. Найдём его по теореме Пифагора:
Таким образом объём равен:
Разделим результат на как указано в условии и запишем ответ.
Ответ: 1
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-23

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
1
Задание 1. Однозначное соотнесение графа и таблицы
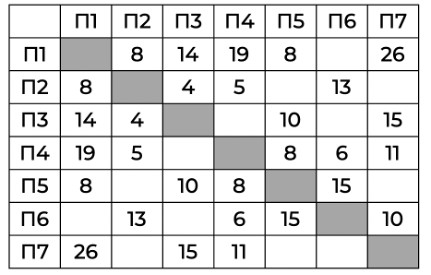
Между населёнными пунктами П1, П2, П3, П4, П5, П6, П7 построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.
Определите длину кратчайшего пути между пунктами П1 и П7, проходящего через пункт П6, минуя пункт П2 (при условии, что передвигаться можно только по построенным дорогам).
2
Задание 2. Заполнение таблицы истинности
Логическая функция F задается выражением ((x→w) ≡ (y→z)) / ¬ (w≡y) / ¬ (k→z). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F,содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w, k.
| ? | ? | ? | ? | F | |
| 1 | 1 | 1 | |||
| 0 | 1 | 1 | 1 | ||
| 1 | 0 | 0 | 1 |
В ответе напишите буквы x, y, z, w, k в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
3
Задание 3. Фильтры и таблицы
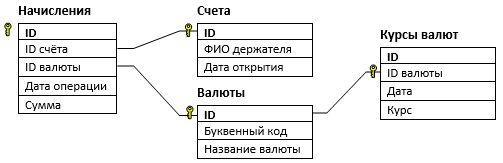
В файле 3-dv.xls приведён фрагмент базы данных «Инвестиционные счета». Таблица «Счета» содержит информацию о владельце счёта и дате его открытия. Таблица «Валюты» содержит информацию о наименованиях валют, которые могут храниться на счетах. Таблица «Курс валют» содержит информацию о курсах валют по отношению к рублю курс валют за период с 24 по 30 декабря 2021 года. Таблица «Начисления» содержит информацию о всех операциях со счетом: код счёта, код валюты, дату операции и сумму начисления (она может быть отрицательной). На рисунке приведена схема указанной базы данных.
Даня и Ваня решили подзаработать, чтобы купить курсы по информатике в лучшей школе 99 баллов. Для этого они хотят найти валюту, которая больше всего прибавила в цене в период с 24 по 30 декабря. Используя информацию из приведённой базы данных, определите буквенное обозначение валюты, которая больше всего прибавила в цене с 24 по 30 декабря. В ответе укажите только 3 заглавные буквы.
4
Задание 4. Минимальная длина кода
По каналу связи передаются сообщения, содержащие девять букв: Х, Д, Б, Р, А, С, Ю, Е, З. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Х — 011, Б-000, Р-111, Ю — 010, З — 001, Е — 110. Какое наименьшее количество символов потребуется, чтобы закодировать сообщение ХАРДБАСС?
5
Задание 5. Двоичные алгоритмы
Автомат получает на вход натуральное число N и строит по нему новое число R по следующему алгоритму:
1) Исходное число переводится в двоичную систему счисления
2) Подсчитывается количество значащих 0. Если их кол-во чётно — из числа убирается последняя цифра, иначе справа дописывается ‘1’.
3) Второй шаг повторяется еще один раз
4) Результат переводится в десятичную систему счисления.
Укажите сколько получится различных R, которые можно получить при исходном N на отрезке [200, 300].
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a,b) (где a, b — целые числа), перемещающую Чертёжника из точки с координатами (x, y) в точку с координатами (x+a, y+b). Если числа a, b положительные, то значение соответствующей координаты увеличивается, если отрицательные — уменьшается. Например, если Чертёжник находится в точке с координатами (4, 2), то команда Сместиться на (2,-3) переместит Чертёжника в точку (6,-1). Запись
Повтори k раз
Команда1 Команда2 Команда3
конец
означает, что последовательность Команда1 Команда2 Команда3 повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 10 раз
Сместиться на (4, 6)
Сместиться на (-4, 6)
Сместиться на (-4, -6)
Сместиться на (4, -6)
конец
Найдите площадь полученной фигуры.
7
Задание 7. Кодирование изображений
Danny Golds делает фотоснимки размером 1920×2550 пикселей. На хранение одного кадра отводится 15600 Кбайт. Определите максимальную глубину цвета (в битах на пиксель), которую можно использовать при фотосъёмке.
8
Задание 8. Составление комбинаций
Вероника составляет 13-буквенные слова из букв М, А, Й, К, О, В, выбирая такие, в которых содержится комбинация МАЙКОВА. Сколько слов сможет составить Вероника?
Откройте файл электронной таблицы 9-107.xls, содержащий в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться величинами углов прямоугольного треугольника, выраженных в градусах. В ответе запишите только число.
С помощью текстового редактора определите, сколько различных чисел встречается в тексте рассказа Валентина Распутина «Уроки французского» (10-d1.docx). Одинаковые числа повторно не считать. В ответе укажите только количество чисел.
11
Задание 11. Пароли с дополнительной информацией
Датчик считывает значения интенсивности поступающего света, которые округляются до одного из 2000 возможных. Каждое считанное значение кодируется одинаковым минимально возможным количеством бит. Известно, что значения считываются сериями по 50 измерений, все серии сохраняются в одном файле. Каждая серия занимает целое количество байт. Если последняя серия содержит меньше 50 значений, она сохраняется в файле с помощью минимально возможного целого количества байт. За время своей работы датчик считал 12312 значений. Какое минимальное целое количество килобайт нужно выделить для хранения файла?
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>3)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 223>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>3)
ТО заменить (>3, 11>)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой ниже программе поступает строка, начинающаяся с символа «>», а затем содержащая 30 цифр 1, 20 цифр 2 и 10 цифр 3, расположенных в произвольном порядке. Определите сумму числовых значений цифр строки, получившейся в результате выполнения программы. Так, например, если результат работы программы представлял бы собой строку, состоящую из 50 цифр 4, то верным ответом было бы число 200.
13
Задание 13. Поиск числа путей
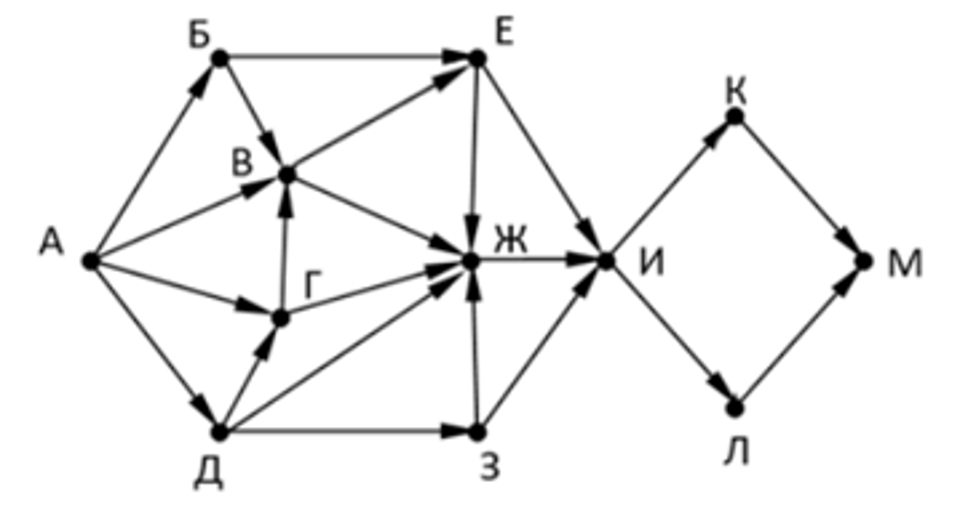
Ваня спешит на пересдачу из общежития (Пункт А) в Иннополис (Пункт М). Чтобы он смог выбрать самый оптимальный маршрут и успеть вовремя, ему нужно знать все возможные варианты добраться до ВУЗа. На рисунке представлена схема дорог, связывающих здания А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из общежития до Иннополиса и не проходящих через военкомат (Пункт В)?
14
Задание 14. Системы счисления (прямое сложение)
Сколько различных цифр в шестнадцатеричной записи числа 2^51 + 2^45 + 2^30 + 4^7 – 2^5
15
Задание 15. Поразрядная коъюнкция
Определите количество натуральных чисел A из интервала [80, 300] таких, что выражение
((X & 55 ≠ 0) (X & 23 ≠ 0)) → (X & A ≠ 0)
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной x)?
16
Задание 16. Рекурсивные алгоритмы
Алгоритм вычисления функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:
F(0) = 1
F(n) = F(n–1) + F(n–2), при чётном n > 0
F(n) = 1,5*F(n–1), при нечётном n > 0
Сколько различных цифр встречается в целой части значения функции F(35)?
17
Задание 17. Числовая последовательность
В файле 17-d5.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от 0 до 1000. Определите сначала количество пар, в которых оба элемента больше, чем сумма всех цифр «3» в шестеричной записи всех чисел в файле, кратных 15, а затем максимальную из сумм таких пар. Под парой подразумевается два идущих подряд элемента последовательности.
18
Задание 18. Двумерное динамическое программирование
Квадрат разлинован на N×N клеток (1 < N < 20). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из трёх команд: вправо, вверх или вправо-вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх – в соседнюю верхнюю, а по команде вправо-вверх – на одну клетку вправо и вверх по диагонали. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата записана величина вознаграждения от 1 до 100. Попав в клетку после хода вправо или вверх, Робот получает указанное в ней вознаграждение, а если он попал в клетку после выполнения команды вправо-вверх, вознаграждение удваивается. Это также относится к начальной и конечной клетке маршрута Робота. Определите максимальное и минимальное вознаграждение, которое может получить Робот, пройдя из левой нижней клетки в правую верхнюю. В ответе укажите два числа без пробелов – сначала максимальное вознаграждение, затем минимальное. Исходные данные записаны в файле 18-5.xls в виде электронной таблице размером N×N, каждая ячейка которой соответствует клетке квадрата.
19
Задание 19. Теория игр (Задания 19)
13. Теория игр. Две кучи Excel
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 40. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 40 или больше камней. В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 30. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
13. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
20
Задание 20. Теория игр (Задания 20)
13. Теория игр. Две кучи Excel
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 40. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 40 или больше камней. В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 30. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
13. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
21
Задание 21. Теория игр (Задания 21)
13. Теория игр. Две кучи Excel
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 40. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 40 или больше камней. В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 30. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
13. Сколько существует значений S, при которых у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22
Задание 22. Параллельные процессы
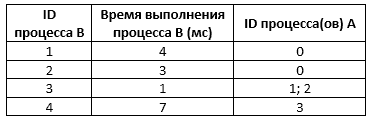
В файле 22d-3 содержится информация о вычислительных процессов проектов P1 и P2, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Найдите время завершения процессов 5 из проектов P1 и P2. В ответ укажите их сумму.
Типовой пример организации данных в файле:
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 – через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
23
Задание 23. Одномерное динамическое программирование
Исполнитель Шахматный Король преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавь 2
2. Прибавь 3
3. Умножь на 2
Программа для исполнителя – это последовательность команд. Сколько существует программ, которые преобразуют исходное число 1 в число 20 и при этом не содержат двух команд умножения подряд?
24
Задание 24. строковая обработка
Текстовый файл 24-d12.txt содержит заглавные латинские буквы и телефонные номера, всего не более чем 106 символов. Телефонный номер – это последовательность цифр, расположенных между буквами. В некоторой стране Z номер телефона состоит из 11 цифр, начинается на 8 и при этом его вторая слева цифра равна предпоследней. Определите количество телефонных номеров страны Z, содержащихся в файле.
25
Задание 25. Поиск делителей
Найдите наименьшее натуральное число, которое имеет ровно 1024 делителя. В ответе запишите сначала само число и затем его наибольший простой делитель. Подсказка: используйте основную теорему арифметики.
26
Задание 26. Сортировки
При проведении эксперимента заряженные частицы попадают на чувствительный экран, представляющий из себя матрицу размером 640 на 480 точек. При попадании очередной частицы на экран в файл записываются координаты чувствительного элемента: номер строки (целое число от 1 до 640) и номер позиции в строке (целое число от 1 до 480). Точка экрана, в которую попала хотя бы одна частица, считается светлой, точка, в которую ни одна частица не попала, – тёмной.
Вам нужно определить наибольшую длину цепочки в одной строке, состоящей только из светлых точек, и строку, в котором она находится. Если таких строк несколько, укажите максимальный из их номеров.
Входные данные представлены в файле 26-73.txt следующим образом. В первой строке входного файла записано целое число N – количество частиц, попавших на экран. В каждой из следующих N строк записаны по два числа, разделённые пробелом: номер строки и номер позиции в строке.
Запишите в ответе два числа: сначала наибольшую длину цепочки из светлых точек, затем – номер строки, в которой находится эта цепочка (если таких строк несколько, запишите максимальный из их номеров).
Пример входного файла:
7
1 2
2 3
3 6
2 4
1 3
2 5
2 4
При таких исходных данных имеется три цепочки светлых точек: в позициях 2 и 3 строки 1, в позициях 4, 5 и 6 строки 2 (это самая длинная цепочка!) и точка в позиции 6 строки 3. Ответ: 3 2.
27
Задание 27. Кратность произведения пары
На вход программы поступает последовательность из N целых положительных чисел, все числа в последовательности различны. Рассматриваются все пары различных элементов последовательности (элементы пары не обязаны стоять в последовательности рядом, порядок элементов в паре не важен). Необходимо определить количество пар, для которых произведение элементов не кратно 10 и 7.
Отличная работа!
Так держать!
Если остались вопросы, напиши своему куратору.
Нужно авторизоваться
Нужно авторизоваться
Введите больше 6 символов
На почту 12345@mail.ru отправлена ссылка для сброса пароля.
Пожалуйста, подтвердите ваш номер телефона
Курс заблокирован
К сожалению, данный курс заблокирован. Необходимо внести доплату
Вывод
средств
Ваше задание
подтверждено!
успешно
Теперь вы можете приступить
к следующему уроку
курса по математике
Перейти к уроку
Подтверждение
замены
Для смены номера телефона
мы отправили Вам код по СМС,
введите его в поле ниже.
Подтвердить
Ты включаешь автопродление — 25-го числа каждого месяца доступ к купленным курсам будет автоматически продлеваться. Деньги будут списываться с одной из привязанных к учетной записи банковских карт. Управлять автопродлением можно из раздела «Финансы»
Для активации регулярного платежа мы спишем небольшую сумму с карты и сразу её вернем
Вы дествительно хотите отменить автопродление?
Благодарим за покупку!
В ближайшее время курс будет доступен в разделе Моё обучение
Материалы будут доступны за сутки до начала урока
Чат будет доступен после выдачи домашнего задания
Укажите вашу электронную почту
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
|
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
|
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
  |
||||
|
Владимiръ |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
Задача 18 Подробности: |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
-
ЕГЭ по математике (база) 2023
- /
-
Задание 10
- /
- Задача 26
- /
Перила лестницы дачного дома для надёжности укреплены посередине вертикальным с…
Разбор сложных заданий в тг-канале:
Сложность:
Среднее время решения: 47 сек.
ЕГЭ по математике (база) 2023 задание 10: номер 26 | 71pac | Перила лестницы дачного дома …
25
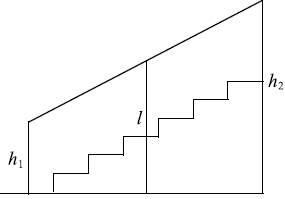
Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту $l$ этого столба, если наименьшая высота $h_1$ перил равна 40 см, а наибольшая высота $h_2$ равна 90 см. Ответ дайте в сантиметрах.
Объект авторского права ООО «Легион»
Вместе с этой задачей также решают:
Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 2:00?
Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 4:00?
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м $×$1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
От столба высотой 29 м к дому натянут провод, который крепится на высоте 5 м от земли. Расстояние от дома до столба 7 м. Найдите длину провода. Ответ дайте в метрах.
Решение и ответы заданий варианта МА2210309 СтатГрад 28 февраля ЕГЭ 2023 по математике (профильный уровень). Тренировочная работа №3. ГДЗ профиль для 11 класса.
+Задания №1, №4, №6, №10 из варианта МА2210311.


Задание 1.
В треугольнике ABC угол C равен 90°, CH – высота, BC = 5, cosA=frac{2sqrt{6}}{5}. Найдите длину отрезка AH.
Задание 1 из варианта 2210311.
Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.
Задание 2.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.
Задание 3.
В группе 16 человек, среди них – Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.
Задание 4.
Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Задание 4 из варианта 2210311.
Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.
Задание 5.
Решите уравнение frac{x–1}{5x+11}=frac{x–1}{3x-7}. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
Задание 6.
Найдите значение выражения frac{(4^{frac{3}{5} }cdot7^{frac{2}{3}})^{15}}{28^{9}} .
Задание 6 из варианта 2210311.
Найдите 98cos2α, если cosα = frac{4}{7}.
Задание 7.
На рисунке изображён график y = f’(x) – производной функции f(x), определённой на интервале (−5; 5). В какой точке отрезка [−4; −1] функция f(x) принимает наибольшее значение?
Задание 8.
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле FA = ρgl3, где l – длина ребра куба в метрах, ρ = 1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте, что g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше чем 2116800 Н? Ответ дайте в метрах.
Задание 9.
Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Задание 10.
На рисунке изображён график функции f(x) = ax2 + bx + c. Найдите значение f(−1).
Задание 10 из варианта 2210311.
На рисунке изображены графики функций f(x) = frac{k}{x} и g(x) = ax + b, которые пересекаются в точках A и B. Найдите абсциссу точки B.
Задание 11.
Найдите точку минимума функции y = x3 − 27x2 + 13.
Задание 12.
а) Решите уравнение 2cos3x = –sin(frac{3pi}{2} + x)
б) Найдите все корни этого уравнения, принадлежащие отрезку [3π; 4π]
Задание 13.
Основанием правильной пирамиды PABCD является квадрат ABCD. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды, если AB = 30.
Задание 14.
Решите неравенство frac{9^{x}–13cdot 3^{x}+30}{3^{x+2}–3^{2x+1}}ge frac{1}{3^{x}}.
Задание 15.
По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n, при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Задание 16.
В треугольнике ABC медианы AA1, BB1 и CC1 пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22.
Задание 17.
Найдите все значения a, при каждом из которых система уравнений
begin{cases} (x-5a+1)^{2}+(y-2a-1)^{2}=a-2 \ 3x-4y=2a+3 end{cases}
не имеет решений.
Задание 18.
У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький – 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять.
а) Может ли Аня купить 24 конверта?
б) Может ли Аня купить 29 конвертов?
в) Какое наибольшее число конвертов может купить Аня?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.