При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Найдите значение выражения 
Ответ:
2
Найдите значение выражения (0,01)2 · 105 : 4−2
Ответ:
3
Площадь земель фермерского хозяйства, отведённых под посадку сельскохозяйственных культур, составляет 42 га и распределена между зерновыми и техническими культурами в отношении 3 : 4. Сколько гектаров занимают технические культуры?
Ответ:
4
5
Найдите значение выражения 
Ответ:
6
По тарифному плану «Просто как день» компания сотовой связи каждый вечер снимает со счёта абонента 18 руб. Если на счету осталось меньше 18 руб., то на следующее утро номер блокируют до пополнения счёта. Сегодня утром у Лизы на счету было 800 руб. Сколько дней (включая сегодняшний) она сможет пользоваться телефоном, не пополняя счёт?
Ответ:
7
Решите уравнение 
Ответ:
8
Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил относительно земли равна 1,5 м, а наибольшая h2 равна 2,5 м. Ответ дайте в метрах.
Ответ:
9
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) длина реки Волги
Б) диаметр монеты
В) ширина окна
Г) высота горы Эверест
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
1) 8848 м
2) 20 мм
3) 120 см
4) 3530 км
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Ответ:
10
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Ответ:
11
В соревнованиях по метанию молота участники показали следующие результаты.
| Спортсмен | Результат попытки, м | |||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | |
| Донников | 49 | 50,5 | 50 | 51 | 51 | 49,5 |
| Мелихов | 51 | 52,5 | 49,5 | 50 | 52 | 51,5 |
| Иванов | 50,5 | 50 | 49 | 51,5 | 51 | 51,5 |
| Теплицын | 52 | 51 | 52 | 50,5 | 51,5 | 51 |
Места распределяются по результатам лучшей попытки каждого спортсмена: чем дальше он метнул молот, тем лучше. Каков результат лучшей попытки (в метрах) спортсмена, занявшего второе место?
Ответ:
12
От дома до дачи можно доехать на автобусе, на электричке или на маршрутном такси. В таблице показано время, которое нужно затратить на каждый участок пути. Какое наименьшее время потребуется на дорогу? Ответ дайте в часах.
| 1 | 2 | 3 | |
| Автобусом | От дома до автобусной станции — 15 мин |
Автобус в пути: 2 ч 15 мин. |
От остановки автобуса до дачи пешком 5 мин. |
| Электричкой | От дома до станции железной дороги — 25 мин. |
Электричка в пути: 1 ч 45 мин. |
От станции до дачи пешком 20 мин. |
| Маршрутным такси | От дома до остановки маршрутного такси — 25 мин. |
Маршрутное такси в дороге: 1 ч 35 мин. |
От остановки маршрутного такси до дачи пешком 40 минут |
Ответ:
13
Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
Ответ:
14
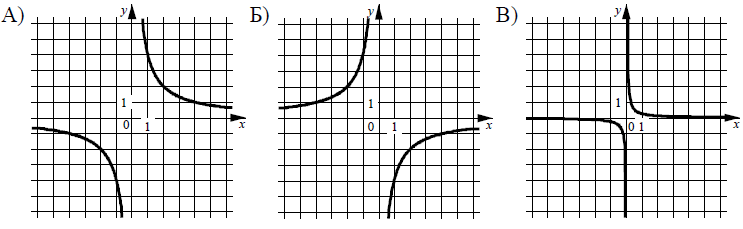
Установите соответствие между графиками линейных функций и угловыми коэффициентами прямых.
ГРАФИКИ
УГЛОВЫЕ КОЭФФИЦИЕНТЫ
1) 
2) 
3) 
4) 1
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Ответ:
15
16
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Ответ:
17
На координатной прямой точками отмечены числа a, b, c, d и m. Установите соответствие между указанными точками и числами из правого столбца.
ТОЧКИ
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Ответ:
18
Учитель математики Иван Петрович обязательно отключает свой телефон, когда ведёт урок. Выберите утверждения, которые следуют из приведённых данных.
1) Если телефон Ивана Петровича включён, значит, он не ведёт урок.
2) Если телефон Ивана Петровича выключен, значит, он ведёт урок.
3) Если Иван Петрович проводит контрольную работу по математике, значит, его телефон выключен.
4) Если Иван Петрович не ведёт урок, значит, его телефон включён.
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ:
19
Сумма цифр трёхзначного натурального числа А делится на 12. Сумма цифр числа (А + 6) также делится на 12. Найдите наименьшее возможное число А.
Ответ:
20
Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 10 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 42 очка, если известно, что по крайней мере один раз он ошибся?
Ответ:
Завершить тестирование, свериться с ответами, увидеть решения.
- 10.03.2023
Шестой тренировочный вариант, составленный на основе демоверсии ЕГЭ 2023 года по информатике от ФИПИ. Вариант включает все задания кодификатора 2023 года и учитывает все изменения, которые произошли в 2023 году (полный список изменений). Вариант содержит правильные ответы и подробные разборы для второй части теста — задания повышенной сложности. Ответы сохранены в конце варианта.
- Другие тренировочные варианты по информатике
Тест может содержать вопросы на различные темы, включая алгоритмы, программирование, базы данных, сети, компьютерную архитектуру и технологии. Вопросы могут быть представлены в различных форматах, таких как выбор одного или нескольких правильных ответов, соответствие, заполнение пропусков, короткий или развернутый ответы. В тесте могут также содержаться задания, требующие написания кода на языке программирования, анализа программного кода, использования различных программных инструментов и знание основных терминов и определений в области информатики.
- Дополнительные файлы для варианта 6
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 
2 .
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
|
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
||||
|
|
||||
|
|
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
| |
||||
|
|
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
| |
||||
|
|
||||
|
|
||||
| Показать сообщения за: Сортировать по: |
Добавлено: Вчера, 09:59 
Решение и ответы заданий варианта МА2290301 СтатГрад 31 января ОГЭ 2023 по математике. ГДЗ профиль для 9 класса. Решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
Все материалы получены из открытых источников и публикуются после окончания тренировочного экзамена в ознакомительных целях.
ЧАСТЬ 1
Задание 1-5.
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
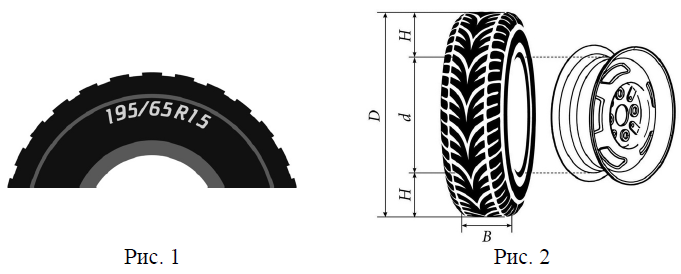
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рис. 2). Второе число (число 65 в приведённом примере) – процентное отношение высоты боковины (параметр H на рис. 2) к ширине шины, то есть 100·frac{H}{B}.
Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 245/45 R18.
Задание 6.
Найдите значение выражения frac{21}{5}:frac{6}{7}.
Задание 7.
Между какими числами заключено число √89?
1) 4 и 5
2) 29 и 31
3) 9 и 10
4) 88 и 90
Задание 8.
Найдите значение выражения frac{(5^{3}cdot 5^{4})^{7}}{(5cdot 5^{7})^{6}}.
Задание 9.
Решите уравнение 6x2 = 36x.
Если уравнение имеет больше одного корня, в ответе запишите меньший из корней.
Задание 10.
В магазине канцтоваров продаётся 100 ручек: 37 красных, 8 зелёных, 17 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или чёрной.
Задание 11.
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
ФОРМУЛЫ
1)y=-frac{4}{x}
2)y=frac{4}{x}
3)y=frac{1}{4x}
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле a = ω2R, где ω – угловая скорость (в с–1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 10 с–1, а центростремительное ускорение равно 54 м/с2. Ответ дайте в метрах.
Задание 13.
Укажите решение системы неравенств
begin{cases} x-5,2ge 0, \ x+4le 10. end{cases}
1) (–∞; 5,2] ∪ [6; +∞)
2) [5,2; +∞)
3) [6; +∞)
4) [5,2; 6]
Задание 14.
В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 9 минут. В начальный момент масса изотопа составляла 400 мг. Найдите массу изотопа через 36 минут. Ответ дайте в миллиграммах.
Задание 15.
В треугольнике ABC известно, что AB = 7, BC = 8, AC = 13. Найдите cos∠ABC.
Задание 16.
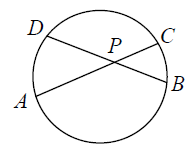
Хорды AC и BD окружности пересекаются в точке P, BP = 10, CP = 8, DP = 12. Найдите длину отрезка AP.
Задание 17.
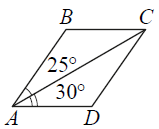
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Задание 18.
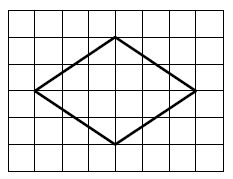
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Задание 19.
Какое из следующих утверждений верно?
1) Средняя линия трапеции равна полусумме её оснований.
2) Диагонали любого прямоугольника делят его на четыре равных треугольника.
3) Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету.
В ответе запишите номер выбранного утверждения.
ЧАСТЬ 2
Задание 20.
Решите неравенство (x – 6)2 < √10(x – 6).
Задание 21.
Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
Задание 22.
Постройте график функции
y=begin{cases} x^{2}-8x+14 ::при ::xge 3,\ x-2 ::при ::xlt 3.end{cases}
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Задание 23.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB = 40, CD = 42, а расстояние от центра окружности до хорды AB равно 21.
Задание 24.
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K. Докажите, что треугольники KAB и KCD подобны.
Задание 25.
На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD = 15, MD = 12, H – точка пересечения высот треугольника ABC. Найдите AH.
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.