Решу егэ второй закон термодинамики - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Идеальный газ получил количество теплоты 300 Дж и совершил работу 100 Дж. Чему равно изменение внутренней энергии газа? Ответ дайте в джоулях.

Идеальный газ получил количество теплоты 300 Дж и при этом внутренняя энергия газа увеличилась на 100 Дж. Какова работа, совершенная газом? (Ответ дать в джоулях.)

Идеальный газ отдал количество теплоты 300 Дж и при этом внутренняя энергия газа увеличилась на 100 Дж. Какова работа, совершенная газом? (Ответ дать в джоулях.)

Идеальный газ отдал количество теплоты 300 Дж и при этом внутренняя энергия газа уменьшилась на 100 Дж. Какова работа, совершенная газом? (Ответ дайте в джоулях.)

Идеальный газ получил количество теплоты 100 Дж и при этом внутренняя энергия газа уменьшилась на 100 Дж. Какова работа, совершенная газом? (Ответ дать в джоулях.)

Пройти тестирование по этим заданиям

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 358 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …

Добавить в вариант

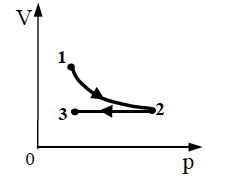
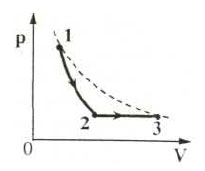
На графиках А и Б приведены диаграммы p−T и p−V для процессов 1−2 и 3−4 (гипербола), проводимых с 1 моль гелия. На диаграммах p – давление, V – объём и T – абсолютная температура газа. Установите соответствие между графиками и утверждениями, характеризующими изображённые на графиках процессы. К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ГРАФИКИ

А)  

Б)  

УТВЕРЖДЕНИЯ

1)  Над газом совершают работу, при этом газ отдаёт положительное количество теплоты.

2)  Газ получает положительное количество теплоты, при этом его внутренняя энергия не изменяется.

3)  Над газом совершают работу, при этом его внутренняя энергия увеличивается.

4)  Газ получает положительное количество теплоты, при этом его внутренняя энергия увеличивается.

Источник: ЕГЭ по физике 2017. Досрочная волна. Вариант 101

В цилиндр с подвижным поршнем накачали ν = 4 моля идеального одноатомного газа при температуре t₁ = 70 °C. Накачивание вели так, что давление газа было постоянным. Затем накачку прекратили и дали газу в цилиндре расшириться без теплообмена с окружающей средой до давления p = 1 атм. При этом газ остыл до температуры t₂  =  30 °C. Какую суммарную работу совершил газ в этих двух процессах? В исходном состоянии цилиндр был пуст и поршень касался дна.

На рисунке показан график зависимости модуля среднеквадратичной скорости V_ср.кв. атомов одноатомного идеального газа от объёма V газа в некотором процессе 1→2. Количество атомов газа в течение этого процесса не изменяется.

На основании анализа представленного графика выберите все верные утверждения.

1)  В процессе 1→2 газ совершает положительную работу.

2)  В процессе 1→2 внутренняя энергия газа уменьшается.

3)  В процессе 1→2 давление p газа возрастает прямо пропорционально объёму V газа.

4)  В процессе 1→2 газ отдаёт некоторое количество теплоты окружающим телам.

5)  Процесс 1→2 является изобарическим.

В вертикальном цилиндре, закрытом лёгким поршнем, находится этиловый спирт при температуре кипения t  =  78 °C. При сообщении спирту количества теплоты Q часть его превращается в пар, который при изобарном расширении совершает работу A. Удельная теплота парообразования спирта L  =  846 · 10³ Дж/кг, а его молярная масса  — 46 · 10^-3 кг/моль. Какая часть подведённого к этиловому спирту количества теплоты переходит в работу? Объёмом жидкого этилового спирта пренебречь.

Источник: ЕГЭ по физике 13.07.2020. Основная волна. ЦФО. Часть C. Вариант 1

В вертикальном цилиндре, закрытом лёгким поршнем, находится ацетон при температуре кипения t  =  56 °C. При сообщении ацетону количества теплоты Q часть его превращается в пар, который при изобарном расширении совершает механическую работу A. Удельная теплота парообразования ацетона L  =  524 · 10³ Дж/кг, а его молярная масса M  =  58 · 10^-3 кг/моль. Какая часть подведённого к ацетону количества теплоты идёт на увеличение внутренней энергии системы? Объёмом жидкого ацетона пренебречь.

Источник: ЕГЭ по физике 13.07.2020. Основная волна. ПФО (Самара). Часть C

В цилиндрическом сосуде, закрытом подвижным поршнем, находится водяной пар и капля воды. С паром в сосуде при постоянной температуре провели процесс a→b→c, pV−диаграмма которого представлена на рисунке. Из приведённого ниже списка выберите все правильные утверждения относительно проведённого процесса.

1)  На участке b→c масса пара уменьшается.

2)  На участке a→b к веществу в сосуде подводится положительное количество теплоты.

3)  В точке с водяной пар является насыщенным.

4)  На участке a→b внутренняя энергия капли уменьшается.

5)  На участке b→c внутренняя энергия пара уменьшается.

Источник: Демонстрационная версия ЕГЭ—2021 по физике

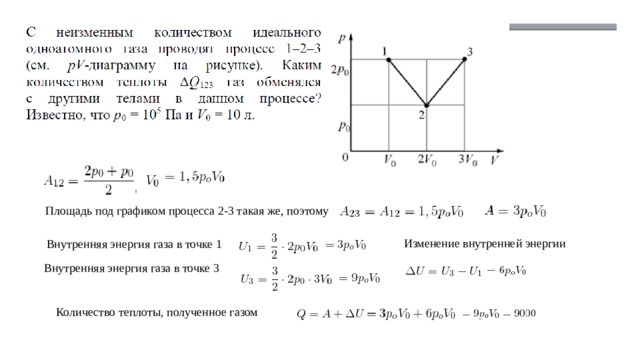
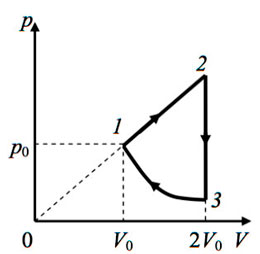
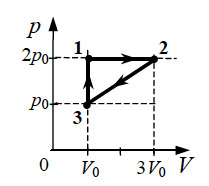
Два моля идеального одноатомного газа совершают циклический процесс, изображённый на диаграмме (см. рис.). Температура газа в состоянии 2 равна 2000 К. Какое количество теплоты получает газ на участке 2−3 этого циклического процесса? Ответ выразите в килоджоулях и округлите до целого числа.

В некотором процессе 1−2 внешние силы совершили над неизменным количеством идеального газа положительную работу 120 Дж. Внутренняя энергия газа в этом процессе изменилась на 100 Дж.

Из приведённого ниже списка выберите все правильные утверждения относительно проведённого процесса.

1)  В результате этого процесса газ отдал количество теплоты окружающим телам ().

2)  В результате этого процесса температура газа могла только повыситься.

3)  Этот процесс представляет собой замкнутый цикл.

4)  Объём газа в этом процессе уменьшился.

5)  Объём газа в этом процессе увеличился.

Идеальный одноатомный газ занимал объём 4 л при давлении 300  кПа. Затем газ расширился и стал занимать объём 6 л при давлении 150 кПа. В этом процессе газ совершил работу 550 Дж. Какое количество теплоты получил газ в этом процессе, если масса газа в сосуде неизменна?

В ходе адиабатного процесса идеальный одноатомный газ совершил работу 2493 Дж. В результате температура газа понизилась на 50 °C. Найдите количество вещества этого газа. Ответ запишите в молях.

На рисунке показан циклический процесс изменения состояния 1 моль одноатомного идеального газа. На каком участке цикла изменение внутренней энергии газа равно полученному газом количеству теплоты?

Источник: Демонстрационная версия ЕГЭ—2022 по физике

В ходе некоторого процесса температура 1 моля гелия повышается на 200 К.

В этом процессе удельная теплоёмкость гелия постоянна и равна 4991,3 Дж/(кг · °C). Какую работу совершает гелий в этом процессе?

Ответ выразите в Дж и округлите до целого числа.

Если идеальный газ получил количество теплоты 100 Дж, и при этом внутренняя энергия газа увеличилась на 100 Дж, то какую работу совершил газ в этом процессе? (Ответ дайте в джоулях.)

Если идеальный газ отдал количество теплоты 100 Дж и при этом внутренняя энергия газа уменьшилась на 100 Дж, то какова работа, совершенная газом? (Ответ дайте в джоулях.)

Всего: 358 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 1000 … 341–360 | 361–380 | 381–400 | 401–420 | 421–440 | 441–460 | 461–480 | 481–500 …

Добавить в вариант

Идеальный колебательный контур состоит из заряженного конденсатора ёмкостью 0,02 мкФ, катушки индуктивностью 0,2 мГн и разомкнутого ключа. После замыкания ключа, которое произошло в момент времени t = 0, в контуре возникли собственные электромагнитные колебания. При этом максимальная сила тока, текущего через катушку, была равна 0,01 Установите соответствие между зависимостями, полученными при исследовании этих колебаний (см. левый столбец), и формулами, выражающими эти зависимости (см. правый столбец; коэффициенты в формулах выражены в соответствующих единицах СИ без кратных и дольных множителей).

К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ЗАВИСИМОСТИ

А)  Зависимость напряжения на конденсаторе от времени

Б)  Зависимость силы тока, текущего через катушку, от времени

ФОРМУЛЫ

1)  f(t)=

2)  f(t)=

3)  f(t)=

4)  f(t)=

Снаряд массой 2 кг, летящий со скоростью 100 м/с, разрывается на два осколка. Один из осколков летит под углом 90° к первоначальному направлению, а второй  — под углом 60°. Какова масса второго осколка, если его скорость равна 400 м/с? Ответ приведите в килограммах.

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 6.

По гладкой горизонтальной плоскости по осям x и y движутся две шайбы с импульсами, равными по модулю p₁ = 1,5 кг·м/с и p₂ = 3,5 кг·м/с, как показано на рисунке. После соударения вторая шайба продолжает двигаться по оси y в прежнем направлении с импульсом, равным по модулю p₃ = 1,5 кг·м/с. Определите модуль импульса первой шайбы после удара. Ответ приведите в килограммах на метр в секунду.

К контактам батарейки с некоторым внутренним сопротивлением подсоединён резистор сопротивлением R, при этом через батарейку течёт ток силой I₁. Параллельно с этим резистором подсоединяют второй такой же резистор, и сила тока, текущего через батарейку, изменяется в 1,5 раза. После этого второй резистор R отсоединяют и подключают его последовательно с первым резистором. В результате через батарейку начинает течь ток силой I₃. Чему равно отношение I₃/I₁?

Три одинаковых резистора сопротивлением 30 Ом каждый подключают к источнику постоянного напряжения: первый раз  — последовательно, второй  — параллельно. При этом показания идеального амперметра (см. рис.) отличаются в 3 раза. Чему равно внутреннее сопротивление источника напряжения?

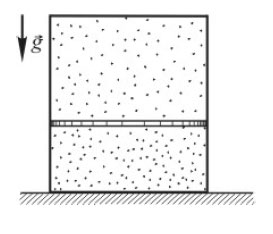
Опыт показывает, что сопротивление R чистых металлов при условиях, близких к нормальным, зависит от температуры по закону где R₀  — сопротивление при температуре 0 °C, а температура t измеряется в градусах Цельсия. Школьник при температуре 0 °C собрал электрическую цепь, состоящую из последовательно соединённых аккумулятора с ЭДС 40 В, амперметра и металлической проволочной спирали (рисунок сверху). Затем он нагрел спираль при помощи спиртовки (рисунок снизу). Пренебрегая сопротивлением аккумулятора, амперметра и проводов, определите сопротивление спирали при температуре 0 °C (в Ом) и найдите температуру (в градусах Цельсия), до которой во втором опыте была нагрета спираль. Показания амперметра можно считать точными. Значения сопротивления и температуры запишите в ответе слитно, не разделяя их пробелом или другим знаком.

Снаряд массой 2 кг, летящий со скоростью 200 м/с, разрывается на два осколка. Один из осколков летит под углом 90° к первоначальному направлению, а второй  — под углом 60°. Какова скорость второго осколка, если его масса равна 1 кг?

Источник: ЕГЭ по физике 07.06.2017. Основная волна

Снаряд массой 2 кг, летящий со скоростью 200 м/с, разрывается на два осколка. Первый осколок массой 1 кг летит под углом 90° к первоначальному направлению со скоростью 300 м/с. Найдите скорость второго осколка.

Источник: Демонстрационная версия ЕГЭ—2018 по физике

В двух идеальных колебательных контурах происходят незатухающие электромагнитные колебания. Максимальное значение заряда конденсатора во втором контуре равно 6 мкКл. Амплитуда колебаний силы тока в первом контуре в 2 раза меньше, а период его колебаний в 3 раза меньше, чем во втором контуре. Определите максимальное значение заряда конденсатора в первом контуре. Ответ дайте в микрокулонах.

Источник: ЕГЭ по физике 13.07.2020. Основная волна

Установите соответствие между физическими законами и формулами для них. К каждой позиции первого столбца подберите нужную позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ЗАКОНЫ

А)  Закон Ампера

Б)  Закон Джоуля-Ленца

Пояснение.

Физические законы  — самое важное, что есть в физике. Чтобы успешно сдать экзамен по физике, надо специально потратить время на выучивание формул и названных физических законов. Задания на «соответствие» помогут в этом. Полезный ориентир: признаком успеха в этом деле будет то, что задачи подобного типа станут казаться вам простыми.

Установите взаимосвязь между физическим явлением и законом, его описывающим

ФИЗИЧЕСКОЕ ЯВЛЕНИЕ

А)  Взаимное притяжение тел

Б)  Наличие силы, действующей на проводник с током в магнитном поле

ЗАКОН

1)  Закон сохранения импульса

2)  Закон сохранения механической энергии

3)  Закон Ампера

4)  Закон всемирного тяготения

В колебательном контуре, состоящем из конденсатора и катушки индуктивности, происходят свободные электромагнитные колебания. В момент, когда конденсатор разряжен, параллельно к нему подключают второй такой же конденсатор. Как после этого изменятся следующие физические величины: запасенная в контуре энергия, частота свободных электромагнитных колебаний, амплитуда напряжения между пластинами первого конденсатора?

Для каждой величины определите соответствующий характер изменения. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А)  Запасенная в контуре энергия

Б)  Частота свободных электромагнитных колебаний

В)  Амплитуда напряжения между пластинами первого конденсатора

ИХ ИЗМЕНЕНИЕ

1)  Увеличится

2)  Уменьшится

3)  Не изменится

При помощи первого электрокипятильника можно вскипятить 200 г воды в стакане за 2 минуты, а при помощи второго, включённого в ту же розетку,  — за 3 минуты. За какое время закипит та же масса воды в стакане, если подключить эти кипятильники параллельно? Теплопотерями пренебречь. Ответ приведите в минутах.

Снаряд массой 2 кг, летящий со скоростью 100 м/с, разрывается на два осколка. Один из осколков летит под углом 90° к первоначальному направлению. Под каким углом к этому направлению полетит второй осколок, если его масса 1 кг, а скорость 400 м/с? Ответ приведите в градусах.

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 2., ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 4.

На рисунке показана цепь постоянного тока. Установите соответствие между физическими величинами и

формулами, по которым их можно рассчитать (   — ЭДС источника напряжения; r  — внутреннее сопротивление источника; R  — сопротивление резистора).

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А)  напряжение на источнике при замкнутом ключе К

Б)  сила тока через источник при разомкнутом ключе К

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Источник: ЕГЭ — 2015. Досрочная волна.

В пробирке находится υ молей атомов β-радиоактивного вещества с периодом полураспада T. Экспериментатор отмеряет время 10T. Потом он берёт другую пробирку с тем же количеством атомов другого радиоактивного вещества с периодом полураспада 5T, и отмеряет то же самое время 10T. Известно, что продуктами распада обоих веществ являются стабильные изотопы.

Как для второй пробирки по сравнению с первой через время 10T изменятся следующие физические величины: количество вещества в пробирке; количество нерадиоактивных атомов в пробирке?

Для каждой величины определите соответствующий характер изменения:

1)  увеличится;

2)  уменьшится;

3)  не изменится.

Запишите в ответ цифры, расположив их в порядке, соответствующем таблице:

Количество вещества в пробирке	Количество нерадиоактивных атомов в пробирке

Металлическое кольцо, обладающее электрическим сопротивлением, находится в однородном магнитном поле. Линии индукции этого поля перпендикулярны плоскости кольца, а величина магнитной индукции изменяется по гармоническому закону с частотой ω. Индуктивность кольца пренебрежимо мала.

Из приведённого ниже списка выберите все правильные утверждения.

1)  В кольце протекает переменный электрический ток.

2)  Сила натяжения проволоки, из которой изготовлено кольцо, изменяется по гармоническому закону с частотой 2ω.

3)  Амплитуда протекающего в кольце электрического тока не зависит от частоты ω.

4)  Амплитуда ЭДС индукции, действующая в кольце, пропорциональна частоте ω.

5)  Средняя тепловая мощность, выделяющаяся в кольце, пропорциональна частоте ω.

Источник: ЕГЭ по физике 11.06.2021. Основная волна. Разные задания

Снаряд массой 4 кг, летящий со скоростью 400 м/с, разрывается на две равные части, одна из которых летит в направлении движения снаряда, а другая  — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличилась на величину Скорость осколка, летящего по направлению движения снаряда, равна 900 м/с. Найдите

Какие законы Вы используете для описания взрыва снаряда? Обоснуйте их применение к данному случаю.

Снаряд массой 4 кг, летящий со скоростью 400 м/с, разрывается на две равные части, одна из которых летит в направлении движения снаряда, а другая  — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличилась на величину Определите скорость осколка, летящего по направлению движения снаряда.

Какие законы Вы используете для описания взрыва снаряда? Обоснуйте их применение к данному случаю.

Всего: 1000 … 341–360 | 361–380 | 381–400 | 401–420 | 421–440 | 441–460 | 461–480 | 481–500 …

Источник

Второй закон термодинамики

Темы кодификатора ЕГЭ: второй закон термодинамики.
Необратимость процессов в природе
Постулаты Клаузиуса и Кельвина
Эквивалентность постулатов Клаузиуса и Кельвина
Обратимые процессы
Обратимость машины Карно

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: второй закон термодинамики.

Не все физические процессы, допускаемые нашим воображением, могут осуществляться в реальности.

Например, в течение нескольких столетий предпринимались попытки изобрести вечный двигатель первого рода — устройство, способное производить неограниченное количество механической работы само по себе, без привлечения внешних источников энергии.

Все подобные проекты, зачастую весьма хитроумные, неизменно терпели крах. В конечном счёте это привело к открытию фундаментального закона природы—закона сохранения энергии. Любой процесс, нарушающий закон сохранения энергии, оказывается невозможным; точнее — не обнаружено ни одного процесса, в котором не выполнялся бы закон сохранения энергии.

В термодинамике закон сохранения энергии принял форму первого закона термодинамики.

к оглавлению ▴

Необратимость процессов в природе

Существуют, однако, и другие ограничения на ход процессов, не связанные с законом сохранения энергии. Оказывается, реальные процессы необратимы: они могут самопроизвольно идти лишь в одном определённом направлении. Обратные им процессы, также не нарушающие закон сохранения энергии, сами по себе никогда не протекают.

Так, если привести в тепловой контакт горячее и холодное тело, то энергия в процессе теплообмена будет передаваться от горячего тела к холодному. Обратный процесс, в результате которого холодное тело ещё больше остывало бы, а горячее — ещё больше нагревалось, хотя и возможен с энергетической точки зрения, в действительности сам по себе не происходит. Теплопередача от горячего тела к холодному является необратимым процессом (подчеркнём ещё раз, что речь идёт о невозможности самопроизвольного протекания обратного процесса. В принципе передать энергию от холодного тела к горячему можно — но только за счёт работы внешнего источника. Именно этим и занимаются холодильные машины).

Подобных примеров можно привести сколько угодно. Ложка падает со стола и остаётся лежать на полу — кинетическая энергия её механического движения переходит во внутреннюю энергию пола и самой ложки.

Энергетически возможен и обратный процесс: молекулы со стороны пола синхронно ударят по ложке так, что она запрыгнет обратно на стол(а участок пола при этом охладится, потеряв внутреннюю энергию). Но такое в природе никогда не наблюдалось. Превращение механической энергии во внутреннюю является необратимым процессом.

к оглавлению ▴

Постулаты Клаузиуса и Кельвина

Необратимость процессов теплопередачи от горячего тела к холодному и превращения механической энергии во внутреннюю была постулирована во втором законе термодинамики. Две эквивалентные формулировки второго закона термодинамики принадлежат Клаузиусу и Томсону (лорду Кельвину).

Постулат Клаузиуса. Невозможен процесс, единственным результатом которого является передача тепла от менее нагретого тела к более нагретому.

Процесс, при котором тепло передаётся от менее нагретого тела к более нагретому, происходит в холодильных машинах. Но эта передача тепла не является единственным результатом данного процесса. Происходят изменения и в других телах — например, работает внешний источник энергии. Постулат Клаузиуса утверждает невозможность самопроизвольной теплопередачи от холодного тела к горячему.

Постулат Кельвина. Невозможен циклический процесс, единственным результатом которого является получение работы за счёт охлаждения теплового резервуара.

В тепловом двигателе работа получается за счёт отвода тепла Q_1 от теплового резервуара — нагревателя. Но получение работы не является единственным результатом данного процесса. Мы уже отмечали, что для обеспечения цикличности работы теплового двигателя какое-то количество теплоты Q_2 должно быть отдано другому резервуару — холодильнику. Поэтому происходят изменения и в других телах.

Фактически постулат Кельвина запрещает существование теплового двигателя с КПД, равным единице.

Гипотетический тепловой двигатель, целиком превращающий в работу поступающее от нагревателя тепло, называется вечным двигателем второго рода. Он не противоречит закону сохранения энергии. Если бы такой двигатель был изобретён, люди получили бы возможность без потерь превращать в работу огромные запасы внутренней энергии морей и океанов. Но невозможность создать вечный двигатель второго рода как раз и утверждается постулатом Кельвина.

к оглавлению ▴

Эквивалентность постулатов Клаузиуса и Кельвина

Постулаты Клаузиуса и Кельвина логически следуют друг из друга. Показать это совсем не сложно.

Предположим сначала, что неверен постулат Клаузиуса. Тогда существует процесс , единственным результатом которого является передача тепла от менее нагретого тела к более нагретому телу .

Возьмём тепловой двигатель, нагревателем которого является тело , а холодильником — тело .

Двигатель подберём так, чтобы за цикл к холодильнику поступало как раз тепло . Совершим один цикл, в ходе которого двигатель производит работу , после чего осуществим процесс . Тепло вернётся к телу .

Тогда окажется, что в результате циклического процесса наш двигатель произвёл работу единственно за счёт тепла, отведённого от нагревателя . Следовательно, неверен постулат Кельвина.

Наоборот, предположим, что неверен постулат Кельвина. Тогда существует циклический процесс , единственным результатом которого является получение работы за счёт тепла, отводимого от некоторого резервуара .

Возьмём тело — более горячее, чем . Запустим процесс . От тела будет отведено тепло . Полученную работу A=Q превратим во внутреннюю энергию тела (например, с помощью трения).

В итоге мы осуществим процесс, единственным результатом которого является передача тепла от менее нагретого тела к более нагретому телу . Никаких других изменений не произошло (ведь процесс — циклический!). Стало быть, постулат Клаузиуса неверен.

В листке «Тепловые машины» мы отметили, что изотермические и адиабатные процессы делают машину Карно обратимой, но не объяснили — почему.

Кроме того, в этом листке было сказано, что все реальные процессы необратимы. Как это увязать с упомянутой обратимостью цикла Карно?

Прежде всего, нужно рассказать о важнейшей (наряду с идеальным газом) идеализации в термодинамике — равновесных обратимых процессах.

к оглавлению ▴

Обратимые процессы

Равновесное состояние газа (и вообще любой термодинамической системы) — это состояние теплового равновесия (вспоминайте листок «Температура»!). В этом состоянии определены значения макроскопических параметров: давления, объёма, температуры…Равновесное состояние может быть изображено точкой на диаграммах состояния (т. е. -, — и -диаграммах).

Равновесный процесс представляет собой последовательную цепочку близких равновесных состояний. Равновесный процесс может быть изображён непрерывной линией на диаграммах состояния.

Как вы теперь понимаете, все процессы, графики которых мы рассматривали в предыдущих листках, предполагались равновесными — ведь только в этом случае можно говорить о «графике процесса».

Процесс можно считать равновесным, если параметры газа меняются достаточно медленно. Настолько медленно, что в каждый момент времени будет успевать устанавливаться новое равновесное состояние. Такие медленные равновесные процессы называют ещё квазистатическими.

Вот пример квазистатического (равновесного) процесса. Пусть имеется вертикальный цилиндр с газом под поршнем. Положим на поршень песчинку. Потом другую, третью, сотую, тысячную. Получим чрезвычайно медленное сжатие газа, представляющее собой череду сменяющих друг друга равновесных состояний.

Теперь начнём снимать песчинки обратно, всё так же по одной. Получим квазистатическое равновесное расширение газа. При этом газ пройдёт в обратном направлении те же самые состояния, которые он проходил в предыдущем процессе равновесного сжатия. Действительно, раз уж при каждом положении поршня успевает установиться тепловое равновесие, то значения макроскопических параметров определяются только самим положением поршня, но не направлением его движения.

Мы видим, что равновесный процесс является обратимым — его можно провести в обратном направлении через ту же самую цепочку равновесных состояний. На диаграммах состояния обратимый процесс идёт по одной и той же линии как в прямом, так и в обратном направлении.

Если же вместо песчинок поставить на поршень увесистую гирьку, то процесс сжатия газа пойдёт весьма быстро. Давление газа непосредственно под поршнем будет больше, чем у дна сосуда, и мы уже не сможем охарактеризовать состояние газа в каждый момент времени каким-то одним значением давления. Состояния, проходимые газом, не будут состояниями теплового равновесия (макроскопические параметры не успевают принимать определённые значения для всего газа). Стало быть, процесс быстрого сжатия газа будет неравновесным.

Кроме того, такой процесс будет необратимым . Ведь если столь же быстро расширять газ, то давление непосредственно под поршнем теперь окажется меньше, чем у дна сосуда. Следовательно, при быстром расширении газ проходит через иную цепочку состояний, чем в процессе сжатия.

Процессы, идущие бесконечно медленно, являются обратимыми. Это идеализация. Реальные процессы идут с конечной скоростью и потому необратимы.

к оглавлению ▴

Обратимость машины Карно

Пусть некоторая тепловая машина осуществляет цикл между нагревателем с фиксированной температурой T_1 и холодильником с фиксированной температурой T_2 . Как сделать этот цикл обратимым?

Разумеется, все процессы цикла должны быть квазистатическими — наша машина будет работать бесконечно медленно (мощность такой машины равна нулю). Но этого не достаточно. То, что машина обязана работать в прямом и обратном направлении (т. е. как тепловой двигатель и как холодильная машина) между одними и теми же нагревателем и холодильником, налагает дополнительные требования.

При работе в прямом направлении рабочее тело (газ) получает от нагревателя тепло Q_1 и отдаёт холодильнику тепло Q_2 . Эти процессы теплопередачи должны быть обратимы: в самом деле, при работе в обратном направлении газ должен забрать у холодильника тепло Q_2 и отдать нагревателю тепло Q_1 , проходя через те же самые состояния, что и в прямом направлении.

Можно ли сделать теплопередачу обратимой? Ведь если температура газа будет отличаться от температуры нагревателя (холодильника),передача тепла будет необратима в силу постулата Клаузиуса!

Единственный выход состоит в том, чтобы тепловое взаимодействие газа с нагревателем и холодильником происходило изотермически. В ходе теплообмена газ имеет ту же температуру, что и нагреватель (холодильник), и бесконечно медленно, обратимым образом обменивается с ними теплом. Вот откуда берутся изотермы в цикле Карно: только они и могут соответствовать тепловому контакту газа с нагревателем и холодильником.

Изменение температуры газа в цикле тоже должно происходить обратимо; значит, и тут нужно исключать необратимый теплообмен. Единственная возможность — теплоизолировать газ и использовать адиабатные процессы. Если проводить их квазистатически, они будут обратимыми.

Таким образом, цикл Карно — это единственный циклический процесс, который можно осуществлять обратимым образом между данными нагревателем и холодильником с фиксированными температурами.

Разумеется, машина Карно является идеализацией — уже потому, что использует бесконечно медленные процессы. Поэтому её часто называют идеальной тепловой машиной.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Второй закон термодинамики» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.03.2023

Источник

Термодинамика 1

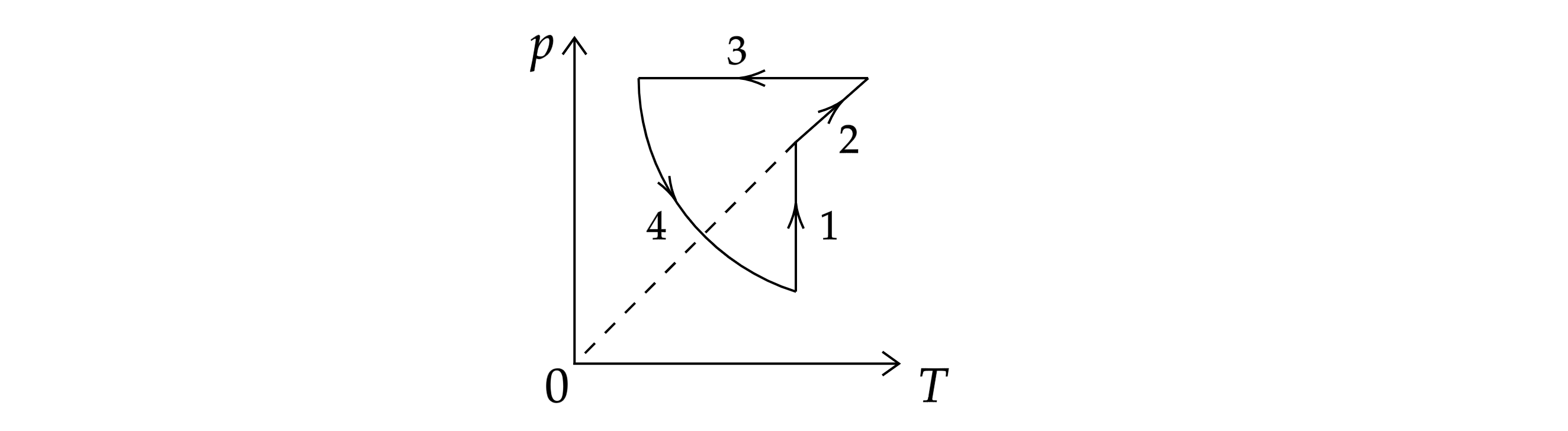
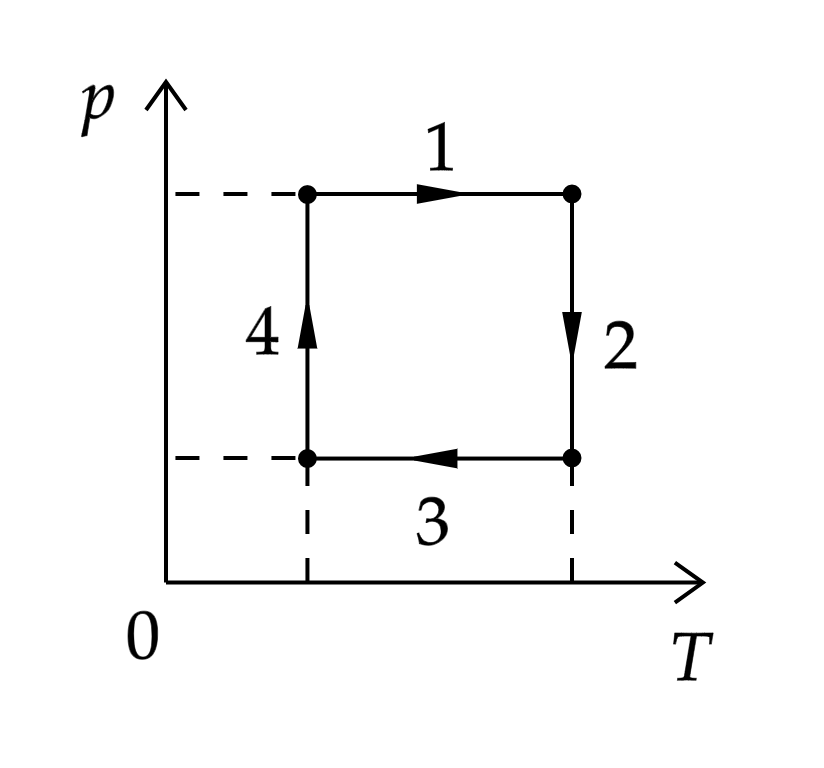
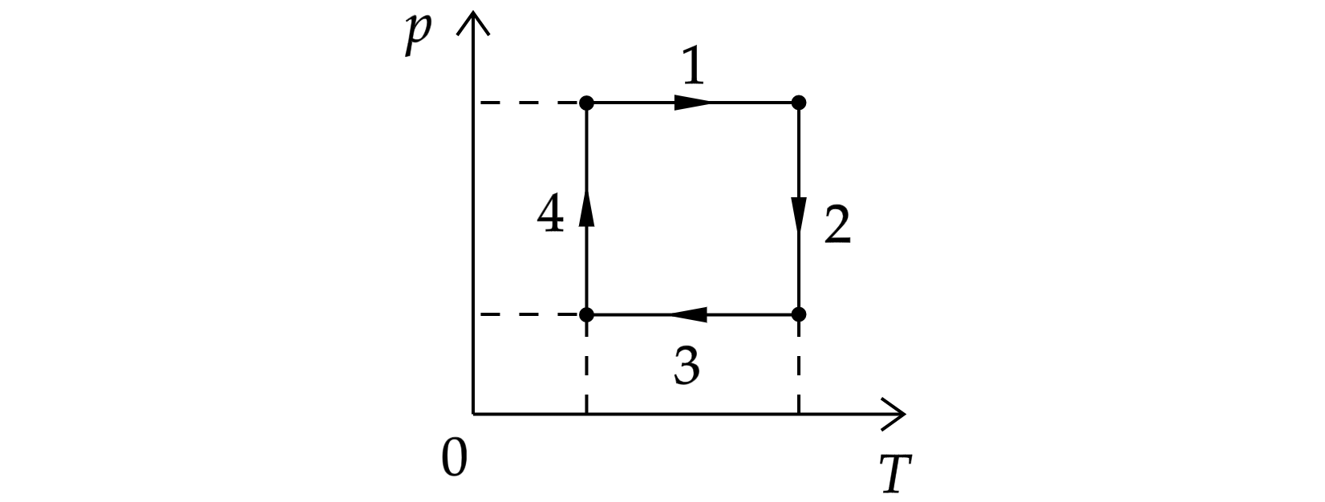
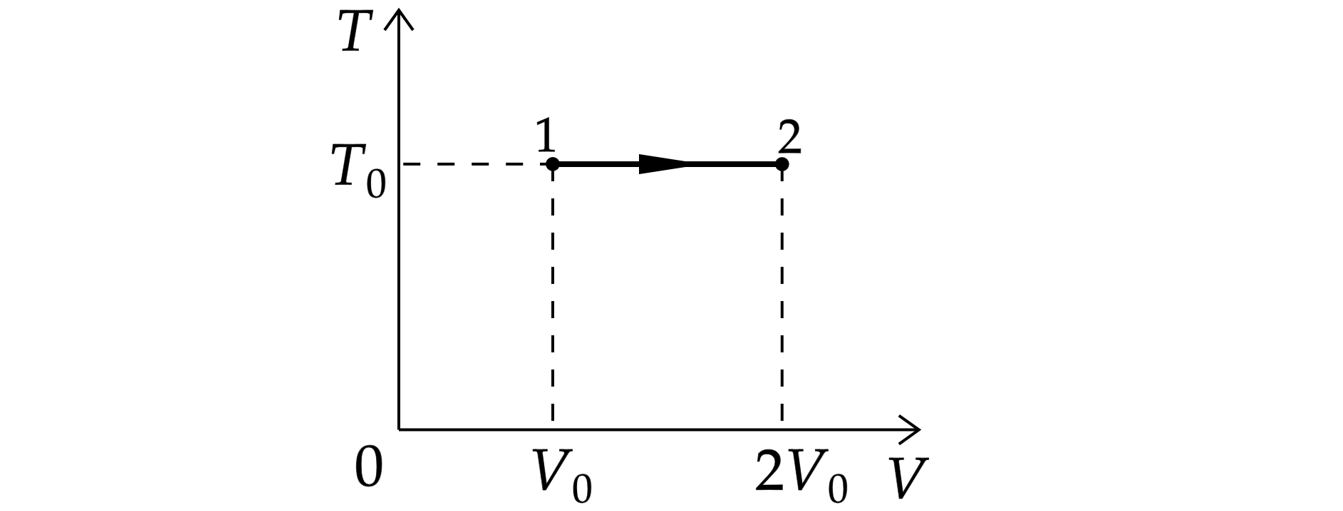
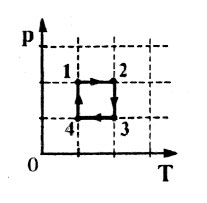
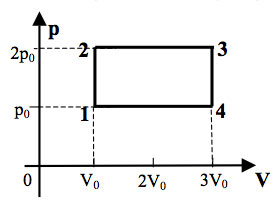
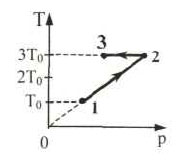
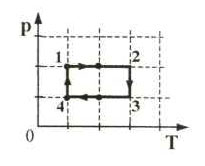
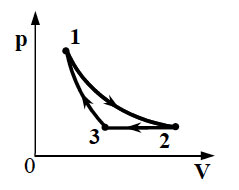
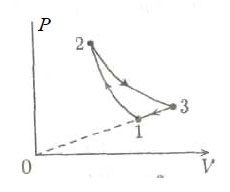
С одним молем идеального газа совершают циклический процесс 1–2–3–4–1, изображенный на Т– р — диаграмме . Определить работу, совершенную газом за цикл, если температуры в состояниях 1 и 3 равны соответственно Т1 и Т3, а температуры в состояниях 2 и 4 одинаковы. Добавим еще одно задание: найти КПД цикла.

Площадь под графиком процесса 2-3 такая же, поэтому

Изменение внутренней энергии

Внутренняя энергия газа в точке 1

Внутренняя энергия газа в точке 3

Количество теплоты, полученное газом

Источник

Первое начало термодинамики

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

термодинамика

9.01Внутренняя энергия газа

9.02Работа идеального газа

9.03Первое начало термодинамики

9.04Термодинамические циклы. КПД тепловых машин

Решаем задачи

Показать ответ и решение

В первом процессе газ расширяется при постоянном давлении от объема 0 до . Так как
, то процесс изобарный и работу газа, совершенную за этот процесс можно найти по
формуле:

Запишем уравнение Менделеева – Клапейрона:

где
— количество вещества газа, — универсальная газовая постоянная, .
Подставим (2) в (1):

Рассмотрим второй процесс. В условии сказано, что газ расширялся без теплообмена с окружающей
средой, то есть второй процесс был адиабатическим.
Запишем первое начало термодинамики для адиабатического процесса (с учетом того, что
Q2 = 0 ):

где
— количество теплоты, ΔU2 — изменение внутренней энергии газа. Выразим работу газа,
совершенную во втором процессе:

A = − ΔU (3)
2 2

Изменение внутренней энергии одноатомного газа во втором процессе равно:

3
ΔU2 = -νR ΔT, (4)
2

где изменение абсолютной температуры газа во втором процессе , причем
T = (273 + t )
2 2 .
Подставим (4) в (3):

3
A2 = − --νR(T2 − T1 )
2

Найдем суммарную работу, которую совершил газ в этих двух процессах:

( )
A = νRT1 + − 3νR (T2 − T1)
2

( )
5- 3-
A = νR 2T1 − 2T2

Д ж ( 5 3 )
A = 2 моля ⋅ 8,31 ---------⋅ --⋅ 323 К − -⋅ 293 К = 6116, 16 Дж ≈ 6 кД ж
моль ⋅ К 2 2

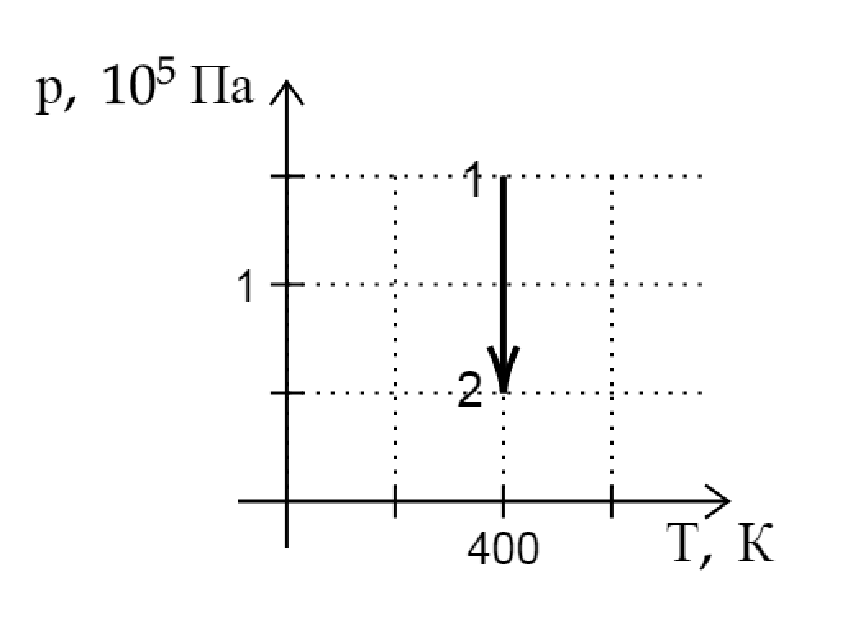
Газ получил количество теплоты, равное 300 Дж, при этом внутренняя энергия газа уменьшилась на 100
Дж. Масса газа не менялась. Какую работу совершил газ в этом процессе? (Ответ дайте в джоулях.)

Демоверсия 2023

Показать ответ и решение

Первое начало термодинамики:

где — количество теплоты, — изменение внутренней энергии газа, — работа газа.
Выразим работу газа:

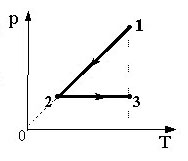
На рисунке показан циклический процесс изменения состояния 1 моль одноатомного идеального газа. На
каком участке цикла изменение внутренней энергии газа равно полученному газом количеству теплоты?

Демоверсия, 2022

Показать ответ и решение

Первое начало термодинамики:

где — количество теплоты, — изменение внутренней энергии газа, — работа
газа.
То есть работа газа должна быть равна нулю, значит, объём постоянен. По уравнению
Клапейрона-Менделеева:

pV- = νR,
T

где – объём газа.
При постоянном давлении имеем:

p
--= νR = const ⇒ p = const ⋅ T,
T

то есть прямая линия под некоторым наклоном (2)

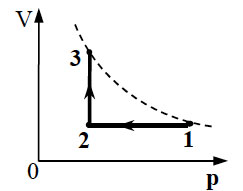
На рисунке показан циклический процесс изменения состояния постоянной массы одноатомного
идеального газа. На каком участке работа газа положительна и равна полученному газом количеству
теплоты

Показать ответ и решение

По первому началу термодинамики:

где
– количество теплоты, полученное газом, – изменение внутренней энергии, – работа
газа.
Так как Q = A , то ΔU = 0 , при этом изменение внутренней энергии равно:

ΔU = 3-νR ΔT,
2

где
– количество вещества, – изменение температуры.
Следовательно, температура не изменялась.
Работа газа положительна, если объём газа увеличивается. По закону Бойля-Мариотта:

где
– объём, то есть объём увеличивается при уменьшении давления, что соответствует графику 2.

Внутреннюю энергию 2 молей одноатомного идеального газа уменьшили на 800 Дж, а внешние силы
совершили над ним работу 400 Дж. Какое количество теплоты отдал газ? Ответ дайте в
Джоулях.

Показать ответ и решение

Запишем первый закон термодинамики

′
Q = ΔU − A ,

где
– изменение внутренней энергии, A ′ – работа внешних сил.

Внутренняя энергия газа в процессе эксперимента увеличилась на 33 кДж, при этом внешние силы
совершили работу на газом, равную 51 кДж. Какое количество теплоты газ отдал окружающей среде?
Ответ выразить в кДж.

Показать ответ и решение

По первому закону термодинамики:

где — количество теплоты, — изменение внутренней энергии газа, а — работа, совершенная
газом.

где A вн — работа внешних сил над газом.
Отсюда:

Q = ΔU − A_вн = 33 кДж − 51 кДж = −18 кДж

Значит, газ отдал окружающей среде количество теплоты, равное 18 кДж.

Показать ответ и решение

По первому закону термодинамики:

Q= ΔU = 3m-RΔT
2M

Осталось выразить :

2QM 2⋅900 Дж ⋅0,04 кг/моль
ΔT = 3mR-= 3⋅0,2-кг⋅8,31-Дж/-(моль-⋅ К)-≈ 14 K

В некотором процессе идеальный газ совершает работу 140 Дж, причем полученное газом количество
теплоты составляет 16/7 от изменения внутренней энергии газа (внутренняя энергия увеличивается).
Чему равно изменение внутренней энергии газа в этом процессе? Ответ дайте в Дж и округлите до
целых.

Показать ответ и решение

По первому закону термодинамики:

где — количество теплоты, полученное газом, — изменение внутренней энергии газа, а —
работа, совершенная газом.

По условию 16
Q = ---ΔU
7 . Отсюда:

16
7-- ΔU = ΔU + A

В процессе адиабатного расширения четырех молей идеального одноатомного газа газ совершил работу
100 Дж. Определите изменение внутренней энергии газа в этом процессе. Ответ дайте в
Дж.

Показать ответ и решение

По первому закону термодинамики:

В адиабатном процессе газ не получает теплоты от внешней среды:

0 = ΔU + A ⇒ ΔU = −A = −100 Дж

В некотором процессе газ получает количество теплоты 97 Дж, внутренняя энергия газа увеличивается,
причём изменение его внутренней энергии составляет 4/7 от работы газа. Какую работу совершает газ в
этом процессе? Ответ дать в Дж и округлить до целых.

Показать ответ и решение

По первому закону термодинамики:

По условию 4
ΔU = -A
7 . Отсюда:

На рисунке показан график изменения состояния постоянной массы идеального газа. В этом процессе
газ отдал количество теплоты, равное 4 кДж. На сколько уменьшилась внутренняя энергия газа? Ответ
дайте в кДж.

Показать ответ и решение

Из графика видно, что данный процесс является изохорным. Поскольку объем газа не изменялся, газ не
совершал работы. Следовательно, согласно первому началу термодинамики:

Идеальный газ совершил работу 161 кДж и при этом внутренняя энергия газа уменьшилась на 140 кДж.
Какое количество теплоты получил газ в этом процессе? (Ответ дать в кДж)

Показать ответ и решение

По первому закону термодинамики:

Q = −140 кДж + 161 кДж = −140 ⋅ 10³ Дж + 161 ⋅ 10³ Дж = 21000 Дж = 21 кДж

В процессе адиабатного сжатия над 2 молями идеального одноатомного газа совершают
работу 980,5 Дж. Определите модуль изменения температуры данной порции газа в результате этого
процесса. Ответ дайте в К и округлите до целых.

Показать ответ и решение

По первому закону термодинамики:

В адиабатном процессе газ не получает теплоты от внешней среды:

ΔU = 3-
2 νRΔT

Отсюда:

−A = 3
--
2 νRΔT

На -диаграмме показан процесс изменения состояния постоянной массы идеального газа. В этом
процессе газ совершает работу, равную 3 кДж. Каково количество теплоты, полученное газом? (Ответ
дайте в кДж.)

Показать ответ и решение

По первому закону термодинамики:

ΔU = 3-
2 νRΔT.

По графику находим, что ΔT = 0 , значит ΔU = 0 . Подставим это в (1):

В процессе эксперимента внутренняя энергия газа увеличилась на 4,7 Дж, при этом газ отдал
окружающей среде количество теплоты, равное Дж. Какую работу совершили над газом внешние
силы в данном эксперименте? Ответ дать в Дж.

Показать ответ и решение

По первому закону термодинамики:

где — количество теплоты (т.к. по условию газ отдает количество теплоты, то при подстановке
значений мы будем писать его со знаком ««), — изменение внутренней энергии газа, а —
работа, совершенная газом.

Отсюда:

Известно, что:

где A вн — работа внешних сил над газом. Подставим сюда (1) и выразим A вн :

A_вн = −A = −(Q − ΔU) = −Q + ΔU = −(−39 Дж) + 4, 7 Дж = 39 Дж + 4, 7 Дж = 43, 7 Дж

На рисунке показан циклический процесс изменения состояния постоянной массы одноатомного
идеального газа. На каком участке работа внешних сил над газом положительна и равна отданному
газом количеству теплоты

Демоверсия 2019

Показать ответ и решение

По первому началу термодинамики:

ΔU = 3-νR ΔT,
2

где
– количество вещества, – изменение температуры.
Следовательно, температура не изменялась.
Работа газа отрицательна, если объём газа уменьшается. По закону Бойля-Мариотта:

где
– объём, то есть объём уменьшается при увеличении давления, что соответствует графику 4.

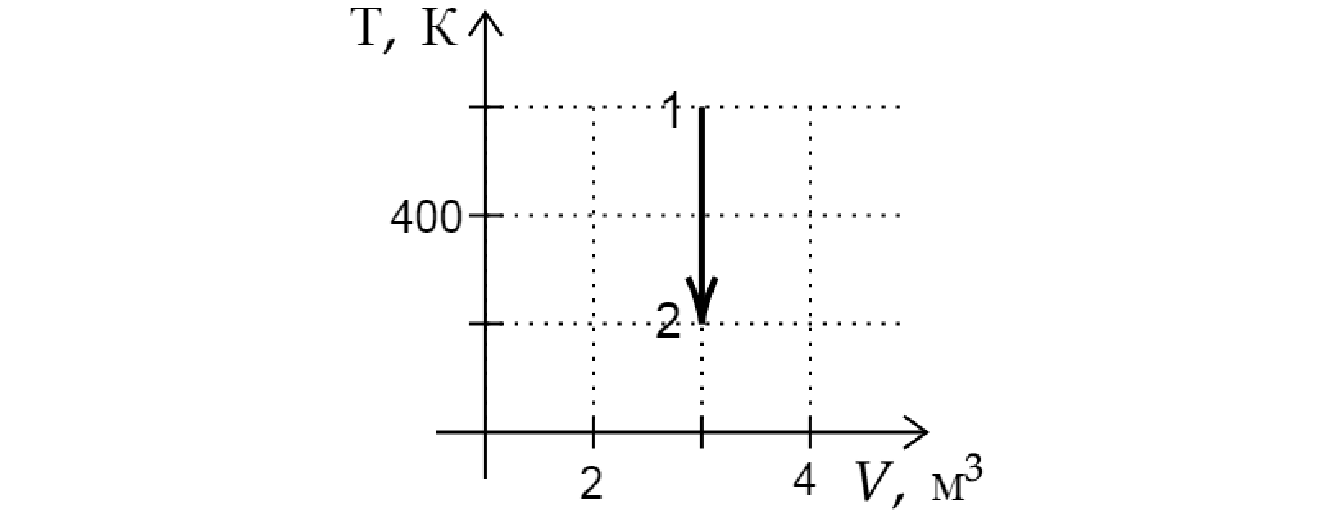
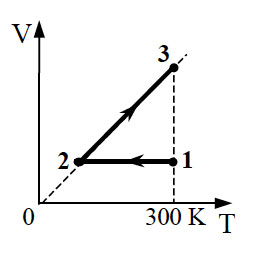
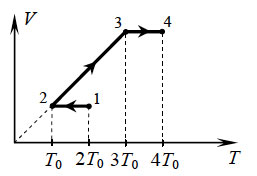
На ТV – диаграмме показан процесс изменения состояния идеального одноатомного газа. Газ получил
количество теплоты, равное 50 кДж. Какую работу совершил газ в этом процессе, если его масса не
меняется? Ответ дайте в кДж.

Демоверсия 2018

Показать ответ и решение

Из первого начала термодинамики для изотермического процесса(изменение внутренней энергии равно
0)

В некотором процессе газ отдал окружающей среде количество теплоты, равное 10 кДж. При этом
внутренняя энергия газа увеличилась на 30 кДж. Определите работу, которую совершили внешние силы,
сжав газ. Ответ дайте в кДж.

Демоверсия 2017

Показать ответ и решение

По первому закону Термодинамики:

где
– переданное количество теплоты, – изменение внутренней энергии, – работа над газом.

Идеальный газ получил количество теплоты 100 Дж и при этом внутренняя энергия газа уменьшилась
на 100 Дж. Какова работа, совершенная газом? (Ответ дайте в джоулях.)

Источник

Задачи из ДЕМОВАРИАНТОВ (с решениями)

1. Воздушный шар, оболочка
которого имеет массу М = 145 кг и объем V =
230 м³, наполняется горячим воздухом при нормальном
атмосферном давлении и температуре окружающего воздуха t_о
= 0^оС. Какую минимальную температуру t должен
иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка
шара нерастяжима и имеет в нижней части небольшое отверстие.
Образец возможного решения

2. Воздушный
шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием.
Он может удерживать в воздухе на высоте, где температура воздуха
17^оС, а давление 10⁵ Па, груз массой 225
кг. Какова масса гелия в оболочке шара? Считать, что оболочка
шара не оказывает сопротивления изменению объема шара.
Образец возможного решения

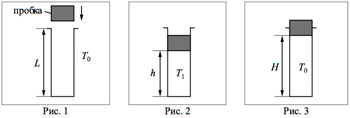
2*. В камере, заполненной азотом, при температуре T = 300 К находится открытый цилиндрический сосуд (см. рис. 1). Высота сосуда L = 50 см. Сосуд плотно закрывают цилиндрической пробкой и охлаждают до температуры T₁. В результате расстояние от дна сосуда до низа пробки становится равным h = 40 см (см. рис. 2). Затем сосуд нагревают до первоначальной температуры T₀. Расстояние от дна сосуда до низа пробки при этой температуре становится равным H = 46 см (см. рис. 3). Чему равна температура T₁? Величину силы трения между пробкой и стенками сосуда считать одинаковой при движении пробки вниз и вверх. Массой пробки пренебречь. Давление азота в камере во время эксперимента поддерживается постоянным.
Образец возможного решения

3. В медный
стакан калориметра массой 200 г, содержащий 150 г воды, опустили
кусок льда, имевший температуру 0°С. Начальная температура калориметра
с водой 25°С. В момент времени, когда наступит тепловое равновесие,
температура воды и калориметра стала равной 5°С. Рассчитайте массу
льда. Удельная теплоемкость меди 390 Дж/кг•К, удельная теплоемкость
воды 4200 Дж/кг•К, удельная теплота плавления льда 3,35•10⁵
Дж/кг. Потери тепла калориметром считать пренебрежимо малыми.
Образец возможного решения

4. Необходимо расплавить лёд массой 0,2 кг,
имеющий температуру 0^оС. Выполнима ли эта задача,
если потребляемая мощность нагревательного элемента – 400 Вт,
тепловые потери составляют 30%, а время работы нагревателя не
должно превышать 5 минут?
Образец возможного решения

4*. Теплоизолированный горизонтальный сосуд разделён пористой перегородкой на две равные части. В начальный момент в левой части сосуда находится ν = 2 моль гелия, а в правой – такое же количество моль аргона. Атомы гелия могут проникать через перегородку, а для атомов аргона перегородка непроницаема. Температура гелия равна температуре аргона: Т = 300 К. Определите отношение внутренних энергий газов по разные стороны перегородки после установления термодинамического равновесия.
Образец возможного решения

4**. Теплоизолированный цилиндр разделён подвижным теплопроводным поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 300 К, а аргона – 900 К; объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Поршень медленно перемещается без трения. Теплоёмкость поршня и цилиндра пренебрежимо мала. Чему равно отношение внутренней энергии гелия после установления теплового равновесия к его энергии в начальный момент?
Образец возможного решения

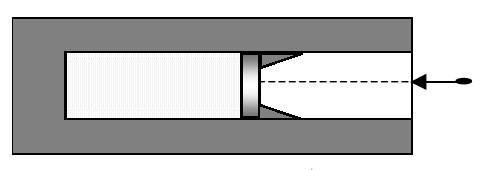
5. В вакууме
закреплен горизонтальный цилиндр с поршнем. В цилиндре находится
0,1 моль гелия. Поршень удерживается упорами и может скользить
влево вдоль стенок цилиндра без трения. В поршень попадает пуля
массой 10 г, летящая горизонтально со скоростью 400 м/с, и застревает
в нем. Температура гелия в момент остановки поршня в крайнем левом
положении возрастает на 64 К. Какова масса поршня? Считать, что
за время движения поршня газ не успевает обменяться теплом с поршнем
и цилиндром.
Образец возможного решения

6. В горизонтальном цилиндрическом сосуде,
закрытом поршнем, находится одноатомный идеальный газ. Первоначальное
давление газа p₁ = 4•10⁵
Па. Расстояние от дна сосуда до поршня равно L. Площадь
поперечного сечения поршня S = 25 см². В
результате медленного нагревания газ получил количество теплоты
Q = 1,65 кДж, а поршень сдвинулся на расстояние x
= 10 см. При движении поршня на него со стороны стенок сосуда
действует сила трения величиной F_тр = 3•10³
Н. Найдите L. Считать, что сосуд находится в вакууме.
Образец возможного решения

7. На pT-диаграмме показан
цикл тепловой машины, у которой рабочим телом является идеальный
газ (см. рисунок). На каком из участков цикла 1 – 2, 2 – 3, 3
– 4, 4 – 1 работа газа наибольшая по модулю?
Образец возможного решения

8. 10 моль одноатомного идеального
газа сначала охладили, уменьшив давление в 3 раза, а затем нагрели
до первоначальной температуры 300 К (см. рисунок). Какое количество
теплоты получил газ на участке 2 — 3?
Образец возможного решения

9. 10 моль идеального одноатомного газа охладили,
уменьшив давление в 3 раза. Затем газ нагрели до первоначальной
температуры 300 К (см. рисунок). Какое количество теплоты сообщено
газу на участке 2 — 3?
Образец возможного решения

10. 1 моль идеального одноатомного газа сначала
охладили, а затем нагрели до первоначальной температуры 300
К, увеличив объем газа в 3 раза (см. рисунок). Какое количество
теплоты отдал газ на участке 1 — 2?
Образец возможного решения

10*. Над одноатомным идеальным газом проводится циклический процесс, показанный на рисунке. На участке 1–2 газ совершает работу А₁₂ = 1000 Дж. На адиабате 3–1 внешние силы сжимают газ, совершая работу |A₃₁| = 370 Дж. Количество вещества газа в ходе процесса не меняется. Найдите количество теплоты |Q_хол|, отданное газом за цикл холодильнику.
Образец возможного решения

11. Рассчитайте КПД тепловой
машины, использующей в качестве рабочего тела одноатомный идеальный
газ и работающей по циклу, изображенному на рисунке.
Образец возможного решения

Избранные задачи прошлых лет (с ответами)

12. Вертикально расположенный
замкнутый цилиндрический сосуд высотой 50 см разделен подвижным
поршнем весом 110 Н на две части, в каждой из которых содержится
одинаковое количество идеального газа при температуре 361 К. Сколько
молей газа находится в каждой части цилиндра, если поршень находится
на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.

13. В калориметре
находился лед при температуре t₁ = — 5 °С.
Какой была масса m₁ льда, если после добавления
в калориметр m₂ = 4 кг воды, имеющей температуру
t₂ = 20 °С, и установления теплового равновесия
температура содержимого калориметра оказалась равной t
= 0 °С, причем в калориметре была только вода?

14. Теплоизолированный
цилиндр разделен подвижным теплопроводным поршнем на две части.
В одной части цилиндра находится гелий, а в другой — аргон. В
начальный момент температура гелия равна 300 К, а аргона — 900
К. При этом объемы, занимаемые газами одинаковы. Какую температуру
будут иметь газы в цилиндре после установления теплового равновесия,
если поршень перемещается без трения? Теплоемкостью сосуда и поршня
пренебречь.

15. Теплоизолированный
сосуд объемом V = 2 м³ разделен теплопроводящей
перегородкой на две части одинакового объема. В одной части находится
m = 1 кг гелия, а в другой части m = 1 кг аргона.
Средняя квадратичная скорость атомов аргона равна средней квадратичной
скорости атомов гелия и составляет υ = 500 м/с. Рассчитайте
парциальное давление гелия после удаления перегородки.

16. Теплоизолированный
сосуд объемом V = 2 м³ разделен пористой перегородкой
на две равные части. В начальный момент в одной части сосуда находится
ν_He = 2 моль гелия, а в другой – ν_Ar
= 1 моль аргона. Температура гелия Т_He = 300
К, а температура аргона Т_Ar = 600 К. Атомы
гелия могут свободно проникать через поры в перегородке, а атомы
аргона – нет. Определите температуру гелия после установления
теплового равновесия в системе.

17. С одним молем идеального
одноатомного газа совершают процесс 1-2-3-4, показанный на рисунке
в координатах V-Т. Во сколько раз количество теплоты,
полученное газом в процессе 1-2-3-4 больше работы газа в этом
процессе?

18. Один моль одноатомного
идеального газа совершает процесс 1-2-3 (см. рисунок). На участке
2 — 3 к газу подводят 3 кДж теплоты. Т₀ =
100 К. Найдите отношение работы, совершаемой газом в ходе всего
процесса А₁₂₃, к соответствующему полному
количеству подведенной к нему теплоты Q₁₂₃.

19. Один моль идеального
одноатомного газа сначала изотермически сжали (Т₁
= 300 К). Затем газ изохорно охладили, понизив давление в 3 раза
(см. рисунок). Какое количество теплоты отдал газ на участке 2
— 3?

20. Идеальный одноатомный
газ расширяется сначала адиабатно, а затем изобарно. Конечная
температура газа равна начальной (см. рисунок). За весь процесс
1-2-3 газом совершается работа, равная 5 кДж. Какую работу совершает
газ при адиабатном расширении?

21. На рисунке в координатах
p,T показан цикл тепловой машины, у которой
рабочим телом является идеальный газ. На каком участке цикла работа
газа наименьшая по модулю?

22. Один моль одноатомного
идеального газа совершает цикл, изображенный на pV-диаграмме
(см. рисунок). Участок 1 – 2 –– изотерма, 2 – 3 –– изобара, 3
– 1 –– адиабата. Работа, совершаемая газом за цикл, равна А.
Разность температур в состояниях 1 и 3 составляет ΔТ.
Какую работу совершает газ при изотермическом процессе?

23. Газообразный гелий находится
в цилиндре под подвижным поршнем. Газ сжимают в адиабатическом
процессе, переводя его из состояния 1 в состояние 2 (см. рис.).
Над газом совершается при этом работа сжатия А₁₂
(А₁₂> 0). Затем газ расширяется в изотермическом
процессе 2-3, и, наконец, из состояния 3 газ переводят в состояние
1 в процессе, когда его давление Р прямо пропорционально
объему V. Найти работу А₂₃, которую
совершил газ в процессе изотермического расширения, если во всем
замкнутом цикле 1-2-3-1 он совершил работу А.

24. Температура
гелия увеличилась в k = 3 раза в процессе P²V
= const (Р — давление, V — объем газа), а его
внутренняя энергия изменилась на 100 Дж. Найти: 1) начальный объем
V₁ газа; 2) начальное давление P₁
газа. Максимальный объем, который занимал газ в процессе нагрева,
равнялся V_max = 3 л.

25. Одноатомный идеальный
газ неизменной массы совершает циклический процесс, показанный
на рисунке. За цикл от нагревателя газ получает количество теплоты
Q_H = 8 кДж. Чему равна работа газа за цикл?

Ответы к избранным задачам
прошлых лет

Источник