Решу егэ высота над землей подброшенного вверх мяча меняется по закону

1

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,4 плюс 9t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?

2

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,2 плюс 9t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 4 метров?

3

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,4 плюс 14t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 8 метров?

4

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,6 плюс 12t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте более 8 метров?

5

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =2 плюс 9t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте более 6 метров?

6

Высота над землёй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,8 плюс 10t минус 5t в квадрате , где h  — высота в метрах, t — время в секундах, прошедшее с момента броска. Какое время мяч будет находиться на высоте не менее 5 метров? Ответ дайте в секундах.

7

Высота над землёй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1 плюс 12t минус 5t в квадрате , где h  — высота в метрах, t — время в секундах, прошедшее с момента броска. Какое время мяч будет находиться на высоте не менее 5 метров? Ответ дайте в секундах.

8

Высота над землёй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =2 плюс 11t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте больше 4 метров?

9

Высота над землёй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =2 плюс 14t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте больше 10 метров?

10

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,2 плюс 10t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?

11

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,6 плюс 13t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 4 метров?

12

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1 плюс 12t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 5 метров?

13

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,8 плюс 10t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 5 метров?

14

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =2 плюс 7t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 4 метров?

15

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =2 плюс 11t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 8 метров?

16

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,4 плюс 9t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 5 метров?

17

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =2 плюс 14t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 11 метров?

18

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =2 плюс 14t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 10 метров?

19

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,6 плюс 12t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 7 метров?

20

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,6 плюс 12t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 8 метров?

21

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =2 плюс 9t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 6 метров?

22

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,4 плюс 11t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 5 метров?

23

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =2 плюс 12t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 9 метров?

24

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,4 плюс 11t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 7 метров?

25

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,8 плюс 7t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?

26

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,6 плюс 13t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 6 метров?

27

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =2 плюс 9t минус 5t в квадрате , где h  — высота в метрах, t  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте более 6 метров?

Источник

Высота над землeй подброшенного вверх мяча меняется по закону h левая круглая скобка t правая круглая скобка =1,6 плюс 8t минус 5t в квадрате , где h − высота в метрах, t − время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трeх метров?

Спрятать решение

Решение.

Определим моменты времени, когда мяч находился на высоте ровно три метра. Для этого решим уравнение h левая круглая скобка t правая круглая скобка =3:

h левая круглая скобка t правая круглая скобка =3 равносильно 1,6 плюс 8t минус 5t в квадрате =3 равносильно 5t в квадрате минус 8t плюс 1,4=0 равносильно совокупность выражений новая строка t=0,2; новая строка t=1,4. конец совокупности .

Проанализируем полученный результат: поскольку по условию задачи мяч брошен снизу вверх, это означает, что в момент времени t=0,2 (с) мяч находился на высоте 3 метра, двигаясь снизу вверх, а в момент времени t=1,4 (с) мяч находился на этой высоте, двигаясь сверху вниз. Поэтому он находился на высоте не менее трёх метров 1,4 − 0,2  =  1,2 секунды.

Ответ: 1,2.

Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 2.

Источник

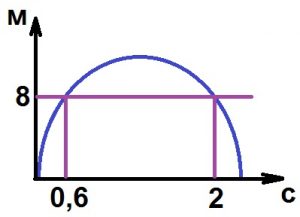
Высота над землёй подброшенного вверх мяча меняется по закону h(t) = 2 + 13t − 5t2, где h − высота в метрах, t − время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 8 метров?

Источники: fipi, os.fipi, Пробный ЕГЭ 2015.

Решение:

    Найдём моменты времени когда мяч был на высоте ровно h = 8 метров.

8 = 2 + 13t − 5t2
5t2 – 13t – 2 + 8 = 0
5t2 – 13t + 6 = 0

  D = (–13)2 – 4·5·6 = 169 – 120 = 49 = 72

 

 

    Первый раз мяч поднялся на высоту 8 метров в 0,6 секунд при взлёте, потом высота увеличивалась, затем начала падать на 2 секунде мят снова оказался на высоте 8 метров, после этого упал.

Высота над землёй подброшенного вверх мяча меняется по закону h(t) = 2 + 13t − 5t^2
    Найдём секунд мяч будет находиться на высоте не менее 8 метров:

2 – 0,6 = 1,4 секунд 

Ответ: 1,4.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.7 / 5. Количество оценок: 11

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Условие

Высота над землёй подброшенного вверх мяча меняется по закону h(t)=1+8t-5t^2, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее четырёх метров?

Показать решение

Решение

Решим относительно t неравенство h(t)geqslant4.

-5t^2+8t+1geqslant4,

5t^2-8t-1leqslant-4,

5t^2-8t+3leqslant0.

Найдем корни уравнения 5t^2-8t+3=0:

Вычислим дискриминант: D=b^2-4ac= -8^2-4cdot5cdot3= 64-60=4,

t_{1,2}= frac{-bpmsqrt D}{2a}= frac{8pmsqrt4}{2cdot5}= frac{8pm2}{10},

t_1=frac35,,t_2=1;

5left ( t-frac35 right ) left ( t-1 right )leqslant0, откуда frac35leqslant tleqslant1. Мяч будет находиться на высоте не мене четырех метров в течение 1-frac35=frac25=0,4 секунды.

Ответ

0,4

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Рассказать друзьям

Лучшие репетиторы для сдачи ЕГЭ

Комментарии

Задавайте ваши вопросы и помогайте друг другу в решении задач

Комментарии содержащие в себе рекламу, нецензурную лексику и не относящиеся к тематике сайта будут удалены

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Задание 10. Математика ЕГЭ. Сколько секунд мяч будет находится на высоте не менее 8 метров

Задание.  Высота над землей подброшенного вверх мяча меняется по закону h(t) = 2 + 17t – 5t2, где h – высота в метрах,  t – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 8 метров?

Решение:

Мяч будет находиться на высоте 8 метров и более, начиная с момента времени t1 (см. рисунок), когда он достигнет при броске 8 метров, и, заканчивая моментом t2 (см. рисунок), когда он опустится снова до 8 метров. Т. е. t = t2 – t1.

Задание10в5

Найдем значения t1 и t2, для этого в формулу h(t) = 2 + 17t – 5t2  вместо h(t) подставим значение 8, получим:

8 = 2 + 17t – 5t2 

5t2 — 17t + 6 = 0

Решим квадратное уравнение, дискриминант равен 169, тогда  t1 = 0,4,  t2 = 3.

t = t2 – t1 = 3 — 0,4 = 2,6.

Ответ: 2,6

Оставить комментарий

Рубрики

  • Демоверсия ЕГЭ по информатике
  • Демоверсия ЕГЭ по математике
  • Демоверсия ОГЭ по информатике
  • Демоверсия ОГЭ по математике
  • Материалы по аттестации
  • Решаем ЕГЭ по математике
    • Задание 1
    • Задание 10
    • Задание 11
    • Задание 12
    • Задание 13
    • Задание 14
    • Задание 15
    • Задание 16
    • Задание 2
    • Задание 3
    • Задание 4
    • Задание 5
    • Задание 6
    • Задание 7
    • Задание 8
    • Задание 9
  • Решаем ОГЭ по математике
    • Задание 21
    • Задание 22
    • Задание 24
  • Скачать экзаменационные варианты по информатике
    • ЕГЭ по информатике
    • ОГЭ по информатике
  • Скачать экзаменационные варианты по математике
    • ЕГЭ по математике
    • ОГЭ по математике
  • Тематическое планирование

Яндекс.Метрика

Источник

Задание

Высота над землёй подброшенного вверх мяча меняется по закону h(t)=1,4+9t-5t2,  где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?

Решение

  1. Найдем время, когда мяч находится на высоте 3 метра:

3 = 1,4+9t-5t2
5t2-9t-1,4+3 = 0
5t2-9t+1,6 = 0

Решим данное квадратное уравнение через дискриминант:

D = b2-4ac
D = 92-4*5*1,6 = 49
t1,2 = (-b ± Высота подброшенного мяча меняется по закону h(t)=1,4+9t-5t^2)/2a
t1 = (9+7)/10 = 1,6 секунд
t2 = (9-7)/10 = 0,2 секунды.

  1. Проанализируем получившейся результат:

Мяч бросают с земли, следовательно, в момент времени t=0,2 секунды  мяч находится на высоте 3м, двигаясь снизу вверх. В момент времени t=1,6 секунд мяч находится на высоте 3 м, двигаясь вниз к земле.  Значит, в промежутки этого интервала мяч находился на высоте не менее 3 м:

1,6-0,2=1,4 секунды мяч находился на высоте не менее 3 м.

Ответ: 1,4

Источник

Понравилась статья? Поделить с друзьями:
  • Решу егэ вход в аккаунт
  • Решу егэ вход биология
  • Решу егэ второй закон термодинамики
  • Решу егэ вторая часть познание
  • Решу егэ вторая часть обществознание