Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.
Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!
Темы для повторения:
New
Решаем задачи из сборника И. В. Ященко, 2021
Квадратичные неравенства
Метод интервалов
Уравнения и неравенства с модулем
Иррациональные неравенства
Показательные неравенства
Логарифмические неравенства
Метод замены множителя (рационализации)
Решение неравенств: основные ошибки и полезные лайфхаки
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15
Логарифмические неравенства повышенной сложности
Разберем неравенства разных типов из вариантов ЕГЭ по математике.
Дробно-рациональные неравенства
1. Решите неравенство:
Сделаем замену
Тогда , а
Получим:
Решим неравенство относительно t методом интервалов:
Получим:
Вернемся к переменной x:
Ответ:
Показательные неравенства
2. Решите неравенство
Сделаем замену Получим:
Умножим неравенство на
Дискриминант квадратного уравнения
Значит, корни этого уравнения:
Разложим квадратный трехчлен на множители.
. Вернемся к переменной x.
Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?
Ответ:
Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ.
3. Решите неравенство
Сделаем замену Получим:
Вернемся к переменной
Первое неравенство решим легко: С неравенством
тоже все просто. Но что делать с неравенством
? Ведь
Представляете, как трудно будет выразить х?
Оценим Для этого рассмотрим функцию
Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом
Мы получили, что
Тогда , и это значит, что
Значение
не достигается ни при каких х.
Но если и
, то
Мы получили:
Ответ:
Логарифмические неравенства
4. Решите неравенство
Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.
Ответ:
Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!
5. Решите неравенство
ОДЗ:
Замена
Ответ:
А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.
6. Решите неравенство:
Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что . Используем также условия
Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,
Поскольку
Согласно методу замены множителя, выражение заменим на
Получим систему:
Решить ее легко.
Ответ: .
Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.
7. Решите неравенство:
ОДЗ:
Привести обе части к одному основанию не получается. Ищем другой способ.
Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.
Функции и
— монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.
Поскольку при x=9 значение монотонно возрастающей функции равно 4, при
значения этой функции меньше 4. Конечно, при этом
, то есть x принадлежит ОДЗ.
Ответ:
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 14. Неравенства u0026#8212; профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
24 февраля 2019
В закладки
Обсудить
Жалоба
Задачи 13 и 15 профильного ЕГЭ по математике.
-
Простые неравенства
-
Cложные неравенства
-
Иррациональные неравенства
-
Неравенства с модулем
Простые неравенства
С простыми неравенствами проблем, как правило, не бывает: решаем уравнение относительно нуля, расставляем точки, соответствующие корням, рисуем интервалы, определяем знаки.
Например: (х — 1)2 (х + 3)6 (х — 5)9 ≥ 0 . Корнями этого выражения будут точки: х1 = 1; х2 = -3; х3 = 5. Но точки х1 и х2 на знак не влияют,так как первые два множителя заведомо положительные, они возводятся в четную степень. Или, другими словами, в первой скобке два одинаковых корня, во второй — четыре. Определяем, какой знак будет иметь выражение, скажем, в точке 10. Положительное. Рисуем числовую ось и расставляем знаки. Ответ: х ∈ { -3 } ∪ { 1} ∪ [ 5; +∞ )
Почему -3 и 1 появились? Потому что они не меняют знак, но являются частью уравнения, так как у нас стоит знак «больше и равно». Если бы было строгое неравенство, то подобные точки, соответствующие четным корням, необходимо было бы выколоть.
Рассмотрим еще одно неравенство:
Ищем нули функции. Это корни числителя: х1,2= ±4, х3 = 3, три корня х4 = -1; корни знаменателя: х5 ≠ -4, х6 ≠ 2. Считаем, какой знак получится у выражения, когда, скажем, х=0. В нуле функция отрицательна. Строим интервалы. Учитываем, что корней х = -4 два, а значит, в этой точке знак не меняется:
Пишем ответ: x ∈ [ -1; 2 ) ∪ [ 3; 4 ]
Сложные неравенства
Решаем сложное неравенство, в котором присутствуют две различные функции в числителе и знаменателе:

положительная. Чтобы расставить все точки над «i», посмотрим, как выглядит график функции.


Отсюда вывод:
- Для того, чтобы решить любое неравенство, достаточно определиться с так называемыми нулями функции, не забывая «выколоть» нули знаменателя, определить знак любого промежутка из получившихся и чередовать знаки.
- Если появились одинаковые корни, количество которых кратно двум, то в них знак не меняется.
Иррациональные неравенства
• Решим неравенство : ≥ 0 . Неравенство несложное, но есть некоторые тонкости, которые следует учитывать, решая выражения с корнем:
- Квадратный корень всегда число неотрицательное по определению, на знак нашего выражения не влияет.
- Квадратный корень можно извлечь только из неотрицательного числа.
- Решать такие выражения очень часто приходится возведением обеих частей неравенства в квадрат, а это — не всегда равносильные выражения.
При решении уравнений все вышесказанное приводит к обязательной проверке корней, что невозможно сделать в неравенстве. Поэтому такие неравенства превращаются в систему неравенств.
Так как в конкретном нашем выражении корень не влияет на знак, мы на него делим. Напомню, что неравенства можно делить или умножать на выражения или числа только, если известен знак этого выражения или числа, так как в противном случае такое деление может изменить знак всего неравенства.
Решаем систему: Первое неравенство имеет решение при х ≤ -3 и х ≥ 3. Второе — при х ≥ 2. Выводим общие для обоих неравенств интервалы.
Ответ: х ∈ [ 3; +∞ )
• Рассмотрим еще одно неравенство: .
Функция ограниченная из-за двух корней, поэтому сначала найдем область определения функции (ООП):
Решение этого неравенства: х ∈ [ -1; 8 ].
Теперь решаем само неравенство. Можно решить стандартно, возводя в квадрат обе части, при этом желательно перенести второй корень в правую часть, а единицу влево, и возвести в квадрат: . Обращаю ваше внимание, что придется возводить в квадрат два раза, так как слева после возведения останется корень от удвоенного произведения первого слагаемого на второе.
Но можно несколько облегчить себе задачу, введя новую переменную . Тогда х+1 = t2 , х = t2 — 1, а
а все выражение превратится в выражение с одним корнем:
— t < -1 ⇒
< t — 1
Возводим в квадрат,…….и т.д. Дальше решать не буду, Думаю, все понятно. Корни будут иррациональными, и это — нормально.
Неравенства с модулем
Отдельная история — неравенства с модулем. Вспомним,что такое модуль числа
Очевидно, что решать уравнения или неравенства с модулем можно только, раскрыв модуль. Модуль раскрывается по правилу в зависимости от знака выражения, стоящего под модулем. Давайте разбираться на конкретных примерах:

Если построить числовую ось, то все значения, удовлетворяющие этому неравенству, окажутся внутри интервала х ∈ ( -3; 3) Неравенство у нас строгое, значит скобки будут круглые.
в). ⇒
Ответ: х ∈ ( — ∞; -3) ∪ ( 3; +∞ ), то есть больше большего корня и меньше меньшего корня.
Если же у нас под знаком модуля будут какие-нибудь функции, модуль будет раскрываться аналогично вышеизложенному, только уже не получится сразу интервалов, а будет системы или объединенные множества неравенств.
1. Решаем следующее неравенство:
I 2x — 7 I ≤ 5
Открываем модуль:
-5 ≤ 2x -7 ≤ 5
Внутри модуля функция линейная, которую можно решить двойным неравенством. Сначала прибавим ко всем трем частям 7, получим :
2 ≤ 2x ≤ 12,
затем разделим все неравенство на 2 :
1 ≤ x ≤ 6
Ответ: х ∈ [ 1; 6 ].
2. Еще одно неравенство:
Сначала найдем область определения функции, т.к. наша функция — ограниченная. ООП: х > -2.
Убираем модуль. Наше неравенство превращается в объединенное множество:
3. Ну, и наконец, неравенство с двумя модулями: В этом неравенстве две точки смены знака под модулем, это точки 3 и 5, следовательно, модули будем открывать на трех промежутках:
Ответ: х∈ ( — ∞; 2 ] ∪ [4; +∞)
Это неравенство можно представить графически. Для этого достаточно построить графики функции (зеленой) с модулями
y = Ix — 3I + Ix — 5I (в неравенстве слева) и (красной) линейной функции
y =6 — x, находящейся на правой стороне неравенства. По условию неравенства нас интересует та часть графиков, где зеленая функция находится выше красной. Как видите, ответ тот же самый!
NB: Кстати, решение уравнений и неравенств при помощи графиков часто очень помогает разобраться с задачами с параметрами — с задачами №18 профильного ЕГЭ. Но это уже тема для другой статьи.
Павел Бердов
уроки математики
- Глава 1.
- Логарифмические неравенства
- § 1.
- Пример решения задачи 15
- § 2.
- Задача 15: системы логарифмических неравенств
- Глава 2.
- Показательные неравенства
- § 1.
- Показательные неравенства в задаче 15
- § 2.
- Что делать, если в показателе стоит логарифм
- § 3.
- Задача 15: тонкости решения систем неравенств
- § 4.
- Особенности сравнения корней в логарифмических неравенствах
- § 5.
- Пример из настоящего ЕГЭ: решение нестандартной системы неравенств
- § 6.
- Задача 15 из пробного ЕГЭ 2016 от 3 марта — решаем неравенство
- § 7.
- Как монотонность логарифма помогает упростить решение неравенства в несколько раз? (абсолютно легальный приём)
- § 8.
- Задание 15: метод интервалов для логарифмов
14 задача ЕГЭ – это всегда неравенство. На реальных ЕГЭ бывают 3 вида неравенств: показательные, логарифмические и смешанные.
Что нужно знать?
- Метод интервалов
- Как решаются дробно-рациональные неравенства
- Как делается замена и обратная замена в неравенствах
- Как решаются показательные неравенства
- Свойства логарифмов
- Как решаются логарифмические неравенства
- Метод рационализации
Задачи, которые были на экзамене за последние 7 лет с решениями на полный балл
2022:

Решение

2021:

Решение

2020:

Решение

2019:

Решение

2018:

Решение

2017:

Решение

2016:

Решение

2015:

Решение

Процент выполнения
А вот данные сколько процентов пишущих экзамен решили задачу на неравенство в разные годы:

Сколько процентов из тех, кто решал экзамен в 2021 году*, набрал в задаче хотя бы 1 балл:

* так как в 2022 году ЕГЭ был сильно скорректирован, то некоторые задачи изменили свой номер, какие-то исчезли совсем, а другие добавились. В таблице приведены данные 2021 года, приведенные к формату экзамена 2022 (поэтому, например, в задачах 9 и 10 стоят прочерки – это новые задачи)
Типичные ошибки
1. Ошибки по невнимательности
Если вы будете готовиться к 14 задаче ЕГЭ, то практически наверняка одной из главных проблем станут ошибки по невнимательности. Из всех задач профильного ЕГЭ эта задача, пожалуй, самая опасная в плане мелких ошибок. Как научиться не допускать их написано в этой статье.
Примеры таких ошибок по невнимательности выделены желтым


2. Неправильно использовать метод интервалов
Метод интервалов – это база для 14 задачи ЕГЭ. Поэтому если вы хотите научиться решать неравенства на ЕГЭ – первым делом освойте метод интервалов, чтоб ошибок не было. Вот как «косячат» в нем школьники на реальном экзамене.



3. Умножить/делить на выражение с переменной
Почему в общем случае неравенство нельзя умножать или делить на выражение с переменной? Все дело в том, что если мы неравенство умножаем (делим) на положительное число, то должны оставить знак сравнения тем же, а если на отрицательное – перевернуть его.
(2x>4) (-2x>4)
(x>2) (x<-2)
Но чаще всего мы не знаем положительно или отрицательно выражение, на которое собрались умножать (делить), потому что при разных значениях переменной знак выражения может меняться. То есть, возникает неясность — переворачивать знак сравнения или оставить тем же? Поэтому в неравенствах так не делают. В уравнении можно, в неравенстве нет.
|
Уравнение (можно и нужно умножать на икс) |
Неравенство (нужно приводить к общему знаменателю) |
| (frac{1}{x}=1) |(·x) | (frac{1}{x}>1) |
| (1=x) | (frac{1}{x}-1>0) |
| (x=1) | (frac{1-x}{x}>0) (|·(-1)) |
| (frac{x-1}{x}<0) | |
| (x∈(0;1)) |
Хотя бывают исключения, когда знак выражения с иксом определен. Например, на (2^x) умножить или разделить неравенство можно, потому что (2^x) положительно всегда, независимо от значения (x).
(frac{2^x-1}{2^x} ≥0) (|cdot2^x)
(2^x-1≥0)
Также бывает, что выражение положительно не всегда, но мы знаем, что в данном конкретном неравенстве это так, поскольку, например, таковы требования ОДЗ.
|
(log_2x+log_2frac{1}{x^2}≥0) (log_2x frac{1}{x^2} ≥log_21) (frac{1}{x}≥ 1) (|cdot x) (1≥x) (x≤1) |
Огр. (begin{cases} x>0 \ frac{1}{x^2} >0 end{cases}) |
Несколько примеров с ошибками:



4. Неправильно привести к общему знаменателю
Чаще всего такую ошибку допускают те ученики, которые ленятся написать лишнюю строчку, делают два, а то и три действия за один ход: сразу и домножаем, и раскрываем скобки, и тут же в уме приводим подобные слагаемые. Вот, например, в примере внизу пропущен шаг домножения дробей на недостающие множители и раскрытие скобок. Подозреваю, что из-за этого и возникла ошибка.

Сравните с этим бланком, где выпускник все сделал постепенно, по шагам и закономерно получил верный ответ.

5. Не сделать обратную замену
Это вообще классика – сделать замену и забыть вернуться к исходной переменной. Вот пример.

6. Неправильно снять квадрат
Такая ошибка редко совершается на самом ЕГЭ, потому что так обычно ошибаются те, кто только начал проходить неравенства. Но зато в начале пути ее делают практически все, поэтому я внесла её в список.
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Решение неравенств
Задание
1
#2500
Уровень задания: Легче ЕГЭ
Решите неравенство [x+10<3x^2]
Перенесем слагаемые в левую часть: [-3x^2+x+10<0] Разложим на множители выражение (-3x^2+x+10): [-3x^2+x+10=0 quad Rightarrow quad x_1=2quadtext{и}quad x_2=-dfrac53] Следовательно, (-3x^2+x+10=-3(x-2)left(x-frac53right)=-(x-2)(3x+5)).
Тогда неравенство примет вид [-(x-2)(3x+5)< 0quad Rightarrow
quad (x-2)(3x+5)>0] Решим его методом интервалов:
Таким образом, подходят (xin
left(-infty;-frac53right)cup(2;+infty)).
Ответ:
(left(-infty;-frac53right)cup(2;+infty))
Задание
2
#2501
Уровень задания: Легче ЕГЭ
Решите неравенство [x^2+34x+289>0]
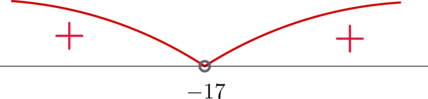
Заметим, что по формуле квадрата суммы (x^2+34x+289=(x+17)^2), следовательно, неравенство принимает вид: [(x+17)^2>0] Решим его методом интервалов:
Таким образом, нам подходят (xin(-infty;-17)cup(-17;+infty)).
Ответ:
((-infty;-17)cup(-17;+infty))
Задание
3
#2502
Уровень задания: Легче ЕГЭ
Решите неравенство [x^2-4x+4leqslant 0]
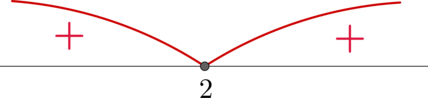
Заметим, что по формуле квадрата разности (x^2-4x+4=(x-2)^2), следовательно, неравенство принимает вид: [(x-2)^2leqslant 0] Решим его методом интервалов:
Таким образом, нам подходят (xin{2}).
Ответ:
({2})
Задание
4
#2503
Уровень задания: Легче ЕГЭ
Решите неравенство [x^2+3x+3geqslant 0]
Разложим на множители выражение (x^2+3x+3), для этого решим уравнение (x^2+3x+3=0). Оно имеет отрицательный дискриминант, следовательно, не разлагается на множители и принимает значения одного знака: либо положительно, либо отрицательно при всех (x). Проверить его знак можно, подставив вместо (x) любое число, например, (x=0): получим (3), следовательно, выражение всегда (>0).
Таким образом, нам подходят (xin mathbb{R}).
Ответ:
(mathbb{R})
Задание
5
#2412
Уровень задания: Легче ЕГЭ
Решите неравенство
[begin{aligned}
dfrac{(x — 1)(x + 2)}{(x — 3)(x + 4)}leqslant 0
end{aligned}]
ОДЗ:
[begin{aligned}
(x — 3)(x + 4)neq 0
end{aligned}]
Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.
1) Нули числителя находятся из уравнения [(x — 1)(x + 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = 1,qquadqquad x = -2]
2) Найдём нули знаменателя: [(x — 3)(x + 4) = 0qquadLeftrightarrowqquad
left[
begin{gathered}
x = 3\
x = -4
end{gathered}
right.]
По методу интервалов:
откуда [xin(-4; -2]cup[1; 3),.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).
Ответ:
((-4; -2]cup[1; 3))
Задание
6
#3762
Уровень задания: Легче ЕГЭ
Решить неравенство [dfrac 6{xsqrt3-3}+dfrac{xsqrt3-6}{xsqrt3-9}geqslant 2]
(Задача от подписчиков)
Пусть (xsqrt3-3=t). Тогда [dfrac 6t+dfrac{t-3}{t-6}geqslant 2quadLeftrightarrowquad
dfrac{t^2-15t+36}{t(t-6)}leqslant 0quadLeftrightarrowquad
dfrac{(t-3)(t-12)}{t(t-6)}leqslant 0] Решая данное неравенство методом интервалов, получим (0<tleqslant 3) или (6<tleqslant 12). Следовательно, [left[begin{gathered}begin{aligned}
&0<xsqrt3-3leqslant 3\
&6<xsqrt3-3leqslant
12end{aligned}end{gathered}right.quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&sqrt3<xleqslant 2sqrt3\
&3sqrt3<xleqslant 5sqrt3
end{aligned}end{gathered}right.]
Ответ:
((sqrt3;2sqrt3]cup(3sqrt3;5sqrt3])
Задание
7
#2413
Уровень задания: Легче ЕГЭ
Решите неравенство
[begin{aligned}
dfrac{(x + 1)(x — 2)}{(x + 3)(x^2 + 4)}leqslant 0
end{aligned}]
ОДЗ:
[begin{aligned}
(x — 3)(x^2 + 4)neq 0
end{aligned}]
Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.
1) Нули числителя находятся из уравнения [(x + 1)(x — 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = -1,qquadqquad x = 2]
2) Найдём нули знаменателя: [(x + 3)(x^2 + 4) = 0] так как (x^2geqslant 0), то (x^2 + 4geqslant 4), следовательно, нули знаменателя: [x = -3]
По методу интервалов:
откуда [xin(-infty; -3)cup[-1; 2],.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).
Ответ:
((-infty; -3)cup[-1; 2])

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Теория
| 1. | Ещё раз про ОДЗ | |
| 2. | Решение неравенств с помощью систем | |
| 3. | Системы неравенств | |
| 4. | Метод интервалов | |
| 5. | Метод рационализации | |
| 6. | Как решать задание ЕГЭ |
Задания
| 1. |
Метод введения новой переменной
Сложность: |
2 |
| 2. |
Дробное рациональное неравенство (теорема Виета)
Сложность: |
2 |
| 3. |
Дробное рациональное неравенство (разность квадратов)
Сложность: |
2 |
| 4. |
Квадратный трёхчлен в знаменателе
Сложность: |
2 |
| 5. |
Дробно-рациональный показатель степени
Сложность: |
2 |
| 6. |
Неизвестное основание
Сложность: |
2 |
| 7. |
Неравенство третьей степени в ОДЗ
Сложность: |
2 |
| 8. |
Логарифм произведения
Сложность: |
2 |
| 9. |
Дробно-рациональное выражение под логарифмом
Сложность: |
2 |
| 10. |
Неравенства с отрицательными степенями
Сложность: |
2 |
| 11. |
Показательное с модулем
Сложность: |
2 |
| 12. |
Монотонность логарифмической функции
Сложность: |
2 |
| 13. |
Трёхчлен в основании логарифма
Сложность: |
2 |
| 14. |
Монотонность квадратного корня
Сложность: |
2 |
| 15. |
Показательное с переменным основанием
Сложность: |
2 |
Экзаменационные задания (подписка)
| 1. |
Как на ЕГЭ (1). Сложное неравенство
Сложность: |
2 |
| 2. |
Как на ЕГЭ (2). Сложное неравенство
Сложность: |
2 |
| 3. |
Как на ЕГЭ (3). Сложное неравенство
Сложность: |
2 |
| 4. |
Как на ЕГЭ (4). Сложное неравенство
Сложность: |
2 |
Тесты
| 1. |
Тренировка по теме Сложное неравенство
Сложность: сложное |
4 |
Материалы для учителей
| 1. | Методическое описание |