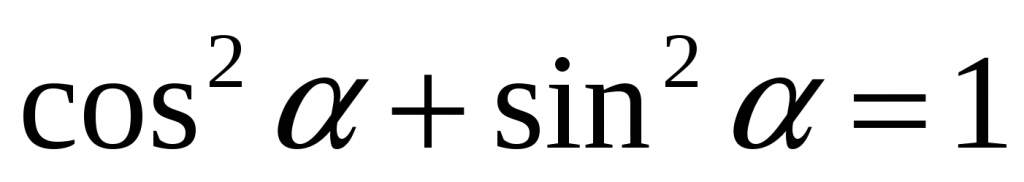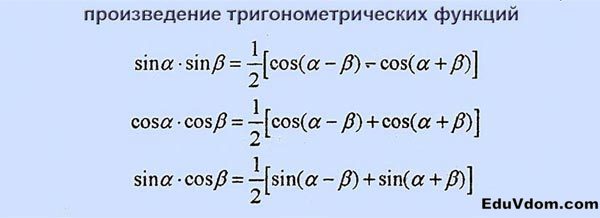Сборник формул для егэ по математике профильный уровень

Ученики, сдающие базовую математику, почти не тратят времени на подготовку к ней, ведь в экзамене нужно решить лишь задания, которые требуют самых основ. Тем же выпускникам, которые хотят поступать в технические вузы, предстоит готовиться не только к предметам по выбору, но и к профилю. В этой статье мы расскажем, какие формулы для ЕГЭ по математике (профильный уровень) сделают подготовку легче, а баллы на экзамене — выше.

Какие формулы необходимы для сдачи ЕГЭ по профильной математике?

Помимо очевидного, что для сдачи профиля нужно уметь складывать, вычитать и умножать, необходимы еще некоторые знания. Все это проходится в течение школы, но повторить или заполнить пробелы перед экзаменом нужно обязательно. Вот, что пригодится:

• Формулы сокращенного умножения;
• Арифметическая и геометрическая прогрессии;
• Вероятность;
• Свойства степеней;
• Свойства логарифмов;
• Тригонометрия;
• Производные;
• Первообразные.

Список внушительный, но вполне реальный, чтобы его выучить. Для того, чтобы лишний раз не гуглить в интернете «формулы для ЕГЭ по математике профильный уровень», приложим их ниже. А начнем по порядку из списка выше.

Формулы сокращённого умножения

Первые в нашем списке – формулы сокращенного умножения – нужны для решения задания №9 из профильного уровня. Вам встретятся задачи на преобразование выражений, поэтому умение это делать будет вознаграждено баллами.

Вот то, что будет вашим спасательным кругом:

Есть те, которые знать не обязательно. Но чем большими знаниями вы будете обладать, тем легче вам будет на экзамене. Вот они:

Умея применять эти формулы для ЕГЭ по математике, профильный уровень вам уже будет решить легче. Но это далеко не все, что нужно знать, чтобы получить сто баллов за ЕГЭ.

Арифметическая и геометрическая прогрессии

Для задания №19 нужно знание арифметической и геометрической прогрессии. Прикладываем формулы для ЕГЭ по математике, профильный уровень которой невозможен без их знания:

Вероятность

Вероятность встречается в задании №4, а ведь в самом начале обычно ставят легкие задания. Тем не менее, придется применять знания, которые представлены ниже:

Перейдем к свойствам степеней, ведь в них тоже есть, что запомнить.

Свойства степеней

Эти свойства нужно знать и для того, чтобы решить «базу», так что гуманитарии тоже могут обратить внимание на это:

Как вы видите, запоминать не очень много, зато формулы не самые простые. Но есть еще сложнее, и сейчас узнаем, какие они.

Свойства логарифмов

Формулы логарифмов лучше всего начать с их определения:

Теперь перейдем к более сложному:

Тригонометрия

Тригонометрические уравнения встречаются в задании №13. Для того, чтобы заработать баллы, нужно знать это:

Но это еще не все. Есть такая вещь, как основное тригонометрическое тождество. Вот оно:

Формулы двойного угла:

Формулы суммы и разности аргументов:

Преобразование суммы и разности в произведение:

Формулы половинного аргумента:

На этом с тригонометрией все.

Производные

Начнем с основных правил дифференцирования:

Уравнение касательной: 

Производные элементарных функций:

Закончим эту статью первообразными.

Первообразные

Она выглядит так:

Таблица первообразных:

Итог

То, что работа предстоит колоссальная — и правда, и нет. Да, придется хорошо постараться, чтобы набрать высокие баллы, так как составители ЕГЭ все больше усложняют экзамен. С другой стороны, хотя бы часть формул, описанных выше, вы уже знаете. А значит, работы хоть на немного, но меньше. А это ли не счастье в такие тяжелые времена подготовки?

Геометрия

• Треугольник
• Четырехугольники
• Окружность и круг
• Призма
• Пирамида
• Усеченная пирамида
• Цилиндр
• Конус
• Усеченный конус
• Сфера и шар

1. Формулы сокращённого умножения

Наверх

2. Модуль числа

Определение:

Основные свойства модуля:

Наверх

3. Степень с действительным показателем

Свойства степени с действительным показателем

Пусть Тогда верны следующие соотношения:

Наверх

4. Корень n-ой степени из числа

Корнем n-ой степени из числа a называется число, n-ая степень которого равна a.
Арифметическим корнем четной степени n из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.

Основные свойства арифметического корня:

Наверх

5. Логарифмы

Определение логарифма:

Основное логарифмическое тождество:

Основные свойства логарифмов

Пусть Тогда верны следующие соотношения:

Наверх

6. Арифметическая прогрессия

Формула n-го члена арифметической прогрессии:

Характеристическое свойство арифметической прогрессии:

Сумма n первых членов арифметической прогрессии:

При решении задач, связанных с арифметической прогрессией, могут оказаться полезными также следующие формулы:

Наверх

7. Геометрическая прогрессия

Формула n-го члена геометрической прогрессии:

Характеристическое свойство геометрической прогрессии:

Сумма n первых членов геометрической прогрессии:

При решении задач, связанных с геометрической прогрессией, могут оказаться полезными также следующие формулы:

Наверх

8. Бесконечно убывающая геометрическая прогрессия

Сумма бесконечно убывающей геометрической прогрессии:

Наверх

9. Основные формулы тригонометрии

Зависимость между тригонометрическими функциями одного аргумента:

Формулы сложения:

Формулы тригонометрических функций двойного аргумента:

Формулы понижения степени:

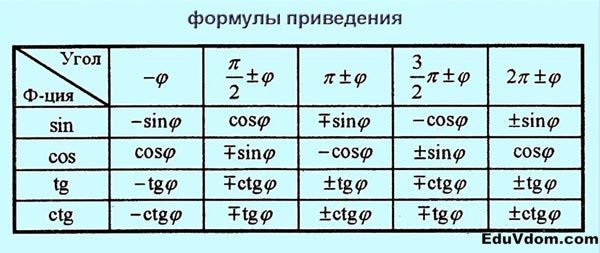
Формулы приведения

Все формулы приведения получаются из соответствующих формул сложения. Например:

Применение формул приведения укладывается в следующую схему:

— определяется координатная четверть, в которой лежит аргумент приводимой функции, считая, что ;

— определяется знак приводимой функции;

— определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид или , то функция меняется на сходственную функцию, если аргумент приводимой функции имеет вид , то функция названия не меняет.

Например, получим формулу :

— — IV четверть;

— в IV четверти тангенс отрицательный;

— аргумент приводимой функции имеет вид , следовательно, название функции меняется. Таким образом,

Формулы преобразования суммы тригонометрических функций в произведение:

Формулы преобразования произведения тригонометрических функций в сумму:

Наверх

10. Производная и интеграл

Таблица производных некоторых элементарных функций

Правила дифференцирования:

1.

2.

3.

4.

5.

Уравнение касательной к графику функции в его точке :

Таблица первообразных для некоторых элементарных функций

Правила нахождения первообразных

Пусть ― первообразные для функций и соответственно, a, b, k ― постоянные, Тогда:

— ― первообразная для функции

— ― первообразная для функции

— ― первообразная для функции

— Формула Ньютона-Лейбница:

1. Треугольник

Пусть ― длины сторон BC, AC, AB треугольника ABC соответственно; ― полупериметр треугольника ABC; A, B, C ― величины углов BAC, ABC, ACB треугольника ABC соответственно; ― длины высот AA₂, BB₂, CC₂ треугольника ABC соответственно; R ― радиус окружности, описанной около треугольника ABC; r — радиус окружности, вписанной в треугольник ABC; ― площадь треугольника ABC. Тогда имеют место следующие соотношения:

(теорема синусов);

(теорема косинусов);

Наверх
2. Четырёхугольники

Параллелограмм

Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.

Прямоугольником называется параллелограмм, у которого все углы прямые.

Ромбом называется параллелограмм, все стороны которого равны.

Квадратом называется прямоугольник, все стороны которого равны. Из определения следует, что квадрат является ромбом, следовательно, он обладает всеми свойствами прямоугольника и ромба.

Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны.

Площадь четырехугольника

Площадь параллелограмма равна произведению его основания на высоту.

Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.

Площадь трапеции равна произведению полусуммы ее оснований на высоту.

Площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.

Наверх

3. Окружность и круг

Соотношения между элементами окружности и круга

Пусть r — радиус окружности, d — ее диаметр, C — длина окружности, S — площадь круга,  — длина дуги в градусов,  — длина дуги в радиан,  — площадь сектора, ограниченного дугой в n градусов,  — площадь сектора, ограниченного дугой в радиан. Тогда имеют место следующие соотношения:

Вписанный угол

Вписанный угол измеряется половиной дуги, на которую он опирается.

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на полуокружность, — прямой.

Вписанная окружность

Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех сторон этого многоугольника, ― точка пересечения биссектрис углов этого многоугольника. Таким образом, в многоугольник можно вписать окружность, и притом только одну, тогда и только тогда, когда биссектрисы его углов пересекаются в одной точке.

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.

Описанная окружность

Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех вершин этого многоугольника, ― точка пересечения серединных перпендикуляров к сторонам этого многоугольника. Таким образом, около многоугольника можно описать окружность, и притом только одну, тогда и только тогда, когда серединные перпендикуляры к сторонам этого многоугольника пересекаются в одной точке.

Около четырехугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны

Наверх

4. Призма

Пусть H ― высота призмы, AA₁ ― боковое ребро призмы,  ― периметр основания призмы,  ― площадь основания призмы,  ― площадь боковой поверхности призмы,  ― площадь полной поверхности призмы, V ― объем призмы,  ― периметр перпендикулярного сечения призмы,  ― площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:

Свойства параллелепипеда:

— противоположные грани параллелепипеда равны и параллельны;

— диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам;

— квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Наверх

5. Пирамида

Пусть H ― высота пирамиды,  ― периметр основания пирамиды,  ― площадь основания пирамиды,  ― площадь боковой поверхности пирамиды,  ― площадь полной поверхности пирамиды, V ― объем пирамиды. Тогда имеют место следующие соотношения:

;

.

Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны , то

Наверх

6. Усечённая пирамида

Пусть H ― высота усеченной пирамиды, и  ― периметры оснований усеченной пирамиды, и  ― площади оснований усеченной пирамиды,  ― площадь боковой поверхности усеченной пирамиды,  ― площадь полной поверхности усеченной пирамиды, V ― объем усеченной пирамиды.

Тогда имеют место следующие соотношения:

Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны , то:

Наверх

7. Цилиндр

Пусть h ― высота цилиндра, r ― радиус цилиндра,  ― площадь боковой поверхности цилиндра,  ― площадь полной поверхности цилиндра, V ― объем цилиндра.

Тогда имеют место следующие соотношения:

Наверх

8. Конус

Пусть h ― высота конуса, r ― радиус основания конуса, l ― образующая конуса,  ― площадь боковой поверхности конуса,  ― площадь полной поверхности конуса, V ― объем конуса.

Тогда имеют место следующие соотношения:

Наверх

9. Усечённый конус

Пусть h ― высота усеченного конуса, r и  ― радиусы основания усеченного конуса, l ― образующая усеченного конуса,  ― площадь боковой поверхности усеченного конуса, V ― объем усеченного конуса. Тогда имеют место следующие соотношения:

Наверх

10. Сфера и шар

Пусть R ― радиус шара, D ― его диаметр, S ― площадь ограничивающей шар сферы,  ― площадь сферической поверхности шарового сегмента (шарового слоя), высота которого равна h, V ― объем шара,  ― объем сегмента, высота которого равна h,  ― объем сектора, ограниченного сегментом, высота которого равна h. Тогда имеют место следующие соотношения:

Наверх

Формулы ЕГЭ по математике

27.09.2013

Полный сборник красиво оформленных школьных формул по алгебре и геометрии.

В пособии содержатся все разделы школьной математики, все формулы и даны подробные описания к каждому из них.

Смотреть в PDF:

Скачайте в pdf файле.

По разделам:

Формулы для профильного ЕГЭ-2022 по математике

Формулы сокращённого умножения
Арифметическая и геометрическая прогрессии
Вероятность
Свойства степеней
Свойства логарифмов
Тригонометрия
Производные
Первообразные
Геометрия

Формулы сокращённого умножения

`(a + b)^2=a^2 + 2ab + b^2`
`(a − b)^2=a^2 − 2ab + b^2`
`a^2 − b^2=(a + b)(a − b)`
`a^3 + b^3=(a + b)(a^2 − ab + b^2)`
`a^3 − b^3=(a − b)(a^2 + ab + b^2)`
`(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3`
`(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3`

Прогрессии

Арифметическая прогрессия:

`a_n=a_(n-1)+d`

`a_n=a_1+(n-1)*d`

`S_n=((a_1+a_n)*n)/2`

Геометрическая прогрессия:

`b_n=b_(n-1)*q`

`b_n=b_1*q^(n-1)`

`S_n=((q^n-1)*b_1)/(q-1)`

Бесконечно убывающая: `S=b_1/(1-q)`

Вероятность

Вероятность события A:	`P(A)=m/n`
События происходят A и B происходят одновременно	`A*B`
Независимые события:	`P(A*B)=P(A)*P(B)`
Зависимые события:	`P(A*B)=P(A)*P(B|A)`
Происходит или событие A, или B	`A+B`
Несовместные события:	`P(A+B)=P(A)+P(B)`
Совместные события:	`P(A+B)=P(A)+P(B)-P(A*B)`

Свойства степеней

`a^0=1`	`a^1=a`
`a^(-1)=1/a`	`a^(-n)=1/a^n`
`a^(1/2)=sqrt(a)`	`a^(1/n)=root(n)(a)`
`a^m*a^n=a^(m+n)`	`a^m/a^n=a^(m-n)`
`(a*b)^n=a^n*b^n`	`(a/b)^n=a^n/b^n`
`(a^m)^n=a^(m*n)`	`a^(m/n)=root(n)(a^m)`

Свойства логарифмов

`log_ab=c``a^c=b`
`log_a1=0`
`log_aa=1`
`log_a(b*c)=log_ab+log_ac`
`log_a(b/c)=log_ab-log_ac`
`log_ab^n=n*log_ab`
`log_(a^m)b=1/m*log_ab`
`log_ab=1/(log_ba)`
`log_ab=(log_cb)/(log_ca)`
`a^(log_cb)=b^(log_ca)`
`a^(log_ab)=b`

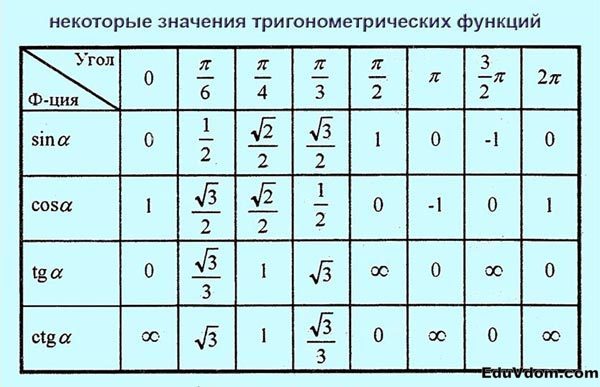
Тригонометрия

`alpha`	`0`	`pi/6`	`pi/4`	`pi/3`	`pi/2`	`pi`	`(3pi)/2`	`2pi`
`0^circ`	`30^circ`	`45^circ`	`60^circ`	`90^circ`	`180^circ`	`270^circ`	`360^circ`
`sinalpha`	`0`	`1/2`	`sqrt(2)/2`	`sqrt(3)/2`	`1`	`0`	`-1`	`0`
`cosalpha`	`1`	`sqrt(3)/2`	`sqrt(2)/2`	`1/2`	`0`	`-1`	`0`	`1`
`text(tg)alpha`	`0`	`sqrt(3)/3`	`1`	`sqrt(3)`	`infty`	`0`	`infty`	`0`
`text(ctg)alpha`	`infty`	`sqrt(3)`	`1`	`sqrt(3)/3`	`0`	`infty`	`0`	`infty`

Основные соотношения

`sin^2alpha+cos^2alpha=1`
`text(tg)alpha=sinalpha/cosalpha=1/(text(ctg)alpha)`

Формулы двойного угла

`cos2alpha={(cos^2alpha-sin^2alpha),(1-2sin^2alpha),(2cos^2alpha-1):}`
`sin2alpha=2sinalphacosalpha`
`text(tg)2alpha=(2text(tg)alpha)/(1-text(tg)^2alpha)`

Формулы суммы и разности аргументов

`sin(alpha+-beta)=sinalphacosbeta+-cosalphasinbeta`

`cos(alpha+-beta)=cosalphacosbeta∓sinalphasinbeta`

`text(tg)(alpha+-beta)=(text(tg)alpha+-text(tg)beta)/(1∓text(tg)alpha*text(tg)beta)`

Преобразование суммы и разности в произведение

`sinalpha+-sinbeta=2sin((alpha+-beta)/2)cos((alpha∓beta)/2)`

`cosalpha+cosbeta=2cos((alpha+beta)/2)cos((alpha-beta)/2)`

`cosalpha-cosbeta=-2sin((alpha+beta)/2)sin((alpha-beta)/2)`

Формулы половинного аргумента

`sin(alpha/2)=+-sqrt((1-cosalpha)/2)`
`cos(alpha/2)=+-sqrt((1+cosalpha)/2)`
`text(tg)(alpha/2)=+-sqrt((1-cosalpha)/(1+cosalpha))=(1-cosalpha)/sinalpha=sinalpha/(1+cosalpha)`

Обратные тригонометрические функции

`sinx=A`	`x=(-1)^k*arcsinA + pik` или `{(x=arcsinA + 2pik),(x=pi-arcsinA+2pik):}`	`kinZZ`
`cosx=A`	`x=±arccosA + 2pik`	`kinZZ`
`tg x=A`	`x=text(arctg) A + pik`	`kinZZ`
`ctg x=A`	`x=text(arcctg) A + pik`	`kinZZ`

Также некоторые тригонометрические соотношения смотрите в разделе Геометрия.

Производные

Основные правила дифференцирования

`(u+-v)’=u’+-v’`
`(u*v)’=u’*v+u*v’`
`(u/v)^’=(u’*v-u*v’)/v^2`
`[f(g(x))]’=f'(g(x))*g'(x)`

Уравнение касательной

`y=f(x_0)+f'(x_0)*(x-x_0)`

Производные элементарных функций

`C’=0`	`(C*x)’=C`
`(x^m)’=mx^(m-1)`	`(sqrtx)’=1/(2sqrtx)`
`(1/x)^’=-1/x^2`
`(e^x)’=e^x`	`(lnx)’=1/x`
`(a^x)’=a^x*lna`	`(log_ax)’=1/(xlna)`
`(sinx)’=cosx`	`(cosx)’=-sinx`
`(text(tg)x)’=1/cos^2x`	`(text(ctg)x)’=-1/sin^2x`
`(arcsinx)’=1/sqrt(1-x^2)`	`(arccosx)’=-1/sqrt(1-x^2)`
`(text(arctg))=1/(1+x^2)’`	`(text(arcctg))’=-1/(1+x^2)`

Также некоторые сведения про производные смотрите в описании задач
№14 (база), №7 (профиль), №12 (профиль).

Первообразные

Первообразная:	`F'(x)=f(x)`
Неопределённый интеграл:	`intf(x)dx=F(x)+C`
Определённый интеграл (формула Ньютона-Лейбница):	`int_a^bf(x)dx=F(b)-F(a)`

Таблица первообразных

`f(x)`	`F(x)`		`f(x)`	`F(x)`
`a`	`ax`
`x^n`	`x^(n+1)/(n+1)`		`1/x`	`lnx`
`e^x`	`e^x`		`a^x`	`a^x/lna`
`sinx`	`-cosx`		`cosx`	`sinx`
`1/cos^2x`	`text(tg)x`		`1/sin^2x`	`-text(ctg)x`
`1/(x^2+a^2)`	`1/atext(arctg)x/a`		`1/(x^2-a^2)`	`1/(2a)ln|(x-a)/(x+a)|`
`1/sqrt(a^2-x^2)`	`text(arcsin)x/a`		`1/sqrt(x^2+a)`	`ln|x+sqrt(x^2+a)|`

Геометрия

Планиметрия (2D)

Площади фигур:

Окружность:	`S=pir^2`
Треугольник:	`S=1/2ah`
Параллелограмм:	`S=ah`
Четырёхугольник:	`S=1/2d_1d_2sinvarphi`
Трапеция:	`S=(a+b)/2*h`

Стереометрия (3D)

Призма:	`V=S_(осн)h`
Пирамида:	`V=1/3S_(осн)h`
Конус:	`V=1/3S_(осн)h`
	`S_(бок)=pirl`
Цилиндр:	`V=pir^2h`
	`S_(бок)=2pirh`
Шар:	`V=4/3pir^3`
	`S=4pir^2`

Как выучить все формулы по математике к ЕГЭ

Чтобы сдать ЕГЭ по математике, необходимо знать математические формулы из школьного курса алгебры и геометрии.

Для того, чтобы запомнить формулы школьной математики, желательно держать в течение всего года на видном месте шпаргалку с красиво написанными формулами. Таким образом подключается зрительная память и формулы лучше запоминаются.

Проверяйте себя время от времени: попробуйте написать все важные математические формулы по памяти, а затем проверьте. На самом деле, формул, которые надо выучить наизусть, не так много. И целого учебного года вполне достаточно, чтобы все выучить.

Многие алгебраические, геометрические, тригонометрические формулы можно быстро вывести прямо на экзамене, если Вы их забыли. Но на это придется потратить какое-то время. Поэтому преимущество получают те школьники, которые выучили формулы.
Зная математические формулы наизусть, можно гораздо быстрей решить сложные задачи по алгебре, тригонометрии и геометрии на ЕГЭ.

Мы собрали самые важные формулы из школьного курса математики, которые надо выучить для успешной сдачи ЕГЭ.

Математические формулы школьного курса алгебры

Степени и корни

Формулы сокращенного умножения

Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители

Логарифмические формулы

Формулы тригонометрии

Основные формулы тригонометрии

Тригонометрические уравнения

Значения тригонометрических функций

Формулы приведения

Сумма и разность углов

Формулы двойного и тройного аргумента

Формулы половинного аргумента

Сумма и разность тригонометрических функций

Произведение тригонометрических функций

Формулы дифференциального исчисления

Формулы векторной алгебры из школьного курса математики

Формулы арифметической и геометрической прогрессии

Геометрические формулы школьного курса математики для ЕГЭ

Планиметрия

Стереометрия

Выучить формулы по математике – это еще не все, что надо для успешной сдачи ЕГЭ. Опыт решения задач, знания правил оформления заданий на экзамене не менее важны. Приглашаем всех школьников 11-х классов на курсы подготовки к ЕГЭ ПАРАГРАФ. С нами Вы подготовитесь к ЕГЭ наиболее продуктивно.

Учите формулы по математике и сдавайте ЕГЭ на максимальные баллы!

DOC-шпаргалка — подборка всех основных формул по разделам, которые нужны при решении заданий ЕГЭ по математике базового или профильного уровня…

Скачать шпаргалку

---

Скриншот:

---

Рейтинг: 3.6 из 5.0
Проголосовало: 17

Комментарии

Всего комментариев: 0

Полный сборник красиво оформленных школьных формул по алгебре и геометрии.

В пособии содержатся все разделы школьной математики, все формулы и даны подробные описания к каждому из них.

Смотреть в PDF: Скачайте pdf файл.

Можете записаться на занятия к репетитору математики, если что-то не понятно.

По разделам:

Степени и корни:

  Сокращенное умножение

:

  Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители:
 

 

Логарифмы:
 
 

Формулы тригонометрии, тождества:
 
 

Тригонометрические уравнения:
 
 

Значения тригонометрических функций:
 
 

Формулы приведения:
 
 

Сумма и разность углов:
 
 

Формулы двойного и тройного аргумента:
 
 

Формулы половинного аргумента:
 
 

Сумма и разность тригонометрических функций:
 
 

Произведение тригонометрических функций:
 
 

Производная: признаки возрастания, убывания, минимума функции:
 
 

Дифференциальное исчисление:
 
 

Геометрия: формулы площадей. Прямоугольники, окружности, трапеции:
 
 

Стереометрия: объёмы, площади поверхностей:

Обратиться к репетитору по математике.

На ЕГЭ формулами пользоваться нельзя, нужно их помнить! 

В этой подборке формул использованы 3 основных принципа, для упрощения запоминания:

• Выбраны только те формулы, которые могут встретиться на ЕГЭ по математике (это лишь часть того, что изучено в школе);
• Формулы разобраны на тематические блоки;
• Блоки формул выделены цветовым фоном, который позволяет, всего после нескольких обращений, вспоминать картинку и буквально читать с нее нужную формулу.

Как легко запомнить именно нужные формулы из всего курса математики? 

Для подготовки нужно выбрать такое оформление математических формул, чтобы они отложились в памятки наиболее эффективно. 

Все формулы по математике. Скачать

Комментарии

Всего комментариев: 0

---

0 комментария