Новый тренировочный вариант №397 Алекса Ларина ЕГЭ 2023 по математике профильный уровень 11 класс с ответами и решением, который вышел на сайте 10 сентября 2022 года, по новой демоверсии ЕГЭ 2023 года ФИПИ.
Скачать вариант с ответами
Демоверсия ЕГЭ 2023 по математике
Тренировочный вариант 397 Ларина ЕГЭ 2023 по математике профиль
ларин-егэ2023-вариант-397-ответы
Ответы для варианта
1)Около окружности, радиус которой равен 8, описан многоугольник, площадь которого равна 208. Найдите периметр этого многоугольника.
Ответ: 52
2)В прямоугольном параллелепипеде АВСDА1B1C1D1 известны длины ребер: АВ = 11, AD = 20, AA1 = 4. Найдите расстояние от вершины С до центра грани АА1D1D.
Ответ: 15
3)Из слова «максимум» случайным образом выбирается одна буква. Найдите вероятность того, что будет выбрана буква, встречающаяся в этом слове только один раз.
Ответ: 0,625
4)Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что извлечённый наугад кубик будет иметь хотя бы одну окрашенную грань.
Ответ: 0,488
9)Имеется три одинаковых по массе сплава. Известно, что процентное содержание никеля во втором сплаве на 25 процентных пункта больше, чем в первом, а процентное содержание никеля в третьем сплаве на 4 процентных пункта больше, чем во втором. Из этих трёх сплавов получили четвертый сплав, содержащий 64% никеля. Сколько процентов никеля содержит первый сплав?
Ответ: 46
13)В правильной шестиугольной пирамиде SABCDEF сторона основания AB = 4, а боковое ребро SA = 7. Точка M лежит на ребре BC, причем BM = 1, точка K лежит на ребре SC, причем SK = 4. А) Докажите, что плоскость MKD перпендикулярна плоскости основания пирамиды. Б) Найдите объем пирамиды CDKM.
15)В июле 2026 года планируется взять кредит на три года. Условия его возврата таковы: — каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; — платежи в 2027 и в 2028 годах должны быть по 300 тыс. руб.; — к июлю 2029 года долг должен быть выплачен полностью. Известно, что платёж в 2029 году будет равен 417,6 тыс. руб. Какую сумму (в тыс. рублей) планируется взять в кредит?
Ответ: 700
16)Две окружности пересекаются в точках Р и Q. Через точку Р проведена прямая, пересекающая вторично первую из окружностей в точке А, а вторую – в точке В. Через точку Q также проведена прямая, пересекающая вторично первую окружность в точке С, а вторую – в точке D. А) Докажите, что прямые АС и BD параллельны. Б) Найдите наибольшее возможное значение суммы длин отрезков АВ и CD, если расстояние между центрами данных окружностей равно 1.
18)Издательство на выставку привезло несколько книг для продажи (каждую книгу привезли в единственном экземпляре). Цена каждой книги — натуральное число рублей. Если цена книги меньше 100 рублей, на неё приклеивают бирку «выгодно». Однако до открытия выставки цену каждой книги увеличили на 10 рублей, из‐за чего количество книг с бирками «выгодно» уменьшилось.
А) Могла ли уменьшиться средняя цена книг с биркой «выгодно» после открытия выставки по сравнению со средней ценой книг с биркой «выгодно» до открытия выставки?
Б) Могла ли уменьшиться средняя цена книг без бирки «выгодно» после открытия выставки по сравнению со средней ценой книг без бирки «выгодно» до открытия выставки?
В) Известно, что первоначально средняя цена всех книг составляла 110 рублей, средняя цена книг с биркой «выгодно» составляла 81 рубль, а средняя цена книг без бирки — 226 рублей. После увеличения цены средняя цена книг с биркой «выгодно» составила 90 рублей, а средняя цена книг без бирки — 210 рублей. При каком наименьшем количестве книг такое возможно?
Видео решение варианта Ларина
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Задание 1
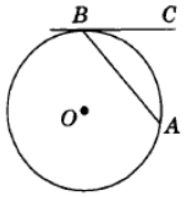
Хорда АВ стягивает дугу окружности в 40°. Найдите угол АВС между этой хордой и касательной к окружности, проведённой через точку В. Ответ дайте в градусах.
Ответ: 20
Скрыть
Угол между касательной и хордой равен половине дуги, заключённой между ними. Поэтому он равен 20.
Задание 2
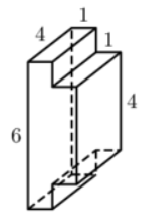
Найдите площадь поверхности многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.
Ответ: 84
Скрыть
Площадь поверхности заданного многогранника равна сумме площадей параллелепипедов с ребрами 1, 6, 4 и 1, 4, 4 уменьшенной на удвоенную площадь квадрата стороной 4:
$$S=2(4cdot1+6cdot1+4cdot6)+2(4cdot1+4cdot1+4cdot4)-2(4cdot4)=84$$
Задание 3
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 35% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 60% яиц высшей категории. Всего высшую категорию получает 55% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Ответ: 0,2
Скрыть
Сначала определим вероятность того, что было куплено яйцо высшего сорта у первого или второго хозяйства. Пусть событие $$A$$ означает яйцо высшей категории, а события $$B_1$$ и $$B_2$$ определяют то, что яйцо высшей категории было произведено 1-м и 2-м хозяйством соответственно. Тогда условные вероятности $$P(A|B_1)$$ и $$P(A|B_2)$$ будут означать, вероятности закупки яйца первой категории у 1-го и 2-го хозяйства соответственно. По формуле полной вероятности найдем вероятность того, что будет куплено яйцо высшей категории, имеем:
$$P(AB_1)+B(AB_2)=P(A|B_1)cdot P(B_1)+P(A|B_2)cdot P(B_2)=$$
$$=0,35cdot P(B_1)+0,6cdot(1-P(B_1))=-0,25cdot P(B_1)+0,6$$
По условию задачи эта вероятность равна 0,55, следовательно, вероятность того, что купленное яйцо произведено в первом хозяйстве, равна:
$$P(B_1)=(0,55-0,6):(-0,25)=0,2$$.
Задание 4
Первый игральный кубик обычный, а на гранях второго кубика нет нечётных чисел, а чётные числа 2, 4 и 6 встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 4 и 6 очков. Какова вероятность того, что бросали первый кубик?
Ответ: 0,2
Скрыть
Предположим, что бросали первый кубик. Тогда вероятность того, что в каком-то порядке выпали 4 и 6 очков, равна $$frac{1}{6}cdotfrac{1}{6}+frac{1}{6}cdotfrac{1}{6}=frac{1}{18}.$$
Теперь предположим, что бросали второй кубик. Поскольку на втором кубике числа 4 и 6 встречаются по два раза, вероятность того, что в каком-то порядке выпали 4 и 6 очков, равна $$frac{2}{6}cdotfrac{2}{6}+frac{2}{6}cdotfrac{2}{6}=frac{2}{9}.$$
Таким образом, искомая вероятность равна $$frac{frac{1}{18}}{frac{1}{18}+frac{2}{9}}=frac{1}{1+4}=0,2.$$
Задание 5
Решите уравнение $$sqrt[x]{64}-sqrt[x]{2^{3x+3}}+12=0.$$
Ответ: 3
Скрыть
$$sqrt[x]{64}-sqrt[x]{2^{3x+3}}+12=0$$
$$sqrt[x]{2^6}-sqrt[x]{2^{3x+3}}+12=0$$
$$(sqrt[x]{2^3})^2-2^{3}cdotsqrt[x]{2^3}+12=0$$
Замена: $$sqrt[x]{2^3}=y>0$$
$$y^2-8y+12=0Rightarrow (y-2)(y-6)=0Rightarrowleft[begin{matrix} y=2\ y=6 end{matrix}right.Leftrightarrowleft[begin{matrix} sqrt[x]{2^3}=2\ sqrt[x]{8}=6 end{matrix}right.Leftrightarrow x=3$$
Предполагается, что $$xin N,$$ поэтому $$sqrt[x]{8}=6$$ не имеет решений.
Задание 6
Найдите $$tg a,$$ если $$frac{5sin a-4cos a-2}{5sin a+cos a-3}=frac{2}{3}.$$
Ответ: 2,8
Скрыть
$$frac{5sin a-4cos a-2}{5sin a+cos a-3}=frac{2}{3}Leftrightarrow 15sin a-12cos a-6=10sin a+2cos a-6Rightarrow$$
$$Rightarrow5sin a=14cos a; |:cos aRightarrow 5tg a=14Rightarrow tg a=2,8$$
Задание 7
На рисунке изображен график производной $$y=f'(x)$$ функции $$f(x),$$ определенной на интервале $$(-4;8).$$ В какой точке отрезка $$[-3;1]$$ функция $$f(x)$$ принимает наименьшее значение?
Ответ: 1
Скрыть
На заданном отрезке производная функции отрицательна, поэтому функция на этом отрезке убывает. Поэтому наименьшее значение функции достигается на правой границе отрезка, т. е. в точке $$1.$$
Задание 8
При температуре $$0^{circ}$$ С рельс имеет длину $$l_0=10$$ м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону $$l(t^{circ})=l_0(1+acdot t^{circ}),$$ где $$a=1,2cdot10^{-5}(^{circ} C)^{-1}$$ — коэффициент теплового расширения, $$t^{circ}$$ — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.
Ответ: 25
Скрыть
Необходимо рассчитать значение $$t,$$ при котором $$l(t)=l_0+3cdot10^{-3}$$ метров. Воспользуемся законом изменения длины рельс от температуры и выразим температуру, получим:
$$l_0+3cdot10^{-3}=l_0+l_0at$$
$$l_0at=3cdot10^{-3}$$
$$t=frac{3cdot10^{-3}}{l_0a}$$
$$t=frac{3cdot10^{-3}}{10cdot1,2cdot10^{-5}}=frac{3cdot10^{-3}}{12cdot10^{-5}}=25$$
Задание 9
По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 300 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 300 метрам.
На сколько километров в час скорость первого сухогруза меньше скорости второго?
Ответ: 4
Скрыть
Необходимо понять, как протекает данный процесс.
За точку, которая передвигается, принимается нос второго сухогруза. В таком случае он проходит сначала расстояние 300 метров, потом длину первого 120 метров, потом свою длину 80 метров, и только с этого момента начинает его опережать, то есть проходит еще 300 метров. В таком случае общий путь S=800 метров = 0,8 км.
Далее можно рассмотреть эту задачу немного иначе.
Раз один догоняет другого, мы можем представить, что первый стоит, а второй двигается к нему со скоростью, равной разности их скоростей, то есть то, что мы ищем.
Время представляем в часах: 0,2 часа и далее применяем стандартную формулу нахождения скорости через расстояние и время.
Получаем: $$v=frac{0,8}{0,2}=4$$
Задание 10
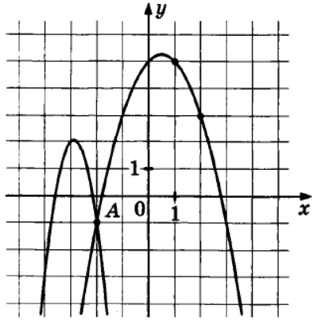
На рисунке изображены графики функций $$f(x)=-4x^2-23x-31$$ и $$g(x)=ax^2+bx+c,$$ которые пересекаются в точках А и В. Найдите абсциссу точки В.
Ответ: -6
Скрыть
Очевидно, что это правый график (у $$f(x)$$: $$a=-4$$ — сужение как у левого). $$g(x)$$ проходит через $$(2;3)$$ и $$(1;5).$$ Получим:
$$left{begin{matrix} 3=acdot2^2+bcdot2+5\ 5=acdot1^2+bcdot1+5 end{matrix}right.Leftrightarrowleft{begin{matrix} 4a+2b=-2\ a+b=0 end{matrix}right.Leftrightarrowleft{begin{matrix} 4a+2b=-2\ 4a+4b=0 end{matrix}right.Leftrightarrowleft{begin{matrix} 2b=2\ 4a+4=0 end{matrix}right.Leftrightarrow$$
$$Leftrightarrowleft{begin{matrix} b=1\ a=-1 end{matrix}right.$$
Получим $$g(x)=-x^2+x+5.$$ Тогда:
$$-4x^2-23x-31=-x^2+x+5Leftrightarrow 3x^2+24x+36=0Rightarrow x^2+8x+12=0Rightarrow$$
$$Rightarrowleft[begin{matrix} x=-2\ x=-6 end{matrix}right.$$
Тогда $$B_x=-6$$
Задание 11
Найдите наибольшее значение функции $$y=sqrt{2lg x-1}-lg x$$
Ответ: 0
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$${y}’=frac{1}{2sqrt{2lg x-1}}*frac{2}{xln 10}-frac{1}{xln10}=0$$
$$frac{1}{xln 10}(frac{1}{2sqrt{2lg x-1}})=0$$
$$left{begin{matrix}xneq 0 \sqrt{2lg x-1}=1(1)end{matrix}right.$$
$$(1): sqrt{2lg x-1}=1Leftrightarrow$$ $$2lg x-1leq 1Leftrightarrow$$ $$2lg x=2Leftrightarrow$$ $$lg x=1Leftrightarrow x=10$$
$$y(10)=y=sqrt{2lg 10-1}-lg 10=1-1=0$$
Задание 12
А) Решите уравнение $$cos x+sqrt{frac{2-sqrt{2}}{2}cdot(sin x+1)}=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-frac{11pi}{2};-4pi]$$
Ответ: А)$$-frac{pi}{2}+2pi n;frac{3pi}{4}+2pi n,nin Z$$ Б)$$-frac{9pi}{2};-frac{21pi}{4}$$
Задание 13
В правильной четырехугольной пирамиде SABCD точка L — середина бокового ребра SB. На ребре SA взята точка К так, что SK:KA=1:2.
А) Докажите, что плоскость DKL параллельна боковому ребру SC.
Б) Найдите площадь сечения пирамиды плоскостью DKL, если все ребра пирамиды равны 24.
Ответ: $$60sqrt{19}$$
Задание 14
Решите неравенство: $$log_5^2(x-8)-6log_5(sqrt{x-8})geq4-25cdot(x-8)cdot(log_5(x-8)-4)$$
Ответ: $$(8;frac{201}{25}],[633;infty)$$
Задание 15
Андрей планирует 19 декабря взять в банке кредит на 3 года в размере 2 029 000 рублей. Сотрудник банка предложил Андрею два различных плана погашения кредита, описание которых приведено в таблице.
| План 1 | — каждый январь долг возрастает на 8% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; — кредит должен быть полностью погашен за три года тремя равными платежами. |
| План 2 | — 1-го числа каждого месяца долг возрастает на 0,8% по сравнению с концом предыдущего месяца; — со 2-го по 18-е число каждого месяца необходимо выплатить часть долга; — 19-го числа каждого месяца со 2-го по 36-й долг должен быть меньше долга на 19-е число предыдущего месяца на одну и ту же сумму; — к 19-му числу 36-го месяца кредит должен быть полностью погашен. |
На сколько рублей меньше окажется общая сумма выплат Андрея банку по более выгодному плану погашения кредита?
Ответ: 32 668
Задание 16
В трапеции ABCD известно, что $$BC || AD, angle ABC=90^{circ}.$$ Прямая, перпендикулярная стороне CD, пересекает сторону АВ в точке М, а сторону CD — в точке N, DH — перпендикуляр, опущенный из точки D на прямую МС.
А) Докажите, что расстояние от точки А до прямой BN равно $$frac{BNcdot DH}{MC}$$
Б) Найдите отношение боковых сторон трапеции, если $$MC = 4, BN = 2$$
Ответ: $$1:2$$
Задание 17
Найдите все значения параметра $$a,$$ при каждом из которых уравнение
$$cossqrt{2pi ax-4x^2}+cos2sqrt{2pi ax-4x^2}=0$$
имеет ровно два решения.
Ответ: $$(-2;-frac{2}{3}),(frac{2}{3};2)$$
Задание 18
А) Уравнения $$ax^2+bx+c=0$$ и $$cx^2+bx+a=0$$ имеют корни, которые являются целыми числами. Коэффициенты уравнений являются натуральными числами (необязательно различными). Причем корни первого уравнения равны корням второго. Решите эти уравнения.
Б) Найдите квадратные уравнения $$ax^2+bx+c=0,$$ для которых коэффициенты $$a,b,c$$ являются корнями.
В) Три числа $$a,b,c$$ отличны от нуля. Квадратные уравнения
$$ax^2+bx+c=0$$
$$bx^2+cx+a=0$$
$$cx^2+ax+b=0$$
имеют общий корень. Решите эти уравнения.
Ответ: $$А)-1,$$ $$Б)-x^2-x=0,x^2+x-2=0,x^2-frac{1}{2}x-frac{1}{2}=0,ax^2+frac{1}{a}x+a=0,a^3+a+1=0,$$ $$В)left{1,frac{c}{a}right},left{1,frac{a}{b}right}left{1,frac{b}{c}right}$$
Критерии
Оценивание
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:
А. Ларин. Тренировочный вариант № 415.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В правильной четырехугольной пирамиде SABCD с вершиной S каждое ребро равно Через середины сторон AD и DC и середину высоты пирамиды проведена плоскость α.
а) Докажите, что плоскость α параллельна ребру SD.
б) Найдите площадь сечения пирамиды плоскостью α.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В июле 2023 года планируется взять кредит в банке на 6 лет в размере S тысяч рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на 16% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо одним платежом выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Дата | Июль 2023 | Июль 2024 | Июль 2025 | Июль 2026 | Июль 2027 | Июль 2028 | Июль 2029 |
|---|---|---|---|---|---|---|---|
| Долг (в тыс. руб.) |
S | 0,9S | 0,8S | 0,7S | 0,6S | 0,5S | 0 |
Найдите, на сколько процентов общая сумма платежей после полного погашения кредита превысит сумму взятого кредита.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
B трапеции ABC боковая сторона AB перпендикулярна основаниям. Из точки A на сторону CD опустили перпендикуляр AH. На стороне AB отмечена точка E так, что прямые CD и CE перпендикулярны.
а) Докажите, что прямые BH и ED параллельны.
б) Найдите отношение BH к ED, если
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, для каждого из которых уравнение
имеет хотя бы одно решение.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Натуральное число называется свободным от квадратов, если оно не делится ни на один квадрат натурального числа, кроме 1. Составим последовательность {an}, состоящую из чисел, свободных от квадратов: пусть и для любых натуральных n
где ai — число, свободное от квадратов.
а) Может ли число, свободное от квадратов, иметь 15 делителей?
б) Чему равно n, если an = 326?
в) Чему равно a100?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
- О сайте
- Карта сайта
- Пользовательское соглашение
- Политика конфиденциальности
© 2020-2023, ege314.ru, ОГЭ и ЕГЭ по математике | Генератор вариантов ЕГЭ 2023.
Частичное или полное копирование решений (включая графические элементы) с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все решения являются собственностью сайта.