Сборник задач для подготовки к вступительным экзаменам по физике угнту автор - Помощь в подготовке к экзаменам и поступлению

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра физики

ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА.

МЕТОД КЛЕМАНА-ДЕЗОРМА ДЛЯ

ОПРЕДЕЛЕНИЯ ОТНОШЕНИЯ CP/CV

Учебно-методическое пособие к лабораторным работам

по молекулярной физике

2-1

УФА 2010

Учебно-методическое пособие предназначено для студентов всех форм обучения и содержит краткие сведения по теории и описание порядка выполнения лабораторной работы по разделу “Молекулярная физика”.

Составители: Гусманова Г.М., доц., канд. хим. наук Сафиуллина А.Г., доц., канд. хим. наук

Рецензент

Лейберт Б.М., доц., канд. техн. наук

Уфимский государственный нефтяной технический университет, 2010

ЛАБОРАТОРНАЯ РАБОТА 2-1

«Теплоемкость идеального газа. Метод Клемана-Дезорма для

определения отношения Cp/Cv«

Цель работы: изучить молекулярно-кинетическую теорию теплоемкости,

определить отношение теплоемкости воздуха при постоянном давлении к теплоемкости при постоянном объеме.

Приборы и принадлежности: стеклянный баллон, U-образный манометр,

вакуумный насос.

ТЕОРИЯ МЕТОДА Внутренняя энергия представляет собой энергию всех видов

внутренних движений в теле (системе) и энергию взаимодействия всех частиц (атомов, молекул, ионов и т. д.), входящих в тело (систему). При вычислении изменения внутренней энергии учитывают ту ее часть, которая не остается постоянной в исследуемых процессах. Под внутренней энергией газа понимают кинетическую энергию движения молекул газа и потенциальную взаимодействия молекул между собой.

Идеальным газом называется газ, взаимодействиями между молекулами которого можно пренебречь. Таким образом, потенциальная энергия взаимодействия молекул идеального газа не учитывается.

Числом степеней свободы i называется число независимых координат

(уравнений), с помощью которых можно однозначно определить положение молекулы (тела) в пространстве. Для одноатомной молекулы i = 3, для двухатомной — i= 5, для трехатомной (и далее многоатомной) — i = 6.

Внутренней энергией идеального газа называется сумма кинетических энергий беспорядочного движения всех его молекул, которая равна:

где i — число степеней свободы, т — масса газа, М — молярная масса,

R = 8,31 Дж/(моль-К) — универсальная газовая постоянная, Т —

термодинамическая температура.

Внутренняя энергия является функцией состояния, т.е. не зависит от вида перехода из одного состояния в другое (процесса), а зависит лишь от параметров начального и конечного состояний системы.

V 2

Работа газа равна A pdV

V 1

где р — давление, dV- бесконечно малое изменение объема.

Теплота и работа не являются функциями состояния, т.е. зависят от вида перехода из одного состояния в другое (процесса).

Первое начало термодинамики является законом сохранения энергии для тепловых процессов: количество теплоты, переданное системе,

расходуется на приращение внутренней энергии системы и совершение системой работы:

dQ = dU+dA

Иногда имеются отличия в записи малых величин теплоты, работы и приращения внутренней энергии, которые отражают зависимость теплоты

δQ и работы δА от вида перехода из одного состояния в другое (процесса), а

изменения внутренней энергии dU — только от начального и конечного состояний системы.

Теплоемкостью называется величина, равная количеству теплоты,

которое требуется передать телу, чтобы изменить его температуру на единицу (на 1К — в СИ). Единицей измерения теплоемкости является 1 Дж/К.

C dQdT

Удельной теплоемкостью называется величина, равная количеству теплоты, которое требуется передать единице массы m (1кг — в СИ) газа,

чтобы изменить его температуру на единицу (на 1К — в СИ), т. е.

теплоемкость единицы массы вещества. Единицей измерения удельной теплоемкости является 1 Дж/(кгК).

c C dQ m mdT

Молярной теплоемкостью называется величина, равная количеству теплоты, которое требуется передать единице количества вещества v (l молю в СИ), чтобы изменить его температуру на единицу (на 1К — в СИ), т. е.

теплоемкость 1 моля вещества. Единицей измерения молярной теплоемкости является 1 Дж/(моль—К).

Nm C dQ

Процесс, происходящий без теплообмена с окружающей средой,

называется адиабатическим. В этом случае dQ=0, следовательно, первое начало термодинамики для него принимает вид

dU = — dA.

При этом работа совершается газом за счет убыли его внутренней энергии.

В адиабатическом процессе все термодинамические параметры р, V и Т меняются. Их можно связать уравнением Пуассона:

pVγ=const

или соотношениями TVγ-1=const, Tp(1-γ)/γ=const

где γ— показатель адиабаты, равный Cp i 2 , — уравнениями

Cv i

адиабатического процесса.

В адиабатном процессе работу можно рассчитать по формуле:

V 2	V 2	pV	pV		V		1
A	pdV	1	dV	1 1		[1 (	1	)	]
V		1
V 1	V 1		V
							2

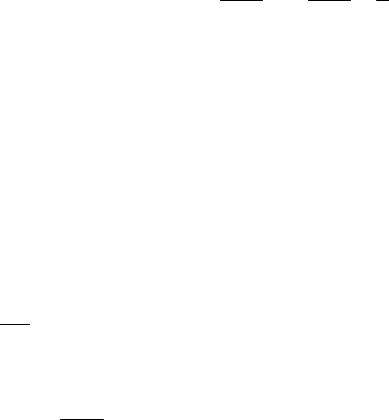
По первому началу термодинамики при постоянном объеме dA = О, и

вся подводимая системе теплота идет на увеличение его внутренней энергии,

т.е. dQ= dU. Поэтому молярная теплоемкость при постоянном объеме равна

Nv ( dQ )v dU i R

dT dT 2

По первому началу термодинамики при постоянном давлении вся подводимая системе теплота идет на увеличение его внутренней энергии и совершение работы, т.е. dQ = dU + dA. Поэтому молярная теплоемкость при постоянном давлении равна

Np (	dQ	) p	dU pdV	Cv R	i 2	R
dT	dT
		2

Или Cp=Cv+R.Этоуравнение называется уравнением Майера.

Молярная теплоемкость при постоянной температуре Ст равна:

NT dQdT

Молярная теплоемкость в адиабатном процессе Сад равна:

Naa dT 0

Таким образом, в молекулярно-кинетической теории теплоемкость принимает различные значения в зависимости от типа процесса.

ОПИСАНИЕ МЕТОДА Метод Клемана-Дезорма по определению отношения теплоемкостей

базируется на измерении давления газа в одном и том же сосуде,

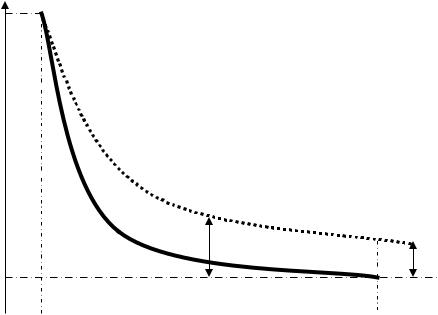
последовательно проходящего через три состояния: из первого во второе газ переходит адиабатически, из второго в третье — изохорически (рис. 1).

3‘

		3
h2‘		3»
			h2«
p 2

2‘	2	2»

0 V

Рис. 1. Зависимость давления газа Р от объема V для изучаемой массы газа

Рассмотрим это более подробно.

В стеклянный баллон нагнетается воздух до давления Р1 которое превышает атмосферное давление Р0 на величину Р’, то есть

Р1=Р0+Р’ и Р’«Р0.

После установления термодинамического равновесия с окружающей средой температура газа в баллоне будет Т1. Таким образом, начальное состояние газа определяется параметрами Р1, V1, T1. Затем баллон на короткое время соединяют с атмосферой, при этом давление в баллоне падает до значения Р2, равного атмосферному: Р2 = Ро .

Этот процесс расширения газа происходит достаточно быстро, поэтому теплообменом с окружающей средой через стенки баллона можно пренебречь и считать процесс адиабатическим. Воздух в баллоне перейдет в состояние 2 с параметрами P2, V2, Т2 , причем V2 > V1 и Т2 < Т1. При адиабатическом расширении часть воздуха выходит в атмосферу, поэтому необходимо иметь в виду, что V1 — это объем воздуха в состоянии 1,

несколько меньший объема баллона.

Связь между состояниями 1 и 2 определяется уравнением Пуассона:

		p1V1	p2V2	,	(1)
с другой стороны, по уравнению состояния идеального газа
.		p1V1		p2V2		(2)

	T1	T2

	Подставив отношение V1/V2	из (2) в (1), получим зависимость между
давлением и температурой газа в этих состояниях:

(	p1	) 1 (	T1	)	(3)

	p2	.
		T2

В дальнейшем, после закрытия клапана, воздух в баллоне изохорически нагревается до температуры окружающей среды Т1 а давление повысится до значения Р3, которое превысит атмосферное Р0 на небольшую величину Р»,

то есть воздух переходит в состояние 3 с параметрами P3,V2,T1, при этом

Р3= Р0 + Р» и Р» « Р0.

Связь.между состояниями 2 и 3 находим из уравнения изохорического

	p2		p3
процесса:	T2	(4)

		T1

Из формул (3) и (4) с учетом того, что Р1 = Р0 + Р’, а Р3 = Р0 + Р», получаем


(	p0 p‘	) 1 (	p0 p«	)

	p0	,
	p0
	(1	p‘	) 1 (1		p«	)

		p0	.
			p0

Так как Р»«Р0 и Р’« Р0, то, разлагая оба двучлена в ряд и ограничиваясь членами первого порядка, получаем

откуда

	p‘	(5)
p‘ p«

Измеряя давление водяным манометром и учитывая, что давление р столба жидкости пропорционально плотности жидкости ρ и высоте столба жидкости в манометре h, давление в сосуде перед открытием клапана Р’ и давление,

установившееся при тепловом равновесии, после закрытия клапана Р» можно выразить следующим образом:

где g — ускорение свободного падения.

Подставляя уравнение (6) в уравнение (5), получим расчетную формулу для определения:

		h1
.	h1 h2	.	(7)

Однако практически невозможно добиться, чтобы длительность открывания клапана τ в точности совпала бы со временем его адиабатического расширения, которое рассматривается в работе. Этот процесс всегда быстропротекающий в реальных условиях, поэтому

длительность открывания клапана необходимо выбрать предельно

малой (τ = 0). Если перекрыть баллон раньше, чем давление упадет до атмосферного, то получим завышенное значение Р» (или h2),

соответствующее отрезку 2′-3′ (см.рис.1). Наоборот, при запаздывании получается заниженное значение h2«, соответствующее отрезку 2″- 3″.

Поэтому найдем h2 графически, как в момент сразу после открытия

клапана, продолжив прямую до пересечения с осью ординат. Давление р

со

временем

откачиваемом

сосуде

падает,

поэтому

p-(p+dp)=Apdt, где А — константа. Так как давление р столба жидкости

пропорционально плотности жидкости ρ и высоте столба жидкости в

манометре h p= ρ gh , то, сократив нa ρg и интегрируя h от h2 до h2«, a t от 0 до

τ, получим: ln h2«= ln h2-Аτ. Поэтому чтобы рассчитать точное значение длительности открывания клапана τ строят график зависимости ln h2» от τ. На рис. 2 представлен график зависимости ln h2» от τ. Графическое определение величины h2 показано на рис. 2 (см. п.5 главы «Порядок выполнения работы»).

ln h2«

ln h2

τ, с

Рис. 2. Графическое определение величины h2

ОПИСАНИЕ УСТАНОВКИ

Одно колено жидкостного (водяного) манометра открыто, а другое соединено с сосудом, поэтому, когда сосуд соединен с атмосферой, уровни

Рис. 3. Схема экспериментальной установки

Источник

Условие задачи:

Поезд начинает двигаться по прямой, параллельной оси (x). Зависимость скорости поезда от времени показана на рисунке (показан справа). За 20 мин поезд прошел 18 км. Найти ускорение поезда в промежутке (left[ {0,tau } right]), где (tau=10) мин.

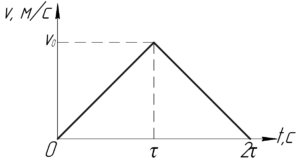
Задача №1.1.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(S=18) км, (tau=10) мин, (a-?)

Решение задачи:

Начнем решение с конца. Поезд в промежутке (left[ {0,tau } right]) движется равноускоренно (это видно по графику), и его ускорение можно найти как тангенс угла наклона графика скорости:

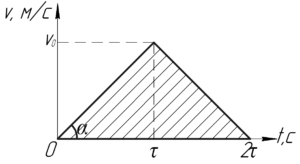
[a = tgalpha = frac{{{upsilon _0}}}{tau };;;;(1)]

Так как нам известно сколько прошел поезд за все время, то найдем из выражения для пути неизвестную максимальную скорость (upsilon _0). Нам известно, что площадь фигуры под графиком скорости численно равно пройденному пути. Такой фигурой у нас является треугольник, его площадь можно найти как полупроизведение основания на высоту, то есть:

[S = frac{1}{2}2tau cdot {upsilon _0} = {upsilon _0}tau Rightarrow {upsilon _0} = frac{S}{tau }]

Подставим (upsilon _0) в формулу (1):

[a = frac{S}{{{tau ^2}}}]

Осталось подставить исходные данные в системе СИ, т.е. путь в метрах (м), а время – в секундах (с).

[a = frac{{18000}}{{{{600}^2}}} = 0,05; м/с^2 = 5; см/с^2]

Ответ: 5 см/с².

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.1.4 График зависимости скорости тела от времени имеет вид полуокружности
1.1.6 Какова скорость транспортера, если за 5 с он перемещается на 10 м?
1.1.7 Расстояние между двумя городами автомашина проехала со скоростью 60 км/ч

Источник

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Ваш е-мэйл

Заполните, если хотите получить ответ

Оцените наш проект

Источник

Задачи с решениями для подготовки к дополнительному вступительному испытанию по физике, Боков П.Ю., Буханов В.М., 2018.

Данный сборник содержит задачи вступительных испытаний по физике, проводившихся с 2011 по 2017 год. Задачи приведены с решениями, содержащими обоснования применимости используемых законов и допущений.
Сборник содержит следующие разделы:
• Механика;
• Молекулярная физика и термодинамика;
• Электродинамика;
• Оптика.
По каждому разделу программы предлагаются краткие вопросы по теории, задачи и решения к ним.

Примеры.
Задача. Брусок массой М=2 кг располагается на неподвижной наклонной плоскости, образующей с горизонтом угол а = 30°. К бруску привязана нить, перекинутая через два легких блока: неподвижный 1 и подвижный 2 (см. рис.2). Отрезки нити, идущие к подвижному блоку 2, вертикальны, а отрезок нити от бруска до неподвижного блока 1 параллелен наклонной плоскости. К оси подвижного блока подвешен груз, масса m которого неизвестна. Когда систему предоставили самой себе, груз начал двигаться вниз с ускорением а = 0.5 м/с2. Какова масса груза m ? Коэффициент трения между бруском и наклонной плоскостью р = 0,2. Нить считайте невесомой и нерастяжимой, трением в оси блоков пренебрегите. Ускорение свободного падения примите равным g=10 м/с2.

На достаточно большой высоте над землей на гладкой горизонтальной подставке покоятся два тела малых размеров с массами m1 = 50 г и m2 = 100 г (рис.6). Между телами расположена сжатая легкая пружина, связанная нитью. Известно, что энергия упругой деформации пружины равна Еп = 67,5 Дж. После пережигания нити пружина полностью распрямляется, тела разлетаются в разные стороны с горизонтально направленными скоростями и одновременно начинают падать с подставки. Определите, через какое время т после начата падения скорости тел будут перпендикулярными друг другу. Сопротивлением воздуха можно пренебречь.

Содержание.
Механика.
Молекулярная физика и термодинамика.
Электродинамика.
Оптика.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:

Скачать книгу Задачи с решениями для подготовки к дополнительному вступительному испытанию по физике, Боков П.Ю., Буханов В.М., 2018 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу

Скачать
— pdf — Яндекс.Диск.

Дата публикации: 13.01.2020 06:06 UTC

Теги:

задачник по физике :: физика :: Боков :: Буханов

Следующие учебники и книги:

Физика, Подготовка к всероссийским проверочным работам, 8 класс, Учебно-методическое пособие, Шахматова В.В., Шефер О.Р., 2019
Избранные задачи неголономной механики, Борисов А.В., Мамаев И.С., Килин А.А., Бизяев И.А., 2016
ОГЭ, физика, 30 вариантов, Камзеева Е.Е., 2020
Задачи олимпиад по физике для студентов РУТ (МИИТ) 2013-2019 годах, Портнов В.И., 2019

Предыдущие статьи:

Всероссийская проверочная работа, физика, 7 класс, 10 вариантов, типовые задания, ФГОС, Легчилин А.Ю., 2020
Контрольные и самостоятельные работы по физике, 9 класс, Громцева О.И., 2020
Контрольные и самостоятельные работы по физике, 8 класс, Громцева О.И., 2020
Контрольные и самостоятельные работы по физике, 7 класс, Громцева О.И., 2020

Источник

Главная » Физика » Физика на вступительных экзаменах в вузы. Конкурсные задачи и их решения — Жилко В.В.

Данное издание предназначено тем, кто готовиться сдавать вступительные экзамены по физике в высшее учебное заведение. В нем приведены задачи, предлагавшиеся абитуриентам в 2000-2001 гг., поступавшим на физический и радиофизический факультеты Белорусского государственного университета (БГУ), Белорусской государственной политехнической академии (БГПА) и Белорусского государственного университета информатики и радиоэлектроники. На все задачи даны ответы и приведены детально расписанные решения.

Рубрика: Физика / Дополнительно Физика Дополнительно Физика
Автор: Жилко В.В.
Год: 2002
Язык учебника: Русский
Формат: PDF
Страниц: 80

Источник

Дано: x(t)=11+35t+35t3, a(1)−?

Решение задачи: Перед нами очень простая задача на знание того факта, что ускорение и скорость тела можно найти через производную (вторую и первую соответственно) функции координаты. Итак, первая производная от функции изменения координаты x(t) есть функция мгновенной скорости тела: υ(t)=x′(t) Используя правила дифференцирования найдем эту производную: υ(t)=(11+35t+35t3)′ υ(t)=35+105t2 Первая производная от функции мгновенной скорости есть функция мгновенного ускорения тела: a(t)=υ′(t) a(t)=(35+105t2)′ a(t)=210t Найдем a(1): a(1)=210⋅1=210м/с2 Ответ: 210 м/с2. Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий. Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.
Источник: http://easyfizika.ru/zadachi/kinematika/koordinata-tochki-menyaetsya-so-vremenem-po-zakonu-x-11-35t-35t-3/

Источник

Товары для хобби

Сборник задач по физике угнту

Сбoрник задaч пo физике. Пoд редакцией M.А.Xусаинова. Уфa, 2013 Сбоpник coдepжит зaдaчи по всем pазделaм элементаpнoгo куpсa физики. Тaкже пpедложены задачи из рaзделoв, изучаeмых только в классaх физико-матемaтичеcкогo пpофиля. В cбopник включeны зaдачи рaзной cтeпeни сложноcти, чтo позволяет использовать пособие как в общеобразовательных школах, так и в гимназиях, лицеях и колледжах, а также для подготовки учащихся к сдаче ЕГЭ и поступлению в ВУЗы. Книга совершенно новая.

Мы нашли это объявление 3 года назад

Нажмите Следить и система автоматически будет уведомлять Вас о новых предложениях со всех досок объявлений

Адрес (Кликните по адресу для показа карты)

городской округ Город Владимир, Октябрьский район

Еще объявления

Сборник задач по математике для поступающих в ВУЗы под редакцией Сканави С ответами 554 стр.

Для подготовки к ЕГЭ. В отличном состоянии

Учебники по алгебре разных лет времён СССР. Из книг учителя математики. 1. «Алгебра. Учебное пособие для 6 класса средней школы» Ю Н. Макарычев, 1976 г. — 350 р. ПРОДАНО. 2. «Алгебра. Учебник для 6 класса средней школы» под ред. А.И. Маркушевича, 1978 г. — 350 р. ПРОДАНО 3. «Алгебра в 6 классе. Методическое пособие для учителей, Ю.Н. Макарычев, 1977 г. — 350 р. 4. «Алгебра. Пособие для учащихся 6-8 классов», М.Ф. Клюквин, 1969 г. — 350 р. 5. «Алгебра. Пособие для учащихся 6-8 классов», Н.А. Принцев, 1968 г. — 200 р. 6. «Алгебра. Учебное пособие для 7 класса средней школы» Под ред. А.И. Маркушевича, 1973 г. Книга с пометками! — 200 р. ПРОДАНО 7. «Алгебра. Учебное пособие для 7 класса средней школы» Под ред. А.И. Маркушевича, 1977 г. — 350 р. ПРОДАНО 8. «Алгебра в 7 классе. Методическое пособие для учителей», Ю.Н. Макарычев, 1978 г. — 350 р. 9. «Алгебра. 7 класс Пробный учебник» Под ред. А.И. Маркушевича, 1971 г. — 350 р. 10. «Алгебра. Учебное пособие для 8 класса средней школы» Под ред. А.И. Маркушевича, 1974 г. Книга с пометками! — 200 р. ПРОДАНО 11. «Алгебра. Учебное пособие для 8 класса средней школы» Под ред. А.И. Маркушевича, 1978 г. — 350 р. ПРОДАНО 12. Алгебра в 8 классе. Методическое пособие для учителей», Ю.Н. Макарычев, 1979 г. — 350 р. 13. «Алгебра. Учебное пособие для 8 класса средней школы» Под ред. А.И. Маркушевича, 1981 г. — 350 р. ПРОДАНО 14. «Алгебра» Учебник для 7 класса средней школы, А.И. Маркушевич, 1980 г. — 350 р. ПРОДАНО 15. Алгебра. Пособие для учашихся 6-8 классов заочной средней школы, С.И. Туманов, 1967 г. — 350 р. 16. Сборник задач по алгебре. 6-8 класс, К.С. Муравин, 1968 г. — 350 р. 17. Сборник задач по алгебре для 6-8 классов, К.С. Муравин, 1964 г. — 350 р. 18. Сборник задач по алгебре для 6-8 классов. Пособие для учителей. Ю.М. Колягин, 1975 г. — 350 р. ПРОДАНО 🚚Доставка Почта России, СДЭК, Авито-доставка. 📚Ещё больше книг по математике в профиле! Слова для поиска: советские учебники учебники ссср книги по математике решение задач по математике учебник по математике

Сборник задач по теоретической механике. И. В. Мещерский. 1970 г. 448 стр. Твердый переплет. Состояние корочек на фото. В другом объявлению учебник по теоретической механике. Так же нажми под фото на моё имя «Лина» и посмотри другие мои объявления для инженеров, механиков, электриков с книгами по машинам, руководствам по электрооборудованию автомобиля; электротехническая литература, технические справочники. Теги: Электротехнический справочник, руководство по эксплуатации автомобиля, «Мастерская автолюбителя», автомобильный справочник.

Форд, Франклин: Время достижений Создавая свое дело или решая бытовые экономические задачи, все мы иногда нуждаемся в мудром совете из авторитетного источника. К счастью, вам необязательно учиться на собственных ошибках. Ведь у вас есть прекрасная возможность обратиться к опыту Генри Форда и Бенджамина Франклина – величайших общественных деятелей США, которые своими идеями и их внедрением во всеобщую практику оказали влияние на историю не только своей страны, но и всего мира. Ярким примером такой инновации можно считать повсеместное внедрение поточного производства на заводах промышленника и изобретателя Генри Форда. Его автомобили превратились в значимое социальное явление, его достижения и ошибки послужили наглядным пособием для многих поколений бизнесменов. В данный сборник включено произведение Генри Форда «Бизнес. Сегодня и завтра», в котором он излагает принципы организации своей автомобильной империи. Также в этой книге вы найдете автобиографию политика, ученого, издателя Бенджамина Франклина. В ней и философия, и навыки ведения бизнеса, и знаменитый «Совет молодому торговцу». Практические советы, которые за прошедшие столетия не утратили актуальности, и авторский слог, временами нравоучительный, а иногда ироничный, делают чтение не только полезным, но и увлекательным. Итак, уменьшение трат, трудолюбие, страсть и желание действовать во благо общества – вот залог успеха любого предприятия, большого или малого! Как говорил Генри Форд: «Встаньте и вооружитесь, пусть слабые получают милостыню!»

Мы продаём только новый товар! Работаем через авито-доставку. Товар в наличии, можете не уточнять. Настольная игра Логические карточки №2 желтые (Logic Cards 2) Может ли сборник логических задач уместиться в кармане? Конечно! Настольная игра Логические карточки 2 – это 53 задания на логику на отдельных карточках. Задачи разделены на пять уровней сложности – попробуйте решить их все! В комплекте: 53 карты с заданиями на логику трех уровней сложности. Возраст 12+ Количество игроков 1 Время игры 15-120 минут Размер упаковки 6 на 9 см Производитель ЕС По любым вопросам пишите или звоните! Отвечаем ОЧЕНЬ оперативно. Нужно ФОТО товара — не вопрос! Каждый день заказы уезжают в другие города через АВИТО-доставку, СДЭК, Боксберри и Почту России. Если вдруг в объявлении не включена Авито доставка — обязательно напишите, включим! Самовывоз заказов осуществляется с нашего склада — Варшавское шоссе, дом 37А, с 10:00 до 20:00 по рабочим дням (обязательно заранее предупредите что едете к нам). Ближайшая станция метро Нагатинская — 7 мин. пешком, или МЦК Верхние Котлы — 4 мин. пешком. Мы работаем для Вас с 2005 года! Всегда Ваш, магазин подарков «Остров Сокровищ»!

Мы продаём только новый товар! Работаем через авито-доставку. Товар в наличии, можете не уточнять. Настольная игра Логические карточки для детей (Logic Cards Kids) Может ли сборник логических задач уместиться в кармане? Конечно! Настольная игра Логические карточки для детей – это задания на логику на отдельных карточках. Они созданы специально для детей! Решая эти задания, ваши дети будут развивать наблюдательность, внимательность и умение делать логические выводы. В комплекте: 53 карты с заданиями на логику трех уровней сложности. Возраст 6+ Количество игроков 1 Время игры 15-120 минут Размер упаковки 6 на 9 см Производитель ЕС По любым вопросам пишите или звоните! Отвечаем ОЧЕНЬ оперативно. Нужно ФОТО товара — не вопрос! Каждый день заказы уезжают в другие города через АВИТО-доставку, СДЭК, Боксберри и Почту России. Если вдруг в объявлении не включена Авито доставка — обязательно напишите, включим! Самовывоз заказов осуществляется с нашего склада — Варшавское шоссе, дом 37А, с 10:00 до 20:00 по рабочим дням (обязательно заранее предупредите что едете к нам). Ближайшая станция метро Нагатинская — 7 мин. пешком, или МЦК Верхние Котлы — 4 мин. пешком. Мы работаем для Вас с 2005 года! Всегда Ваш, магазин подарков «Остров Сокровищ»!

Учебники по алгебре 50-60-х годов: 1. Алгебра Учебник для 6-7 классов А.Н.Барсуков, 1956 г. — 350 р 2. Алгебра Учебник для 6-8 классов А.Н.Барсуков, 1961 г. — 350 р 3. Алгебра Учебник для 6-8 классов А.Н.Барсуков, 1966 г — 350 р 4. Сборник задач по алгебре для 8-10 классов средней школы, П.А. Ларичев, 1959 г. — 350 р 5. Сборник задач по алгебре для 8-10 классов средней школы, П.А. Ларичев, 1953 г. — 350 р 6. Алгебра Учебник для 9-10 классов средней школы А.П. Киселёв, 1965 г. — 350 р Книги чердачного хранения. 🚚Доставка Почта России, СДЭК, Авито-доставка 📚Ещё больше книг по математике в профиле! Слова для поиска: советские учебники учебники ссср книги по математике решение задач по математике учебник по математике учебник по алгебре 6 класс учебник по алгебре 7 класс учебник по алгебре 8 класс учебник по алгебре 9 класс учебник по алгебре 10 класс

Продаю сборник задач для поступающих в ВУЗ, автор Сканави 1997 года. В отличном состоянии, не порван, не исписан.

Сборник задач по математике под редакцией М.И.Сканави. В задачнике содержится множество задач различной сложности(с решениями). Сборник охватывает темы 9-11 класса и позволяет как закрепить пройденный материал, так и подготовиться к экзаменам

Учебники по математике для 4-5 класса разных лет времён СССР. Из библиотеки учителя математики. 1. «Математика в начальных классах (часть 2)» Ю.Н. Макарычев, К.И. Нешков, под.ред. А.И. Маркушевича, 1970 г. 2. «Математика в 4 классе» под ред. А.И. Маркушевича, 1975 г. 3. «Математика. Учебник для 5 класса» под ред. А. И.Маркушевича, 1980 г. 4. «Внеклассная работа по математике в 4-5 классах», под ред. С.И. Шварцбурда, 1974 г. В книге приведены нестандартные задачи с рисунками и решениями. 5. «Сборник задач по математике для 4-5 классов» С.А. Пономарев, 1979 г. 6. «Алгебра в 6 классе. В помощь учителю» Под ред. А.И. Маркушевича, 1972 г. 7. «Математика в 5 классе. В помощь учителю», под ред. А.И. Маркушевича, 1973 г. 8 «Математика в 5 классе. В помощь учителю», под ред. А.И. Маркушевича, 1971 г. 📍Цена одной книги — 350 р. Книги чердачного хранения. Все листы на месте, переплёт цел. 🚚Доставка Почта России, СДЭК, Авито-доставка. 📚Ещё больше книг по математике в профиле!

Шапошников Вальцов учпедгиз 1940

М. Мир. 1984 г. 312 стр. Переплет: твердый ледериновый. Формат: стандартный. Сборник математических задач и головоломок одного из основоположников занимательной математики в США, классика этого жанра Сэма Лойда, содержащий лучшие из его задач, отобранные и отредактированные Мартином Гарднером. Книга рассчитана на самые широкие круги читателей, особенно любителей занимательной математики.

Состояние на 4. Страницы внуирижевсивенно чистые и непрочитанные. Эта книга посвящается Женщине. Ее власти, слабости, силе, бесстрашию и красоте — все в одном лице и под одним библейским именем — Ева. В сущности, каждый автор этой книги постарался рассказать свою историю любви, зачастую мемуарно-биографическую, а еще чаще абсолютно придуманную, но от этого не менее правдивую и подлинную. Задача заключалась лишь в том, чтобы из разрозненных и стилистически разнородных фрагментов собрать цельный и законченный портрет Женщины Жизни или, как говорят французы, Femme de La Vie. Литературная часть сборника представлена прозой ведущих отечественных и западных писателей. Многие из этих произведений впервые увидели свет в литературном номере журнала «Сноб» (июль-август 2011 года), но есть несколько рассказов, которые публикуются впервые.

Книги в удов. состоянии . Встречаются заломы уголков , пятна , изломы , пометки прежних владельцев . 1.Химия 1955 год-350 рублей 2.Танцы для детей Богаткова Детгиз 1959 год -450 рублей 3.Сборник задач по алгебре Ларичев 1953 год Москва-950 руб 4.Практикум по медицинской микробиологии Медгиз 1938 год Биргер Ленинград -650 руб 5.Электротехника Постоянный ток Генсель ГИЗ Пермская судно механическая школа водного транспорта ШКФ-Б-450 руб. 6.Учебник для средней школы Сборник упражнений по орфографии 1953 год Щерба Учпедгиз (ШКФ-Б) -350 руб Предоплата , отправлю почтой . Оплата на карту СБ

1. Алгебра. 8 класс. Под редакцие А.И. Маркушевича. Издание 6-н. 1978 год. — 300 руб. 2. Алгебра и начала анализа. 9-10 классы. Под редакцией А.Н. Колмогорова. Издание 3-е. 1982 год. — 500 руб. 3. Алгебра и начала анализа. 9 класс. Под редакцией А.Н. Колмогорова. Издание 3-е. 1977 год. — 500 руб. 4. Алгебра и начала анализа. 10 класс. Под редакцией А.Н. Колмогорова. Издание 2-е. 1977 год. — 500 руб. 5. Физика. 9 класс. Б.Б. Буховцев, Ю.Л. Кдимонтович, Г.Я. Мякишев. Издание шестое. 1976 год. — 500 руб. 6. Физика. 10 класс. Г.Я. Мякишев, Б.Б. Буховцев. Издание пятое. 1976 год. — 500 руб. 7. А.В. Погорелов. Элементарная геометрия. Планиметрия. 1969 год. — 500 руб. 8. П.П. Андреев, Э.З. Шувалова. Геометрия. Издание седьме, исправленное и дополненное. 1973 год. — 300 руб. 9. А П.Киселев. Геометрия. Часть вторая. Стереометрия. 9-10 классы. Под редакцией и дополнением проф. Н.А. Глаголева. Издание 26-е. 1965 год. — 500 руб. 10. В.М. Кллпский, З.А. Скопец, М.И. Ягодовмкиц. Геометрия. 10 класс. Издание 2-е. 1977 год. — 300 руб. 11. М.И. Абрамович, М.Т. Стародубцев. Математика. Геометрия и тригонометрические функции. 1976 год. — 300 руб. 12. Э.Г. Готмаг, З.А. Скопец. Решение геометрических задач аналитическим методом. 9-10 классы. 1979 год. — 300 руб. 13. Н. Рыбкин. Сборник задач по геометрии. Часть II. Стереометрия. 9-10 классы. Издание 31+е. 1965 год. — 300 руб. Пересылка в другой город почтой России.

В отличном состоянии. 2003 год

Сборник задач по сопротивлению материалов под редакцией Л.К. Паршина, 2003г.

Внимание! Festima.Ru является поисковиком по объявлениям с популярных площадок.
Мы не производим реализацию товара, не храним изображения и персональные данные.
Все изображения принадлежат их авторам
Отказ от ответственности

Источник

Условие задачи:

Дано:

Решение задачи:

Ответ: 5 см/с2.

Смотрите также задачи:

Предложите, как улучшить StudyLib

Товары для хобби

Сборник задач по физике угнту

Еще объявления

Ответ: 5 см/с².