Сечения геометрия егэ - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В основании правильной треугольной призмы ABCA₁B₁C₁ лежит треугольник со стороной 6. Высота призмы равна 4. Точка N  — середина ребра A₁C₁.

а)  Постройте сечение призмы плоскостью BAN.

б)  Найдите периметр этого сечения.

В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP.

а)  Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.

б)  Найдите площадь сечения.

Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1.

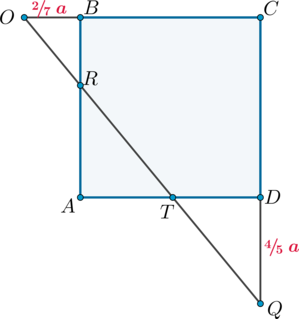
На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка E так, что A₁E : EA = 5 : 3, на ребре BB₁  — точка F так, что B₁F : FB = 5 : 11, а точка T − середина ребра B₁C₁. Известно, что AD = 10, AA₁  =  16.

а)  Докажите, что плоскость EFT проходит через вершину D₁.

б)  Найдите площадь сечения параллелепипеда плоскостью EFT.

На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка E так, что A₁E  =  6EA. Точка T  — середина ребра B₁C₁. Известно, что AD  =  12, AA₁  =  14.

а)  Докажите, что плоскость ETD₁ делит ребро BB₁ в отношении 4 : 3.

б)  Найдите площадь сечения параллелепипеда плоскостью ETD₁.

Основанием прямой четырехугольной призмы ABCDA’B’C’D’ является квадрат ABCD со стороной высота призмы равна Точка K  — середина ребра BB’. Через точки K и С’ проведена плоскость α, параллельная прямой BD’.

а)  Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.

б)  Найдите периметр треугольника, являющегося сечением призмы плоскостью α.

Источник: ЕГЭ по математике 2015. Досрочная волна, резервная волна (часть С)

Пройти тестирование по этим заданиям

Источник

14. Задачи по стереометрии

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи на построение сечений

Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.

Важные факты и теоремы, необходимые для построения сечений

(blacktriangleright) Определение: две прямые параллельны, если они лежат в одной плоскости и не пересекаются.
Если через две прямые нельзя провести одну плоскость, то такие прямые скрещиваются.

(blacktriangleright) Теорема о параллельности трех прямых: если (aparallel b, bparallel c), то и (aparallel c).

(blacktriangleright) Определение: прямая и плоскость параллельны, если они не имеют общих точек.

Признак параллельности прямой и плоскости: прямая, не лежащая в плоскости, параллельна этой плоскости, если она параллельна некоторой прямой из этой плоскости.

(blacktriangleright) Определение: две плоскости параллельны, если они не имеют общих точек.

Признак параллельности двух плоскостей: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости параллельны.

(blacktriangleright) Если две плоскости пересекаются, то их линия пересечения — прямая.

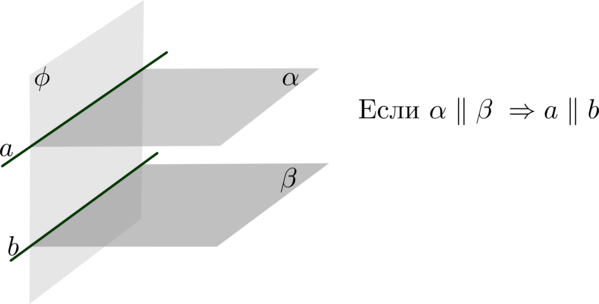
(blacktriangleright) Если две параллельные плоскости пересечены третьей, то их линии пересечения параллельны (см. рис.)

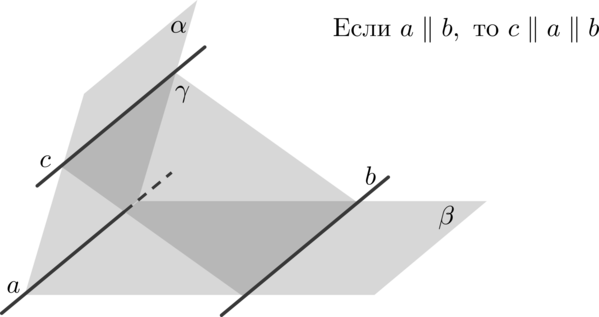
(blacktriangleright) Если плоскости (alpha) и (beta) пересекаются по прямой (a), а плоскости (beta) и (gamma) пересекаются по прямой (b), причем (aparallel b), то плоскости (alpha) и (gamma) пересекутся по прямой (cparallel aparallel b).

Задание
1

#999

Уровень задания: Легче ЕГЭ

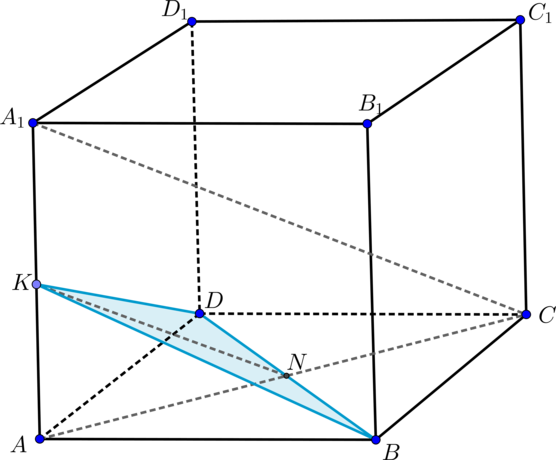
Дан куб (ABCDA_1B_1C_1D_1). Через точку (K), середину ребра (AA_1), и точку (B) проведите плоскость (alpha) параллельно диагонали (A_1C).

Т.к. (A_1Cparallel alpha Rightarrow A_1C) параллельна некоторой прямой, содержащейся в (alpha). Рассмотрим плоскость (AA_1C_1C), в которой находится (A_1C). Т.к. точка (Kin AA_1C_1C), то проведем в этой плоскости (KN parallel A_1C) (по теореме Фалеса (N) – середина (AC)).

Т.к. (ABCDA_1B_1C_1D_1) – куб, то (N) – точка пересечения диагоналей квадрата (ABCD), следовательно, (Nin BD). Таким образом, получили сечение (KBD) куба плоскостью (alpha).

Ответ:

Рисунок.

Задание
2

#3981

Уровень задания: Легче ЕГЭ

Дан куб (ABCDA_1B_1C_1D_1). На ребрах (AA_1) и (BC) отмечены точки (M) и (N) соответственно, причем (AM:MA_1=2:1), а (N) – середина (BC). Найдите сечение куба плоскостью (DMN).

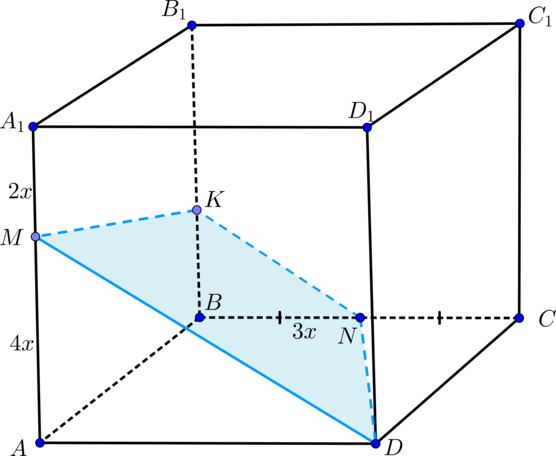
Т.к. грани (ADD_1A_1) и (BCC_1B_1) куба параллельны, то плоскость (DMN) пересечет их по параллельным прямым. Таким образом, проведем (NKparallel DM). Таким образом, (DNKM) – искомое сечение.

Необходимо найти точное расположение точки (K).

Обозначим ребро куба за (6x). Т.к. (bigtriangleup ADM sim
bigtriangleup BNK Rightarrow dfrac{BK}{AM}=dfrac{BN}{AD}
Rightarrow BK=2x). Таким образом, (BK:KB_1=1:2).

Ответ:

Рисунок.

Задание
3

#3804

Уровень задания: Равен ЕГЭ

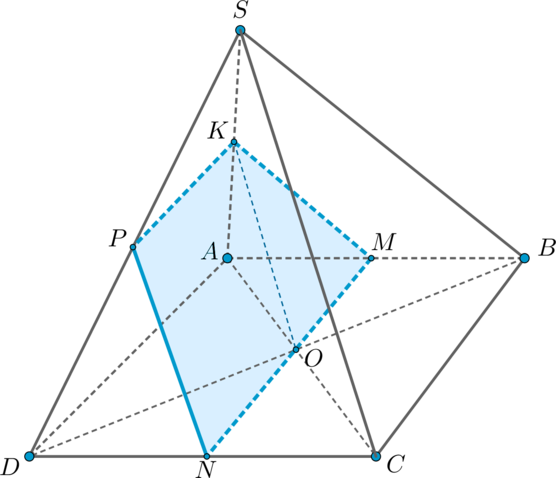
(SABCD) – четырехугольная пирамида, в основании которой лежит квадрат (ABCD), а две боковые грани (SAB) и (SAD) представляют собой прямоугольные треугольники с прямым углом (angle A).

1) Проведите плоскость (alpha) через точку пересечения диагоналей основания параллельно грани (SBC).

2) Найдите площадь сечения пирамиды плоскостью (alpha), если (SA=AB=a).

1) Пусть (ACcap BD=O). Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Заметим, что т.к. (angle SAB=angle SAD=90^circ Rightarrow
SAperp
(ABC)).

Проведем в плоскости (SAC) прямую (OKparallel SC). Т.к. (O) – середина (AC), то по теореме Фалеса (K) – середина (SA). Через точку (K) в плоскости (SAB) проведем (KMparallel SB) (следовательно, (M) – середина (AB)). Таким образом, плоскость, проходящая через прямые (OK) и (KM), и будет искомой плоскостью.

Необходимо найти сечение пирамиды этой плоскостью. Соединив точки (O) и (M), получим прямую (MN).

Т.к. (alphaparallel (SBC)),то (alpha) пересечет плоскость (SCD) по прямой (NPparallel SC) (если (NPcap SC ne varnothing), то (alphacap (SBC)ne varnothing), что невозможно ввиду их параллельности).

Таким образом, (KMNP) – искомое сечение, причем (KPparallel
ADparallel MN Rightarrow) это трапеция.

2) Т.к. все точки (K,M,N,P) – середины отрезков (SA, AB, CD, SD) соответственно, то:

а) (MN=AD=a)

б) (KP=dfrac{1}{2}AD=dfrac{a}{2})

в) (KM=dfrac{1}{2}SB=dfrac{asqrt2}{2})

Заметим, что по теореме о трех перпендикулярах (SBperp BC
Rightarrow KMperp MN). Таким образом, (KMNP) – прямоугольная трапеция.

(S_{KMNP}=dfrac{KP+MN}{2}cdot KM=dfrac{3sqrt2}{8}a^2)

Ответ:

1) Рисунок.

2) (dfrac{3sqrt2}{8}a^2)

Задание
4

#1003

Уровень задания: Равен ЕГЭ

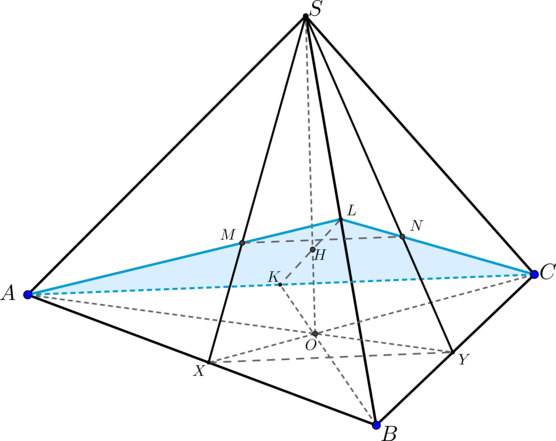
Дана правильная треугольная пирамида (SABC) с вершиной (S). Проведите плоскость через середину ребра (AC) и точки пересечения медиан граней (ASB) и (CSB). Найдите площадь сечения пирамиды этой плоскостью, если (AB=21, AS=12sqrt2).

1) Пусть(K) – середина (AC), (SX, AL) – медианы грани (ASB), (CL,
SY) – медианы грани (CSB), (ALcap SX=M, CLcap SY=N). (SO) – высота пирамиды.

Найдем сечение пирамиды плоскостью (MNK).
Т.к. пирамида правильная, то (triangle SXY) – равнобедренный, (SM=SN=dfrac{2}{3}SX Rightarrow MNparallel XY Rightarrow
MNparallel (ABC)). Таким образом, плоскость (MNK) содержит прямую (MN), параллельную (ABC), следовательно, плоскость (MNK) пересечет плоскость (ABC) по прямой, параллельной (MN) (если это не так, то линия пересечения этих плоскостей (lcap MN=E Rightarrow Ein
(ABC)) и (Ein MN Rightarrow MN) не может быть параллельна ((ABC))).

Прямая, проходящая через точку (K) и параллельная (MN) (или (XY)) – это (AC). Следовательно, сечением является равнобедренный треугольник (ALC).

2) Пусть (LKcap SO=H). Тогда по теореме о трех перпендикулярах (HKperp AC) как наклонная ((HOperp (ABC), OKperp AC) как проекция). Следовательно, и (LKperp AC).

Тогда (S_{ALC}=dfrac{1}{2}ACcdot LK).

Рассмотрим (triangle SKB: BK=ABcdot
dfrac{sqrt3}{2}=dfrac{21sqrt3}{2} Rightarrow cos
B=dfrac{7sqrt3}{12sqrt2}).

Тогда по теореме косинусов для (triangle KLB):

(KL^2=dfrac{729}{4} Rightarrow KL=dfrac{27}{2})

Значит, (S_{ALC}=dfrac{567}{4}).

Ответ:

(dfrac{567}{4}).

Задание
5

#3792

Уровень задания: Сложнее ЕГЭ

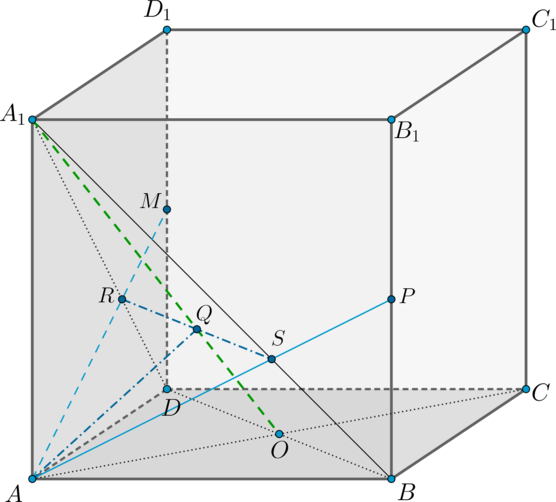
Дан куб (ABCDA_1B_1C_1D_1). Диагонали основания (AC) и (BD) пересекаются в точке (O). Найдите сечение куба плоскостью (alpha), проходящей через точку (A) перпендикулярно прямой (A_1O).

1) Если (A_1Operp alpha), то (A_1O) перпендикулярно двум пересекающимся прямым, лежащим в плоскости (alpha). Построим эти две прямые.

Рассмотрим плоскость (AA_1C_1C) ((A_1O) лежит в этой плоскости). Проведем в ней (AQperp A_1O). Теперь необходимо через их точку пересечения (точку (Q)) провести еще одну прямую перпендикулярно (A_1O).

Рассмотрим для этого плоскость (A_1BD) ((A_1O) лежит в этой плоскости). Проведем через точку (Q) прямую (RSperp A_1O). Т.к. по теореме о трех перпендикулярах (A_1Operp BD) как наклонная ((A_1Aperp (ABC), AOperp BD) – проекция), то (RSparallel BD).

2) Проведем прямые (AR) и (AS). Они могут пересечь либо сами ребра (DD_1) и (BB_1), либо их продолжения. Т.к. от этого зависит вид сечения, определим расположение точек (R) и (S).

Обозначим ребро куба за (a). Тогда (AO=dfrac{asqrt2}{2}=dfrac
a{sqrt2}). Рассмотрим прямоугольный (triangle AA_1O). Так как (AQperp A_1O), то по свойству прямоугольного треугольника (triangle AA_1Qsim triangle AA_1O). Следовательно, [dfrac{A_1Q}{AA_1}=dfrac{AA_1}{A_1O}] Так как по теореме Пифагора (A_1O=sqrt{a^2+frac{a^2}2}=dfrac{sqrt6 a}2), то [A_1Q=dfrac{AA_1^2}{A_1O}=dfrac{sqrt6}3a]

Так как (RSparallel BD), то (triangle A_1DOsim triangle A_1RQ), следовательно, [dfrac{A_1R}{A_1D}=dfrac{A_1Q}{A_1O}=dfrac{sqrt6}3:dfrac{sqrt6}2=
dfrac23] Аналогично (A_1S:A_1B=2:3).

Заметим, что (triangle AA_1Rsim triangle MDR) с коэффициентом подобия (2) ((A_1R:RD=2:1)), следовательно, (MD=frac12AA_1).
Аналогично (PB=frac12AA_1).

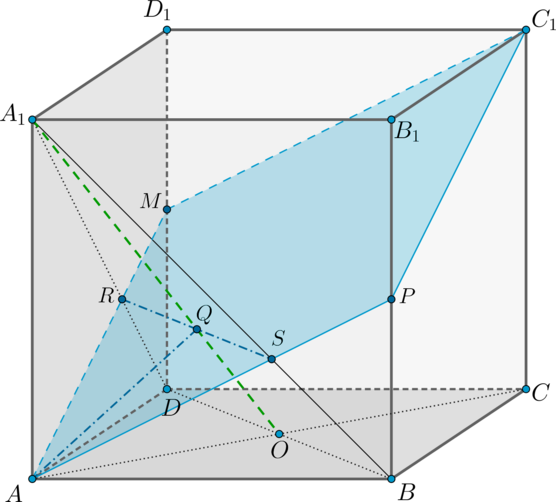
Таким образом, получили линии пересечения плоскостей (AA_1D_1) и (AA_1B_1) с плоскостью (alpha) – прямые (AM) и (AP).

3) Так как плоскости (AA_1B_1) и (DD_1C_1) параллельны, то плоскость (alpha) пересечет их по параллельным прямым. Следовательно, в плоскости (DD_1C_1) через точку (M) нужно провести прямую, параллельную (AP).
Так как (M) и (P) – середины (DD_1) и (BB_1), то (MC_1parallel
AP).

Таким образом, сечение куба плоскостью (alpha) – это четырехугольник (AMC_1P) (который, вообще говоря, является ромбом, так как (AM=AP=MC_1) и (MC_1parallel AP)).

Ответ:

Рисунок.

Задание
6

#2451

Уровень задания: Сложнее ЕГЭ

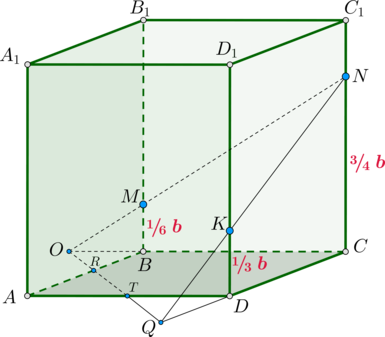
Дан прямоугольный параллелепипед (ABCDA_1B_1C_1D_1), в основании которого лежит квадрат (ABCD). На ребрах (BB_1), (CC_1), (DD_1) отмечены точки (M, N, K) соответственно так, что (BM:MB_1=1:5), (CN:NC_1=3:1), (DK:KD_1=1:2).
Найдите отношение отрезков, на которые делит плоскость (MNK) диагональ (AC).

Обозначим ребро основания за (a), а боковое ребро за (b). Тогда из условия задачи следует, что (BM=frac16b), (CN=frac34b), (DK=frac13b).

Найдем положение точек (R) и (T), в которых плоскость пересекает ребра (AB) и (AD) соответственно.

1) Продлим отрезки (NK) и (CD) до пересечения в точке (Q). Тогда (triangle QDKsim triangle QNC). Следовательно,

[dfrac{QD}{QC}=dfrac{KD}{NC} quad Rightarrow quad
dfrac{QD}{QD+a}=dfrac{frac13b}{frac34b}=dfrac49 quad
Rightarrow quad QD=dfrac45a.]

Аналогично из (triangle OMBsim triangle ONC) получаем, что [OB=dfrac27a.]

Соединив точки (Q) и (O), получим точки пересечения плоскости с ребрами (AB) и (AD).

2) Рассмотрим основание.

(triangle OBRsim triangle OCQ), следовательно,

[dfrac{OB}{OC}=dfrac{BR}{CQ} quad Rightarrow quad
dfrac{frac27a}{frac97a}=dfrac{BR}{frac95a} quad Rightarrow
quad BR=dfrac25a.]

(triangle OBRsim triangle TAR), следовательно,

[dfrac{OB}{AT}=dfrac{BR}{AR}quad Rightarrow quad
dfrac{frac27a}{AT}=dfrac{frac25a}{frac35a} quad Rightarrow
quad AT=dfrac37a.]

3) Для того, чтобы найти, в каком отношении (RT) поделит (AC), проведем прямую (RGparallel AD), (Gin AC).

Тогда (triangle ARG) – прямоугольный и (angle RAG=45^circ), то есть он равнобедренный и (RG=frac35a). Тогда по теореме Фалеса (AG:AC=AR:AB=3:5), следовательно, т.к. (AC=asqrt2), то (AG=frac{3sqrt2}5a).

(triangle ASTsim triangle RSG), следовательно,

[dfrac{AT}{RG}=dfrac{AS}{SG} quad Rightarrow quad
dfrac{frac37a}{frac35a}=dfrac{AS}{frac{3sqrt2}5a-AS} quad
Rightarrow quad AS=dfrac{sqrt2}4a.]

Тогда (SC=asqrt2-frac{sqrt2}4a=frac{3sqrt2}4a) и (AS:SC=1:3).

Ответ:

(1:3)

Теме «Построение сечения» в ЕГЭ по математике профильного уровня посвящается, как правило, несколько заданий. Они могут требовать от школьника как краткого ответа, так и полного развернутого решения. Если одним из ваших слабых мест являются именно задачи на сечения (в ЕГЭ при этом вы хотите получить конкурентные баллы), непременно стоит повторить или вновь разобраться в материале.

Сделать это наиболее эффективно вам поможет образовательный математический проект «Школково». Наши специалисты подготовили теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко справиться с решением задач на сечение.

Полезная информация

Для того чтобы выполнить построение сечений в ЕГЭ, нужно отметить точки пересечения пространственной фигуры с ребрами и произвести их соединение, начертив отрезки.

Необходимо запомнить

Производится соединение только двух точек, которые лежат в плоскости одной грани. Прежде чем приступить к решению задачи на построение сечений, полезно повторить материал о параллельных прямых. Сделать это вы можете, посетив раздел «Теоретическая справка».

Также необходимо запомнить, что пересечение секущей плоскости параллельных граней возможно только по параллельным отрезкам.

В том случае, когда в плоскости грани обозначена только одна точка, которая принадлежит плоскости сечения, следует отметить еще одну дополнительную. Для того чтобы это сделать, нужно определить точки пересечения прямых, которые уже построены, с теми, которые лежат в тех же гранях.

Выполнив построение сечений многогранников в задачах, которые представлены в нашем «Каталоге», вы сможете закрепить изученный материал и успешно справиться с подобным заданием на ЕГЭ в Москве.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Скачать материал

Курс добавлен 16.12.2022
Сейчас обучается 20 человек из 14 регионов

Сейчас обучается 342 человека из 70 регионов

Сейчас обучается 25 человек из 13 регионов

Описание презентации по отдельным слайдам:

1 слайд

Сечения.
Стереометрия
в задачах ЕГЭ
Сечение многогранников и круглых тел
М.Г.КИМ, учитель маоу сош № 77
г. Хабаровск-2017
2 слайд

Подготовительные задачи
3 слайд

В прямоугольном параллепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 ребро 𝐴𝐵=2, ребро 𝐴𝐷= 5 , ребро 𝐴 𝐴 1 =2. Точка 𝐾 — середина ребра 𝐵 𝐵 1 . Найдите площадь сечения, проходящего через точки 𝐴 1 , 𝐷 1 и 𝐾.
Решение.
Сечение пересекает параллельные грани по параллельным отрезкам. Поэтому четырехугольник 𝐴 1 𝐾 𝐾 1 𝐷 1 — параллелограмм. Кроме того, ребро 𝐴 1 𝐷 1 перпендикулярно граням 𝐷 𝐷 1 𝐶 1 𝐶 и 𝐴 𝐴 1 𝐵 1 𝐵, поэтому углы 𝐴 1 𝐷 1 𝐾 1 и 𝐷 1 𝐴 1 𝐾 — прямые. Следовательно, сечение 𝐴 1 𝐾 𝐾 1 𝐷 1 — прямоугольник.
Из прямоугольного треугольника 𝐴 1 𝐵 1 𝐾 по теореме Пифагора найдем 𝐴 1 𝐾:
𝐴 1 𝐾= 𝐴 1 𝐵 1 2 + 𝐵 1 𝐾 2 = 4+1 = 5
Тогда площадь прямоугольника 𝐴 1 𝐾 𝐾 1 𝐷 1 равна:
𝐴 1 𝐷 1 ∙ 𝐴 1 𝐾= 5 ∙ 5 =5.
Ответ. 5
4 слайд

В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 ребро 𝐶𝐷=2, ребро
𝐵𝐶=2 2 , ребро 𝐶 𝐶 1 =4. Точка 𝐾 — середина ребра 𝐷 𝐷 1 . Найдите площадь сечения, проходящего через точки 𝐶 1 , 𝐵 1 и 𝐾.
Ответ. 8
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 ребро 𝐴𝐷=6, ребро
𝐶𝐷= 37 , ребро 𝐷 𝐷 1 =2. Точка 𝐾 — середина ребра 𝐴 𝐴 1 . Найдите площадь сечения, проходящего через точки 𝐷 1 , 𝐶 1 и 𝐾.
Ответ. 37
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 ребро 𝐶𝐷=4, ребро
𝐵𝐶= 17 , ребро 𝐶 𝐶 1 =2. Точка 𝐾 — середина ребра 𝐷 𝐷 1 . Найдите площадь сечения, проходящего через точки 𝐶 1 , 𝐵 1 и 𝐾.
Ответ. 17
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 ребро 𝐴𝐷=2, ребро
𝐶𝐷=2 2 , ребро 𝐷 𝐷 1 =4. Точка 𝐾 — середина ребра 𝐴 𝐴 1 . Найдите площадь сечения, проходящего через точки 𝐷 1 , 𝐶 1 и 𝐾.
Ответ. 8
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 ребро 𝐴𝐷=2, ребро
𝐶𝐷= 5 , ребро 𝐷 𝐷 1 =2. Точка 𝐾 — середина ребра 𝐴 𝐴 1 . Найдите площадь сечения, проходящего через точки 𝐷 1 , 𝐶 1 и 𝐾.
Ответ. 5
5 слайд

В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 известны длины рёбер: 𝐴𝐵=24, 𝐴𝐷=10, 𝐴 𝐴 1 =22. Найдите площадь сечения, проходящего через вершины 𝐴, 𝐴 1 и 𝐶.
Решение.
Сечение пересекает параллельные грани по параллельным отрезкам. Поэтому сечение 𝐴 𝐴 1 𝐶 1 𝐶 − параллелограмм. Кроме того, ребро 𝐴 1 𝐴 перпендикулярно граням 𝐴𝐵𝐶𝐷 и 𝐴 1 𝐵 1 𝐶 1 𝐷 1 . Поэтому углы 𝐴 𝐴 1 𝐶 1 и 𝐴 1 𝐴𝐶 − прямые. Поэтому сечение 𝐴 𝐴 1 𝐶 1 𝐶 — прямоугольник.
Из прямоугольного треугольника 𝐴𝐵𝐶 найдем 𝐴𝐶
𝐴𝐶= 𝐴𝐵 2 + 𝐵𝐶 2 = 24 2 + 10 2 = 676 =26
Тогда площадь прямоугольника 𝐴 𝐴 1 𝐶 1 𝐶 равна:
𝐴 𝐴 1 ∙𝐴𝐶=22∙26=572
Ответ. 572
6 слайд

В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 известны длины рёбер: 𝐴𝐵=44, 𝐴𝐷=33, 𝐴 𝐴 1 =6. Найдите площадь сечения, проходящего через вершины 𝐷, 𝐷 1 и 𝐵.
Ответ. 330
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 известны длины рёбер: 𝐴𝐵=21, 𝐴𝐷=28, 𝐴 𝐴 1 =25. Найдите площадь сечения, проходящего через вершины 𝐷, 𝐷 1 и 𝐵.
Ответ. 875
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 известны длины рёбер: 𝐴𝐵=12, 𝐴𝐷=16, 𝐴 𝐴 1 =3. Найдите площадь сечения, проходящего через вершины 𝐵, 𝐵 1 и 𝐷.
Ответ. 60
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 известны длины рёбер: 𝐴𝐵=40, 𝐴𝐷=30, 𝐴 𝐴 1 =48. Найдите площадь сечения, проходящего через вершины 𝐴, 𝐴 1 и 𝐶.
Ответ. 2400
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 известны длины рёбер: 𝐴𝐵=36, 𝐴𝐷=15, 𝐴 𝐴 1 =48. Найдите площадь сечения, проходящего через вершины 𝐶, 𝐶 1 и 𝐴.
Ответ. 1872
8 слайд

Точка 𝐸 — середина ребра 𝐶 𝐶 1 куба 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 . Найдите площадь сечения куба плоскостью 𝐴 1 𝐵𝐸, если ребра куба равны 2.
Решение.
Прямая 𝐵𝐸 пересекает прямую 𝐵 1 𝐶 1 в точке 𝐾. Прямая 𝐴 1 𝐾 пересекает ребро 𝐶 1 𝐷 1 в его середине — точке 𝐹. 𝐴 1 𝐵𝐸𝐹 — сечение куба плоскостью 𝐴 1 𝐵𝐸.
Равнобедренный треугольник 𝐴 1 𝐵𝐾 подобен треугольнику 𝐾𝐹𝐸 𝐴 1 𝐾=𝐵𝐾=2𝐵𝐸=2 5 ,
𝐴 1 𝐵= 2 ∙𝐴𝐵=2 2 и высота 𝐾𝐻= 𝐵 𝐾 2 − 𝐴 1 𝐵 2 2 =3 2 .
Поскольку 𝐸𝐹 — средняя линия треугольника 𝐴 1 𝐵𝐾, получаем:
𝑆 𝐾𝐸𝐹 = 1 4 𝑆 𝐴 1 𝐵𝐾
𝑆 𝐴 1 𝐵𝐸𝐹 = 𝑆 𝐴 1 𝐵𝐾 − 𝑆 𝐾𝐸𝐹 = 3 4 𝑆 𝐴 1 𝐵𝐾 = 3 4 ∙ 1 2 ∙𝐾𝐻∙ 𝐴 1 𝐵=4,5
Ответ. 4,5
9 слайд

Точка 𝐸 — середина ребра 𝐵 𝐵 1 куба 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 . Найдите площадь сечения куба плоскостью 𝐷 1 𝐴𝐸, если ребра куба равны 4.
Решение.
Прямая 𝐴𝐸 пересекает прямую 𝐴 1 𝐵 1 в точке 𝐾. Прямая 𝐷 1 𝐾 пересекает ребро 𝐵 1 𝐶 1 в его середине — точке 𝐹. 𝐴𝐸𝐹 𝐷 1 — сечение куба плоскостью 𝐷 1 𝐴𝐸.
В равнобедренном треугольнике 𝐴𝐾 𝐷 1 имеем
𝐷 1 𝐾=𝐴𝐾=2𝐴𝐸=4 5 𝐴 𝐷 1 = 2 ∙𝐴𝐷=4 2 и высота
𝐾𝐻= 𝐴 𝐾 2 − 𝐴 𝐷 1 2 2 =6 2 .
Поскольку 𝐸𝐹 — средняя линия треугольника 𝐴𝐾 𝐷 1 , получаем:
𝑆 𝐾𝐸𝐹 = 1 4 𝑆 𝐴𝐾 𝐷 1
𝑆 𝐴𝐸𝐹 𝐷 1 = 𝑆 𝐴𝐾 𝐷 1 − 𝑆 𝐾𝐸𝐹 = 3 4 𝑆 𝐴𝐾 𝐷 1 = 3 4 ∙ 1 2 ∙𝐾𝐻∙𝐴 𝐷 1 =18.
Ответ. 18
10 слайд

В правильной четырёхугольной пирамиде SABCD с основанием ABCD проведено сечение через середины ребер АВ и ВС и вершину S. Найдите площадь этого сечения, если все ребра пирамиды равны 8.
Решение.
Пусть M — середина AB, а N — середина BC. Тогда площадь сечения равна площади треугольника SMN. Найдем последовательно SM, MN и SN.
SM и SN — медианы треугольников SAB и SBC соответственно. Т. к. эти треугольники равносторонние (поскольку все ребра пирамиды одинаковой длины),
𝑆𝑀=𝑆𝑁= 3 2 ∙8=4 3 .
Найдем теперь MN из прямоугольного треугольника MBN.
В нем катеты равны 4. Гипотенуза MN, по теореме Пифагора, будет равна 4 2 .
Теперь найдем площадь равнобедренного треугольника SMN. Для этого проведем высоту SH, по теореме Пифагора равную 2 10 , и вычислим площадь:
𝑆= 1 2 ∙𝑆𝐻∙𝑀𝑁= 1 2 ∙2 10 ∙4 2 =8 5 .
Ответ. 8 5
11 слайд

В правильной четырёхугольной пирамиде 𝑆𝐴𝐵𝐶𝐷
с основанием 𝐴𝐵𝐶𝐷 проведено сечение через середины рёбер 𝐴𝐵 и 𝐵𝐶 и вершину 𝑆. Найдите площадь этого сечения, если боковое ребро пирамиды равно 5, а сторона основания равна 4.
Решение.
Пусть 𝑀 — середина 𝐴𝐵, а 𝑁 — середина 𝐵𝐶 Тогда площадь сечения равна площади треугольника 𝑆𝑀𝑁 Найдем последовательно 𝑆𝑀, 𝑆𝑁 и 𝑀𝑁. 𝑆𝑀 и 𝑆𝑁 — медианы треугольников 𝑆𝐴𝐵 и 𝑆𝐵𝐶 соответственно. Так как эти треугольники равнобедренные (поскольку пирамида правильная),
𝑆𝑀=𝑆𝑁= 𝑆 𝐵 2 − 1 2 𝐴𝐵 2 = 𝑆 𝐵 2 − 1 2 𝐵𝐶 2 = 5 2 − 2 2 = 21
Найдем теперь 𝑀𝑁 из прямоугольного треугольника 𝑀𝐵𝑁. В нем катеты равны 2. Гипотенуза 𝑀𝑁 по теореме Пифагора, будет равна 2 2.
Теперь найдем площадь равнобедренного треугольника 𝑆𝑀𝑁. Для этого проведем высоту 𝑆𝐻, которая, по теореме Пифагора, равна 19 и вычислим площадь:
𝑆= 1 2 ∙𝑆𝐻∙𝑀𝑁= 1 2 ∙ 19 ∙2 2 = 38 .
Ответ. 38
12 слайд

В правильной треугольной пирамиде 𝑆𝐴𝐵𝐶 с основанием 𝐴𝐵𝐶 сторона основания равна 8, а угол 𝐴𝑆𝐵 равен 36°. На ребре 𝑆𝐶 взята точка 𝑀 так, что 𝐴𝑀 — биссектриса угла 𝑆𝐴𝐶 Найдите площадь сечения пирамиды, проходящего через точки 𝐴, 𝑀 и 𝐵.
Решение.

Нужное сечение — треугольник 𝐴𝑀𝐵.
Рассмотрим треугольник 𝐴𝑆𝐶 .Он равнобедренный.
∠𝐴𝑆𝐶=∠𝐴𝑆𝐵=36°, поэтому ∠𝑆𝐴𝐶=∠𝑆𝐶𝐴=72°.
Значит, ∠𝑀𝐴𝐶=36°.
Рассмотрим теперь треугольник 𝐶𝐴𝑀. Сумма его углов 180°, значит, ∠𝐴𝑀𝐶=72°.
Следовательно, треугольник 𝐶𝐴𝑀 равнобедренный, и поэтому 𝐴𝑀=𝐴𝐶=8. Аналогично находим, что 𝐵𝑀=8.
Таким образом, треугольник 𝐴𝑀𝐵 равносторонний со стороной 8. Его площадь равна 8 2 3 4 =16 3 .
Ответ. 16 3
13 слайд

В правильной треугольной призме 𝐴𝐵𝐶 𝐴 1 𝐵 1 𝐶 1 стороны основания равны 6, боковые рёбра равны 4. Изобразите сечение, проходящее через вершины 𝐴,𝐵 и середину ребра 𝐴 1 𝐶 1 . Найдите его площадь.
Решение.

Обозначим через 𝑀 и 𝑁 средины ребер 𝐴 1 𝐶 1 и 𝐵 1 𝐶 1 соответственно.
По теореме о средней линии треугольника 𝑀𝑁∥ 𝐴 1 𝐵 1 ∥𝐴𝐵, так что прямые 𝑀𝑁 и 𝐴𝐵лежат в одной плоскости. Сечение про которое спрашивается в условии, − это сечение призмы этой плоскостью. Оно представляет собой равнобокую трапецию 𝐴𝑀𝑁𝐵.
Основания трапеции 𝐴𝐵=6, 𝑀𝑁=3, по теореме Пифагора найдем боковую сторону: 𝐴𝑀= 𝐴 𝐴 1 2 + 𝐴 1 𝑀 2 = 16+9 =5.
Проведем в трапеции высоту 𝑀𝐻. Отрезок 𝐴𝐻 равен полуразности оснований трапеции: 𝐴𝐻= 𝐴𝐵−𝑀𝑁 2 =3/2
Следовательно, высота трапеции 𝑀𝐻= 5 2 − 3 2 2 = 91 2 . Зная её, находим площадь трапеции: 𝑆 𝐴𝑀𝑁𝐵 = 𝑀𝑁+𝐴𝐵 2 ∙𝑀𝐻= 9 2 ∙ 91 2 = 9 4 91
Ответ. 9 4 91
14 слайд

В правильной треугольной призме ABCA’B’C’ стороны основания равны 6, а боковые ребра равны 4. Изобразите сечение, проходящее через вершины A, B и середину ребра A’C’. Найдите его площадь.
Решение.

Параллельные грани оснований сечение пересекает по параллельным прямым, поэтому сечение — трапеция. Пусть точка М — середина A’C’, точка N — середина B’С’. Боковые стороны трапеции ABNM являются гипотенузами равных прямоугольных треугольников AA’M и BB’N, катеты которых равны 3 и 4. Тем самым, трапеция является равнобедренной, а ее боковые стороны равны 5.
Отрезок MN — средняя линия треугольника A’B’C’, поэтому
MN = 0,5 A’C’ = 3. Пусть MН — высота трапеции, тогда
𝑀Н= 𝐴 𝑀 2 −𝐴 Н 2 = 5 2 − 3 2 2 = 91 2 .
Следовательно,
𝑆 трап = 𝐴𝐵+𝑀𝑁 2 ∙𝑀Н= 9 2 ∙ 91 2 = 9 91 4 .
Ответ. 9 91 4
15 слайд

В правильной четырехугольной пирамиде 𝑀𝐴𝐵𝐶𝐷 с вершиной 𝑀 стороны основания равны 15, а боковые ребра равны 16. Найдите площадь сечения пирамиды плоскостью, проходящей через точку 𝐵 и середину ребра 𝑀𝐷 параллельно прямой 𝐴𝐶.
Решение.

𝑀𝐹:𝐹𝐴=𝑀𝐺:𝐺𝐶=𝑀𝑃:𝑃𝑂=2:1,
𝐹𝐺= 2 3 𝐴𝐶= 2 2 ∙𝐴𝐵 3 =10 2 .
Четырёхугольник BFEG — искомое сечение. Отрезок BE — медиана треугольника MBD, значит,
𝐵𝐸= 2𝐵 𝐷 2 +2𝑀 𝐵 2 −𝑀 𝐷 2 2 = 4𝐴 𝐵 2 +𝑀 𝐵 2 2 =17.
Поскольку прямая BD перпендикулярна плоскости MAC, диагонали BE и FG четырёхугольника BFEG перпендикулярны, следовательно, 𝑆 𝐵𝐶𝐹𝐸𝐺 = 𝐵𝐸∙𝐹𝐺 2 =85 2 .
Ответ. 85 2
16 слайд

В правильной четырёхугольной призме 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 сторона основания равна 20, а боковое ребро 𝐴 𝐴 1 =7.Точка 𝑀 принадлежит ребру 𝐴 1 𝐷 1 и делит его в отношении 2:3 считая от вершины 𝐷 1 . Найдите площадь сечения этой призмы плоскостью, проходящей через точки 𝐵, 𝐷 и 𝑀.
Решение.
Отрезок 𝑀𝑁 параллелен диагонали 𝐵𝐷 (точка 𝑁 принадлежит ребру 𝐴 1 𝐵 1 ), следовательно, искомое сечение — трапеция 𝐵𝐷𝑀𝑁 (рис. 1). Плоскость сечения пересекает нижнее основание по прямой 𝐵𝐷 параллельной 𝐵 1 𝐷 1 значит, 𝑀𝑁 параллелен 𝐵 1 𝐷 1 .
Треугольники 𝑁 𝐴 1 𝑀 и 𝐵 1 𝐴 1 𝐷 1 подобны, следовательно,
𝐴 1 𝑁: 𝐴 1 𝐵 1 = 𝐴 1 𝑀: 𝐴 1 𝐷 1 =𝑀𝑁: 𝐵 1 𝐷 1 =3:5.
Значит, 𝐵𝐷= 𝐵 1 𝐷 1 =20 2 , 𝑀𝑁=12 2 .
В равных прямоугольных треугольниках 𝐵 𝐵 1 𝑁 и 𝐷 𝐷 1 𝑀
𝐷𝑀=𝐵𝑁= 𝐵 𝐵 1 2 + 𝐵 1 𝑁 2 = 113 , значит, трапеция 𝐵𝐷𝑀𝑁 равнобедренная.
Пусть 𝑁𝐻 — высота трапеции 𝐵𝐷𝑀𝑁, проведённая к основанию 𝐵𝐷 (рис. 2), тогда:
𝐵𝐻= 𝐵𝐷−𝑀𝑁 2 =4 2 ⇔𝑁𝐻= 𝐵 𝑁 2 −𝐵 𝐻 2 =9⇔
𝑆 𝐵𝐷𝑀𝑁 = 𝐵𝐷+𝑀𝑁 2 ∙𝑁𝐻=144 2 .

Ответ. 144 2
17 слайд

В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 известны рёбра 𝐴𝐵=8, 𝐴𝐷=7,𝐴 𝐴 1 =5. Точка 𝑊 принадлежит ребру 𝐷 𝐷 1 и делит его в отношении 1:4, считая от вершины 𝐷. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки 𝐶,𝑊 и 𝐴 1 .
Решение.
Отрезок 𝐶𝑇 параллелен 𝐴 1 𝑊 (точка 𝑇 принадлежит ребру 𝐵 𝐵 1 ). Плоскость сечения пересекает плоскость 𝐴 𝐴 1 𝐵 1 по прямой 𝐴 1 𝑇 параллельной 𝐶𝑊, следовательно, искомое сечение — параллелограмм 𝐶𝑇 𝐴 1 𝑊 (рис. 1).
Треугольники 𝐶𝐵𝑇 и 𝐴 1 𝐷 1 𝑊 равны, следовательно,
𝐵𝑇= 𝐷 1 𝑊= 4 5 𝐷 𝐷 1 =4;𝐷𝑊=𝐷 𝐷 1 − 𝐷 1 𝑊=1.
𝐶𝑇= 𝐵 𝐶 2 +𝐵 𝑇 2 = 65 ; 𝐶𝑊= 𝐶 𝐷 2 +𝐷 𝑊 2 = 65 ,
значит, 𝐶𝑇 𝐴 1 𝑊 — ромб со стороной 65 и диагональю
𝐶 𝐴 1 = 𝐶 𝐵 2 +𝐵 𝐴 2 +𝐴 𝐴 1 2 = 138 (рис. 2).
Тогда диагональ
𝑊𝑇=2 𝐶 𝑇 2 − 𝐶 𝐴 1 2 2 = 122 ; 𝑆 𝐶𝑇 𝐴 1 𝑊 = 𝐶 𝐴 1 ∙𝑊𝑇 2 = 4209 .

Ответ. 4209
18 слайд

В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 известны рёбра: 𝐴𝐵=3, 𝐴𝐷=2, 𝐴 𝐴 1 =5. Точка 𝑂 принадлежит ребру 𝐵 𝐵 1 и делит его в отношении 2:3 считая от вершины 𝐵. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки 𝐴,𝑂 и 𝐶 1 .
Решение.
Сечение плоскостью 𝐴𝑂 𝐶 1 пересекает ребро 𝐷 𝐷 1 в точке 𝑃.
Отрезок 𝐴𝑃 параллелен 𝐶 1 𝑂, отрезок 𝐶 1 𝑃 параллелен 𝐴𝑂.
Следовательно, искомое сечение — параллелограмм 𝐴𝑂 𝐶 1 𝑃 (рис.1). Далее имеем:
𝐵𝑂= 2 5 𝐵 𝐵 1 =2, 𝐵 1 𝑂=3, 𝐶 1 𝑂= 𝐶 1 𝐵 1 2 + 𝐵 1 𝑂 2 = 4+9 = 13 ,
𝐴𝑂= 𝐴 𝐵 2 +𝐵 𝑂 2 = 9+4 = 13 .
Значит, 𝐴𝑂 𝐶 1 𝑃 — ромб. Найдем его диагонали:
𝐴 𝐶 1 = 𝐴 𝐵 2 +𝐵 𝐶 2 +𝐶 𝐶 1 2 = 9+4+25 = 38 ;
𝑂𝑃=2 𝐴 𝑂 2 − 1 4 𝐴 𝐶 1 2 = 4∙13−38 = 14 .
Площадь ромба равна половине произведения его диагоналей. Поэтому
𝑆 𝐴𝑂 𝐶 1 𝑃 = 𝐴 𝐶 1 ∙𝑂𝑃 2 = 1 2 38 ∙ 14 = 133 .
Ответ. 133
19 слайд

В правильной четырёхугольной пирамиде 𝑀𝐴𝐵𝐶𝐷 с вершиной 𝑀 стороны основания равны 3, а боковые рёбра равны 8. Найдите площадь сечения пирамиды плоскостью, проходящей через точку 𝐵 и середину ребра 𝑀𝐷 параллельно прямой 𝐴𝐶.
Решение.
Пусть точка 𝐸 — середина ребра 𝑀𝐷. Отрезок 𝐵𝐸 пересекает плоскость 𝑀𝐴𝐶 в точке 𝑃. В треугольнике 𝑀𝐵𝐷 точка 𝑃 является точкой пересечения медиан, следовательно, 𝑀𝑃:𝑃𝑂=2:1, где 𝑂 — центр основания пирамиды. Отрезок 𝐹𝐺 параллелен 𝐴𝐶 и проходит через точку 𝑃 (точка 𝐹 принадлежит ребру 𝑀𝐴, 𝐺 — ребру 𝑀𝐶), откуда
𝑀𝐹:𝐹𝐴=𝑀𝐺:𝐺𝐶=𝑀𝑃:𝑃𝑂=2:1, 𝐹𝐺= 2 3 𝐴𝐶=2 2 .
Четырёхугольник 𝐵𝐸𝐹𝐺 — искомое сечение. Отрезок 𝐵𝐸 — медиана треугольника 𝑀𝐵𝐷 значит,
𝐵𝐸= 2𝐵 𝐷 2 +2𝑀 𝐵 2 −𝑀 𝐷 2 2 = 4𝐴 𝐵 2 +𝑀 𝐵 2 2 =5.
Поскольку прямая 𝐵𝐷 перпендикулярна плоскости 𝑀𝐴𝐶, диагонали 𝐵𝐸 и 𝐹𝐺 четырёхугольника 𝐵𝐹𝐸𝐺 перпендикулярны, следовательно, 𝑆 𝐵𝐹𝐸𝐺 = 𝐵𝐸∙𝐹𝐺 2 =5 2 .
Ответ. 5 2
20 слайд

Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 8. Плоскость β, параллельная плоскости α, касается меньшего шара, а площадь сечения этой плоскостью большего шара равна 5. Найдите площадь сечения большего шара плоскостью α.
Решение.
Сечение шара плоскостью — круг. Рассмотрим сечение, проходящее через общий центр шаров и центры кругов. Обозначение центра, точки касания и точек пересечения поверхностей шаров с плоскостями α и β дано на рисунке.
FD — радиус круга, полученного в сечении меньшего шара
плоскостью α, тогда 𝑆 𝛼 =𝜋∙𝐹 𝐷 2 =8 — площадь сечения меньшего шара
плоскостью α.
AB — радиус круга, полученного в сечении большего шара
плоскостью β, тогда 𝑆 𝛽 =𝜋∙𝐴 𝐵 2 =5 — площадь сечения большего шара
плоскостью β.
CF — радиус круга, полученного в сечении большего шара плоскостью α.
Параллельные прямые AB и CF перпендикулярны прямой AF.
Из прямоугольных треугольников получаем:
𝑂 𝐹 2 =𝑂 𝐶 2 −𝐶 𝐹 2 =𝑂 𝐷 2 −𝐹 𝐷 2 ,
откуда 𝐶 𝐹 2 =𝑂 𝐶 2 −𝑂 𝐷 2 +𝐹 𝐷 2 =𝑂 𝐵 2 −𝑂 𝐴 2 +𝐹 𝐷 2 =𝐴 𝐵 2 +𝐹 𝐷 2 .
Площадь сечения большего шара плоскостью α:
𝑆=𝜋∙𝐶 𝐹 2 =𝜋∙𝐴 𝐵 2 +𝜋∙𝐹 𝐷 2 =13.
Ответ. 13
21 слайд

Плоскость 𝛼 пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 6. Плоскость 𝛽, параллельная плоскости 𝛼, касается меньшего шара, а площадь сечения этой плоскостью большего шара равна 4. Найдите площадь сечения большего шара плоскостью 𝛼.
Решение.
Сечение шара плоскостью — круг. Рассмотрим сечение, проходящее через общий центр шаров и центры кругов.
Обозначение центра, точки касания и точек пересечения поверхностей шаров с плоскостями 𝛼 и 𝛽 дано на рисунке.
𝐹𝐷 — радиус круга, полученного в сечении меньшего шара
плоскостью 𝛼 тогда 𝑆 𝛼 =𝜋∙𝐹 𝐷 2 =6 — площадь сечения меньшего шара
плоскостью 𝛼.
𝐴𝐵 — радиус круга, полученного в сечении большего шара
плоскостью 𝛽, тогда 𝑆 𝛽 =𝜋∙𝐴 𝐵 2 =4 — площадь сечения большего шара
плоскостью 𝛽.
𝐶𝐹 — радиус круга, полученного в сечении большего шара плоскостью 𝛼. Параллельные прямые 𝐴𝐵 и 𝐶𝐹 перпендикулярны прямой 𝐴𝐹.
Из прямоугольных треугольников получаем: 𝑂 𝐹 2 =𝑂 𝐶 2 −𝐶 𝐹 2 =𝑂 𝐷 2 −𝐹 𝐷 2 , откуда 𝐶 𝐹 2 =𝑂 𝐶 2 −𝑂 𝐷 2 +𝐹 𝐷 2 =𝑂 𝐵 2 −𝑂 𝐴 2 +𝐹 𝐷 2 =𝐴 𝐵 2 +𝐹 𝐷 2 .
Площадь сечения большего шара плоскостью 𝛼:
𝑆=𝜋∙𝐶 𝐹 2 =𝜋∙𝐴 𝐵 2 +𝜋∙𝐹 𝐷 2 =10.
Ответ. 10
22 слайд

В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания равна 11, а боковое ребро AA1=7. Точка K принадлежит ребру B1C1 и делит его в отношении 8:3, считая от вершины B1. Найдите площадь сечения этой призмы плоскостью, проходящей через точки B, D и K.
Решение.
Пусть L — точка, в которой плоскость сечения пересекает ребро C1D1. Отрезок KL параллелен диагонали BD. Искомое сечение — трапеция BDLK (рис. 1). Плоскость сечения пересекает нижнее основание по прямой BD, параллельной B1D1, значит, KL
параллельно B1D1.
Треугольники LC1K и D1C1B1 подобны, следовательно,
𝐶 1 𝐿: 𝐶 1 𝐷 1 = 𝐶 1 𝐿: 𝐶 1 𝐵 1 =𝐾𝐿: 𝐵 1 𝐷 1 =3:11.
Значит, 𝐵𝐷= 𝐵 1 𝐷 1 =11 2 , 𝐾𝐿=3 2 .
В равных прямоугольных треугольниках DD1L и BB1K имеем
𝐵𝐾=𝐷𝐿= 𝐷 𝐷 1 2 + 𝐷 1 𝐿 2 = 113 , значит, трапеция BDLK равнобедренная.
Пусть LH — высота трапеции BDLK, проведённая к основанию BD (рис.2), тогда: 𝐷𝐻= 𝐵𝐷−𝐾𝐿 2 =4 2 ; 𝐿𝐻= 𝐷 𝐿 2 −𝐷 𝐻 2 =9;

𝑆 𝐵𝐷𝐿𝐾 = 𝐵𝐷+𝐾𝐿 2 ∙𝐿𝐻=63 2 .
Ответ. 63 2
23 слайд

В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 известны рёбра 𝐴𝐵=5, 𝐴𝐷=4, 𝐴 𝐴 1 =9. Точка 𝑂 принадлежит ребру 𝐵 𝐵 1 и делит его в отношении 4:5, считая от вершины 𝐵. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки 𝐴,𝑂 и 𝐶 1 .
Решение.

Пусть плоскость 𝐴𝑂 𝐶 1 пересекает ребро 𝐷 𝐷 1 в точке 𝑃. Плоскость сечения пересекает плоскость 𝐶 𝐶 1 𝐷 1 по прямой 𝐶 1 𝑃 параллельной 𝐴𝑂 следовательно, искомое сечение — параллелограмм 𝐴𝑂 𝐶 1 𝑃 (рис. 1).
Треугольники 𝐴𝐷𝑃 и 𝐶 1 𝐵 1 𝑂 равны, следовательно,
𝐷𝑃= 𝐵 1 𝑂= 5 9 𝐵 𝐵 1 =5;𝐵𝑂=𝐵 𝐵 1 − 𝐵 1 𝑂=4
Далее, 𝐴𝑃= 𝐴 𝐷 2 +𝐷 𝑃 2 = 41 ;𝐴𝑂= 𝐴 𝐵 2 +𝐵 𝑂 2 = 41 ,
значит, 𝐴𝑂 𝐶 1 𝑃 и — ромб со стороной 41 и диагональю 𝐴 𝐶 1 = 𝐴 𝐵 2 +𝐵 𝐶 2 +𝐶 𝐶 1 2 = 122 (рис. 2).
Тогда другая диагональ
𝑂𝑃=2 𝐴 𝑂 2 − 𝐴 𝐶 1 2 2 = 42 ; 𝑆 𝐴𝑂 𝐶 1 𝑃 = 𝐴 𝐶 1 2 = 1281 .
Ответ. 1281
24 слайд

Две параллельные плоскости, расстояние между которыми 2, пересекают шар. Одна из плоскостей проходит через центр шара. Отношение площадей сечений шара этими плоскостями равно 0,84. Найдите радиус шара.
Решение.

Сечение шара плоскостью — круг. Рассмотрим сечение плоскостью, проходящей через центры сечений. Обозначения даны на рисунке. OA — радиус шара, тогда
S1 = π · OA2 — площадь сечения шара плоскостью, проходящей через его центр. BC — радиус меньшего круга, полученного в сечении, тогда S2 = π · BC2 — площадь сечения шара второй плоскостью.
Из отношения площадей сечений получаем:
𝐵𝐶 𝑂𝐴 = 21 5 . OB — расстояние между плоскостями, равное 2.
В прямоугольном треугольнике OBC: OC2 = BC2 + OB2, откуда получаем:
𝑂 𝐴 2 = 21 5 𝑂𝐴 2 +4; 𝑂𝐴=5.
Ответ. 5
25 слайд

В правильной треугольной пирамиде SABC боковое ребро SA = 5, а сторона основания AB = 4. Найдите площадь сечения пирамиды плоскостью, проходящей через ребро AB перпендикулярно ребру SC.
Решение.

В треугольнике BCS проведём высоту BK , тогда искомое сечение — треугольник ABK . Пусть Q — площадь треугольника ABK . Сечение из условия разбивает пирамиду на тетраэдры CAKB и SAKB . Их суммарный объём
1 3 ∙𝑄∙𝑆𝐾+ 1 3 ∙𝑄∙𝐶𝐾= 1 3 ∙𝑄∙𝑆𝐶= 5𝑄 3 равен объёму пирамиды.
Пусть — SO высота пирамиды. В треугольнике SCO имеем:
𝐶𝑂= 𝐴𝐵 3 = 4 3 3 , 𝑆𝑂= 𝑆 𝐶 2 −𝑂 𝐶 2 = 25− 16 3 = 59 3 .
Объём пирамиды SABC равен 1 3 ∙𝑆𝑂∙ 𝑆 𝐴𝐵𝐶 = 59 3 3 ∙ 16 3 4 = 4 59 3 .
Приравнивая два найденных значения для объёма,
получаем 𝑄= 4 59 5 .
Ответ. 4 59 5
26 слайд

В правильной треугольной пирамиде SABC боковое ребро SA = 6, а сторона основания AB = 4. Найдите площадь сечения пирамиды плоскостью, проходящей через ребро AB перпендикулярно ребру SC.
Решение.

В треугольнике BCS проведём высоту BK , тогда искомое сечение — треугольник ABK . Пусть Q — площадь треугольника ABK . Сечение из условия разбивает пирамиду на тетраэдры CAKB и SAKB . Их суммарный объём
1 3 ∙𝑄∙𝑆𝐾+ 1 3 ∙𝑄∙𝐶𝐾= 1 3 ∙𝑄∙𝑆𝐶=2𝑄 равен объёму пирамиды.
Пусть — SO высота пирамиды. В треугольнике SCO имеем:
𝐶𝑂= 𝐴𝐵 3 = 4 3 3 , 𝑆𝑂= 𝑆 𝐶 2 −𝑂 𝐶 2 = 36− 16 3 = 2 69 3 .
Объём пирамиды SABC равен
1 3 ∙𝑆𝑂∙ 𝑆 𝐴𝐵𝐶 = 1 3 ∙ 2 69 3 ∙ 16 3 4 = 8 23 3 .
Приравнивая два найденных значения для объёма,
получаем 𝑄= 4 23 3 .
Ответ. 4 23 3
27 слайд

Сфера, вписанная в правильную шестиугольную пирамиду
28 слайд

В правильную шестиугольную пирамиду, боковое ребро которой равно 10, а высота равна 6, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение.

Пусть MH — высота правильной шестиугольной пирамиды MABCDEF с вершиной M, тогда треугольник AMH прямоугольный,
MA = 10, MH = 6, откуда 𝐴𝐻= 𝑀 𝐴 2 −𝑀 𝐻 2 =8.
Треугольник ABH равносторонний, следовательно, AB = AH = 8.
В треугольнике AMB высота𝑀𝑁= 𝑀 𝐴 2 − 𝐴𝐵 2 2 =2 21 .
В правильном треугольнике AHB высота 𝑁𝐻= 𝐴𝐵 3 2 =4 3 .
Центр O сферы, вписанной в правильную шестиугольную пирамиду, лежит на её высоте MH, точка K касания сферы и боковой грани AMB лежит на отрезке MN. Треугольники MOK и MNH подобны, поэтому
𝑀𝑂:𝑂𝐾=𝑀𝐻:𝐻𝑁⇔ 6−𝑟 ∙4 3 =2 21 ∙𝑟⇔𝑟=4 7 −8,
где r — радиус сферы. Площадь сферы 𝑆=4𝜋 𝑟 2 =64 11−4 7 𝜋.
Ответ.
64 11−4 7 𝜋
29 слайд

В правильную шестиугольную пирамиду, боковое ребро которой равно 5 , а высота равна 1, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение.

Пусть МН — высота правильной шестиугольной пирамиды MABCDEF с вершиной М, тогда треугольник АМН прямоугольный, 𝑀𝐴= 5 , 𝑀𝐻=1, откуда 𝐴𝐻= 𝑀 𝐴 2 −𝑀 𝐻 2 =2.
Треугольник АВН равносторонний, следовательно, 𝐴𝐵=𝐴𝐻=2.
В треугольнике АМВ высота 𝑀𝑁= 𝑀 𝐴 2 − 𝐴𝐵 2 2 =2.
В правильном треугольнике АНВ высота 𝐻𝑁= 𝐴𝐵 3 2 = 3 .
Центр О сферы, вписанной в правильную шестиугольную пирамиду, лежит на её высоте МН, точка К касания сферы и боковой грани AMB лежит на отрезке MN. Треугольники МОК и MNH подобны, поэтому
𝑀𝑂:𝑂𝐾=𝑀𝑁:𝐻𝑁⇔ 1−𝑟 ∙ 3 =2∙𝑟⇔𝑟=2 3 −3,
где r — радиус сферы.
Площадь сферы 𝑆=4𝜋 𝑟 2 =12 7−4 3 𝜋.
Ответ.
12 7−4 3 𝜋
30 слайд

Радиус основания конуса равен 6, а его высота равна 8. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 4. Найдите расстояние от центра основания конуса до плоскости сечения.
Решение.

Сечение конуса плоскостью, содержащей его вершину S и хорду
AB = 4, — треугольник ASB.
В равных прямоугольных треугольниках SOA и SOB, где O — центр основания конуса, OA = OB = 6, SO = 8, откуда
𝑆𝐴=𝑆𝐵= 𝑂 𝐵 2 +𝑆 𝑂 2 =10.
Пусть SH — высота и медиана равнобедренного треугольника ASB, 𝑆𝐻= 𝑆 𝐴 2 −𝐴 𝐻 2 =4 6 , Тогда отрезок OH — высота и медиана равнобедренного треугольника AOB, 𝑂𝐻= 𝐴 𝑂 2 −𝐴 𝐻 2 =4 2 .
Прямые SH и OH перпендикулярны прямой AB, поэтому плоскость SOH перпендикулярна плоскости ASB. Следовательно, расстояние от точки O до плоскости ASB равно высоте OM прямоугольного треугольника SOH, проведённой к гипотенузе: 𝑂𝑀= 𝑂𝐻∙𝑆𝑂 𝑆𝐻 = 8 3 3 .
Ответ. 8 3 3
31 слайд

Радиус основания конуса равен 5, а его высота равна 12. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 6. Найдите расстояние от центра основания конуса до плоскости сечения.
Решение.

Сечение конуса плоскостью, содержащей его вершину S и хорду 𝐴𝐵=6 — треугольник ASB.
В равных прямоугольных треугольниках SOA и SOB, где О — центр основания конуса, 𝑂𝐴=𝑂𝐵=5, 𝑆𝑂=12, откуда
𝑆𝐴=𝑆𝐵= 𝑂 𝐵 2 +𝑆 𝑂 2 =13.
Пусть SH — высота и медиана равнобедренного треугольника ASB, 𝑆𝐻= 𝑆 𝐴 2 −𝐴 𝐻 2 =4 10 . Тогда отрезок ОН — высота и медиана равнобедренного треугольника AOB 𝑂𝐻= 𝑂 𝐴 2 −𝐴 𝐻 2 =4.
Прямые SH и ОН перпендикулярны прямой AB, поэтому плоскость SOH перпендикулярна плоскости ASB. Следовательно, расстояние от точки О до плоскости ASB равно высоте ОМ прямоугольного треугольника SOH, проведенной к гипотенузе: 𝑂𝑀= 𝑂𝐻∙𝑆𝑂 𝑆𝐻 = 6 10 5 .
Ответ. 6 10 5
32 слайд

Сфера, вписанная в четырехугольную пирамиду
33 слайд

В правильную четырёхугольную пирамиду, боковое ребро которой равно 10, а высота равна 6, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение.
Пусть МН — высота правильной четырёхугольной пирамиды MABCD с вершиной М. тогда треугольник АМН прямоугольный.
МA = 10, МН = 6, откуда 𝐴𝐻= 𝑀 𝐴 2 −𝑀 𝐻 2 =8.
Треугольник АВН прямоугольный равнобедренный, следовательно, 𝐴𝐵=𝐴𝐻 2 =8 2 .В треугольнике AMB высота
𝑀𝐻= 𝑀 𝐴 2 − 𝐴𝐵 2 2 =2 17 .
В равнобедренном прямоугольном треугольнике АВН высота
𝑁𝐻= 𝐴𝐵 2 =4 2 .
Центр О сферы, вписанной в правильную четырёхугольную пирамиду, лежит на её высоте MH, точка K касания сферы и боковой грани АМВ лежит на отрезке MN. Треугольники MOK и MNH подобны, поэтому
𝑀𝑂:𝑂𝐾=𝑀𝑁:𝐻𝑁⇔ 6−𝑟 ∙4 2 =2 17 ∙𝑟⇔𝑟= 4 34 −16 3 ,
где 𝑟 — радиус сферы.
Площадь сферы 𝑆=4𝜋 𝑟 2 = 128 25−4 34 𝜋 9 .
Ответ.
128 25−4 34 𝜋 9
34 слайд

В правильную четырёхугольную пирамиду, боковое ребро которой равно 17, а высота равна 7, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение.
Пусть 𝑀𝐻 — высота правильной четырёхугольной пирамиды 𝑀𝐴𝐵𝐶𝐷 с вершиной 𝑀 тогда треугольник 𝐴𝑀𝐻 — прямоугольный,
𝑀𝐴=17, 𝑀𝐻=7, откуда 𝐴𝐻= 𝑀 𝐴 2 −𝑀 𝐻 2 =4 15 .
Треугольник 𝐴𝐵𝐻 — прямоугольный равнобедренный, следовательно, 𝐴𝐵=𝐴𝐻 2 =4 30 . В треугольнике 𝐴𝑀𝐵 высота
𝑀𝑁= 𝑀 𝐴 2 − 𝐴𝐵 2 2 =13.
В равнобедренном прямоугольном треугольнике 𝐴𝐵𝐻 высота
𝐻𝑁= 𝐴𝐵 2 =2 30 .
Центр 𝑂 сферы, вписанной в правильную четырёхугольную пирамиду, лежит на её высоте 𝑀𝐻 точка 𝐾 касания сферы и боковой грани 𝐴𝑀𝐵 лежит на отрезке 𝑀𝑁. Треугольники 𝑀𝑂𝐾 и 𝑀𝑁𝐻 подобны, поэтому
𝑀𝑂:𝑂𝐾=𝑀𝑁:𝐻𝑁⇔ 7−𝑟 𝑟 = 13 2 30 ⇔ 7−𝑟 ∙2 30 =13∙𝑟⇔
⇔𝑟= 26 30 −120 7 , где 𝑟 — радиус сферы.
Площадь сферы 𝑆=4𝜋 𝑟 2 = 480 289−52 30 𝜋 49 .
Ответ.
480 289−52 30 𝜋 49
35 слайд

В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 4, а боковые рёбра равны 8. Найдите площадь сечения пирамиды плоскостью, проходящей через точку B и середину ребра MD параллельно прямой AC.
Ответ.
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 18, а боковые рёбра равны 15. Точка R принадлежит ребру MB, причём MR : RB = 2 : 1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки C и R параллельно прямой BD.
Ответ.
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 12, а боковые рёбра равны 24. Точка G принадлежит ребру MA, причём MG : GA = 2 : 1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки B и G параллельно прямой AC.
Ответ.
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания равна 22, а боковое ребро AA1 = 7. Точка K принадлежит ребру B1C1 и делит его в отношении 6 : 5, считая от вершины B1. Найдите площадь сечения этой призмы плоскостью, проходящей через точки B, D и K.
Ответ.
36 слайд

В правильной четырёхугольной призме 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 сторона основания равна 10, а боковое ребро 𝐴 𝐴 1 =2. Точка O принадлежит ребру 𝐴 1 𝐵 1 и делит его в отношении 4 : 1, считая от вершины 𝐴 1 . Найдите площадь сечения этой призмы плоскостью, проходящей через точки A, C и O.
Ответ.
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 известны рёбра
𝐴𝐵=4, 𝐴𝐷=3, 𝐴 𝐴 1 =7. Точка O принадлежит ребру 𝐵 𝐵 1 и делит его в отношении 3 : 4, считая от вершины B. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки A, O и C1.
Ответ.
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷 𝐴 1 𝐵 1 𝐶 1 𝐷 1 известны рёбра
𝐴𝐵=5, 𝐴𝐷=3, 𝐴 𝐴 1 =8. Точка R принадлежит ребру 𝐴 𝐴 1 и делит его в отношении 3 : 5, считая от вершины A. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки B, R и D1.
Ответ.
37 слайд

Спасибо за внимание!

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 155 172 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

Другие материалы

03.05.2020
327
0

03.05.2020
268
10

03.05.2020
868
7

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Правовое обеспечение деятельности коммерческой организации и индивидуальных предпринимателей»
Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
Курс повышения квалификации «Введение в сетевые технологии»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
Курс профессиональной переподготовки «Организация деятельности специалиста оценщика-эксперта по оценке имущества»
Курс профессиональной переподготовки «Эксплуатация и обслуживание общего имущества многоквартирного дома»
Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»
Курс профессиональной переподготовки «Стандартизация и метрология»

Источник

Геометрия, 11 класс

Урок №18. Сечения многогранников

Перечень вопросов, рассматриваемых в теме:

Решение задач, сводящихся к доказательству, связанному с построением сечения многогранника

Построение сечения многогранников

Решение задач на нахождение площадей сечений многогранников

Площадь

треугольника S=½hа

трапеции S=½h(а+b)

параллелограмма S=hа

Основная литература:

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10–11 классы : учеб.для общеобразоват. организаций : базовый и углубл. уровни – М.: Просвещение, 2014. – 255, сс. 121-126.

Дополнительная литература:

Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб.для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.

Потоскуев Е.В., Звавич Л.И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.

Открытые электронные ресурс:

Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.

Определение: две прямые параллельны, если они лежат в одной плоскости и не пересекаются. Если через две прямые нельзя провести одну плоскость, то такие прямые скрещиваются.

Теорема о параллельности трех прямых: если a∥b, b∥c, то и a∥c. Определение: прямая и плоскость параллельны, если они не имеют общих точек. Признак параллельности прямой и плоскости: прямая, не лежащая в плоскости, параллельна этой плоскости, если она параллельна некоторой прямой из этой плоскости.

Определение: две плоскости параллельны, если они не имеют общих точек.

Признак параллельности двух плоскостей: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости параллельны.

Если две плоскости пересекаются, то их линия пересечения — прямая.

Если две параллельные плоскости пересечены третьей, то их линии пересечения параллельны (см. рис.)

Если плоскости α и β пересекаются по прямой a, а плоскости β и γ пересекаются по прямой b, причем a∥b, то плоскости α и γ пересекутся по прямой c∥a∥b.

Следом называется прямая, по которой плоскость сечения пересекает плоскость любой из граней многогранника.

Примеры и разбор решения заданий тренировочного модуля

№1 SABCD – четырехугольная пирамида, в основании которой лежит квадрат ABCD, а две боковые грани SAB и SAD представляют собой прямоугольные треугольники с прямым углом ∠A. Найдите площадь сечения пирамиды плоскостью α, если SA=AB=a.

Решение:

сначала построим сечение по условию задачи.

1)Пусть AC∩BD=O. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Заметим, что т.к. ∠SAB=∠SAD=90∘⇒SA⊥(ABC). Проведем в плоскости SAC прямую OK∥SC. Т.к. O – середина AC, то по теореме Фалеса K – середина SA. Через точку K в плоскости SAB проведем KM∥SB (следовательно, M – середина AB). Таким образом, плоскость, проходящая через прямые OK и KM, и будет искомой плоскостью. Необходимо найти сечение пирамиды этой плоскостью. Соединив точки O и M, получим прямую MN. Т.к. α∥(SBC),то α пересечет плоскость SCD по прямой NP∥SC (если NP∩SC≠∅, то α∩(SBC)≠∅, что невозможно ввиду их параллельности). Таким образом, KMNP – искомое сечение, причем KP∥AD∥MN⇒ это трапеция.

2)Т.к. все точки K,M,N,P – середины отрезков SA,AB,CD,SD соответственно, то: а) MN=AD=a б) KP=1/2AD=a/2 в) KM=1/2SB=a 2/2 Заметим, что по теореме о трех перпендикулярах SB⊥BC⇒KM⊥MN. Таким образом, KMNP – прямоугольная трапеция. S_KMNP=(KP+MN)* KM/ 2 =3 a²/8

Ответ:3 a²/8

№2 Найди площадь сечения прямой призмы, проходящей через середины ребер, если =120°, АВ=5 см, ВС=3см и наибольшая из площадей боковых граней равна 35см² .

Решение:

боковая грань прямой призмы является прямоугольником.

Площадь каждой боковой грани равна произведению высоты призмы на сторону основания.

То есть большая боковая грань содержит большую сторону основания.

По условию =120°, – тупой, а поскольку напротив большей стороны лежит больший угол, то большей стороной основания будет сторона АС. Вычислим длину стороны АС по теореме косинусов.

Получим, что длина стороны АС=7см.

Зная большую сторону основания и площадь наибольшей боковой грани призмы, длину высоты призмы вычислить нетрудно.

Получим, что длина высоты призмы равна .

Найдем площадь основания, а оно равно площади сечения, по формуле .

Мы воспользуемся второй формулой. Получим, что площадь основания равна .

Ответ: 15 /4 см²

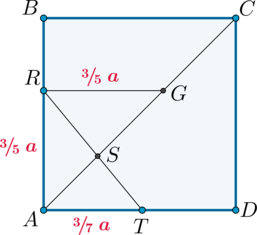
№3 На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q, причём AQ:QB=1:2. Точка P — середина ребра AS.

Найдите площадь сечения DPQ, если площадь сечения DSB равна 6.

Решение:

пусть сторона основания пирамиды равна 3а, а высота пирамиды равна h. Тогда площадь сечения DSB равна

S=BD*SO/2= 3 =6

откуда ah=2 .

Площадь сечения DPQ равна

Ответ:

№4

Дана правильная треугольная пирамида SABC с вершиной S. Через середину ребра AC и точки пересечения медиан граней ASB и CSB проведена плоскость. Найдите площадь сечения пирамиды этой плоскостью, если AB=21,AS=12 .

Решение:

пусть LK∩SO=H. Тогда по теореме о трех перпендикулярах HK⊥AC как наклонная (HO⊥(ABC),OK⊥AC как проекция). Следовательно, и LK⊥AC.

Тогда S_ALC=AC⋅LK/2 Рассмотрим △SKB: BK=AB⋅ /2=21 /2⇒cosB=7 /12 .

Тогда по теореме косинусов для △KLB: KL²=729/4⇒KL=27/2

Значит, S_ALC=567/4=141,75

Ответ : 141,75

№5

Дана правильная четырехугольная призма ABCDA₁B₁C₁D₁. На ребре AA₁ отмечена точка K так, что AK : KA₁ = 1 : 2. Плоскость α проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD₁ в точке M, АВ=4, АА₁=6. Найдите площадь сечения.

Решение:

По теореме о трех перпендикулярах прямые BM и AC перпендикулярны, а значит, прямые BM и KL перпендикулярны. Площадь четырехугольника, диагонали которого взаимно перпендикулярны, равна половине произведения диагоналей. Найдем их: KL=AC=4 как диагональ квадрата, лежащего в основании призмы, тогда

по теореме Пифагора.

Тогда

Ответ: 8

Источник