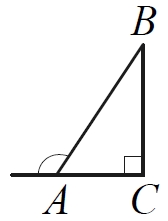Решение заданий Открытого варианта досрочного периода ЕГЭ 2022 по математике (базовый уровень). Официальный досрочный вариант. Досрочник КИМ ФИПИ. Досрочная волна 2022. Полный разбор. ГДЗ база решебник для 11 класса. Ответы с решением.
Задание 1.
Найдите значение выражения 8,4⋅1,5 + 6,9.
Задание 2.
В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 600 листов. Какого наименьшего количества пачек бумаги хватит на 6 недель?
Задание 3.
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
| А) площадь города Санкт-Петербурга Б) площадь Краснодарского края В) площадь экрана монитора компьютера Г) площадь ногтя на пальце взрослого человека |
1) 100 кв. мм |
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Задание 4.
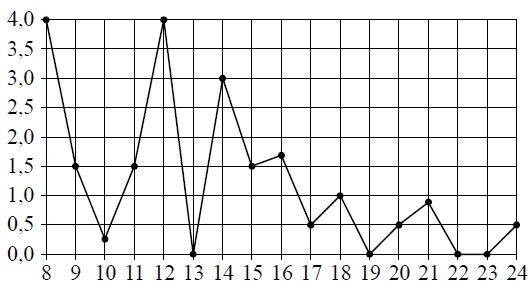
На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указаны числа месяца, по вертикали – количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линиями.
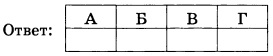
Задание 5.
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
Задание 6.
Товар на распродаже уценили на 50 %, при этом он стал стоить 820 рублей. Сколько рублей стоил товар до распродажи?
Задание 7.
Найдите значение выражения frac{4^{7}}{2^{7}}:2^{3}.
Задание 8.
Площадь четырёхугольника можно вычислить по формуле S=frac{1}{2}d1d2sinα, где d1 и d2 – длины диагоналей четырёхугольника, α – угол между диагоналями. Пользуясь этой формулой, найдите площадь S, если d1 = 4, d2 = 3 и sinα = frac{5}{6}.
Задание 9.
Найдите корень уравнения 6 − 2x = 3x − 10.
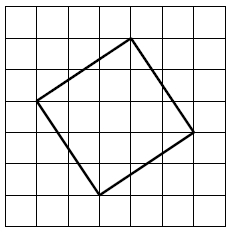
Задание 10.
На рисунке показано, как выглядит колесо с 7 спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 20°?
Задание 11.
Вероятность того, что стекло мобильного телефона разобьётся при падении на твёрдую поверхность, равна 0,84. Найдите вероятность того, что при падении на твёрдую поверхность стекло мобильного телефона не разобьётся.
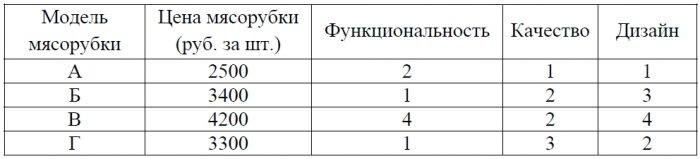
Задание 12.
Независимая экспертная лаборатория определяет рейтинг мясорубок на основе коэффициента ценности, равного 0,01 средней цены P (в рублях за штуку), показателей функциональности F, качества Q и дизайна D. Рейтинг R вычисляется по формуле
R = 4(2F + 2Q + D) − 0,01P.
В таблице даны цены и показатели четырёх моделей мясорубок.
Найдите наивысший рейтинг мясорубки из представленных в таблице моделей.
Задание 13.
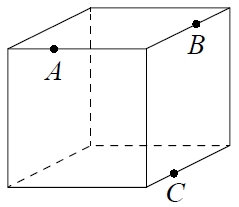
Плоскость, проходящая через точки A, B и C (см. рисунок), разбивает куб на два многогранника. Сколько вершин у получившегося многогранника с бо́льшим числом граней?
Задание 14.
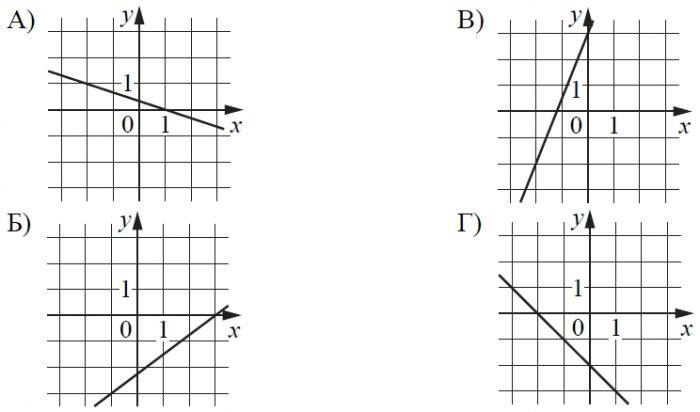
На рисунках изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и угловыми коэффициентами прямых.
ГРАФИКИ
УГЛОВЫЕ КОЭФФИЦИЕНТЫ
1) -frac{1}{3}
2) −1
3) 0,75
4) 2,5
В таблице под каждой буквой укажите соответствующий номер.
Задание 15.
В прямоугольном треугольнике ABC внешний угол при вершине A равен 120°. Катет AC = 23. Найдите длину гипотенузы AB.
Задание 16.
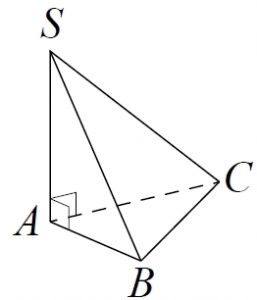
В основании пирамиды SABC лежит правильный треугольник ABC со стороной 2, а боковое ребро SA перпендикулярно основанию и равно 4√3. Найдите объём пирамиды SABC.
Задание 17.
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) log2 (x – 1) < 1 Б) 3–x > frac{1}{3} В) (x – 3)(x – 1) > 0 Г) frac{x-1}{(x-3)^{2}}>0 |
1) (1; 3)∪(3; +∞) 2) (–∞; 1)∪(3; +∞) 3) (–∞; 1) 4) (1; 3) |
Впишите в приведённую в ответе таблицу под каждой буквой соответствующий номер решения.
Задание 18.
В фирме работает 50 сотрудников, из них 40 человек знают английский язык, а 20 – немецкий. Выберите все утверждения, которые верны при указанных условиях.
1) В этой фирме нет ни одного сотрудника, знающего и английский, и немецкий языки.
2) Не больше 20 сотрудников этой фирмы знают и английский, и немецкий языки.
3) В этой фирме хотя бы три сотрудника знают и английский, и немецкий языки.
4) Если сотрудник этой фирмы знает английский язык, то он знает и немецкий.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Задание 19.
Найдите четырёхзначное натуральное число, меньшее 1360, которое делится на каждую свою цифру и все цифры которого различны и не равны нулю. В ответе запишите какое-нибудь одно такое число.
Задание 20.
Один мастер может выполнить заказ за 42 часа, а другой – за 21 час. За сколько часов выполнят заказ оба мастера, работая вместе?
Задание 21.
Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами – 324, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.8 / 5. Количество оценок: 5
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
-
Главная
-
ЕГЭ
-
ЕГЭ 2022
-
Реальные варианты ЕГЭ 2022
- 29.03.2022
Дата обновления: 07.06.2022
СОХРАНИ СТРАНИЦУ С ЗАКЛАДКИ!
Общая страница, на которой мы будем собирать все реальные варианты, которые будут появляться по ЕГЭ в 2022 году. Все варианты будут публиковаться после проведения экзамена.
- 02.04.2022 — Варианты досрочного ЕГЭ 2022 по всем предметам
- 01.05.2022 — Опубликованы открытые варианты по всем предметам
- 26.05.2022 — Началась основная волна ЕГЭ 2022 (см ссылки ниже)
- 07.06.2022 — Обновлены задания по тем предметам, которые прошли — история, физика, русский, математика
Реальные варианты 2022 ПО ПРЕДМЕТАМ (по алфавиту)
- Английский язык
- Биология от 07.04.2022
- География от 26.05.2022
- История от 06.06.2022
- Литература от 26.05.2022
- Математика профильная обновлено от 06.06.2022
- Математика базовая — обновлено 05.06.2022
- Обществознание от 07.04.2022
- Русский язык от 30.05.2022, 31.05.2022
- Физика от 06.06.2022
- Химия от 26.05.2022
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить
3 июня 2022
В закладки
Обсудить
Жалоба
Вариант собран по заданиям прошедшего ЕГЭ 3 июня.
Ответы прилагаются.
Экзаменационная работа включает в себя 21 задание.
На выполнение работы отводится 3 часа.
→ rm-ege2022-baza.pdf
→ Профильный уровень.
Каждое из заданий 1–21 считается выполненными верно, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби.
Каждое верно выполненное задание оценивается 1 баллом.
Перевод баллов в оценку
0-6 → 2
7-11 → 3
12-16 → 4
17-21 → 5
Источник: yagubov.ru
Задание 1
Найдите корень уравнения $$9^{2x+5}=3,24cdot 5^{2x+5}$$
Ответ: -1,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 2
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,25. Вероятность того, что это вопрос по теме «Площадь», равна 0,3. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Ответ: 0,55
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 3
В тупоугольном треугольнике АВС известно, что АС=ВС, высота АН равна 3, $$CH=sqrt{7}$$. Найдите синус угла АСВ.
Ответ: 0,75
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 4
Найдите значение выражения $$frac{4cos 121^{circ}}{cos 59^{circ}}$$
Ответ: -4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 5
Цилиндр вписан в правильную шестиугольную призму. Радиус основания цилиндра равен $$sqrt{3}$$, а высота равна 2. Найдите площадь боковой поверхности призмы.
Ответ: 24
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 6
На рисунке изображён график y=f(x). На оси абсцисс отмечены точки -2, -1, 1, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 7
При температуре 0°C рельс имеет длину l0=15 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону $$l(t_{0})=l_{0}(1+alphacdot t^{circ})$$, где $$alpha=1,2cdot 10^{-5}$$(оС)-1 — коэффициент теплового расширения, t° — температура (в градусах Цельсия). При какой температуре рельс удлинится на 7,2 мм? Ответ дайте в градусах Цельсия.
Ответ: 40
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 8
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 135 км. На следующий день он отправился обратно со скоростью на 9 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Ответ: 13,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

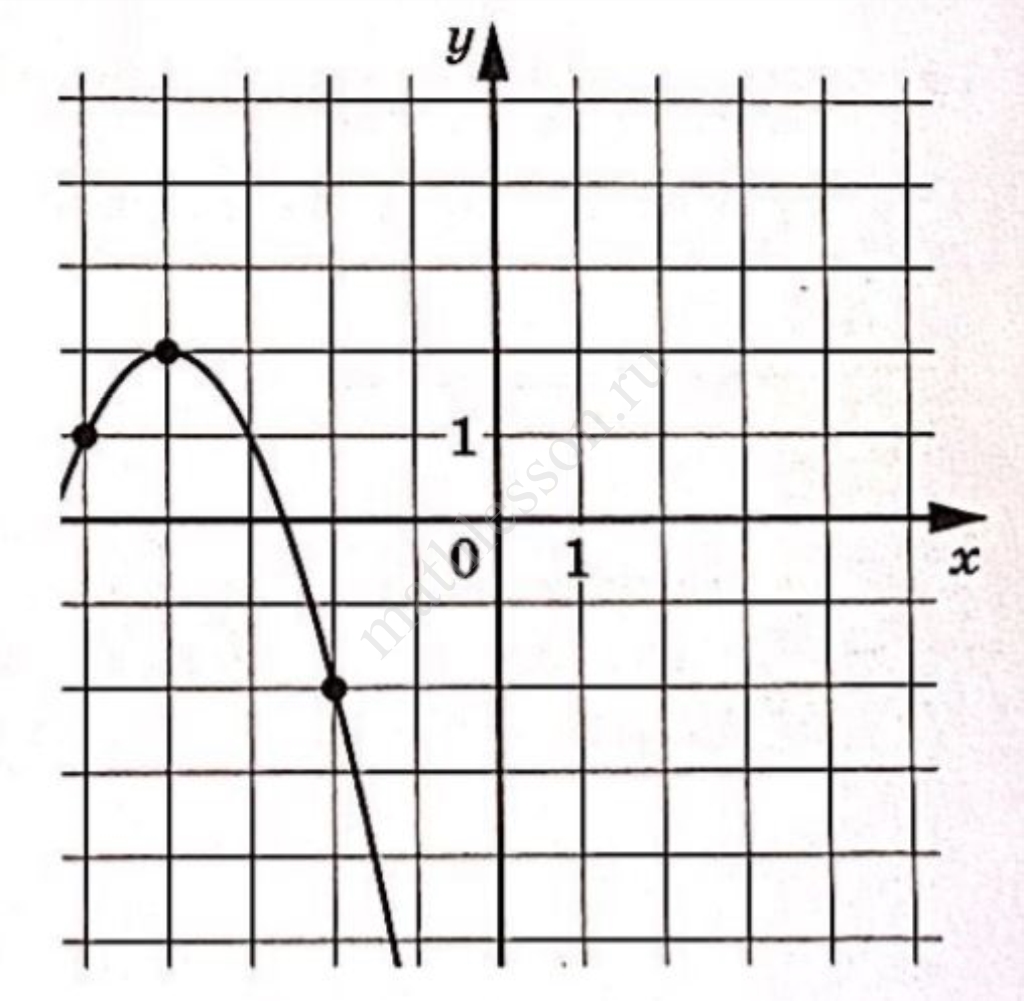
Задание 9
На рисунке изображён график функции $$f(x)=ax^{2}+bx+c$$. Найдите $$f(-9)$$.
Ответ: -23
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 10
Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 25% этих стёкол, вторая — 75%. Первая фабрика выпускает 5 % бракованных стёкол, а вторая — 1 %. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Ответ: 0,02
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 11
Найдите точку минимума функции $$y=frac{4}{3}xsqrt{x}-5x+4$$
Ответ: 6,25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 12
а) Решите уравнение $$2cos^{3}(x-pi)=sin (frac{3pi}{2}+x)$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[frac{9pi}{2};frac{11pi}{2}]$$
Ответ: а)$$frac{pi}{2}+pi k;frac{pi}{4}+frac{pi n}{2}$$ б)$$frac{9pi}{2};frac{19pi}{4};frac{21pi}{4};frac{11pi}{2}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 13
В правильной четырёхугольной пирамиде SABCD сторона основания AD равна 10, высота SH равна 12. Точка К — середина бокового ребра SD. Плоскость АКB пересекает боковое ребро SC в точке Р.
а) Докажите, что площадь четырёхугольника CDKP составляет $$frac{3}{4}$$ треугольника SCD.
б) Найдите объём пирамиды ACDKP.
Ответ: 150
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 14
Решите неравенство $$(25^{x}-4cdot 5^{x})^2+8cdot 5^{x}<2cdot 25^{x}+15$$
Ответ: $$(-infty;0);(log_{5}3;1)$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 15
В июле 2023 года планируется взять кредит на 10 лет на некоторую сумму. Условия возврата таковы:
— каждый январь с 2024 по 2028 год долг возрастает на 18 % по сравнению с концом предыдущего года;
— каждый январь с 2029 по 2033 год долг возрастает на 16 % по сравнению с концом предыдущего года;
— с февраля по июнь необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года;
— к июлю 2033 года кредит должен быть полностью погашен.
Найдите сумму, которую планируется взять в кредит, если общая сумма выплат по кредиту должна составить 1470 тыс. рублей.
Ответ: 750 тыс. руб.
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 16
Точки А, В, С, D и Е лежат на окружности в указанном порядке, причём ВС=CD=DE, а AC $$perp$$ BE. Точка К — пересечение прямых BE и AD.
а) Докажите, что прямая СЕ делит отрезок KD пополам.
б) Найдите площадь треугольника АВК, если AD=4, $$DC=sqrt{3}$$ .
Ответ: $$frac{25sqrt{39}}{64}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 17
Найдите все значения а, при каждом из которых уравнение $$|x^{2}-a^{2}|=|x+a|sqrt{x^{2}-5ax+4a}$$ имеет ровно два различных корня
Ответ: $$a<-2;-2<a<-frac{2}{3};a>0$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 18
На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго.
а) Может ли сумма этих чисел быть равна 3456?
б) Может ли сумма этих чисел быть равна 2345?
в) В тройке чисел первое число трёхзначное, а третье равно 5. Сколько существует таких троек?
Ответ: а) да б) нет в) 85
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!