Сфера формулы егэ - Помощь в подготовке к экзаменам и поступлению

Сфера, шар, сегмент и сектор. Формулы и свойства сферы

Определение.

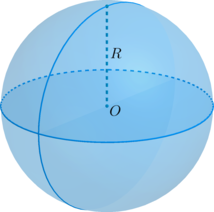
Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула. Объём шара:

V =	4	πR³ =	1	πD³
3	6

Формула. Площадь поверхности сферы через радиус или диаметр:

S = 4πR² = πD²

Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:

x² + y² + z² = R²

2. Уравнение сферы с радиусом R и центром в точке с координатами (x₀, y₀, z₀) в декартовой системе координат:

(x — x₀)² + (y — y₀)² + (z — z₀)² = R²

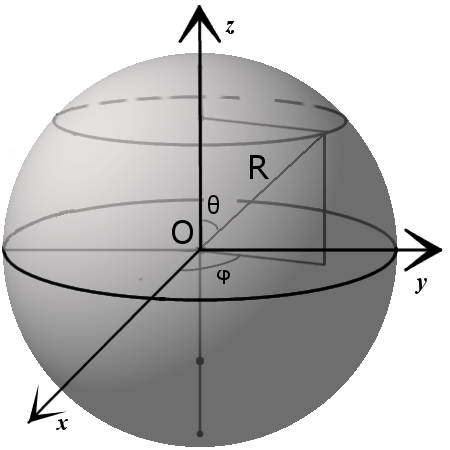
3. Параметрическое уравнение сферы с центром в точке (x₀, y₀, z₀):

x = x₀ + R · sin θ · cos φ
y = y₀ + R · sin θ · sin φ
z = z₀ + R · cos θ

где θ ϵ [0,π], φ ϵ [0,2π].

Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.

6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.

7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.

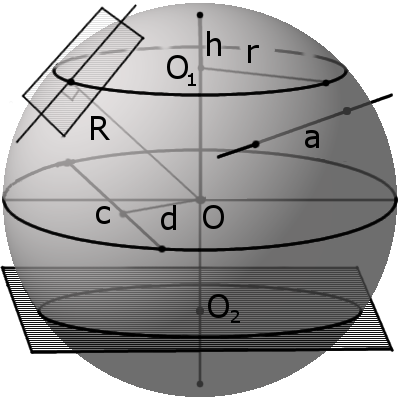
Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.

Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость — это плоскость, которая пересекает сферу.

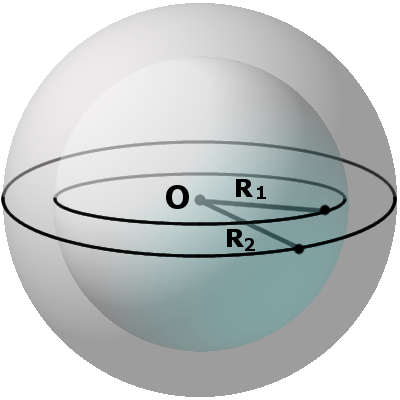
Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сечение образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:

d < R

Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m < R

Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:

r = √R² — m²,

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.

Касательная, касательная плоскость к сфере и их свойства

Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.

Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

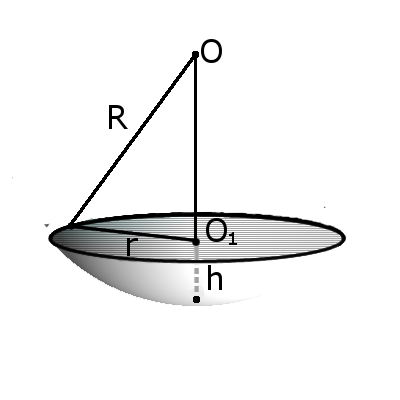
Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:

S = 2πRh

Формула. Объём сегмента сферы с высотой h через радиус сферы R:

Определение. Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.

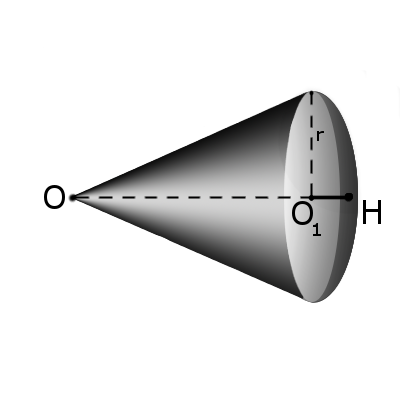
Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

Формула. Площадь поверхности сектора S с высотой O₁H (h) через радиус шара OH (R):

S = πR(2h + √2hR — h²)

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.

Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.

Источник

8. Геометрия в пространстве (стереометрия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи по теме «Сфера и шар»

(blacktriangleright) Сфера – это множество точек пространства, находящихся на одинаковом расстоянии от заданной точки (O) (называемой центром сферы).

(blacktriangleright) Шар – это сфера вместе со своей внутренностью.

Основные формулы (где (R) – радиус сферы или шара):

(blacktriangleright) площадь сферы ({large{S=4pi R^2}})

(blacktriangleright) объем шара ({large{V=dfrac{4}{3}pi R^3}})

Задание
1

#1878

Уровень задания: Равен ЕГЭ

Объем шара равен (displaystyle frac{36}{sqrtpi}). Чему будет равна площадь поверхности шара, если его радиус увеличить на (displaystyle frac{6}{sqrtpi})?

(displaystyle V_{text{шара}} = frac{4}{3}pi R^3 = frac{36}{sqrtpi}) (Rightarrow) (displaystyle R = frac{3}{sqrtpi}). Радиус нового шара равен: (displaystyle R_{text{нов.}} = R + frac{6}{sqrtpi} = frac{9}{sqrtpi}). Тогда найдем площадь поверхности: (displaystyle {S_{text{пов.}} = 4pi R_{text{нов.}}^2 = 4pi left(frac{9}{sqrtpi}right)^2 = 4pifrac{81}{pi} = 324}.)

Ответ: 324

Задание
2

#1877

Уровень задания: Равен ЕГЭ

Во сколько раз объем шара больше объема сегмента, высота которого равна половине радиуса?

Необходимо объем шара разделить на объем соответствующего сегмента, высота которого равна (H = frac{1}{2}R)

[frac{V_{text{шара}}}{V_{text{сегм.}}} = frac{frac{4}{3}pi R^3}{pi left(frac{1}{2}Rright)^2left(R — frac{1}{3}left(frac{1}{2}Rright)right)} = frac{frac{4}{3}pi R^3}{frac{5}{24}pi R^3} = frac{4}{3} cdot frac{24}{5} = frac{32}{5} = 6,4.]

Ответ: 6,4

Задание
3

#2674

Уровень задания: Сложнее ЕГЭ

Имеются две сферы (S_1) и (S_2), про которые известно, что радиус первой сферы в (2) раза больше, чем радиус второй сферы. Кроме того, сфера (S_2) целиком находится внутри сферы (S_1). Пусть объём шара, ограниченного второй сферой, равен (V_2), а объём тела, заключённого между сферами, равен (V). Найдите (V : V_2).

Пусть (V_1) – объём шара, ограниченного первой сферой. Так как радиус (S_1) в два раза больше, чем радиус (S_2), то (V_1 : V_2 = .

[V = V_1 — V_2 = 8V_2 — V_2 = 7V_2,,] следовательно, (V : V_2 = 7).

Ответ: 7

Задание
4

#2306

Уровень задания: Сложнее ЕГЭ

Площадь поверхности шара равна (frac{37}{pi}). На расстоянии (frac1{2pi}) от центра шара проведена плоскость. Найдите длину полученной в сечении окружности.

Т.к. площадь поверхности сферы ищется по формуле (S=4pi R^2), то

[4pi R^2=dfrac{37}{pi} quad Rightarrow quad R^2=dfrac{37}{4pi^2}]

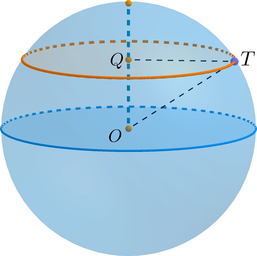
По условию задачи (OQ=frac1{2pi}). Рассмотрим (triangle OQT): он прямоугольный ((angle OQT=90^circ)), гипотенуза (OT=R), катет (QT) равен радиусу (r) окружности сечения.

Таким образом, по теореме Пифагора [QT^2=r^2=OT^2-OQ^2=dfrac{37}{4pi^2}-dfrac1{4pi^2}=dfrac{9}{pi^2}
quad Rightarrow quad r=dfrac3{pi}]

Таким образом, длина окружности сечения равна [C=2pi
r=2picdotfrac3{pi}=6.]

Ответ: 6

Задание
5

#2307

Уровень задания: Сложнее ЕГЭ

Площадь поверхности шара равна (64). На расстоянии (frac3{2sqrt{pi}}) от центра шара проведена плоскость. Найдите площадь полученного сечения.

Т.к. площадь поверхности сферы ищется по формуле (S=4pi R^2), то

[4pi R^2=64 quad Rightarrow quad R^2=dfrac{64}{4pi}]

По условию задачи (OQ=frac3{2sqrt{pi}}). Рассмотрим (triangle
OQT): он прямоугольный ((angle OQT=90^circ)), гипотенуза (OT=R), катет (QT) равен радиусу (r) окружности сечения.

Таким образом, по теореме Пифагора [QT^2=r^2=OT^2-OQ^2=dfrac{64}{4pi}-dfrac9{4pi}=dfrac{55}{4pi}]

Таким образом, площадь сечения равна

[S=picdot r^2=picdot dfrac{55}{4pi}=dfrac{55}4=13,75.]

Ответ: 13,75

Задание
6

#951

Уровень задания: Сложнее ЕГЭ

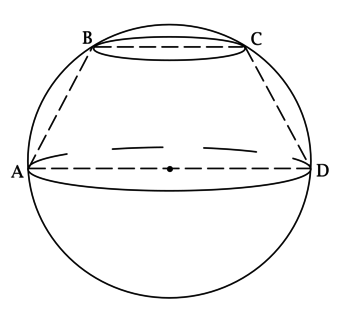
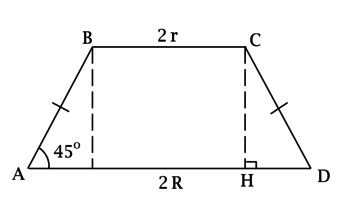
Центр большего основания усечённого конуса совпадает с центром сферы, а окружность его меньшего основания лежит на сфере. Отрезки (BC) и (AD) – диаметры меньшего и большего оснований этого усечённого конуса соответственно, (BCparallel AD), [S_{ABCD} = dfrac{210}{sqrt[3]{pi^2}},qquadqquad dfrac{r}{R} = dfrac{1}{sqrt{15}},] где (R) и (r) – радиусы большего и меньшего оснований усечённого конуса соответственно, (angle ADC = 45^circ). Найдите объём шара, ограниченного данной сферой.

Рассмотрим (ABCD): т.к. (BCparallel AD), то (ABCD) – трапеция. Так как (AB) и (CD) – образующие усечённого конуса, то (AB = CD) и трапеция (ABCD) – равнобедренная.

Построим (CHperp AD). Так как (angle ADC = 45^circ), то (triangle CHD) – равнобедренный и (CH = HD).
[HD = dfrac{AD — BC}{2} = R — r,qquadqquad S_{ABCD} = dfrac{BC + AD}{2}cdot CH = (R + r)(R — r) = R^2 — r^2 = dfrac{210}{sqrt[3]{pi^2}},] но (r = dfrac{R}{sqrt{15}}), тогда [R^2left(1-dfrac{1}{15}right) = dfrac{210}{sqrt[3]{pi^2}}qquadRightarrowqquad R = dfrac{15}{sqrt[3]{pi}}qquadRightarrowqquad V_{text{шара}} = dfrac{4}{3}pi R^3 = dfrac{4}{3}cdotpicdotdfrac{15^3}{pi} = 4500.]

Ответ: 4500

Задание
7

#3114

Уровень задания: Сложнее ЕГЭ

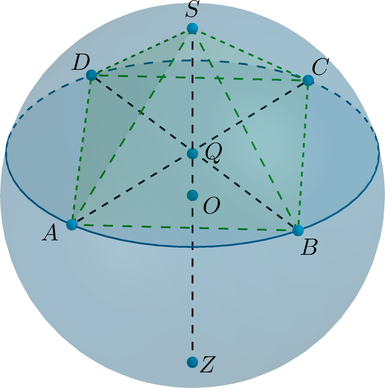
Дан шар, диаметр которого равен (9). Плоскость (alpha) пересекает диаметр (SZ) шара под углом (90^circ) и делит его точкой пересечения в отношении (1:2), считая от вершины (S). Найдите объем пирамиды с вершиной в точке (S), в основании которой лежит квадрат, вписанный в сечение шара плоскостью (alpha).

Пусть (O) – центр шара, (Q) – точка пересечения (SZ) и плоскости (alpha). Пусть (SABCD) – пирамида, объем которой нужно найти.
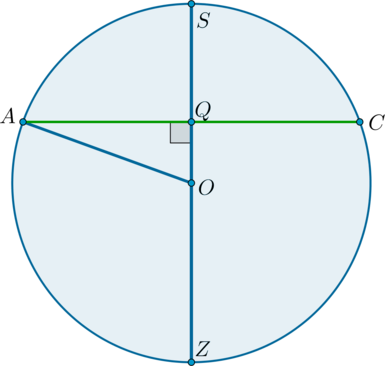
Рассмотрим сечение шара плоскостью (ASC).

Так как (SQ:QZ=1:2), то (SQ:SZ=1:3), следовательно, (SQ:SO=2:3), следовательно, (OQ:SO=1:3). Тогда [AQ=sqrt{AO^2-OQ^2}=sqrt{AO^2-left(dfrac13AOright)^2}=dfrac{2sqrt2}3AO
=dfrac{2sqrt2}3cdot dfrac92=3sqrt2] Следовательно, (AC=6sqrt2). Следовательно, (AB=AC:sqrt2=6).
Также [SQ=dfrac23SO=dfrac23cdot dfrac92=3] Заметим, что (SQ) – высота пирамиды, так как (SQperp alpha). Следовательно, [V=dfrac13cdot SQcdot AB^2=36.]

Ответ: 36

Задачи по стереометрии, в которых требуется произвести расчет объема сферы и измерение других неизвестных параметров, встречаются в ЕГЭ каждый год. Это означает, что знать основные формулы и уметь оперативно находить правильный ответ должны выпускники с разным уровнем подготовки. Понимая принцип решения задач ЕГЭ, в которых требуется вычислить объем или, к примеру, площадь сферы, старшеклассники смогут выполнять упражнения с любым количеством действий и при этом получить достаточно высокие баллы по итогам прохождения экзаменационного испытания.

Базовая информация

Сферой называется поверхность, которая состоит из множества точек пространства. Все они располагаются на одинаковом расстоянии от точки О. Она является центром сферы.
Геометрическое тело, которое ограничено сферой, называется шаром. Его осевое сечение представляет собой круг. Радиус последнего равен радиусу шара.
Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в n2 раз, а объем — в n3 раз.

Занимайтесь с образовательным порталом «Школково» для качественной подготовки к экзамену!

Проблема поиска необходимой информации встает перед старшеклассниками достаточно остро. Не всегда школьный учебник оказывается под рукой. А поиск базовых формул для вычисления площади, объема шара и других неизвестных параметров бывает достаточно трудоемким даже в онлайн-режиме.

Наш образовательный проект поможет сэкономить время и эффективно подготовиться к сдаче экзаменационного испытания. Мы предлагаем учащимся и их преподавателям выстроить процесс подготовки к ЕГЭ от простого к сложному. Такой подход позволит старшеклассникам понять, какие темы требуют более детального изучения, и улучшить имеющиеся знания.

Базовая информация, которую стоит повторить еще до выполнения задач на нахождение объема шара, представлена в разделе «Теоретическая справка». Материал, подготовленный опытными преподавателями «Школково», поможет вам восполнить пробелы в знаниях без помощи репетитора.

Чтобы задачи ЕГЭ по теме «Шар» или, например, по теме «Цилиндр», не вызывали затруднений, мы предлагаем также потренироваться в выполнении соответствующих упражнений. Множество заданий разной степени сложности вы найдете в разделе «Каталог». Каждое упражнение содержит подробный алгоритм решения. Попрактиковавшись в режиме онлайн и поняв принцип нахождения правильного ответа, школьники смогут без труда вычислить объем сферы.

При необходимости любое задание можно сохранить в разделе «Избранное». Это позволит в дальнейшем вернуться к нему.

Выполнять онлайн-задания на нахождение площади боковой сферы могут не только школьники из столицы, но и выпускники из других российских городов.