Каталог заданий.
Шар
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 2 № 27059
Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Аналоги к заданию № 27059: 5049 27185 72765 72719 72721 72723 72725 72727 72729 72731 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 2 № 27072
Даны два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Аналоги к заданию № 27072: 5075 73287 520653 520694 26551 73243 73245 73247 73249 73251 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур
Классификатор стереометрии: Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
3
Тип 2 № 27097
Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Аналоги к заданию № 27097: 74403 74405 74407 74409 74411 74413 74415 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур, Подобие
Классификатор стереометрии: Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
4
Тип 2 № 27125
Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Аналоги к заданию № 27125: 75307 75309 75311 75313 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор стереометрии: Объём цилиндра, конуса, шара
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
5
Тип 2 № 27162
Объем первого шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Аналоги к заданию № 27162: 76349 76355 505443 76351 76353 76357 76359 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур, Подобие
Классификатор стереометрии: Объём цилиндра, конуса, шара, Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по теме «Сфера и шар»
(blacktriangleright) Сфера – это множество точек пространства, находящихся на одинаковом расстоянии от заданной точки (O) (называемой центром сферы).
(blacktriangleright) Шар – это сфера вместе со своей внутренностью.
Основные формулы (где (R) – радиус сферы или шара):
(blacktriangleright) площадь сферы ({large{S=4pi R^2}})
(blacktriangleright) объем шара ({large{V=dfrac{4}{3}pi R^3}})
Задание
1
#1878
Уровень задания: Равен ЕГЭ
Объем шара равен (displaystyle frac{36}{sqrtpi}). Чему будет равна площадь поверхности шара, если его радиус увеличить на (displaystyle frac{6}{sqrtpi})?
(displaystyle V_{text{шара}} = frac{4}{3}pi R^3 = frac{36}{sqrtpi}) (Rightarrow) (displaystyle R = frac{3}{sqrtpi}). Радиус нового шара равен: (displaystyle R_{text{нов.}} = R + frac{6}{sqrtpi} = frac{9}{sqrtpi}). Тогда найдем площадь поверхности: (displaystyle {S_{text{пов.}} = 4pi R_{text{нов.}}^2 = 4pi left(frac{9}{sqrtpi}right)^2 = 4pifrac{81}{pi} = 324}.)
Ответ: 324
Задание
2
#1877
Уровень задания: Равен ЕГЭ
Во сколько раз объем шара больше объема сегмента, высота которого равна половине радиуса?
Необходимо объем шара разделить на объем соответствующего сегмента, высота которого равна (H = frac{1}{2}R)
[frac{V_{text{шара}}}{V_{text{сегм.}}} = frac{frac{4}{3}pi R^3}{pi left(frac{1}{2}Rright)^2left(R — frac{1}{3}left(frac{1}{2}Rright)right)} = frac{frac{4}{3}pi R^3}{frac{5}{24}pi R^3} = frac{4}{3} cdot frac{24}{5} = frac{32}{5} = 6,4.]
Ответ: 6,4
Задание
3
#2674
Уровень задания: Сложнее ЕГЭ
Имеются две сферы (S_1) и (S_2), про которые известно, что радиус первой сферы в (2) раза больше, чем радиус второй сферы. Кроме того, сфера (S_2) целиком находится внутри сферы (S_1). Пусть объём шара, ограниченного второй сферой, равен (V_2), а объём тела, заключённого между сферами, равен (V). Найдите (V : V_2).
Пусть (V_1) – объём шара, ограниченного первой сферой. Так как радиус (S_1) в два раза больше, чем радиус (S_2), то (V_1 : V_2 = 
[V = V_1 — V_2 = 8V_2 — V_2 = 7V_2,,] следовательно, (V : V_2 = 7).
Ответ: 7
Задание
4
#2306
Уровень задания: Сложнее ЕГЭ
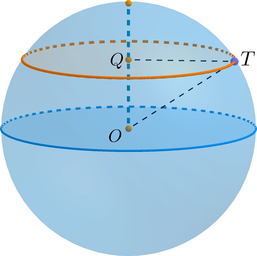
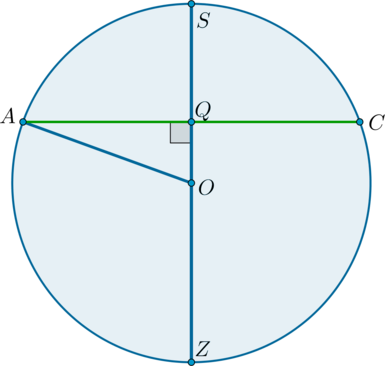
Площадь поверхности шара равна (frac{37}{pi}). На расстоянии (frac1{2pi}) от центра шара проведена плоскость. Найдите длину полученной в сечении окружности.
Т.к. площадь поверхности сферы ищется по формуле (S=4pi R^2), то
[4pi R^2=dfrac{37}{pi} quad Rightarrow quad R^2=dfrac{37}{4pi^2}]
По условию задачи (OQ=frac1{2pi}). Рассмотрим (triangle OQT): он прямоугольный ((angle OQT=90^circ)), гипотенуза (OT=R), катет (QT) равен радиусу (r) окружности сечения.
Таким образом, по теореме Пифагора [QT^2=r^2=OT^2-OQ^2=dfrac{37}{4pi^2}-dfrac1{4pi^2}=dfrac{9}{pi^2}
quad Rightarrow quad r=dfrac3{pi}]
Таким образом, длина окружности сечения равна [C=2pi
r=2picdotfrac3{pi}=6.]
Ответ: 6
Задание
5
#2307
Уровень задания: Сложнее ЕГЭ
Площадь поверхности шара равна (64). На расстоянии (frac3{2sqrt{pi}}) от центра шара проведена плоскость. Найдите площадь полученного сечения.
Т.к. площадь поверхности сферы ищется по формуле (S=4pi R^2), то
[4pi R^2=64 quad Rightarrow quad R^2=dfrac{64}{4pi}]
По условию задачи (OQ=frac3{2sqrt{pi}}). Рассмотрим (triangle
OQT): он прямоугольный ((angle OQT=90^circ)), гипотенуза (OT=R), катет (QT) равен радиусу (r) окружности сечения.
Таким образом, по теореме Пифагора [QT^2=r^2=OT^2-OQ^2=dfrac{64}{4pi}-dfrac9{4pi}=dfrac{55}{4pi}]
Таким образом, площадь сечения равна
[S=picdot r^2=picdot dfrac{55}{4pi}=dfrac{55}4=13,75.]
Ответ: 13,75
Задание
6
#951
Уровень задания: Сложнее ЕГЭ
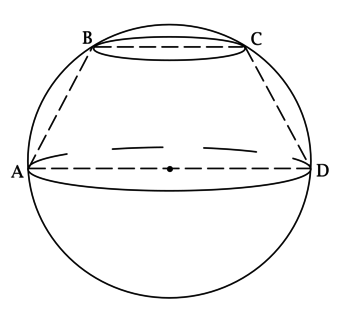
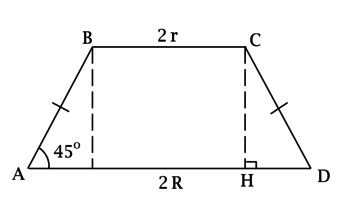
Центр большего основания усечённого конуса совпадает с центром сферы, а окружность его меньшего основания лежит на сфере. Отрезки (BC) и (AD) – диаметры меньшего и большего оснований этого усечённого конуса соответственно, (BCparallel AD), [S_{ABCD} = dfrac{210}{sqrt[3]{pi^2}},qquadqquad dfrac{r}{R} = dfrac{1}{sqrt{15}},] где (R) и (r) – радиусы большего и меньшего оснований усечённого конуса соответственно, (angle ADC = 45^circ). Найдите объём шара, ограниченного данной сферой.
Рассмотрим (ABCD): т.к. (BCparallel AD), то (ABCD) – трапеция. Так как (AB) и (CD) – образующие усечённого конуса, то (AB = CD) и трапеция (ABCD) – равнобедренная.
Построим (CHperp AD). Так как (angle ADC = 45^circ), то (triangle CHD) – равнобедренный и (CH = HD).
[HD = dfrac{AD — BC}{2} = R — r,qquadqquad S_{ABCD} = dfrac{BC + AD}{2}cdot CH = (R + r)(R — r) = R^2 — r^2 = dfrac{210}{sqrt[3]{pi^2}},] но (r = dfrac{R}{sqrt{15}}), тогда [R^2left(1-dfrac{1}{15}right) = dfrac{210}{sqrt[3]{pi^2}}qquadRightarrowqquad R = dfrac{15}{sqrt[3]{pi}}qquadRightarrowqquad V_{text{шара}} = dfrac{4}{3}pi R^3 = dfrac{4}{3}cdotpicdotdfrac{15^3}{pi} = 4500.]
Ответ: 4500
Задание
7
#3114
Уровень задания: Сложнее ЕГЭ
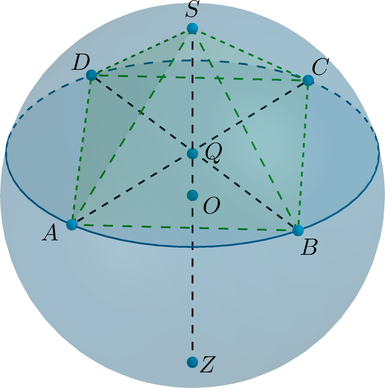
Дан шар, диаметр которого равен (9). Плоскость (alpha) пересекает диаметр (SZ) шара под углом (90^circ) и делит его точкой пересечения в отношении (1:2), считая от вершины (S). Найдите объем пирамиды с вершиной в точке (S), в основании которой лежит квадрат, вписанный в сечение шара плоскостью (alpha).
Пусть (O) – центр шара, (Q) – точка пересечения (SZ) и плоскости (alpha). Пусть (SABCD) – пирамида, объем которой нужно найти.
Рассмотрим сечение шара плоскостью (ASC).
Так как (SQ:QZ=1:2), то (SQ:SZ=1:3), следовательно, (SQ:SO=2:3), следовательно, (OQ:SO=1:3). Тогда [AQ=sqrt{AO^2-OQ^2}=sqrt{AO^2-left(dfrac13AOright)^2}=dfrac{2sqrt2}3AO
=dfrac{2sqrt2}3cdot dfrac92=3sqrt2] Следовательно, (AC=6sqrt2). Следовательно, (AB=AC:sqrt2=6).
Также [SQ=dfrac23SO=dfrac23cdot dfrac92=3] Заметим, что (SQ) – высота пирамиды, так как (SQperp alpha). Следовательно, [V=dfrac13cdot SQcdot AB^2=36.]
Ответ: 36
Задачи по стереометрии, в которых требуется произвести расчет объема сферы и измерение других неизвестных параметров, встречаются в ЕГЭ каждый год. Это означает, что знать основные формулы и уметь оперативно находить правильный ответ должны выпускники с разным уровнем подготовки. Понимая принцип решения задач ЕГЭ, в которых требуется вычислить объем или, к примеру, площадь сферы, старшеклассники смогут выполнять упражнения с любым количеством действий и при этом получить достаточно высокие баллы по итогам прохождения экзаменационного испытания.
Базовая информация
- Сферой называется поверхность, которая состоит из множества точек пространства. Все они располагаются на одинаковом расстоянии от точки О. Она является центром сферы.
- Геометрическое тело, которое ограничено сферой, называется шаром. Его осевое сечение представляет собой круг. Радиус последнего равен радиусу шара.
- Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в n2 раз, а объем — в n3 раз.
Занимайтесь с образовательным порталом «Школково» для качественной подготовки к экзамену!
Проблема поиска необходимой информации встает перед старшеклассниками достаточно остро. Не всегда школьный учебник оказывается под рукой. А поиск базовых формул для вычисления площади, объема шара и других неизвестных параметров бывает достаточно трудоемким даже в онлайн-режиме.
Наш образовательный проект поможет сэкономить время и эффективно подготовиться к сдаче экзаменационного испытания. Мы предлагаем учащимся и их преподавателям выстроить процесс подготовки к ЕГЭ от простого к сложному. Такой подход позволит старшеклассникам понять, какие темы требуют более детального изучения, и улучшить имеющиеся знания.
Базовая информация, которую стоит повторить еще до выполнения задач на нахождение объема шара, представлена в разделе «Теоретическая справка». Материал, подготовленный опытными преподавателями «Школково», поможет вам восполнить пробелы в знаниях без помощи репетитора.
Чтобы задачи ЕГЭ по теме «Шар» или, например, по теме «Цилиндр», не вызывали затруднений, мы предлагаем также потренироваться в выполнении соответствующих упражнений. Множество заданий разной степени сложности вы найдете в разделе «Каталог». Каждое упражнение содержит подробный алгоритм решения. Попрактиковавшись в режиме онлайн и поняв принцип нахождения правильного ответа, школьники смогут без труда вычислить объем сферы.
При необходимости любое задание можно сохранить в разделе «Избранное». Это позволит в дальнейшем вернуться к нему.
Выполнять онлайн-задания на нахождение площади боковой сферы могут не только школьники из столицы, но и выпускники из других российских городов.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
По теме: методические разработки, презентации и конспекты
мини-сборник для подготовки ГИА: «Уравнение с одной переменной»
сборник составлен для подготовки к ГИА по теме «Уравнения с одной переменной»…
Сборник заданий части С для подготовки к ЕГЭ по химии
Здесь собраны задания части С из материалов ЕГЭ по химии….
Сборник по подготовке к ЕГЭ авт.Щеголева Л.М. и Тимченко И.В. издан в журнале «Французский язык»
Сборник содержит различные виды заданий по подготовке к ЕГЭ….
Сборник по подготовке к ЕГЭ, ГИА по темам «Сказуемое и его основные виды», «Тире между подлежащим и сказуемым», «Односоставное предложение».
В связи с переходом образовательных учреждений РФ и в частности школ на новую форму итоговой аттестации в 9 классе возникает необходимость и в новом подходе к планировани…
Сборник по подготовке к ЕГЭ, ГИА по темам «Сказуемое и его основные виды», «Тире между подлежащим и сказуемым», «Односоставное предложение».
В связи с переходом образовательных учреждений РФ и в частности школ на новую форму итоговой аттестации в 9 классе возникает необходимость и в новом подходе к планировани…
Задания из сборника.Часть В 14 (по старому В 13)
Этот документ содержит основные задания из части.В-13.Для успешной сдачи экзамена рекомендую решить самим или с помощью учителя! Успехов!…
Устная часть ОГЭ. Задание 2. Сборник вопросов
Во втором задании устной части ученику предлагается принять участие в телефонном опросе, где у него есть 40 секунд, чтобы ответить на каждый из 6 вопросов….
План изучения темы
- Понятие сферы и отличие от шара.
- Уравнение сферы.
- Площадь поверхности сферы.
- Объём шара.
- Решение задач на тему «Сфера. Шар».
Понятие сферы и отличие от шара
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

Тело, ограниченное сферой, называется шаром. Простыми словами — сфера полая, а шар имеет объём.
Уравнение сферы

По рисунку мы видим, что точка С — это центр сферы, а точка М — лежит на поверхности сферы. У каждой из них свои координаты. Так как расстояние МС равно радиусу сферы, то можно легко получить уравнение сферы:
Площадь поверхности сферы
Площадь поверхности сферы достаточно легко запоминается:
 Объём шара
Объём шара
Объём шара вычисляется по формуле:
 Решение задач на тему «Сфера. Шар»
Решение задач на тему «Сфера. Шар»
Пример 1 (Ященко 36 вариантов, 2021 год, вариант 3)
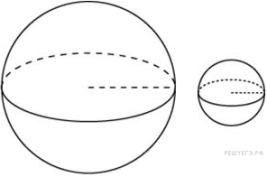
Радиусы двух шаров равны 7 и 24. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
Решение: по формуле находим площадь поверхности каждого шара.
Площадь поверхности нового шара состоит из суммы двух найденных, значит:
Ну и отсюда находим радиус нового шара:
Ответ: 25
Пример 2 (Ященко 36 вариантов, 2021 год, вариант 13)
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 188. Найдите объём конуса.
Решение:


Видим, что и тут всплыл радиус в кубе. Значит, нужно всего лишь посчитать объём конуса:
Ответ: 47
Пример 3
Напишите уравнение сферы с центром в точке А(3;0;-5) и радиусом R=5.
Решение: уравнение сферы:
В нашем случае:
Подставляем и пишем уравнение сферы:
Шар
1. 
2. 
3. 
4. 
5. 
6. 
7. 
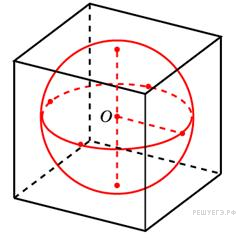
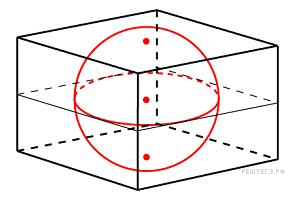
8. В куб вписан шар радиуса 1. Найдите объем куба.
-
Около шара описан цилиндр, площадь поверхности которого равна 6. Найдите площадь поверхности шара.
-
Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.
-
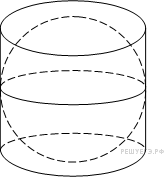
Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
-
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна
. Найдите радиус сферы.
-
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен
. Найдите образующую конуса.
-
Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.








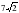 . Найдите радиус сферы.
. Найдите радиус сферы.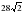 . Найдите образующую конуса.
. Найдите образующую конуса.