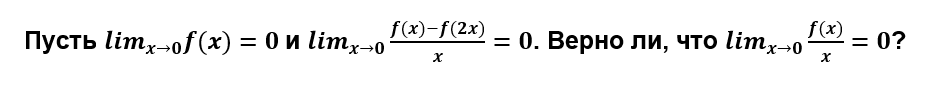Шад экзамен по математике - Помощь в подготовке к экзаменам и поступлению

Приём в 2022

Те, кто готовится к поступлению, могут посмотреть решения нескольких заданий из вариантов письменного экзамена, демонстрирующие полезные факты и приёмы.

Запись дня открытых дверей ШАД от 2021 года. Вы можете узнать все подробности о поступлении и обучении в ШАДе, о различиях между направлениями и карьерных перспективах после выпуска, а также о совместных магистерских программах с вузами.

Набор 2022 закрыт. Новый набор стартует ориентировочно в апреле 2023 года. Вы можете подписаться на новости и получить письмо о начале набора.

ШАД подходит тем, кто:

интересуется анализом данных или архитектурой распределенных систем;
готов тратить не менее 30 часов в неделю на учебу;
обладает хорошей математической подготовкой и знаком с каким-нибудь языком программирования или имеет опыт в IT и обладает некоторой математической культурой.

При поступлении в ШАД проверяются знания в рамках общей программы, включающей базовые разделы высшей алгебры, математического анализа, комбинаторики, теории вероятностей, а также основы программирования и анализа данных.

Также доступен альтернативный трек поступления в ШАД. Он предназначен в первую очередь для тех, у кого уже есть опыт промышленной разработки или научных исследований в области Data Science. На втором этапе отбора и на собеседовании вам не придётся решать трудных задач по высшей математике, но зато нужно будет показать хорошее умение программировать. Кроме того, при отборе мы будем учитывать участие в проектах, наличие статей и в целом индустриальный опыт.

Набор проходит в три этапа

1. Онлайн-тестирование

После заполнения анкеты поступающего вы получите письмо со ссылкой. На решение заданий теста отводится пять часов.

2. Второй этап

Для поступающих в московское отделение ШАД второй этап состоит из двух частей: первая — математика и алгоритмы, вторая — программирование и основы анализа данных.
Для проступающих в филиалы ШАД или на заочное отделение второй этап отбора — онлайн-экзамен.

3. Собеседование

Собеседования пройдут очно и онлайн с конца июня по конец июля в филиалах ШАД. На собеседовании нужно будет решать задачи по математике, алгоритмам и программированию. Также нужно пройти собеседование по мотивации.

Платное обучение

Поступающие, хорошо показавшие себя на собеседовании, но не прошедшие по общему конкурсу, смогут начать учиться на платной основе. Платное обучение возможно только в Москве.

Обучение на платной основе ничем не отличается от бесплатного — нужно выполнять всё те же непростые задания, укладываясь в жёсткие сроки.

Обучение стоит 150 000 рублей за семестр. Стоимость обучения будет снижена до 75 000, если студент заканчивает семестр на «хорошо» и «отлично». Сдавший на «хорошо» и «отлично» две сессии подряд дальше учится бесплатно.

Примеры заданий

Если вы хотите получше подготовиться и знать, что вас ждёт, порешайте варианты прошлых лет.

Часто задаваемые вопросы

Поступление

Как поступить в Школу анализа данных?
Чтобы поступить в Школу анализа данных, нужно пройти три этапа отбора: онлайн-тестирование, экзамен и собеседование.Онлайн-тестирование — это тест с задачами по математике и программированию, где нужно выбрать один ответ. Сдать тест можно в любое время в течение месяца, но есть всего одна попытка.Во время экзамена нужно решить задачи по математике, алгоритмам, программированию и основам анализа данных.Поступающие в Москве сдают экзамен в два этапа: — математика и алгоритмы; — программирование и основы анализа данных.Поступающие в филиалы ШАД пишут один онлайн-экзамен на все темы.Собеседование проходит по трем секциями: алгоритмы, программирование, мотивация. О времени собеседования договариваемся индивидуально.Новый набор в ШАД стартует в апреле. Чтобы записаться, оставьте свои данные в разделе «Подробнее о поступлении».
Как происходит отбор на заочное отделение?
Чтобы поступить на заочное отделение, нужно пройти онлайн-тестирование, онлайн-экзамен и собеседование.
Существуют ли подготовительные курсы в ШАД?
Нет.
Чем отличается альтернативный трек поступления от классического?
Альтернативный трек подходит тем, у кого есть опыт промышленной разработки или научных исследований в области Data Science. Во время экзамена и на собеседовании не нужно решать задачи по высшей математике, но важно показать умение программировать. Мы также учитываем участие в проектах, наличие статей и опыт.
Возьмут ли меня, если я уже не студент? А если я вообще не выпускник вуза? Или имею только юридическое образование? Или я — гражданин другой страны?
Да, никаких ограничений нет. Если вы поступаете по классическому треку, главное иметь необходимые знания по высшей алгебре, математическому анализу, комбинаторике, теории вероятностей и основам программирования. Если вы поступаете по альтернативному треку, важно иметь опыт в IT, базовую математическую культуру и хорошие навыки программирования.Темы для поступления и список рекомендованной литературы найдете в Программе поступления
Можно ли сразу поступить на платное очное или заочное без экзаменов?
Нет. Во всех отделениях Школы обучение бесплатное. Учиться платно можно только в Москве, если вы хорошо показали себя на собеседовании, но не прошли по конкурсу.
Сколько людей возьмут в ШАД?
Всё зависит от конкурса. Фиксированного количества мест нет.
Стоит ли идти в ШАД, если я хочу заниматься наукой?
Да. В ШАД проходят научные семинары и исследовательские проекты. У нас можно пообщаться с ведущими исследователями Data Science и сделать первые шаги в научной карьере.

Обучение

Как проходит обучение в ШАД?
Занятия проходят с 18:00 до 21:00 по московскому времени. Записи всех актуальных лекций и семинаров есть в личном кабинете, там же можно сдавать домашние задания.
Можно ли совмещать учёбу в ШАД и работу?
Занятия проходят вечером. Вместе с домашними заданиями обучение занимает около 30 часов в неделю. Если вы сможете работать и учиться при таких условиях, с нашей стороны ограничений нет.
Эквивалентно ли обучение в ШАДе обучению в магистратуре?
Нет, ШАД — это дополнительное профессиональное образование. В конце обучения вы получаете диплом о профессиональной переподготовке.
Чем отличается очное обучение от заочного?
Некоторые формы отчётности на очном и заочном обучении устроены по-разному. Других отличий нет: студенты очного отделения могут заниматься в онлайне, им не обязательно посещать занятия. Дипломы одинаковые и там, и там.
Получу ли я диплом об окончании обучения в ШАДе?
Да, вы получите диплом о профессиональной переподготовке.

Источник

Экзамены в ШАД — это серьёзная проверка и стресс даже для абитуриентов с хорошей подготовкой: нужно глубоко знать теорию математики, программировать и решать олимпиадные задачи. С наскока освоить такой объём информации не получится. Поэтому первым делом внимательно изучите программу на сайте и определите, какие темы вы знаете хорошо, а что нужно подтянуть.

Дисциплина — ключ к успеху

Начинайте готовиться сразу, как только определились с темами. Чётко распишите план подготовки, учитывая текущую загрузку, и обязательно сделайте скидку на то, что всё может пойти не так. Занимайтесь регулярно, но без фанатизма. Не нужно зубрить 24/7: в какой-то момент наступит перенасыщение знаниями и от подготовки не будет толка.

Хорошее самочувствие тоже часть подготовки. Не забывайте переключаться и делать передышки. Это поможет не перегореть и сохранить силы для поступления.

Выбор трека как стратегия

Есть разные подходы к подготовке в зависимости от выбранного трека, но база неизменна. Повторите все формулировки и определения из программы, откройте варианты и контесты прошлых лет — и решайте все задачи, которые с ходу не даются. Навыки программирования оттачивайте на LeetCode, Codeforces или TopCoder, а умение рассуждать — объясняя решение задач друзьям, далёким от математики. Тренируйтесь, пока не начнёте описывать выводы стройно и понятно, на собеседованиях, помимо знаний, оценивается умение излагать ход мыслей. Учитесь задавать вопросы по задаче, это поможет, если запутаетесь в решении.

Не злоупотребляйте готовыми разборами. Во-первых, в интернете многие задачи, особенно по теории вероятностей, разбираются неправильно. Во-вторых, заучивание готового не поможет на экзаменах. Лучше просидеть над задачей три дня, самостоятельно прийти к какому-то некрасивому решению и только после этого прочитать правильное. Так вы запомните его гораздо лучше и сможете объяснить.

— Михаил Берновский, студент 1-го курса ШАДа, альтернативный трек.

Насколько глубоко погружаться в каждую тему, зависит от того, на какой трек вы поступаете. Если на классическом треке ожидается, что вы понимаете связь между размерностью ядра, размерностью образа и кратностью нуля как собственного значения матрицы, то на альтернативном треке достаточно помнить, что для нахождения ядра нужно решить систему. Поступая на альтернативный трек, нужно понимать, как что-то посчитать, а поступая на классический — нужно уметь свободно рассуждать на тему решения и на близкие темы.

Но это не значит, что альтернативный трек — лёгкий способ попасть в ШАД. При поступлении на него требуется опыт в IT: промышленная разработка или исследования в области data science.

Классический трек и три математических столпа

Есть три больших области знаний, в которых надо ориентироваться: математический анализ, линейная алгебра и теория вероятностей. Хорошая стратегия — досконально изучить хотя бы две, а лучше все три.

Я поступала в ШАД на 4-м курсе мехмата, поэтому математику более-менее помнила. Из книг читала «Комбинаторику» Виленкина и «Основы теории вероятностей» Жуковского. Но это всё не помогает, пока не решишь минимум 100 задач на каждый жанр.

— Евгения Елистратова, выпускница ШАДа, разработчица в Яндекс Погоде.

В матанализе огромное количество теории, но для успешного прохождения экзаменов важнее решать задачи, очень много задач. Без умения хорошо считать не обойтись: нужно уметь брать интегралы, дифференцировать, находить минимумы и максимумы.

Пример экзаменационной задачи по математическому анализу.

Линейная алгебра также нужна во многом на уровне языка. Теория пригодится ровно настолько, чтобы хорошо решать задачи. На практике важнее всего будет уметь работать с матрицами, но вы сильно выиграете, если сможете, глядя на абстрактные матричные выражения, вспомнить соответствующую теорию.

Пример экзаменационной задачи по линейной алгебре.

К экзамену по теории вероятностей, в отличие от матанализа и линейной алгебры, готовиться нужно намного основательнее. Есть много условий и ограничений в теоремах, которые важно повторить. Например, есть разные типы сходимости, и нужно помнить, какой из какого следует, какой — в центральной предельной теореме, а какой — в законе больших чисел. Желательно также повторить основные распределения и уметь с ними работать.

Пример экзаменационной задачи по теории вероятностей.

Альтернативный трек: алгоритмы и IT-опыт

Если вы выбрали альтернативный трек, то бóльшую часть математической теории можно опустить, максимально сосредоточившись на написании кода и алгоритмах.

Хотя совсем без математики не обойтись. Необходимо уметь объяснять математические задачи, а также знать базовые алгоритмы и определения из матанализа и линейной алгебры. Как минимум, дифференцировать точно нужно уметь.

Я поступал в ШАД через несколько лет после окончания вуза и понимал, что не конкурент свежим выпускникам мехмата. Поэтому сразу выбрал альтернативный трек. На всю программу по математике у меня времени не было, и я стал решать ШАДовские задачи с прошлых экзаменов. Параллельно читал разборы, чтобы освежить теорию.

— Леонид Курахтенков, студент 1-го курса ШАДа, альтернативный трек.

Задачи по теории вероятностей здесь будут немного проще, чем в классическом треке. Скорее всего, потребуется вычислить дискретную вероятность — решить «задачу с цветными шариками». Также нужно будет показать, что вы умеете рассуждать логически, не путаете причину и следствие и не считаете, что пример доказывает утверждение.

Повторите теорию алгоритмов и структур данных: сортировки, обходы графов, устройство хэш-таблиц и «жадные» алгоритмы. Рекомендуем пройти тренировки по алгоритмам: в них собрана хорошая база теории, а также задачи с разбором для прокачки практических навыков.

Что касается машинного обучения, то здесь достаточно разбираться в основах. Строить сложные модели, требующие больших вычислительных ресурсов, на экзамене не потребуется, но нужно уметь анализировать данные и понимать, как решаются нетривиальные задачи обучения с учителем и без.

Какой опыт необходим для поступления на альтернативный трек? В первую очередь, конечно, индустриальная разработка, ML и продуктовая аналитика. Если у вас есть исследовательский опыт или опубликованные научные статьи, расскажите об этом в своей анкете и на собеседовании.

Как определить мотивацию

Итак, вы прошли все этапы, осталось собеседование по мотивации. Как к нему подготовиться и о чём говорить с куратором? Сначала честно ответьте на вопрос: «Зачем вам ШАД». Вы хотите подняться на новый карьерный уровень, сменить профессиональный трек или углубиться в то направление, которое уже изучаете?

Если вы учитесь в вузе на математической специальности и ищете прикладное применение своим знаниям в IT, то ШАД поможет объединить теорию и практику.

ШАД — это хорошая возможность развиться в профессиональном плане как дата-саентист или разработчик машинного обучения. В университете я изучаю науку, а ШАД даёт этой базе конкретное практическое применение.

— Константин Гордеев, студент 1-го курса ШАДа, классический трек.

Сформулируйте мотивацию заранее, так вы поймёте, какие моменты подсветить на собеседовании, а что звучит не слишком убедительно. Обдумайте на берегу, готовы ли вы вкладываться в учёбу на 200%: важно показать, что вы не просто загорелись идеей поступить в ШАД, но и полны решимости трудиться два года. И если это так — дерзайте!

Полезные материалы

Здесь собран минимум, который пригодится для подготовки к экзаменам. Но, конечно, мы рассчитываем, что вы знакомы со всем списком рекомендуемой литературы.

1. Алгоритмы: построение и анализ (Т. Кормен, Ч. Лейзерсон, Р. Риверст, К. Штайн)

2. Задачи и теоремы линейной алгебры (В. Прасолов)

3. Основные понятия теории вероятностей (А. Колмогоров)

4. Курс теории вероятностей и математической статистики (Б. Севастьянов)

5. Курс комбинаторики А. М. Райгородского в YouTube

6. Тренажёры по написанию кода: Codeforces, LeetCode или TopCoder

7. Контесты прошлых лет

8. Задачи с экзаменов в ШАДе для классического и альтернативного треков

9. Тренировки Яндекса по алгоритмам

10. Разбор задач для поступления в ШАД

11. Архив олимпиады Putman Competition

Также рекомендуем почитать статью Виктора Рогуленко о том, как он готовился к поступлению в ШАД в 2019 году. Ждём ваших заявок и желаем удачи!

Источник

Алгоритмы, Занимательные задачки, Математика

Рекомендация: подборка платных и бесплатных курсов таргетированной рекламе — https://katalog-kursov.ru/

Привет! С вами Азат Калмыков, куратор в «ШАД Helper». Мы продолжаем наш цикл статей, в которых разбираем задачи для поступления в ШАД. На этот раз мы (я, Николай Проскурин и Александр Курилкин) посмотрим на решения первого этапа отбора в ШАД в этом году, который закончился совсем недавно. Итак, приступим.

A. Локальный минимум

При каких значениях параметра a первообразная функции

$f(x)=left(x^{4}-(a+1) x^{3}+(a-2) x^{2}+2 a xright) exp ^{frac{sin x^{2}+2}{5 x^{2}+2}}$ имеет не более одного локального минимума?

Решение

Заметим, что производная от первообразной — это исходная функция. Значит, нам нужно исследовать на смену знака нашу исходную функцию. Конкретно, надо понять, сколько раз функция меняет знак с минуса на плюс (то есть посчитать количество точек локального минимума).

Заметим, что экспонента всегда положительна, не влияет на знак, поэтому её можно откинуть и считать, что

. Многочлен легко раскладывается на множители, потому что все его корни можно угадать: это

. Значит,

Если многочлен имеет четыре различных корня, то он меняет знак в порядке

, и потому имеет хотя бы два локальных минимума. Значит, нам могут подойти только

. Прямая проверка показывает, что все они являются ответами.

B. Предел

Определите, при каком значении

$a$ данный предел равен

$frac{1}{e}$ :

$lim _{x rightarrow +inf }left(cos sqrt{frac{1}{x}}right)^{frac{x}{a}}$

Решение

Сначала посчитаем предел, приняв

$a = 1$ . Поскольку

$sqrt{frac{1}{x}} to 0$ , мы можем разложить функцию в ряд Тейлора в нуле:

$cos{sqrt{frac{1}{x}}} = 1 - frac{1}{2!x} + frac{1}{4!x^2} - frac{1}{6!x^3} + ldots$

Ограничим ряд сверху и снизу и воспользуемся теоремой о двух милиционерах. Заметим, что сумма больше первых двух слагаемых, так как группируя последующие слагаемые по два, мы получим бесконечное число положительных чисел, которые мы откидываем. Аналогично, сверху сумму можно оценить суммой первых трёх слагаемых. Значит:

$1 - frac{1}{2x} < cos{sqrt{frac{1}{x}}} < 1 - frac{1}{2x} + frac{1}{24x^2}$

Поскольку

, от возведения в степень

$x$ неравенство сохранится, а при переходе к пределу изменится только строгость знаков. Левую часть можно посчитать сразу как следствие из второго замечательного предела, она равна

$e^{-1/2}$ . Покажем, что правая равна тому же:

$lim_{x to +infty} left( 1 - frac{1}{2x} + frac{1}{24x^2} right)^x = expleft(lim_{x to +infty} x lnleft( 1 - frac{1}{2x} + frac{1}{24x^2} right)right) =$

$= expleft(lim_{x to +0} frac{lnleft( 1 - frac{x}{2} + frac{x^2}{24} right)}{x}right)$

Применяя правило Лопиталя, получаем требуемое. Значит:

$lim_{x to +infty} left(cos{sqrt{frac{1}{x}}}right)^x = e^{-1/2} Rightarrow lim_{x to +infty} left(cos{sqrt{frac{1}{x}}}right)^{x/a} = e^{-1/2a}$

Откуда

$a = frac{1}{2}$ .

Примечание: зная, что степенной ряд можно бесконечно дифференцировать в области сходимости, можно было пропустить шаг с оценкой ряда и сразу применить Лопиталя.

C. Локальный минимум

При какой минимальной длине шага градиентный спуск не сможет найти минимум функции

, если

$x_0=1$ ?

Решение

Вспомним, что шаг градиентного спуска при константной длине шага считатеся следующим образом:

В нашем случае градиент — это обычная одномерная производная, так что наша задача проще градиентного спуска в общем случае.

$x_0$ нам известно, давайте посчитаем

$x_1$ :

Давайте заметим что, при

значение градиента будет таким же по модулю, как в точке

$x_0$ , но иметь обратный знак. Таким образом, можно понять, что при таком варианте градиентный спуск будет «скакать» туда-сюда из точки

$1$ в

$-1$ и обратно. Таким образом, можно понять, что при

градиентный спуск уже не найдёт точку минимума (это точка

$0$ ). Но надо показать, что при меньших

она будет найдена.

Это можно понять и интуитивно, но давайте попробуем доказать строго. Можно доказать что

$|x_{n+1}| leq |x_n||1-4lambda|$ по индукции. Здесь нам важно, что

База:

Переход.

$|x_{n+1}| = |x_n - 4lambda x_n^3| = |x_n| |1-4lambda x_n^2|$ . За счёт предположения индукции можем получить что

. Тогда

$|x_{n+1}| leq |x_n||1-4lambda|$ . Всё доказано.

Пользуясь доказанным, можно получить, что

. Так как знаем, что

, то получим что

$|x_n|$ сходится к нулю. Значит градиент находит минимум.

D. Собственный вектор

Определите, при каких значениях параметра a вектор

$left(begin{array}{l} 1 \ 1 \ a end{array}right)$ является собственным вектором матрицы

$left(begin{array}{ccc} a & 1 & -1 \ 1 & 2 & -1 \ 0 & 0 & 1 end{array}right)$

Решение

По определению, вектор

является собственным для матрицы

$A$ , если

. Получаем уравнение:

$begin{pmatrix} a & 1 & -1 \ 1 & 2 & -1\ 0 & 0 & 1\ end{pmatrix} begin{pmatrix} 1 \ 1 \ a \ end{pmatrix} = begin{pmatrix} 1 \ 3 - a \ a \ end{pmatrix} = lambda begin{pmatrix} 1 \ 1 \ a \ end{pmatrix}$

По первой координате получаем. что

, по второй — что

$a = 2$ , проверяем, что третья координата согласуется с ответом. Значит,

$a = 2$ .

E. Определитель

При каких значениях параметра

$a$ максимален определитель матрицы, обратной к этой?

$left(begin{array}{ccc} a & -7 & -3 \ 6 & -10 & -a^{2} \ 0 & a & 9 end{array}right)$

Решение

Посчитаем определитель исходной матрицы:

$det(a) = begin{vmatrix} a & -7 & -3 \ 6 & -10 & -a^2 \ 0 & a & 9 \ end{vmatrix} = a begin{vmatrix} -10 & -a^2 \ a & 9 \ end{vmatrix} - 6 begin{vmatrix} -7& -3 \ a & 9 \ end{vmatrix} = a^4 - 108a + 376$

Несложно понять, что производная строго возрастает, значит, точка, в которой производная обнуляется, это точка минимума функции

, откуда

и минимум достигается в точности в

$a = 3$ . Тогда, пользуясь формулой

$det(A^{-1}) = det(A)^{-1}$ , получаем, что максимум определителя обратной матрицы достигается в

$a = 3$ .

F. Проекции

Даны точки

, а также плоскости

$alpha$ :

$?$ :

. Найдите координаты точки

$A$ , если известно, что её ортогональная проекция на

$alpha$ совпадает с проекцией точки

$B$ , а на

$beta$ — с проекцией точки

$С$ .

Решение

Если

имеет ту же проекцию на плоскость, что и

$B$ , то она лежит на прямой, перпендикулярной плоскости и содержащей

$B$ . Эту прямую можно задать параметрически, поскольку мы знаем точку и направляющий вектор, который совпадает с вектором нормали к

$alpha$ и потому равен

$overline{n}_1(2, -2, 1)$ . Система для прямой:

$begin{cases} x = 2t_1 + 1\ y = -2t_1 + 2\ z = t_1 - 3\ end{cases}$

Аналогично,

$A$ лежит на прямой, проходящей через

$C$ и перпендикулярной

$beta$ . Вектор нормали:

$overline{n}_2(-1, 2, 3)$ , система:

$begin{cases} x = -t_2 + 2\ y = -2t_2 + 2\ z = 3t_2 + 1\ end{cases}$

Пересечение прямых и будет являться искомой точкой. Для её нахождения нужно определить

$t_1$ и

$t_2$ , для этого достаточно приравнять первые два уравнения систем:

$begin{cases} 2t_1 + 1 = -t_2 + 2\ -2t_1 + 2 = 2t_2 + 2\ end{cases} Leftrightarrow begin{cases} 3 = t_2 + 4\ -2t_1 + 2 = 2t_2 + 2\ end{cases} Leftrightarrow begin{cases} t_2 = -1\ t_1 = 1\ end{cases}$

Подставив параметры в обе системы, убеждаемся, что получили одну и ту же точку

, которая и является искомой.

G. Домино

В далёком созвездии Тау-Кита на каждой половинке костяшки домино стоит от

$0$ до

$N$ точек, причём для каждой пары чисел

$(a,b)$ таких, что

$a$ и

$b$ целые от

$0$ до

$N$ , существует ровно одна доминошка, содержащая оба этих числа. Космический турист прилетел и выбрал наугад перевёрнутую костяшку. При каком

$N$ математическое ожидание модуля разности количеств точек на одной и на другой половине этой доминошки будет равно

$2$ ?

Решение

Обозначим случайную величину за

$xi$ , вероятностное пространство за

$Omega$ и образ случайной величины за

. Будем считать матожидание по формуле:

$E(xi) = sum_{k in xi(Omega)} k Pr[xi = k] = 2$

Пусть

$A_k$ — событие, что величина примет значение

$K$ , тогда

$Pr[xi = k] = frac{|A_k|}{|Omega|}$ . Домножив на

, получаем:

$sum_{k in xi(Omega)} k |A_k|= 2 |Omega|$

Посчитаем

. Во-первых, в него входят доминошки с одинаковыми числами на половинках. Во-вторых, в него входят все возможные пары различных чисел, причем каждая по одному разу. Значит,

$|Omega| = n + 1 + frac{n(n + 1)}{2}$

Теперь посчитаем сумму. Понятно, что величина принимает значения от 0 до

$n$ . Сколько раз она принимает значение

$k$ ? Ровно

: благоприятные исходы — это доминошки

. Значит:

$sum_{k in xi(Omega)} k |A_k| = sum_{k = 0}^n k(n - k + 1) = (n + 1)sum_{k = 0}^n k - sum_{k = 0}^n k^2 = frac{n(n + 1)^2}{2} -$

$- frac{n(n + 1)(2n + 1)}{6} = frac{n(n + 1)(n + 2)}{6}$

Получаем уравнение:

$frac{n(n + 1)(n + 2)}{6} = (n + 1)(n + 2)$

Поскольку

$n > 0$ , получаем, что

$n = 6$ .

H. Экзамен

Два друга решили вместе пойти на экзамены в ШАД и договорились встретиться у входа с 14:00 до 15:00, но не договорились во сколько именно. Момент времени прихода каждого из них распределён равномерно на этом отрезке времени, но друзья нетерпеливые, поэтому через 15 минут ожидания они отчаиваются дождаться и заходят одни. Известно, что они встретились.

Найдите вероятность того, что оба пришли до 14:45.

Решение

Для того, чтобы решить эту задачу, нам нужно немного порисовать. А именно, давайте нарисуем квадрат 60×60. Ось x будет обозночать время прихода первого, y — второго.

Событие «друзья встретились» изображено на рисунке красной областью. Событие «каждый пришёл до 14:45» обозначено пересечением 2 зелёных областей. Пользуясь тем, что время прихода каждого из друзей распределено равномерно, можем понять, что вероятность того, что «каждый пришёл до 14:45» при условии, что «друзья встретились» это отношение площади пересечения всех 3 областей к площади красной области. Применяя теорему пифагора и простой счёт, можем получить ответ

$frac{5}{7}$ .

I. Случайная величина

Плотность распределения случайной величиы

$xi$ равна

$p(x)=frac{1}{sin x}$ при

$x$ от

$pi/2$ до

и нулю при всех остальных

$x$ .

Найдите значение, которое эта случайная величина не превосходит с вероятностью

$frac{1}{2}$ .

Решение

Выразим искомую величину через плотность и воспользуемся универсальной тригонометрической подстановкой:

$Pr(xi leq x) = intlimits_{pi/2}^x frac{dt}{sin{t}} = intlimits_{1}^{tan{x/2}} frac{du}{u} = ln{tan{frac{x}{2}}}$

Получили уравнение:

$ln{tan{frac{x}{2}}} = frac{1}{2} Leftrightarrow tan{frac{x}{2}} = e^{1/2} Leftrightarrow x = 2 tan^{-1}{e^{1/2}}$

J. Найти среднее

Условие

Костя разрабатывает модуль статистики для высоконагруженного сервиса. Накопилось много исторических данных: n вещественных чисел

$a_0, a_1, dots, a_{n-1}$ .

Из-за частого обращения к его модулю за вычислением среднего геометрического эту функцию необходимо ускорить!

На вход поступают множество запросов по поиску среднего на интервале индексов от l до r. Найдите необходимые значения.

Для запроса от

$l$ до

$r$ необходимо вернуть величину:

$sqrt[r-l+1]{a_{l} cdot a_{l+1} cdot ldots cdot a_{r}}$

Формат ввода

В первой строке входных данных записано число

$n$ (

Во второй строке записаны n вещественных чисел

$a_i$ (

) с двумя десятичными знаками.

В третьей строке входных данных записано число

$q$ (

) — количество запросов.

Далее в

$q$ строках записано по два целых числа

$l_i$ и

$r_i$ (

) —

$i$ -й запрос на вычисление среднего.

Формат вывода

Для каждого запроса на вычисление среднего выведите найденное значение с 6 верными знаками после точки.

Ответы должны следовать в соответствии с порядком запросов.

Пример 1

Пример 2

Пример 3

Примечания

Костя считает, что его реализация функции эффективно использует соотношение

$xy = e^{ln x + ln y}$ . Но вы можете это соотношение не использовать.

Решение

Для простоты сначала рассмотрим вариацию со средним арифметическим. Чтобы вычислять его для отрезка за

$О(1)$ , необходимо находить сумму на отрезке за

$O(1)$ .

Это делается с помощью следующего трюка. Насчитаем массив sums, где

. Так как

, то это можно сделать за

$O(n)$ . Теперь сумма на отрезке с

$l$ по

$r$ — это просто

. Чтобы вычислить среднее арифметическое на отрезке, нужно еще поделить эту сумму на

. Итого

$O(1)$ на запрос и

$O(n)$ на предподсчёт.

В вариации со средним геометрическим чуть посложнее. Так как теперь вместо суммы у нас умножение, числа могут расти довольно быстро, и произведение чисел на префиксе может быть настолько большим или маленьким, что не будет влезать в стандартные типы данных. Чтобы решить эту проблему, будем считать натуральный логарифм среднего геометрического, а потом просто возведем

$e$ в эту степень. Школьная математика гласит, что

$ln ((a[l] cdot ... cdot a[r])^{frac{1}{r - l + 1}}) = frac{ln a[l] cdot dots cdot a[r]}{r - l + 1} = frac{ln a[l] + dots + ln a[r]}{r - l + 1}$ , а сумму логарифмов можно посчитать за

$О(1)$ с помощью описанного выше трюка.

Код: gist.github.com/Azatik1000/0b0d8496785169a8ac0d35a8c9e8e59f