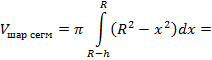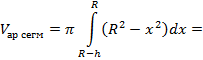Каталог заданий.
Шар
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 2 № 27059
Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Аналоги к заданию № 27059: 5049 27185 72765 72719 72721 72723 72725 72727 72729 72731 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 2 № 27072
Даны два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Аналоги к заданию № 27072: 5075 73287 520653 520694 26551 73243 73245 73247 73249 73251 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур
Классификатор стереометрии: Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
3
Тип 2 № 27097
Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Аналоги к заданию № 27097: 74403 74405 74407 74409 74411 74413 74415 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур, Подобие
Классификатор стереометрии: Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
4
Тип 2 № 27125
Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Аналоги к заданию № 27125: 75307 75309 75311 75313 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор стереометрии: Объём цилиндра, конуса, шара
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
5
Тип 2 № 27162
Объем первого шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Аналоги к заданию № 27162: 76349 76355 505443 76351 76353 76357 76359 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур, Подобие
Классификатор стереометрии: Объём цилиндра, конуса, шара, Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
({color{red}{{small{textbf{Факт 1. Про шаровой сегмент}}}}})
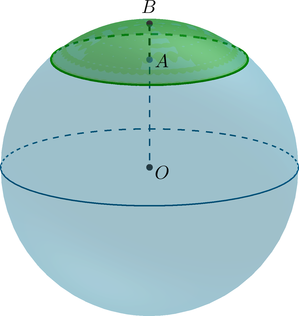
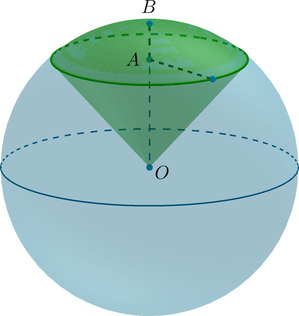
(bullet) Шаровой сегмент – шасть шара, отсекаемая от него плоскостью ((alpha)).
(bullet) Если (O) – центр шара, (OB=R) – радиус шара, перпендикулярный плоскости (alpha), (A) – центр круга (основания шарового сегмента), а также точка пересечения радиуса (OB) c этим кругом, то
(H=AB) – высота шарового сегмента.
(bullet) Площадь сферического сегмента (часть сферы, отсекаемая от нее плоскостью (alpha)) вычисляется по формуле [S=2pi cdot RH] (bullet) Объем шарового сегмента вычисляется по формуле [V=pi H^2cdot left(R-frac13Hright)]
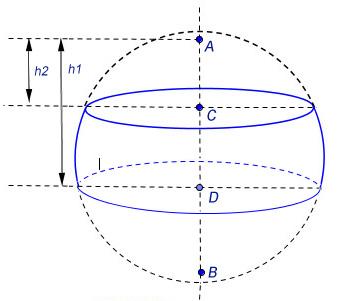
({color{red}{{small{textbf{Факт 2. Про шаровой слой}}}}})
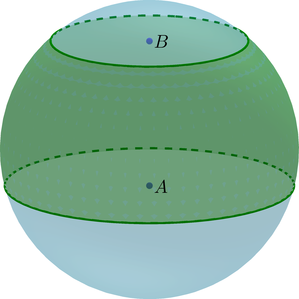
(bullet) Шаровой слой – часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.
(bullet) Основания шарового слоя – это сечения шара плоскостями.
(bullet) Высота (H=AB) шарового слоя – это расстояние между основаниями.
(bullet) Площадь сферической части шарового слоя равна [S=2pi RH] где (R) – радиус шара.
(bullet) Объем шарового слоя равен разности объемов двух шаровых сегментов: [V=V_{A}-V_{B}]
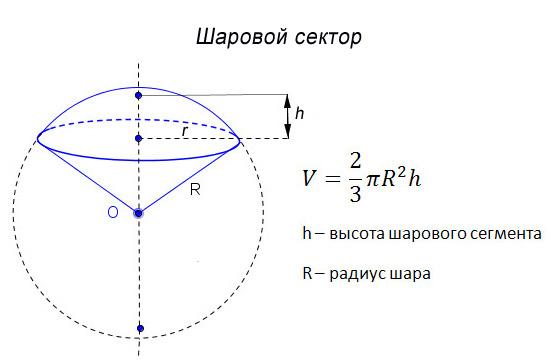
({color{red}{{small{textbf{Факт 3. Про шаровой сектор}}}}})
(bullet) Шаровой сектор – часть шара, ограниченная сферической частью шарового сегмента и боковой поверхностью конуса, имеющего то же основание, что и шаровой сегмент.
(bullet) Если (H=AB), то объем шарового сектора равен [V=dfrac23pi R^2cdot H]
Комментарии преподавателя
Задача 1 (вычисление объёма шарового сектора)
Найти объём шарового сектора, если известен радиус шара – 75 см, и радиус окружности, лежащей в основании соответствующего шарового сегмента – 60 см (рис. 1).
Рис. 1. Иллюстрация к задаче
Дано: r = 60 см; R = 75 см
Найти:
Решение:
1. Введём обозначения:



2. Для того чтобы вычислить объём шарового сектора, необходимо знать радиус шара (он нам известен) и высоту сегмента 
Рассмотрим прямоугольный треугольник 




3. Найдём высоту сегмента H:


4. Подставим в формулу объёма шарового сектора известные величины:



Ответ: 
Задача 2 (определение объёма шарового сегмента)
Высота шарового сегмента составляет 0,1 диаметра шара. Определить, какую часть объёма шара составляет объём шарового сегмента.
Дано:
Найти:
Решение:
1. Так как высота H шарового сегмента – это 

2. Найдём объём шарового сегмента:


3. Найдём отношение объёма сегмента к объёму шара, то есть узнаем, какую часть объёма шара составляет объём шарового сегмента.
Объём сегмента:

Объём шара:

Отношение объёма сегмента к объёму шара:

Ответ: объём шарового сегмента составляет 
Задача 3 (определение объёма шарового сегмента)
В шаре проведена плоскость, которая перпендикулярна диаметру и делит диаметр на два отрезка длиной 6 см и 12 см. Найти объёмы частей, на которые делит плоскость шар.
Рис. 2. Иллюстрация к задаче
Дано: 

Найти:
Решение:
На рисунке 2 изображено осевое сечение шара (окружность) и плоскости (DC), AB – диаметр шара.
1. Диаметр шара равен:


Следовательно, радиус шара:


2. Плоскость разделила шар на два сегмента, найдём объём меньшего с высотой 


3. Объём второго сегмента можно аналогично найти по формуле объёма шарового сегмента или как разность объёма шара и объёма сегмента с высотой 

Объём шара:


Ответ: 



Разветвление: задача 4
В III веке до нашей эры жил великий учёный своих дней – Архимед. Он сделал множество открытий, но, согласно легенде, больше всего он гордился тем, что получил соотношение между объёмом цилиндра и объёмом вписанного в этот цилиндр шара. Согласно этой же легенде, на могиле Архимеда, которая не сохранилась до наших дней, был изображен цилиндр и вписанный в него шар, а также написано соотношение объёмов цилиндра и шара.
В то время это было великое достижение, так как точных формул для нахождения объёмов цилиндра и шара ещё не было.
Найдём это соотношение.

Рис. 3. Иллюстрация к задаче


Объём шара:

Объём цилиндра:

Отношение этих объёмов:


Отношение площадей этих фигур будет таким же. Докажем это. Площадь шара:

Площадь цилиндра

Отношение этих площадей:


Разветвление: задача 5
Диаметр шара, равный 12 см, разделён в отношении 1:3:4. Через точки деления проведены две параллельные плоскости. Найти объём шарового слоя, отсечённого этими плоскостями (рис. 4).
Рис. 4. Иллюстрация к задаче
Дано:
Найти:
Решение:
1. Введём следующие обозначения:

Так как диаметр 


2. 




Радиус шара равен половине диаметра, то есть:


3. Найдём объём шарового слоя. Это будет разность объёма полушара и объёма шарового сегмента.
Объём полушара:

Объём шарового сегмента:

Объём шарового слоя:


Ответ: 
Подведение итогов урока
На данном уроке мы разобрали решение нескольких задач по теме «Объём шара и его частей».
ИСТОЧНИК
http://x-uni.com/geometriya/11-klass/video/reshenie-zadach-po-teme-ob-em-shara-i-ego-chastey
http://www.youtube.com/watch?v=kzgro70ZsCI
http://www.youtube.com/watch?v=Ai3DO-Ppr54
https://www.youtube.com/watch?v=Ll73wyXzuVw
http://prezentacii.com/uploads/ppt/05-13/obem-shara-i-ego-chastey.rar
http://900igr.net/datas/geometrija/Objom-shara/0003-003-Obem-sharovogo-sektora.jpg
http://mtable.narod.ru/math/vrash/vrash.jpg
http://mypresentation.ru/documents/a7548ea4ce0e9520bb410ab789dcdbab/img4.jpg
http://interneturok.ru/ru/school/geometry/11-klass/povtorenie/kruglye-tela-sfera?seconds=0&chapter_id=865
������� ������
�������� �����: ������� ������, ������� �������, ������� ����, ���, �����, �������
- ������� ��������� ���������� ����� ����, ���������� �� ���� ����������.
- ������� ����� ���������� ����� ����, ������������� ����� ����� ������������� �����������, ������������� ���.
- ������� ������ ���������� �� �������� �������� � ������.
- ���� ������� ������� ������ ��������, �� ������� ������� ����������� �������, � �������� ������� � ������ ����, � ���������� �������� ��������� ��������.
- ���� �� ������� ������ ��������, �� ��������� ����� �� ���� ���������.

��. �����:
���
ЕГЭ Профиль №13. Фигуры вращения: цилиндр, конус, шар
Скачать файл в формате pdf.
ЕГЭ Профиль №13. Фигуры вращения: цилиндр, конус, шар
Цилиндр
Прямым круговым цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону. Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Осью цилиндра называется прямая, проходящая через центры оснований.
Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник. Две его стороны – образующие цилиндра, а две другие – параллельные хорды оснований. В частности, прямоугольником является осевое сечение. Это – сечение цилиндра плоскостью, проходящей через его ось.
Площадь боковой поверхности цилиндра находится по формуле: ({S_{{text{б}}{text{.п}}{text{.}}}} = 2,pi ,R,H); площадь полной поверхности цилиндра находится по формуле: (S = 2,pi ,R,H + 2pi ,{R^2}); объем цилиндра находится по формуле: (V = pi ,{R^2},H), где R – радиус основания; H – длина высоты цилиндра.
Конус
Прямым круговым конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет. Другой катет треугольника, вращаясь вокруг этой же оси, дает круг, который называется основанием. При вращении вокруг этой оси гипотенузы получается фигура, называемая боковой поверхностью конуса. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса. Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Осью конуса называется прямая, содержащая его высоту.
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса. В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса.
Площадь боковой поверхности конуса находится по формуле: ({S_{{text{б}}{text{.п}}{text{.}}}} = pi ,R,L,); площадь полной поверхности конуса находится по формуле: (S = pi ,R,L, + pi ,{R^2}); объем конуса находится по формуле: (V = frac{1}{3}pi ,{R^2},H), где R – радиус основания; L – длина образующей; H – длина высоты конуса.
Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом.
Площадь боковой поверхности усеченного конуса находится по формуле:({S_{{text{б}}{text{.п}}}} = pi ,left( {,{R_1} + {R_2},} right),L); объем усеченного конуса находится по формуле:(V = frac{1}{3}pi ,H,left( {,R_1^2 + {R_1} cdot {R_2} + R_2^2,} right)), где ({R_1}) и ({R_2}) – радиусы оснований; L – длина образующей; H – длина высоты конуса.
Шар
Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии от данной точки, не большем данного положительного числа. Эта точка называется центром шара, а данное расстояние радиусом шара. Шаровой поверхностью или сферой шара называется множество всех точек пространства, находящихся на равном положительном расстоянии от некоторой точки. Эта точка называется центром сферы, а данное расстояние радиусом сферы. Таким образом, точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, также называется радиусом. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром.
Площадь поверхности шара находится по формуле: (S = 4,pi ,{R^2}); объем шара находится по формуле: (V = frac{4}{3}pi ,{R^3}), где R – радиус шара.
Шар, так же как цилиндр и конус, является телом вращения. Он получается при вращении полукруга вокруг его диаметра как оси. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость. Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы – большой окружностью. Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Шаровой сегмент можно получить, вращая круговой сегмент вокруг диаметра, перпендикулярного его хорде.
Площадь сегментной поверхности находится по формуле: (S = 2,pi ,R,H); объем шарового сегмента находится по формуле: (V = pi ,{H^2},left( {,R — frac{H}{3},} right)), где H – высота сегмента; R – радиус шара.
Шаровым сектором называется тело, которое получается из шарового сегмента и конуса следующим образом. Если шаровой сегмент меньше полушара, то он дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.
Объем шарового сектора находится по формуле: (V = frac{2}{3}pi ,{R^2}H); площадь полной поверхности шарового сектора складывается из площади сегментной поверхности и площади боковой поверхности конуса и находится по формуле:({S_{{text{шар}}{text{.}};{text{сект}}}} = {S_{{text{шар}}{text{.}};{text{сегм}}}} + {S_{{text{б}}{text{.}};{text{п}}{text{.}};{text{кон}}}} = 2,pi ,R,H + pi ,R,sqrt {,2,R,H — {H^2}} ), где H – высота соответствующего шарового сегмента; R – радиус шара.
1В. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка C1, причём CC1 — образующая цилиндра, а AC — диаметр основания. Известно, что (angle ,ACB = 30^circ ,;;AB = sqrt 2 ,) (C{C_1} = 2.)
а) Докажите, что угол между прямыми AC1 и BC равен (45^circ ).
б) Найдите объём цилиндра.
2В. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
б) Найдите угол между прямыми ВВ1 и АС1, если АВ = 6, ВВ1 = 15, В1С1 = 8.
ОТВЕТ: ({rm{arctg}}frac{2}{3}).
3В. В конус, радиус основания которого равен 3, вписан шар радиуса 1,5.
а) Изобразите осевое сечение комбинации этих тел.
б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.
4В. Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно (sqrt {730} ).
а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
ОТВЕТ: ({rm{arctg}}frac{{21}}{{17}}).
5В. Прямоугольник ABCD и цилиндр расположены таким образом, что AB — диаметр верхнего основания цилиндра, а CD лежит в плоскости нижнего основания и касается его окружности, при этом плоскость прямоугольника наклонена к плоскости основания цилиндра под углом 60°.
а) Докажите, что ABCD — квадрат.
б) Найдите длину той части отрезка BD, которая находится снаружи цилиндра, если радиус цилиндра равен (sqrt 2 ).
6В. В одном основании прямого кругового цилиндра с высотой 3 и радиусом основания 8 проведена хорда AB, равная радиусу основания, а в другом его основании проведён диаметр CD, перпендикулярный AB. Построено сечение ABNM, проходящее через прямую AB перпендикулярно прямой CD так, что точка C и центр основания цилиндра, в котором проведён диаметр CD, лежат с одной стороны от сечения.
а) Докажите, что диагонали этого сечения равны между собой.
б) Найдите объём пирамиды CABNM.
ОТВЕТ: (64 + 32sqrt 3 ).
7В. Отрезок AB — диаметр верхнего основания цилиндра, CD — диаметр нижнего, причём отрезки AB и CD не лежат на параллельных прямых.
а) Докажите, что у тетраэдра ABCD скрещивающиеся рёбра попарно равны.
б) Найдите объём этого тетраэдра, если AC = 6, AD = 8, а радиус цилиндра равен 3.
ОТВЕТ: (frac{{64}}{3}).
8В. Высота конуса равна 6, а радиус основания равен 8.
а) Докажите, что наибольшая площадь сечения конуса плоскостью, проходящей через его вершину, равна 50.
б) Найдите расстояние от центра основания конуса до этой плоскости.
ОТВЕТ: (frac{{6sqrt 7 }}{5}.)
9В. Проведены две параллельные плоскости по одну сторону от центра сферы на расстоянии 3 друг от друга. Эти плоскости дают в сечении две окружности, длины которых равны 18π и 24π.
а) Точка H — ортогональная проекция произвольной точки меньшей окружности на плоскость большей. Докажите, что точка H делит проходящий через неё диаметр большей окружности в отношении 1 : 7.
б) Найдите объём шара, ограниченного данной сферой.
ОТВЕТ: (4500{rm{pi }}).
10В. Плоскость α проходит через диаметр AB сферы. Через произвольную точку M, лежащую на сфере, но не лежащую в плоскости α, проведена плоскость β, перпендикулярная прямой AB. Отрезок CD — общая хорда окружностей сечений сферы плоскостями α и β.
а) Докажите, что (angle ,CMD = 90^circ ).
б) Вершина конуса совпадает с точкой A, а окружность основания — с окружностью сечения сферы плоскостью β. Найдите объём конуса, если диаметр сферы равен 15, а (MB = 3sqrt 5 ).
ОТВЕТ: (144{rm{pi }}).
11В. На окружности основания конуса с вершиной P выбраны точки A и B, делящие окружность на две дуги, длины которых относятся как 1 : 2.
а) Пусть MN — диаметр окружности основания, перпендикулярный хорде AB. Докажите, что объём одной из пирамид PABN и PABM втрое больше объёма другой.
б) Найдите площадь сечения конуса плоскостью ABP, если радиус основания конуса равен 6, а длина его образующей равна 7.
12В. Угол при вершине осевого сечения конуса равен (arccos frac{7}{8}).
а) Докажите, что площадь полной поверхности конуса в пять раз больше площади его основания.
б) Найдите угол в развёртке боковой поверхности.
13В. Радиус основания конуса с вершиной S и центром основания О равен 13, а его высота равна (3sqrt {41} ). Точки А и В – концы образующих, М – середина SA, N – точка в плоскости основания такая, что прямая MN параллельна прямой SB.
а) Докажите, что угол ANO – прямой.
б) Найдите угол между прямой ВМ и плоскостью основания конуса, если АВ = 10.
14В. Два конуса имеют общее основание, причем один из них находится внутри другого. Образующие этих конусов составляют с плоскостью основания углы ({60^ circ }) и ({30^ circ }).
а) Докажите, что вершина меньшего конуса делит высоту большего конуса в отношении (2:1), считая от вершины большего конуса.
б) Найдите объем тела, заключенного между боковыми поверхностями этих конусов, если известно, что сумма высот обоих конусов равна 4.
15В. В конус вписан шар.
а) Докажите, что отношение площади полной поверхности конуса к площади поверхности шара равно отношению их объемов.
б) Найдите угол между образующей конуса и плоскостью основания конуса, если отношение объема конуса к объему вписанного шара равно (frac{9}{4}), а отношение радиуса шара к радиусу основания конуса меньше (frac{3}{5}).
16В. Точки А, В и С лежат на окружности основания конуса с вершиной S, причем А и С диаметрально противоположны. Точка М – середина ВС.
а) Докажите, что прямая SM образует с плоскостью АВС такой же угол, как и прямая АВ с плоскостью SBC.
б) Найдите угол между прямой SA и плоскостью SBC, если АВ = 6, ВС = 8 и (SC = 5sqrt 2 .)
ОТВЕТ: (arcsin frac{{3sqrt {17} }}{{17}}.)
17В. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А, В и С, а на окружности другого основания – точка С1, причем СС1 – образующая цилиндра, а АС – диаметр основания. Известно, что (angle ACB = {45^ circ },,,,AB = 3sqrt 2 ,,,,C{C_1} = 6.)
а) Докажите, что угол между прямыми АС1 и ВС равен (60^circ ).
б) Найдите расстояние от точки В до прямой АС1.
ОТВЕТ: (frac{{3sqrt 6 }}{2}.)
18В. Полушар и вписанный в него конус имеют общее основание и общую высоту.
а) Докажите, что объем части полушара, лежащей вне конуса равен объему конуса.
б) Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите площадь сечения, заключенного между боковой поверхностью конуса и поверхностью полушара, если радиус полушара равен 4.
19В. На окружности основания конуса с вершиной S отмечены точки A, B и С так, что AB = BC. Медиана АМ треугольника ACS пересекает высоту конуса.
а) Точка N – середина отрезка АС. Докажите, что угол MNB прямой.
б) Найдите угол между прямыми АМ и SB, если (AS = 2,,,,AC = sqrt 6 .)
ОТВЕТ: (arccos frac{5}{{16}}.)
20В. Трапеция ABCD и цилиндр расположены таким образом, что AD — диаметр нижнего основания цилиндра, а точки C и B лежат на окружности верхнего основания и хорда CB равна радиусу основания. Прямая AB образует с плоскостью основания цилиндра угол равный (arccos frac{2}{3}.)
а) Докажите, что в трапецию ABCD можно вписать окружность.
б) Найдите угол между плоскостью основания цилиндра и плоскостью ABCD.
ОТВЕТ: (arccos frac{{sqrt 6 }}{4}.)
21В. Прямоугольник ABCD является осевым сечением цилиндра (AB и CD — образующие). Диаметры AD и KM пересекаются в точке О под прямым углом и (DO = CD.)
а) Докажите, что площадь поверхности цилиндра относится к площади описанной около этого цилиндра сферы как 4 : 5.
б) Найдите площадь сечения цилиндра, проходящего через точки K, M и B, если (AB = 
ОТВЕТ: (32sqrt 2 {rm{pi }}.)
- Взрослым: Skillbox, Geekbrains, Хекслет, Eduson, XYZ, Яндекс.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
Объёмы шарового сегмента, шарового слоя и шарового сектора
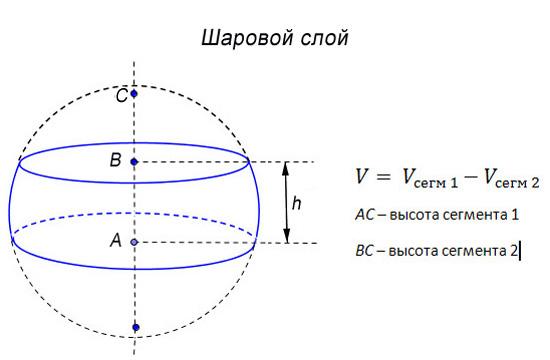
При пересечении шара плоскостью от целого отделяется два фрагмента, образующие шаровые сегменты. Например, на центральной оси шара или диаметре, расположена точка В. Если точка пересекается секущей плоскостью α под прямым углом к оси, то каждая из получившихся частей имеет свою высоту. Например, отрезок АС представляет собой диаметр, тогда высоты сегментов будут АВ и ВС. Основанием называется фигура, образуемая сечением на концах высот.
В формуле объёма используются значения высоты сегмента h и радиус шара R:
При выполнении условия площадь сечения, образованного под прямым углом к оси, вычисляется так:
Шаровой слой образуется парой параллельно расположенных плоскостей, разделяющих шаровое тело. Шаровой слой зажат основаниями, отдалёнными друг от друга на расстояние высоты шарового слоя.
Вычитание объёмов сегментов шара, расположенных внутри и по обе стороны от шарового слоя, позволяет получить его объём.
Сочленение шарового сегмента и конуса составляет шаровой сектор, также формируемый при повороте сектора круга, образованного острым углом, вокруг оси в границах радиуса сектора.
Условная высота сегмента h и шаровой радиус R - необходимые значения для выяснения объёма сектора:
- Взрослым: Skillbox, Geekbrains, Хекслет, Eduson, XYZ, Яндекс.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
Объем шарового сегмента, шарового слоя и шарового сектора
На уроке мы рассмотрим части шара: шаровой сегмент, шаровой слой и шаровой сектор
Определение. Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.
Секущая плоскость разбивает шар на два шаровых сегмента.
Круг, получающийся в сечении, называется основанием каждого из этих сегментов, а длины отрезков диаметра, перпендикулярного к секущей плоскости, называются высотами сегмента.
На экране высоты сегментов обозначены
Теорема. Объем шарового сегмента равен
где R – радиус шара;
h – высота сегмента.
Доказательство.
Применим уже известную нам интегральную формулу для вычисления объемов тел.
Проведем ось Ox перпендикулярно к плоскости основания.
Тогда произвольное сечение, проведенное перпендикулярно к оси Ox, будет кругом, а его площадь S выражается формулой:
, при R- hxR.
Эту формулу мы получили при выводе формулы объема шара.
Вычислив соответствующий определенный интеграл, получаем:
.
Итак,
Ч. т. д.
Теорема. Объем шарового сегмента равен
где R – радиус шара;
h– высота сегмента.
Доказательство.
Проведем ось Oxк плоскости основания.
Тогда произвольное сечение, проведенное Ox, будет кругом, а его площадь S выражается формулой:
, при R- hxR.
Вычислим соответствующий интеграл:
.
Итак,
Ч. т. д.
Определение. Шаровым слоем называется часть шара, заключенная между двумя параллельными сечениями.
Расстояние h между сечениями называется высотой слоя, а сами сечения – основаниями слоя.
Объем шарового слоя можно вычислить как разность объемов двух шаровых сегментов.
Например, объем шарового слоя, изображенного на экране, равен разности объемов шаровых сегментов с высотами AC и BC.
Определение. Шаровым сектором называется тело, полученное вращением кругового сектора с углом меньшим 900, вокруг прямой, содержащей один из ограничивающих сектор радиусов.
Шаровой сектор состоит из шарового сегмента и конуса.
Если радиус шара равен R, а высота шарового сегмента равна h, то объем V шарового сектора вычисляется по формуле:
Переходим к решению задач.
Задача 1
Диаметр шара разделен на три равные части и через точки деления проведены плоскости, перпендикулярные к диаметру. Найдите объем получившегося шарового слоя, если радиус шара равен R.
Дано:
Шаровой слой.
R – радиус шара
D –диаметр, точки C, D делят диаметр на три равные части:
AC = CD = DC
Нужно найти:
Задача 1
Диаметр шара разделен на три равные части и через точки деления проведены плоскости, перпендикулярные к диаметру. Найдите объем получившегося шарового слоя, если радиус шара равен R.
Дано:
Шаровой слой
R – радиус шара
AB–диаметр,
AC = CD = DC
Найти :
81
Решение:
Объем шарового слоя можно найти как разность объемов двух шаровых сегментов, с высотами AD и AC.
Обозначим высоты сегментов через
На чертеже отрезок AB – диаметр шара и он равен двум радиусам, высота первого сегмента h1 — отрезок AD, высота второго h2 — отрезок AC.
Так как по условию задачи, точки C и D делят диаметр шара AB на три равные части (AC = СD = DB), то
Общая формула для нахождения объема шарового сегмента:
Найдем объем большего сегмента:
Найдем объем меньшего сегмента:
Теперь мы можем вычислить объем шарового слоя, вычислив их разность:
Ответ:
Решение.
Обозначим высоты сегментов через
На чертеже AB – диаметр шара, AB = 2R,
.
Ответ:
Задача 2
Радиус основания шарового сегмента 8 см, а его высота – 4 см.
Найти объем сегмента.
Дано:
Шаровой сегмент.
Радиус основания r=8 см.
Высота h = 4 см.
Нужно найти объем шарового сегмента V.
Задача2.
Радиус основания шарового сегмента 8 см, а его высота – 4 см.
Найти объем сегмента.
Дано:
Шаровой сегмент
r= 8 см
h = 4 см
Найти: Vсегм.
Решение.
Формула для вычисления объема шарового сегмента:
где R – радиус шара;
h – высота сегмента.
-
Найдем радиус шара R.
Проведем ось Ox перпендикулярно основанию шарового сектора. Она пройдет через центр основания (свойство высоты, опущенной из центра шара на секущую плоскость) и будет перпендикулярна его радиусу ().
Рассмотрим осевое сечение.
Так как OA = OB = R, то OC = R –AC = R – 4
– прямоугольный (
.
По теореме Пифагора:
После подстановки значений получим уравнение с одной переменной:
Решая это уравнение, найдем R.
8R= 80;
R = 10
-
Теперь можно вычислить объем
Ответ:
Решение.
Формула для вычисления объема шарового сегмента:
где R – радиус шара;
h– высота сегмента.
-
Найдем радиус шара R.
Проведем ось Ox перпендикулярно основанию шарового сектора.
Рассмотрим осевое сечение.
Так как OA =OB = R, то OC = R –AC = R – 4
– прямоугольный (
.
По теореме Пифагора
.
Подставив значения, получим уравнение:
Решая его, найдем R.
8R = 80;
R = 10
-
Вычисляем объем
Ответ:
Задача 3.
Найдите объем шарового сектора, если радиус окружности основания соответствующего шарового сегмента равен 60 см, а радиус шара равен 75 см.
Дано:
Шаровой сектор.
r = 60 см
R = 75 см
Найти:
Решение.
Формула для нахождения объема шарового сектора:
,
где R – радиус шара;
h – высота шарового сегмента.
Радиус шара нам известен по условию задачи.
Не известно значение высоты h.
Для нахождения h проведем ось Ox перпендикулярно основанию шарового сектора и рассмотрим осевое сечение.
На чертеже AO = OB = R, поэтому h = CB = R – CO.
Отрезок CO можно найти из треугольника ACO.
Так как ось Ox перпендикулярна основанию сегмента, то она перпендикулярна его радиусу (.
Треугольник AOC – прямоугольный.
По теореме Пифагора:
= 45см
Теперь можно найти h:
h = R – CO=75 – 45=30 см
Осталось вычислить объем:
Ответ: 112 500 πсм3.
Задача 3.
Найдите объем шарового сектора, если радиус окружности основания соответствующего шарового сегмента равен 60 см, а радиус шара равен 75 см.
Дано: шаровой сектор
r= 60 см
R = 75 см
Найти:
Решение.
Формула для нахождения объема шарового сектора:
,
где R – радиус шара;
h – высота шарового сегмента.
Для нахождения h проведем ось Ox перпендикулярно основанию шарового сектора и рассмотрим осевое сечение.
Так как AO = OB = R, то h = CB = R – CO.
ΔACO– прямоугольный ():
=45см
Находим h:
h = R –CO=75 – 45=30 см
Вычисляем объем:
Ответ: 112 500 πсм3.