Шестиугольная пирамида егэ - Помощь в подготовке к экзаменам и поступлению

Правильная шестиугольная пирамида — пирамида, в основании которой лежит правильный шестиугольник.

Обозначения

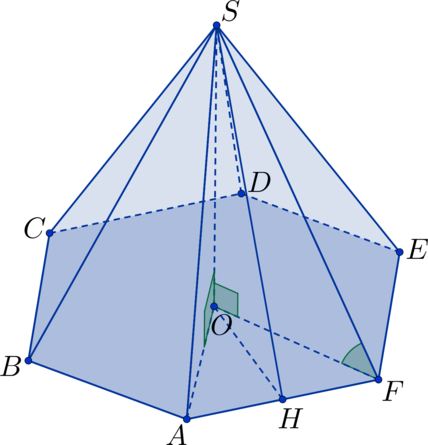
$SABCDEF$ — правильная шестиугольная пирамида
$O$ — центр основания пирамиды
$a$ — длина стороны основания пирамиды
$h$ — длина бокового ребра пирамиды
$S_{text{осн.}}$ — площадь основания пирамиды
$V_{text{пирамиды}}$ — объем пирамиды

Площадь основания пирамиды

В основаниях пирамиды находится правильный шестиугольник со стороной $a$. По свойствам правильного шестиугольника, площадь основания пирамиды равна $$ S_{text{осн.}}=frac{3sqrt{3}}{2}cdot a^2 $$

Правильный шестиугольник в основании пирамиды

По свойствам правильного шестиугольника, треугольники AOB, BOC, COD, DOE, EOF, FOA являются правильными треугольниками. Отсюда следует, что $$ AO=OD=EO=OB=CO=OF=a $$ Проводим отрезок AE, пересекающийся с отрезком CF в точке M. Треугольник AEO равнобедренный, в нём $AO=OE=a, angle EOA=120^{circ}$. По свойствам равнобедренного треугольника $$ AE=acdotsqrt{2(1-cos EOA)}=sqrt{3}cdot a $$ Аналогичным образом приходим к заключению, что $ AC=CE=sqrt{3}cdot a $, $FM=MO=frac{1}{2}cdot a$.

Находим $SO$

Прямая $SO$ является высотой пирамиды, поэтому $angle SOF=90^{circ}$. Треугольник $SOF$ прямоугольный, в нем $FO=a, FS=h$. По свойствам прямоугольного треугольника $$ SO=sqrt{FS^2-FO^2}=sqrt{h^2-a^2} $$

Объем пирамиды

Объем пирамиды вычисляется как треть произведения площади ее основания на ее высоту. Высотой правильной пирамиды является отрезок $SO$. В основании правильной шестиугольной призмы находится правильный шестиугольник, площадь которого нам известна. Получаем $$ V_{text{пирамиды}}=frac{1}{3}cdot S_{text{осн.}}cdot SO=frac{sqrt{3}}{2}cdot a^2 cdot sqrt{h^2-a^2} $$

Находим $ST$ и $TO$

Пусть точка $T$ является серединой ребра $AF$. Треугольник $AOF$ правильный, поэтому, по свойствам правильного треугольника $$ TO=frac{sqrt{3}}{2}cdot a $$ Треугольник $STO$ прямоугольный, высота $SO$ равна $sqrt{h^2-a^2}$. По теореме Пифагора $$ ST=sqrt{SO^2+TO^2}=sqrt{h^2-frac{1}{4}cdot a^2} $$

Источник

Объем правильной треугольной пирамиды

Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle H).

( displaystyle {{S}_{осн}}) – это площадь правильного треугольника ( displaystyle ABC).

Вспомним, как искать эту площадь.

Используем формулу площади:

( displaystyle S=frac{1}{2}abcdot sin gamma )

У нас «( displaystyle a)» – это ( displaystyle a), а «( displaystyle b)» – это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2})

Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).

Теперь найдем ( displaystyle H).

По теореме Пифагора для ( displaystyle Delta SOC)

( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}})

Чему же равно ( displaystyle OC)?

Это радиус описанной окружности в ( displaystyle Delta ABC), потому что пирамида правильная и, значит, ( displaystyle O) – центр ( displaystyle Delta ABC)

Найдем ( displaystyle OC) (Подробнее смотри в теме «Правильный треугольник»).

( displaystyle OC=frac{2}{3}CK), так как ( displaystyle O) – точка пересечения и медиан тоже.

( displaystyle C{{K}^{2}}=A{{C}^{2}}-A{{K}^{2}}) (теорема Пифагора для ( displaystyle Delta ACK))

( displaystyle C{{K}^{2}}-{{a}^{2}}-frac{{{a}^{2}}}{4}=frac{3{{a}^{2}}}{4}); ( displaystyle CK=frac{asqrt{3}}{2})

Значит, ( displaystyle OC=frac{2}{3}cdot frac{asqrt{3}}{2}=frac{asqrt{3}}{3})

Подставим ( displaystyle OC) в формулу для ( displaystyle H).

( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}={{b}^{2}}-{{left( frac{asqrt{3}}{3} right)}^{2}}={{b}^{2}}-frac{{{a}^{2}}}{3})

И подставим все в формулу объема:

( displaystyle V=frac{1}{3}{{S}_{ABC}}cdot H=frac{1}{3}cdot frac{{{a}^{2}}sqrt{3}}{4}cdot sqrt{{{b}^{2}}-frac{{{a}^{2}}}{3}})

( displaystyle V=frac{{{a}^{2}}sqrt{3}}{12}sqrt{{{b}^{2}}-frac{{{a}^{2}}}{3}}).

Внимание: если у тебя правильный тетраэдр (т.е. ( displaystyle b=a)), то формула получается такой:

( displaystyle V=frac{{{a}^{3}}}{6sqrt{2}}).

Источник

В правильной шестиугольной пирамиде SABCDEF сторона основания АВ равна 2, а боковое ребро SA равно 8. Точка М – середина ребра АВ. Плоскость α перпендикулярна плоскости АВС и содержит точки М и D. Прямая SC пересекает плоскость α в точке К.

А) Докажите, что КМ = КВ.

Б) Найдите объём пирамиды CDKM.

Решение:

А) SO – высота пирамиды, т.е. SO⊥(ABC); прямые MD и FC пересекаются в точке K₁.

Вспомним признак перпендикулярности плоскостей: если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Т.к. SO⊥(ABC) и SO∈(SFC), то (ABC)⊥(SFC).

Тогда KK₁⊥(ABC) → KK₁– высота треугольника MKD.

Рассмотрим правильный шестиугольник ABCDEF:

Правильный шестиугольник состоит из шести правильных треугольников, значит соответственные углы DAM и DOK₁ равны, т.е. ∠DAM= ∠DOK₁=60°.

По признаку параллельности прямых AM||OK₁.

AO=DO, AM||OK₁ → OK₁ – средняя линия ΔADM → MK₁=K₁D → KK₁ – высота и медиана в ΔMKD → ΔMKD – равнобедренный, т.е. KМ=KD.

Б) Построим пирамиду CDKM:

Источник

8. Геометрия в пространстве (стереометрия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

(blacktriangleright) Пирамида называется прямоугольной, если одно из ее боковых ребер ((SR)) перпендикулярно основанию (оно же будет и высотой).
Грани, образованные этим ребром, будут представлять собой прямоугольные треугольники ((triangle SMR, triangle SPR)).

(blacktriangleright) Пирамида называется правильной, если в основании лежит правильный многоугольник (все углы равны и все стороны равны) и выполнено одно из эквивалентных условий:

(sim) боковые ребра равны;
(sim) высота пирамиды проходит через центр описанной около основания окружности;
(sim) боковые ребра наклонены к основанию под одинаковым углом.

(blacktriangleright) Заметим, что у правильных многоугольников центры описанной и вписанной окружностей совпадают.

(blacktriangleright) Заметим, что у правильной пирамиды все боковые грани – равные равнобедренные треугольники.
Высота этих треугольников, проведенная из вершины пирамиды, называется апофемой.

Задание
8

#1867

Уровень задания: Сложнее ЕГЭ

Найдите апофему в правильной шестиугольной пирамиде, если сторона шестиугольника равна (7), а тангенс угла наклона бокового ребра к основанию равен (displaystyle frac{1}{2}).

(SABCDEF) – правильная шестиугольная пирамида, (SO) – высота пирамиды, (ABCDEF) – правильный шестиугольник. (triangle AOF) – равносторонний треугольник (Rightarrow) (FO = 7). Рассмотрим треугольник (SOF): (SO) – перпендикуляр, (SF) – наклонная к плоскости шестиугольника, (OF) – проекция наклонной (SF) (Rightarrow) (displaystyle mathrm{tg},angle SFO = frac{1}{2}) (Rightarrow) (displaystyle SO = FOcdotmathrm{tg},angle SFO = frac{7}{2}). (OH) – высота в равностороннем треугольнике (triangle AOF) (Rightarrow) (displaystyle OH = frac{sqrt3}{2}cdot AF = frac{sqrt3}{2}cdot7). Тогда апофему можно найти из прямоугольного треугольника (triangle SOH) по теореме Пифагора: (displaystyle SH^2 = SO^2 + OH^2 = left(frac{7}{2}right)^{2} + left(frac{sqrt3}{2}cdot7right)^{2} = 7).

Ответ: 7

Задание
9

#3077

Уровень задания: Сложнее ЕГЭ

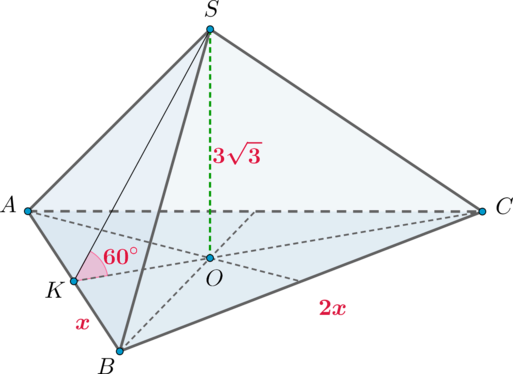
Высота правильной треугольной пирамиды равна (3sqrt3), а двугранный угол при основании равен (60^circ). Найдите объем пирамиды.

Так как пирамида правильная, то высота (SO) падает в точку пересечения медиан (которые являются также высотами и биссектрисами) основания. Пусть (CKperp AB). Тогда (OKperp AB). Тогда по теореме о трех перпендикулярах наклонная (SK), проекцией которой является (OK), также будет перпендикулярна (AB). Следовательно, (angle SKC) – линейный угол двугранного угла при основании, то есть (angle
SKC=60^circ).

Из прямоугольного (triangle SKO): [mathrm{tg},angle K=sqrt3=dfrac{SO}{OK} quadRightarrowquad
OK=dfrac{3sqrt3}{sqrt3}=3.] Так как (OK) – медиана, а (O) – точка пересечения медиан, и медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то (CK=3OK=9).
Пусть (KB=x), тогда (BC=2x). Рассмотрим прямоугольный (triangle
CKB): [BC^2=KB^2+CK^2 quadRightarrowquad 4x^2=x^2+81
quadRightarrowquad x=3sqrt3 quad Rightarrowquad
BC=6sqrt3=AB.] Следовательно, объем пирамиды равен [V=dfrac 13cdot SOcdot dfrac 12 ABcdot CK=
dfrac13cdot 3sqrt3cdot dfrac12cdot 6sqrt3cdot 9=81.]

Ответ: 81

Задание
10

#2855

Уровень задания: Сложнее ЕГЭ

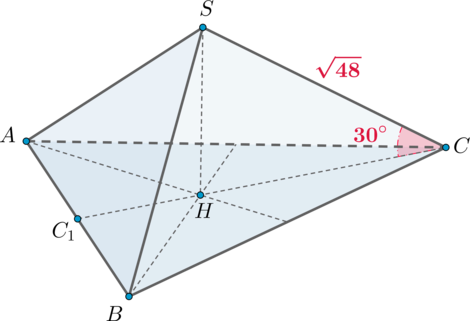
Дана правильная треугольная пирамида (SABC) с вершиной (S). Известно, что боковое ребро пирамиды равно (sqrt{48}), а угол между боковым ребром и плоскостью основания (30^circ). Найдите объем пирамиды.

Пусть (SH) – высота пирамиды. Так как пирамида правильная, то высота падает в центр основания, то есть в точку пересечения медиан (высот, биссектрис).
Заметим, что (sqrt{48}=4sqrt3).
Пусть (CC_1) – высота (а значит и медиана) основания. Тогда [CC_1=dfrac{sqrt3}2AB.] Так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то [CH=dfrac23CC_1=dfrac{sqrt3}3AB.]
Так как угол между прямой и плоскостью – это угол между прямой и ее проекцией на эту плоскость, а (CH) – проекция (SC) на плоскость основания, то (angle SCH=30^circ).
Из прямоугольного (triangle
SHC): [cos 30^circ=dfrac{CH}{SC}quadRightarrowquad
CH=SCcdot cos30^circ quadRightarrowquad CH=4sqrt3cdot
dfrac{sqrt3}2=6.] Так как еще (CH=dfrac{sqrt3}3AB), то можно найти (AB): [6=dfrac{sqrt3}3AB quadRightarrowquad
AB=6sqrt3.] Также из прямоугольного (triangle SHC): [sin30^circ=dfrac{SH}{SC} quadRightarrowquad
SH=dfrac12SC=2sqrt3.]
Следовательно, объем пирамиды равен [V=dfrac13cdot SHcdot S_{ABC}=dfrac13cdot 2sqrt3cdot
dfrac12cdot dfrac{sqrt3}2cdot 6sqrt3cdot 6sqrt3=54.]

Ответ: 54

Задание
11

#2640

Уровень задания: Сложнее ЕГЭ

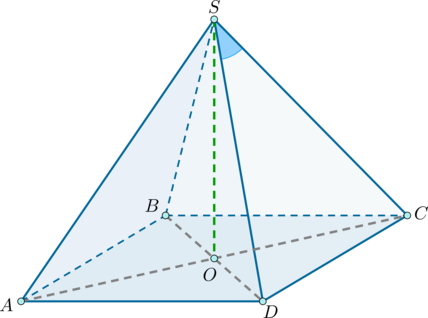
Найдите объем правильной четырехугольной пирамиды, если стороны основания равны (6sqrt2), а плоский угол при вершине пирамиды равен (60^circ).

(SABCD) – правильная четырехугольная пирамида. Значит, в ее основании лежит квадрат, а высота (SO) пирамиды падает в точку пересечения диагоналей этого квадрата.
(angle DSC=angle CSB=angle BSA=angle ASD=60^circ), (AB=6sqrt2).

Найдем объем пирамиды, если (AB=a), а затем подставим вместо (a=6sqrt2).

Т.к. объем пирамиды равен [V=dfrac13 cdot S_{ABCD}cdot
SO=dfrac13cdot a^2cdot SO,]

то необходимо найти (SO).

(triangle CSD) — равнобедренный ((SD=SC)), следовательно, (angle D=angle C=frac12(180^circ-60^circ)=60^circ).

Следовательно, он равносторонний и (SD=SC=CD=a).

Т.к. (BD=ABsqrt2 quad Rightarrow quad
OD=0,5BD=frac{sqrt2}2cdot a).

Тогда по теореме Пифагора из прямоугольного треугольника (SOD) ((angle SOD=90^circ)):

[SO^2=SD^2-OD^2=a^2-left(dfrac{sqrt2}2cdot aright)^2=dfrac{a^2}2 quad
Rightarrow quad SO=frac{sqrt2}2cdot a.]

Тогда объем равен

[V=dfrac13cdot a^2cdot frac{sqrt2}2cdot a=dfrac{a^3}{3sqrt2}=
dfrac{6^3cdot 2sqrt2}{3sqrt2}=144.]

Ответ: 144

Задание
12

#2915

Уровень задания: Сложнее ЕГЭ

(EABCD) – прямоугольная пирамида (отрезок (BE) перпендикулярен плоскости основания ((ABCD))), (ABCD) – параллелограмм со сторонами (a), (b), причем [angle BCD = 77^{circ},qquadqquad BE = dfrac{abcdotsin 77^{circ}}{sqrt{a^2 + b^2 + 2abcdotcos 77^{circ}}}.] Найдите угол между плоскостями ((ABCD)) и ((ACE)). Ответ дайте в градусах.

Построим (BK) перпендикулярно (AC), как показано на рисунке.

Так как (BK) – проекция (EK) на плоскость ((ABCD)), то по теореме о трех перпендикулярах (EK) перпендикулярен (AC), следовательно, угол между плоскостями ((ABCD)) и ((ACE)) есть (angle BKE).

Найдем (BK):
рассмотрим параллелограмм (ABCD). С одной стороны, его площадь [S_{ABCD} = abcdotsin 77^{circ}.] С другой стороны, его площадь равна удвоенной площади треугольника (ABC), то есть [S_{ABCD} = BKcdot AC.] Найдем (AC), используя теорему косинусов для треугольника (ACD): [AC^2 = a^2 + b^2 — 2abcdotcosangle ADC = a^2 + b^2 — 2abcdotcos(180^{circ} — angle BCD) = a^2 + b^2 + 2abcdotcosangle BCD = a^2 + b^2 + 2abcdotcos 77^{circ},] откуда (AC = sqrt{a^2 + b^2 + 2abcdotcos 77^{circ}}).

Приравняв площади параллелограмма, получим: [abcdotsin 77^{circ} = BKcdotsqrt{a^2 + b^2 + 2abcdotcos 77^{circ}},] откуда [BK = dfrac{abcdotsin 77^{circ}}{sqrt{a^2 + b^2 + 2abcdotcos 77^{circ}}} = BE,] тогда треугольник (BKE) прямоугольный равнобедренный, откуда (angle BKE = 45^{circ}).

Ответ: 45

Задание
13

#2916

Уровень задания: Сложнее ЕГЭ

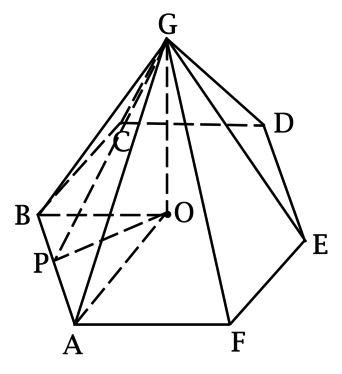
(GABCDEF) – правильная пирамида ((ABCDEF) – шестиугольник), (AB = 2), площадь полной поверхности пирамиды равна (12 + 6sqrt{3}). Найдите расстояние от точки (G) до плоскости ((ABC)).

Расстояние от точки до плоскости – длина перпендикуляра, опущенного из этой точки на плоскость.

Так как в основании пирамиды (GABCDEF) правильный шестиугольник, то [S_{ABCDEF} = dfrac{3sqrt{3}}{2}a^2] при (a = 2), то есть [S_{ABCDEF} = 6sqrt{3}.]

Тогда суммарная площадь оставшихся граней пирамиды равна (12 + 6sqrt{3} — 6sqrt{3} = 12). Так как у правильной пирамиды все грани – равные треугольники, то площадь каждой боковой грани равна (12 : 6 = 2), откуда с учётом того, что (AB = 2) находим высоту треугольника (ABG): она равна 2.

Так как (GABCDEF) – правильная пирамида, то точка (O) – основание перпендикуляра, опущенного из точки (G) на плоскость ((ABC)) – центр описанной около (ABCDEF) окружности, (BO = AO = AB = 2).

Пусть (OP) высота в треугольнике (ABO), тогда (OP = sqrt{3}), (BP = PA), но треугольник (ABG) – равнобедренный, тогда (GP) – высота (в нём) и, значит, (GP = 2).

По теореме Пифагора [GO^2 = GP^2 — PO^2 = 4 — 3 = 1,] откуда (GO = 1), то есть расстояние от точки (G) до плоскости ((ABC)) равно 1.

Ответ: 1

Задание
14

#2917

Уровень задания: Сложнее ЕГЭ

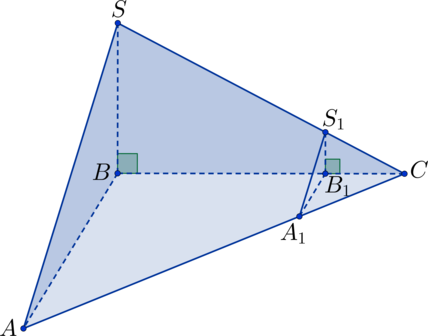
Пирамида (SABC) прямоугольная, (SB) – высота пирамиды. Точки (A_1), (S_1), (B_1) лежат соответственно на сторонах (AC), (SC), (BC), причем (S_1B_1 || SB), (A_1B_1 || AB), а (BB_1:B_1C = 3:1). Найдите площадь поверхности пирамиды (SABC), если площадь поверхности пирамиды (S_1A_1B_1C) равна (10).

Треугольник (triangle A_1B_1C) и (triangle ABC) подобны, т.к. у них общий угол (angle C) и по теореме Фалеса параллельные стороны (AB) и (A_1B_1) отсекают пропорциональные отрезки. Аналогичным образом подобны треугольники (triangle B_1S_1C) и (triangle BSC). Тогда из пропорциональности соответствующих сторон вытекает подобие треугольников (triangle A_1S_1C), (triangle A_1B_1S_1), соответственно треугольникам (triangle ASC), (triangle ABS). Коэффициент подобия (k = frac{B_1C}{BC} = frac{B_1C}{BB_1 + B_1C}
= frac{1}{4}). Тогда (S_{triangle A_1B_1C}:S_{triangle ABC} =
S_{triangle A_1S_1C}:S_{triangle ASC} = S_{triangle
A_1B_1S_1}:S_{triangle ABS} = S_{triangle B_1S_1C}:S_{triangle
BSC} = k^2 = frac{1}{16}) (Rightarrow) [begin{aligned}
&S_{text{пов.}S_1A_1B_1C}:S_{text{пов.}SABC} = frac{S_{triangle A_1B_1C} + S_{triangle A_1S_1C} + S_{triangle A_1B_1S_1} + S_{triangle B_1S_1C}}{S_{triangle ABC} + S_{triangle ASC} + S_{triangle ABS} + S_{triangle BSC}} = \[3ex]
&= frac{frac{1}{16}cdot S_{triangle ABC} + frac{1}{16}cdot S_{triangle ASC} + frac{1}{16}cdot S_{triangle ABS} + frac{1}{16}cdot S_{triangle BSC}}{S_{triangle ABC} + S_{triangle ASC} + S_{triangle ABS} + S_{triangle BSC}} = \[3ex]
&= frac{frac{1}{16}cdot(S_{triangle ABC} + S_{triangle ASC} +
S_{triangle ABS} + S_{triangle BSC})}{S_{triangle ABC} +
S_{triangle ASC} + S_{triangle ABS} + S_{triangle BSC}} = 1:16
end{aligned}] (Rightarrow) (S_{text{пов.}SABC} = 16cdot10 = 160).

Ответ: 160

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

22 января 2014

Основная проблема всех стереометрических задач (и B13 в частности) — понять, где расположен линейный угол двугранного угла, либо просто угла между плоскостью и прямой.

Просто запомните: углы в стереометрии всегда связаны с перпендикулярами. Именно поэтому в задаче B13 так часто дается высота. Как ее использовать — смотрите в сегодняшнем видеоуроке.

Задача B13. Высота правильной шестиугольной пирамиды равна 42. Боковое ребро наклонено к плоскости основания под углом 30°. Найдите боковое ребро пирамиды.

Практика показывает, что после небольшой тренировки большинство учеников начинают решать такие задачи вообще устно. Поэтому не поленитесь и прорешайте несколько аналогичных примеров.

Смотрите также:

Углы и отрезки в стереометрии — 2
Пример простейшего перехода
Тест к уроку «Что такое логарифм» (тяжелый)
Сводный тест по задачам B12 (1 вариант)
Как решать простейшие логарифмические уравнения
Задача B4: резка стекол

Источник