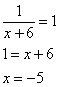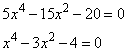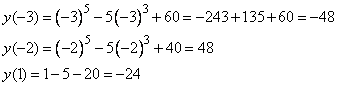Шпаргалка для 12 задания егэ профиль математика

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Задачи из сборников Ященко, 2021 год

Квадратные уравнения

Показательные уравнения

Логарифмические уравнения

Модуль числа

Уравнения с модулем

Тригонометрический круг

Формулы тригонометрии

Формулы приведения

Простейшие тригонометрические уравнения 1

Простейшие тригонометрические уравнения 2

Тригонометрические уравнения

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка . От нее и будем отсчитывать. Получим:

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

Давайте потренируемся.

а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку

Упростим левую часть по формуле приведения.

Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

б) Отметим на тригонометрическом круге найденные серии решений и отрезок

Видим, что указанному отрезку принадлежат решения

Ответ:

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка От нее и отсчитываем.

Получим:

2. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

а)

Степени равны, их основания равны. Значит, равны и показатели.

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку

Отметим на тригонометрическом круге отрезок и найденные серии решений.

Видим, что указанному отрезку принадлежат точки и из серии

Точки серии не входят в указанный отрезок.

А из серии в указанный отрезок входит точка

Ответ в пункте (б):

3. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

а)

Применим формулу косинуса двойного угла:

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.

Сначала серия

Теперь серия

Ответ: .

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть

ОДЗ:

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси .

Ответ в пункте а)

б) Отметим на тригонометрическом круге найденные серии решений и отрезок

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

и

5. а) Решите уравнение

б) Найдите корни, принадлежащие отрезку

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или . Заметим, что среди них находятся и углы, для которых

Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

На отрезке нам подходит корень .

На отрезке нам подходят корни .

На отрезке — корни

Ответ в пункте б):

ЕГЭ по математике профиль

10 июля 2022

В закладки

Обсудить

Жалоба

Шпаргалка по задачам профильного ЕГЭ по математике

Сжатая информация по всем задачам профильного ЕГЭ по математике.

Часть 1

Все ответы к заданиям 1-11 по условиям экзамена даются в виде целого числа или десятичной дроби.

sh-m1.pdf

Часть 2

Для успешного решения заданий второй части нужно знать весь материал, относящийся к первой части плюс факты, перечисленные ниже.
Желательно уметь всё это доказывать!

sh-m2.pdf

Автор: Андрей Павликов.

Источник: vk.com/lomonosov_math

Всё варианты 12 задания математика ЕГЭ Профиль 2022admin2022-08-03T22:19:54+03:00

Скачать задания в формате pdf.

Задания 12 ЕГЭ по математике профильного уровня 2022 год (уравнения)

1) (28.03.2022 досрочная волна) а) Решите уравнение    ({4^{sin x}} + {4^{sin left( {pi  + x} right)}} = frac{5}{2}.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{5}}pi }}{2};;4pi } right]).

ОТВЕТ: а) ( pm frac{pi }{6} + pi k;;;k in Z;)  б) (frac{{17pi }}{6};,,,,,frac{{19pi }}{6};,,,,,frac{{{text{23}}pi }}{6}.)

---

2) (28.03.2022 досрочная волна) а) Решите уравнение     ({81^{cos x}} — 12 cdot {9^{cos x}} + 27 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,4pi ;,,, — frac{{{text{5}}pi }}{2}} right]).

ОТВЕТ: а) ( pm frac{pi }{3} + 2pi k;;;2pi k;;;k in Z;)  б) ( — frac{{11pi }}{3};,,,, — 4pi .)

---

3) (28.03.2022 досрочная волна) а) Решите уравнение     ({16^{sin x}} — 1,5 cdot {4^{sin x + 1}} + 8 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,5pi ;,,, — frac{{{text{7}}pi }}{2}} right]).

ОТВЕТ:  а) (frac{pi }{6} + 2pi k;,,;frac{{{text{5}}pi }}{6} + 2pi k;;;frac{pi }{2} + 2pi k;;;k in Z;)  б) ( — frac{{{text{23}}pi }}{6};,,,, — frac{{7pi }}{2}.)

---

4) (02.06.2022 основная волна) а) Решите уравнение      (2{sin ^2}x — cos left( { — x} right) — 1 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,pi ;,,,frac{pi }{2}} right]).

ОТВЕТ:  а) ( pm frac{pi }{3} + 2pi k;,,;pi  + 2pi k;;;k in Z;)  б) ( — pi ;,,, — frac{pi }{3};,,,,frac{pi }{3}.)

---

5) (06.2022 основная волна) а) Решите уравнение      (2{cos ^2}x — 3sinleft( { — x} right) — 3 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{5}}pi }}{2};,,4pi } right]).

ОТВЕТ:  а) (frac{pi }{6} + 2pi k;,,;frac{{{text{5}}pi }}{6} + 2pi k;;;frac{pi }{2} + 2pi k;;;k in Z;)  б) (frac{{{text{17}}pi }}{6};,,,,frac{{{text{5}}pi }}{2}.)

---

6) (06.2022 основная волна) а) Решите уравнение     (cos 2x + sinleft( { — x} right) — 1 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{pi }{2};,,2pi } right]).

ОТВЕТ:  а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;;pi k;;;k in Z;)  б) (pi ;,,,,frac{{{text{7}}pi }}{6};,,,,frac{{{text{11}}pi }}{6};,,,2pi .)

---

7) (06.2022 основная волна) а) Решите уравнение     (cos 2x + 3sinleft( { — x} right) — 2 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{3}}pi }}{2};,,3pi } right]).

ОТВЕТ:  а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;; — frac{pi }{{text{2}}}{text{ + 2}}pi k;;;k in Z;)  б) (frac{{{text{3}}pi }}{2};,,,,frac{{{text{11}}pi }}{6}.)

---

(06.2022 основная волна) а) Решите уравнение     (sin 2x — 2sin x + 2cos x — 2 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {{text{3}}pi ;,,frac{{{text{9}}pi }}{2}} right]).

ОТВЕТ:  а) ( — frac{pi }{2} + 2pi k;,,;2pi k;;;;k in Z;)  б) (frac{{{text{7}}pi }}{2};,,,4pi .)

---

9) (06.2022 основная волна) а) Решите уравнение     (sin 2x + 2sin left( { — x} right) + cos left( { — x} right) — 1 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {{text{2}}pi ;,,frac{{{text{7}}pi }}{2}} right]).

ОТВЕТ:  а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;;2pi k;;;k in Z;)  б) (frac{{{text{19}}pi }}{6};,,,2pi .)

---

10) (27.06.2022 резервная волна) а) Решите уравнение     ({log _{11}}left( {2{{sin }^2}x + 7sqrt 3 sin x — 11} right) = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{3}}pi }}{2};,,3pi } right]).

ОТВЕТ:  а) (frac{pi }{3} + 2pi k;,,;frac{{{text{2}}pi }}{3} + 2pi k;;;k in Z;)  б) (frac{{{text{7}}pi }}{3};,,,frac{{{text{8}}pi }}{3}.)

---

11) (27.06.2022 резервная волна) а) Решите уравнение    ({log _9}left( {sqrt 2 sin x + sin 2x + 9} right) = 1.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — frac{{{text{7}}pi }}{2};,, — 2pi } right]).

ОТВЕТ:  а) ( pm frac{{{text{3}}pi }}{4} + 2pi k;,,;;pi k;;;k in Z;)  б) ( — frac{{{text{13}}pi }}{4};,, — 3pi ;,,, — frac{{{text{11}}pi }}{4};,, — 2pi .)

---

Значения функции: наибольшее и наименьшее

---

В задании №12 ЕГЭ по математике профильного уровня нам необходимо найти наибольшее или наименьшее значение функции. Для этого необходимо воспользоваться, очевидно, производной. Посмотрим на типовом примере.

---

Разбор типовых вариантов заданий №12 ЕГЭ по математике профильного уровня

---

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

Найти точку максимума функции y = ln(x+4)²+2x+7.

[/su_note]

Алгоритм решения:

1. Определяем область определения функции.
2. Находим производную.
3. Определяем, в каких точках производная равна 0.
4. Исключаем точки, не принадлежащие области определения.
5. Среди оставшихся точек ищем значения х, в которых функция имеет максимум.
6. Записываем ответ.

Решение:

1. Ищем значения х, при которых логарифм имеет смысл. Для этого решаем неравенство:

(x+4)² > 0

Поскольку квадрат любого числа неотрицателен. Решением неравенства будет лишь то значение х, при котором х+4≠ 0, т.е. при х≠-4.

2. Находим производную:

у’=(ln(x+4)² + 2x + 7)’

По свойству логарифма получаем:

у’=(ln(x+4)² )’+(2x)’+(7)’.

По формуле производной сложной функции:

(lnf)’=(1/f)∙f’. У нас f=(x+4)²

у^, = (ln(x+4)² )’+ 2 + 0 = (1/(x+4)² )∙((x+4)²)’ + 2=(1/(x+4)² 2)∙(х² + 8х + 16)’ +2=2(х + 4) /((х + 4)²) + 2

у’= 2/(х + 4) + 2

3. Приравниваем производную к нулю:

у^, = 0 → (2+2∙(х + 4))/(х + 4)=0,

2 +2х +8 =0, 2х + 10 = 0,

2х = -10,

х = -5

Ответ: -5.

---

Второй вариант задания (из Ященко, №1)

[su_note note_color=”#defae6″]

Найдите точку минимума функции y = x – ln(x+6) + 3.

[/su_note]

Алгоритм решения:

1. Определяем область определения функции.
2. Находим производную.
3. Определяем, в каких точках производная равна 0.
4. Исключаем точки, не принадлежащие области определения.
5. Среди оставшихся точек ищем значения х, в которых функция имеет минимум.
6. Записываем ответ.

Решение:

1. ОДЗ: .

2. Найдем производную функции:

3. Приравниваем полученное выражение к нулю:

4. Получили одну точку x=-5, принадлежащую области определения функции.

5. В этой точке функция имеет экстремум. Проверим, минимум ли это. При х=-4

При х=-5,5 производная функции отрицательна, так как

Значит, точка х=-5 является точкой минимума.

Ответ: -5.

---

Третий вариант задания (из Ященко, №12)

[su_note note_color=”#defae6″]

Найдите наибольшее значение функции  на отрезке [-3; 1].

[/su_note]

Алгоритм решения:.

1. Находим производную.
2. Определяем, в каких точках производная равна 0.
3. Исключаем точки, не принадлежащие заданному отрезку.
4. Среди оставшихся точек ищем значения х, в которых функция имеет максимум.
5. Находим значения функции на концах отрезка.
6. Ищем среди полученных значений наибольшее.
7. Записываем ответ.

Решение:

1. Вычисляем производную от функции, получим

2. Приравниваем производную к нулю:

Решение уравнения дает два корня

 – не принадлежит множеству действительных чисел

.

3. Значение  и остается одна точка .

4. Вычисляем значения функции в точке -2 и на концах отрезка -3 и 1, получим:

Наибольшее значение функции на заданном отрезке равно 48 в точке х=-2.

Ответ: 48.

Даниил Романович | Просмотров: 11.9k

Все уравнения можно разделить на несколько групп:

— Целые рациональные уравнения

— Дробно-рациональные уравнения

— Иррациональные уравнения

— Тригонометрические уравнения

— Показательные уравнения

Каждая группа уравнений имеет свои особенности. На первый взгляд может показаться, что это очень большой материал и на его изучение понадобится много времени, однако на самом деле для подготовки в экзамену и выполнению задания номер 12 можно подготовиться достаточно быстро, используя верно подобранные материалы и разбирая примеры заданий

Комбинируя все представленные в данных материалах способы и обладая базовыми знаниями математики, можно успешно решить большинство уравнений, которые могут встретиться учащимся во время обучения в средней и старшей школе а так же успешно решить задания на данную тему в контрольно-измерительных материалах

СОВЕТ: после прохождения какой-либо темы в моём пособии, необходимо прорешать похожие уравнения (этой же группы) на одном из подобранных мной сайтов (смотрите ниже)

Часть I. Способы решения уравнений. Метод “Замена переменной”

Уравнение вида af²(x)+bf (x)+c=0 Такие уравнения (их иногда называют трехчленными) являются одними из наиболее распространенных. Скорее всего, самый известный и яркий пример этого типа уравнений — биквадратное уравнение ax⁴ + bx2 + c = 0 (здесь f (x) = x 2 ). Заменой переменной t = f (x) трехчленное уравнение сводится к квадратному относительно переменной t уравнению at² + bt + c = 0

Решить уравнение (2x² – 3x + 1) = 22x² – 33x + 1.

Решение:

Пример1

Перепишем уравнение в виде

(2x² – 3x + 1)² = 11(2x² – 3x) + 1. Произведем замену. Пусть 2x² – 3x = a, тогда уравнение примет вид:

(a + 1)² = 11a + 1.

a² + 2a + 1 = 11a + 1;

a² – 9a = 0.

В получившемся неполном квадратном уравнении вынесем общий множитель за скобки и получим следующее:

a(a – 9) = 0;

a= 0 или a= 9 (записывается как система).

2x² – 3x = 0 или 2x² – 3x = 9

x = 0 или x = 3/2 x = 3 или x = -3/2

Ответ: x=0, x=3, x=+-3/2

Пример 2

Решить уравнение (x – 1)(x – 3)(x + 5)(x + 7) = 297

Решение: Попытаемся перемножить между собой множители и получим

((x – 1)(x + 5))((x – 3)(x + 7)) = 297;

(x² + 5x – x – 5)(x² + 7x – 3x – 21) = 297;

(x² + 4x – 5)(x² + 4x – 21) = 297.

Замечаем замену x² + 4x = a, тогда уравнение будет выглядеть следующим образом:

(a – 5)(a – 21) = 297.

Раскроем скобки, приведем подобные слагаемые:

a² – 21a – 5a + 105 = 297;

a² – 26t – 192 = 0.

По теореме Виета определяем, что корнями полученного уравнения будут числа -6 и 32.

После обратной замены будем иметь:

x² + 4x = -6 или x² + 4x = 32

x² + 4x + 6 = 0 x² + 4x – 32 = 0

D = 16 – 24 < 0 D = 16 + 128 > 0

Нет корней x1 = -8; x2 = 4

Ответ: x=-8; x=4

Метод “Применение свойств функции”

Некоторые (не обязательно целые) уравнения могут быть решены с помощью таких свойств функций, как монотонность и ограниченность. Приведем простой пример решения уравнения таким методом

Решим данное нам уравнение:

Решение.

Каждая из корней в правой части уравнения — возрастающая функция, которая при любом x будет принимать только положительные значения. Значит и их сумму тоже будет принимать значение больше или равные нулю. Значение в правой части уравнения меньше 0, из этого следует, что уравнение не будет иметь решения

Ответ: нет корней

Для дробно-рациональных уравнений метод “применения свойств” функции также будет очень эффективным

Алгебраические преобразования для решения уравнений

Одним из основных способов сведения уравнения к одному или нескольким простейшим являются алгебраические преобразования одной или обеих его частей, позволяющие свести дробно-рациональное уравнение к целому. В некоторых случаях для решения рациональных уравнений приходится применять искусственные приемы: добавление и вычитание одного и того же числа и т. п.

Тригонометрические уравнения

Основной идеей при решении тригонометрических уравнений является сведение большого многочлена к простейшему уравнению вида sin x = a, cos x = a, tg x = a, ctg x = a. А потом они уже решаются при помощи числовой окружности. Но при этом для решения этого типа уравнений так же подходят изученные нами ранее способы: замена переменной, алгебраические преобразования и, конечно, применение свойств функции

Представленный выше пример является простейшим тригонометрическим уравнением вида tg x = a, который мы решали используя тригонометрический круг

Теперь рассмотрим пример уравнения, где необходимо выполнить преобразования для того, чтобы прийти к простейшему тригонометрическому уравнению

Теперь предлагаю разобрать одно из самых сложных заданий на эту тему по данным сайта Решуегэ.РФ

Логарифмические уравнения

Основная идея решения любого логарифмического уравнения —

сведение его к одному или нескольким простейшим уравнениям, а ос-

новными средствами реализации этой идеи являются следующие:

• равносильные преобразования,

• переход к уравнению-следствию,

• разложение на множители,

• замена переменной,

• применение свойств функций.

Решение большинства логарифмических уравнений после некото-

рых преобразований сводится к решению логарифмического уравне-

ния вида logh(x)

f (x)=logh(x)

g(x) или совокупности таких уравнений.

Приведем соответствующее равносильное преобразование:

Часть II. Решение систем уравнений. Системы целых алгебраических уравнений

Основными методами решения систем, содержащих нелинейные урав-

нения, являются следующие:

• подстановка,

• замена переменной,

• алгебраическое сложение,

• разложение на множители.

Рассмотрим пример решения систем целых алгебраических уравнений:

При возможности, нужно решать по одному уравнению день за днём. Причём я рекомендую делать так: 2 дня решать тригонометрические уравнения, 1 день показательные и 1 день логарифмические. Это будет наиболее эффективный метод подготовки к решению задания номер 12 из егэ по профильной математике

Ссылки для тренировки:

Тригонометрические уравнения

Иррациональные уравнения

Показательные уравнения

Уравнения смешанного типа

Банк заданий с уравнениями от ФИПИ