Лучшие шпаргалки по математике. Качественно. Ничего лишнего.
Просто кликните по картинке. Подробно — в разделе «Решение задач ЕГЭ по математике».
Самое популярное. Тригонометрия и площади фигур
Тригонометрический круг
Синус, косинус, тангенс…
Формулы тригонометрии
Геометрия. Площади фигур
Геометрия на ЕГЭ по математике. Треугольники, четырехугольники, окружности.
Высоты, медианы, биссектрисы
Параллелограмм, ромб, квадрат и их свойства
Касательная к окружности
Центральные и вписанные углы
Стереометрия: формулы объема и площади поверхности.
Вписанные и описанные треугольники
Вписанные и описанные четырехугольники
Стереометрия: Формулы объема и площади поверхности.
Чертежи в задачах по стереометрии
Классическая стереометрия и метод координат
Основы стереометрии. Часть 1.
Основы стереометрии. Часть 2.
Стереометрия: Векторы и координаты.
Как расположить прямоугольную систему координат
Алгебра
Таблица производных.
Преобразования графиков функций. Задача С5.
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Лучшие шпаргалки по математике. Качественно. Ничего лишнего.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
База 11
1). Плоскость, проходящая через три точки A, B и C,
разбивает куб на два многогранника. Сколько граней у многогранника, у
которого больше граней? Ответ. 7.
2). Плоскость, проходящая через три точки A, B и C,
разбивает куб на два многогранника. Сколько ребер у многогранника, у
которого больше? Ответ. 15.
3). Плоскость, проходящая через три точки A, B и C,
разбивает куб на два многогранника. Сколько вершин у многогранника, у
которого больше? Ответ. 10.
4). Плоскость, проходящая через три точки A, B и C,
разбивает куб на два многогранника. Сколько граней у многогранника, у
которого меньше граней? Ответ. 5.
5). Плоскость, проходящая через три точки A, B и C,
разбивает куб на два многогранника. Сколько ребер у многогранника, у
которого меньше? Ответ. 9.
6). Плоскость, проходящая через три точки A, B и C,
разбивает куб на два многогранника. Сколько вершин у многогранника, у
которого меньше? Ответ. 6.
7). Плоскость, проходящая через три точки A, B и С,
разбивает правильную треугольную призму на два многогранника. Сколько рёбер
у многогранника, у которого больше вершин? Ответ. 12.
8). Плоскость, проходящая через три точки A, B и С,
разбивает правильную треугольную призму на два многогранника. Сколько граней
у многогранника, у которого больше ? Ответ. 6.
9). Плоскость, проходящая через три точки A, B и С,
разбивает правильную треугольную призму на два многогранника. Сколько вершин
у многогранника, у которого больше? Ответ. 8.
10). Плоскость, проходящая через три точки A, B и С,
разбивает правильную треугольную призму на два многогранника. Сколько рёбер
у многогранника, у которого меньше? Ответ. 9.
11). Плоскость, проходящая через три точки A, B и С,
разбивает правильную треугольную призму на два многогранника. Сколько граней
у многогранника, у которого меньше? Ответ. 5.
12). Плоскость, проходящая через три точки A, B и С,
разбивает правильную треугольную призму на два многогранника. Сколько вершин
у многогранника, у которого меньше? Ответ. 6.
13). Плоскость, проходящая через точки A, B и C (см.
рис.), разбивает тетраэдр на два многогранника. Сколько рёбер у
получившегося многогранника с большим числом вершин? Ответ. 9.
14). Плоскость, проходящая через точки A, B и C (см.
рис.), разбивает тетраэдр на два многогранника. Сколько вершин у
получившегося многогранника с большим? Ответ. 6.
15). Плоскость, проходящая через точки A, B и C (см.
рис.), разбивает тетраэдр на два многогранника. Сколько граней у
получившегося многогранника с большим? Ответ. 5
16). Плоскость, проходящая через точки A, B и C (см.
рис.), разбивает тетраэдр на два многогранника. Сколько вершин у
получившегося многогранника с меньшим? Ответ. 4.
17). Плоскость, проходящая через точки A, B и C (см.
рис.), разбивает тетраэдр на два многогранника. Сколько ребер у
получившегося многогранника с меньшим? Ответ. 6.
18). Плоскость, проходящая через точки A, B и C (см.
рис.), разбивает тетраэдр на два многогранника. Сколько граней у
получившегося многогранника с меньшим? Ответ. 4.
19). Пирамида Снофру имеет форму правильной четырёхугольной пирамиды,
сторона основания которой равна 220 м, а высота — 104 м. Сторона основания
точной музейной копии этой пирамиды равна 44 см. Найдите высоту
музейной копии. Ответ дайте в сантиметрах.
220м = 22000см, 22000 : 44 = 500, 10400 : 500
= 20,8см. Ответ. 20,8
20). От деревянной правильной пятиугольной призмы отпилили все
её вершины (см. рис.). Сколько граней у получившегося многогранника
(невидимые рёбра на рисунке не изображены)? Ответ. 17.
21). От деревянной правильной пятиугольной призмы отпилили все
её вершины (см. рис.). Сколько ребер у получившегося многогранника
(невидимые рёбра на рисунке не изображены)? Ответ. 45.
22). От деревянной правильной пятиугольной призмы отпилили все
её вершины (см. рис.). Сколько вершин у получившегося многогранника
(невидимые рёбра на рисунке не изображены)? Ответ. 30.
23). От деревянного кубика отпилили все её вершины (см. рис.). Сколько
граней у получившегося многогранника (невидимые рёбра на рисунке не
изображены)? Ответ. 14.
24). От деревянного кубика отпилили все её вершины (см. рис.). Сколько
ребер у получившегося многогранника (невидимые рёбра на рисунке не
изображены)? Ответ. 36.
25). От деревянного кубика отпилили все её вершины (см. рис.). Сколько
вершин у получившегося многогранника (невидимые рёбра на рисунке не
изображены)? Ответ. 24.
26). От деревянной правильной треугольной призмы отпилили все
её вершины (см. рис.). Сколько граней у получившегося многогранника
(невидимые рёбра на рисунке не изображены)? Ответ. 11.
27). От деревянной правильной треугольной призмы отпилили все
её вершины (см. рис.). Сколько ребер у получившегося многогранника
(невидимые рёбра на рисунке не изображены)? Ответ. 27.
28). От деревянной правильной треугольной призмы отпилили все
её вершины (см. рис.). Сколько вершин у получившегося многогранника
(невидимые рёбра на рисунке не изображены)? Ответ. 18.
29). Двускатную крышу дома, имеющего в основании прямоугольник (см.
рис.), необходимо полностью покрыть рубероидом. Высота крыши равна 4 м, длины
стен дома равны 6 м и 8 м. Найдите, сколько рубероида.
1) 6 : 2 = 3; ; 3)
Ответ.80
30). К правильной треугольной призме со стороной основания 1
приклеили правильную треугольную пирамиду с ребром 1 так, что основания
совпали. Сколько граней у получившегося многогранника.Ответ.7.
31). К правильной треугольной призме со стороной основания 1
приклеили правильную треугольную пирамиду с ребром 1 так, что основания
совпали. Сколько ребер у получившегося многогранника? Ответ. 12.
32). К правильной треугольной призме со стороной основания 1
приклеили правильную треугольную пирамиду с ребром 1 так, что основания
совпали. Сколько вершин у получившегося многогранника? Ответ. 7.
33). К кубу с ребром 1 приклеили правильную четырёхугольную
пирамиду с ребром 1 так, что квадратные грани совпали. Сколько рёбер у
получившегося многогранника (невидимые рёбра на рисунке не изображены)? Ответ. 16.
34). К кубу с ребром 1 приклеили правильную четырёхугольную
пирамиду с ребром 1 так, что квадратные грани совпали. Сколько граней у
получившегося многогранника (невидимые рёбра на рисунке не изображены)? Ответ. 9.
35). К кубу с ребром 1 приклеили правильную четырёхугольную
пирамиду с ребром 1 так, что квадратные грани совпали. Сколько вершин у
получившегося многогранника (невидимые рёбра на рисунке )? Ответ. 9.
36). К правильной шестиугольной призме с ребром основания 1
приклеили правильную шестиугольную пирамиду с ребром основания 1 так, что
основания совпали. Сколько граней у получившегося многогранника? Ответ.
13.
37). К правильной шестиугольной призме с ребром основания 1
приклеили правильную шестиугольную пирамиду с ребром основания 1 так, что
основания совпали. Сколько ребер у получившегося многогранника ? Ответ.
24.
38). К правильной шестиугольной призме с ребром основания 1
приклеили правильную шестиугольную пирамиду с ребром основания 1 так, что
основания совпали. Сколько вершин у получившегося многогранника ?
Ответ. 13.
39). Ящик, имеющий форму куба с ребром 20 см без одной грани,
нужно покрасить со всех сторон снаружи. Найдите площадь поверхности,
которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
Ответ. 2000
40). Аквариум имеет форму прямоугольного параллелепипеда с
размерами 80 см × 30 см × 40 см. Сколько
литров составляет объём аквариума? В одном литре 1000 кубических
сантиметров.
Ответ. 96.
41). В бак, имеющий форму правильной четырёхугольной призмы со
стороной основания, равной 40 см, налита жидкость. Чтобы
измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите
объём детали, если после её погружения уровень жидкости в баке поднялся на 10 см.
Ответ. 16000.
42). В бак, имеющий форму прямой призмы, налито 5 л
воды. После полного погружения в воду детали уровень воды в баке
увеличился в 1,8 раза. Найдите объём детали. Ответ дайте в
кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров. Ответ. 4000.
43). Вода в сосуде, имеющем форму правильной четырёхугольной призмы,
находится на уровне h = 90 см. На каком уровне окажется вода,
если её перелить в другой сосуд, имеющий форму правильной четырёхугольной
призмы, у которого сторона основания втрое больше, чем у данного? Ответ. 10.
44). Вода в сосуде, имеющем форму правильной четырёхугольной призмы,
находится на уровне h= 20 см. На каком уровне окажется вода,
если её перелить в другой сосуд, имеющий форму правильной четырёхугольной
призмы, у которого сторона основания вдвое меньше, чем у данного? Ответ. 80.
45). Даны две коробки, имеющие форму правильной четырёхугольной призмы,
стоящей на основании. Первая коробка в полтора раза выше второй, а вторая
втрое шире первой. Во сколько раз объём первой коробки меньше
объёма второй?
46). Высота бака цилиндрической формы равна 40 см, а площадь
его основания равна 150 квадратным сантиметрам. Чему равен объём этого
бака (в литрах)? В одном литре 1000 кубических сантиметров.
Ответ. 6.
47). Даны две кружки цилиндрической формы. Первая кружка в четыре с
половиной раза выше второй, а вторая в полтора раза шире первой. Во сколько
раз объём второй кружки меньше объёма первой?
48). Даны два конуса. Радиус основания и высота первого конуса равны
соответственно 4 и 9, а второго — 6 и 8. Во
сколько раз объём второго конуса больше объёма первого?
49). Однородный шар диаметром 3 см весит 162 грамма.
Сколько граммов весит шар диаметром 2 см, изготовленный из того же
материала? Ответ. 48.
50). Даны два шара с радиусами 8 и 2. Во сколько раз
объём большего шара больше объёма другого?
Ответ. 64.
51). Даны два цилиндра. Радиус основания и высота первого цилиндра
равны соответственно 4 и 18, а второго — 2
и 3. Во сколько раз площадь боковой поверхности первого цилиндра
больше площади боковой поверхности второго? Ответ. 12.
51). В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты.
Объём сосуда 1600 мл. Чему равен объём налитой жидкости? . Ответ. 200.
52). В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты.
Объём жидкости равен
30 мл. Найдите объём сосуда. ответ. 240.
53). В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты.
Объём жидкости равен 30 мл. Сколько миллилитров жидкости нужно
долить, чтобы наполнить сосуд доверху?
ответ. 210.
54). Деталь имеет форму изображённого на рисунке многогранника (все
двугранные углы прямые). Числа на
рисунке обозначают длины рёбер в сантиметрах. Найдите объём
этой детали.
ответ. 24.
55). Деталь имеет форму изображённого на рисунке многогранника (все
двугранные углы прямые). Числа на рисунке обозначают длины рёбер в
сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в
квадратных сантиметрах.
56). Найдите площадь поверхности многогранника, изображённого
на рисунке (все двугранные углы – прямые).
База 12
1). На
прямой AB взята точка M. Луч MD — биссектриса
угла CMB. Известно, что ∠DMC=51°. Найдите величину угла CMA. Ответ дайте
в градусах.
2). На
прямой AB взята точка M. Луч MD — биссектриса
угла CMB. Известно, что ∠CMA=36°. Найдите угол DMB. Ответ дайте в
градусах.
3). Прямые m и n параллельны
(см. рис.). Найдите если
4). В
треугольнике ABC проведена биссектриса AL,
угол ALC равен 145°, угол ABC равен 113°.
Найдите угол ACB. Ответ дайте в градусах.
5). В
треугольнике ABC сторона AC=56,
BM — медиана, BH — высота, BC=BM. Найдите
длину отрезка AH.
6). В
прямоугольном треугольнике ABC внешний угол при вершине А равен 150 °. Катет BC=30. Найдите
длину гипотенузы AB.
7). В
треугольнике ABC внешние углы при
вершинах A и C равны 150°, AB=54. Найдите
длину биссектрисы BK.
8). В
треугольнике ABC угол B равен 120°.
Медиана BM делит угол B пополам и равна 27. Найдите
длину стороны AB.
9). В выпуклом
четырёхугольнике ABCD известно, что AB=BC, AD=CD, ∠B=61°, ∠D=151°. Найдите
угол A. Ответ дайте в градусах.
10). Обе диагонали
параллелограмма равны 13. Одна из сторон параллелограмма равна 5.
Найдите сторону параллелограмма, соседнюю с данной.
11). В
трапеции ABCD известно, что AB=CD, ∠BDA=54° и ∠BDC=23°.
Найдите угол ABD. Ответ дайте в градусах.
12). Основания
трапеции равны 8 и 16, боковая сторона, равная 6, образует
с одним из оснований трапеции угол 150°. Найдите площадь
трапеции.
13). В
прямоугольной трапеции основания равны 3 и 5, а один из
углов равен 135°. Найдите меньшую боковую сторону.
14). В
параллелограмме диагонали являются биссектрисами его углов и равны 16 и 30.
Найдите периметр параллелограмма.
15). Сумма двух
углов ромба равна 120°, а его меньшая диагональ равна 8. Найдите
периметр ромба .
16). Сумма двух
углов ромба равна 120°, а его периметр равен 84. Найдите длину
меньшей диагонали ромба.
17). Стороны
параллелограмма равны 9 и 12. Высота, опущенная на меньшую
сторону, равна 8. Найдите высоту, опущенную на большую сторону параллелограмма.
18). Найдите
площадь ромба, если его высота равна 6, а острый угол равен 30°.
19). Ромб и
квадрат имеют равные стороны. Найдите площадь ромба, если его острый
угол равен 30°, а площадь квадрата равна 16.
20). В
треугольнике ABC АВ = ВС =25 АС = 14 .Найдите
длину медианы ВМ.
21). В треугольнике
каждая из двух сторон равна 10, а третья сторона равна 12.Найдите
длину медианы, проведенной к третьей стороне.
22). Найдите
площадь прямоугольного треугольника, если его гипотенуза равна , а один из катетов равен 1.
23). На
стороне BC прямоугольника ABCD, у которого AB=15 и AD=23,
отмечена точка E так, что треугольник ABE равнобедренный. Найдите ED.
24). Основания
равнобедренной трапеции равны 10 и 24, боковая сторона
равна 25. Найдите высоту трапеции.
25). В
треугольнике ABC известно, что AB=BC=13, AC=10.
Найдите площадь треугольника ABC.
26). В
равнобедренном треугольнике ABC основание AC равно 32,
площадь треугольника равна 192. Найдите длину боковой
стороны AB.
27). В
треугольнике АВС АВ = ВС, медиана ВМ равна
6. Площадь треугольника АВС равна .Найдите AB.
28). В
параллелограмме АВСD отмечена точка M —середина
стороны ВС. Отрезки ВD и A M
пересекаются в точке K. Найдите длину отрезка ВK, если ВD=15.
29).
Катет прямоугольного треугольника равен 24, одна из средних линий равна 3,5.
Найдите гипотенузу этого треугольника.
30). В
равнобедренном треугольнике ABC медиана BK=16, боковая
сторона BC=34. Найдите длину отрезка MN, если известно,
что он соединяет середины боковых сторон.
31). В
равнобедренном треугольнике ABC с
основанием AC медиана BK=9, отрезок MN,
соединяющий середины боковых сторон, равен 40. Найдите боковую
сторону AB.
32).
В треугольнике ABC угол C равен 90°, AB=12, AC=3. Найдите sinA.
33). В
треугольнике ABC угол C равен 90°, AB=25, AC=24.
Найдите cosB.
34). В
треугольнике ABC угол C равен 90° АВ = , ВС = 3. Найдите
35). В
равнобедренном треугольнике ABC боковые стороны AB=BC=20, АС=32.
Найдите синус угла ВАС.
36). В
равнобедренном треугольнике ABC боковые стороны AB=BC=5,
медиана BM=3.Найдите cos∠BAC.
37). В
треугольнике ABC угол C равен 90°, AB=15, sinA=0,6.
Найдите AC.
38). В
треугольнике ABC угол C равен 90°, AB=39, . Найдите ВC.
39). В
треугольнике ABC угол C равен 90°, BС=32, тангенс
угла А равна . Найдите АВ.
40). В
прямоугольнике ABCD сторона ВС равна 48, тангенс угла CAD равна . Найдите площадь прямоугольника.
41). В
равнобедренной трапеции одно из оснований равно 5,
а другое — 9. Высота трапеции равна 6. Найдите
тангенс острого угла трапеции.
42). В
равнобедренном треугольнике ABC медиана BM, проведённая к
основанию, равна 12, а tgA=12/5. Найдите длину боковой
стороны треугольника ABC.
43). В
треугольнике АВС известно, что АВ=ВС, АС=8, tg∠ВАС=√5/2. Найдите
длину стороны АВ.
44). В
равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5.
Найдите площадь треугольника ABC.
45). В
равнобедренном треугольнике ABC высота BM, проведённая к
основанию, равна 6, а tgA=0,3. Найдите площадь
треугольника ABC.
46).
В равнобедренном треугольнике ABC боковая сторона AС=32, . Найдите площадь треугольника ABC.
47). Площадь
прямоугольника ABCD равна 400, сторона АВ=14. Найдите тангенс угла CAD.
48). В окружности
с центром O отрезки AC и BD — диаметры.
Центральный угол AOD равен 124°. Найдите
угол ACB. Ответ дайте в градусах.
49). На
окружности по разные стороны от диаметра AB отмечены
точки D и C. Известно, что ∠DBA=41°. Найдите
угол DCB. Ответ дайте в градусах.
50).
Четырёхугольник ABCD вписан в окружность.
Угол ABC равен 56°, угол CAD равен 42°.
Найдите угол ABD. Ответ дайте в градусах.
51). На
окружности с центром O и диаметром AB отмечена
точка C так, что угол COB равен 120°, AC=34.
Найдите диаметр окружности.
52). На окружности
радиуса 3 отмечена точка С. Отрезок АВ — диаметр
окружности, AC=. Найдите BC.
53).
На окружности радиуса 5 отмечена точка С. Отрезок АВ — диаметр
окружности, AC=6. Найдите cos∠BAC.
54). На окружности
радиуса 5 отмечена точка С. Отрезок АВ — диаметр
окружности, AC=8. Найдите sin∠ABC.
55). В
прямоугольной трапеции АВСD с основаниями ВС и АD
угол ВAD прямой, АВ=8, ВС= CD=10. Найдите
среднюю линию трапеции.
56). В
окружности с
центром O отрезки AC и BD — диаметры.
Вписанный угол ACB равен 36°. Найдите угол AOD.
Ответ дайте в градусах.
57). Найдите
вписанный угол, опирающийся на дугу, длина которой равна 1/5 длины
окружности. Ответ дайте в градусах.
58). В угол C,
равный 68°, вписана окружность с центром O, которая касается
сторон угла в точках A и B. Найдите угол AOB.
Ответ дайте в градусах.
59). На
окружности отмечена точка С. Отрезок АВ — диаметр
окружности, AC=9, BC=12. Найдите радиус окружности.
База 13
1). Два ребра прямоугольного параллелепипеда равны 8 и 5, а
объём параллелепипеда равен 280. Найдите площадь поверхности
этого параллелепипеда.
2). В прямоугольном
параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и
диагональ DA1 боковой грани равны соответственно 3, 5 и . Найдите объём параллелепипеда.
3). В основании прямой призмы лежит прямоугольный треугольник, катеты
которого равны 3 и 16. Найдите объём призмы, если её высота равна
3.
4). В основании прямой призмы лежит прямоугольный треугольник, один из
катетов которого равен 3, а гипотенуза равна . Найдите объём призмы, если её высота равна 6.
5). Сторона основания правильной треугольной
призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4. Найдите объём призмы ABCA1B1C1.
6). В треугольной
пирамиде ABCD рёбра AB, AC и AD взаимно
перпендикулярны. Найдите объём этой пирамиды, если AB=5, AC=24 и AD=3.
7). В основании пирамиды SABCSABC лежит правильный
треугольник ABCABC со стороной 6, а боковое
ребро SASA перпендикулярно основанию и равно 6. Найдите объём пирамиды SABC.
8). Основанием четырёхугольной пирамиды является прямоугольник со
сторонами 9 и 4. Найдите высоту этой пирамиды, если её
объём равен 48.
9). Найдите объём правильной четырёхугольной пирамиды,
сторона основания которой равна 4, а боковое ребро равно .
10). Сторона основания правильной треугольной пирамиды равна 3,
а высота пирамиды равна 4. Найдите объём этой пирамиды.
11). Стороны основания правильной треугольной пирамиды равны 16,
а боковые рёбра равны 17. Найдите площадь боковой поверхности этой
пирамиды.
12). Сторона основания правильной шестиугольной пирамиды равна 22,
боковое ребро равно 61. Найдите площадь боковой поверхности этой
пирамиды.
13). Даны два цилиндра. Радиус основания и высота первого цилиндра
равны соответственно 2 и 6, а второго — 6 и 4. Во
сколько раз объем второго цилиндра больше объема первого?
14). Даны два цилиндра. Радиус основания и высота первого цилиндра
равны соответственно 4 и 18, а второго — 2 и 3. Во
сколько раз площадь боковой поверхности первого цилиндра больше площади боковой
поверхности второго?
15). Радиус основания цилиндра равен 15, а его
образующая равна 19. Сечение, параллельное оси цилиндра,
удалено от неё на расстояние, равное 9. Найдите площадь сечения.
16). Объём конуса равен 32π, а его высота равна 6. Найдите
радиус основания конуса.
17). Объём конуса равен 16π, а радиус его основания равен 2.
Найдите высоту конуса.
18). Даны два конуса. Радиус основания и высота первого конуса равны
соответственно 4 и 9, а второго 6 и 8. Во
сколько раз объём второго конуса больше объёма первого?
19). Даны два конуса. Радиус основания и образующая первого конуса
равны соответственно 5 и 6, а второго
2 и 3. Во сколько раз площадь боковой поверхности
первого конуса больше второго?
20). Объём конуса равен 27. Через точку, делящую высоту конуса в
отношении 1:2, считая от вершины, проведена плоскость, параллельная
основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой
плоскостью.
21). Через точку, делящую высоту конуса в отношении 1:4,
считая от вершины, проведена плоскость, параллельная основанию. Найдите объём
этого конуса, если объём конуса, отсекаемого от данного конуса проведённой
плоскостью, равен 8.
22). Даны два шара с радиусами 8 и 2. Во сколько раз объём
большего шара больше объёма другого?
23). Даны два шара с радиусами 9 и 3. Во сколько раз площадь
поверхности большего шара больше объёма другого?
База 20
1). В сосуд, содержащий 5 литров 12−процентного водного
раствора некоторого вещества, добавили 7 литров воды. Сколько процентов
составляет концентрация получившегося раствора?
2). Смешали некоторое количество 15−процентного раствора
некоторого вещества с таким же количеством 19−процентного раствора этого
вещества. Сколько процентов составляет концентрация получившегося раствора?
3). Смешали 4 литра 15−процентного водного раствора
некоторого вещества с 6 литрами 25−процентного водного раствора
этого же вещества. Сколько процентов составляет концентрация получившегося
раствора?
4). Имеется два сплава. Первый сплав содержит 10% меди, второй
− 30% меди. Из этих двух сплавов получили третий сплав, содержащий 25%
меди. Масса первого сплава равна 200кг. Найдите массу третьего?
5). Имеется два сплава. Первый сплав содержит 15% меди, второй
− 35% меди. Из этих двух сплавов получили третий сплав, содержащий 30%
меди. Масса первого сплава равна 35кг. На сколько кг масса первого
сплава меньше массы второго?
6). Из городов A и B, расстояние между
которыми равно 330 км, навстречу друг другу одновременно выехали два
автомобиля и встретились через 3 часа на расстоянии 180 км от
города Найдите скорость автомобиля,
выехавшего из города
7). Дорога между пунктами А и В состоит
из подъёма и спуска, а её длина равна 8 км. Турист прошёл путь из А в В за
5 часов. Время его движения на спуске составило 1 час. С какой
скоростью турист шёл на спуске, если скорость его движения на
подъёме меньше скорости движения на спуске на 3 км/ч?
8). Расстояние между городами A и B равно
470 км. Из города A в город B выехал
первый автомобиль, а через 3 часа после этого навстречу ему из
города B выехал со скоростью 60 км/ч второй автомобиль.
Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км
от города
9). Расстояние между городами A и B равно
435 км. Из города A в город B со
скоростью 60 км/ч выехал первый автомобиль, а через час после
этого навстречу ему из города B выехал со скоростью 65 км/ч
второй автомобиль. На каком расстоянии от города A автомобили
встретятся? Ответ дайте в километрах.
10). Два человека отправляются из одного и того же места
на прогулку до опушки леса, находящейся в 4,4 км от места отправления.
Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч.
Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком
расстоянии от точки отправления произойдёт их встреча?
11). Теплоход, скорость которого в неподвижной воде равна 25 км/ч,
проходит по течению реки и после стоянки возвращается в исходный пункт.
Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в
исходный пункт теплоход возвращается через 30 часов после отплытия из
него. Сколько километров прошел теплоход за весь рейс?
12). Первые два часа автомобиль ехал со скоростью 50 км/ч,
следующий час — со скоростью 100 км/ч, а затем два часа —
со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении
всего пути.
13). Первые 190 км автомобиль ехал со скоростью 50 км/ч,
следующие 180 км — со скоростью 90 км/ч, а затем 170 км —
со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на
протяжении всего пути.
14). Первую треть трассы автомобиль ехал со скоростью 60 км/ч,
вторую треть — со скоростью 120 км/ч, а последнюю — со скоростью 110 км/ч.
Найдите среднюю скорость автомобиля на протяжении всего пути.
15). Путешественник переплыл море на яхте со средней скоростью 20 км/ч.
Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите
среднюю скорость путешественника на протяжении всего пути.
16). Один мастер может выполнить заказ за 12 часов, а другой — за
6 часов. За сколько часов выполнят заказ оба мастера, работая вместе?
17). Первый насос наполняет бак за 20 минут, второй — за 30
минут, а третий — за 1 час. За сколько минут наполнят бак три насоса,
работая одновременно?
18). Даша и Маша пропалывают грядку за 12 минут, а одна Маша —
за 20 минут. За сколько минут пропалывает грядку одна Даша?
19). Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8
вопросов теста, а Ваня — на 9. Они одновременно начали отвечать на
вопросы теста, и Петя закончил свой тест позже Вани на 20 минут. Сколько
вопросов содержит тест?
9). В понедельник акции компании подорожали на некоторое количество
процентов, а во вторник подешевели на то же самое количество процентов. В
результате они стали стоить на дешевле, чем при открытии торгов в
понедельник. На сколько процентов подорожали акции компании в понедельник?
Дополнительные задачи.
10). Изюм получается в процессе сушки винограда. Сколько килограммов
винограда потребуется для получения 78 килограммов изюма, если виноград
содержит 82% воды, а изюм содержит 19% воды?
11). Девять одинаковых рубашек дешевле куртки на 10%. На сколько
процентов одиннадцать таких же рубашек дороже куртки?
12). Семья состоит из мужа, жены и их дочери студентки. Если бы
зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы
стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на
4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
13). Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий
час — со скоростью 100 км/ч, а затем два часа — со скоростью 75 км/ч. Найдите
среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
17). Велосипедист выехал с постоянной скоростью из города А в город В,
расстояние между которыми равно 187 км. На следующий день он отправился
обратно в А со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку
на 6 часов. В результате велосипедист затратил на обратный путь столько же
времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из
А в В. ответ.
18). Велосипедист выехал с постоянной скоростью из города А в город В,
расстояние между которыми равно 143 км. На следующий день он отправился
обратно в А со скоростью на 2 км/ч больше прежней. По дороге он сделал
остановку на 2 часов. В результате велосипедист затратил на обратный путь
столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на
пути из B в A.
ответ.
19). Два велосипедиста одновременно отправились в 240-километровый
пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и
прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста,
пришедшего к финишу первым. ответ.
20). Два велосипедиста одновременно отправились в 88−километровый
пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и
прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста,
пришедшего к финишу вторым. ответ.
21). Из пункта А в пункт В, расстояние между которыми 30 км,
одновременно выехали автомобилист и велосипедист. За час автомобилист проезжает
на 70 км больше, чем велосипедист. Определите скорость велосипедиста,
если известно, что он прибыл в пункт В на 1 час 10 минут позже автомобилиста.
ответ.
22). Расстояние между городами A и B равно 420 км. Из города A в
город B выехал автомобиль, а через 1 час следом за ним со скоростью
80 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул
обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите
расстояние от A до C. Ответ дайте в километрах.
ответ.
23). Из городов А и В навстречу друг другу одновременно выехали
мотоциклист и велосипедист. Мотоциклист приехал в город В на 12 часов раньше,
чем велосипедист приехал в город А, а встретились они через 2 часа 30 минут
после выезда. Сколько часов затратил на путь из города В в город А
велосипедист?
24). По двум параллельным железнодорожным путям друг навстречу другу
следуют скорый и пассажирский поезда, скорости которых равны соответственно
65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину
скорого поезда, если время, за которое он прошел мимо пассажирского поезда,
равно 36 секундам.
25). От пристани A к пристани B, расстояние между которыми равно
153 км, отправился с постоянной скоростью первый теплоход, а через 8 часов
после этого следом за ним со скоростью на 8 км/ч большей отправился второй.
Найдите скорость первого теплохода, если в пункт B оба теплохода прибыли
одновременно. Ответ дайте в км/ч. ответ.
26). Пристани A и B расположены на
озере, расстояние между ними 390 км. Баржа отправилась с постоянной скоростью
из A в На следующий день после прибытия она
отправилась обратно со скоростью на 3 км/ч больше прежней, сделав по пути
остановку на 9 часов. В результате она затратила на обратный путь столько же
времени, сколько на путь из A в Найдите
скорость баржи на пути из A в Ответ
дайте в км/ч. ответ.
27). Теплоход, скорость которого в неподвижной воде равна 25 км/ч,
проходит по течению реки и после стоянки возвращается в исходный пункт.
Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт
теплоход возвращается через 30 часов после отплытия из него. Сколько километров
прошел теплоход за весь рейс?
28). Теплоход проходит по течению реки до пункта назначения
384 км и после стоянки возвращается в пункт отправления. Найдите
скорость теплохода в неподвижной воде, если скорость течения равна
4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход
возвращается через 48 часов.
ответ.
29). Теплоход проходит по течению реки до пункта назначения
468 км и после стоянки возвращается в пункт отправления. Найдите
скорость скорость течения, если скорость теплохода равна 22 км/ч,
стоянка длится 3 часа, а в пункт отправления теплоход возвращается через
47 часов. ответ.
30). Моторная лодка прошла против течения реки 165 км и вернулась
в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость
лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ
дайте в км/ч. ответ.
31). Моторная лодка прошла против течения реки 252 км и вернулась
в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость
течения, если скорость лодки в неподвижной воде равна 16 км/ч. Ответ
дайте в км/ч. ответ.
32). Байдарка в 10 : 00 вышла из пункта А в пункт В,
расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, байдарка
отправилась назад и вернулась в пункт А в 16:00 того же дня.
Определите (в км/ч) собственную скорость байдарки, если известно, что
скорость течения реки равна 2 км/ч.
ответ.
33). Баржа в 10:00 вышла из пункта А в пункт В,
расположенный в 30 км от А. Пробыв в пункте В 4 часа, баржа отправилась
назад и вернулась в пункт А в 22:00 того же дня. Определите (в
км/ч) скорость течения реки, если известно, что собственная скорость баржи
равна 8 км/ч. ответ.
34). Расстояние между пристанями A и B равно 192 км. Из A в B по
течению реки отправился плот, а через 3 часа вслед за ним отправилась яхта,
которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому
времени плот проплыл 92 км. Найдите скорость яхты в неподвижной воде,
если скорость течения реки равна 4 км/ч.
ответ.
35). Заказ на 140 деталей первый рабочий выполняет на 4 часа
быстрее, чем второй. Сколько деталей в час делает второй рабочий, если
известно, что первый за час делает на 4 детали больше? ответ.
36). Заказ на 176 деталей первый рабочий выполняет на 5 часов быстрее,
чем второй. Сколько деталей в час делает первый рабочий, если
известно, что он за час делает на 5 деталей больше, чем второй?
ответ.
37). На изготовление 720 деталей первый рабочий затрачивает на 6 часов
меньше, чем второй рабочий на изготовление 840 деталей. Известно, что первый
рабочий за час делает на 2 детали больше, чем второй. Сколько деталей в
час делает первый рабочий? ответ.
38). На изготовление 696 деталей первый рабочий затрачивает на 5 часов
меньше, чем второй рабочий на изготовление 725 деталей. Известно, что первый
рабочий за час делает на 4 детали больше, чем второй. Сколько деталей в
час делает второй рабочий? ответ.
39). Первая труба пропускает на 8 литров воды в минуту меньше, чем
вторая. Сколько литров воды в минуту пропускает первая
труба, если резервуар объёмом 180 литров она заполняет на 8 минут дольше, чем
вторая труба? ответ.
40). Первая труба пропускает на 4 литров воды в минуту меньше, чем
вторая. Сколько литров воды в минуту пропускает вторая
труба, если резервуар объёмом 252 литров она заполняет на 4 минут быстрее, чем
первая труба? ответ.
41). Первая труба наполняет резервуар на 13 минут дольше, чем
вторая. Обе трубы, работая одновременно, наполняют этот же
резервуар за 42 минуты. За сколько минут наполняет этот резервуар одна
вторая труба? ? ответ.
База 21
1). Кузнечик прыгает: данное число плюс один.
2). В корзине лежат грибы: Сколько рыжиков в корзине?
Грузди минус один. Сколько груздей? Рыжик минус один.
3). Восемь столбов соединены: Перемножить данные два числа и
разделить на два.
4). Из десяти стран: Перемножить первые два числа, перемножаем
вторые два числа, складываем их и делим на два.
5). На поверхности глобуса: Параллель плюс один и умножаем на
меридиан.
6). В таблице три столбца и несколько строк. 119, 125, 133.
Больше 15, но меньше 18.
Значит это числа 16 или 17. Складываем все три числа
119+125+133=377.Затем делим 377 на 16. 377:16=23.
7). В конце четверти Петя: Разлагаем данное число на простые
множители.
(2+3+3+2+3):5=2,6. Ответ. 3
8). Миша, Коля и Леша играют в теннис: Надо из большего числа
вычесть меньшее.
9). Из книги выпало несколько листов: 298. 289, 829,
892, 928, 982.
289 не подходит, оно меньше 298. Из оставшихся чисел
выбираем нечетное число, это 829. =265.
10).На ленте по разные стороны: Складываем данные
числа и делим на два.
11). На палке отмечены поперечные линии: Складываем все три
числа и вычитаем два.
12). На кольцевой дороге: Из первого числа вычитаем второе.
13). Про натуральные числа A, B и C известно, что каждое из них больше 4, но меньше 8.
Загадали натуральное число, затем его умножили А, потом прибавили B и вычли С. Получилось
165. .
А, B, С =5 или 6 или 7. Ответ. 33
14). Если каждый множитель увеличить на 1, то их произведение
увеличилось бы на 3.
Каждый из них увеличится на 5. Решение:
15). Список заданий викторины: правильный ответ 7, а
неправильный 13. Набрал 56 очков. . Ответ. 21.
16). Клетки таблицы 4х5. 15 и 11.
17). Прямоугольник разбить на четыре части. Найдите периметр.
14-12=2. 13-2=11.
18). Прямоугольник разбить на четыре части. Найдите площадь.
Ответ. 20.
19). Саша пригласил Петю в гости, сказав живет в 8 подъезде,
квартира №468, а этаж сказать забыл. Дом двенадцатиэтажный. На каком
этаже живет Саша?
На каждом этаже по 5 квартир. 7 подъезд заканчивается
№420. . Ответ. 10.
20). Во всех подъездах дома одинаковое число этажей: . Берем из них большее число. Ответ. 11.
21). Петя меняет маленькие фишки на большие за один обмен
получает 4 большие отдав 10 маленьких. Было 100 фишек, осталось 64. Ответ.6
22). В доме всего 18 квартир с номерами от 1 до 18. В квартирах
с 1по 13 включительно живет 15 человек. А с 11 по 18 включительно живет 20
человек. 15+15 = 30. Ответ. 30
23). Маша и Медведь съели 51печенье…Медведь ест в четыре
раза быстрее.
4² =16;
24). В обменном пункте: за 4 золотых получить 5 серебряных.
За 8 серебряных получить 5
золотых. 45 медных.
25). Взяли несколько досок и распилили: Из большего вычесть
меньшее.
26). Среднее арифметическое 5 чисел равно 7.
Среднее арифметическое этих пяти чисел и шестого равно 8. . Ответ. 13.
27). Хозяин договорился с рабочим: 4200; 1300; 11. 117700.
28). В магазине квас на разлив: 1л-36р; 2л-66р. Сколько 1,5?
29). Три луча разбивают на 3 разных угла. Наибольший угол в 2 раза
больше.
.
90-72-1=17. Ответ.17.
- 09.09.2012
Подборка шпаргалок по МАТЕМАТИКЕ.
Дата обновления: 01.11.2022
Полный набор теоретического материала для подготовки к ЕГЭ по математике — профильной и базовой. Таблицы, схемы, формулы, вся теория по заданимя. Всё, что необходимо для самостоятельной работы по математике.
- Тренировочные варианты ЕГЭ по профильной математике
- Тренировочные варианты по базовой математике
Что содержите в себе сборник шпаргалок по математике
- Числа, степени, модуль
- Уравнения, углы, прямые
- Справочные материалы по тригонометрии
- Решение текстовых задач
- Производная и первообразная
- Шпаргалка для экономических задач
- Шпоры по тригонометрии
- Шпаргалки по математике в картинках
Для чтения шпаргалок необходимы бесплатные программы: WinDJView и Adobe Reader
СКАЧАТЬ
https://down.ctege.info/ege/obshee/shpory/matem-ege-shpora.zip
10+ формул, которые помогут тебе сдать базовую математику на отлично
Математика — один из самых сложных предметов для сдачи ЕГЭ. Особенно, если ты гуманитарий. Какие основные формулы помогут тебе хорошо сдать базовый экзамен? Делимся с тобой необходимым материалом для подготовки к ЕГЭ по математике.
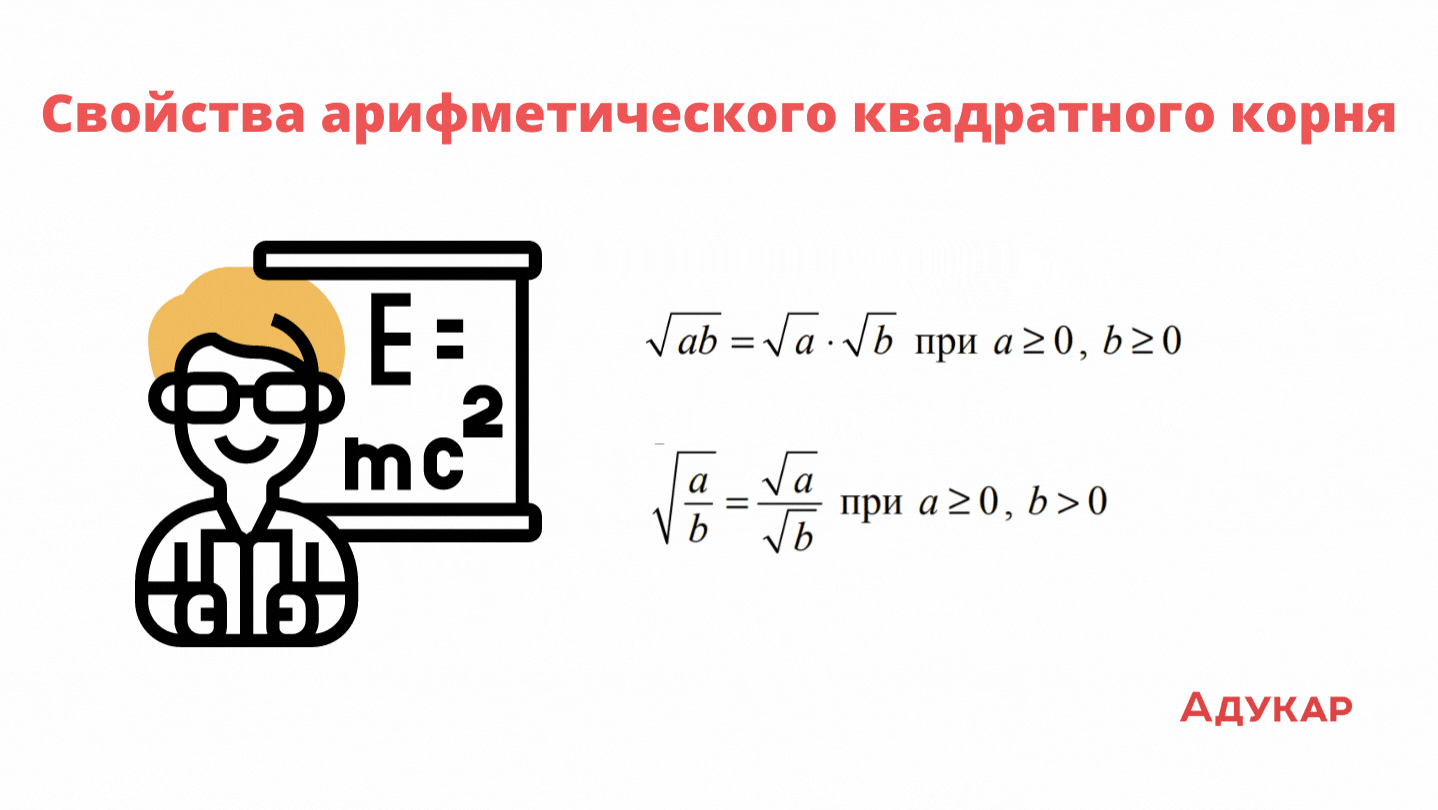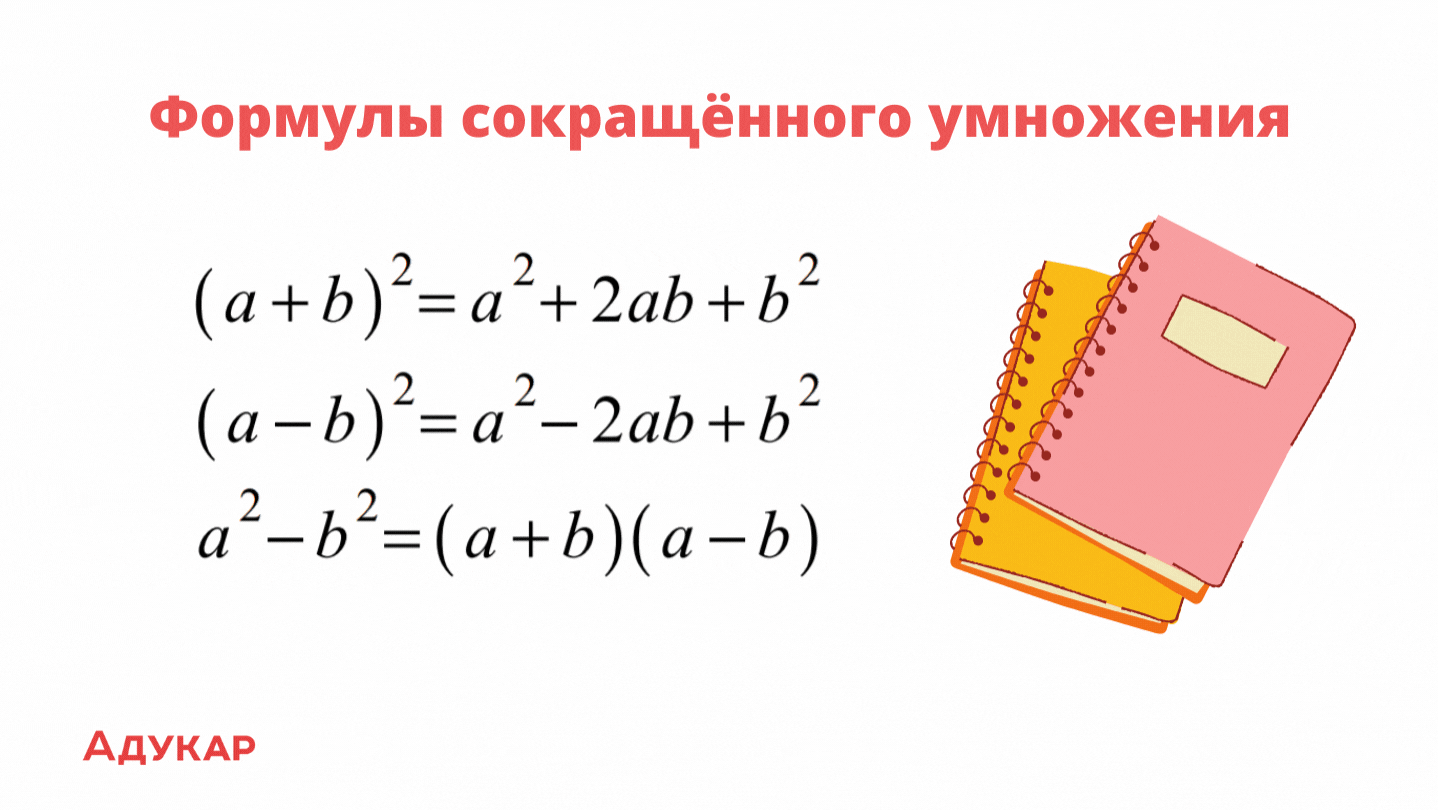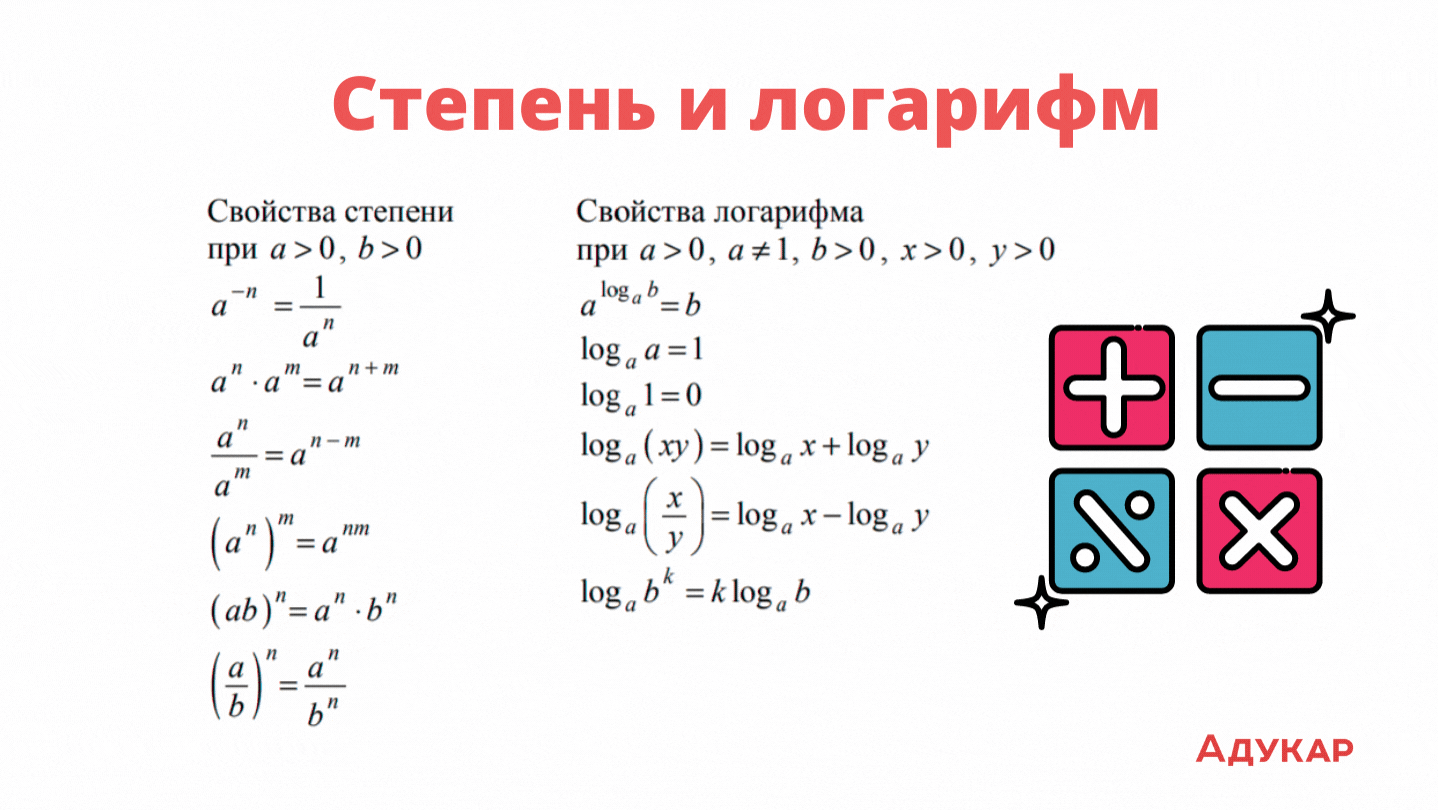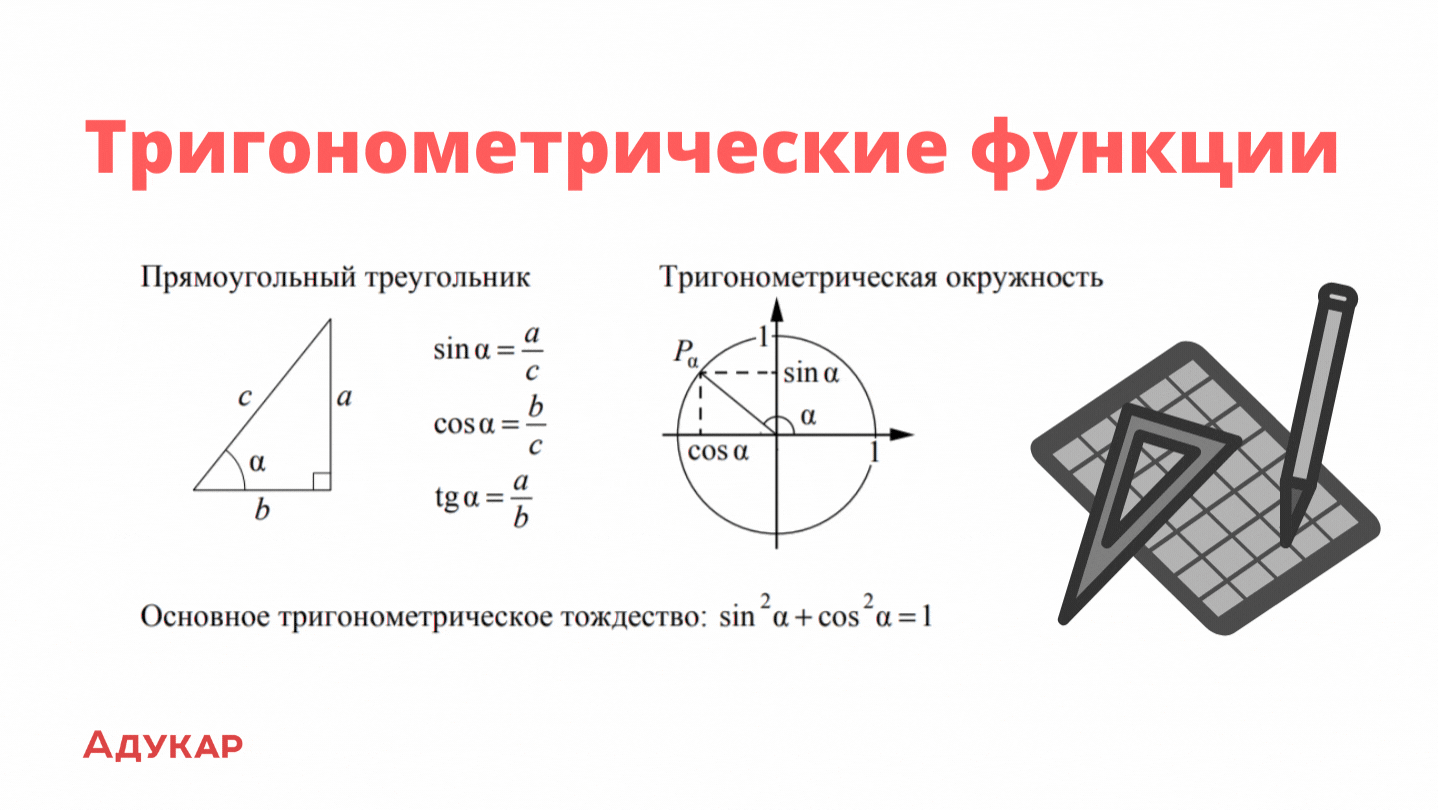
Свойства арифметического квадратного корня
Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a. Если нужно прочитай это утверждение ещё раз, чтобы понять его. Этот арифметический корень имеет свойства, представленные на картинке. Заучи их, ведь задания на подобную тематику встречаются в семнадцатом вопросе ЕГЭ.
Демоверсия ЕГЭ-2022 по математике. Базовый уровень
Корни квадратного уравнения
Напоминаем, что уравнение является равенством, содержащим в себе переменную, значение которой нужно найти. А когда переменная, входящая в уравнение, возведена во вторую степень (в квадрат), то такое уравнение называют уравнением второй степени или квадратным уравнением. Чтобы решить его без проблем, нужно выучить несколько формул. Не забивай на это, так как квадратные уравнения будут в девятом вопросе.
Формулы сокращенного умножения
Тут всё сложнее, чем дважды два — четыре. Но тебя снова выручат формулы. Они облегчат работу с объёмными вычислениями. Есть вероятность, что на ЕГЭ ты встретишь задания на сокращённое умножение в седьмом вопросе.
Стоит сказать, что на картинке выше собраны не все формулы. На самом деле их больше.
Степень и логарифм
Логарифмы считаются одной из самых сложных тем в курсе школьной математики, поэтому не жалей времени на её разбор. Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x. В неравенстве всё выглядит так: loga x = b, где a — основание, x — аргумент, b — собственно, чему равен логарифм. На картинке ниже мы собрали формулы со свойствами степени и логарифма. Их стоит приберечь (в уме, а не шпаргалках) для седьмого и семнадцатого заданий.
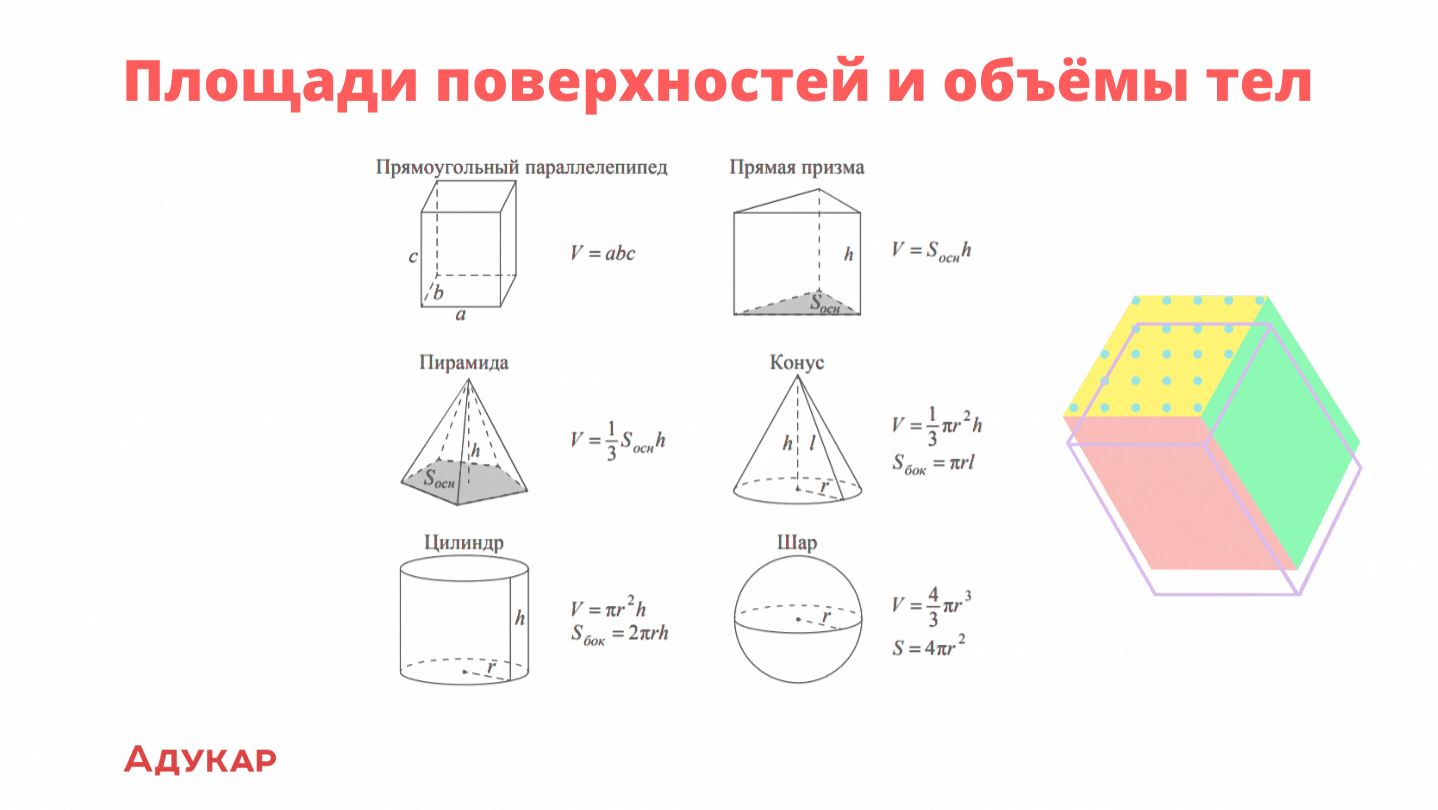
Площади поверхностей и объёмы тел
Спроси любого школьника и он ответит: площадь геометрической фигуры — это величина, характеризующая её размер. Объём — это величина фигуры в длину, высоту и ширину, измеряемая в кубических единицах. Если ты тоже знаешь эти правила, значит в формулах ниже разберёшься без проблем и с шестнадцатым вопросом ЕГЭ справишься.
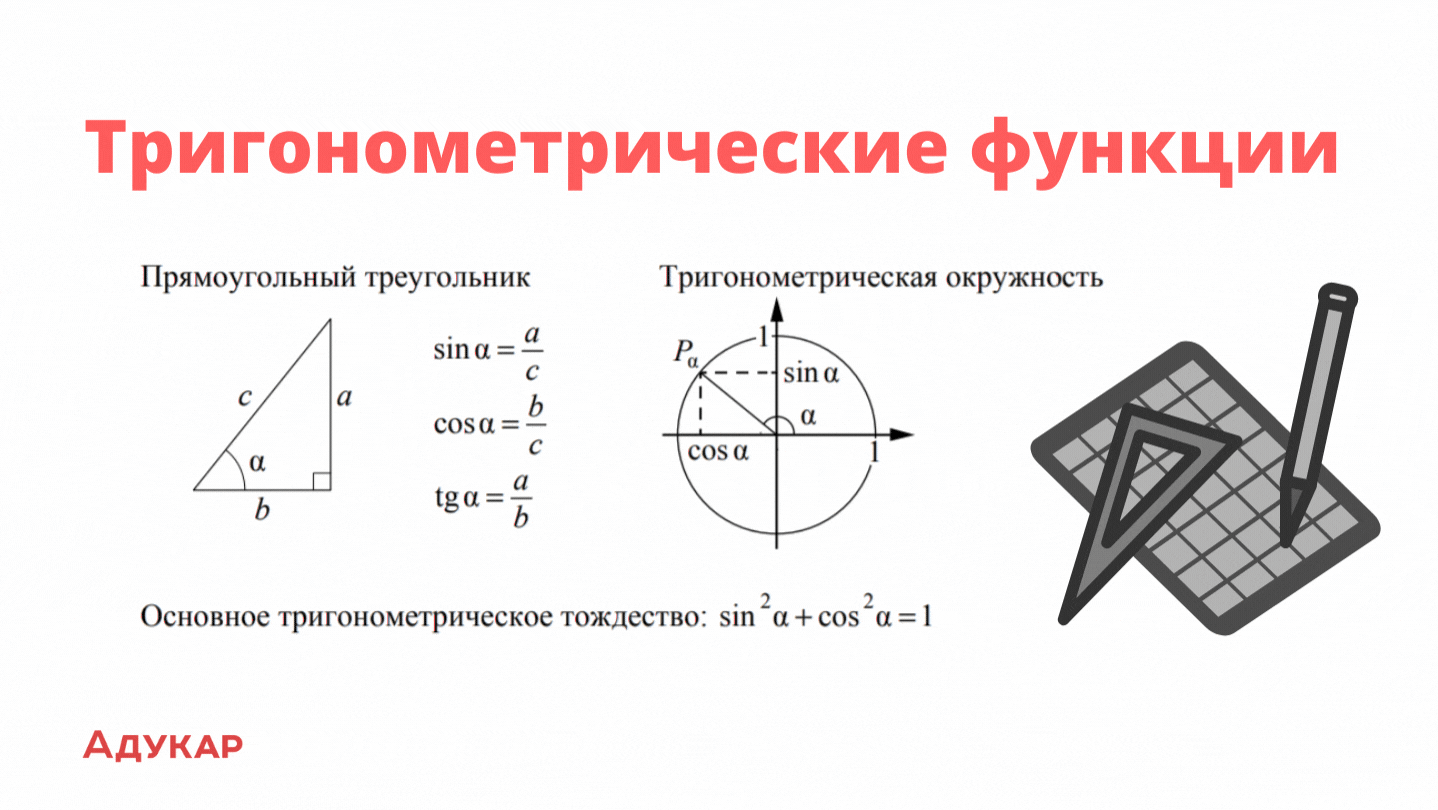
Тригонометрические функции
Напоследок повторим, что такое тригонометрические функции. Это элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе. Синус, косинус, тангенс, котангенс — ключевые понятия тригонометрии. Чтобы запомнить, как они работают, тебе пригодится картинка ниже. Задания на тригонометрию есть в седьмом вопросе ЕГЭ.
Справочные материалы базового ЕГЭ-2022 по математике
Теперь ты знаешь всё о наиболее распространённых формулах в базовом ЕГЭ по математике. К сожалению, подготовку к экзамену на этом закончить нельзя. Но ты можешь записаться на бесплатное пробное занятие по математике в Адукар.
Cпасибо, что дочитал до конца. Мы рады, что были полезны. Чтобы получить больше информации, посмотри ещё:
Типичные ошибки при выборе профессии
ЕГЭ по математике: что изменится в 2022 году?
Итоговое сочинение 2022: всё, что о нём нужно знать
Не пропускай важные новости и подписывайся на наш YouTube, ВК, Instagram, Telegram.
***
Если хотите разместить этот текст на своём сайте или в социальной сети, свяжись с нами по адресу info@adukar.by. Перепечатка материалов возможна только с письменного согласия редакции.
Хочешь быть в курсе новостей ЦТ?
Подписывайся на Адукар в соцсетях!
Начни подготовку к ЦТ и ЦЭ прямо сейчас!

Адукар обещает крутых преподавателей и много полезной практики.
итоговые занятия перед ЦТ? Такие занятия мы проводим уже четвёртый год, и преподаватели нашего учебного центра
научились достаточно точно предсказывать, какие вопросы будут на ЦТ. На этом занятии мы прорешаем их вместе с тобой!
Регистрируйся,
если еще не сделал этого — и увеличь свои шансы на поступление!