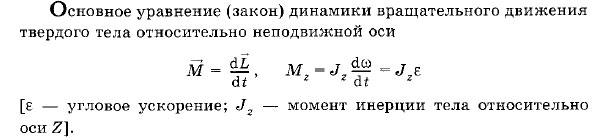Шпаргалка к экзамену по физике 1 семестр

☺ Механическое
движение. Механическая система.
Материальная точка. Абсолютно твердое
тело. Система отсчета.

☺ Координатный
способ задания положения м.т.

☺ Путь
м.т. Перемещение м.т. Мгновенная скорость.
Средняя. Средняя путевая.

☺ Ускорение.
Нормальное. Тангенсальное

☺ Вычисление
пути м.т. Перемещения.

☺ Кинематика
вращательного движения твердого тела.
Равномерное и равнопеременное движение.

☺ Кинематика
вращательного движения твердого тела.
Вектор элементарного угла поворота.
Угловая скорость. Угловое ускорение.

☺ Частный
случай вращательного движения. Равномерное
вращение. Частота. Период. Равнопеременное
вращение.

☺ Связь
угловых и линейных характеристик
вращательного движения. Тангенсальное
ускорение. Нормальное.

☺ 1
закон Ньютона. Сила. Масса. Ускорение.
2 закон Ньютона.

☺ Импульс
тела.
Элементарный
импульс силы.

☺ 3
закон Ньютона.

☺ Движение
тела переменной массы. Уравнение
Мещерского.
Уравнение Циолковского.

☺ Работа.
Механическая энергия.

☺ Консервативные
силы. Неконсервативные. Потенциальная
энергия. Закон сохранения энергии
консервативной системы.

☺ Основное
уравнение динамики вращательного
движения твердого тела.

☺ Момент
силы относительно Точки. Неподвижной
оси. Момент импульса.

☺ Момент
инерции м.т., системы материальных точек
и тела относительно оси. Т. Штейнера
(док.)

☺ Кинетическая
энергия тела, вращающегося вокруг
неподвижной оси. Работа и мощность, для
вращательного движения тела.

☺ Центр
масс и закон его движения.

☺ Абсолютно
упругий удар. Неупругий. Пример прямого,
центрального соударения шаров.

☺ Движение
в поле центральных сил. Гравитационное
поле. Напряженность. Потенциал. Связь
между силой и потенциальной энергией.

☺ Закон
всемирного тяготения. Космические
скорости.

☺ Неинерциальные
системы отсчета.
Скорость
в Н.С.О.

☺ Ускорение
в Н.С.О. Абсолютное, переносное кориолисово
ускорения.

☺ Гармонические
колебания. Дифференциальное уравнение
гармонических колебаний. Решение
уравнения.

☺ Метод
векторных диаграмм. Сложение двух
одинаково направленных гармонических
колебаний.

☺ Кинетическая
и потенциальная энергия м.т., совершающей
прямолинейные гармонические колебания.

☺ Когерентные
гармонические колебания. Некогерентные.
Биения.

☺ Затухающие
колебания. Дифференциальное уравнение
затухающих колебаний. Его решение.
Условный период.
Логарифмический
декремент затухания.

☺ Вынужденные
механические колебания. Дифференциальное
уравнение. Его решение.

☺ Сложение взаимно
перпендикулярных колебаний.

☺ Элементы теории
относительности. Преобразования Лоренца.

☺ Следствия из
преобразования Лоренца.

☺ Связь массы и
энергии. Полной энергии массы и импульса
в релятивистской механике.

☺ Термодинамическая
система. Ее параметры и процессы.
Уравнение Менделеева – Клайперона.

☺ Внутренняя
энергия. Работа. Теплота. 1 начало
термодинамики.

☺ Теплоемкость
в-ва удельная. Малярная. Уравнение
Майера. Связь между теплоемкостями.

☺ 1 начало
термодинамики для изопроцессов.

☺ Адиабатный
процесс. Уравнение адиабаты.

☺ Работа, совершаемая
газом в адиабатном процессе и изопроцессах.

☺ Политропный
процесс. Работа.

☺ Теплоемкость
в-ва. Для различных изопроцессов.

☺ Обратимые
процессы. Необратимые. Энтропия.

☺ Диаграмма T-S
для изопроцессов.

☺ Энергия Гельмгольца.

☺ 2
и 3 начало термодинамики.

☺ Круговые процессы.
Цикл Карно прямой. Обратный. Термодинамический
коэффициент полезного действия.

☺ Теоремы
Карно.

☺ Молекулярно-кинематическая
теория строения в-ва. Закон Дальтона.

☺ Закон равномерного
распределения энергии по степеням
свободы.

☺ Средняя
арифметическая скорость поступательного
движения молекул идеального газа.
Средняя квадратичная. Наиболее вероятная.

☺ Распределение
Максвелла. Опыт Штерна.

☺ Барометрическая
формула. Закон Больцмана для распределения
частиц во внешнем потенциальном поле.

☺ Реальные газы.
Уравнение Ван-дер-Ваальса.

☺ Явление переноса.
Законы Ньютона, Фурье, Фика.

☺ Механическое движение изменение положения тела в пространстве относительно других тел, с течением времени. Механическая система – совокупность материальных точек (тел), рассматриваемых, как единое целое. Абсолютно твердое тело тело, расстояние между любыми двумя точками которого остается постоянным. Система отсчета тело отсчета, система координат, часы. Поступательное движение такое движение, при котором прямая, соединяющая любые две точки тела остается параллельной самой себе при движении тела.	☺ Координатный способ задания положения м.т. положение м.т. в пространстве можно задать радиус вектором (вектор, проведенный из начала координат к м.т.)	☺ Путь м.т. расстояние измеряемое по траектории (линии, описываемой точкой при ее движении) вдоль движения м.т. Перемещение м.т. за данный промежуток времени вектор, соединяющий начальное и ее конечное положение. Мгновенная скорость первая производная от радиус вектора по времени. Средняя вектор, равный отношению перемещения м.т. за промежуток времени ∆t к этому промежутку времени. Средняя путевая скалярная величина, равная отношению пути, пройденному за промежуток времени ∆t к этому промежутку времени.
☺ Ускорение первая производная от скорости по времени или вторая производная то радиус вектора по времени. Нормальное Тангенсальное Модуль тангенсального ускорения характеризует быстроту изменения модуля скорости м.т. Модуль ускорения	☺ Вычисление пути м.т. Перемещения. Равномерное прямолинейное: Равнопеременное прямолинейное:	☺ Кинематика вращательного движения твердого тела. Равномерное и равнопеременное движение. Вращение тела вокруг неподвижной оси АВ – движение твердого тела при котором все точки прямой АВ жестко связанны с телом остаются неподвижными. Мерой перемещения всего тела за малый промежуток времени ∆t для вращательного движения служит вектор элементарного угла поворота ∆φ
☺ Кинематика вращательного движения твердого тела. Вектор элементарного угла поворота – вектор, модуль которого равен самому углу поворота dφ за промежуток времени dt, направленный вдоль лси вращения по правилу правого буравчика: если рукоятку буравчика вращать в сторону увеличения угла φ, то поступательное движение буравчика даст направление вектора dφ). Угловая скорость – отношение вектора элементарного угла поворота dφ к некоторому промежутку времени dt, в течение которого происходил этот поворот. Угловое ускорение – первая производная от угловой скорости по времени.	☺ Частный случай вращательного движения. Равномерное вращение – такое вращение, при котором угловая скорость = const. Частота – число полных оборотов, совершаемых телом при равномерном движении по окружности в единицу времени. Период – время, за которое точка совершает один полный оборот. Равнопеременное вращение – вращение при котором угловое ускорение = const.	☺ Связь угловых и линейных характеристик вращательного движения. Тангециальное и нормальное ускорения. Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением .
☺ 1 закон Ньютона: м.т. сохраняет состояние покоя или прямолинейного равномерного движения, пока внешняя сила не выведет ее из этого состояния. Сила – векторная физическая величина, являющаяся мерой механического воздействия других тел или полей, в результате которого тело приобретает ускорение или деформируется. Масса – скалярная величина, которая является мерой инертности тела. Масса – величина аддитивная, те масса всего тела равна сумме масс частей этого тела Ускорение – первая производная от скорости по времени или вторая производная от пути по времени. 2 закон Ньютона: скорость изменения импульса м.т. равна действующей на нее силе.	☺ Импульс тела – величина, численно равная произведению массы на скорость тела и имеющая направление. Количество движения. Элементарный импульс силы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени.	☺ 3 закон Ньютона: две м.т. действуют друг на лдруга с силами равными по модулю, и направленными в противоположные стороны, вдоль прямой, соединяющей эти точки. F=-F
☺ Движение тела переменной массы. Уравнение Мещерского— основное уравнение в механике тел переменной массы, полученное И. В. Мещерским для материальной точки переменной массы. Уравнение Циолковского. где  — число Циолковского.	☺ Работа – скалярное произведение силы на перемещение. Механическая энергия – мера механического движения тел и механического воздействия системы тел друг с другом и с внешними телами.	☺ Консервативные силы – силы, действующие в потенциальных полях. Неконсервативные. Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Закон сохранения энергии консервативной системы: в системе тел, между которыми действуют только консервативные силы (внутренние и внешние).
☺ Основное уравнение динамики вращательного движения твердого тела: производная по времени момента импульса механической системы относительно неподвижной точки равна главному моменту всех внешних сил, приложенных к системе относительно той же точки.	☺ Момент силы относительно точки: векторное произведение радиус вектора r проведенного из неподвижной точки к точке приложения силы на эту силу. M=[rF] Неподвижной оси: проекция на эту ось вектора момента силы относительно произвольной точки, взятой на этой оси. Момент импульса: L=[rP].	☺ Момент инерции м.т.: произведение массы на квадрат ее расстояния до оси. М системы материальных точек тела относительно оси: сумма произведения масс на квадрат их расстояния до оси. Т. Штейнера (док.)
☺ Кинетическая энергия малого элемента тела массой dm, вращающегося вокруг неподвижной оси Кинетическая энергия всего тела: Работа для вращательного движения тела Мощность Различают среднюю мощность за промежуток времени : и мгновенную мощность в данный момент времени:	☺ Центр масс и закон его движения.	☺ Абсолютно упругий удар. Неупругий. Пример прямого, центрального соударения шаров.
☺ Движение в поле центральных сил. Сила, действ. На м.т. называется центральной, если она зависит только от расстояния между м.т. и некой неподвижной точкой, называемой центром силы и направлена всюду: либо от центра, либо к центру. Гравитационное поле – поле центральных сил. Силы тяготения всегда направлены вдоль прямой, соединяющей взаимодействующие тела Вектор g не зависит от m и наз. напряж. Напряженность поля тяготения определяется силой, действующей на м.т. единичной массой со стороны поля и совпадает по направлению с действующей силой. Потенциал φ – скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля или работой по перемещению единичной массы в поле. Связь между силой и потенциальной энергией. П=mGMh/R02=mgh. F=GmM/R2	☺ Закон всемирного тяготения: между любыми двумя материальными точками действует сила взаимного притяжения, прямопропорц… и обратнопропорц…. F=Gm1m2/r2 Первая космическая скорость — такая минимальная скорость, которую надо сообщить телу, чтобы оно могло двигаться вокруг Земли по круговой орбите, те превратиться в искусственный спутник Земли. По 2 зН: GmM/r2=mv2/r, g=GM/R02, а у поверхности Земли R0≈r то v2=gR0=7,9км/с Вторая космическая скорость – та наименьшая скорость, которую надо сообщить телу, чтобы оно могло преодолеть притяжение Земли, и привратиться в спутник Солнца. V2=2gR0≈11,2 км/с Третья космическая скорость – скорость, кот необходимо сообщить телу на земле, чтобы оно покинуло пределы солнечной системы, преодолев притяжение Солнца. V=16,7 км/с	☺ Неинерциальные системы отсчета – системы отсчета, движущиеся относительно инерциальной системы с ускорением. Но к ним можно применять законы динамики, если ввести силы инерции.с Скорость в Н.С.О.
☺ Ускорение в Н.С.О. Абсолютное, переносное кориолисово ускорения.	☺ Колебания – прочесы повторяющиеся во времени. Гармонические колебания – периодические колебания, в которых колеблющаяся величина изменяется по закону sin или cos. Периодические – колебания при которых колеблющиеся величины, характеризующие систему, повторяются через равные промежутки времени. Дифференциальное уравнение гармонических колебаний. Решение уравнения.	☺ Метод векторных диаграмм. Сложение двух одинаково направленных гармонических колебаний.
☺ Кинетическая и потенциальная энергия м.т., совершающей прямолинейные гармонические колебания.	☺ Когерентные гармонические колебания – такие колебания у которых разность фаз остается постоянной во времени. Биения – негармонические колебания, получившиеся в результате наложения двух одинаково направленных гармонических колебаний с близкими частотами.	☺ Затухающие колебания. Затухание – трение с окружающей средой. Е колебаний системы уменьшается – уменьшается амплитуда колебаний. Дифференциальное уравнение затухающих колебаний. Его решение. Условный период. Логарифмический декремент затухания.
☺ Вынужденные механические колебания – колебания, возникающие в системе под влиянием переменного внешнего воздействия. Дифференциальное уравнение. Его решение.	☺ Сложение взаимно перпендикулярных колебаний.	☺ Элементы теории относительности. Преобразования Лоренца.
☺ Следствия из преобразования Лоренца.	☺ Связь массы и энергии. Полной энергии массы и импульса в релятивистской механике.	☺ Термодинамическая система. Ее параметры и процессы. Уравнение Менделеева – Клайперона.
☺ Внутренняя энергия. Работа. Теплота. 1 начало термодинамики.	☺ Теплоемкость в-ва удельная. Малярная. Уравнение Майера. Связь между теплоемкостями.	☺ Адиабатный процесс. Уравнение адиабаты.
☺ Работа, совершаемая газом в адиабатном процессе и изопроцессах.	☺ 1 начало термодинамики для изопроцессов.	☺ Теплоемкость в-ва. Для различных изопроцесса.
☺ Обратимые процессы. Необратимые. Термодинамический процесс – обратимый, если после него можно вернуть систему в исходное состояние так, что в окружающей среде не останется никаких изменений. В противном случае, процесс – необратимый. Все реальные процессы – необратимые, тк они сопровождаются трением. Энтропия – функция S состояния системы, дифференциал которого в обратимом процессе равен отношению малого количества δQ, сообщаемого системе к абсолютной температуре системы. dS= (δQ/T)обр. Энтропия сложной системы равна сумме энтропий всех ее однородных частей, те S – величина – аддитивная. При нагревании системы, dS>0. При охлаждении dS<0.	☺ Политропный процесс. Работа.	☺ Энергия Гельмгольца.
☺ 2 начало термодинамики. Процесс, при котором не происходит никаких изменений, кроме передачи тепла от горячего тела к холодному является необратным. 3 начало термодинамики. Энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к абсолютному нулю.	☺ Диаграмма T—S для изопроцессов.	☺ Теоремы Карно. т.1 Термический КПД не зависит от природы рабочего тела и определяется только температурой нагревателя и холодильника. т.2 Термический КПД любого обратимого цикла не может превосходить термический кпд цикла Корно, проведенного между экстремальными точками рабочего тела, рассматриваемого цикла.
☺ Молекулярно-кинематическая теория строения в-ва. Закон Дальтона.	☺ Круговые процессы. Цикл Карно прямой. Обратный. Термодинамический коэффициент полезного действия.	☺ Средняя арифметическая скорость поступательного движения молекул идеального газа. Средняя квадратичная. Наиболее вероятная.
☺ Распределение Максвелла. Опыт Штерна.	☺ Закон равномерного распределения энергии по степеням свободы.	☺ Реальные газы. Уравнение Ван-дер-Ваальса.
☺ Явление переноса. Законы Ньютона, Фурье, Фика.	☺ Барометрическая формула. Закон Больцмана для распределения частиц во внешнем потенциальном поле.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #

  09.05.2015260.29 Кб28шпоры по Материаловедению 1 курс.docx

• #
• #
• #
• #
• #
• #
• #

1-1) Область прим клас. нерелятивист. механики.

V< >> λ, где λ = h/mV – длина волны Дебройля

1-2) Что такое материальная точка?

МТ – это тело, формами и размерами которого можно пренебречь в условиях данной задачи. Для описания движения необходимо ввести систему отсчета: 1) тело отсчета 2) система координат 3) часы

1-3) Что такое траектория, скорость и путь?

Траектория – линия, по которой движется в пространстве мат. точка.

r(t) = x(t)*i + y(t)*j + z(t) * k. Движение можно определить, если известны x(t), y(t), z(t).

Скорость – это вектор, равный отношению dr / dt. Из определения скорости следует, что скорость направлена всегда по касательной к траектории. V = V(x)*i + V(y)*j + V(z)*k, написать |V| = …

Путь – это длина траектории, пройденной телом за рассматриваемый интервал времени. При бесконечно малом инт-ле времени, путь тоже бесконечно малая величина. dS = V * dt

1-4) Что такое ускорение, нормальное ускорение, τ-ускорение?

a = dV/dt = d^2r/dt^2, расписать по осям и написать модуль

В общем случае ускорение направлено произвольным образом.

Тангенциальное ускорение характеризует изменение скорости по величине. Нормальное ускорение характеризует изменение скорости по направлению.

2-1) 1-ый з-н Ньютона

Тело находится в состоянии покоя или прямолинейного равномер. движения до тех пор, пока на него не действуют другие тела. СО называется инерциальной, если в ней выполняется 1-ый з-н Ньютона. ИСО много, тк любая СО, движущаяся равномерно и прямолинейно относительно ИСО, также является ИСО.

(Нарисовать СО в ИСО) r(t) = Vt + r’(t), V(t) = V + V’(t)

2-2) 2-ой з-н Ньютона

Скорость изменения импульса тела равна действующей на тело силе F: dp/dt = F

2-3) 3-ий з-н Ньютона

Силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению.

F₁₂ = -F₂₁

2-4) Типы фундаментальных взаимодействий

Сила – это вектор, характеризующий меру взаимодействия тел.

С точки зрения фундаментальной физики существует 4 вида взаимодействий.

1) СИЛЬНОЕ взаимодействие (между нуклонами в ядре атомов). Это взаимодействие короткодействующее на расстояниях порядка размеров одного ядра (10e-15 метра).

2) ЭЛЕКТРОМАГНИТНОЕ взаимодействие (з-н Кулона). Отвечают за электронную структуру атома. К ним относятся силы упругости, трения.

3) СЛАБЫЕ взаимодействия – они отвечают за ряд процессов в мире элек. частиц, одним из которых явл. распад свободного нейтрона.

4) ГРАВИТАЦИОННОЕ вз. – з-н всемирного тяготения Ньютона.

2-5) Закон Гука

В основе силы упругости лежит электромагнитное взаимодействие. З-н Гука: сила упругости пропорциональна величине деформации тела. F = -kx. k – коэф. жесткости, x – величина деформации

З-н Гука справедлив и для малых деформаций. Для тел существует понятие предела прочности – силы, при воздействии которых нарушается з-н Гука и происходит разрушение.

2-6) З-н сухого трения

Вызывается путем скольжения одной поверхности по другой или попытками вызвать это скольжение. В основе лежит электромагнитное взаимодействие.

если F

если F>kN, то F(тр) = kN

3-1) З-н изменения момента импульса системы

опр: p_i = m_iV_i , P_{cистемы} = ΣP_i

dP_сист/dt = ΣF^{внешних}

3-2) З-н сохранения импульса системы

Это следствие из закона изменения импульса системы

P_сист = const, если ΣF^внеш = 0

Частные случаи з-на сохранения импульса системы:

а) система замкнута (нет взаимодействия с внешним миром)

б) ΣF^внеш <> 0, но ΣF_x^внеш = 0

т.е. сумма проекций внешних сил на какую либо ось = 0

3-3) Что такое центр масс системы?

ЦМС – это точка, которая задается радиусом вектором R

R = Σr_im_i / Σm_i  x_цм = Σx_im_i/M_сист y_цм = Σy_im_i / M_сист

3-4) З-н движения центра масс

V_цм = ΣV_im_i /M = P_сист /M, a_цм = P’_сист/M = ΣF_внеш/M

з-н движения: M_систa_цм = ΣF_внещ

Если сумма внешних сил = 0 или если система замкнута ( все внешние силы = 0), то ц.м. тела покоится или движется прямолинейно.

3-5) Что такое момент импульса системы?

опр: момент силы M_i = r_i x F_i

Моментом импульса относительно точки О называется вектор

L = r x p

Моментом импульса системы относительно точки О наз. вектор

L = Σ_i M_i = Σ_i r_i x p_i

3-6) З-н изменения момента импульса системы

dL_сист/dt = ΣM_внеш

3-7) З-н сохранения момента импульса системы

Следует из закона изменения момента импульса системы

Момент импульса системы сохраняется, если сумма моментов внешних сил = 0

L_сист = const, если ΣM_внеш = 0

а) Момент импульса в замкнутой системе не изменяется

б) если ΣM_x^внеш = 0, то сохраняется проекция импульса системы на эту ось ΣL_x^сист = const

3-8) Теорема о моменте импульса тела, движущемся в центр силовом поле.

Момент импульса тела, движущемся в центральном силовом поле, сохраняется. ( F(r) = kr )

4-1) Что такое работа силы? + мощность

Опр: dA = Fdr (A>0, A=0, A<0)

Если на тело действует несколько сил, то работа результирующей силы равна сумме работ всех сил в отдельности.

dA_рез = F_резdr = ΣF_idbr = ΣdA_i

Работа на конечном участке траектории: A = S₁² Fdr

опр: мошностью называется величина P = dA/dt (мгн. мощность)

4-2) Определение потенциального поля.

Если на тело в каждой точке пространства действует сила, то говорят, что тело находится в силовом поле. Если сила не зависит от времени во всех точках пространства, то говорят, что поле стационарно. (F_кул F_грав)

Стационарное силовое поле назыввается потенциальным, если работа сил поля при перемещении тела из одной точки в другую не зависит от траектории, по которой перемещали тело.

СЛЕДСТВИЕ: работа сил поля, при перемещении тела по замкнутой траектории для потенциальных полей = 0.

4-3) Определение потенциальной энергии.

В потенциальном поле можно ввести ф-ию, зависящую от координаты точки пространства, такую, что работа при перемещении из 1 в 2: A₁₂ = U(r₁) – U(r₂).

Ф-ия U(r) называется потенциальной энергией тела, находящемся в данном потенциальном поле.

СВЯЗЬ между пот.энергией и силой:

F’ = -grad U = -(i dU/dx + j dU/dy + k dU/dz)

4-4) Потенциальная энергия различных полей.

а) гравитационного и кулоновского поля

Эти поля центральные. Пусть U_кул(бескон) = 0

U(r) = -G * Mm/r

U(r) = qQ/4πεε₀r

б) пот. энергия в однородном гравитационном поле

Пусть пот. энергия на поверхности = 0, тогда U_пот = mgh

в) деформации

Пусть, когда пружина не сдвинута, пот. энергия деформации = 0

Тогда U_упруг = kx² / 2

5-1) З-н изм-ия кинет. энергии материальной точки

Величина T = mV²/2 назыв. кинетической энергией

Изменение кинетической энергии = работе всех сил, приложенных к телу. T₂ – T₁ = A_1—>2^{всех сил}

5-2) Что такое механическая энергия тела?

Величина, равная сумме кинетических и потенциальных энергий называется механической энергией. E = T + U

5-3) З-н изменения механической энергии тела

(T₂ + U₂) – (T₁ + U₁) = A₁₂^{непот сил}

E₂ — E₁ = A₁₂^{непот сил}

Работа непотенциальных сил равна изменению механической энергии тела.

непотенц. силы: трение, силы сопротивления

потенциальные: гравитация, кулон (упругость)

Если тело находится в потенциальных полях, то у него сохраняется механическая энергия.

5-4) Что такое финитное и инфинитное движение?

Пусть мат. точак движется в произвольном потенциальном поле. В точках x₁, x₂, x₃ – кинетическая энергия обращается в 0.

В ост. области кинетическая

энергия положительна, значит тело

обладает скоростью.

На рисунке x₂x₃ – это потенциальный

барьер, а x₁x₂ – потенциальная яма.

Если частица при своем движении не

может удалиться на бесконечность,

движение называется финитным (в

потенциальной яме). Если же частица

может уходить сколь угодно далеко,

движение называют инфинитным.

Например финиттное – электрон в ядре

атома или планеты вокруг солнца.

5-5) Что такое абс-но упругий и неупругий удары?

При столкновении тел, в области соприкосновения возникают большие силы, которые приводят к деформации тел. Если к концу столкновения, тела полностью восстанавливают форму, то эти столкновения абсолютно упругие.

Если тела слипаются и движутся вместе, то это абсолютно неупругое столкновение.

При абсолютно упругом столкновении сохраняется суммарная кинет. энергия сталк. тел. При неупругом столкновении кинет энергия тел не сохраняется, т.к. часть ее переходит во внутреннюю энергию тел (остаточная деформация, тепловая…)

При всех видах столкновений и взрывах выполняется ЗСИ.

АУУ: m₁V₁² + m₂V₂² = m₁U₁² + m₂U₂², m₁V₁ + m₂V₂ = m₁U₁ + m₂U₂

AНУ: m₁V₁² + m₂V₂² = (m₁+ m₂)U² + Q_внутр , m₁V₁ + m₂V₂ = (m₁+m₂)U

6-1) Что такое поступательное движение?

Это движение, при котором любая прямая, связанная с телом, перемещается параллельно самой себе. В этом случае скорость всех точек тела в любой момент времени одинаковы (в век смысле)

6-2) Что такое вращательное движение?

Это движение, при котором все точки движутся по окружностям относительно некоторой оси вращения.

6-3) Как описать движение твердого тела?

Твердое тело – это тело, деформациями которого в усл данной задачи можно пренебречь.

Введем связанную с телом систему координат o’x’, o’y’, o’z’.

Пусть в начальный момент времени эта система совпадает с ox, oy, oz. Для однозначного задания положения тела в пространстве в произвольный момент времени t, необходимо знать 6 величин:

Три координаты радиус-вектора R(t), которые характеризуют начало координат о’ и три угла, которые ориентируют штриховую систему координат в пространстве.

6-4) З-н, опр движение ц.м. твердого тела.

Чаще всего, начало штриховой системы координат помещают в центр масс тела, т.к. в этом случае наиболее просто описывается движение точки o’.

Ma_цм = ΣF_внеш, a_ц.м. = d²R(t) / dt²

Это означает, что ц.м. твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием всех приложенных к нему сил.

6-5) З-н динамики вращения твердого тела.

ОПР: угл скорость: ω = dφ/dt, угл. уск: β = dω/dt = d²φ/dt²

V = ωR, a = βR

Получим з-н динамики вращения тв. тела вокруг закрепленной оси:

dL / dt = ΣM^внеш, где L = Σm_ir_ixV_i, M_k^внеш = r x F

Тот же з-н, на ось Z.

6-6) Что такое момент инерции?

Величина I, равная сумме произведений элементарных масс на квадраты их расстояний от некоторой оси, называют моментом инерции тела относительно данной оси.

I = Σ m_i R_i²

Шпаргалки по физике

Шпаргалки по физике

Инфоурок

›

Физика

›Другие методич. материалы›Шпаргалки для подготовки к экзаменам по физике

Шпаргалки для подготовки к экзаменам по физике