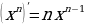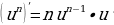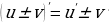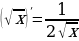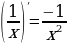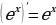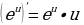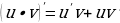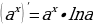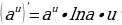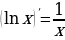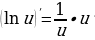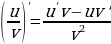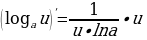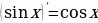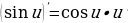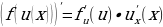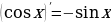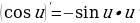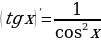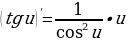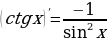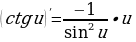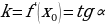Шпаргалка по производной функции егэ - Помощь в подготовке к экзаменам и поступлению

Таблица производных и правила дифференцирования

О том, что такое производная, мы рассказали в статье «Геометрический смысл производной». Если функция задана графиком, её производная в каждой точке равна тангенсу угла наклона касательной к графику функции. А если функция задана формулой — вам помогут таблица производных и правила дифференцирования, то есть правила нахождения производной.

Для решения задач на исследование функции в вариантах ЕГЭ необходима таблица производных и правила дифференцирования, а также знания о том, как связана производная с поведением функции.

Смотри также, как решаются задачи ЕГЭ на применение производной: задача 7 и задача 11.

Прокомментируем несколько строк из таблицы производных.

1. Производная постоянной величины, то есть константы, равна ей самой. Так и должно быть. Ведь константа не меняется. Это постоянная величина, она всегда принимает одинаковые значения.

А производная функции, как мы знаем, – это скорость изменения функции. Подробнее об этом здесь:
Производная функции.
И поэтому производная константы равна нулю.

2. Производная функции у=х равна 1. Вспомним, что производная функции в точке – это тангенс угла наклона касательной, проведенной к графику функции в этой точке. График функции у=х образует угол 45 градусов с положительным направлением оси Х. А тангенс 45 градусов равен 1.

3. Производная функции $y=e^{x}$ равна самой этой функции. И действительно, чем больше значение х, тем больше значение функции $y=e^{x}$ … и тем круче вверх идет график по отношению к оси Х. Вот такая это функция, экспонента. Чем дальше, тем быстрее она растет.

4. Производная синуса и косинуса – тоже тригонометрические функции. Например, производная синуса – это косинус. Как это отражается в физике? Если координата тела меняется по закону синуса, то производная координаты, скорость, будет меняться по закону косинуса. Это описание гармонических колебаний: и координата, и скорость, и ускорение тела меняются по законам синуса и косинуса.

5. Производная логарифма в точке $x_{0}$ обратно пропорциональна $x_{0}$ . Чем дальше, тем медленнее растет логарифмическая функция.

Вспомним, как связаны производная и поведение функции.

Если производная {f} положительна, то функция f(x) возрастает.

Если производная отрицательная, то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

Запишем эти выводы в виде таблицы:

	возрастает	точка максимума	убывает	точка минимума	возрастает
	+	0	—	0	+

Разберем задачи ЕГЭ по теме «Таблица производных, нахождение наибольших и наименьших значений функции, нахождение точек максимума и минимума». Во всех этих примерах мы пользуемся формулами из таблицы производных.

Задача 1. Найдите точки максимумам функции $displaystyle y=-frac{x^{2}+25}{x}.$

Решение:

Область определения функции:

Найдем производную функции, пользуясь формулой производной частного из таблицы.

{y} если x=pm 5.

Точки х = 5 и х = -5, а также точка ноль, разбивают числовую прямую на интервалы, на каждом из которых производная сохраняет свой знак. Это метод интервалов.

Найдем знаки производной на каждом интервале.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». Это точка 5 на рисунке.

Ответ: 5.

Задача 2. Найдите точки минимума функции $y=e^{x+10}(8x-3).$

Решение:

Применим формулу производной произведения.

{y}

Приравняем производную к нулю:

{y} , если 8x-5=0, $displaystyle x=frac{5}{8}=0,625.$

Если то {y} функция убывает.

Если то {y} функция возрастает, значит, x=0,625 – точка минимума функции y(x).

В этой точке производная равна нулю и меняет знак с «минуса» на «плюс».

Ответ: 0,625.

Задача 3. Найдите значение функции $f(x)=x^{4}-4x^{3}-2x^{2}+12x+9$ в точке максимума.

Решение:

Найдем производную функции:

Мы применили формулы производной степени.

Решим уравнение:

$3x^{3}-12x^{2}-4x+12=0Leftrightarrow 3x^{3}(x-3)-4(x-3)=0Leftrightarrow$
$Leftrightarrow (x-3)cdot 4cdot (x-1)cdot (x+1)=0Leftrightarrow left[begin{array}{c}x=3\x=1\x=-1\end{array}right. .$

Получили критические точки, в которых производная равна нулю. Отметим их на оси Х и найдём знаки производной.

x=1 – точка максимума.

Найдём значение функции в этой точке:

Ответ: 16.

Рассмотрим задачи ЕГЭ на нахождение наибольших и наименьших значений функций.

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке:

Это значит, что у нас есть алгоритм для нахождения наибольших и наименьших значений функции на интервале.

Пусть функция f(x) определена на некотором интервале. Чтобы найти ее наибольшее или наименьшее значение, действуем следующим образом:

Находим производную функции.
Приравниваем производную к нулю, находим точки, в которых она равна нулю.
Если производная меняет знак с «плюса» на «минус» в точке $x_{0}$ , то $x_{0}$ – точка максимума функции.
Если производная меняет знак с «минуса» на «плюс» в точке $x_{0}$ , то $x_{0}$ – точка минимума функции.
Чтобы найти наибольшее значение функции на отрезке, сравниваем значения в точке максимума и концах отрезка.
Чтобы найти наименьшее значение функции на отрезке, сравниваем значения в точке минимума и концах отрезка.

Задача 4. Найдите наибольшее значение функции на отрезке

Решение:

Найдем производную:

Приравняем производную к нулю:

$displaystyle Leftrightarrow x=frac{pi }{4}+pi n, nin Z.$

Если то $displaystyle x=frac{pi }{4}.$

Так как

Точка $displaystyle x=frac{pi }{4}$ – точка максимума функции $displaystyle y(x); y_{max}(x)=yleft (frac{pi }{4}right )=4.$

В этой точке функция принимает наибольшее значение на указанном отрезке.

Ответ: 4.

Задача 5. Найдите наименьшее значение функции $y=(x-21)e^{x-20}$ на отрезке

Решение:

Найдем производную функции:

при x=20.

Найдем знаки производной слева и справа от точки x=20.

Если то {y}

Значит, x=20 – точка минимума. Наименьшее значение функции на отрезке достигается при x=20.

Это значение равно

Ответ: -1.

Задача 6. Найдите наибольшее значение функции $y=3x^{2}-13x+7ln+5$ на отрезке $displaystyle left [ frac{13}{14};frac{15}{14} right ].$

Решение:

Область определения функции:

Найдем производную функции и приравняем ее к нулю:

$displaystyle =frac{6(x-1)left ( x-frac{7}{6} right )}{x}.$

если $6x^{2}-13x+7=0.$

или $displaystyle x=frac{7}{6}.$ Второй корень не принадлежит отрезку $displaystyle left [ frac{13}{14};frac{15}{14} right ].$

Найдем знаки производной на отрезке:

В точке x=1 производная равна нулю и меняет знак с «плюса» на «минус». Значит, это точка максимума, и наибольшее значение функции на отрезке $displaystyle left [ frac{13}{14};frac{15}{14} right ]$ достигается при x=1.

Найдем значение функции при x=1:

Ответ: -5.

В следующих задачах наименьшее значение функции достигается на конце отрезка.

Задача 7. Найдите наименьшее значение функции $y=3cosx-pi x+pi ^{2}$ на отрезке

Решение:

Найдем производную функции и приравняем ее к нулю.

У этого уравнения нет решений, так как $displaystyle-frac{pi }{3}textless -1.$

Это значит, что при любых то есть а это означает, что y(x) – убывает, наименьшее значение функции достигается в правом конце отрезка

$y_{min}=y(pi )=-3.$

Ответ: -3.

Задача 8. Найдите наибольшее значение функции на отрезке $displaystyle left [ -frac{pi }{2}; 0 right ].$

Решение:

Найдем производную функции:

Производная функции не равна нулю ни при каком .

Мы знаем, что Тогда

Прибавим 7 ко всем частям неравенства:

для всех

Значит, производная положительна при любом значении переменной, функция монотонно возрастает. Наибольшее значение функции будет достигаться в правом конце отрезка, то есть при x=0.

$y_{naim}=y(0)=7cdot 0-6sin0+8=8.$

Ответ: 8.

Задача 9. Найдите наименьшее значение функции $displaystyle y=13+frac{sqrt{3}pi }{3}-2sqrt{3}cdot x-4sqrt{3}cdot cosx$ на отрезке $displaystyleleft [ 0; frac{pi }{2} right ].$

Решение:

Найдем производную функции и приравняем ее к нулю:

тогда $displaystyle sinx=frac{1}{2}.$

На указанном отрезке это уравнение имеет единственное решение $displaystyle x=frac{pi }{6}.$

Слева от этой точки Если производная отрицательна.

Справа от этой точки производная положительна.

Значит, $displaystyle x=frac{pi }{6}$ – точка минимума функции, и наименьшее значение функции на отрезке достигается в этой точке.

Найдем значения функции в этой точке:

$displaystyle yleft ( frac{pi }{6} right )=13+frac{sqrt{3}pi }{3}-2sqrt{3}cdot frac{pi }{6}-4sqrt{3}cdot cosfrac{pi }{6}=$

$displaystyle =13+frac{sqrt{3}pi }{3}-frac{sqrt{3}pi }{3}-4sqrt{3}cdot frac{sqrt{3}}{2}=13-6=7.$

Ответ: 7.

В задачах ЕГЭ встречаются сложные функции. И найти нужно их точки максимума или минимума, наибольшие или наименьшие значения. Но производную сложной функции в школьной программе по-настоящему не проходят. Как же быть? Покажем полезные приемы, помогающие решить такие задания ЕГЭ.

Задача 10. Найдите наименьшее значение функции $y=log_{2}(x^{2}+x+0,5).$

Решение:

Рассмотрим функцию $y=log_{2}t.$

Так как функция $y=log_{2}t$ монотонно возрастает, точка минимума функции $y=log_{2}(x^{2}+x+0,5)$ будет при том же значении , что и точка минимума функции $t(x)=x^{2}+x+0,5.$ А ее найти легко:

при $displaystyle x=-frac{1}{2}.$

В точке $displaystyle x=-frac{1}{2}$ производная меняет знак с «минуса» на «плюс». Значит, $displaystyle x=-frac{1}{2}$ – единственная точка минимума функции t(x) и функции $y=log_{2}(x^{2}+x+0,5).$

$displaystyle y_{min}=yleft ( -frac{1}{2} right )=log_{2}left ( frac{1}{4}-frac{1}{2}+0,5 right )=log_{2}frac{1}{4}=-2.$

Ответ: -2.

Задача 11. Найдите наибольшее значение функции $y=sqrt{x^{2}-4x+13}$ на отрезке

Решение:

$y=sqrt{x^{2}-4x+13}, xin [-0,5; 6].$

Так как функция монотонно возрастает при tgeq 0, точка минимума функции $y=sqrt{x^{2}-4x+13}$ соответствует точке минимума подкоренного выражения $t(x)={x^{2}-4x+13}.$

Заметим, что подкоренное выражение всегда положительно.

Функция $t(x)={x^{2}-4x+13}.$ задает квадратичную параболу с ветвями вверх и точкой минимума в вершине параболы, то есть при $displaystyle x=frac{4}{2}=2.$

Если $xin [-0,5; 2], y=sqrt{x^{2}-4x+13}$ – монотонно убывает.

Если $xin [2; 6], y=sqrt{x^{2}-4x+13}$ – монотонно возрастает.

Значит, наибольшее значение функции $y=sqrt{x^{2}-4x+13}$ на отрезке достигается в одном из концов этого отрезка.

Сравним и y=(6):

$y_{max}=6.$

Ответ: 6.

Задача 12. Найдите точку максимума функции $y=log_{2}(2+2x-x^{2})-2.$

Решение:

Рассмотрим функцию $t(x)=2+2x-x^{2}.$

Ее график – парабола с ветвями вниз, и точка максимума будет в вершине параболы, при x=1. Функция $y(t)=log_{2}t$ монотонно возрастает, и значит, большему значению будет соответствовать большее значение y(t).

Точка максимума функции $y=log_{2}(2+2x-x^{2})-2$ будет такой же, как у функции $t(x)=2+2x-x^{2},$ то есть x=1.

Ответ: 1.

Читайте также: Задание 11 на ЕГЭ по математике.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Таблица производных и правила дифференцирования» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

ФОРМУЛЫ И ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Формулы	Правила
Элементарные функции	Сложные функции	(c∙f(x))=c∙f  (x) (c – постоянная) Постоянный множитель можно выносить за знак производной
c=0 (c – постоянная)
x=1
(n – постоянная)		Производная суммы (разности) Производная суммы (разности) функций равна сумме их производных
Частные случаи

		Производная произведения
(a0 – постоянная)
		Производная частного

		Производная сложной функции (функции от функции) Если y=f(u) и u=u(x), т.е. y=f(u(x)), то



Геометрический смысл производной
Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке, а также тангенсу угла наклона касательной к оси Х.
Физический смысл производной
Скорость –это производная пути по времени, а ускорение – это производная скорости по времени.	S=S(t) v=S(t) a=v(t)
Исследование функции y=f(x) на монотонность и экстремумы
Найти область определения и интервалы, на которых функция непрерывна. Найти производную f  (x). Найти критические точки, т.е. внутренние точки области определения, в которых f  (x)=0 или не существует. Отметить критические точки на области определения; найти знак производной и характер поведения функции на каждом из интервалов, на которые разбивается область определения. Относительно каждой точки определить, является ли она точкой максимума или минимума или не является точкой экстремума. Записать результат исследования (промежутки монотонности и экстремумы)
Нахождение наибольшего и наименьшего значения функции, непрерывной на отрезке
Найти производную f  (x). Найти критические точки ( f  (x)=0 или не существует). Выбрать критические точки, принадлежащие данному отрезку. Вычислить значение функции в критических точках и на концах отрезка. Сравнить полученные значения и выбрать из них наименьшее и наибольшее

Источник

Справочник

Задание №7 профильная математика

Производной функции y=f(x)в точке x0 называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю. То есть,

Геометрический смысл производной	Физический смысл производной
Значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке (тангенсу угла между касательной и осью Ох) f’(хo) = k = tg α	Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки: V(t)=x’(t)
Если f’(x) > 0 на промежутке, то функция f(x) возрастает на этом промежутке. Если f’(x) < 0 на промежутке, то функция f(x) убывает на этом промежутке	Если функция f(x) возрастает на промежутке, то f’(x) > 0 на этом промежутке. Если функция f(x) убывает на промежутке, то f’(x) < 0 на этом промежутке

Если прямые параллельны, то их угловые коэффициенты равны
Точка хo называется точкой максимума функции f(х), если существует такая окрестность точки хo, что для всех х≠ хo из этой окрестности выполняется неравенство f(х) < f(хo). Точка хo называется точкой минимума функции f(х), если существует такая окрестность точки хo, что для всех х≠ хo из этой окрестности выполняется неравенство f(х) > f(хo) = 0. Если хo – точка экстремума функции f(х), то f’(хo) = 0.	Пусть функция f(х) дифференцируема на интервале (a;b), хo Є (a; b) и f’(хo) = 0, то: при переходе через стационарную точку хo функции f(х) ее производная меняет знак с «плюса» на «минус», то хo – точка максимума функции f(х); при переходе через стационарную точку хo функции f(х) ее производная меняет знак с «минуса» на «плюс», то хo – точка минимума функции f(х).

Примеры заданий

№	Задание	Что делать?
	На рисунке изображен график функции y=f(x) и касательная к нему в точке х0. Найдите значение производной функции f(x) в точке x0.	Найти тангенс угла наклона касательной к оси абсцисс (отношение противолежащего катета к прилежащему катету). На рисунке выделены точки на касательной, на которых как на гипотенузе надо достроить прямоугольный треугольник. Если α <900, то tg α >0, если α >900, то tg α <0.
	На рисунке изображен график функции y=f(x), определённый на интервале (-10;2). Найдите количество точек, в которых производная функции f(x) равна 0.	Подсчитать количество точек экстремума(минимумы и максимумы)
	На рисунке изображен график функции y=f(x), определённый на интервале (-1;12). Найдите количество целых точек, в которых производная функции отрицательна.	Подсчитать целые точки на промежутках убывания функции
	На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 2, 3. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.	x=-2, то f ↓ => f’ <0 x=-1, то f имеет экстремум =>f’=0 x=2, то f ↑ => f’ >0 x=3, то f ↓ => f’ <0
	На рисунке изображён график дифференцируемой функции y=f(x), и отмечены семь точек на оси абсцисс: х1, х2, х3, х4, х5, х6, х7, х8,х9 . В скольких из этих точек производная функции f(x) отрицательна?	В скольких точках функция убывает
	На рисунке изображен график функции y=f’(x ) – производной функции f(x), определённой на интервале (-6;5). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.	Промежутки убывания функции =производная на данном графике отрицательна, т.е.расположена ниже оси Ох. Найти сумму целых точек.
	На рисунке изображен график функции y=f’(x ) – производной функции f(x), определённой на интервале (-8;6). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.	Промежутки возрастания функции =производная на данном графике положительна, т.е.расположена выше оси Ох. Записать длину большего промежутка
	На рисунке изображены график функции y=f’(x ) – производной функции f(x) и семь точек на оси абсцисс: х1, х2, х3, х4, х5, х6, х7. В скольких из этих точек функция f(x) возрастает?	Сосчитать количество точек, в которых производная на данном графике положительна
	Прямая y=6x+9 параллельна касательной к графику функции y=x2+7х-6. Найдите абсциссу точки касания.	Если прямые параллельны, то их угловые коэффициенты равны. Найти производную функции (x2+7х-6)’=2x+7=kкас=6 => x=-0,5
	Прямая y=-9x+5 параллельна касательной к графику функции y=аx2+15х+11. Найдите a.	Найти производную функции (аx2+15х+11)’=2a+15= -9 => a= -12
	На рисунке изображён график y=f’(x) – производной функции f(x), определённой на интервале (-9;3). Найдите количество точек, в которых касательная к графику f(x) параллельна прямой y=2x-19 или совпадает с ней.	Провести горизонтальную прямую y=2 и сосчитать количество точек пересечения с графиком.
	На рисунке изображён график функции y=f(x), определённой на интервале (-3;9). Найдите количество точек, в которых касательная к графику f(x) параллельна прямой y=12.	Т.к. угловой коэффициент прямой y=12 равен 0, то считаем количество точек пересечения с осью Ох.
	На рисунке изображен график производной функции y=f’(x). Найдите абсциссу точки, в которых касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает ней.	Находим точку на графике y=f’(x), в которой у=0, т.е.точку пересечения данного графика с осью Ох => -3
	На рисунке изображен график производной функции y=f’(x), определенной на интервале (-7;4). В какой точке отрезка [-6;-1] функция f(x) принимает наибольшее значение?	На отрезке [-6;-1] производная положительна (лежит выше Ох) => функция возрастает, т.е. достигает наибольшего значения при наибольшем значении аргумента => -1 Значит в х=-6 достигает наименьшего значения.
	На рисунке изображён график y=f’(x) – производной функции f(x), определённой на интервале (-7;4). Найдите точку максимума функции f(x).	Находим точку на оси Ох, в которой производная меняет свой знак с «+» на «-» => -1
	На рисунке изображён график y=f’(x) – производной функции f(x), определённой на интервале (-6;5). Найдите точку экстремума функции f(x), принадлежащую отрезку [-5;4].	Находим точку на оси Ох, в которой производная меняет свой знак => -2
	На рисунке изображён график функции y=f(x), определённой на интервале (-5;7). Найдите сумму точек экстремума функции f(x).	Считаем сумму «горбов и впадин» по оси Ох: -3 + (-1) +0+2+3+5+6=12
	На рисунке изображён график y=f’(x) – производной функции f(x), определённой на интервале (-10;8). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-9;6].	Находим точки на оси Ох, в которой производная меняет свой знак с «+» на «-» => х= -4 и х=4 => 2
	На рисунке изображён график y=f’(x) – производной функции f(x), определённой на интервале (-16;4). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-14;2].	Считаем количество точек пересечения графика производной на рисунке с осью Ох => 5
	Материальная точка движется прямолинейно по закону x(t)=t2-3t-29, где x – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t=3с.	V(t=3)=x’(t)=( t2-3t-29)’= =2t-3=2*3-3=3
	Материальная точка движется прямолинейно по закону x(t)=1/6t3-2t2-4t+39, где x – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. В какой момент времени (в секундах) её скорость была равной 38м/с.	V(t)=x’(t)=( 1/6t3-2t2-4t+39)’= =1/6 3t2-22t-4=0.5t-4t-4 Если V=38, то 0.5t2-4t-4=38 0.5t2-4t-4-38=0 t2-8t-84=0 Решая уравнение через D, находим t=14

Источник