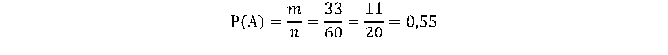Шпаргалка по теории вероятности профиль егэ

17 декабря 2015

В закладки

Обсудить

Жалоба

Всё о теории вероятности в кратком виде.

arhiv.rar

Случайности не случайны… Всё решает вероятность событий!

В ЕГЭ по математике целых два задания на теорию вероятностей, поэтому стоит уделить ей в два раза больше внимания! Первое решается по основной формуле вероятности, а вот над вторым придётся подумать и вспомнить, какие бывают события.

Мы структурировали типы задач, которые могут попасться на экзамене, и сделали эту полезную шпаргалку с формулами и теорией — сохраняйте карточки, чтобы подготовка к ЕГЭ по математике была ещё продуктивнее.

Задание 3. Теория вероятностей на ЕГЭ по математике.

Мы начнем с простых задач и основных понятий теории вероятностей.
Случайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет.
Вы выиграли в лотерею — случайное событие. Пригласили друзей отпраздновать выигрыш, а они по дороге к вам застряли в лифте — тоже случайное событие. Правда, мастер оказался поблизости и освободил всю компанию через десять минут — и это тоже можно считать счастливой случайностью…

Наша жизнь полна случайных событий. О каждом из них можно сказать, что оно произойдет с некоторой вероятностью. Скорее всего, вы интуитивно знакомы с этим понятием. Теперь мы дадим математическое определение вероятности.

Начнем с самого простого примера. Вы бросаете монетку. Орел или решка?

Такое действие, которое может привести к одному из нескольких результатов, в теории вероятностей называют испытанием.

Орел и решка — два возможных исхода испытания.

Орел выпадет в одном случае из двух возможных. Говорят, что вероятность того, что монетка упадет орлом, равна .

Бросим игральную кость. У кубика шесть граней, поэтому возможных исходов тоже шесть.

Например, вы загадали, что выпадет три очка. Это один исход из шести возможных. В теории вероятностей он будет называться благоприятным исходом.

Вероятность выпадения тройки равна (один благоприятный исход из шести возможных).

Вероятность четверки — тоже .

А вот вероятность появления семерки равна нулю. Ведь грани с семью точками на кубике нет.

Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.

Очевидно, что вероятность не может быть больше единицы.

Вот другой пример. В пакете  яблок, из них  — красные, остальные — зеленые. Ни формой, ни размером яблоки не отличаются. Вы запускаете в пакет руку и наугад вынимаете яблоко. Вероятность вытащить красное яблоко равна , а зеленое — .

Вероятность достать красное или зеленое яблоко равна .
 

БЕСПЛАТНЫЙ МИНИ-КУРС ПО ТЕОРВЕРУ

Определение вероятности. Простые задачи из вариантов ЕГЭ.

Разберем задачи по теории вероятностей, входящие в сборники для подготовки к ЕГЭ.

В фирме такси в данный момент свободно  машин:  красных,  желтых и  зеленых. По вызову выехала одна из машин, случайно оказавшихся ближе всего к заказчице. Найдите вероятность того, что к ней приедет желтое такси.

Всего имеется  машин, то есть к заказчице приедет одна из пятнадцати. Желтых — девять, и значит, вероятность приезда именно желтой машины равна , то есть .

 В сборнике билетов по биологии всего  билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет. Найдите вероятность того, что в этом билете не будет вопроса о грибах.

Очевидно, вероятность вытащить билет без вопроса о грибах равна , то есть .

Родительский комитет закупил  пазлов для подарков детям на окончание учебного года, из них  с картинами известных художников и  с изображениями животных. Подарки распределяются случайным образом. Найдите вероятность того, что Вовочке достанется пазл с животным.

Задача решается аналогично.

Ответ: .

В чемпионате по гимнастике участвуют  спортсменок: — из России,  — из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая последней, окажется из Китая.

Давайте представим, что все спортсменки одновременно подошли к шляпе и вытянули из нее бумажки с номерами. Кому-то из них достанется двадцатый номер. Вероятность того, что его вытянет китайская спортсменка, равен (поскольку из Китая —  спортсменок). Ответ: .

Ученика попросили назвать число от  до . Какова вероятность того, что он назовет число кратное пяти?

Каждое пятое число из данного множества делится на . Значит, вероятность равна .

Брошена игральная кость. Найдите вероятность того, что выпадет нечетное число очков.

 — нечетные числа;  — четные. Вероятность нечетного числа очков равна .

Ответ: .

Монета брошена три раза. Какова вероятность двух «орлов» и одной «решки»?

Заметим, что задачу можно сформулировать по-другому: бросили три монеты одновременно. На решение это не повлияет.

Как вы думаете, сколько здесь возможных исходов?

Бросаем монету. У этого действия два возможных исхода: орел и решка.

Две монеты — уже четыре исхода:

орел	орел
орел	решка
решка	орел
решка	решка

Три монеты? Правильно,  исходов, так как .

Вот они:

орел	орел	орел
орел	орел	решка
орел	решка	орел
решка	орел	орел
орел	решка	решка
решка	орел	решка
решка	решка	орел
решка	решка	решка

Два орла и одна решка выпадают в трех случаях из восьми.

Ответ: .

В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет  очков. Результат округлите до сотых.

Бросаем первую кость — шесть исходов. И для каждого из них возможны еще шесть — когда мы бросаем вторую кость.

Получаем, что у данного действия — бросания двух игральных костей — всего  возможных исходов, так как .

А теперь — благоприятные исходы:

Вероятность выпадения восьми очков равна .

Стрелок попадает в цель с вероятностью . Найдите вероятность того, что он попадёт в цель четыре выстрела подряд.

Если вероятность попадания равна  — следовательно, вероятность промаха . Рассуждаем так же, как и в предыдущей задаче. Вероятность двух попадания подряд равна . А вероятность четырех попаданий подряд равна .

Лень разбираться самому?
Присоединяйся к мини-курсу по теории вероятностей

ПОДРОБНЕЕ

Вероятность: логика перебора.

 В кармане у Пети было монеты по  рублей и  монеты по  рублей. Петя не глядя переложил какие-то  монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.

Мы знаем, что вероятность события равна отношению числа благоприятных исходов к общему числу исходов. Но как посчитать все эти исходы?

Можно, конечно, обозначить пятирублевые монеты цифрами , а десятирублевые цифрами  — а затем посчитать, сколькими способами можно выбрать три элемента из набора .

Однако есть более простое решение:

Кодируем монеты числами: ,  (это пятирублёвые),  (это десятирублёвые). Условие задачи можно теперь сформулировать так:

Есть шесть фишек с номерами от  до . Сколькими способами можно разложить их по двум карманам поровну, так чтобы фишки с номерами  и  не оказались вместе?

Давайте запишем, что у нас в первом кармане.

Для этого составим все возможные комбинации из набора . Набор из трёх фишек будет трёхзначным числом. Очевидно, что в наших условиях  и  — это один и тот же набор фишек. Чтобы ничего не пропустить и не повториться, располагаем соответствующие трехзначные числа по возрастанию:

…

А дальше? Мы же говорили, что располагаем числа по возрастанию. Значит, следующее — , а затем:

.

Все! Мы перебрали все возможные комбинации, начинающиеся на . Продолжаем:

.

Всего  возможных исходов.

У нас есть условие — фишки с номерами  и  не должны оказаться вместе. Это значит, например, что комбинация нам не подходит — она означает, что фишки  и  обе оказались не в первом, а во втором кармане. Благоприятные для нас исходы — такие, где есть либо только , либо только . Вот они:

134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 256 – всего  благоприятных исходов.

Тогда искомая вероятность равна .

Ответ: .

Сумма событий, произведение событий и их комбинации

Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Проработав год, чайник может либо сломаться на второй год, либо благополучно служить и после 2 лет работы.
Пусть – вероятность того, что чайник прослужил больше года.

– вероятность того, что он сломается на второй год, – вероятность того, что он прослужит больше двух лет.

Очевидно,

Тогда

Ответ: 0,06.

События, взаимоисключающие друг друга в рамках данной задачи, называются несовместными. Появление одного из несовместных событий исключает появление других.

Сумма двух событий – термин, означающий, что произошло или первое событие, или второе, или оба сразу.

Вероятность суммы несовместных событий равна сумме их вероятностей.

В нашей задаче события «чайник сломался на второй год работы» и «чайник работает больше двух лет» — несовместные. Чайник или сломался, или остается в рабочем состоянии.

На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук выйдет через выход А.

Пронумеруем развилки, на которых паук может случайным образом свернуть в ту или другую сторону.

Он может либо выйти в выход D, и вероятность этого события равна Либо уйти дальше в лабиринт. На второй развилке он может либо свернуть в тупик, либо выйти в выход В (с вероятностью На каждой развилке вероятность свернуть в ту или другую сторону равна а поскольку развилок пять, вероятность выбраться через выход А равна то есть 0,03125.

События А и В называют независимыми, если вероятность появления события А не меняет вероятности появления события В.

В нашей задаче так и есть: неразумный паук сворачивает налево или направо случайным образом, независимо от того, что он делал до этого.

Для нескольких независимых событий вероятность того, что все они произойдут, равна произведению вероятностей.

(А) Два грузовика, работая совместно, вывозят снег с улицы Нижняя Подгорная, причем первый грузовик должен сделать три рейса с грузом снега, а второй — два. Вероятность застрять с грузом снега при подъеме в горку равна 0,2 для первого грузовика и 0,25 — для второго. С какой вероятностью грузовики вывезут снег с улицы Нижняя Подгорная, ни разу не застряв на горке?

Вероятность для первого грузовика благополучно одолеть горку Для второго Поскольку первый грузовик должен сделать 3 рейса, а второй – два, грузовики ни разу не застрянут на горке с вероятностью

Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Нарисуем все возможные исходы ситуации. Покупатель пришел в магазин, который принадлежит агрофирме, и купил яйцо. Надо найти вероятность того, что это яйцо из первого хозяйства.

Яйца могут быть только или из первого домашнего хозяйства, или из второго, причем эти два события несовместны. Других яиц в этот магазин не поступает.

Пусть вероятность того, что купленное яйцо из первого хозяйства, равна . Тогда вероятность того, что яйцо из второго хозяйства (противоположного события), равна .

Яйца могут быть высшей категории и не высшей.
В первом хозяйстве 40% яиц имеют высшую категорию, а 60% — не высшую. Это значит, что случайно выбранное яйцо из первого хозяйства с вероятностью 40% будет высшей категории.

Во втором хозяйстве 20% яиц высшей категории, а 80% — не высшей.

Пусть случайно выбранное в магазине яйцо — из первого хозяйства и высшей категории. Вероятность этого события равна произведению вероятностей:

Вероятность того, что яйцо из второго хозяйства и высшей категории, равна

Если мы сложим эти две вероятности, мы получим вероятность того, что яйцо имеет высшую категорию. По условию, высшую категорию имеют 35% яиц, значит, эта вероятность равна 0,35.

Мы получили уравнение:

Решаем это уравнение и находим, что – вероятность того, что яйцо, купленное у этой агрофирмы, оказалось из первого хозяйства.

Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

С чем пришел пациент в клинику? – С подозрением на гепатит. Возможно, он действительно болен гепатитом, а возможно, у его плохого самочувствия другая причина. Может быть, он просто съел что-нибудь. Вероятность того, что он болен гепатитом, равна 0,05 (то есть 5%). Вероятность того, что он здоров, равна 0,95 (то есть 95%).

Пациенту делают анализ. Покажем на схеме все возможные исходы:

Если он болен гепатитом, анализ дает положительный результат с вероятностью 0,9. То есть анализ покажет: «есть гепатит».
Заметим, что анализ не во всех случаях выявляет гепатит у того, кто действительно им болен. С вероятностью 0,1 анализ не распознает гепатит у больного.

Более того. Анализ может ошибочно дать положительный результат у того, кто не болеет гепатитом. Вероятность такого ложного положительного результата 0,01. Тогда с вероятностью 0,99 анализ даст отрицательный результат, если человек здоров.

Найдем вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

Благоприятные для этой ситуации исходы: человек болен, и анализ положительный (вероятность одновременного наступления этих двух событий равна ), или человек здоров, и анализ ложный положительный (вероятность одновременного наступления этих двух событий равна ). Так как события «человек болен» и «человек не болен» несовместны, то вероятность того, что результат анализа будет положительным, равна

Ответ: 0,0545.

Чтобы поступить в институт на специальность «Лингвистика», абитуриент З. должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.

Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.

Заметим, что в задаче не спрашивается, будет ли абитуриент по фамилии З. учиться и лингвистике, и коммерции сразу и получать два диплома. Здесь надо найти вероятность того, что З. сможет поступить хотя бы на одну из двух данных специальностей – то есть наберет необходимое количество баллов.
Для того чтобы поступить хотя бы на одну из двух специальностей, З. должен набрать не менее 70 баллов по математике. И по русскому. И еще – обществознание или иностранный.
Вероятность набрать 70 баллов по математике для него равна 0,6.
Вероятность набрать баллы по математике и русскому равна

Разберемся с иностранным и обществознанием. Нам подходят варианты, когда абитуриент набрал баллы по обществознанию, по иностранному или по обоим. Не подходит вариант, когда ни по языку, ни по «обществу» он не набрал баллов. Значит, вероятность сдать обществознание или иностранный не ниже чем на 70 баллов равна

В результате вероятность сдать математику, русский и обществознание или иностранный равна Это ответ.

Чтобы полностью освоить тему, смотрите видеокурс по теории вероятностей. Это бесплатно.

Еще задачи ЕГЭ по теме «Теория вероятностей».

Смотрите также: парадокс Монти Холла.

1.Ве­ро­ят­ность того, что в слу­чай­ный мо­мент вре­ме­ни тем­пе­ра­ту­ра тела здо­ро­во­го че­ло­ве­ка ока­жет­ся ниже чем 36,8 °С, равна 0,81. Най­ди­те ве­ро­ят­ность того, что в слу­чай­ный мо­мент вре­ме­ни у здо­ро­во­го че­ло­ве­ка тем­пе­ра­ту­ра ока­жет­ся 36,8 °С или выше.

1 − 0,81 = 0,19.

2.Ве­ро­ят­ность того, что новый элек­три­че­ский чай­ник про­слу­жит боль­ше года, равна 0,97. Ве­ро­ят­ность того, что он про­слу­жит боль­ше двух лет, равна 0,89. Най­ди­те ве­ро­ят­ность того, что он про­слу­жит мень­ше двух лет, но боль­ше года.

P(A) = 0,97 − 0,89 = 0,08.

3.По­ме­ще­ние осве­ща­ет­ся фонарём с двумя лам­па­ми. Ве­ро­ят­ность пе­ре­го­ра­ния лампы в те­че­ние года равна 0,3. Най­ди­те ве­ро­ят­ность того, что в те­че­ние года хотя бы одна лампа не пе­ре­го­рит.

0,3·0,3 = 0,09. 1 − 0,09 = 0,91.

4.В тор­го­вом цен­тре два оди­на­ко­вых ав­то­ма­та про­да­ют кофе. Ве­ро­ят­ность того, что к концу дня в ав­то­ма­те за­кон­чит­ся кофе, равна 0,3. Ве­ро­ят­ность того, что кофе за­кон­чит­ся в обоих ав­то­ма­тах, равна 0,12. Най­ди­те ве­ро­ят­ность того, что к концу дня кофе оста­нет­ся в обоих ав­то­ма­тах.

0,3 + 0,3 − 0,12 = 0,48. 1 − 0,48 = 0,52.

5.При ар­тил­ле­рий­ской стрель­бе ав­то­ма­ти­че­ская си­сте­ма де­ла­ет вы­стрел по цели. Если цель не уни­что­же­на, то си­сте­ма де­ла­ет по­втор­ный вы­стрел. Вы­стре­лы по­вто­ря­ют­ся до тех пор, пока цель не будет уни­что­же­на. Ве­ро­ят­ность уни­что­же­ния не­ко­то­рой цели при пер­вом вы­стре­ле равна 0,4, а при каж­дом по­сле­ду­ю­щем — 0,6. Сколь­ко вы­стре­лов по­тре­бу­ет­ся для того, чтобы ве­ро­ят­ность уни­что­же­ния цели была не менее 0,98?

Р(1) = 0,6. Р(2) = Р(1)·0,4 = 0,24.

Р(3) = Р(2)·0,4 = 0,096. Р(4) = Р(3)·0,4 = 0,0384;

Р(5) = Р(4)·0,4 = 0,01536.  

По­след­няя ве­ро­ят­ность мень­ше 0,02, по­это­му до­ста­точ­но пяти вы­стре­лов по ми­ше­ни.

6.Две фаб­ри­ки вы­пус­ка­ют оди­на­ко­вые стек­ла для ав­то­мо­биль­ных фар. Пер­вая фаб­ри­ка вы­пус­ка­ет 45% этих сте­кол, вто­рая — 55%. Пер­вая фаб­ри­ка вы­пус­ка­ет 3% бра­ко­ван­ных сте­кол, а вто­рая — 1%. Най­ди­те ве­ро­ят­ность того, что слу­чай­но куп­лен­ное в ма­га­зи­не стек­ло ока­жет­ся бра­ко­ван­ным.

0,45 · 0,03 = 0,0135. 0,55 · 0,01 = 0,0055.

0,0135 + 0,0055 = 0,019.

 7. В клас­се 26 че­ло­век, среди них два близ­не­ца — Ан­дрей и Сер­гей. Класс слу­чай­ным об­ра­зом делят на две груп­пы по 13 че­ло­век в каж­дой. Най­ди­те ве­ро­ят­ность того, что Ан­дрей и Сер­гей ока­жут­ся в одной груп­пе. Пусть один из близ­не­цов на­хо­дит­ся в не­ко­то­рой груп­пе. Вме­сте с ним в груп­пе ока­жут­ся 12 че­ло­век из 25 остав­ших­ся од­но­класс­ни­ков 12 : 25 = 0,48.

8.В Вол­шеб­ной стра­не бы­ва­ет два типа по­го­ды: хо­ро­шая и от­лич­ная, причём по­го­да, уста­но­вив­шись утром, дер­жит­ся не­из­мен­ной весь день. Из­вест­но, что с ве­ро­ят­но­стью 0,8 по­го­да зав­тра будет такой же, как и се­год­ня. Се­год­ня 3 июля, по­го­да в Вол­шеб­ной стра­не хо­ро­шая. Най­ди­те ве­ро­ят­ность того, что 6 июля в Вол­шеб­ной стра­не будет от­лич­ная по­го­да.

Ре­ше­ние.

Для по­го­ды на 4, 5 и 6 июля есть 4 ва­ри­ан­та: ХХО, ХОО, ОХО, ООО 

P(XXO) = 0,8·0,8·0,2 = 0,128;

P(XOO) = 0,8·0,2·0,8 = 0,128;

P(OXO) = 0,2·0,2·0,2 = 0,008;

P(OOO) = 0,2·0,8·0,8 = 0,128.

 P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392.

9.Ков­бой Джон по­па­да­ет в муху на стене с ве­ро­ят­но­стью 0,9, если стре­ля­ет из при­стре­лян­но­го ре­воль­ве­ра. Если Джон стре­ля­ет из не­при­стре­лян­но­го ре­воль­ве­ра, то он по­па­да­ет в муху с ве­ро­ят­но­стью 0,2. На столе лежит 10 ре­воль­ве­ров, из них толь­ко 4 при­стре­лян­ные. Ков­бой Джон видит на стене муху, на­уда­чу хва­та­ет пер­вый по­пав­ший­ся ре­воль­вер и стре­ля­ет в муху. Най­ди­те ве­ро­ят­ность того, что Джон про­махнётся.

Ре­ше­ние.

0,4·(1 − 0,9) = 0,04 и 0,6·(1 − 0,2) = 0,48. Эти со­бы­тия не­сов­мест­ны, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий: 0,04 + 0,48 = 0,52.

10.Аг­ро­фир­ма за­ку­па­ет ку­ри­ные яйца в двух до­маш­них хо­зяй­ствах. 40% яиц из пер­во­го хо­зяй­ства — яйца выс­шей ка­те­го­рии, а из вто­ро­го хо­зяй­ства — 20% яиц выс­шей ка­те­го­рии. Всего выс­шую ка­те­го­рию по­лу­ча­ет 35% яиц. Най­ди­те ве­ро­ят­ность того, что яйцо, куп­лен­ное у этой аг­ро­фир­мы, ока­жет­ся из пер­во­го хо­зяй­ства.

Ответ 0,75

11. Стре­лок стре­ля­ет по ми­ше­ни один раз. В слу­чае про­ма­ха стре­лок де­ла­ет вто­рой вы­стрел по той же ми­ше­ни. Ве­ро­ят­ность по­пасть в ми­шень при одном вы­стре­ле равна 0,7. Най­ди­те ве­ро­ят­ность того, что ми­шень будет по­ра­же­на (либо пер­вым, либо вто­рым вы­стре­лом).

0,7+(1-0,7) ·0,7=0,91

12.Чтобы по­сту­пить в ин­сти­тут на спе­ци­аль­ность «Линг­ви­сти­ка», аби­ту­ри­ент дол­жен на­брать на ЕГЭ не менее 70 бал­лов по каж­до­му из трёх пред­ме­тов — ма­те­ма­ти­ка, рус­ский язык и ино­стран­ный язык. Чтобы по­сту­пить на спе­ци­аль­ность «Ком­мер­ция», нужно на­брать не менее 70 бал­лов по каж­до­му из трёх пред­ме­тов — ма­те­ма­ти­ка, рус­ский язык и об­ще­ст­во­зна­ние.

Ве­ро­ят­ность того, что аби­ту­ри­ент З. по­лу­чит не менее 70 бал­лов по ма­те­ма­ти­ке, равна 0,6, по рус­ско­му языку — 0,8, по ино­стран­но­му языку — 0,7 и по об­ще­ст­во­зна­нию — 0,5.

Най­ди­те ве­ро­ят­ность того, что З. смо­жет по­сту­пить хотя бы на одну из двух упо­мя­ну­тых спе­ци­аль­но­стей.

0,6·0,8·(1 –(1-0,7)(1-0,5)) =0,48·(1-0,3·0,5)=0,408

13. На фаб­ри­ке ке­ра­ми­че­ской по­су­ды 10% про­из­ведённых та­ре­лок имеют де­фект. При кон­тро­ле ка­че­ства про­дук­ции вы­яв­ля­ет­ся 80% де­фект­ных та­ре­лок. Осталь­ные та­рел­ки по­сту­па­ют в про­да­жу. Най­ди­те ве­ро­ят­ность того, что слу­чай­но вы­бран­ная при по­куп­ке та­рел­ка не имеет де­фек­тов. Ре­зуль­тат округ­ли­те до сотых.

0,1·0,8=0,08, 1-0,08=0,92 0,9 : 0,92=0,98

14.Всем па­ци­ен­там с по­до­зре­ни­ем на ге­па­тит де­ла­ют ана­лиз крови. Если ана­лиз вы­яв­ля­ет ге­па­тит, то ре­зуль­тат ана­ли­за на­зы­ва­ет­ся по­ло­жи­тель­ным. У боль­ных ге­па­ти­том па­ци­ен­тов ана­лиз даёт по­ло­жи­тель­ный ре­зуль­тат с ве­ро­ят­но­стью 0,9. Если па­ци­ент не болен ге­па­ти­том, то ана­лиз может дать лож­ный по­ло­жи­тель­ный ре­зуль­тат с ве­ро­ят­но­стью 0,01. Из­вест­но, что 5% па­ци­ен­тов, по­сту­па­ю­щих с по­до­зре­ни­ем на ге­па­тит, дей­стви­тель­но боль­ны ге­па­ти­том. Най­ди­те ве­ро­ят­ность того, что ре­зуль­тат ана­ли­за у па­ци­ен­та, по­сту­пив­ше­го в кли­ни­ку с по­до­зре­ни­ем на ге­па­тит, будет по­ло­жи­тель­ным.

0,05·0,9+0,95·0,01 =0,0545

15. У Вити в ко­пил­ке лежит 12 рублёвых, 6 двух­рублёвых, 4 пя­ти­рублёвых и 3 де­ся­ти­рублёвых мо­не­ты. Витя на­у­гад достаёт из ко­пил­ки одну мо­не­ту. Най­ди­те ве­ро­ят­ность того, что остав­ша­я­ся в ко­пил­ке сумма со­ста­вит более 70 руб­лей.

Ре­ше­ние.

У Вити в ко­пил­ке лежит 12 + 6 + 4 + 3 = 25 монет на сумму 12 + 12 + 20 + 30 = 74 рубля. Боль­ше 70 руб­лей оста­нет­ся, если до­стать из ко­пил­ки либо рублёвую, либо двух­рублёвую мо­не­ту. Ис­ко­мая ве­ро­ят­ность равна 18 : 25 = 0,72.

16.В кар­ма­не у Пети было 2 мо­не­ты по 5 руб­лей и 4 мо­не­ты по 10 руб­лей. Петя, не глядя, пе­ре­ло­жил какие-то 3 мо­не­ты в дру­гой кар­ман. Най­ди­те ве­ро­ят­ность того, что пя­ти­руб­ле­вые мо­не­ты лежат те­перь в раз­ных кар­ма­нах. Всего 6 монет. Ве­ро­ят­ность того, что Петя взял пя­ти­руб­ле­вую мо­не­ту, затем де­ся­ти­руб­ле­вую, и затем еще одну де­ся­ти­руб­ле­вую (в ука­зан­ном по­ряд­ке) равна 2/6·4/5·3/4=0,2  По­сколь­ку Петя мог до­стать пя­ти­руб­ле­вую мо­не­ту не толь­ко пер­вой, но и вто­рой или тре­тьей, ве­ро­ят­ность до­стать набор из одной пя­ти­руб­ле­вой и двух де­ся­ти­руб­ле­вых монет в 3 раза боль­ше. Тем самым, она равна 0,6.

17. За круг­лый стол на 101 сту­л в слу­чай­ном по­ряд­ке рас­са­жи­ва­ют­ся 99 маль­чи­ков и 2 де­воч­ки. Най­ди­те ве­ро­ят­ность того, что между двумя де­воч­ка­ми будет си­деть один маль­чик.

Ре­ше­ние.

Пусть пер­вой за стол сядет де­воч­ка, тогда для каж­до­го из остав­ших­ся ребят (в том числе и для вто­рой де­воч­ки ) ве­ро­ят­ность ока­зать­ся на любом из остав­ших­ся сту­льев равна 0,01 . А мест, удо­вле­тво­ря­ю­щих усло­вию за­да­чи, толь­ко два. Таким об­ра­зом ве­ро­ят­ность, что между двумя де­воч­ка­ми будет си­деть один маль­чик равна 2·0,01 = 0,02

18. За круг­лый стол на 17 сту­льев в слу­чай­ном по­ряд­ке рас­са­жи­ва­ют­ся 15 маль­чи­ков и 2 де­воч­ки. Най­ди­те ве­ро­ят­ность того, что обе де­воч­ки будут си­деть рядом. 

Ре­ше­ние.

Пусть пер­вой за стол сядет де­воч­ка, тогда рядом с ней есть два места, на каж­дое из ко­то­рых пре­тен­ду­ет 16 че­ло­ве­ка, из ко­то­рых толь­ко одна де­воч­ка. Таким об­ра­зом, ве­ро­ят­ность, что де­воч­ки будут си­деть рядом равна 2·1/16 =1/8 =0,125

Не будут сидеть рядом 1-0,125=0,875

19. Про паука.

Вероятностью события $А$ называется отношение числа благоприятных для $А$ исходов к числу всех
равновозможных исходов

$P(A)={m}/{n}$, где $n$ – общее количество возможных исходов, а $m$ – количество исходов, благоприятствующих событию
$А$.

Вероятность события — это число из отрезка $[0; 1]$

Противоположные события

Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно
происходит. Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
${(А)}↖{-}$.

$Р(А)+Р{(А)}↖{-}=1$

Независимые события

Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.

Несовместные события

Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)

Совместные события

Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же
испытании. В противном случае события называются несовместными.

Задание четыре егэ математика профиль

Банковская задача (дифференцированные платежи)

На занятии решены задачи на кредиты с дифференцированными платежами из прошедших тренировочных работ и досрочных ЕГЭ.

Понятие о базах данных

База данных обеспечивает хранение информации и представляет собой поименованную совокупность данных, организованных по определенным правилам, включающим общие принципы описания, хранения и манипулирования данными.

Шпаргалка к заданию №4 ЕГЭ по математике

На занятии решены задачи на кредиты с дифференцированными платежами из прошедших тренировочных работ и досрочных ЕГЭ.

Шпаргалка к заданию 4 ЕГЭ по математике.

4ege. ru

27.10.2017 4:56:49

2017-10-27 04:56:49

Источники:

Http://4ege. ru/matematika/52364-shpargalka-k-zadaniyu-4-ege-po-matematike. html

Задание 4 ЕГЭ математика (профильный уровень) » /> » /> .keyword { color: red; } Задание четыре егэ математика профиль

Задание 4 ЕГЭ математика (профильный уровень)

Задание 4 ЕГЭ математика (профильный уровень)

В четвертом задании предстоит вычислить вероятность события. Вычисления довольно простые, достаточно знать определение вероятности и простейшие способы ее вычисления. Также надо уметь работать с обыкновенными дробями, переводить обыкновенные дроби в десятичные, округлять десятичные дроби, составлять и решать линейные уравнения.

Тип задания: с кратким ответом
Уровень сложности: базовый
Количество баллов: 1
Примерное время на выполнение: 2 минуты

Вероятность всегда выражается дробью, в знаменателе которой стоит общее число исходов, а в числителе – число исходов, удовлетворяющих условию. Чаще всего задача сводится именно к вычислению числа исходов (примеры 1-2). Иногда к сложению или умножению вероятностей отдельных событий (примеры 3-6), и очень редко к нескольким действиям (примеры 7-8).

Знать определения и правила надо. Но при решении задач на вероятность важнее иметь хороший практический навык. Это позволит на экзамене не углубляться в простом задании в сложные математические законы и сэкономить время и собственные нервы. На самом деле трудных задач в четвертом задании нет вообще.

Пример №1.

Для призов участникам технического конкурса в магазине приобрели 30 раскрасок, из которых 10 с танками, 11 с самолетами, а остальные с космическими кораблями. Призы определяются жеребьевкой. Дима хочет получить раскраску с космическими кораблями. Какова вероятность, что его желание исполнится?

Решение: Сначала определим число раскрасок с космическими кораблями: 30-10-11=9
Теперь можем вычислить вероятность: 9/30=0,3

Пример №2

В упаковке лежат блокноты с цветными обложками: 12 с красной, 7 с синей, 9 с черной, 8 с желтой и 14 с белой. Из упаковки вынимают 1 блокнот. Найдите вероятность того, что обложка этого блокнота желтая.

Решение: Всего блокнотов: 12+7+9+8+14=50
Вероятность того, что попадется блокнот с желтой обложкой: 8/50=0,16

Пример №3

В киоске продаются уцененные авторучки. Вероятность неисправности авторучки составляет 0,09. Найдите вероятность того, что приобретенная наугад авторучка исправна.

Решение: Сумма вероятностей купить исправную или неисправную авторучку равна единице. Чтобы определить вероятность покупки хорошей ручки надо из единицы вычесть вероятность покупки неисправной ручки: 1-0,09=0,91

Пример №4

Два кубика бросают одновременно. Найти вероятность выбросить 9 очков.

Решение: Подберем пары чисел от 1 до 6, которые в сумме дают 9
3+6
4+5
5+4
6+3
Понятно, что на первом кубике может выпасть 4 из 6 возможных чисел. Вероятность составляет: 4/6=2/3
При бросании второго кубика должно выпасть 1 число из 6, вероятность этого события 1/6.
Тогда вероятность того, что сумма очков составит 9, равна произведению вероятностей: 2/3*1/6=2/18=1/9=0,11

Эту задачу можно решить с помощью таблицы, где в верхней строке указано число на перовом кубике, в левом столбце – число на втором, а в ячейках – их сумма. (Такую таблицу можно за минуту набросать на черновике)

Из таблицы видно, что из 36 возможных исходов, 9 очков выпадает в 4-х случаях. Т. е. вероятность составляет 4/36=1/9=0,11

Пример №5

Дима хорошо подготовился к олимпиаде по физике. С вероятностью 0,98 он станет призером и с вероятностью 0,84 – победителем олимпиады. С какой вероятностью Дима станет призером, но не станет победителем олимпиады по физике?

Решение: Победитель одновременно является и призером олимпиады. Поэтому вероятность стать призером (0,98) можно представить в виде суммы вероятности стать победителем (0,84) и вероятности стать просто призером (Х).
Х+0,84=0,98
Х=0,98-0,84
Х=0,14

Пример №6

В дежурном отряде 7 мальчиков и 14 девочек. Дежурство распределяется по жребию. На центральные ворота лагеря нужны двое дежурных. Найти вероятность, что дежурить на воротах будут двое мальчиков.

Решение: Первым дежурным окажется мальчик с вероятностью: 7/21=1/3
Второй дежурный выбирается из 20 оставшихся детей, из которых мальчиков осталось только 6: 6/20=3/10
Вероятность, что на воротах будут дежурить два мальчика: 1/3*3/10=0,1

Пример №7

В сквере имеется сеть дорожек, ведущих к смотровым площадкам. Водопад можно наблюдать с площадок F и G. Турист отправляется из точки А. На каждой развилке он выбирает произвольное направление (кроме направления назад). С какой вероятностью турист сможет увидеть водопад?

Решение: Так как водопад виден с двух площадок, то для решения задачи нужно сложить вероятность того, что турист попадет на площадку F, и вероятность того, что он попадет на площадку G
Для площадки F: 1/2*1/3=1/6
Для площадки G: 1/2*1/2=1/4
Для двух площадок: 1/6+1/4=4/24+6/24=10/24=0,42

Пример №8

К зачету надо выучить 10 вопросов. Саша выучил 2, а остальные только прочитал. Если Саше попадется выученный билет, то он сдаст зачет с вероятностью 0,9. Если Саше попадется вопрос, который он только прочитал, то вероятность сдать зачет 0,3. Вопросы на зачете распределяются случайным образом. Найти вероятность того, что Саша сдаст зачет.

Решение: Из 10 билетов выучены 2, не выучены 8. Вероятность получить выученный вопрос 2/10, вероятность получить не выученный вопрос 8/10.
Вероятность сдать зачет по выученному билету: 2/10*0,9=0,18
Вероятность сдать по невыученному билету: 8/10*0,3=0,24
Итоговая вероятность: 0,18+0,24=0,42

Несколько советов по решению 2 задания

Сложнее всего определить, когда вероятности двух событий надо перемножать, а когда складывать. Попадаются задачи, когда надо сделать и то, и другое. Если вы нашли вероятности отдельных событий, но не можете определиться, что с ними делать дальше – доверьтесь интуиции.

Если вы понимаете что вероятность двух событий больше, чем вероятность каждого в отдельности – складывайте. (Например, вероятность выбросить решку на одной из двух монет очевидно больше, чем выбросить решку на одной монете.)

Если вероятность двух событий меньше, чем каждого в отдельности – перемножайте. (Например, вероятность выбросить решку на обеих монетах меньше, чем вероятность выбросить решку на одной из них.)

Понятно, что интуиция – подход ненаучный. Но на ЕГЭ в задании с кратким ответом лучше дать какой-нибудь ответ, чем не дать никакого.

Однако не забывайте, что профильный ЕГЭ по математике является не только выпускным, но и вступительным испытанием. Большинство школьных задач на вероятность можно решить путем логических рассуждений. Это создает иллюзию легкости теории вероятности и математической статистики. Но на самом деле это одна из самых передовых и востребованных областей математики, и в ВУЗе вы ощутите её сложность в полной мере.

Чаще всего задача сводится именно к вычислению числа исходов примеры 1-2.

Uroknadom. ru

04.01.2020 1:25:29

2020-01-04 01:25:29

Источники:

Http://uroknadom. ru/blog/zadaniye-4-ege-matematika/

Задание №4 ЕГЭ по математике профильного уровня ⋆ СПАДИЛО » /> » /> .keyword { color: red; } Задание четыре егэ математика профиль

Задание №4 ЕГЭ по математике профильного уровня

Задание №4 ЕГЭ по математике профильного уровня

В задании №4 профильного уровня ЕГЭ по математике необходимо решить простую задачу по теории вероятностей. Задача совсем простая, достаточно поделить одно число на другое, ну или перед этим вычесть из одного числа другое. Задание интуитивно понятно, и решить его можно даже не зная основных формул комбинаторики. Разберем несколько примеров.

Разбор типовых вариантов заданий №4 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.

Алгоритм решения:

Обозначаем событие А. Определяем число всех событий. Находим число благоприятствующих исходов. Подсчитываем вероятность. Записываем ответ.

Решение:

1. Пусть А –событие, при котором ученику попадает билет с вопросом о грибах. 2. Всего билетов 25, значит всех событий n=25. 3. Благоприятствующих исходов m=2, т. к. только 2 билета содержат вопрос о грибах. 4. Вероятность события А равна Р(А) = m/n=2/25 = 0,08. Ответ: 0,08.

Второй вариант задания (из Ященко, №1)

В среднем из 600 садовых насосов, поступивших в продажу, 3 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

Алгоритм решения:

Обозначим событие «купленный контрольный насос не подтекает» буквой А. Найдем число всех событий. Найдем число благоприятствующих событий. Определим вероятность события А. Запишем ответ.

Решение:

1. Пусть событие А: выбранный случайным образом насос не протекает. 2. Число всех событий n=600. 3. Число благоприятствующих исходов равно m=600-3=597. Тогда вероятность того, что выбранный насос не подтекает, определяется так: m/n = 597/600 = 0,995 Ответ: 0,995

Третий вариант задания (из Ященко, №7)

В фирме такси в наличии 60 легковых автомобилей; 27 из них чёрного цвета с жёлтыми надписями на боках, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.

Алгоритм решения:

Обозначим событие «на вызов придет желтая машина» буквой А. Найдем число всех возможных событий. Найдем число благоприятствующих событий. Вычислим вероятность события А. Запишем ответ.

Решение:

1. Пусть событие А: на вызов придет желтое такси. 2. Число всех событий n=60. 3. Число благоприятствующих исходов равно m=60-27= 33. Тогда вероятность того, что выбранное для поездки будет желтым, определяется так: Ответ: 0,55.

Четвертый вариант задания (из Ященко, №21)

На фабрике керамической посуды 20% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 70% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.

Алгоритм решения:

Обозначим х число всех тарелок, произведенных на фабрике. Найдем число дефектных тарелок. Найдем число всех изымаемых при проверке тарелок. Определим вероятность события А: куплена качественная тарелка. Запишем ответ.

Решение:

1. Пусть на фабрике изготовлено х тарелок.

2. Бракованных тарелок на фабрике изготовлено 20%. Это всего 0,2x штук. Тогда в торговую сеть поступает 0,8х качественных тарелок.

3. При проверке качества изымается 70% бракованных тарелок, значит, из них 30% поступает в продажу. Получается, на прилавок идет 0,2x · 0,3 = 0,06x бракованных.

Всего в торговую сеть поступает 0,8x + 0,06x = 0,86x тарелок.

4. Пусть событие А: купленная тарелка качественная. Тогда число благоприятствующих событий m=N(A) = 0,8x. Всего число исходов n = 0,86x.

5. Вероятность события А определяем формулой вероятности: P(A) = m/n = 0,8x/0,86x = 0,9302325… ≈ 0,93

1. Пусть событие А: на вызов придет желтое такси. 2. Число всех событий n=60. 3. Число благоприятствующих исходов равно m=60-27= 33. Тогда вероятность того, что выбранное для поездки будет желтым, определяется так: Ответ: 0,55.

Задание №4 ЕГЭ по математике профильного уровня

В задании №4 профильного уровня ЕГЭ по математике необходимо решить простую задачу по теории вероятностей. Задача совсем простая, достаточно поделить одно число на другое, ну или перед этим вычесть из одного числа другое. Задание интуитивно понятно, и решить его можно даже не зная основных формул комбинаторики. Разберем несколько примеров.

В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.

Алгоритм решения:

Обозначаем событие А. Определяем число всех событий. Находим число благоприятствующих исходов. Подсчитываем вероятность. Записываем ответ.

Решение:

1. Пусть А –событие, при котором ученику попадает билет с вопросом о грибах. 2. Всего билетов 25, значит всех событий n=25. 3. Благоприятствующих исходов m=2, т. к. только 2 билета содержат вопрос о грибах. 4. Вероятность события А равна Р(А) = m/n=2/25 = 0,08. Ответ: 0,08.

Третий вариант задания из Ященко, 7.

Spadilo. ru

07.01.2019 8:51:22

2019-01-07 08:51:22

Источники:

Http://spadilo. ru/zadanie-4-ege-po-matematike-profilnyj/

События, которые происходят реально или в нашем воображении, можно разделить на 3 группы. Это достоверные события, которые обязательно произойдут, невозможные события и случайные события. Теория вероятностей изучает случайные события, т.е. события, которые могут произойти или не произойти. В данной статье будет представлена в кратком виде теория вероятности формулы и примеры решения задач по теории вероятности, которые будут в 4 задании ЕГЭ по математике (профильный уровень).

Зачем нужна теория вероятности

Исторически потребность исследования этих проблем возникла в XVII веке в связи с развитием и профессионализацией азартных игр и появлением казино. Это было реальное явление, которое требовало своего изучения и исследования.

Игра в карты, кости, рулетку создавала ситуации, когда могло произойти любое из конечного числа равновозможных событий. Возникла необходимость дать числовые оценки возможности наступления того или иного события.

В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей.

Основные понятия теории вероятности

Объектом изучения теории вероятностей являются события и их вероятности. Если событие является сложным, то его можно разбить на простые составляющие, вероятности которых найти несложно.

Суммой событий А и В называется событие С, заключающееся в том, что произошло либо событие А, либо событие В, либо события А и В одновременно.

Произведением событий А и В называется событие С, заключающееся в том, что произошло и событие А и событие В.

События А и В называется несовместными, если они не могут произойти одновременно.

Событие А называется невозможным, если оно не может произойти. Такое событие обозначается символом .

Событие А называется достоверным, если оно обязательно произойдет. Такое событие обозначается символом .

Пусть каждому событию А поставлено в соответствие число P{А). Это число P(А) называется вероятностью события А, если при таком соответствии выполнены следующие условия.

1. Вероятность принимает значения на отрезке от 0 до 1, т.е. .
2. Вероятность невозможного события равна 0, т.е. .
3. Вероятность достоверного события равна 1, т.e. .
4. Если события A и В несовместные, то вероятность их суммы равна сумме их вероятностей, т.е. .

Важным частным случаем является ситуация, когда имеется равновероятных элементарных исходов, и произвольные  из этих исходов образуют события А. В этом случае вероятность можно ввести по формуле . Вероятность, введенная таким образом, называется классической вероятностью. Можно доказать, что в этом случае свойства 1-4 выполнены.

Задачи по теории вероятностей, которые встречаются на ЕГЭ по математике, в основном связаны с классической вероятностью. Такие задачи могут быть очень простыми. Особенно простыми являются задачи по теории вероятностей в демонстрационных вариантах. Легко вычислить число благоприятных исходов , прямо в условии написано число всех исходов .

Ответ получаем по формуле .

Пример задачи из ЕГЭ по математике по определению вероятности

На столе лежат 20 пирожков – 5 с капустой, 7 с яблоками и 8 с рисом. Марина хочет взять пирожок. Какова вероятность, что она возьмет пирожок с рисом?

Решение.

Всего равновероятных элементарных исходов 20, то есть Марина может взять любой из 20 пирожков. Но нам нужно оценить вероятность того, что Марина возьмет пирожок с рисом, то есть , где А – это выбор пирожка с рисом. Значит у нас количество благоприятных исходов (выборов пирожков с рисом) всего 8. Тогда вероятность будет определяться по формуле:

   

Ответ: 0,4

Независимые, противоположные и произвольные события

Однако в открытом банке заданий стали встречаться и более сложные задания. Поэтому обратим внимание читателя и на другие вопросы, изучаемые в теории вероятностей.

События А и В называется независимыми, если вероятность каждого из них не зависит от того, произошло ли другое событие.

Событие B состоит в том, что событие А не произошло, т.е. событие B является противоположным к событию А. Вероятность противоположного события равна единице минус вероятность прямого события,т.е. .

Теоремы сложения и умножения вероятностей, формулы

Для произвольных событий А и В вероятность суммы этих событий равна сумме их вероятностей без вероятности их совместного события, т.е. .

Для независимых событий А и В вероятность произведения этих событий равна произведению их вероятностей, т.е. в этом случае .

Последние 2 утверждения называются теоремами сложения и умножения вероятностей.

Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям. Иногда такого рода подсчеты могут становиться самостоятельными заданиями.

Сколькими способами можно усадить 6 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Для третьего ученика остается 4 свободных места, для четвертого — 3, для пятого — 2, шестой займет единственное оставшееся место. Чтобы найти число всех вариантов, надо найти произведение , которое обозначается символом 6! и читается “шесть факториал”.

В общем случае ответ на этот вопрос дает формула для числа перестановок из п элементов  В нашем случае .

Рассмотрим теперь другой случай с нашими учениками. Сколькими способами можно усадить 2 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Чтобы найти число всех вариантов, надо найти произведение .

В общем случае ответ на этот вопрос дает формула для числа размещений из n элементов по k элементам

   

В нашем случае .

И последний случай из этой серии. Сколькими способами можно выбрать трех учеников из 6? Первого ученика можно выбрать 6 способами, второго — 5 способами, третьего — четырьмя. Но среди этих вариантов 6 раз встречается одна и та же тройка учеников. Чтобы найти число всех вариантов, надо вычислить величину: . В общем случае ответ на этот вопрос дает формула для числа сочетаний из элементов по элементам:

   

В нашем случае .

Примеры решения задач из ЕГЭ по математике на определение вероятности

Задача 1. Из сборника под ред. Ященко.

На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Саша наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.

Решение:

.

Ответ: 0,3.

Задача 2. Из сборника под ред. Ященко.

В каждой партии из 1000 лампочек в среднем 20 бракованных. Найдите вероятность того, что наугад взятая лампочка из партии будет исправной.

Решение: Количество исправных лампочек 1000-20=980. Тогда вероятность того, что взятая наугад лампочка из партии будет исправной:

Ответ: 0,98.

Задача 3.

Вероятность того, что на тестировании по математике учащийся У. верно решит больше 9 задач, равна 0,67. Вероятность того, что У. верно решит больше 8 задач, равна 0,73. Найдите вероятность того, что У. верно решит ровно 9 задач.

Решение:

Если мы вообразим числовую прямую и на ней отметим точки 8 и 9, то мы увидим, что условие “У. верно решит ровно 9 задач” входит в условие “У. верно решит больше 8 задач”, но не относится к условию “У. верно решит больше 9 задач”.

Однако, условие “У. верно решит больше 9 задач” содержится в условии “У. верно решит больше 8 задач”. Таким образом, если мы обозначим события: “У. верно решит ровно 9 задач” – через А, “У. верно решит больше 8 задач” – через B, “У. верно решит больше 9 задач” через С. То решение будет выглядеть следующим образом:

.

Ответ: 0,06.

Задача 4.

На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,2. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение.

Давайте подумаем какие у нас даны события. Нам даны два несовместных события. То есть либо вопрос будет относиться к теме “Тригонометрия”, либо к теме “Внешние углы”. По теореме вероятности вероятность несовместных событий равна сумме вероятностей каждого события, мы должны найти сумму вероятностей этих событий, то есть:

Ответ: 0,35.

Задача 5.

Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,29. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

Решение:

Рассмотрим возможные события. У нас есть три лампочки, каждая из которых может перегореть или не перегореть независимо от любой другой лампочки. Это независимые события.

Тогда укажем варианты таких событий. Примем обозначения: – лампочка горит, – лампочка перегорела. И сразу рядом подсчитаем вероятность события. Например, вероятность события, в котором произошли три независимых события “лампочка перегорела”, “лампочка горит”, “лампочка горит”: , где вероятность события “лампочка горит” подсчитывается как вероятность события, противоположного событию “лампочка не горит”, а именно: .

 

 

 

 

 

Заметим, что благоприятных нам несовместных событий всего 7. Вероятность таких событий равна сумме вероятностей каждого из событий: .

Ответ: 0,975608.

Еще одну задачку вы можете посмотреть на рисунке:

Таким образом, мы с вами поняли, что такое теория вероятности формулы и примеры решения задач по которой вам могут встретиться в варианте ЕГЭ.