Шпаргалка по тригонометрии егэ профильный уровень - Помощь в подготовке к экзаменам и поступлению

Алгебра — ЕГЭ Тригонометрия — ЕГЭ Геометрия — ЕГЭ Стереометрия — ЕГЭ Алгебра — ОГЭ Геометрия — ОГЭ

Формулы по тригонометрии

Шпаргалка по тригонометрическим формулам

Таблица формул тригонометрии

Единичный круг — тригонометрия

Самые необходимые тригонометрические формулы

Для того чтобы сдать ЕГЭ по математике, вам понадобится около 20 формул тригонометрии. Это не много. Но их надо знать наизусть!

Вот таблица, в которой собраны основные тригонометрические формулы. Здесь все самое необходимое. Их легко выучить и применять.

Эти формулы применяются и в заданиях 1 части ЕГЭ по математике, и в заданиях 2 части.

Эта полезная табличка – только одна из многих страниц Справочника Анны Малковой для подготовки к ЕГЭ. Скачай Справочник бесплатно здесь.

Кроме того, надо знать определения синуса, косинуса и тангенса, а также значения этих функций для основных углов.

Первые 3 блока формул из нашей таблицы часто встречаются в заданиях 1 части ЕГЭ и в задаче из второй части, где надо решить тригонометрическое уравнение.

В первую очередь это основное тригонометрическое тождество:

sin ${}^2 alpha +$ cos ${}^2 alpha =1.$

Это формулы, которые показывают, как выразить тангенс через косинус и котангенс через синус угла.

tg ${}^2alpha +1=displaystyle frac{1}{{{cos}^2 alpha }};$

1 + ctg ${}^2alpha =displaystyle frac{1}{{{sin}^2 alpha }}.$

Формулы синуса и косинуса двойного угла, формулы синуса суммы, косинуса разности, – все это надо знать, чтобы без ошибок решать тригонометрические уравнения.

А вот формулы суммы синусов и косинусов, а также преобразование произведения в сумму могут пригодиться при решении задач с параметрами.

Где же могут встретиться формулы из двух последних блоков, внизу таблицы?

Формулы понижения степени могут присутствовать и в тригонометрических уравнениях, и в «параметрах». И даже в задачах с физическим содержанием из 1 части ЕГЭ, если там вдруг попадется тригонометрия.

А универсальная тригонометрическая замена, когда мы выражаем синус и косинус угла альфа через тангенс половинного угла? А формулы синуса и косинуса тройных углов? Где же они применяются? Оказывается, они помогают решать задачи по геометрии из 2 части ЕГЭ. Так что их тоже стоит знать, если хотите сдать на высокий балл.

Обратите внимание, что в этой таблице нет формул приведения. О них мы рассказываем в отдельной статье нашего сайта.

Как же выучить тригонометрические формулы?

1. Учите формулы сразу. Не рассказывайте себе сказки о том, что в последнюю ночь перед ЕГЭ все выучите. Каждый день – один блок, то есть три-четыре формулы из нашей таблицы.

2. Тренируйтесь. Выучить иностранный язык проще всего тому, кто вынужден постоянно на нем говорить. Так и здесь. Для тренировки можно из классического задачника Сканави выбрать 20-50 заданий на преобразование тригонометрических выражений и доказательство тождеств.

3. Универсальный способ: ежедневно, садясь за уроки, берите чистый листок и выписывайте наизусть все тригонометрические формулы, какие помните. Когда всё готово — сверяете. И к экзамену вы будете помнить всё.

4. Еще один отличный способ. Вырежьте из плотной бумаги карточки. На одной пишете левую часть формулы. На другой – правую. Перемешиваете. И собираете. Любые формулы запоминаются легко и быстро!

5. И конечно, решаем задания ЕГЭ на применение этих формул. Начнем с задач 1 части, преобразование тригонометрических выражений.

Задача 1.

Найдите tg alpha , если cos $alpha =displaystyle frac{sqrt{10}}{10}$ и $alpha in left(displaystyle frac{3pi }{2};2pi right).$

Решение:

Воспользуемся формулой:

tg ${}^2x+1=displaystyle frac{1}{{cos}^2x} Rightarrow$ tg x $=pm sqrt{displaystyle frac{1}{{cos}^2x}-1}.$

Какой знак будет у тангенса, «плюс» или «минус»?

В условии дано, что $alpha in left(displaystyle frac{3pi }{2};2pi right)$ , то есть это угол из четвертой четверти, значит tgx

tgx $=-sqrt{displaystyle frac{100}{10}-1}=-3.$

Ответ: -3.

Задача 2.

Найдите $displaystyle frac{10{sin 6alpha }}{3{cos 3alpha }},$ если sin

Решение:

Воспользуемся формулой синуса двойного угла: sin2 alpha = 2sin alpha cos alpha :

$displaystyle frac{10{sin 6alpha }}{3{sin 3alpha }}=displaystyle frac{10cdot 2{sin 3alpha }{cos 3alpha }}{3{sin 3alpha }}=displaystyle frac{20cdot {cos 3alpha }}{3}=displaystyle frac{20cdot 0,6}{3}=4.$

Ответ: 4.

Задача 3.

Найдите 24cos если sin

Решение:

Воспользуемся формулой косинуса двойного угла: cos 2 alpha = 1 — 2sin ${}^2$ alpha :

24cos2 alpha = 24(1 — 2sin ${}^2 alpha )=24left(1-2{left(-0,2right)}^2right)=$

Ответ: 22,08.

Задача 4.

Найдите $displaystyle frac{3{cos alpha }-4{sin alpha }}{2{sin alpha }-5{cos alpha }},$ если tg alpha =3.

Решение:

Вынесем косинус альфа за скобки в числителе и знаменателе:

$displaystyle frac{3{cos alpha }-4{sin alpha }}{2{sin alpha }-5{cos alpha }}=displaystyle frac{{cos alpha }left(3-4tgalpha right)}{{cos alpha }left(2tgalpha -5right)}=displaystyle frac{3-4cdot 3}{2cdot 3-5}=displaystyle frac{-9}{1}=-9.$

Ответ: -9.

Задача 5.

Найдите значение выражения: $displaystyle frac{5{sin 98{}^circ }}{{sin 49{}^circ }cdot {sin 41{}^circ }}.$

Решение:

Воспользуемся формулой синуса двойного угла:

sin2 alpha = 2sin alpha cos alpha ; тогда sin alpha cos alpha = $displaystyle frac{1}{2}{sin 2alpha } .$

$displaystyle frac{5{sin 98{}^circ }}{{sin 49{}^circ cdot {sin 41{}^circ } }}=displaystyle frac{10{sin 49{}^circ }cdot {cos 49{}^circ }}{{sin 49{}^circ cdot {sin 41{}^circ } }}=displaystyle frac{10{sin 41{}^circ }}{{sin 41{}^circ }}=10.$

Ответ: 10.

Задача 6.

Найдите значение выражения: sqrt{3} cos ${}^2 displaystyle frac{5pi }{12}-sqrt{3}$ sin ${}^2 displaystyle frac{5pi }{12} .$

Решение:

Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:

cos alpha = cos ${}^2$ alpha — sin ${}^2$ alpha.

$sqrt{3}{{cos}^2 displaystyle frac{5pi }{12} }-sqrt{3}{{sin}^2 displaystyle frac{5pi }{12}=sqrt{3}left({{cos}^2 displaystyle frac{5pi }{12} }-{{sin}^2 displaystyle frac{5pi }{12} }right) }=$

cos $displaystyle frac{5pi }{6}=sqrt{3}cdot left(-displaystyle frac{sqrt{3}}{2}right)=-1,5.$

Ответ: -1,5.

Задача 7.

Найдите значение выражения: $-50tg 9{}^circ cdot$ tg $81{}^circ +31.$

Решение:

Используя формулы приведения, получим: tg $81{}^circ$ = tg $left(90{}^circ -9{}^circ right)$ = ctg $9{}^circ.$

Пользуемся также тем, что тангенс и котангенс угла альфа — взаимно обратные величины,

Получим:

-50tg $9{}^circ cdot$ ctg $9{}^circ +31=-50+31 = - 19.$

Ответ: -19.

Задача 8.

Найдите значение выражения: sin ${}^2 displaystyle frac{21pi }{8}.$

Решение:

sin ${}^2 displaystyle frac{21pi }{8}=6sqrt{2}-12sqrt{2}$ sin ${}^2 displaystyle frac{21pi }{8}=6sqrt{2}cdot left(1-2{}^2 displaystyle frac{21pi }{8} right)=$

cos $(2cdot displaystyle frac{21pi }{8})=6sqrt{2}$ cos $displaystyle frac{21pi }{4}=6sqrt{2}$ cos $displaystyle frac{5pi }{4}=6sqrt{2}cdot displaystyle frac{sqrt{2}}{2}=6.$

Мы вынесли за скобки множитель и применили формулу косинуса двойного угла, выразив его через квадрат синуса угла.

Ответ: 6.

Задача 9.

Найдите значение выражения: 5sin $displaystyle frac{11pi }{12}cdot$ cos $displaystyle frac{11pi }{12}.$

Решение:

Воспользуемся формулой синуса двойного угла: sin alpha = 2sin alpha cos alpha . Также применим одну из формул приведения: sin = -sin alpha .

5sin $displaystyle frac{11pi }{12}$ cos $displaystyle frac{11pi }{12}=displaystyle frac{5}{2}cdot$ sin $displaystyle frac{11pi }{6}=displaystyle frac{5}{2}cdot$ sin $left(2pi -displaystyle frac{pi }{6}right)=-displaystyle frac{5}{2}cdot$ sin $displaystyle frac{pi }{6}=-displaystyle frac{5}{2}cdot displaystyle frac{1}{2}=-1,25.$

Ответ: -1,25.

Задача 10.

Найдите значение выражения: $2sqrt{3}-4sqrt{3}{{sin}^2 displaystyle frac{7pi }{12}}.$

Решение:

Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:

cos2 alpha = 1 — 2 ${sin}^2 alpha.$

$2sqrt{3}-4sqrt{3}{{sin}^2 displaystyle frac{7pi }{12}= }2sqrt{3}(1-2{{sin}^2 displaystyle frac{7pi }{12})= }$

cos $displaystyle frac{7pi }{6}=2sqrt{3}cdot$ cos $left(pi +displaystyle frac{pi }{6}right)=-2sqrt{3}cdot$ cos $displaystyle frac{pi }{6}=-2sqrt{3}cdot displaystyle frac{sqrt{3}}{2}=-3.$

Ответ: -3.

Задача 11.

Найдите значение выражения: $sqrt{108}{{cos}^2 displaystyle frac{pi }{12} }-sqrt{27}.$

Решение:

Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:

cos2 alpha = ${cos}^2 alpha -sin{}^2 alpha = 2cos{}^2 alpha -1.$

cos ${}^2 displaystyle frac{pi }{12}-sqrt{27}=6sqrt{3}$ cos ${}^2 displaystyle frac{pi }{12}-3sqrt{3}=3sqrt{3}left(2{{cos}^2 displaystyle frac{pi }{12} }-1right)=3sqrt{3}cdot$ cos $displaystyle frac{pi }{6}=$

$=3sqrt{3}cdot displaystyle frac{sqrt{3}}{2} =4,5.$

Ответ: 4,5.

Задача 12.

Найдите значение выражения: $-displaystyle frac{6{sin 374{}^circ }}{{sin 14{}^circ }}.$

$displaystyle frac{-6{sin 374{}^circ }}{{sin 14{}^circ }}=displaystyle frac{-6{sin 14{}^circ }}{{sin 14{}^circ }}=-6.$

Мы воспользовались периодичностью функции синус: sinsin alpha . В нашей задаче 374 = 360 + 14.

Ответ: — 6.

Задача 13.

Найдите значение выражения: $7sqrt{2}{sin displaystyle frac{15pi }{8}cdot {cos displaystyle frac{15pi }{8} } }.$

Решение:

Воспользуемся формулой синуса двойного угла: sin2 alpha = 2sin alpha cos alpha.

sin $displaystyle frac{15pi }{8}cdot$ cos $displaystyle frac{15pi }{8}=displaystyle frac{7sqrt{2}}{2}cdot$ sin $displaystyle frac{15pi }{4}=displaystyle frac{7sqrt{2}}{2}cdot$ sin $left(4pi -displaystyle frac{pi }{4}right)=displaystyle frac{7sqrt{2}}{2}cdot$ sin $displaystyle frac{pi }{4}=displaystyle frac{7sqrt{2}}{2}cdot displaystyle frac{sqrt{2}}{2}=3,5.$

Ответ: 3,5.

Заметим, что если в задаче нам встретилось произведение синуса альфа на косинус альфа, то, скорее всего, нужно будет применять формулу синуса двойного угла.

Задача 14.

Найдите tg alpha , если cos alpha $=-displaystyle frac{5sqrt{41}}{41}$ и $alpha in left(pi ;displaystyle frac{3pi }{2}right).$

Решение:

Вспомним основное тригонометрическое тождество: ${{cos}^2 alpha }+ {{sin}^2 alpha }=1.$ Выразим из этой формулы синус альфа:

sin alpha $=pm sqrt{1-{{cos}^2 alpha }}.$

Какой же знак выбрать, «плюс» или «минус»?

Угол альфа в третьей четверти, значит, его синус отрицателен.

sin alpha $=-sqrt{1-{left(-displaystyle frac{5sqrt{41}}{41}right)}^2}=-sqrt{1-displaystyle frac{25}{41}}=-sqrt{displaystyle frac{16}{41}}=-displaystyle frac{4}{sqrt{41}}.$

tg $alpha =displaystyle frac{{sin alpha }}{{cos alpha }}=left(-displaystyle frac{5sqrt{41}}{41}right):left(-displaystyle frac{4}{sqrt{41}}right)=displaystyle frac{5}{4}=1,25.$

Ответ: 1,25.

Задача 15.

Найдите sin alpha , если cos alpha $=-displaystyle frac{sqrt{19}}{10}$ и $alpha in left(displaystyle frac{pi }{2};pi right).$

Решение:

Как и в предыдущей задаче, выразим синус альфа из основного тригонометрического тождества:

sin $alpha =pm sqrt{1-{{cos}^2 alpha }}.$

Дан угол альфа, принадлежащий второй четверти, значит, его синус положителен.

sin $alpha =sqrt{1-{left(displaystyle frac{sqrt{19}}{10}right)}^2}=sqrt{displaystyle frac{81}{100}}=0,9.$

Ответ: 0,9.

Задача 16.

Найдите tg alpha , если sin alpha $=-displaystyle frac{4sqrt{41}}{41}$ и $alpha in left(pi ;displaystyle frac{3pi }{2}right).$

Решение:

Аналогично предыдущим задачам, выразим косинус альфа из основного тригонометрического тождества:

cos alpha $=pm sqrt{1-{{sin}^2 alpha }}.$

Угол альфа в третьей четверти, значит, его косинус отрицателен.

cos alpha $=-sqrt{1-displaystyle frac{16}{41}}=-sqrt{displaystyle frac{25}{41}}=-displaystyle frac{5}{sqrt{41}}$ , тогда tg $alpha =displaystyle frac{{sin alpha }}{{cos alpha }}=-displaystyle frac{4}{sqrt{41}}div left(-displaystyle frac{5}{sqrt{41}}right)=displaystyle frac{4}{5}=0,8.$

Ответ: 0,8.

Задача 17.

Найдите значение выражения: — 42tg $34{}^circ cdot$ tg $56{}^circ +6.$

Решение:

-42tg $34{}^circ cdot$ tg ${56}^circ =$ -42tg $34{}^circ cdot$ tg $left(90{}^circ -34{}^circ right)=$ -42tg $34{}^circ cdot$ ctg $34{}^circ =-42.$

Мы применили формулу приведения, а также то, что тангенс и котангенс угла альфа — взаимно обратные величины, и их произведение равно единице.

Ответ: -42.

Задача 18.

Найдите значение выражения: $displaystyle frac{24}{{{sin}^2 127{}^circ }}+4+$ sin ${}^2 217{}^circ .$

Решение:

Воспользуемся формулами приведения:

$displaystyle frac{24}{{{sin}^2 127+4+sin{}^2 217}}=displaystyle frac{24}{{{sin}^2 left(90{}^circ +37{}^circ right)+4+{{sin}^2 left(180{}^circ +37{}^circ right) } }}=$

$=displaystyle frac{24}{{{cos}^2 37{}^circ +4+{{sin}^2 37{}^circ } }}=displaystyle frac{24}{5}=4,8.$

Также мы применили основное тригонометрическое тождество. Сумма квадратов синуса и косинуса угла альфа равна единице.

Ответ: 4,8.

Задача 19.

Найдите значение выражения: $displaystyle frac{2{sin 136{}^circ }}{{sin 68{}^circ }cdot {sin 22{}^circ }}.$

Решение:

Так как $68{}^circ +22{}^circ =90{}^circ ,$ то заменим ${sin 68{}^circ }$ на ${cos 22 }^circ$ по формуле приведения и воспользуемся формулой синуса двойного угла:

sin2 alpha = 2sin alpha cos alpha.

$displaystyle frac{2{sin 136{}^circ }}{{sin 68{}^circ }{sin 22{}^circ }}=displaystyle frac{2{sin 136{}^circ }}{{cos 22{}^circ }{sin 22{}^circ }}=displaystyle frac{4{sin left(180{}^circ -44{}^circ right) }}{{sin 44{}^circ }}=$

$=displaystyle frac{4{sin 44{}^circ }}{{sin 44{}^circ }}=4.$

Ответ: 4.

Задача 20.

Найдите значение выражения: $displaystyle frac{21left({{sin}^2 66{}^circ }-{{cos}^2 66{}^circ }right)}{{cos 132{}^circ }}.$

Решение:

Воспользуемся формулой косинуса двойного угла:

${cos 2alpha ={{cos}^2 alpha }-{{sin}^2 alpha } }.$

$displaystyle frac{21left({{sin}^2 66{}^circ }-{{cos}^2 66{}^circ }right)}{{cos 132{}^circ }}=displaystyle frac{-21{cos 132{}^circ }}{{cos 132{}^circ }}=-21.$

Ответ: -21.

Задача 21.

Найдите значение выражения: $sqrt{2}{sin displaystyle frac{7pi }{8}cdot {cos displaystyle frac{7pi }{8}} }.$

Решение:

Воспользуемся формулой синуса двойного угла:

$sqrt{2}{sin displaystyle frac{7pi }{8} }cdot {cos displaystyle frac{7pi }{8}=displaystyle frac{sqrt{2}}{2}{sin displaystyle frac{7pi }{4} } }=displaystyle frac{sqrt{2}}{2}{sin left(2pi -displaystyle frac{pi }{4}right) }=-displaystyle frac{sqrt{2}}{2}sin displaystyle frac{pi }{4}=$

$= -displaystyle frac{sqrt{2}}{2}cdot displaystyle frac{sqrt{2}}{2}=-0,25.$

Ответ: -0,25.

Задача 22.

Найдите значение выражения: $3sqrt{2}{{cos}^2 displaystyle frac{9pi }{8} }-3sqrt{2}{{sin}^2 displaystyle frac{9pi }{8} }.$

Решение:

$3sqrt{2}{cos}^2 displaystyle frac{9pi }{8} -3sqrt{2}{{sin}^2 displaystyle frac{9pi }{8} }=3sqrt{2}left({{cos}^2 displaystyle frac{9pi }{8} }-{{sin}^2 displaystyle frac{9pi }{8} }right)=3sqrt{2}{cos displaystyle frac{9pi }{4} }=$

$=3sqrt{2}cos left(2pi +displaystyle frac{pi }{4}right)=3sqrt{2}cos displaystyle frac{pi }{4}=3sqrt{2}cdot displaystyle frac{sqrt{2}}{2}=3.$

И здесь тоже была формула косинуса двойного угла, но только в другой форме.

Ответ: 3.

Задача 23.

Найдите значение выражения: $26sqrt{2}{cos displaystyle frac{pi }{4} }{cos displaystyle frac{4pi }{3} }.$

Решение:

$26sqrt{2}{cos displaystyle frac{pi }{4} }{cos displaystyle frac{4pi }{4} }=26sqrt{2}cdot displaystyle frac{sqrt{2}}{2}cdot left(-displaystyle frac{1}{2}right)=-13.$

А здесь мы просто вычислили косинус и синус табличного угла $displaystyle frac{pi }{4}.$

Ответ: -13.

Задача 24.

Найдите значение выражения: $18sqrt{2}tgdisplaystyle frac{pi }{4}{sin displaystyle frac{pi }{4} }.$

Решение:

$18sqrt{2}cdot tgdisplaystyle frac{pi }{4}{cdot sin displaystyle frac{pi }{4}= }18sqrt{2}cdot 1cdot displaystyle frac{sqrt{2}}{2}=18.$

Это задача на вычисление тригонометрических функций для табличного угла $displaystyle frac{pi }{4}.$ Если этот угол выразить в градусах, то он равен 45 градусов.

Ответ: 18.

Задача 25.

Найдите значение выражения: $displaystyle frac{2{cos left(2pi -beta right) }-3{sin left(-displaystyle frac{pi }{2}+beta right) }}{2{cos left(beta -3pi right) }}.$

Решение:

Используя формулы приведения, получим:

$displaystyle frac{2{cos left(2pi -beta right) }-3{sin left(-displaystyle frac{pi }{2}+beta right) }}{2{cos left(beta -3pi right) }}=displaystyle frac{2{cos beta }+3{cos beta }}{-2{cos beta }}=$

$=-displaystyle frac{5{cos beta }}{2{cos beta }}=-2,5.$

Лайфхак: если вам сложно запомнить формулы приведения, вы можете вместо них использовать формулы косинуса разности и синуса суммы.

Ответ: -2,5.

Посмотрим, как формулы тригонометрии применяются при решении уравнений.

Задача 26.

Решите уравнение: ${{sin}^2 left(displaystyle frac{pi }{4}-xright) }={{sin}^2 left(displaystyle frac{pi }{4}+xright) }.$

Решение:

Воспользуемся формулой понижения степени: sin ${}^2 x=displaystyle frac{1-{cos 2x }}{2}.$

$displaystyle frac{1-{cos left(displaystyle frac{pi }{2}-2xright) }}{2}=displaystyle frac{1-{cos left(displaystyle frac{pi }{2}+2xright) }}{2}Leftrightarrow {cos left(displaystyle frac{pi }{2}-2xright) }={cos left(displaystyle frac{pi }{2}+2xright)Leftrightarrow }$

$Leftrightarrow {cos 2x=-{cos 2xLeftrightarrow 2 } }{cos 2x=0 }Leftrightarrow 2x=displaystyle frac{pi }{2}+pi kLeftrightarrow x=displaystyle frac{pi }{4}+displaystyle frac{pi k}{2}; kin Z.$

Ответ: $x=displaystyle frac{pi }{4}+displaystyle frac{pi k}{2}; kin Z.$

Задача 27.

Решите уравнение: ${{cos}^2 3x }+{{cos}^2 4x }+{{cos}^2 5x }=displaystyle frac{3}{2}.$

Решение:

Воспользуемся формулой понижения степени: ${{cos}^2 x }=displaystyle frac{1+{cos 2x }}{2}.$

${cos}^2 3x+{cos}^2 4x+{cos}^2 5x=displaystyle frac{3}{2}Leftrightarrow displaystyle frac{1+{cos 6x }}{2}+$

$+displaystyle frac{1+{cos 8x }}{2}+displaystyle frac{1+{cos 10x }}{2}=displaystyle frac{3}{2}.$

Умножим обе части на два:

Воспользуемся формулой суммы косинусов: cos alpha + cos beta = 2cos $displaystyle frac{alpha +beta }{2}$ cos $displaystyle frac{alpha -beta }{2};$

cos6x + cos10x = 2cos8x cos2x.

Уравнение примет вид:

2cos8x cos2x + cos8x =0.

Вынесем общий множитель за скобки. Теперь произведение двух множителей равно нулю, а с этим мы умеем работать.

${cos 8xleft(2{cos 2x+1 }right)=0Leftrightarrow left[ begin{array}{c}{cos 8x=0 } \{cos 2x=-displaystyle frac{1}{2} } end{array}Leftrightarrow left[ begin{array}{c}8x=displaystyle frac{pi }{2}+pi k \2x=pm displaystyle frac{2pi }{3}+2pi k;kin Z end{array}right.right. }Leftrightarrow left[ begin{array}{c}x=displaystyle frac{pi }{16}+displaystyle frac{pi k}{8} \x=pm displaystyle frac{pi }{3}+pi k;kin Z end{array}right. .$

Ответ: $left[ begin{array}{c}x=displaystyle frac{pi }{16}+displaystyle frac{pi k}{8} \x=pm displaystyle frac{pi }{3}+pi k;kin Z end{array}right. .$

Все о решении тригонометрических уравнений здесь.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Самые необходимые тригонометрические формулы» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

11 декабря 2020

В закладки

Обсудить

Жалоба

Шпаргалка по тригонометрии

Основные тригонометрические тождества и формулы.

shpargalka_po_trigonometrii.pdf

Содержание

Основные тригонометрические тождества.
Формулы приведения.
Формулы периодических углов.
Формулы суммы и разности углов.
Формулы двойного угла.
Формулы половинного угла (формулы понижения степени).
Формулы произведения тригонометрических функций.
Формулы суммы и разности тригонометрических функций.
Универсальная тригонометрическая подстановка (УТП).
Обратные тригонометрические функции (аркфункции).
Простые тригонометрические уравнения.

Источник

3621

На ЕГЭ по профильной математике с собой можно взять только черные гелевые ручки и линейку. На экзамене профильного уровня, в отличие от базового, не выдаются справочные материалы – выпускникам не предоставляются формулы, необходимые для решения задач. Исключение составляют лишь 5 формул по тригонометрии, но, естественно, они не помогут набрать максимальные баллы, если экзаменуемые не будут знать об остальных важных сведениях и математических свойствах.

Содержание

Формулы для ЕГЭ по профильной математике. Алгебра

Формулы сокращенного умножения

Квадрат суммы: (a + b)² = a² + 2ab + b²

Квадрат разности: (a – b)² = a² – 2ab + b²

Разность квадратов: a² – b² = (a + b)(a – b)

Сумма кубов: a³ + b³ = (a + b)(a² – ab + b²)

Разность кубов: a³ – b³ = (a – b)(a² + ab + b²)

Прогрессия

Арифметическая

Геометрическая

Таблица степеней

Свойства степеней

Таблица квадратов

Интенсивы по подготовке к региональному этапу ВсОШ

Все, что нужно знать
для победы, за 7 дней!

Свойства корней

Тригонометрия

Таблица значений тригонометрических функций

Тригонометрическая окружность

Тригонометрические формулы

Обратные тригонометрические функции

Преобразование суммы и разности в произведение

Регулярные курсы по подготовке к олимпиадам и ЕГЭ

Поступаем в вуз мечты без проблем!

Вероятность

Вероятность события А: m – благоприятные, n – общее число событий

P(A) = m/n

События А и В происходят одновременно: A · B

Независимые события: P(A · B) = P(A) · P(B)

Зависимые события: P(A · B) = P(A) · P(B | A)

Происходит или А, или В: A + B

Несовместные события: P(A + B) = P(A) + P(B)

Совместные события: P(A + B) = P(A) + P(B) – P(A · B)

Свойства модуля

Производные

Основные правила дифференцирования

Таблица производных

Первообразные

Логарифмы

Квадратные уравнения

Дискриминант

Теорема Виета

Разложение на множители

3528

Формулы для ЕГЭ по профильной математике. Геометрия

Планиметрия

Треугольник

Следствие из теоремы косинусов:

Длина биссектрисы (через угол):

Длина биссектрисы (через отрезки):

Прямоугольный треугольник

24 декабря – 20 января

5-11 классы

Онлайн-олимпиада Коалиции

Равносторонний треугольник

Аргументы для итогового сочинения

Подборка лучших аргументов

Равносторонний шестиугольник

Площадь внутреннего треугольника:

Площадь внутреннего прямоугольника:

Ромб

Трапеция

Произвольный четырёхугольник

Окружность

Стереометрия

Выводы

Не заучивайте формулы без осознания того, откуда берутся числа. Как можно чаще применяйте формулы при решении задач, тренируйте гибкость мышления, чтобы на ЕГЭ по профильной математике справиться со всеми заданиями.

А чтобы в разы повысить шансы на успех и разобраться в тонкостях непростой науки, можно обратиться за помощью к преподавателю онлайн-курса по подготовке к ЕГЭ.

Поделиться в социальных сетях

Какими формулами вам приходится пользоваться чаще всего?

Межтекстовые Отзывы

Посмотреть все комментарии

Читайте также

Источник

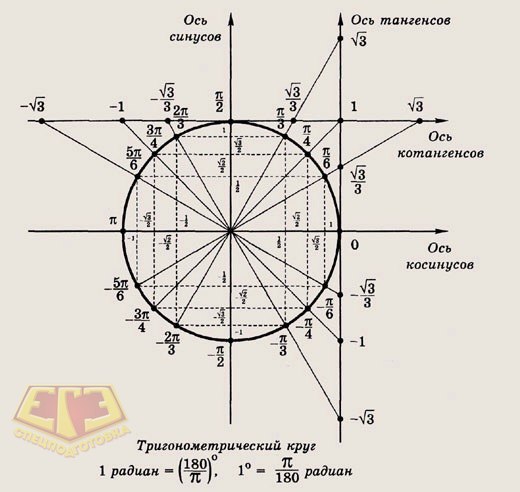
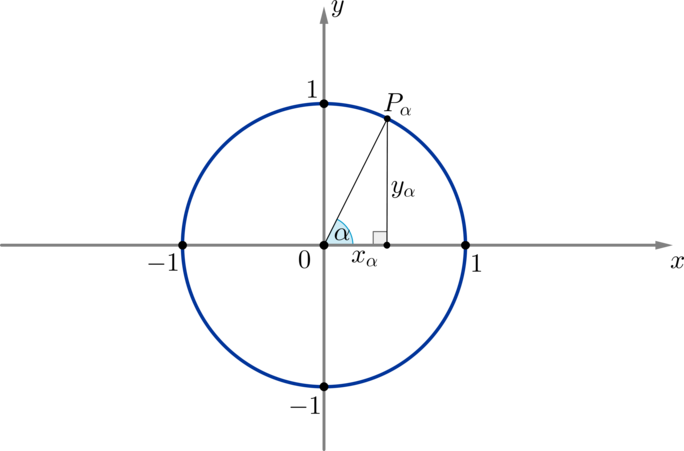
(blacktriangleright) Рассмотрим прямоугольную систему координат и в ней окружность с единичным радиусом и центром в начале координат.

Угол в (1^circ) — это такой центральный угол, который опирается на дугу, длина которой равна (dfrac1{360}) длины всей окружности.

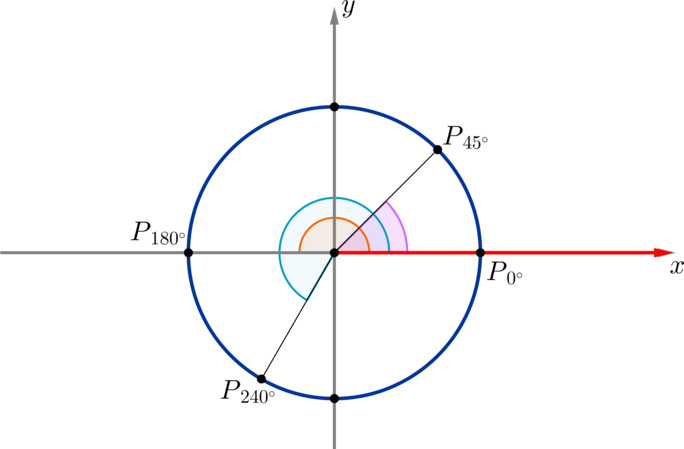
(blacktriangleright) Будем рассматривать на окружности такие углы, у которых вершина находится в центре окружности, а одна сторона всегда совпадает с положительным направлением оси (Ox) (на рисунке выделено красным).
На рисунке таким образом отмечены углы (45^circ, 180^circ,
240^circ):

Заметим, что угол (0^circ) — это угол, обе стороны которого совпадают с положительным направлением оси (Ox).

Точку, в которой вторая сторона такого угла (alpha) пересекает окружность, будет называть (P_{alpha}).
Положение точки (P_{0}) будем называть начальным положением.

Таким образом, можно сказать, что мы совершаем поворот по окружности из начального положения (P_0) до положения (P_{alpha}) на угол (alpha).

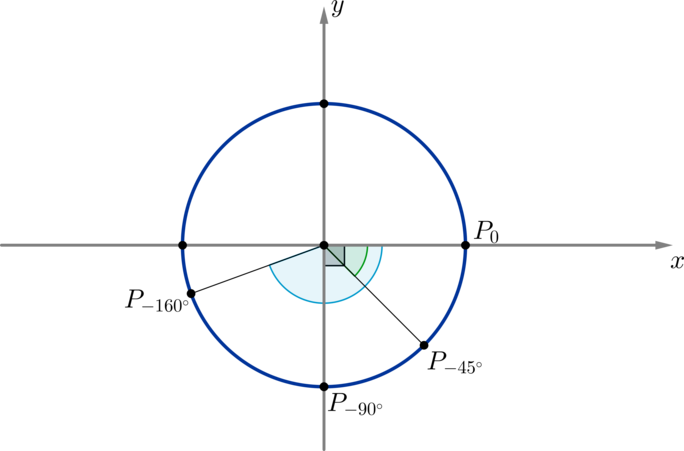
(blacktriangleright) Поворот по окружности против часовой стрелки — это поворот на положительный угол. Поворот по часовой стрелке — это поворот на отрицательный угол.

Например, на рисунке отмечены углы (-45^circ, -90^circ,
-160^circ):

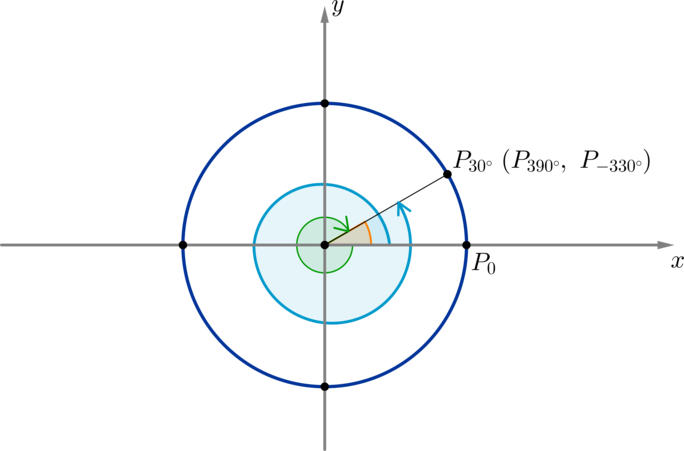
(blacktriangleright) Рассмотрим точку (P_{30^circ}) на окружности. Для того, чтобы совершить поворот по окружности из начального положения до точки (P_{30^circ}), необходимо совершить поворот на угол (30^circ) (оранжевый). Если мы совершим полный оборот (то есть на (360^circ)) и еще поворот на (30^circ), то мы снова попадем в эту точку, хотя уже был совершен поворот на угол (390^circ=360^circ+30^circ) (голубой). Также попасть в эту точку мы можем, совершив поворот на (-330^circ) (зеленый), на (750^circ=360^circ+360^circ+30^circ) и т.д.

Таким образом, каждой точке на окружности соответствует бесконечное множество углов, причем отличаются эти углы друг от друга на целое число полных оборотов ((ncdot360^circ, ninmathbb{Z})).
Например, угол (30^circ) на (360^circ) больше, чем угол (-330^circ), и на (2cdot 360^circ) меньше, чем угол (750^circ).

Все углы, находящиеся в точке (P_{30^circ}) можно записать в виде: (alpha=30^circ+ncdot 360^circ, ninmathbb{Z}).

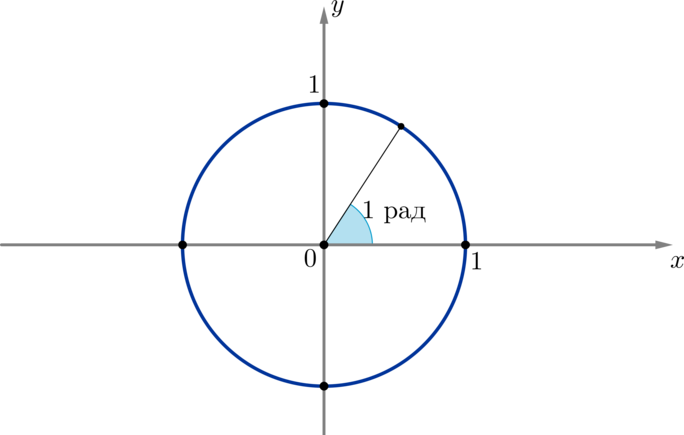
(blacktriangleright) Угол в (1) радиан — это такой центральный угол, который опирается на дугу, длина которой равна радиусу окружности:

Т.к. длина всей окружности радиусом (R) равна (2pi R), а в градусной мере — (360^circ), то имеем (360^circ=2pi cdot
1textbf{ рад}), откуда [180^circ=pi textbf{ рад}] Это основная формула, с помощью которой можно переводить градусы в радианы и наоборот.

Пример 1. Найти радианную меру угла (60^circ).

Т.к. (180^circ = pi Rightarrow 1^circ = dfrac{pi}{180}
Rightarrow 60^circ=dfrac{pi}3)

Пример 2. Найти градусную меру угла (dfrac34 pi).

Т.к. (pi=180^circ Rightarrow dfrac34 pi=dfrac34 cdot
180^circ=135^circ).

Обычно пишут, например, не (dfrac{pi}4 text{ рад}), а просто (dfrac{pi}4) (т.е. единицу измерения “рад” опускают). Обратим внимание, что обозначение градуса при записи угла не опускают. Таким образом, под записью “угол равен (1)” понимают, что “угол равен (1) радиану”, а не “угол равен (1) градусу”.

Т.к. (pi thickapprox 3,14 Rightarrow 180^circ thickapprox 3,14
textbf{ рад} Rightarrow 1 textbf{ рад} thickapprox 57^circ).
Такую приблизительную подстановку делать в задачах нельзя, но знание того, чему приближенно равен (1) радиан в градусах часто помогает при решении некоторых задач. Например, таким образом проще найти на окружности угол в (5) радиан: он примерно равен (285^circ).

(blacktriangleright) Из курса планиметрии (геометрии на плоскости) мы знаем, что для углов (0<alpha< 90^circ) определены синус, косинус, тангенс и котангенс следующим образом:
если дан прямоугольный треугольник со сторонами (a, b, c) и углом (alpha), то:

Т.к. на единичной окружности определены любые углы (alphain(-infty;+infty)), то нужно определить синус, косинус, тангенс и котангенс для любого угла.
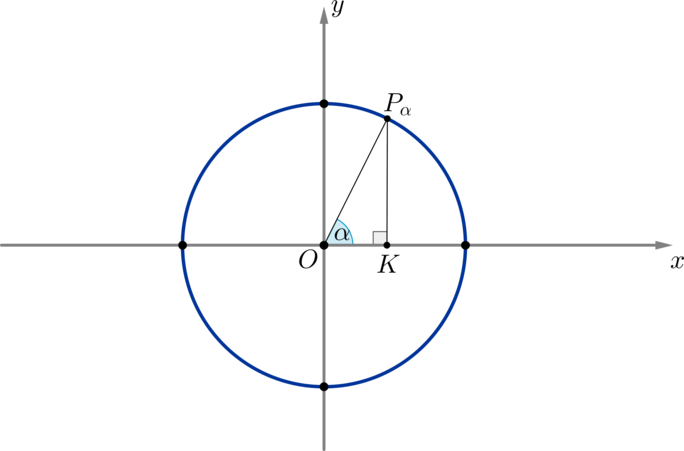
Рассмотрим единичную окружность и на ней угол (alpha) и соответствующую ему точку (P_{alpha}):

Опустим перпендикуляр (P_{alpha}K) из точки (P_{alpha}) на ось (Ox). Мы получим прямоугольный треугольник (triangle OP_{alpha}K), из которого имеем: [sinalpha=dfrac{P_{alpha}K}{P_{alpha}O} qquad cos alpha=dfrac{OK}{P_{alpha}O}] Заметим, что отрезок (OK) есть не что иное, как абсцисса (x_{alpha}) точки (P_{alpha}), а отрезок (P_{alpha}K) — ордината (y_{alpha}). Заметим также, что т.к. мы брали единичную окружность, то (P_{alpha}O=1) — ее радиус.
Таким образом, [sinalpha=y_{alpha}, qquad cos alpha=x_{alpha}]

Таким образом, если точка (P_{alpha}) имела координаты ((x_{alpha},;y_{alpha})), то через соответствующий ей угол ее координаты можно переписать как ((cosalpha,;sinalpha)).

Определение: 1. Синусом угла (alpha) называется ордината точки (P_{alpha}), соответствующей этому углу, на единичной окружности.

2. Косинусом угла (alpha) называется абсцисса точки (P_{alpha}), соответствующей этому углу, на единичной окружности.

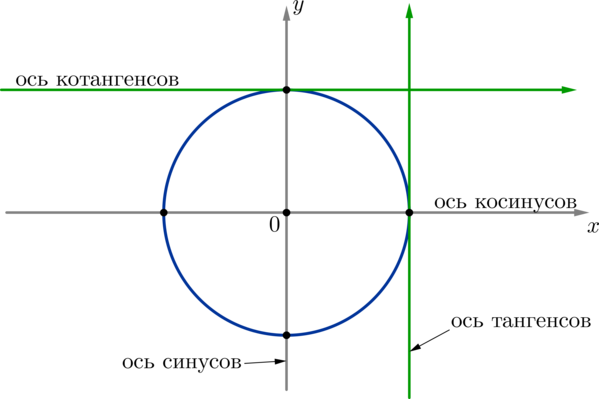
Поэтому ось (Oy) называют осью синусов, ось (Ox) — осью косинусов.

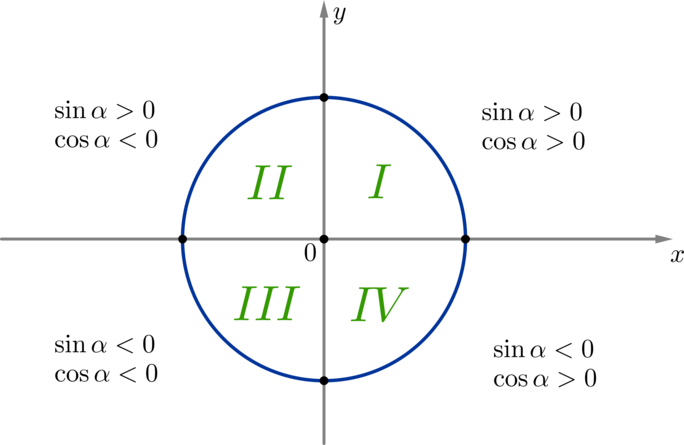
(blacktriangleright) Окружность можно разбить на (4) четверти, как показано на рисунке.

Т.к. в (I) четверти и абсциссы, и ординаты всех точек положительны, то косинусы и синусы всех углов из этой четверти также положительны.
Т.к. во (II) четверти ординаты всех точек положительны, а абсциссы — отрицательны, то косинусы всех углов из этой четверти — отрицательны, синусы — положительны.
Аналогично можно определить знак синуса и косинуса для оставшихся четвертей.

Пример 3. Так как, например, точки (P_{frac{pi}{6}}) и (P_{-frac{11pi}6}) совпадают, то их координаты равны, т.е. (sindfrac{pi}6=sin left(-dfrac{11pi}6right), cos
dfrac{pi}6=cos
left(-dfrac{11pi}6right)).

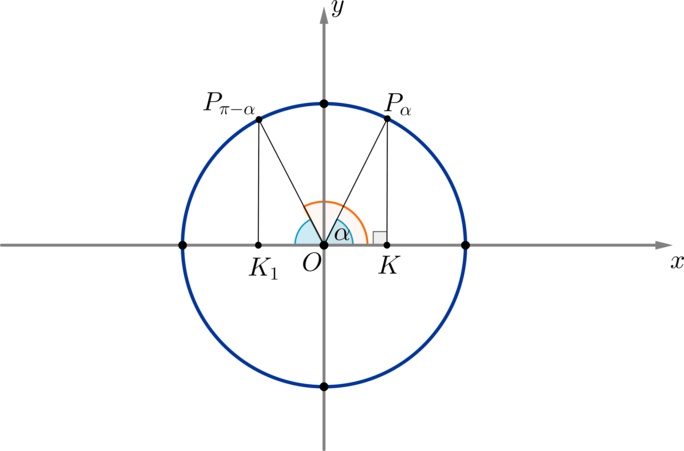
Пример 4. Рассмотрим точки (P_{alpha}) и (P_{pi-alpha}). Пусть для удобства (0<alpha<dfrac{pi}2).

Проведем перпендикуляры на ось (Ox): (OK) и (OK_1). Треугольники (OKP_{alpha}) и (OK_1P_{pi-alpha}) равны по гипотенузе и углу ((angle P_{alpha}OK=angle P_{pi-alpha}OK_1=alpha)).

Следовательно, (OK=OK_1, KP_{alpha}=K_1P_{pi-alpha}).

Т.к. координаты точки (P_{alpha}=(OK;KP_{alpha})=(cosalpha,;sinalpha)), а точки (P_{pi-alpha}=(-OK_1;K_1P_{pi-alpha})=(cos(pi-alpha),;sin(pi-alpha))), следовательно, [cos(pi-alpha)=-cosalpha, qquad sin(pi-alpha)=sinalpha]

Таким образом доказываются и другие формулы, называемые формулами приведения: [{large{begin{array}{l|r}
hline sin(pi-alpha)=sinalpha &
cos(pi-alpha)=-cosalpha\[2ex]
sin(pi+alpha)=-sinalpha &
cos(pi+alpha)=-cosalpha\[2ex]
sin(2pipmalpha)=pmsinalpha & cos
(2pipmalpha)=cosalpha\[2ex]
sin left(dfrac{pi}2pmalpharight)=cosalpha &
cosleft(dfrac{pi}2pmalpharight)=pmsinalpha\[2ex]
hline
end{array}}}]

С помощью этих формул можно найти синус или косинус любого угла, сведя это значение к синусу или косинусу угла из (I) четверти.

Таблица синусов, косинусов, тангенсов и котангенсов углов из первой четверти:
[{large{begin{array}{|c|c|c|c|c|c|}
hline &&&&&\[-17pt]
& quad 0 quad (0^ circ)& quad dfrac{pi}6 quad (30^circ)
& quad dfrac{pi}4
quad (45^circ) & quad dfrac{pi}3 quad (60^circ)& quad dfrac{pi}2 quad
(90^circ) \
&&&&&\[-17pt]
hline sin & 0 &frac12&frac{sqrt2}2&frac{sqrt3}2&1\[4pt]
hline cos &1&frac{sqrt3}2&frac{sqrt2}2&frac12&0\[4pt]
hline mathrm{tg} &0 &frac{sqrt3}3&1&sqrt3&infty\[4pt]
hline mathrm{ctg} &infty &sqrt3&1&frac{sqrt3}3&0\[4pt]
hline
end{array}}}]

Заметим, что данные значения были выведены в разделе “Геометрия на плоскости (планиметрия). Часть II” в теме “Начальные сведения о синусе, косинусе, тангенсе и котангенсе”.

Пример 5. Найдите (sin{dfrac{3pi}4}).

Преобразуем угол: (dfrac{3pi}4=dfrac{4pi-pi}{4}=pi-dfrac{pi}4)

Таким образом, (sin{dfrac{3pi}4}=sinleft(pi-dfrac{pi}4right)=sindfrac{pi}4=dfrac{sqrt2}2).

(blacktriangleright) Для упрощения запоминания и использования формул приведения можно следовать следующему правилу.

Случай 1. Если угол можно представить в виде (ncdot pipm
alpha), где (ninmathbb{N}), то [sin(ncdot pipm
alpha)=bigodot sinalpha] где на месте (bigodot) стоит знак синуса угла (ncdot pipm alpha). [cos(ncdot pipm
alpha)=bigodot cosalpha] где на месте (bigodot) стоит знак косинуса угла (ncdot pipm alpha).

Знак угла можно найти, определив, в какой четверти он находится. Пользуясь таким правилом, предполагаем, что угол (alpha) находится в (I) четверти.

Случай 2. Если угол можно представить в виде (ncdot
pi+dfrac{pi}2pmalpha), где (ninmathbb{N}), то [sin(ncdot pi+dfrac{pi}2pm
alpha)=bigodot cosalpha] где на месте (bigodot) стоит знак синуса угла (ncdot pipm alpha). [cos(ncdot pi+dfrac{pi}2pm
alpha)=bigodot sinalpha] где на месте (bigodot) стоит знак косинуса угла (ncdot pipm alpha).

Знак определяется таким же образом, как и в случае (1).

Заметим, что в первом случае функция остается неизменной, а во втором случае — меняется (говорят, что функция меняется на кофункцию).

Пример 6. Найти (sin dfrac{13pi}{3}).

Преобразуем угол: (dfrac{13pi}{3}=dfrac{12pi+pi}{3}=4pi+dfrac{pi}3), следовательно, (sin dfrac{13pi}{3}=sin
left(4pi+dfrac{pi}3right)=sindfrac{pi}3=dfrac{sqrt3}2)

Пример 7. Найти (cos dfrac{17pi}{6}).

Преобразуем угол: (dfrac{17pi}{6}=dfrac{18pi-pi}{6}=3pi-dfrac{pi}6), следовательно, (cos dfrac{17pi}{6}=cos
left(3pi-dfrac{pi}6right)=-cosdfrac{pi}6=-dfrac{sqrt3}2)

(blacktriangleright) Область значений синуса и косинуса.
Т.к. координаты (x_{alpha}) и (y_{alpha}) любой точки (P_{alpha}) на единичной окружности находятся в пределах от (-1) до (1), а (cosalpha) и (sinalpha) — абсцисса и ордината соответственно этой точки, то [{large{-1leq cosalphaleq 1 ,qquad -1leqsinalphaleq 1}}]

Из прямоугольного треугольника по теореме Пифагора имеем: (x^2_{alpha}+y^2_{alpha}=1^2)
Т.к. (x_{alpha}=cosalpha, y_{alpha}=sinalpha Rightarrow) [{large{sin^2alpha+cos^2alpha=1}} — textbf{основное тригонометрическое тождество (ОТТ)}]

(blacktriangleright) Тангенс и котангенс.

Т.к. (mathrm{tg},alpha=dfrac{sinalpha}{cosalpha}, cosalphane 0)

(mathrm{ctg},alpha=dfrac{cosalpha}{sinalpha}, sinalphane 0), то:

1) ({large{mathrm{tg},alphacdot mathrm{ctg},alpha=1, cosalphane 0, sinalpha ne 0}})

2) тангенс и котангенс положительны в (I) и (III) четвертях и отрицательны в (II) и (IV) четвертях.

3) область значений тангенса и котангенса — все вещественные числа, т.е. (mathrm{tg},alphainmathbb{R},
mathrm{ctg},alphainmathbb{R})

4) для тангенса и котангенса также определены формулы приведения.

Случай 1. Если угол можно представить в виде (ncdot pipm
alpha), где (ninmathbb{N}), то [mathrm{tg},(ncdot pipm
alpha)=bigodot mathrm{tg},alpha] где на месте (bigodot) стоит знак тангенса угла (ncdot pipm alpha) ((cosalphane 0)). [mathrm{ctg},(ncdot pipm
alpha)=bigodot mathrm{ctg},alpha] где на месте (bigodot) стоит знак котангенса угла (ncdot pipm alpha) ((sinalphane 0)).

Случай 2. Если угол можно представить в виде (ncdot
pi+dfrac{pi}2pmalpha), где (ninmathbb{N}), то [mathrm{tg},(ncdot pi+dfrac{pi}2pm
alpha)=bigodot mathrm{ctg},alpha] где на месте (bigodot) стоит знак тангенса угла (ncdot pipm alpha) ((sinalphane 0)). [mathrm{ctg},(ncdot pi+dfrac{pi}2pm
alpha)=bigodot mathrm{tg},alpha] где на месте (bigodot) стоит знак котангенса угла (ncdot pipm alpha) ((cosalphane 0)).

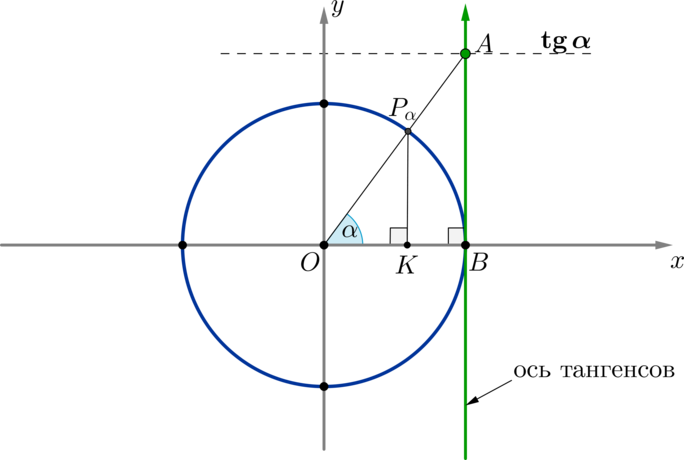
5) ось тангенсов проходит через точку ((1;0)) параллельно оси синусов, причем положительное направление оси тангенсов совпадает с положительным направлением оси синусов;
ось котангенсов — через точку ((0;1)) параллельно оси косинусов, причем положительное направление оси котангенсов совпадает с положительным направлением оси косинусов.

Доказательство этого факта приведем на примере оси тангенсов.

(triangle OP_{alpha}K sim triangle AOB Rightarrow
dfrac{P_{alpha}K}{OK}=dfrac{BA}{OB} Rightarrow
dfrac{sinalpha}{cosalpha}=dfrac{BA}1 Rightarrow
BA=mathrm{tg},alpha).

Таким образом, если точку (P_{alpha}) соединить прямой с центром окружности, то эта прямая пересечет линию тангенсов в точке, значение которой равно (mathrm{tg},alpha).

6) из основного тригонометрического тождества вытекают следующие формулы: [1+mathrm{tg},^2alpha=dfrac1{cos^2alpha},cosalphane 0 qquad qquad 1+mathrm{ctg},^2alpha=dfrac1{sin^2alpha}, sinalphane 0] Первую формулу получают делением правой и левой частей ОТТ на (cos^2alpha), вторую — делением на (sin^2alpha).

Обращаем внимание, что тангенс не определен в углах, где косинус равен нулю (это (alpha=dfrac{pi}2+pi n, ninmathbb{Z}));
котангенс не определен в углах, где синус равен нулю (это (alpha=pi+pi n, ninmathbb{Z})).

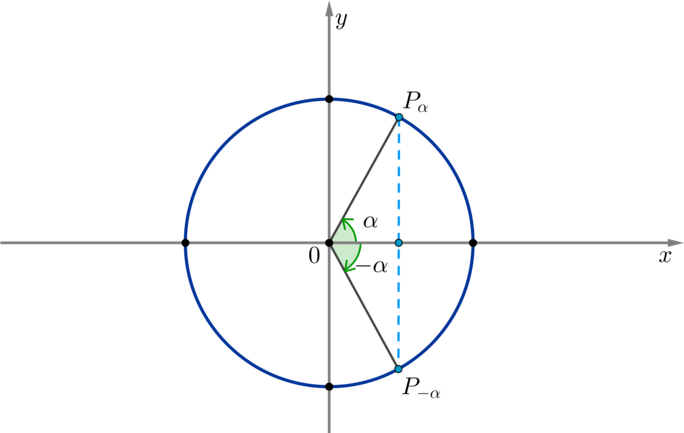
(blacktriangleright) Четность косинуса и нечетность синуса, тангенса, котангенса.

Напомним, что функция (f(x)) называется четной, если (f(-x)=f(x)).

Функция называется нечетной, если (f(-x)=-f(x)).

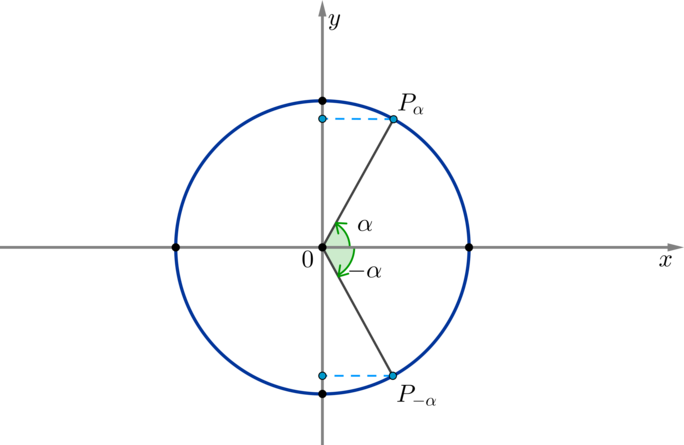
По окружности видно, что косинус угла (alpha) равен косинусу угла (-alpha) при любых значениях (alpha):

Таким образом, косинус — четная функция, значит, верна формула [{Large{cos(-x)=cos x}}]

По окружности видно, что синус угла (alpha) противоположен синусу угла (-alpha) при любых значениях (alpha):

Таким образом, синус — нечетная функция, значит, верна формула [{Large{sin(-x)=-sin x}}]

Тангенс и котангенс также нечетные функции: [{Large{mathrm{tg},(-x)=-mathrm{tg},x}}] [{Large{mathrm{ctg},(-x)=-mathrm{ctg},x}}]

Т.к. (mathrm{tg},(-x)=dfrac{sin (-x)}{cos(-x)}=dfrac{-sin
x}{cos x}=-mathrm{tg},x qquad mathrm{ctg},(-x)=dfrac{cos(-x)}{sin(-x)}=-mathrm{ctg},x))

Источник

На странице вы найдете все формулы тригонометрии в удобном для использования оформлении. Формулы структурированы в блоки по количеству аргументов, степеням, арифметическим операциям над ними.

Содержание:

Основные тригонометрические тождества
Формулы двойного угла
Формулы тройного угла
Формулы понижения степени
1. Вторая степень
2. Третья степень
3. Четвертая степень
4. Пятая степень
Формулы половинного угла
Формулы понижения степени половинного угла
Формулы сложения аргументов
Формулы вычитания аргументов
Формулы суммы
Формулы разности
Формулы произведения
Формулы произведения в степени
Все формулы на одном листе

Все формулы тригонометрии

Основные тригонометрические тождества

tg alpha = dfrac {sin alpha}{ cos alpha} = dfrac{1}{ctg alpha}

ctg alpha = dfrac {cos alpha}{ sin alpha} = dfrac{1}{tg alpha}

sin ^2 alpha + cos ^2 alpha = 1

1+tg^2alpha=dfrac{1}{cos^2alpha}

1+ctg^2alpha=dfrac{1}{sin^2alpha}

tgalpha cdot ctgalpha=1

Формулы двойного угла (аргумента)

sin(2alpha)=2 cdot cos alpha cdot sin alpha

sin(2alpha)=dfrac{2 cdot tg alpha}{1+tg ^2 alpha}=dfrac{2 cdot ctg alpha}{1+ctg ^2 alpha}=dfrac{2}{tg alpha + ctg alpha}

cos(2alpha)=cos ^2 alpha- sin ^2 alpha = 2 cdot cos ^2 alpha- 1 = 1- 2 cdot sin ^2 alpha

cos(2alpha)=dfrac{1 -tg ^2 alpha}{1+tg ^2 alpha}=dfrac{ctg ^2 alpha- 1}{ctg ^2 alpha +1}=dfrac{ctg alpha-tg alpha}{ctg alpha + tg alpha}

tg(2alpha) = dfrac{2 cdot tg alpha}{1-tg ^2 alpha}=dfrac{2 cdot ctg alpha}{ctg ^2 alpha- 1}=dfrac{2}{ctg alpha- tg alpha}

ctg(2alpha) = dfrac{ctg ^2 alpha-1}{2 cdot ctg alpha}=dfrac{ctg alpha- tg alpha}{2}

Формулы тройного угла (аргумента)

sin(3alpha)=3 cdot sin alpha- 4 cdot sin ^3 alpha

cos(3alpha)= 4 cdot cos ^3 alpha- 3 cdot cos alpha

tg(3alpha)= dfrac{3 cdot tg alpha- tg ^3 alpha}{1-3 cdot tg ^2 alpha}

ctg(3alpha)= dfrac{ctg ^3 alpha- 3 cdot ctg alpha}{3 cdot ctg ^2 alpha -1}

Формулы понижения степени тригонометрических функций

Вторая степень

sin ^2 alpha = dfrac{1-cos(2alpha)}{2}

cos ^2 alpha = dfrac{1+cos(2alpha)}{2}

tg ^2 alpha = dfrac{1-cos(2alpha)}{1+cos(2alpha)}

ctg ^2 alpha = dfrac{1+cos(2alpha)}{1-cos(2alpha)}

(sin alpha- cos alpha)^2=1-sin(2 alpha)

(sin alpha+ cos alpha)^2=1+sin(2 alpha)

Третья степень

sin ^3 alpha = dfrac{3 cdot sin(alpha)-sin(3 alpha)}{4}

cos ^3 alpha = dfrac{3 cdot cos(alpha)+cos(3 alpha)}{4}

tg ^3 alpha = dfrac{3 cdot sin (alpha)-sin(3 alpha)}{3 cdot cos (alpha)+cos(3 alpha)}

ctg ^3 alpha = dfrac{3 cdot cos (alpha)+cos(3 alpha)}{3 cdot sin (alpha)-sin(3 alpha)}

Четвёртая степень

sin ^4 alpha = dfrac{3-4 cdot cos(2 alpha)+cos(4 alpha)}{8}

cos ^4 alpha = dfrac{3+4 cdot cos(2 alpha)+cos(4 alpha)}{8}

Пятая степень

sin ^5 alpha = dfrac{10 cdot sin(alpha)-5 cdot sin(3 alpha)+sin(5 alpha)}{16}

cos ^5 alpha = dfrac{10 cdot cos(alpha)+5 cdot cos(3 alpha)+cos(5 alpha)}{16}

Формулы половинного угла (аргумента)

sin Big( dfrac{alpha}{2} Big)=pm sqrt{dfrac{1-cos alpha}{2}}

cos Big( dfrac{alpha}{2} Big)=pm sqrt{dfrac{1+cos alpha}{2}}

tg Big( dfrac{alpha}{2} Big)= dfrac{1-cos alpha}{sin alpha}= dfrac{sin alpha}{1+cos alpha}

ctg Big( dfrac{alpha}{2} Big)= dfrac{1+cos alpha}{sin alpha}= dfrac{sin alpha}{1-cos alpha}

Формулы понижения степени половинного угла (аргумента)

sin ^2 Big( dfrac{alpha}{2} Big)=dfrac{1-cos alpha}{2}

cos ^2 Big( dfrac{alpha}{2} Big)=dfrac{1+cos alpha}{2}

tg ^2 Big( dfrac{alpha}{2} Big)=dfrac{1-cos alpha}{1+cos alpha}

ctg ^2 Big( dfrac{alpha}{2} Big)=dfrac{1+cos alpha}{1-cos alpha}

Формулы сложения аргументов

sin(alpha + beta)=sin alpha cdot cos beta + cos alpha cdot sin beta

cos(alpha + beta)=cos alpha cdot cos beta- sin alpha cdot sin beta

tg(alpha + beta)= dfrac{tg alpha + tg beta}{1-tg alpha cdot tg beta}

ctg(alpha + beta)= dfrac{ctg alpha cdot ctg beta-1}{ctg alpha + ctg beta}

Формулы вычитания аргументов

sin(alpha- beta)=sin alpha cdot cos beta- cos alpha cdot sin beta

cos(alpha- beta)=cos alpha cdot cos beta+ sin alpha cdot sin beta

tg(alpha- beta)= dfrac{tg alpha- tg beta}{1+tg alpha cdot tg beta}

ctg(alpha- beta)= dfrac{ctg alpha cdot ctg beta+1}{ctg beta — ctg alpha}

Формулы суммы тригонометрических функций

sin alpha+ sin beta=2 cdot sin big( dfrac{alpha + beta}{2} big) cdot cos big( dfrac{alpha- beta}{2} big)

cos alpha+ cos beta=2 cdot cos big( dfrac{alpha + beta}{2} big) cdot cos big( dfrac{alpha- beta}{2} big)

tg alpha + tg beta = dfrac{sin(alpha + beta)}{cos alpha cdot cos beta}

ctg alpha + ctg beta = dfrac{sin(alpha + beta)}{cos alpha cdot cos beta}

sin (alpha)+cos(alpha)=sqrt{2} cdot sin Big( alpha+ dfrac{pi}{4} Big)

Формулы разности тригонометрических функций

sin alpha- sin beta=2 cdot sin big( dfrac{alpha- beta}{2} big) cdot cos big( dfrac{alpha+ beta}{2} big)

cos alpha- cos beta=-2 cdot sin big( dfrac{alpha + beta}{2} big) cdot sin big( dfrac{alpha- beta}{2} big)

tg alpha- tg beta = dfrac{sin(alpha- beta)}{cos alpha cdot cos beta}

ctg alpha- ctg beta = dfrac{sin(alpha + beta)}{sin alpha cdot sin beta}

sin (alpha)-cos(alpha)=sqrt{2} cdot sin Big( alpha- dfrac{pi}{4} Big)

Формулы произведения тригонометрических функций

sin alpha cdot sin beta = dfrac{cos (alpha- beta)-cos(alpha + beta)}{2}

sin alpha cdot cos beta = dfrac{sin (alpha- beta)+sin(alpha + beta)}{2}

cos alpha cdot cos beta = dfrac{cos (alpha- beta)+cos(alpha + beta)}{2}

tg alpha cdot tg beta = dfrac{cos(alpha- beta)- cos(alpha+beta)}{cos(alpha- beta)+ cos(alpha+beta)}=dfrac{tg alpha + tg beta}{ctg alpha + ctg beta}

ctg alpha cdot ctg beta = dfrac{cos(alpha- beta)+ cos(alpha+beta)}{cos(alpha- beta)- cos(alpha+beta)}=dfrac{ctg alpha + ctg beta}{tg alpha + tg beta}

tg alpha cdot ctg beta = dfrac{sin(alpha- beta)+ sin(alpha+beta)}{sin(alpha+ beta)- sin(alpha-beta)}

Формулы произведения тригонометрических функций в степени

sin ^2 (alpha) cdot cos ^2 (alpha) = dfrac{1-cos(4 alpha)}{8}

sin ^3 (alpha) cdot cos ^3 (alpha) = dfrac{3 cdot sin(2 alpha)- sin(6 alpha)}{32}

sin ^4 (alpha) cdot cos ^4 (alpha) = dfrac{3-4 cdot cos(4 alpha)+ cos(8 alpha)}{128}

sin ^5 (alpha) cdot cos ^5 (alpha) = dfrac{10 cdot sin (2 alpha)-5 cdot sin(6 alpha)+sin (10 alpha)}{512}

Все формулы тригонометрии на одном листе

На этой картинке собраны все формулы тригонометрии для печати. Лист можно распечатать и использовать при решении задач ЕГЭ или вырезать таблицы и использовать как шпаргалку. Распечатанный лист можно применять как справочный материал при решении задач по тригонометрии в 10 и 11 классе.

Источник