Шпаргалка стереометрия математика профиль егэ

8 декабря 2019

В закладки

Обсудить

Жалоба

Шпаргалка по стереометрии

Краткие пояснения и алгоритмы по стереометрии.

В 8 и 14 заданиях проверяют знания стереометрии: умение разбираться с геометрическими фигурами, координатами и векторами.

Многие не решают это задание из-за того, что пугает его сложность. Но на самом деле это одно из простых заданий, на которых можно получить 14 баллов. Достаточно знать последовательность действий.

shpargalka_po_stereometrii.pdf

Источник: vk.com/hsege

Алгебра — ЕГЭ                Тригонометрия — ЕГЭ                Геометрия — ЕГЭ                Стереометрия — ЕГЭ                Алгебра — ОГЭ                Геометрия — ОГЭ

Шпаргалка по стереометрии для ЕГЭ

Формулы по стереометрии для ЕГЭ

Советская шпора по стереометрии

Площадь поверхности, объем, радиусы вписанной и описанной сфер

Формулы для многогранников

Формулы для пирамиды

Формулы для тел вращения

Лучшие шпаргалки по математике. Качественно. Ничего лишнего.

Просто кликните по картинке. Подробно — в разделе «Решение задач ЕГЭ по математике».

---

 Самое популярное. Тригонометрия и площади фигур

 Геометрия на ЕГЭ по математике. Треугольники, четырехугольники, окружности.

 Стереометрия: формулы объема и площади поверхности.

 Классическая стереометрия и метод координат

 Алгебра

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

1.Ве­ро­ят­ность того, что в слу­чай­ный мо­мент вре­ме­ни тем­пе­ра­ту­ра тела здо­ро­во­го че­ло­ве­ка ока­жет­ся ниже чем 36,8 °С, равна 0,81. Най­ди­те ве­ро­ят­ность того, что в слу­чай­ный мо­мент вре­ме­ни у здо­ро­во­го че­ло­ве­ка тем­пе­ра­ту­ра ока­жет­ся 36,8 °С или выше.

1 − 0,81 = 0,19.

2.Ве­ро­ят­ность того, что новый элек­три­че­ский чай­ник про­слу­жит боль­ше года, равна 0,97. Ве­ро­ят­ность того, что он про­слу­жит боль­ше двух лет, равна 0,89. Най­ди­те ве­ро­ят­ность того, что он про­слу­жит мень­ше двух лет, но боль­ше года.

P(A) = 0,97 − 0,89 = 0,08.

3.По­ме­ще­ние осве­ща­ет­ся фонарём с двумя лам­па­ми. Ве­ро­ят­ность пе­ре­го­ра­ния лампы в те­че­ние года равна 0,3. Най­ди­те ве­ро­ят­ность того, что в те­че­ние года хотя бы одна лампа не пе­ре­го­рит.

0,3·0,3 = 0,09. 1 − 0,09 = 0,91.

4.В тор­го­вом цен­тре два оди­на­ко­вых ав­то­ма­та про­да­ют кофе. Ве­ро­ят­ность того, что к концу дня в ав­то­ма­те за­кон­чит­ся кофе, равна 0,3. Ве­ро­ят­ность того, что кофе за­кон­чит­ся в обоих ав­то­ма­тах, равна 0,12. Най­ди­те ве­ро­ят­ность того, что к концу дня кофе оста­нет­ся в обоих ав­то­ма­тах.

0,3 + 0,3 − 0,12 = 0,48. 1 − 0,48 = 0,52.

5.При ар­тил­ле­рий­ской стрель­бе ав­то­ма­ти­че­ская си­сте­ма де­ла­ет вы­стрел по цели. Если цель не уни­что­же­на, то си­сте­ма де­ла­ет по­втор­ный вы­стрел. Вы­стре­лы по­вто­ря­ют­ся до тех пор, пока цель не будет уни­что­же­на. Ве­ро­ят­ность уни­что­же­ния не­ко­то­рой цели при пер­вом вы­стре­ле равна 0,4, а при каж­дом по­сле­ду­ю­щем — 0,6. Сколь­ко вы­стре­лов по­тре­бу­ет­ся для того, чтобы ве­ро­ят­ность уни­что­же­ния цели была не менее 0,98?

Р(1) = 0,6. Р(2) = Р(1)·0,4 = 0,24.

Р(3) = Р(2)·0,4 = 0,096. Р(4) = Р(3)·0,4 = 0,0384;

Р(5) = Р(4)·0,4 = 0,01536.  

По­след­няя ве­ро­ят­ность мень­ше 0,02, по­это­му до­ста­точ­но пяти вы­стре­лов по ми­ше­ни.

6.Две фаб­ри­ки вы­пус­ка­ют оди­на­ко­вые стек­ла для ав­то­мо­биль­ных фар. Пер­вая фаб­ри­ка вы­пус­ка­ет 45% этих сте­кол, вто­рая — 55%. Пер­вая фаб­ри­ка вы­пус­ка­ет 3% бра­ко­ван­ных сте­кол, а вто­рая — 1%. Най­ди­те ве­ро­ят­ность того, что слу­чай­но куп­лен­ное в ма­га­зи­не стек­ло ока­жет­ся бра­ко­ван­ным.

0,45 · 0,03 = 0,0135. 0,55 · 0,01 = 0,0055.

0,0135 + 0,0055 = 0,019.

 7. В клас­се 26 че­ло­век, среди них два близ­не­ца — Ан­дрей и Сер­гей. Класс слу­чай­ным об­ра­зом делят на две груп­пы по 13 че­ло­век в каж­дой. Най­ди­те ве­ро­ят­ность того, что Ан­дрей и Сер­гей ока­жут­ся в одной груп­пе. Пусть один из близ­не­цов на­хо­дит­ся в не­ко­то­рой груп­пе. Вме­сте с ним в груп­пе ока­жут­ся 12 че­ло­век из 25 остав­ших­ся од­но­класс­ни­ков 12 : 25 = 0,48.

8.В Вол­шеб­ной стра­не бы­ва­ет два типа по­го­ды: хо­ро­шая и от­лич­ная, причём по­го­да, уста­но­вив­шись утром, дер­жит­ся не­из­мен­ной весь день. Из­вест­но, что с ве­ро­ят­но­стью 0,8 по­го­да зав­тра будет такой же, как и се­год­ня. Се­год­ня 3 июля, по­го­да в Вол­шеб­ной стра­не хо­ро­шая. Най­ди­те ве­ро­ят­ность того, что 6 июля в Вол­шеб­ной стра­не будет от­лич­ная по­го­да.

Ре­ше­ние.

Для по­го­ды на 4, 5 и 6 июля есть 4 ва­ри­ан­та: ХХО, ХОО, ОХО, ООО 

P(XXO) = 0,8·0,8·0,2 = 0,128;

P(XOO) = 0,8·0,2·0,8 = 0,128;

P(OXO) = 0,2·0,2·0,2 = 0,008;

P(OOO) = 0,2·0,8·0,8 = 0,128.

 P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392.

9.Ков­бой Джон по­па­да­ет в муху на стене с ве­ро­ят­но­стью 0,9, если стре­ля­ет из при­стре­лян­но­го ре­воль­ве­ра. Если Джон стре­ля­ет из не­при­стре­лян­но­го ре­воль­ве­ра, то он по­па­да­ет в муху с ве­ро­ят­но­стью 0,2. На столе лежит 10 ре­воль­ве­ров, из них толь­ко 4 при­стре­лян­ные. Ков­бой Джон видит на стене муху, на­уда­чу хва­та­ет пер­вый по­пав­ший­ся ре­воль­вер и стре­ля­ет в муху. Най­ди­те ве­ро­ят­ность того, что Джон про­махнётся.

Ре­ше­ние.

0,4·(1 − 0,9) = 0,04 и 0,6·(1 − 0,2) = 0,48. Эти со­бы­тия не­сов­мест­ны, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий: 0,04 + 0,48 = 0,52.

10.Аг­ро­фир­ма за­ку­па­ет ку­ри­ные яйца в двух до­маш­них хо­зяй­ствах. 40% яиц из пер­во­го хо­зяй­ства — яйца выс­шей ка­те­го­рии, а из вто­ро­го хо­зяй­ства — 20% яиц выс­шей ка­те­го­рии. Всего выс­шую ка­те­го­рию по­лу­ча­ет 35% яиц. Най­ди­те ве­ро­ят­ность того, что яйцо, куп­лен­ное у этой аг­ро­фир­мы, ока­жет­ся из пер­во­го хо­зяй­ства.

Ответ 0,75

11. Стре­лок стре­ля­ет по ми­ше­ни один раз. В слу­чае про­ма­ха стре­лок де­ла­ет вто­рой вы­стрел по той же ми­ше­ни. Ве­ро­ят­ность по­пасть в ми­шень при одном вы­стре­ле равна 0,7. Най­ди­те ве­ро­ят­ность того, что ми­шень будет по­ра­же­на (либо пер­вым, либо вто­рым вы­стре­лом).

0,7+(1-0,7) ·0,7=0,91

12.Чтобы по­сту­пить в ин­сти­тут на спе­ци­аль­ность «Линг­ви­сти­ка», аби­ту­ри­ент дол­жен на­брать на ЕГЭ не менее 70 бал­лов по каж­до­му из трёх пред­ме­тов — ма­те­ма­ти­ка, рус­ский язык и ино­стран­ный язык. Чтобы по­сту­пить на спе­ци­аль­ность «Ком­мер­ция», нужно на­брать не менее 70 бал­лов по каж­до­му из трёх пред­ме­тов — ма­те­ма­ти­ка, рус­ский язык и об­ще­ст­во­зна­ние.

Ве­ро­ят­ность того, что аби­ту­ри­ент З. по­лу­чит не менее 70 бал­лов по ма­те­ма­ти­ке, равна 0,6, по рус­ско­му языку — 0,8, по ино­стран­но­му языку — 0,7 и по об­ще­ст­во­зна­нию — 0,5.

Най­ди­те ве­ро­ят­ность того, что З. смо­жет по­сту­пить хотя бы на одну из двух упо­мя­ну­тых спе­ци­аль­но­стей.

0,6·0,8·(1 –(1-0,7)(1-0,5)) =0,48·(1-0,3·0,5)=0,408

13. На фаб­ри­ке ке­ра­ми­че­ской по­су­ды 10% про­из­ведённых та­ре­лок имеют де­фект. При кон­тро­ле ка­че­ства про­дук­ции вы­яв­ля­ет­ся 80% де­фект­ных та­ре­лок. Осталь­ные та­рел­ки по­сту­па­ют в про­да­жу. Най­ди­те ве­ро­ят­ность того, что слу­чай­но вы­бран­ная при по­куп­ке та­рел­ка не имеет де­фек­тов. Ре­зуль­тат округ­ли­те до сотых.

0,1·0,8=0,08, 1-0,08=0,92 0,9 : 0,92=0,98

14.Всем па­ци­ен­там с по­до­зре­ни­ем на ге­па­тит де­ла­ют ана­лиз крови. Если ана­лиз вы­яв­ля­ет ге­па­тит, то ре­зуль­тат ана­ли­за на­зы­ва­ет­ся по­ло­жи­тель­ным. У боль­ных ге­па­ти­том па­ци­ен­тов ана­лиз даёт по­ло­жи­тель­ный ре­зуль­тат с ве­ро­ят­но­стью 0,9. Если па­ци­ент не болен ге­па­ти­том, то ана­лиз может дать лож­ный по­ло­жи­тель­ный ре­зуль­тат с ве­ро­ят­но­стью 0,01. Из­вест­но, что 5% па­ци­ен­тов, по­сту­па­ю­щих с по­до­зре­ни­ем на ге­па­тит, дей­стви­тель­но боль­ны ге­па­ти­том. Най­ди­те ве­ро­ят­ность того, что ре­зуль­тат ана­ли­за у па­ци­ен­та, по­сту­пив­ше­го в кли­ни­ку с по­до­зре­ни­ем на ге­па­тит, будет по­ло­жи­тель­ным.

0,05·0,9+0,95·0,01 =0,0545

15. У Вити в ко­пил­ке лежит 12 рублёвых, 6 двух­рублёвых, 4 пя­ти­рублёвых и 3 де­ся­ти­рублёвых мо­не­ты. Витя на­у­гад достаёт из ко­пил­ки одну мо­не­ту. Най­ди­те ве­ро­ят­ность того, что остав­ша­я­ся в ко­пил­ке сумма со­ста­вит более 70 руб­лей.

Ре­ше­ние.

У Вити в ко­пил­ке лежит 12 + 6 + 4 + 3 = 25 монет на сумму 12 + 12 + 20 + 30 = 74 рубля. Боль­ше 70 руб­лей оста­нет­ся, если до­стать из ко­пил­ки либо рублёвую, либо двух­рублёвую мо­не­ту. Ис­ко­мая ве­ро­ят­ность равна 18 : 25 = 0,72.

16.В кар­ма­не у Пети было 2 мо­не­ты по 5 руб­лей и 4 мо­не­ты по 10 руб­лей. Петя, не глядя, пе­ре­ло­жил какие-то 3 мо­не­ты в дру­гой кар­ман. Най­ди­те ве­ро­ят­ность того, что пя­ти­руб­ле­вые мо­не­ты лежат те­перь в раз­ных кар­ма­нах. Всего 6 монет. Ве­ро­ят­ность того, что Петя взял пя­ти­руб­ле­вую мо­не­ту, затем де­ся­ти­руб­ле­вую, и затем еще одну де­ся­ти­руб­ле­вую (в ука­зан­ном по­ряд­ке) равна 2/6·4/5·3/4=0,2  По­сколь­ку Петя мог до­стать пя­ти­руб­ле­вую мо­не­ту не толь­ко пер­вой, но и вто­рой или тре­тьей, ве­ро­ят­ность до­стать набор из одной пя­ти­руб­ле­вой и двух де­ся­ти­руб­ле­вых монет в 3 раза боль­ше. Тем самым, она равна 0,6.

17. За круг­лый стол на 101 сту­л в слу­чай­ном по­ряд­ке рас­са­жи­ва­ют­ся 99 маль­чи­ков и 2 де­воч­ки. Най­ди­те ве­ро­ят­ность того, что между двумя де­воч­ка­ми будет си­деть один маль­чик.

Ре­ше­ние.

Пусть пер­вой за стол сядет де­воч­ка, тогда для каж­до­го из остав­ших­ся ребят (в том числе и для вто­рой де­воч­ки ) ве­ро­ят­ность ока­зать­ся на любом из остав­ших­ся сту­льев равна 0,01 . А мест, удо­вле­тво­ря­ю­щих усло­вию за­да­чи, толь­ко два. Таким об­ра­зом ве­ро­ят­ность, что между двумя де­воч­ка­ми будет си­деть один маль­чик равна 2·0,01 = 0,02

18. За круг­лый стол на 17 сту­льев в слу­чай­ном по­ряд­ке рас­са­жи­ва­ют­ся 15 маль­чи­ков и 2 де­воч­ки. Най­ди­те ве­ро­ят­ность того, что обе де­воч­ки будут си­деть рядом. 

Ре­ше­ние.

Пусть пер­вой за стол сядет де­воч­ка, тогда рядом с ней есть два места, на каж­дое из ко­то­рых пре­тен­ду­ет 16 че­ло­ве­ка, из ко­то­рых толь­ко одна де­воч­ка. Таким об­ра­зом, ве­ро­ят­ность, что де­воч­ки будут си­деть рядом равна 2·1/16 =1/8 =0,125

Не будут сидеть рядом 1-0,125=0,875

19. Про паука.

Формулы стереометрии. Общий обзор!

Категория: Формулы Теория | ЕГЭ-№2Формулы

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

Параллельность в пространстве

• Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.
• Если две прямые на плоскости перпендикулярны к третьей прямой, то они параллельны.
• Если две прямые в трехмерном пространстве перпендикулярны к одной плоскости, то они параллельны.
• Если прямая a, не лежащая в плоскости $α$, параллельна некоторой прямой $b$, которая лежит в плоскости $α$, то прямая a параллельна плоскости $α$.
• Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.

Перпендикулярность в пространстве

• Две прямые называются перпендикулярными, если угол между ними равен $90°$.
• Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
• Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то заданные плоскости перпендикулярны.
• Теорема о трех перпендикулярах: если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и самой наклонной.
• Если из одной точки проведены к плоскости перпендикуляр и наклонные, то:

1. Перпендикуляр короче наклонных.
2. Равные наклонные имеют равные проекции на плоскости.
3. Большей наклонной соответствует большая проекция на плоскости.

Скрещивающиеся прямые

• Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.
• Через две скрещивающиеся прямые проходит единственная пара параллельных плоскостей.
• Расстояние между скрещивающимися прямыми – это расстояние от некоторой точки одной из скрещивающихся прямых до плоскости, проходящей через другую прямую параллельно первой прямой.
• Угол между скрещивающимися прямыми – это острый угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым.

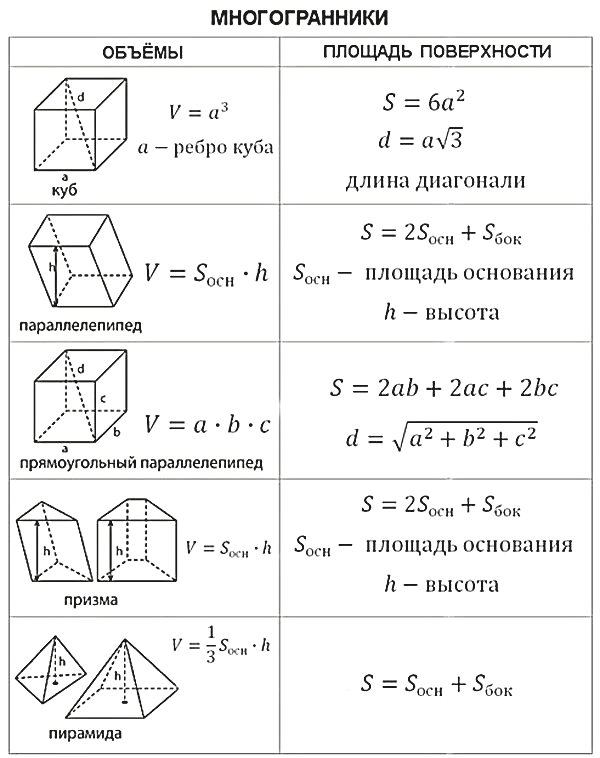
Многогранники

Введем общие обозначения

$P_{осн}$ — периметр основания;

$S_{осн}$ — площадь основания;

$S_{бок}$ — площадь боковой поверхности;

$S_{п.п}$ — площадь полной поверхности;

$V$ — объем фигуры.

Название	Определение и свойства фигуры	Обозначения и формулы объема, площади
Прямоугольный параллелепипед	1. Все двугранные углы прямоугольного параллелепипеда – прямые. 2. Противоположные грани попарно равны и параллельны. 3. Диагонали прямоугольного параллелепипеда равны. 4. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты). $B_1D^2=AD^2+DC^2+C_1C^2$	$V=a·b·c$, где $a, b$ и $с$ – длина, ширина и высота. $S_{бок}=P_{осн}·c=2(a+b)·c$ $S_{п.п}=2(ab+bc+ac)$.
Куб	1. Противоположные грани попарно параллельны. 2. Все двугранные углы куба – прямые. 3. Диагональ куба в $√3$ раз больше его ребра. $B_1 D=АВ√3$ 4. Диагональ грани куба в $√2$ раза больше длины ребра. $DС1=DC√2$	Пусть $а$ — длина ребра куба, $d$ — диагональ куба, тогда справедливы формулы: $V=a^3={d^3}/{3√3}$. $S_{п.п}=6а^2=2d^2$ $R={a√3}/{2}$, где $R$ — радиус сферы, описанной около куба. $r={a}/{2}$, где $r$ — радиус сферы, вписанной в куб.
Призма	Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов. Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру. Прямая призма называется правильной, если ее основания – правильные многоугольники. В правильной четырехугольной призме диагонали точкой пересечения делятся пополам.	$S_{бок}=P_{осн}·h$ $S_{п.п}=S_{бок}+2S_{осн}$ $V=S_{осн}·h$
Пирамида	У треугольной пирамиды есть еще одно название – тетраэдр (четырехгранник). Пирамида называется правильной, если в ее основании лежит правильный многоугольник, а ее высота приходит в центр основания (в центр описанной окружности). Все боковые ребра правильной пирамиды равны, следовательно, все боковые грани являются равнобедренными треугольниками.	Формулы вычисления объема и площади поверхности правильной пирамиды. $h_a$ — высота боковой грани (апофема) $S_{бок}={P_{осн}·h_a}/{2}$ $S_{п.п}=S_{бок}+S_{осн}$ $V={1}/{3} S_{осн}·h$
Усеченная пирамида	Усеченной пирамидой называется многогранник, заключенный между пирамидой и секущей плоскостью, параллельной. Правильная усечённая пирамида получается при сечении правильной пирамиды плоскостью, параллельной основанию. У правильной усеченной пирамиды апофемы равны	$V={h(F+f+√{Ff})}/{3}$ Где $F,f$ — площади оснований; $h$ — высота (расстояние между основаниями); Для правильной ус. пирамиды $S_{бок}={(P+p)·a}/{2}$, где $P$ и $p$ – периметры оснований; $а$ – апофема.
Цилиндр	Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра. Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра. Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра. Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра. $R_{сферы}=R_{цилиндра}={h_{цилиндра}}/{2}$	$S_{бок.пов.}=2πR·h$ $S_{полной.пов.}=2πR(R+h)$ $V=πR^2·h$
Конус	Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса. Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$. Если радиус или диаметр конуса увеличить в $n$ раз, то его объем увеличится в $n^2$ раз. Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.	$S_{бок.пов.}=πR·l$ $S_{полной.пов.}=πR^2+πR·l=πR(R+l)$ $V={πR^2·h}/{3}$
Усеченный конус	Усеченным конусом называется часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию. Осевым сечением усеченного конуса является равнобедренная трапеция.	$S_{бок}=πl(R+r)$ $S_{п.п.}=π(R^2+r^2+l(R+r))$ $V={πH(R^2+r^2+Rr)}/{3}$ Где $R$ и $r$ – радиусы оснований; $Н$ — высота усеченного конуса.
Сфера, шар	Тело, ограниченное сферой, называется шаром. Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара. Если радиус или диаметр шара увеличить в $n$ раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.	$S_{п.п}=4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ — радиус шара, $d$ — диаметр шара.

Тетраэдр

Радиус описанной сферы тетраэдра.

Вокруг тетраэдра можно описать сферу, радиус которой находим по формуле, где $R$ — радиус описанной сферы, $a$ — ребро тетраэдра.

$R={a√6}/{4}$

Радиус вписанной в тетраэдр сферы.

В тетраэдр можно вписать сферу, радиус вписанной сферы находим по формуле, приведенной ниже.

Где $r$ — радиус вписанной в тетраэдр сферы,

$a$ — ребро тетраэдра.

$r={a√6}/{12}$

Составные многогранники

Задачи на нахождение объема составного многогранника:

1. Разделить составной многогранник на несколько параллелепипедов.
2. Найти объем каждого параллелепипеда.
3. Сложить объемы.

Задачи на нахождение площади поверхности составного многогранника.

— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:

$S_{полн.пов.}=P_{осн}·h+2S_{осн}$

Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.

— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

Задачи на нахождение расстояния между точками составного многогранника.

В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.

Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Связь между сторонами правильного n-угольника и радиусами описанной и вписанной окружностей

$АВ=a_n$ — сторона правильного многоугольника

$R$ — радиус описанной окружности

$r$ — радиус вписанной окружности

$n$ — количество сторон и углов

$a_n=2·R·sin{180°}/{n}$;

$r=R·cos{180°}/{n}$;

$a_n=2·r·tg{180°}/{n}$.

Формула нахождения градусной меры угла в правильном многоугольнике:

$α={(n-2)·180°}/{n}$

Формулы площадей треугольников и многоугольников, которые могут находиться в основании многогранников

В основании лежит треугольник

1. $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне а

2. $S={a·b·sin⁡α}/{2}$, где $a, b$ — соседние стороны, $α$ — угол между этими соседними сторонами.

3. $S=p·r$, где $r$ — радиус вписанной окружности

4. $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности

5. Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.

В основании лежит четырехугольник

Прямоугольник

$S=a·b$, где $а$ и $b$ — смежные стороны.

Ромб

$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба

$S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.

Трапеция

$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.

Площади правильных многоугольников:

1. Для равностороннего треугольника $S={a^{2}√3}/{4}$, где $а$ — длина стороны.

2. Квадрат

$S=a^2$, где $а$ — сторона квадрата.

3. Правильный шестиугольник

Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:

$S=6·S_{треугольника}={6·a^{2}√3}/{4}={3·a^{2}√3}/{2}$, где $а$ — сторона правильного шестиугольника.

---

Подборка по базе: Тестовые вопросы к Разделу 5. Стереометрия_ просмотр попытки.pdf, 2 сабақ_ Стереометрия_10 сынып_Түзу мен жазықтықтың перпендикуля, Геометрия 10 сынып Бөлім Стереометрия аксиомалары Тақырыбы Екі т, Геометрия 10 сынып Бөлім Стереометрия аксиомалары Тақырыбы Кеңіс, Тестовые вопросы к Разделу 5. Стереометрия.docx, Лекция 4 Стереометрия.doc

---