10 июля 2022
В закладки
Обсудить
Жалоба
Шпаргалка по задачам профильного ЕГЭ по математике
Сжатая информация по всем задачам профильного ЕГЭ по математике.
Часть 1
Все ответы к заданиям 1-11 по условиям экзамена даются в виде целого числа или десятичной дроби.
sh-m1.pdf
Часть 2
Для успешного решения заданий второй части нужно знать весь материал, относящийся к первой части плюс факты, перечисленные ниже.
Желательно уметь всё это доказывать!
sh-m2.pdf
Автор: Андрей Павликов.
Источник: vk.com/lomonosov_math
- ЕГЭ по математике профиль
Для профильной математики на ЕГЭ в компактном виде для распечатки на принтере.
→ скачать docx
→ скачать pdf
Включены основные формулы:
— по алгебре (Формулы сокращенного умножения, Арифметическая прогрессия, Делимость натуральных чисел, Правила вычисления первообразной функции и т.д.)
— основные тригонометрические формулы (Формулы суммы функций, Формулы суммы аргументов, Формулы произведения функций, Формулы половинного аргумента и т.д.)
— по геометрии (Теорема косинусов, синусов; Конус; Длина окружности, площадь; Основные соотношения в треугольнике и т.д.)
Связанные страницы:
От Мои ответы и задания 18 июня, 2020 Сборники ЕГЭ и ОГЭ
Полезная шпаргалка для 11 класса по математике профильный уровень ЕГЭ. Справочные материалы и все формулы для решения заданий. Можно взять на ЕГЭ, чтобы было легче решать задания на экзамене.
Ссылка для скачивания шпаргалки ЕГЭ: скачать в формате PDF
Шпаргалка ЕГЭ по математике профильный уровень онлайн:
Смотрите также на нашем сайте полезные материалы:
МА1900201-МА1900212 статград математика 10 класс ответы и задания 6 февраля 2020
29 января 2020 ответы и задания по математике 11 класс статград МА1910301-МА1910312
Метки: ЕГЭматематика 11 классшпаргалка
- 09.09.2012
Подборка шпаргалок по МАТЕМАТИКЕ.
Дата обновления: 01.11.2022
Полный набор теоретического материала для подготовки к ЕГЭ по математике — профильной и базовой. Таблицы, схемы, формулы, вся теория по заданимя. Всё, что необходимо для самостоятельной работы по математике.
- Тренировочные варианты ЕГЭ по профильной математике
- Тренировочные варианты по базовой математике
Что содержите в себе сборник шпаргалок по математике
- Числа, степени, модуль
- Уравнения, углы, прямые
- Справочные материалы по тригонометрии
- Решение текстовых задач
- Производная и первообразная
- Шпаргалка для экономических задач
- Шпоры по тригонометрии
- Шпаргалки по математике в картинках
Для чтения шпаргалок необходимы бесплатные программы: WinDJView и Adobe Reader
СКАЧАТЬ
https://down.ctege.info/ege/obshee/shpory/matem-ege-shpora.zip
Лучшие шпаргалки по математике. Качественно. Ничего лишнего.
Просто кликните по картинке. Подробно — в разделе «Решение задач ЕГЭ по математике».
Самое популярное. Тригонометрия и площади фигур
Тригонометрический круг
Синус, косинус, тангенс…
Формулы тригонометрии
Геометрия. Площади фигур
Геометрия на ЕГЭ по математике. Треугольники, четырехугольники, окружности.
Высоты, медианы, биссектрисы
Параллелограмм, ромб, квадрат и их свойства
Касательная к окружности
Центральные и вписанные углы
Стереометрия: формулы объема и площади поверхности.
Вписанные и описанные треугольники
Вписанные и описанные четырехугольники
Стереометрия: Формулы объема и площади поверхности.
Чертежи в задачах по стереометрии
Классическая стереометрия и метод координат
Основы стереометрии. Часть 1.
Основы стереометрии. Часть 2.
Стереометрия: Векторы и координаты.
Как расположить прямоугольную систему координат
Алгебра
Таблица производных.
Преобразования графиков функций. Задача С5.
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Лучшие шпаргалки по математике. Качественно. Ничего лишнего.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Основные формулы и свойства на одном листе
Вернуться назад на сайт »
- ЕГЭ по математике профиль
ФИПИ опубликовал Методические рекомендации обучающимся по организации индивидуальной подготовки к ЕГЭ 2022 по математике профильного уровня.
В них приведены тренировочные задания новых типов, ответы на задания и критерии оценивания.
Линия 9 – задания повышенного уровня сложности с кратким ответом интегрированного характера, для выполнения которых необходимо привлекать знания из разных разделов курса математики: элементарные функции; решение линейных, квадратных, иррациональных, рациональных, логарифмических, показательных уравнений и их систем.
→ Новое задание 9 ЕГЭ 2022 по математике
Связанные страницы:
Решение заданий варианта досрочного периода ЕГЭ 2022 от 28 марта 2022 по математике (профильный уровень). Досрочник КИМ. Досрочная волна 2022. Полный разбор. ГДЗ профиль решебник для 11 класса. Ответы с решением.

Задание 1.
Найдите корень уравнения log2(7 – x) = 5.
Задание 2.
В чемпионате по гимнастике участвуют 4 спортсменки из Аргентины, 7 из Бразилии, 5 из Германии и 4 из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Бразилии.
ИЛИ
В чемпионате по гимнастике участвуют 70 спортсменок: 25 из США, 17 из Мексики, остальные из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.
Задание 3.
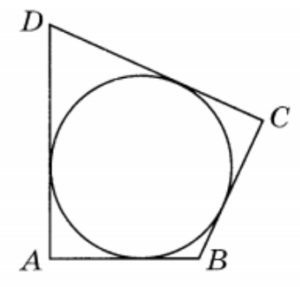
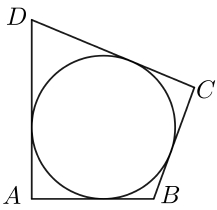
В четырёхугольник ABCD вписана окружность, AB = 8, BC = 5 и CD = 27. Найдите четвёртую сторону четырёхугольника.
ИЛИ
В четырехугольник ABCD, периметр которого равен 56, вписана окружность. Найдите AB, если CD = 13.
Задание 4.
Найдите значение выражения 4^{frac{1}{5}}cdot 16^{frac{9}{10}}
ИЛИ
Найдите значение выражения frac{5^{3,7}cdot 6^{4,7}}{30^{2,7}}
Задание 5.
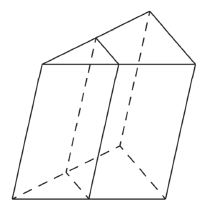
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
ИЛИ
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 37. Найдите площадь боковой поверхности исходной призмы.
Задание 6.
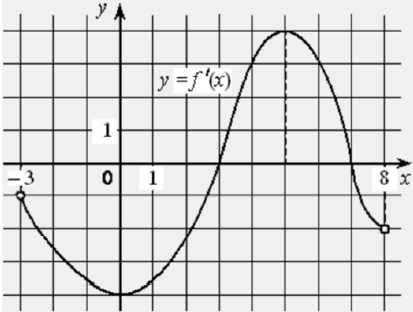
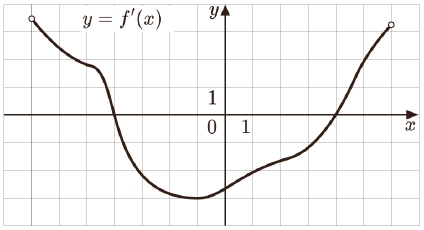
На рисунке изображён график функции y = f ′(x) − производной функции f(x), определённой на интервале (−3; 8). Найдите точку максимума функции f(x).
ИЛИ
На рисунке изображён график y = f ′(x) – производной функции f(x), определённой на интервале (−7; 6). Найдите точку минимума функции f(x).
Задание 7.
При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу со скоростями u и v (в м/с) соответственно, частота звукового сигнала f (в Гц), регистрируемого приёмником, вычисляется по формуле: , где f0 = 170 Гц – частота исходного сигнала, c – скорость распространения сигнала в среде (в м/с), а u = 2 м/с и v = 17 м/с – скорости приёмника и источника относительно среды. При какой скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет равна 180 Гц? Ответ дайте в м/с.
ИЛИ
В розетку электросети подключены приборы, общее сопротивление которых составляет R1 = 90 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R2 этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R1 Ом и R2 Ом их общее сопротивление дается формулой Rобщ = (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в Омах.
Задание 8.
Имеется два сплава. Первый содержит 50% никеля, второй – 15% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
ИЛИ
Имеется два сплава. Первый сплав содержит 5 % меди, второй – 14 % меди. Масса второго сплава больше массы первого на 5 кг. Из этих двух сплавов получили третий сплав, содержащий 12 % меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Задание 9.
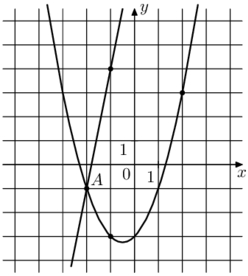
На рисунке изображён график функции f(x) = 5x + 9 и g(x) = ax2 + bx + c, которые пересекаются в точках А и В. Найдите абсциссу точки В.
ИЛИ
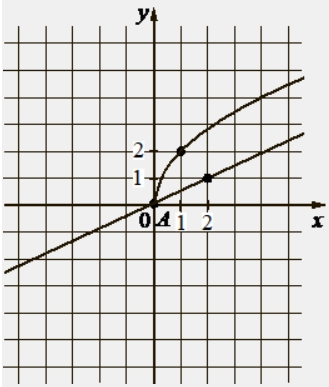
На рисунке изображены графики функций видов f(x) = a√x и g(x) = kx, пересекающиеся в точках A и B. Найдите абсциссу точки B.
Задание 10.
Помещение освещается тремя лампами. Вероятность перегорания каждой лампы в течение года равна 0,3. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
ИЛИ
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Задание 11.
Найдите точку минимума функции y = x√x – 5x + 4.
Задание 12.
а) Решите уравнение 4sin x + 4sin(x + π) = frac{5}{2}.
б) Найдите все корни этого уравнения, принадлежащие отрезку [frac{5pi}{2};4pi].
Задание 13.
Вне плоскости правильного треугольника ABC взята точка D так, что cos∠DAB = cos∠DAC = 0, 2.
а) Докажите, что прямые AD и BC перпендикулярны.
б) Найдите расстояние между прямыми AD и BC, если известно, что AB = 2.
Задание 14.
Решите неравенство frac{log_{2}^{}(32x)-1}{log_{2}^{2}x-log_{2}^{}x^{5}}ge -1
Задание 15.
15-го декабря планируется взять кредит размером 600 тыс. рублей в банке на 26 месяцев. Условия возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца с 1-го по 25-й долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца;
– к 15-му числу 26-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 25-го месяца, если общая сумма выплат после полного погашения кредита составит 691 тысяч рублей?
Задание 16.
В треугольник ABC вписана окружность, которая касается AB в точке P. Точка М середина стороны AB.
а) Докажите, что MP=frac{|BC-AC|}{2}.
б) Найдите углы треугольника ABC, если известно, что отрезок MP равен половине радиуса окружности вписанной в треугольник ABC, BC > AC, отрезки MC и MA равны.
Задание 17.
Найдите всe значения параметра a, при каждом их которых система
begin{cases} frac{xy^{2}-2xy-4y+8}{sqrt{4-y}}=0, y=ax. end{cases}
имеет ровно 3 различных решения.
Задание 18.
Каждое из четырех последовательных натуральных чисел поделили на его первую цифру и сложили все полученные числа, а полученную сумму обозначили за S.
а) Может ли S = 41frac{11}{24}?
б) Может ли S = 569frac{29}{72}?
в) Какое наибольшее целое значение может принимать S, если известно, что 4 исходных числа не меньше 400 и не больше 999?
Источники заданий варианта: школа Пифагора, Профиматика, беседы vk.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 12
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Формулы сокращённого умножения
Арифметическая и геометрическая прогрессии
Вероятность
Свойства степеней
Свойства логарифмов
Тригонометрия
Производные
Первообразные
Геометрия
Формулы сокращённого умножения
| `(a + b)^2=a^2 + 2ab + b^2` | |
| `(a − b)^2=a^2 − 2ab + b^2` | |
| `a^2 − b^2=(a + b)(a − b)` | |
| `a^3 + b^3=(a + b)(a^2 − ab + b^2)` | |
| `a^3 − b^3=(a − b)(a^2 + ab + b^2)` | |
| `(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3` | |
| `(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3` |
Прогрессии
Арифметическая прогрессия:
| `a_n=a_(n-1)+d` |
| `a_n=a_1+(n-1)*d` |
| `S_n=((a_1+a_n)*n)/2` |
Геометрическая прогрессия:
| `b_n=b_(n-1)*q` |
| `b_n=b_1*q^(n-1)` |
| `S_n=((q^n-1)*b_1)/(q-1)` |
| Бесконечно убывающая: `S=b_1/(1-q)` |
Вероятность
| Вероятность события A: | `P(A)=m/n` | |
| События происходят A и B происходят одновременно | `A*B` | |
| Независимые события: | `P(A*B)=P(A)*P(B)` | |
| Зависимые события: | `P(A*B)=P(A)*P(B|A)` | |
| Происходит или событие A, или B | `A+B` | |
| Несовместные события: | `P(A+B)=P(A)+P(B)` | |
| Совместные события: | `P(A+B)=P(A)+P(B)-P(A*B)` |
Свойства степеней
| `a^0=1` | `a^1=a` |
| `a^(-1)=1/a` | `a^(-n)=1/a^n` |
| `a^(1/2)=sqrt(a)` | `a^(1/n)=root(n)(a)` |
| `a^m*a^n=a^(m+n)` | `a^m/a^n=a^(m-n)` |
| `(a*b)^n=a^n*b^n` | `(a/b)^n=a^n/b^n` |
| `(a^m)^n=a^(m*n)` | `a^(m/n)=root(n)(a^m)` |
Свойства логарифмов
| `log_ab=c``a^c=b` | |
| `log_a1=0` | |
| `log_aa=1` | |
| `log_a(b*c)=log_ab+log_ac` | |
| `log_a(b/c)=log_ab-log_ac` | |
| `log_ab^n=n*log_ab` | |
| `log_(a^m)b=1/m*log_ab` | |
| `log_ab=1/(log_ba)` | |
| `log_ab=(log_cb)/(log_ca)` | |
| `a^(log_cb)=b^(log_ca)` | |
| `a^(log_ab)=b` |
Тригонометрия
| `alpha` | `0` | `pi/6` | `pi/4` | `pi/3` | `pi/2` | `pi` | `(3pi)/2` | `2pi` |
|---|---|---|---|---|---|---|---|---|
| `0^circ` | `30^circ` | `45^circ` | `60^circ` | `90^circ` | `180^circ` | `270^circ` | `360^circ` | |
| `sinalpha` | `0` | `1/2` | `sqrt(2)/2` | `sqrt(3)/2` | `1` | `0` | `-1` | `0` |
| `cosalpha` | `1` | `sqrt(3)/2` | `sqrt(2)/2` | `1/2` | `0` | `-1` | `0` | `1` |
| `text(tg)alpha` | `0` | `sqrt(3)/3` | `1` | `sqrt(3)` | `infty` | `0` | `infty` | `0` |
| `text(ctg)alpha` | `infty` | `sqrt(3)` | `1` | `sqrt(3)/3` | `0` | `infty` | `0` | `infty` |
Основные соотношения
| `sin^2alpha+cos^2alpha=1` | |
| `text(tg)alpha=sinalpha/cosalpha=1/(text(ctg)alpha)` |
Формулы двойного угла
| `cos2alpha={(cos^2alpha-sin^2alpha),(1-2sin^2alpha),(2cos^2alpha-1):}` | |
| `sin2alpha=2sinalphacosalpha` | |
| `text(tg)2alpha=(2text(tg)alpha)/(1-text(tg)^2alpha)` |
Формулы суммы и разности аргументов
| `sin(alpha+-beta)=sinalphacosbeta+-cosalphasinbeta` |
| `cos(alpha+-beta)=cosalphacosbeta∓sinalphasinbeta` |
| `text(tg)(alpha+-beta)=(text(tg)alpha+-text(tg)beta)/(1∓text(tg)alpha*text(tg)beta)` |
Преобразование суммы и разности в произведение
| `sinalpha+-sinbeta=2sin((alpha+-beta)/2)cos((alpha∓beta)/2)` |
| `cosalpha+cosbeta=2cos((alpha+beta)/2)cos((alpha-beta)/2)` |
| `cosalpha-cosbeta=-2sin((alpha+beta)/2)sin((alpha-beta)/2)` |
Формулы половинного аргумента
| `sin(alpha/2)=+-sqrt((1-cosalpha)/2)` | |
| `cos(alpha/2)=+-sqrt((1+cosalpha)/2)` | |
| `text(tg)(alpha/2)=+-sqrt((1-cosalpha)/(1+cosalpha))=(1-cosalpha)/sinalpha=sinalpha/(1+cosalpha)` |
Обратные тригонометрические функции
| `sinx=A` | `x=(-1)^k*arcsinA + pik` или `{(x=arcsinA + 2pik),(x=pi-arcsinA+2pik):}` |
`kinZZ` |
| `cosx=A` | `x=±arccosA + 2pik` | `kinZZ` |
| `tg x=A` | `x=text(arctg) A + pik` | `kinZZ` |
| `ctg x=A` | `x=text(arcctg) A + pik` | `kinZZ` |
Также некоторые тригонометрические соотношения смотрите в разделе Геометрия.
Производные
Основные правила дифференцирования
| `(u+-v)’=u’+-v’` | |
| `(u*v)’=u’*v+u*v’` | |
| `(u/v)^’=(u’*v-u*v’)/v^2` | |
| `[f(g(x))]’=f'(g(x))*g'(x)` |
Уравнение касательной
| `y=f(x_0)+f'(x_0)*(x-x_0)` |
Производные элементарных функций
| `C’=0` | `(C*x)’=C` | |
| `(x^m)’=mx^(m-1)` | `(sqrtx)’=1/(2sqrtx)` | |
| `(1/x)^’=-1/x^2` | ||
| `(e^x)’=e^x` | `(lnx)’=1/x` | |
| `(a^x)’=a^x*lna` | `(log_ax)’=1/(xlna)` | |
| `(sinx)’=cosx` | `(cosx)’=-sinx` | |
| `(text(tg)x)’=1/cos^2x` | `(text(ctg)x)’=-1/sin^2x` | |
| `(arcsinx)’=1/sqrt(1-x^2)` | `(arccosx)’=-1/sqrt(1-x^2)` | |
| `(text(arctg))=1/(1+x^2)’` | `(text(arcctg))’=-1/(1+x^2)` |
Также некоторые сведения про производные смотрите в описании задач
№14 (база), №7 (профиль), №12 (профиль).
Первообразные
| Первообразная: | `F'(x)=f(x)` | |||
| Неопределённый интеграл: | `intf(x)dx=F(x)+C` | |||
| Определённый интеграл (формула Ньютона-Лейбница): | `int_a^bf(x)dx=F(b)-F(a)` |
Таблица первообразных
| `f(x)` | `F(x)` | `f(x)` | `F(x)` | |
|---|---|---|---|---|
| `a` | `ax` | |||
| `x^n` | `x^(n+1)/(n+1)` | `1/x` | `lnx` | |
| `e^x` | `e^x` | `a^x` | `a^x/lna` | |
| `sinx` | `-cosx` | `cosx` | `sinx` | |
| `1/cos^2x` | `text(tg)x` | `1/sin^2x` | `-text(ctg)x` | |
| `1/(x^2+a^2)` | `1/atext(arctg)x/a` | `1/(x^2-a^2)` | `1/(2a)ln|(x-a)/(x+a)|` | |
| `1/sqrt(a^2-x^2)` | `text(arcsin)x/a` | `1/sqrt(x^2+a)` | `ln|x+sqrt(x^2+a)|` |
Геометрия
Планиметрия (2D)
Площади фигур:
| Окружность: | `S=pir^2` | |
| Треугольник: | `S=1/2ah` | |
| Параллелограмм: | `S=ah` | |
| Четырёхугольник: | `S=1/2d_1d_2sinvarphi` | |
| Трапеция: | `S=(a+b)/2*h` |
Стереометрия (3D)
| Призма: | `V=S_(осн)h` | |
| Пирамида: | `V=1/3S_(осн)h` | |
| Конус: | `V=1/3S_(осн)h` | |
| `S_(бок)=pirl` | ||
| Цилиндр: | `V=pir^2h` | |
| `S_(бок)=2pirh` | ||
| Шар: | `V=4/3pir^3` | |
| `S=4pir^2` |
Программа экзамена, как и в прошлые годы, составлена из материалов основных математических дисциплин. В билетах будут присутствовать и математические, и геометрические, и алгебраические задачи.
Изменений в КИМ ЕГЭ 2022 по математике профильного уровня нет.
Особенности заданий ЕГЭ по математике-2022
- Осуществляя подготовку к ЕГЭ по математике (профильной), обратите внимание на основные требования экзаменационной программы. Она призвана проверить знания углубленной программы: векторные и математические модели, функции и логарифмы, алгебраические уравнения и неравенства.
- Отдельно потренируйтесь решать задания по теории вероятности.
- Важно проявить нестандартность мышления.
Структура экзамена
Задания ЕГЭ профильной математики разделены на два блока.
- Часть — краткие ответы, включает 8 задач, проверяющих базовую математическую подготовку и умение применять знания по математике в повседневности.
- Часть — краткие и развернутые ответы. Состоит из 11 задач, 4 из которых требуют короткого ответа, и 7 – развернутого с аргументацией выполненных действий.
- Повышенной сложности — задания 9-17 второй части КИМа.
- Высокого уровня сложности — задачи 18-19 –. Эта часть экзаменационных заданий проверяет не только уровень математических знаний, но и наличие или отсутствие творческого подхода к решению сухих «циферных» заданий, а также эффективность умения использовать знания и навыки в качестве профессионального инструмента.
Важно! Поэтому при подготовке к ЕГЭ теорию по математике всегда подкрепляйте решением практических задач.
Как будут распределять баллы
Задания части первой КИМов по математике близки к тестам ЕГЭ базового уровня, поэтому высокого балла на них набрать невозможно.
Баллы за каждое задание по математике профильного уровня распределились так:
- за правильные ответы на задачи №1-12 – по 1 баллу;
- №13-15 – по 2;
- №16-17 – по 3;
- №18-19 – по 4.
Длительность экзамена и правила поведения на ЕГЭ
Для выполнения экзаменационной работы отведено 3 часа 55 минут (235 минут).
В это время ученик не должен:
- вести себя шумно;
- использовать гаджеты и другие технические средства;
- списывать;
- пытаться помогать другим, или просить помощи для себя.
За подобные действия экзаменующегося могут выдворить из аудитории.
На государственный экзамен по математике разрешено приносить с собой только линейку, остальные материалы вам выдадут непосредственно перед ЕГЭ. Справочные материалы выдаются на месте.
Эффективная подготовка — это решение онлайн тестов по математике 2022. Выбирай тренировочные задания и получай максимальный балл!