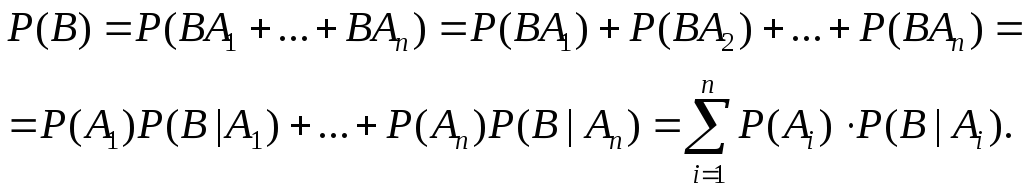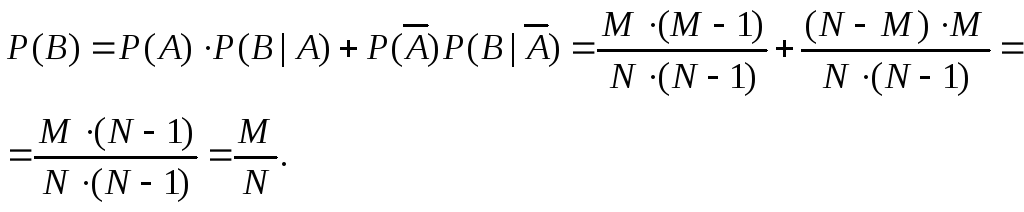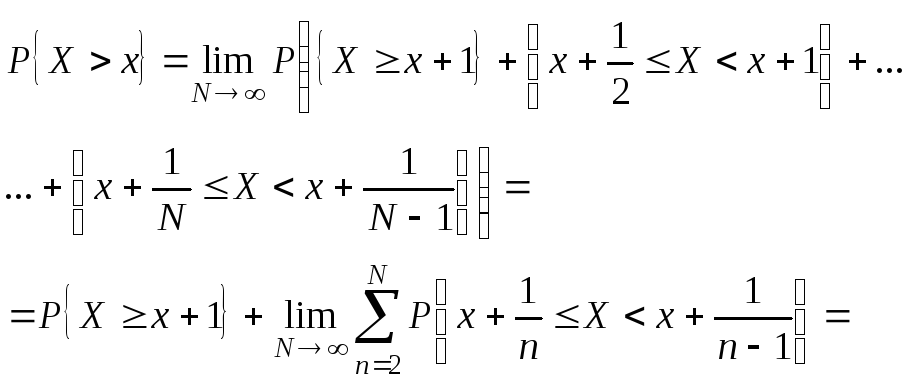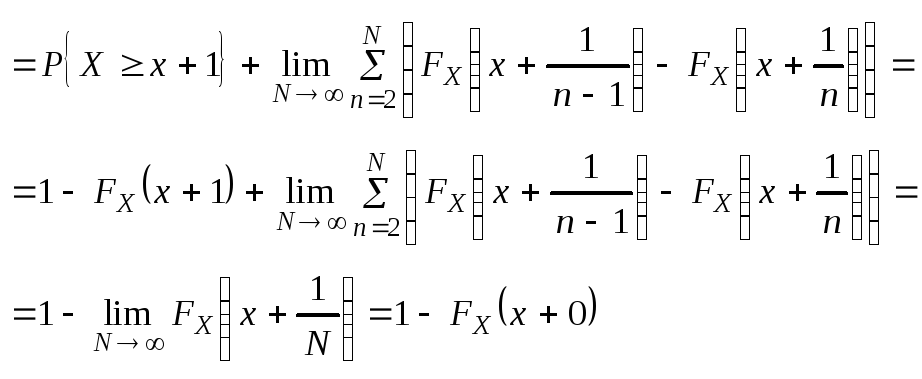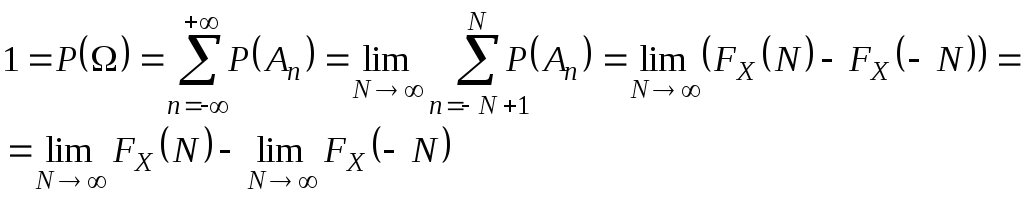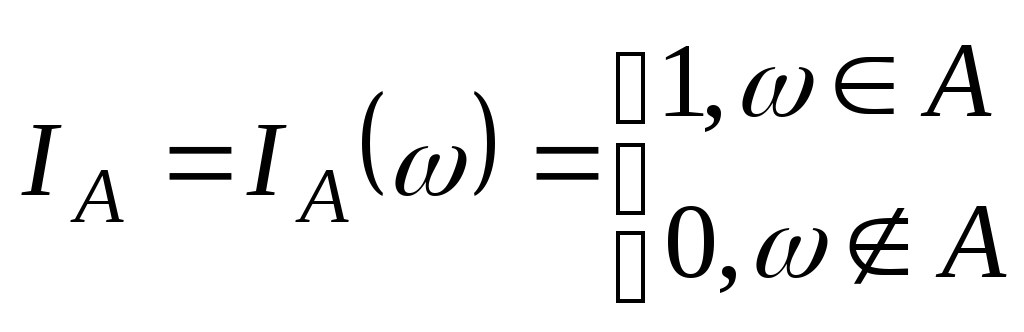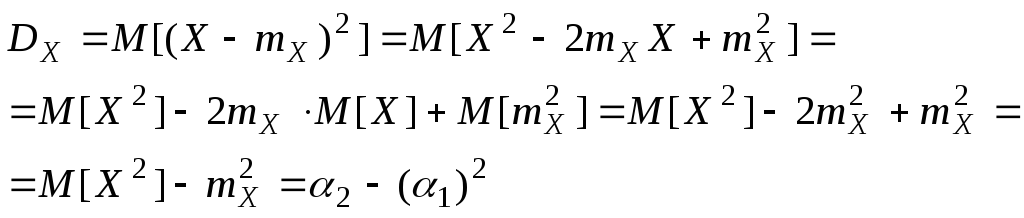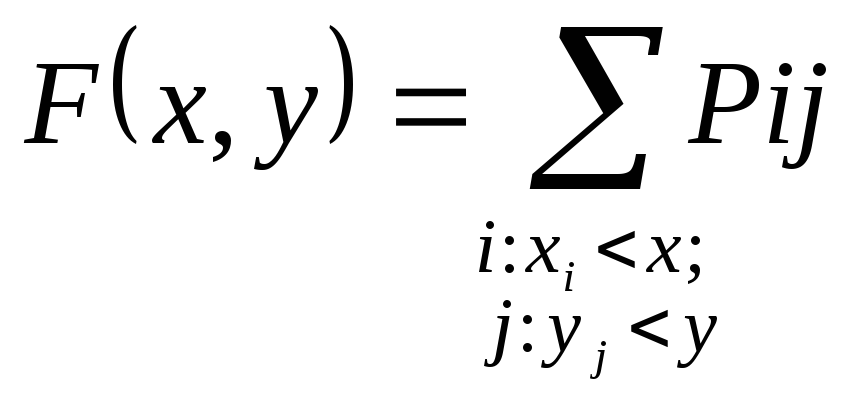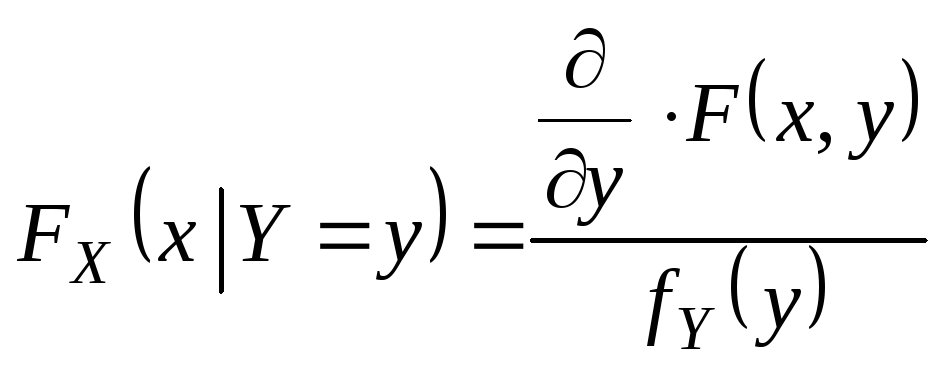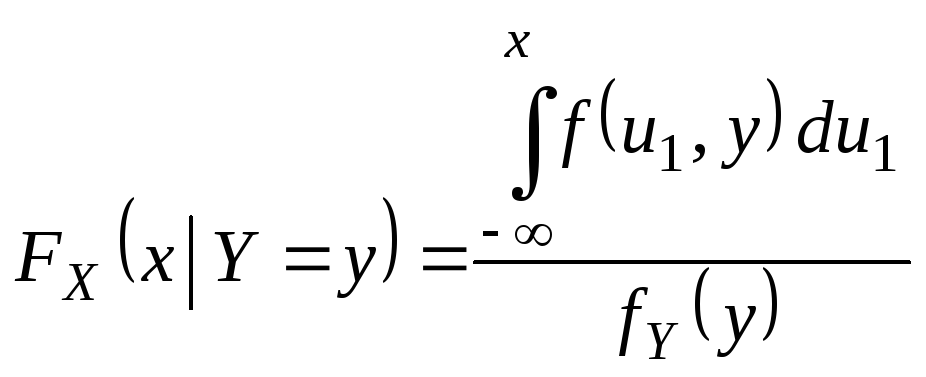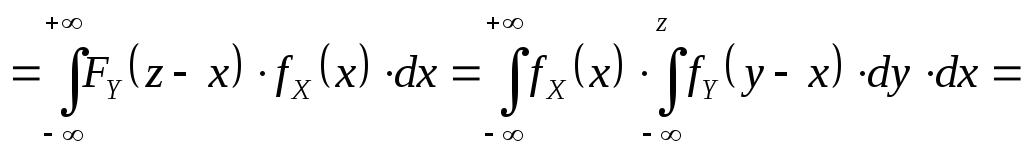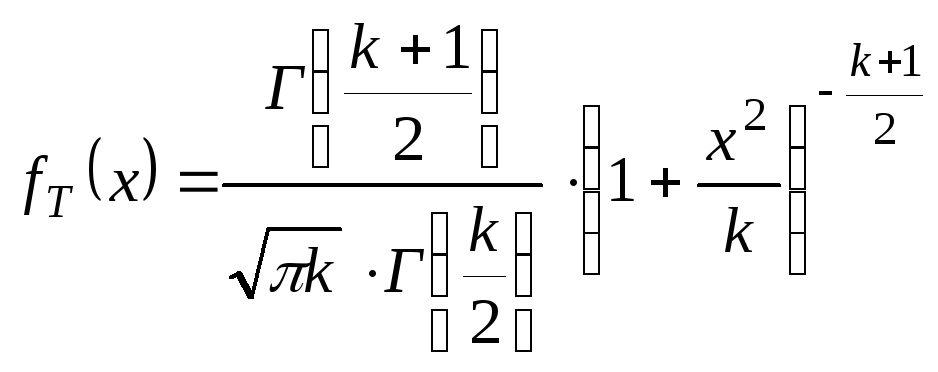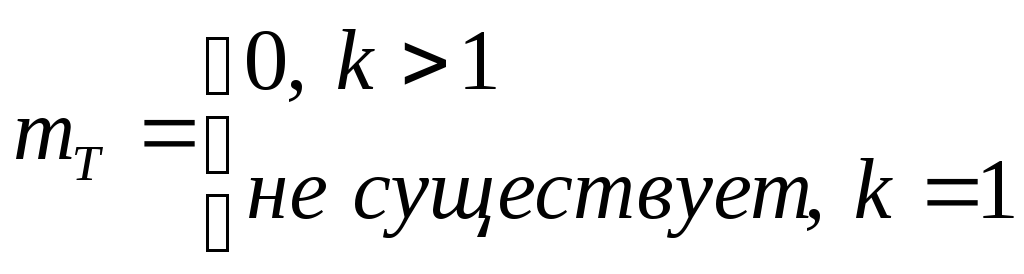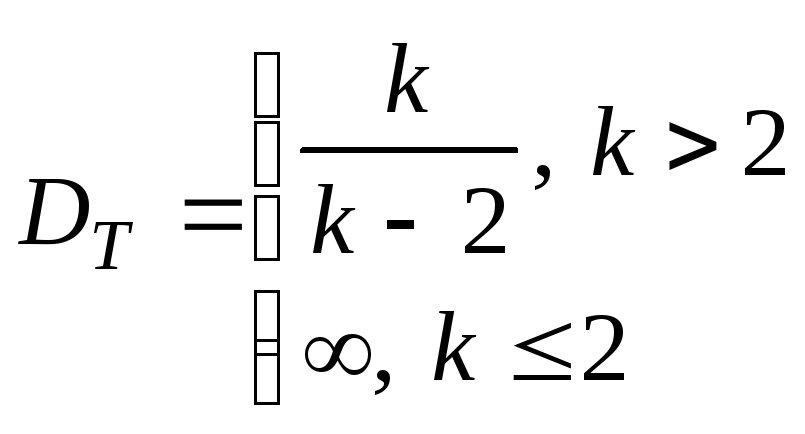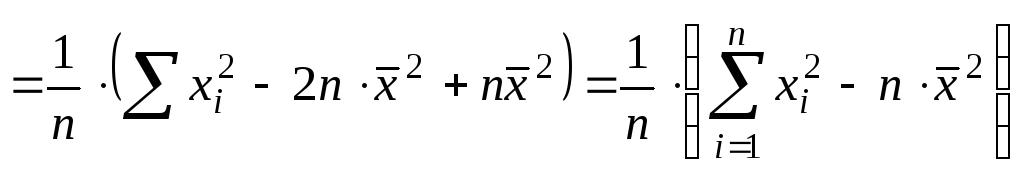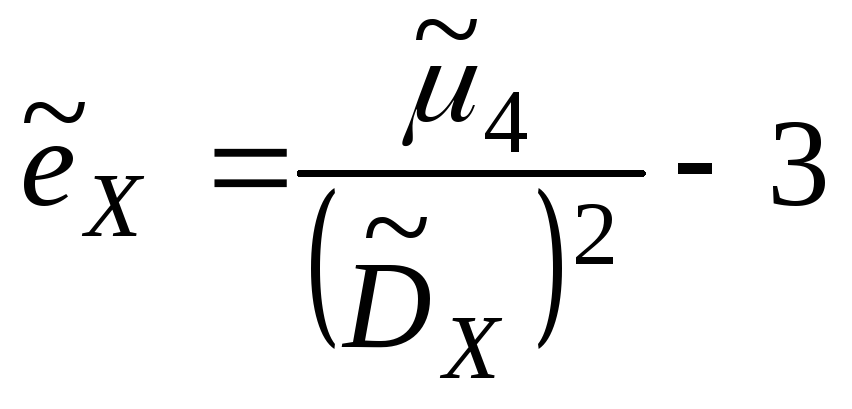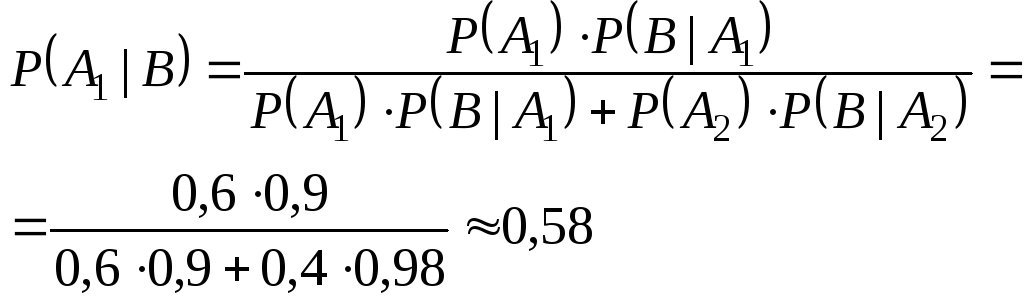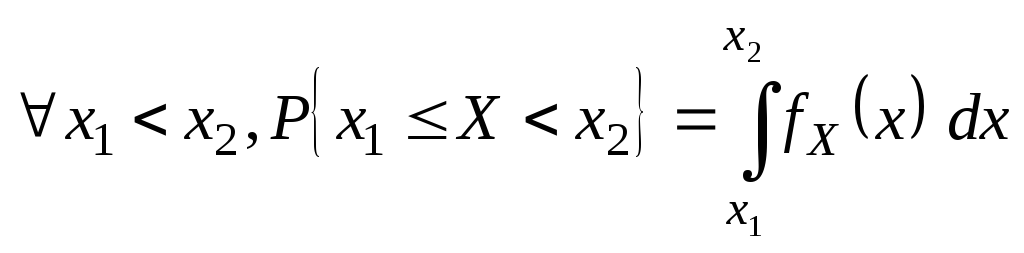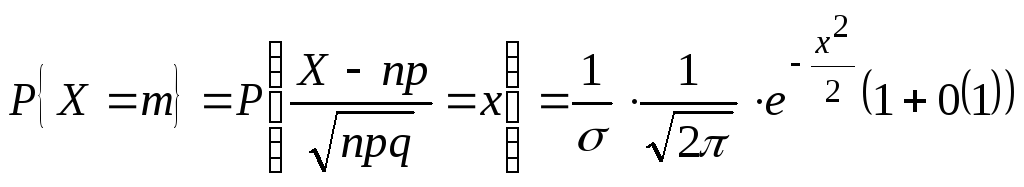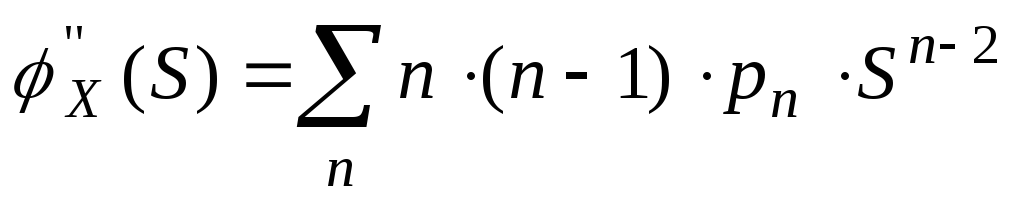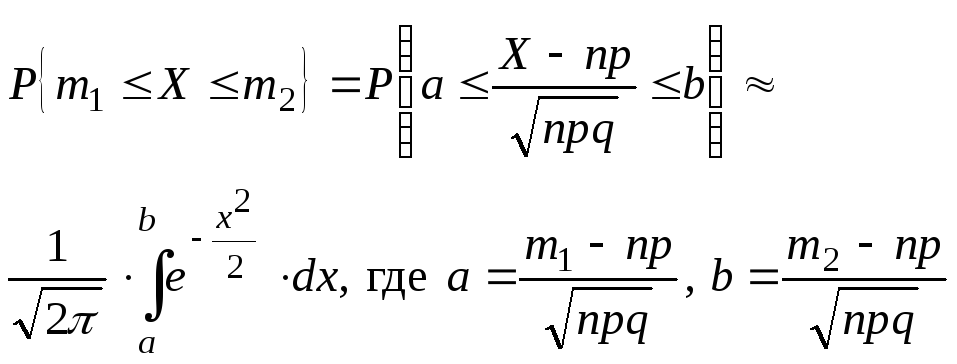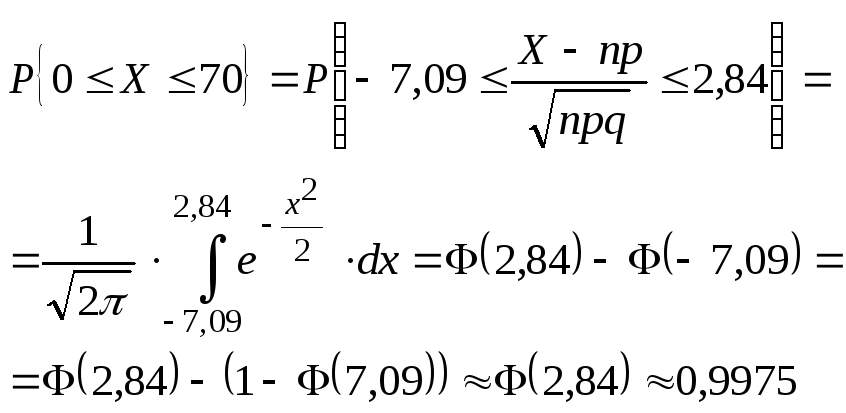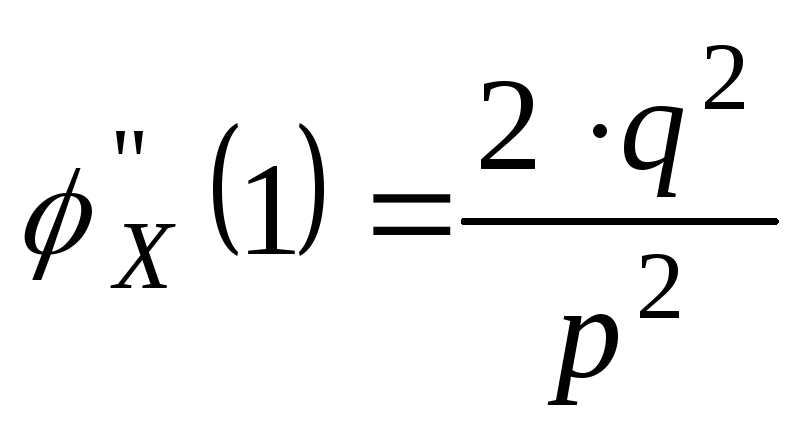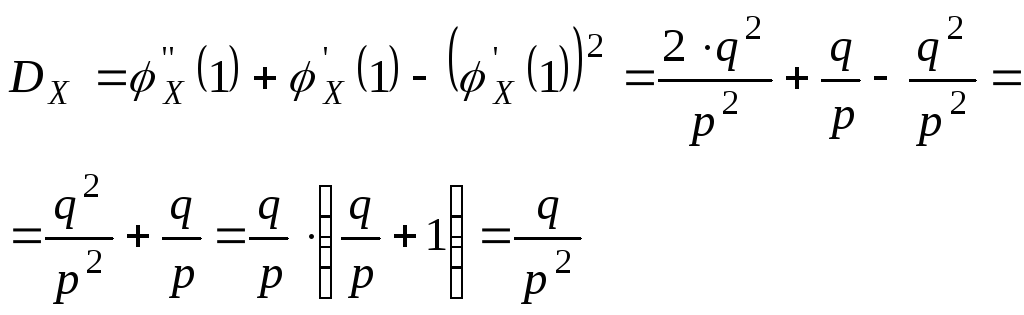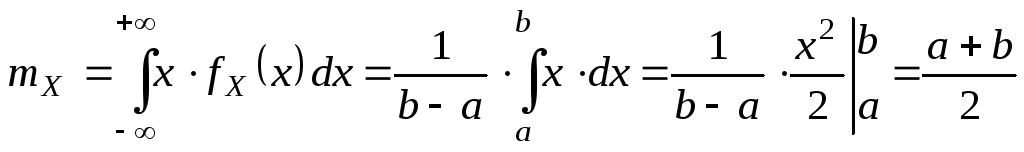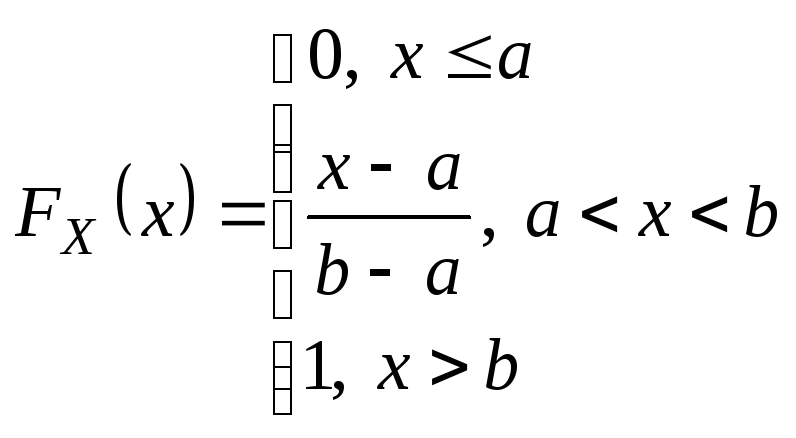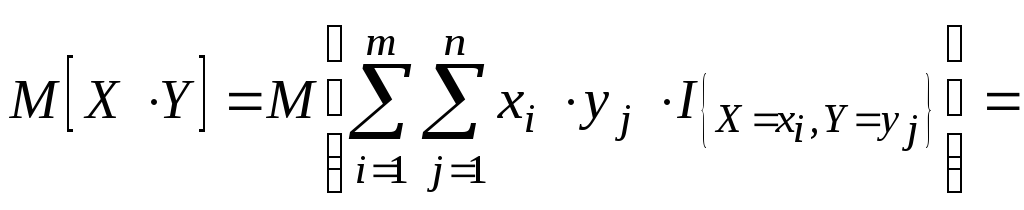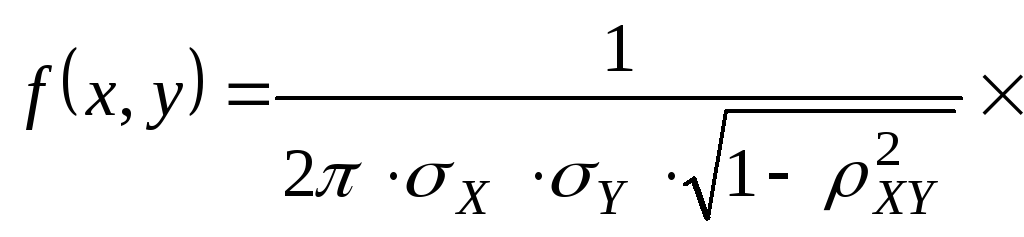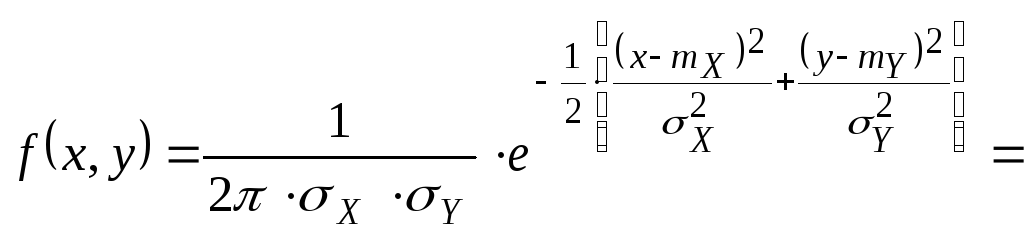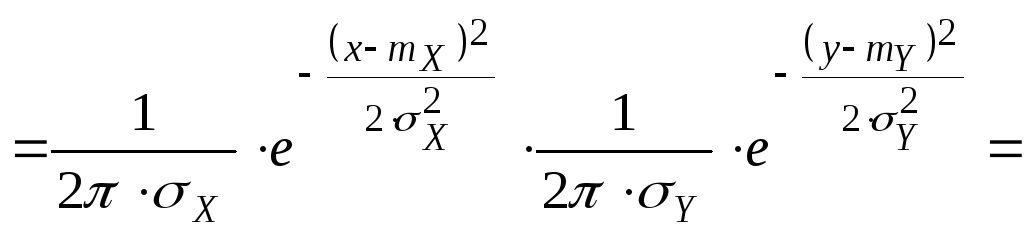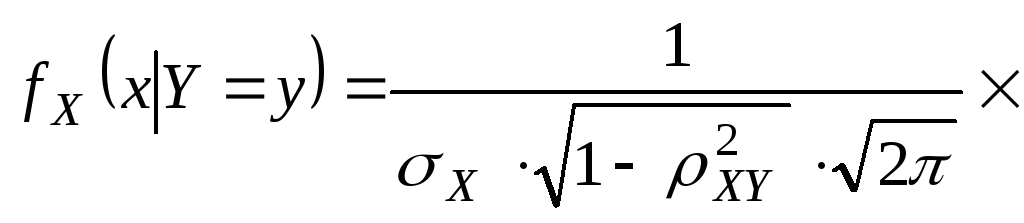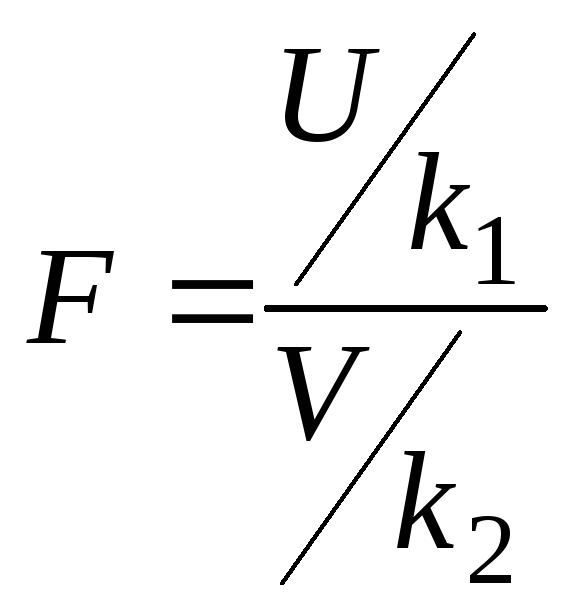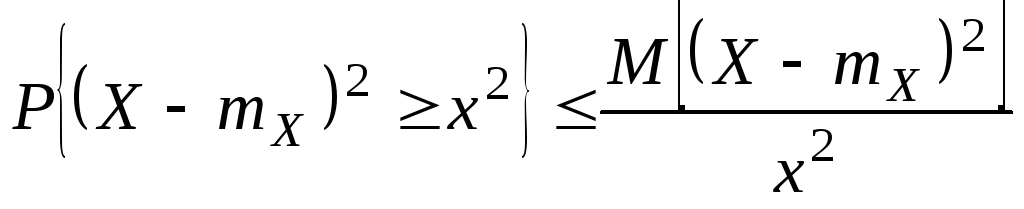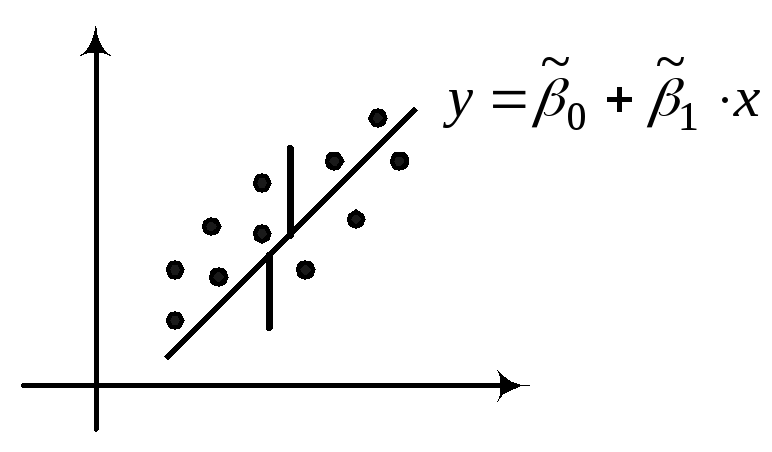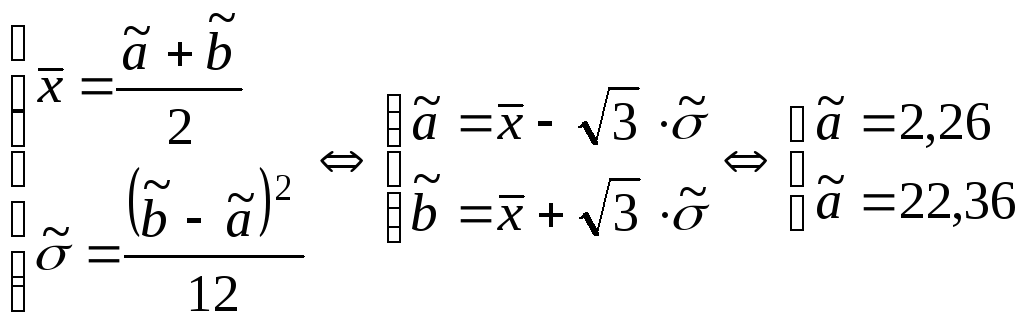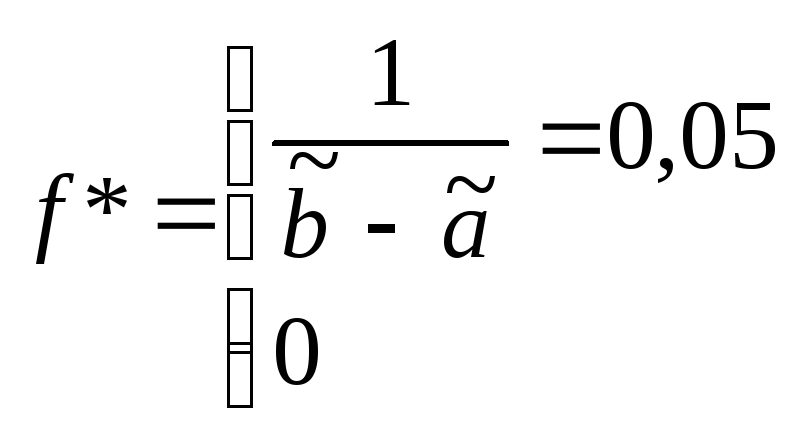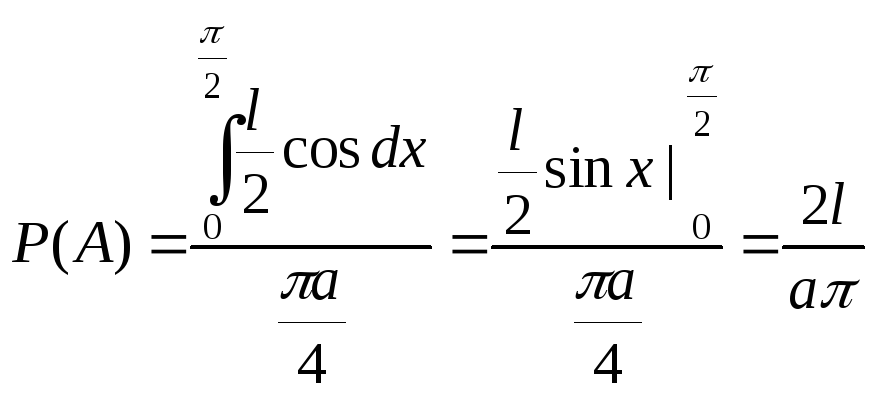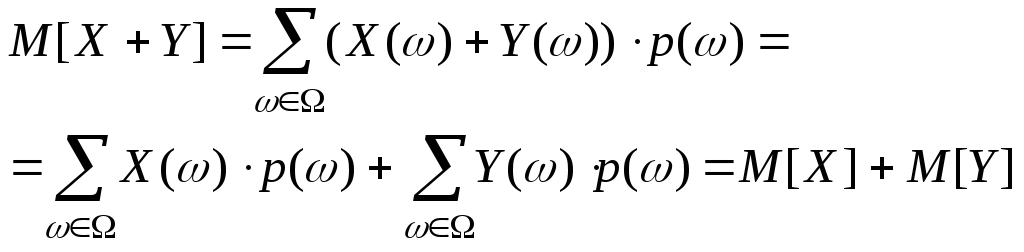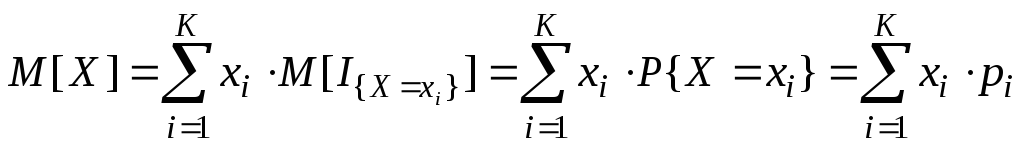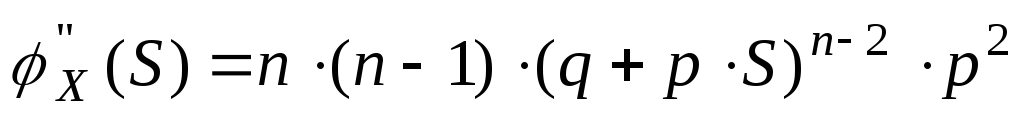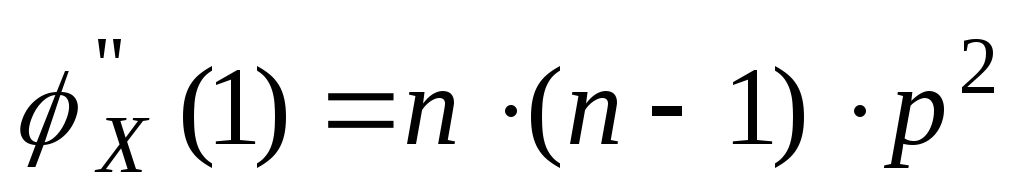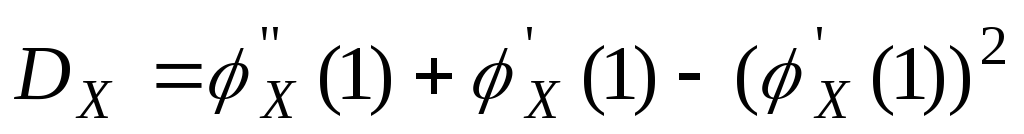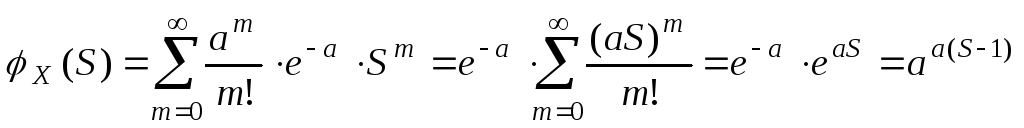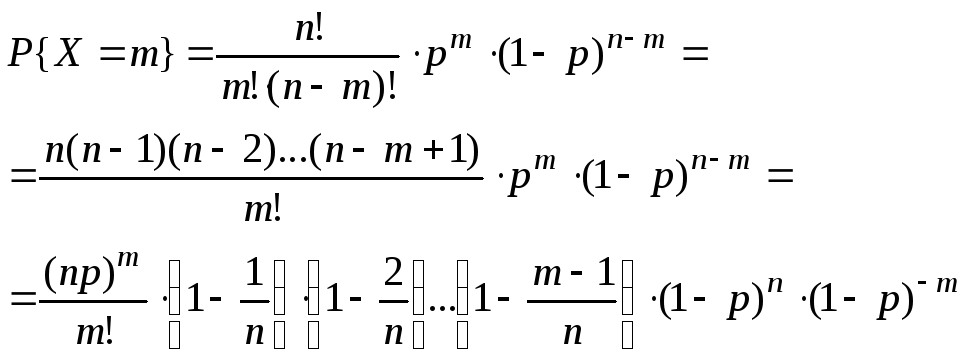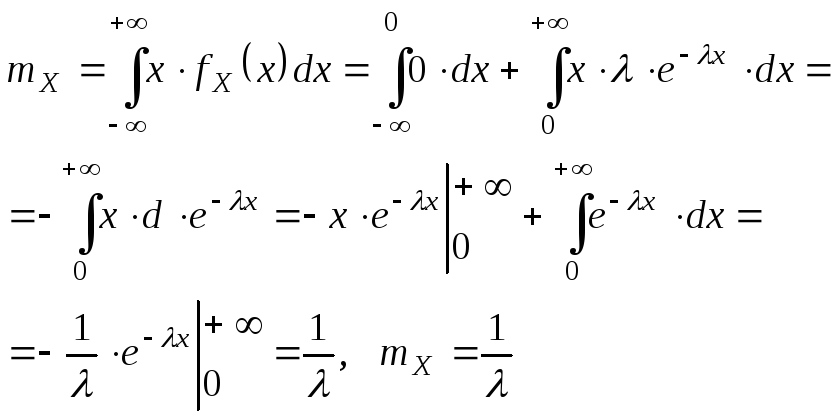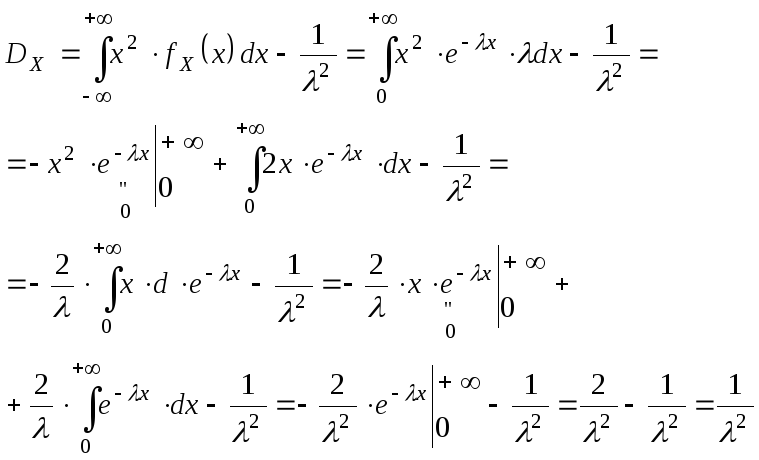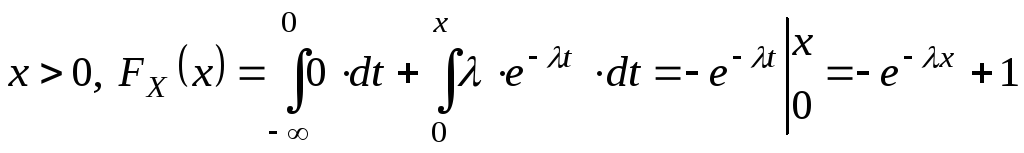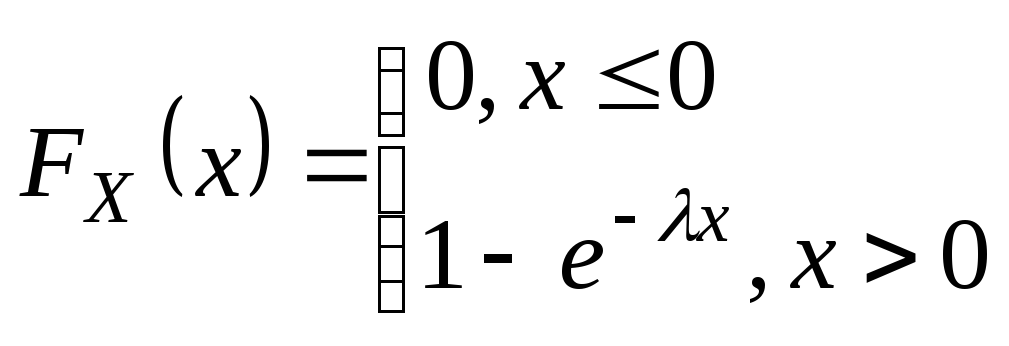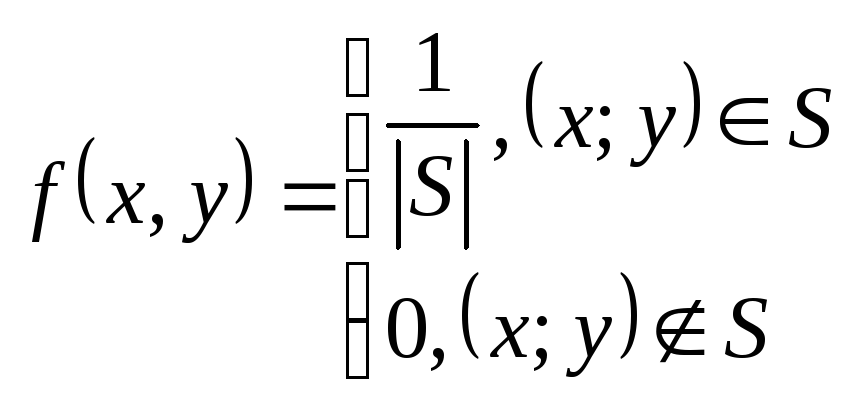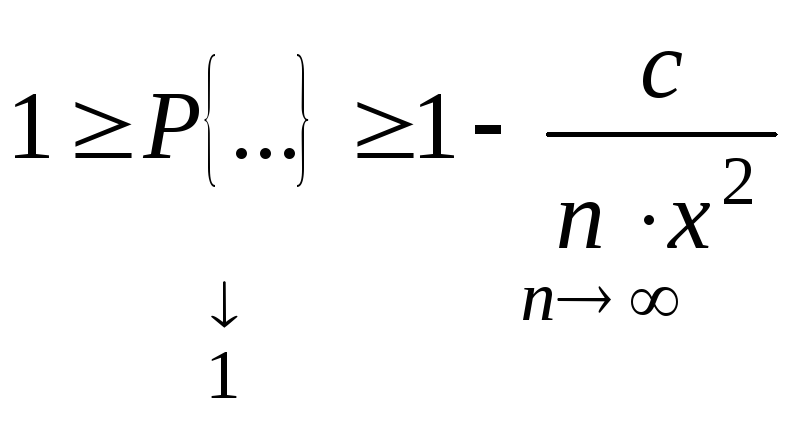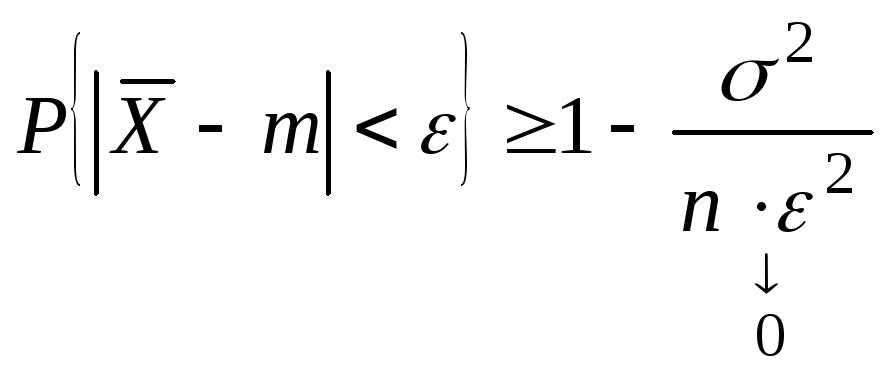Случайности не случайны… Всё решает вероятность событий!
В ЕГЭ по математике целых два задания на теорию вероятностей, поэтому стоит уделить ей в два раза больше внимания! Первое решается по основной формуле вероятности, а вот над вторым придётся подумать и вспомнить, какие бывают события.
Мы структурировали типы задач, которые могут попасться на экзамене, и сделали эту полезную шпаргалку с формулами и теорией — сохраняйте карточки, чтобы подготовка к ЕГЭ по математике была ещё продуктивнее.
















Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
шпора по ТЕРВЕРУ (Шпоры по курсу — Теория вероятностей)
2018-01-112018-01-11СтудИзба
Описание файла
Файл «шпора по ТЕРВЕРУ» внутри архива находится в папке «Шпоры по курсу — Теория вероятностей». Документ из архива «Шпоры по курсу — Теория вероятностей»,
который расположен в категории «».
Всё это находится в предмете «теория вероятностей и математическая статистика» из 4 семестр, которые можно найти в файловом архиве РТУ МИРЭА.
Не смотря на прямую связь этого архива с РТУ МИРЭА, его также можно найти и в других разделах. Архив можно найти в разделе «к экзамену/зачёту», в предмете «теория вероятности» в общих файлах.
Онлайн просмотр документа «шпора по ТЕРВЕРУ»
Текст из документа «шпора по ТЕРВЕРУ»
|
Теорема сложения несовместных: Теорема сложения совместных: P(A+B)=P(A)+P(B) P(A+B)=P(A)+P(B)-P(AB) Теорема умножения незав.соб. Теорема умножения зав.соб. P(AB)=P(A)*P(B) P(AB)=P(A)*PA(B) P(A)+P( Формула полной вероятности: верть соб.А к-е может наступить лишь при появл. 1 из несовм. соб.(гипотез)= P(A)=P(B1)*PB1(A)+P(B2)*PB2(A)+… Формула Байеса: событие А уже произошло, т.е. известен результат
Формула Бернулли: вероятность того что в n незав. испыт-х. в каждом из которых вер-ть появ-я события = p , событие наступит ровно k раз = Менее k раз Pn(0)+Pn(1)+Pn(k-1) Более k раз Pn(k+1)+Pn(k+2)+…+Pn(n) или вычитать из единицы вероятность k раз!!! Не менее k раз Pn(k)+Pn(k+1)+…+Pn(n) Не более k раз Pn(0)+Pn(1)+…+Pn(k) Локальная теорема Лапласа: вероятность того что в n испытания в каждом из которых в-ть появления события =p, событие наступит k раз(без учёта последовательности)т.е. после 100 выстрелов, найти в-ть попадения 75 раз. Интегральная теорема Лапласа :в-ть того что в n событиях вер-ть каждого p, событие наступит не менее k1 раз но не более k2 раз.
|
Плотность распределения вероятностей непрерывной случайной величины X называют функцию f(x) – первую производную от функции распределения F(x): Дисперсия через плотность для не прерывной случ.вел.:
Дисперсия для дискретной сл.вел.:D(x)=M(x2)-M2(x) Математическое ожидание дискретной с.в.: среднее значение случайной величины
Математическое ожидание непрерывной с.в.:
Биномиальное распределение: проводится n испытаний, вероятность появл. соб. А в каждом исп. p. Случайная вел. X-количество появление соб. А в n испытаниях. M(x)=np D(x)=npq Распределение Пуассона: если p мало, a n велико т.е. стремится к бесконечности, то Беном-е распр. переходит в распределение Пуассона. M(x)=a D(x)=a a=np Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью: |
=
|
Теорема сложения несовместных: Теорема сложения совместных: P(A+B)=P(A)+P(B) P(A+B)=P(A)+P(B)-P(AB) Теорема умножения незав.соб. Теорема умножения зав.соб. P(AB)=P(A)*P(B) P(AB)=P(A)*PA(B) P(A)+P( Формула полной вероятности: верть соб.А к-е может наступить лишь при появл. 1 из несовм. соб.(гипотез)= P(A)=P(B1)*PB1(A)+P(B2)*PB2(A)+… Формула Байеса: событие А уже произошло, т.е. известен результат
Формула Бернулли: вероятнось того что в n незав. испыт-х. в каждом из которых вер-ть появ-я события = p , событие наступит ровно k раз = Менее k раз Pn(0)+Pn(1)+Pn(k-1) Более k раз Pn(k+1)+Pn(k+2)+…+Pn(n) или вычитать из единицы вероятность k раз!!! Не менее k раз Pn(k)+Pn(k+1)+…+Pn(n) Не более k раз Pn(0)+Pn(1)+…+Pn(k) Локальная теорема Лапласа: вероятность того что в n испытания в каждом из которых в-ть появления события =p, событие наступит k раз(без учёта последовательности)т.е. после 100 выстрелов, найти в-ть попадения 75 раз. Интегральная теорема Лапласа :в-ть того что в n событиях вер-ть каждого p, событие наступит не менее k1 раз но не более k2 раз.
|
Плотность распределения вероятностей непрерывной случайной величины X называют функцию f(x) – первую производную от функции распределения F(x): Дисперсия через плотность для не прерывной случ.вел.:
Дисперсия для дискретной сл.вел.:D(x)=M(x2)-M2(x) Математическое ожидание дискретной с.в.: среднее значение случайной величины
Математическое ожидание непрерывной с.в.:
Биномиальное распределение: проводится n испытаний, вероятность появл. соб. А в каждом исп. p. Случайная вел. X-количество появление соб. А в n испытаниях. M(x)=np D(x)=npq Распределение Пуассона: если p мало, a n велико т.е. стремится к бесконечности, то Беном-е распр. переходит в распределение Пуассона. M(x)=a D(x)=a a=np Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью: |
|
Теорема сложения несовместных: Теорема сложения совместных: P(A+B)=P(A)+P(B) P(A+B)=P(A)+P(B)-P(AB) Теорема умножения незав.соб. Теорема умножения зав.соб. P(AB)=P(A)*P(B) P(AB)=P(A)*PA(B) P(A)+P( Формула полной вероятности: верть соб.А к-е может наступить лишь при появл. 1 из несовм. соб.(гипотез)= P(A)=P(B1)*PB1(A)+P(B2)*PB2(A)+… Формула Байеса: событие А уже произошло, т.е. известен результат
Формула Бернулли: вероятнось того что в n незав. испыт-х. в каждом из которых вер-ть появ-я события = p , событие наступит ровно k раз = Менее k раз Pn(0)+Pn(1)+Pn(k-1) Более k раз Pn(k+1)+Pn(k+2)+…+Pn(n) или вычитать из единицы вероятность k раз!!! Не менее k раз Pn(k)+Pn(k+1)+…+Pn(n) Не более k раз Pn(0)+Pn(1)+…+Pn(k) Локальная теорема Лапласа: вероятность того что в n испытания в каждом из которых в-ть появления события =p, событие наступит k раз(без учёта последовательности)т.е. после 100 выстрелов, найти в-ть попадения 75 раз. Интегральная теорема Лапласа: в-ть того что в n событиях вер-ть каждого p, событие наступит не менее k1 раз но не более k2 раз.
|
Плотность распределения вероятностей непрерывной случайной величины X называют функцию f(x) – первую производную от функции распределения F(x): Дисперсия через плотность для не прерывной случ.вел.:
Дисперсия для дискретной сл.вел.: D(x)=M(x2)-M2(x) Математическое ожидание дискретной с.в.: среднее значение случайной величины
Математическое ожидание непрерывной с.в.:
Биномиальное распределение:проводится n испытаний, вероятность появл. соб. А в каждом исп. p. Случайная вел. X-количество появление соб. А в n испытаниях. M(x)=np D(x)=npq Распределение Пуассона: если p мало, a n велико т.е. стремится к бесконечности, то Беном-е распр. переходит в распределение Пуассона. M(x)=a D(x)=a a=np Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью: |
Свежие статьи
Популярно сейчас
Зачем заказывать выполнение своего задания, если оно уже было выполнено много много раз? Его можно просто купить или даже скачать бесплатно на СтудИзбе. Найдите нужный учебный материал у нас!
Ответы на популярные вопросы
То есть уже всё готово?
Да! Наши авторы собирают и выкладывают те работы, которые сдаются в Вашем учебном заведении ежегодно и уже проверены преподавателями.
А я могу что-то выложить?
Да! У нас любой человек может выложить любую учебную работу и зарабатывать на её продажах! Но каждый учебный материал публикуется только после тщательной проверки администрацией.
А если в купленном файле ошибка?
Вернём деньги! А если быть более точными, то автору даётся немного времени на исправление, а если не исправит или выйдет время, то вернём деньги в полном объёме!
Отзывы студентов
Добавляйте материалы
и зарабатывайте!
Продажи идут автоматически
650
Средний доход
с одного платного файла
Обучение Подробнее
1.Предмет
теории вероятностей.События.Алгебра
событий.Теория
вероятностей–раздел
математики, изучающий закономерности
случайных явлений.Разница между
закономерными и случайными
событиями.Закономерное
событие–это
событие, которое всегда осуществляется,
как только создаются определённые
условия.Закономерное
явление –
это система закономерных событий.Случайные
события–это
события, которые при одних и тех же
условиях иногда происходят, а иногда
нет.Однако случайные события подчиняются
некоторым закономерностям, которые
называются вероятностными
закономерностями, при этом надо
условится, что мы будем иметь дело не
со всякими случайными событиями, а с
массовыми,
то есть будем предполагать, что в
принципе можно создать много раз одни
и те же условия, при каждом из которых
могут произойти или нет некоторые
случайные события.Пусть при осуществлении
некоторых условий (N
раз), случайное событие A,
будет осуществляться N(А)
раз.Число N(А)
– называется частотой событий A,
а отношение
– относительной частотой события
А.Если
N
велико, относительная частота для
случайных массовых событий обладает
свойством устойчивости.Пример:–серия
испытаний.–
относительная частота испытаний.
…
Относительная
частота колеблется около определенного
числа, которое характеризует данное
случайное событие.Р(А)
– вероятность события А.
Примеры:1)Пусть
случайное событие A
– выпадение герба при одном подбрасывании
симметричной однородной монеты,Р(А)
= 1/2 – вероятность выпадения
герба.2)Статистика рождений показывает,
что мальчиков рождается несколько
больше, чем девочек. Доля рождения
мальчиков 0,51-0,52.Р(А)
= 0,51; 0,51 – вероятность рождения
мальчиков.
События.
Достоверное
событие
– событие, которое всегда происходит
(Ω).Невозможное
событие –
событие, которое не происходит никогда
().Событие
Ā
– событие противоположное событию
A.
Ā
происходит тогда и только тогда, когда
не происходит событие A.Суммой
событий A
и B
называется событие A+B,
которое происходит тогда и только
тогда, когда происходит или A,
или B,
или оба вместе.
Произведением
событий A
и B
называется событие AB,
которое происходит тогда и только
тогда, когда происходят A
и B
вместе.Разностью
событий A
и B
называется событие A—B,
которое происходит тогда и только
тогда, когда происходит A
и не происходит B.События
A
и B
несовместны,
если AB=.Событие
A
влечет за собой событие B,
если из наступления события A
следует наступление события B
(A
B).События
A
и B
называются равносильными
A=B,
если выполняются одновременно два
включения A=B
A
B
и B
A.Пример:
Бросается игральная кость. A
= {выпадает четное число очков} и B
= {выпало
число очков, не большее трех}Решение:
Выпало число очков отличное от 5
(A+B).Выпало
2 (AB).Выпало
число очков равное 4 или 6 (A—B).Выпадает
нечетное число очков (Ā).
3.Конечное
вероятностное пространство. Классическое
определение вероятности. Рассмотрим
случай конечного вероятностного
пространства. В этом случае
состоит из конечного числа элементарных
событий .
= {}
A
– алгебра всех подмножеств
(ввиду конечности вероятностного
пространства алгебра автоматически
является -алгеброй),
тогда вероятность P(A)
для любого подмножества A
задаем следующим образом. Пусть заданы
неотрицательные числа P,
которые удовлетворяют следующему
требованию
,
тогда вероятность события
(*) (способ введения вероятности на
конечном вероятностном
пространстве).Очевидно, что так
определенная вероятность вместе
P()=0
будет удовлетворять всем аксиомам.
Обозначим через -
– количество элементов в множестве
A.
Частным случаем определения вероятности
по формуле (*) будет так называемое
классическое определение вероятностей,
когда все P
будут равны друг другу, так как;
;
–
формула классической вероятности
(**)
Замечание:Модель
вероятностного пространства, приводящая
к классическому определению
вероятностей, когда элементарные
события обладают свойствами «симметрии».
Пример:Бросается кубик на стол. 1
= {выпадает 1} 2
= {выпадает 2} – свойства симметрии
9.Формула
полной вероятности
Система
событий A1,…,An
называется
конечным разбиением(разбиением)
пространства ,
если они:
1)попарно
несовместны, т.е. AiAj=,
если i
j.
2)
A1+A2
+… An
=.
Теорема
(Формула полной вероятности)
Если
A1,…,An
–
разбиение
и все P(Ai)>0,
то для всех событий B
.
Доказательство:B=B=B(A1+…+An)=BA1+…+BAn
Пример.
В урне находятся M-белых
шаров и N—M-черных
шаров. По схеме выборки без возвращения,
последовательно выбираются два шара.
Найти вероятность события B={второй
вынутый шар белый}. A
= {первый шар белый}. Ā={ первый шар
черный}
Решение
A
Ā =
, A
+
Ā
=
Пример
показывает, что при правильно
организованной жеребьевке шансы
будут равны.
8.Условные
вероятности; теорема умножения
N
– число испытаний;
A,
B,
AB
– события;
N(A),
N(B),
N(AB)
– частоты
событий;
–
условная
относительная частота события A
при условии, что произошло событие
B;
;
;

Если
все относительные частоты событий
устойчивы, тогда условная относительная
частота тоже устойчива. Пусть
P(B)>0.Условной
вероятностью
P(A|B)
события A
при условии, что событие B
произошло, называется отношение
.
P(A|B)
= PB(A)
(встречается в литературе).
Теорема
умножения
Если P(A)>0,
P(B)>0,
а P(A|B),
то вероятность произведения
.
Доказательство:
Доказательство
следует из определения.
Пример:
1 способ. В урне
находятся M-белых
шаров и N—M-черных
шаров. По схеме выборки без возвращения,
последовательно выбираются два шара.
Найти вероятность того, что оба шара
будут белыми.
A
= {1 вынутый шар белый} B
= {2 вынутый
шар белый} AB
= {оба шара белых}
,
.
2 способ.
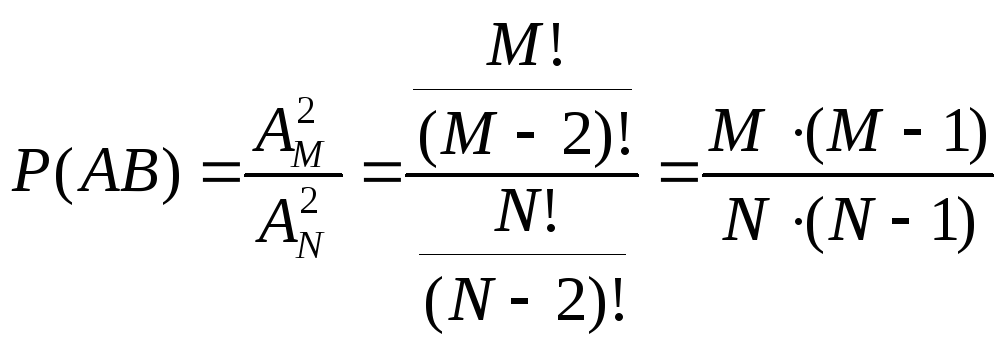
Следствие.
Пусть события
A1,…,An
таковы,
что
P(A1…An-1
)>0 тогда.
Доказательство:
Доказательство проводится методом
математической индукции.
13.Функция
распределения случайной величины.
Её свойства. Функция распределения
СВДТ. Ряд
распределения может быть построен
только для СВДТ, для недискретных
случайных величин из-за несчетности
множества возможных значений такое
представление невозможно. Наиболее
общей формой закона распределения
пригодной для всех
типов
случайных величин является функция
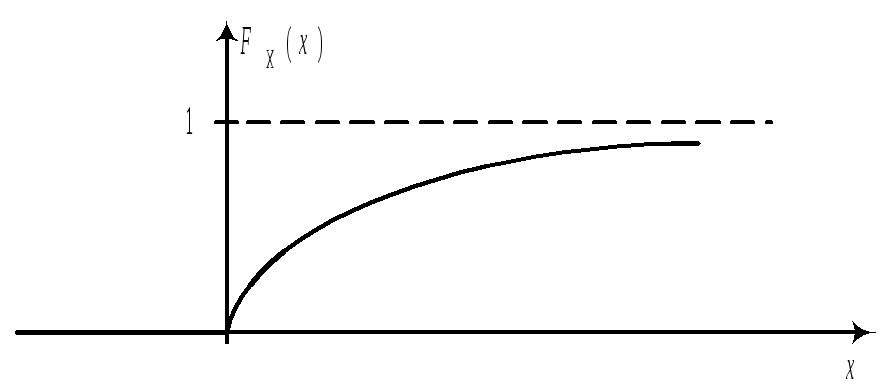
распределения. Функция F(x)=Fx(x)=P{X<x},
xR
называется функцией
распределения
СВ Х.
С помощью функции распределения можно
выразить вероятности попадания CB Х
в различные интервалы вида x1X<
x2
, x1X
x2
, x1<X
x2
, x1<X<
x2
. Пусть x1
< x2
, тогда {X<
x2}
разложим в сумму двух несовместных
событий {X<x2}={X<
x1}+{
x1
X<x2},
тогда P{X<x2}=P({X<
x1}
+{ x1
X<x2})=P{X<
x1}+
P{
x1
X<x2};
FX(x2)=FX(x1)+
P{
x1Xx2};P{
x1Xx2}=
FX(x2)-FX(x1)
(**) Событие {X>x}
можно представить, как счетную сумму
несовместных событий
Согласно (**).
P{X>x}=1-
FX(x+0);
P{Xx}=1-
P{X>x}=FX(x+0);
P{x1Xx2}=FX(x2+0)-
FX(x1);
P{
x1Xx2}=FX(x2+0)-
FX(x1+0);P{
x1Xx2}=FX(x2)-
FX(x1+0);
P{
X=x}=FX(x+0)-
FX(x);
Теорема.
Функция
FX(x)
обладает следующими свойствами:
1.
FX(x)
– не убывает;
2.
FX(x)
– непрерывна слева;
3.
FX(+)=1;
4.
FX(-)=0;.
Доказательство
3 и 4:
1.Следует
из (**), т.к. P{x1Xx2
}0.
2.Следует
из аксиомы непрерывности 4,
т.к. события
FX(x)=
FX(x-0)
.
Свойства
3, 4 вытекают из аксиомы счетной
аддитивности (3*), т.к. =ΣAn
(-<n<),
где
An={
n-1X()<n},
тогда
Пусть
(по теореме Вейeрштрасса).
(0
FX(N)
1 )
Из
равенства P{X=x}=FX(x+0)-FX(x)
следует, что в точках разрыва функции
FX(x)
имеет место положительная вероятность.
P{X=x}>0
Так
как при каждом натуральном n
может быть не более n-точек
x
с вероятностями P{X=x}1/n,
то у функции FX(x)
имеется не более счетного числа точек
разрыва.Обозначим через x1,x2,..
все точки разрыва функции FX(x),
если вероятности P{X=x}=Pk
таковы, что Σpk=1,
то это равносильно тому, что СВ X
имеет дискретное распределение, то
есть является СВДТ.Замечание.
Для СВДТ
FX(x)
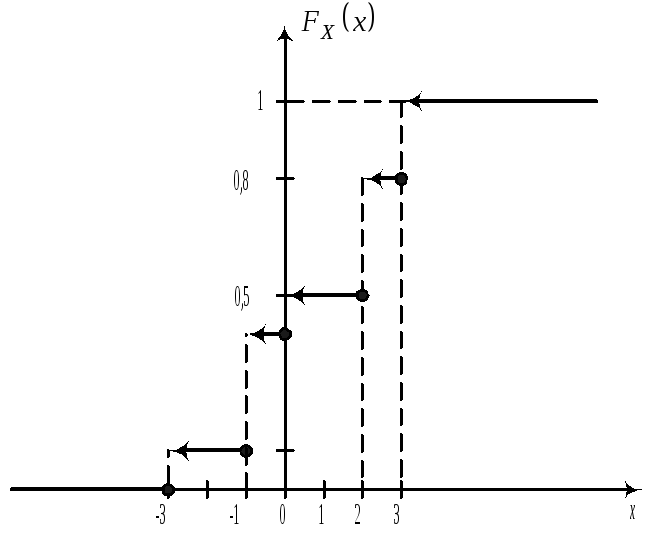
имеет ступенчатый вид. Пример.
X
-3 -1 0 2 3
P
0,1 0,3 0,1 0,3 0,2
Получить
функцию распределения и построить
ее график. Решение. FX(x)=P{X<x},
т.е. FX(x)=0(x-3);
FX(x)=0,1(-3<x-1);
FX(x)=0,4(-1<x0);
FX(x)=0,5(0<x2);
FX(x)=0,8(2<x3);
FX(x)=1(x>3);
P{X=2}=
FX(2+0)-
FX(2)=0,8-0,5=0,3;
P{-1<X2}=FX(2+0)-FX(-1+0)=0,8-0,4=0,4
Введем
новое важное понятие индикатора
события.
Опр:Индикатором
события A
A
называется
СВ :
.
Ряд
распределения случайной величины IA
имеет следующий вид
|
IA |
0 |
1 |
|
P |
1–p |
p |
где
р-вероятность
события А.
16.Моменты
n-го порядка. Дисперсия. Среднее
квадратическое отклонение.
МО в теории
вероятностей относится к типу
характеристик положения (см. далее
мода, медиана), кроме них используется
еще ряд числовых характеристик
различного назначения, среди них
особое значение имеют моменты
(начальные, центральные).Положим
g(x)=xS.
Опр.Начальным
моментом S-го
порядка СВ Х
называется S=M[XS].
Замечание:
Иногда
используются абсолютные начальные
моменты S-го
порядка M[XS].
Для СВДТ:
Для СВНТ:
.
Замечание.
– начальный
момент 1-го
порядка.
Обозначим
.
Определение.
Центральным моментом S-го
порядка называется
.
Замечание.
Иногда используются
абсолютные центральные моменты S-го
порядка.
.
Для СВДТ:
.
Для СВНТ:
.
Определение.
Центральный момент II-го
порядка ()
называется дисперсией
СВ Х
и обозначается
.
Для СВДТ:
.
Для СВНТ:
.
Опр.
– называется средним квадратическим
отклонением СВ Х
(стандартным отклонением в литературе).
Свойства
дисперсии:
1.
.
Доказательство:
.
2.
.
Доказательство:
.
(*).
По свойству 4 МО
и с учетом неравенства (*) получаем
доказательство свойства 2 для дисперсии.
3.
.
Доказательство:
Пример.
Пусть на прямой
в точках x1
<x2
<…<xk
расположены
точечные массы p1,p2.,
pk
Σpi=1:
M[X]=Σxipi
(1<i<k)
– центр тяжести
D[X]=
Σ(xi-mi)pi
(1<i<k)
– момент
инерции масс pi
относительно центра тяжести.
Таким образом,
МО характеризует место, вокруг которого
группируются массы pi,
а дисперсия – степень разбросанности
этих масс относительно МО.
21. Простейший
Пуассоновский поток
На
практике часто встречаются ситуации,
где имеет место распределение Пуассона.
Задача.
Пусть
на оси времени 0t
случайным образом возникают точки
моменты появления каких-то однородных
событий. (Например, вызовы на телефонной
станции, приход посетителей в магазин
и т.д.)). Последовательность таких
моментов назовем потоком
событий.Предположим, что поток обладает
следующими свойствами.
Свойства.
1)Стационарность.Это
свойство означает, что вероятность
попадания, того или иного числа
событий, на участок времени длиной
не зависит от того, где на оси 0t
расположен этот участок, а зависит
только от его длины .Из
этого следует, что среднее число
событий, появляющееся в единицу ()
времени , постоянно.
– интенсивность потока.
2)Ординарность.Это
свойство заключается в том, что
вероятность попадания на малый участок
t
двух или более событий пренебрежимо
мала с вероятностью попадания на него
одного события.
Т.е.
при t0
вероятность двух или более событий
является бесконечно малой более
высокого порядка малости, чем
вероятность попадания на него одного
события.
3)Отсутствие
последствия.Это
свойство означает, что вероятность
попадания некоторого числа событий
на заданный участок оси 0t
не зависит от того сколько событий
попало на любой другой не пересекающийся
с ним участок (в частности “будущее”
потока не зависит от его “прошлого”).
Опр.Поток
событий, обладающий этими 3-мя свойствами
называется простейшим
(или стационарным) Пуассоновским
потоком.
Покажем, как
простейший Пуассоновский поток связан
с распределением Пуассона.
СВ
Х
– количество событий, попадающих на
участок 0t,
длиной .
Покажем, что Х
имеет распределение Пуассона.
Доказательство:
Разделим
участок длины
на n
равных частей
t
=/n.
МО числа событий, попадающих на
элементарный участок t,
равно t*.
Согласно свойству 2 (ординарности)
можно пренебречь вероятностью
попадания на элементарный участок
t,
двух или более событий. Назовем
элементарный участок t
– занятым, если на нем появилось
событие из потока. Назовем элементарный
участок t
– свободным, если на нем не появилось
событие из потока.A
= {участок t
занят} IA=
1(участок t
занят) IA=
0 (участок t
свободен).
M[IA]=pt–
вероятность того, что участок t
занят. Среднее число, то есть МО числа
событий, попадающих на участок длины
t,
будет равно M[IA]=
t*.
pt=
t*.
pt=*/n
Рассмотрим
теперь n-участков
на временной оси, как n-независимых
испытаний (опытов), в каждом из которых
(независимость этих испытаний
из свойства 3) может появиться событие
А
и вероятность этого события
.
Число занятых элементарных участков
– это и есть Х.
СВ
Х
имеет биномиальное распределение
.
Будем
теперь неограниченно увеличивать
число элементарных участков и найдем
при
.
Согласно
теореме Пуассона, при
,
28.Оценка
отклонения теоретического распределения
от нормального; асимметрия и эксцесс.
При
изучении распределений, отличных от
нормального, возникает необходимость
количественно оценить это различие.
С этой целью вводят специальные
характеристики (асимметрию и эксцесс).
Для
нормального распределения эти
характеристики равны 0, поэтому, если
для изучаемого теоретического
распределения асимметрия и эксцесс
имеют небольшие значения, то можно
предположить близость этого
распределения к нормальному. Наоборот
большие значения
aX
и eX,
указывают значительные отклонения
от нормального.
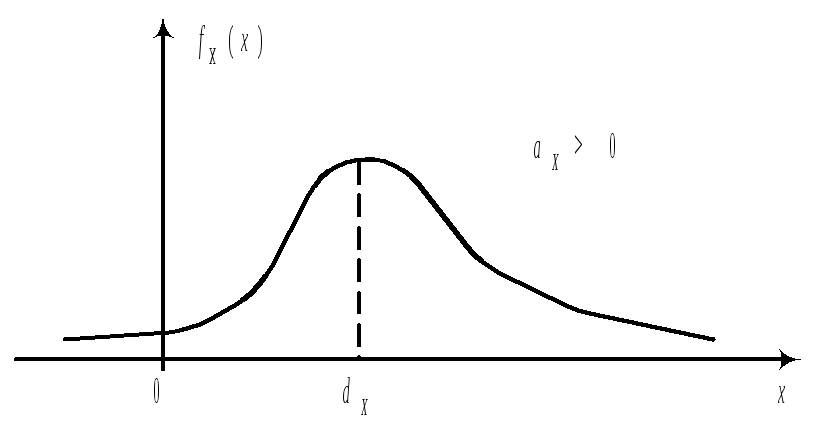
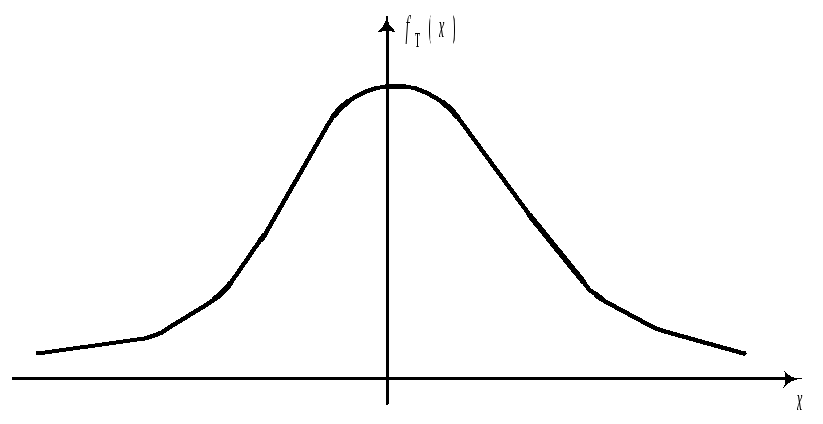
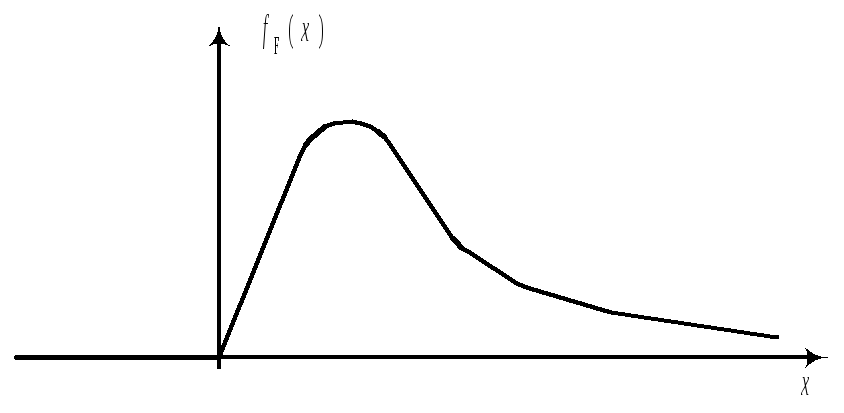
Пологая
часть правее моды, значит aX>0.
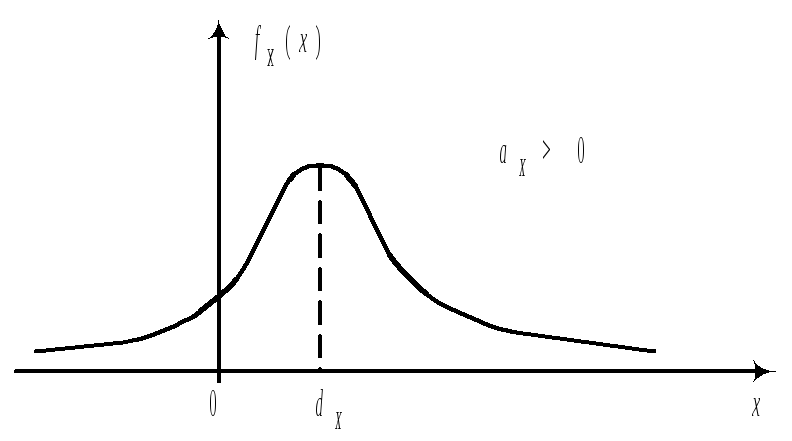
Пологая
часть левее моды, значит aX<0.
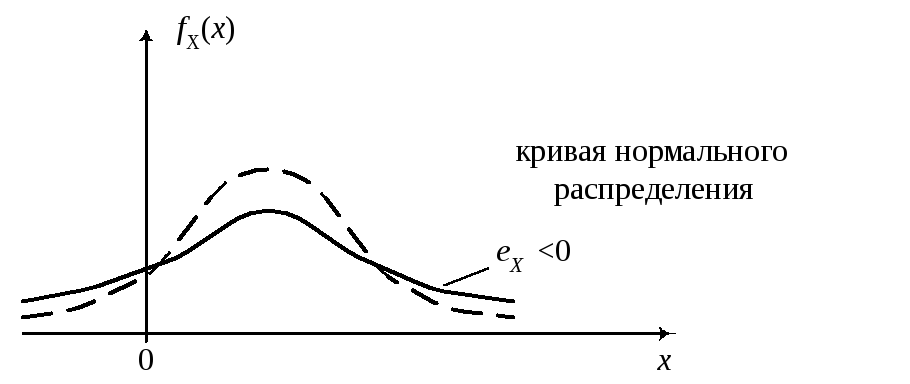
Замечание.При
исследовании эксцесса надо считать,
что нормальное исследуемое распределение,
имеют одинаковое МО и дисперсию.
30.Дискретные
двумерные случайные величины
Опр.
Двумерная
СВ (X,
Y)
называется дискретной, если каждая
из СВ и Х
и Y
является
дискретной.
Пусть
СВ Х
может принимать значения
,
а СВ Y
принимает дискретные значения
.
|
Y X |
y1 |
y2 |
… |
ym |
P{X=xi} |
|
x1 |
P11 |
P12 |
… |
P1m |
P1 |
|
x2 |
P21 |
P22 |
… |
P2m |
P2 |
|
… |
… |
… |
… |
… |
… |
|
xn |
Pn1 |
Pn2 |
… |
Pnm |
Pn |
|
P{Y=yj} |
P1 |
P2 |
… |
Pm |
|
Двумерный
случайные вектор может принимать
только пары значений
По этой таблице
нетрудно определить функцию
распределения.
.
33.Условные
законы распределения для системы СВ.
Если СВ
образующие систему зависимы, то для
нахождения закона распределения
системы не достаточно знать законы
распределения отдельных величин,
входящих в систему, требуется знать
так называемый условный закон
распределения одной из них.
ОпрУсловным
законом распределения одной из величин
системы (X,
Y)
называется ее закон распределения
вычисленный при условии, что другая
СВ приняла определенное значение.
Начнем
с наиболее простого случая, а именно
со случая, когда СВ Y
является дискретной.
Опр.Условной
функцией распределения
называется условная вероятность
события
Замечание
1.Условная
функция распределения обладает всеми
свойствами, которые присущи обычной
(т.е. безусловной) функции распределения.
Замечание
2Если
СВ X
также дискретная, причем
,
то удобно рассматривать условную
вероятность
,
СВ X
принять значения
при условии, что
,
В
общем случае условную функцию
распределения
,
однако, это не всегда возможно. Потому,
что для непрерывного типа P{Y=y}=0.
Чтобы отстроиться от этих неприятностей,
попытаемся воспользоваться предельным
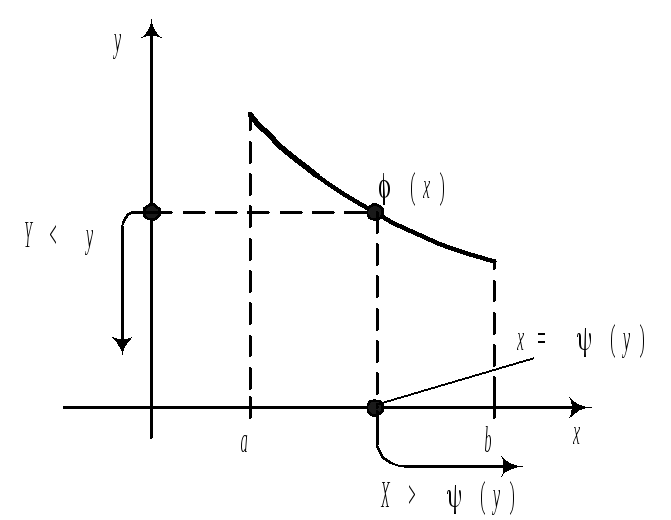
переходом, заменяя событие {Y=y},
событием {yY<y+}
и устремив
0.
Получим.
Назовем
условной функцией распределения
Оказывается
такой предел всегда существует.Если
СВ Y
– непрерывна, то условную функцию
распределения можно определить
следующим выражением
В
наиболее важных для приложений случаях
вектор (X,
Y)
представляет собой двумерную
непрерывную СВ с совместной плотностью
.
Так
как функция
имеет производную по x,
то мы получаем окончательное выражение
для условной плотности.
36.
Коэффициент корреляции. Связь между…
Опр.
Величина XY
называется коэффициентом корреляции
СВ X
и Y.
Коэффициент
XY
характеризует степень зависимости
СВ X
и Y,
но не любой, а только линейной
зависимости, которая проявляется в
том, что при возрастании одной СВ X
, другая также проявляет тенденцию
возрастания, в этом случае XY>0.
Если одна возрастает, а другая убывает,
то XY<0.
В первом
случае говорят, что две СВ связаны
положительной корреляцией. Во втором
случае говорят, что две СВ связаны
отрицательной корреляцией. Модуль
XY
характеризует степень тесноты линейной
зависимости между СВ X
и Y.
Если линейной зависимости нет, то
XY=0.
Теорема
Если же СВ
X
и Y
связывает жесткая функциональная
линейная зависимость Y=aX+b,
то XY=1
при a>0,
XY=
–1 при
a<0.
Доказательство:
;
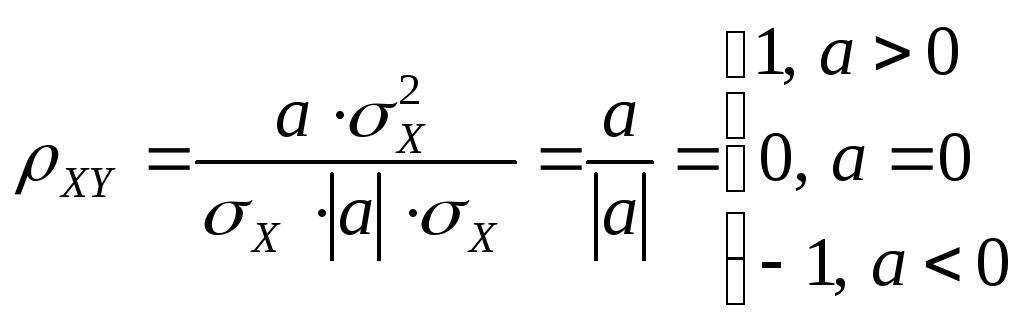
Теорема:
XY1
Доказательство:
Рассмотрим СВ
,
тогда
;
;
;
.
Опр.
СВ X
и Y
называется
не коррелированными, если XY
=0 (или KXY=0).
Замечание.Из
независимости СВ следует их не
коррелированность. Обратное не верно.
Из коррелированности не вытекает их
независимость
Теорема.
D[X+Y]
= DX+DY+2
KXY
Доказательство:
D[X+Y]=M[((X+Y)–(mX
–
mY))2]=
M[((X– mX)+(Y
–
mY))2]=
M[(X–
mX)2+
2(X– mX)(
Y
–
mY)+
(Y
–
mY)2]=
DX+DY+2
M[(X–
mX)(Y
– mY)]=
DX+DY+2
KXY
Следствие:
(доказательство
проводится методом математической
индукции).
40.Функции
от многомерных СВ. Формула
композиции.Функция
от многомерной СВ определяется точно
также, как и функция от одномерной
СВ. Мы рассмотрим это понятие на
примере двумерной СВ. Пусть на
вероятностном пространстве (,
A,
P),
задана двумерная СВ (X,
Y).
Предположим, что у нас имеется
измеренная числовая функция g(X,Y)
числовых аргументов X
и Y.
СВ Z=g(X,Y)
= g(X(),Y())
, назовем функцией от двумерной СВ
(X,
Y).
а)
Функция g(X,Y)от
двумерной дискретной
СВ (X,
Y)
снова является дискретной СВ,
принимающей значения g(xi
,
yj)
с вероятностями Pij=P{X=xi
,Y=yj
}
Чтобы построить ряд распределения
СВ Z=g(X,Y)
надо:1) Исключить все те значения g(xi
,
yj)
, вероятность которых равна нулю; 2)
Объединить в один столбец все одинаковые
значения g(xi
,
yj),
приписав этому столбцу суммарную
вероятность.
б)
В случае когда СВ (X,
Y)
непрерывного типа с плотностью f(x,y),
функция распределения Z=g(X,Y)
будет определяться формулой
Область
интегрирования здесь состоит из всех
точек (x,
y)
для которых g(X,Y)<Z.
особо важным для практики представляется
случай, когда X
и Y
– независимые
СВ, а функция Z=X
+ Y,
тогда g(x,y)=x+y.
Получается так называемая формула
композиции:
fX(x)
— ф-я плотности композиции от х
fY(y)
— ф-я плотности композиции от у
f(x,y)=
fX
(x)
fY
(y)
Интеграл (*)
вычисляется, как повторный, поэтому
.
Дифференцируя
по z
получаем
– формулы
композиции (свертки).
С помощью этих
формул легко выражаются формулы
плотности и функции распределения
суммы независимых СВ.
42.Распределение
Стьюдента.Пусть
Z~N(0;1).
V–
независимая от Z
СВ, которая распределена по закону
2
с k
степенями свободы.
Рассмотрим
СВ

СВ
Т
имеет распределение, которое называется
t–распределением
или распределением Стьюдента с k
степенями свободы.
t–распределение
определяется одним параметром –
числом степеней свободы.
С
возрастанием числа степеней свободы
t–распределение
асимптотически (довольно быстро)
приближается к стандартному нормальному
распределению с параметрами (0; 1).
Для
СВ, имеющих распределение Стьюдента,
имеется таблица квантилей, причем в
силу четности
.
46.Выборка
и способы ее представления Задачи
математической статистики: Установления
закономерностей, которым подчинены
массовые случайные явления основано
на изучении методами теории вероятностей
статистических данных (результатов
наблюдений)1.
Задача математической статистики :
Указать
способы сбора и группировки
статистических сведений, полученных
в результате наблюдений или в результате
специально составленных экспериментов.2.
Задача математической статистики:
1) Разработать
методы анализа статистических данных
в зависимости от целей исследования:
а)
оценка неизвестной вероятности
событий; б)
оценка неизвестной функции распределения;
в)
оценка параметров распределения, вид
которого известен; г)
оценка
зависимости СВ от одной или нескольких
других СВ. 2) Проверка статистических
гипотез о виде неизвестного распределения
или о величине параметров распределения
вид, которого известен.
Современную
математическую статистику определяют
как науку о принятии решений в условиях
неопределенности.
Выборка
и способы ее представления: Математическая
статистика позволяет получить
обоснованные выводы о параметрах,
видах распределений и других свойствах
СВ о конечной совокупности наблюдений
над этими величинами.
Выборка
понимается следующим образом. Пусть
СВ Х
наблюдается на каком либо эксперименте,
повторим этот эксперимент n
раз при одинаковых
условиях. Получаем Х1,..,
Хn
где каждая Хj
– СВ соответствующая j-му
эксперименту. Очевидно, что Хj
– независимые в совокупности СВ,
причем каждая из этих СВ имеет один
и тот же закон распределения, что и
СВ Х.
Опр.
Закон
распределения СВ Х
называется распределением генеральной
совокупности.
СВ
вектор Х1,..,
Хn
называется выборочным вектором, а
конкретные числа x1,..,
xn,
получаемые на практике при n
кратном повторении эксперимента в
неизменных условиях представляет
собой реализацию выборочного вектора
и называются выборкой объема n.
Что такое
вариационный ряд, размах выборки,
статистический ряд, группированный
статистический ряд, частоты,
относительные частоты, накопленные
частоты, относительные накопленные
частоты, всевозможные полигоны и
гистограммы, а также, что такое
эмпирическая функция распределения
изучили самостоятельно.
47.Числовые
характеристики выборки Пусть
x1,..,
xn
выборка объема n
из генеральной совокупности с функцией
распределения FX(x).
Рассмотрим выборочное
распределение,
т.е. распределение дискретной СВ,
принимающей эти значения с вероятностями,
равными 1/n.
Соответственно числовые характеристики
этого выборочного распределения
называют выборочными (эмпирическими)
числовыми характеристиками. Замечание.
Выборочные
числовые характеристики являются
характеристиками данной выборки, но
не являются характеристиками
распределения генеральной совокупности.
“~” – при обозначении этих числовых
характеристик.
.
.
– унимодального, т.е. одновершинного
распределения называется элемент
выборки, встречающийся с наибольшей
частотой. Выборочной медианой
называется
,
которое делит вариационный ряд на
две части, содержащие равное число
элементов. Если n
– нечетное число, т.е. n
= 2l+1,
то
.
Если n
– четное число, т.е. n
= 2l,
то
.
Можно доказать, что выборочные
начальные
и центральные
моменты порядка s
для негруппированных выборок объема
и определяются по следующим формулам
;
.
Форма распределения СВ характеризуется
выборочными коэффициентами асимметрии
и эксцесса.
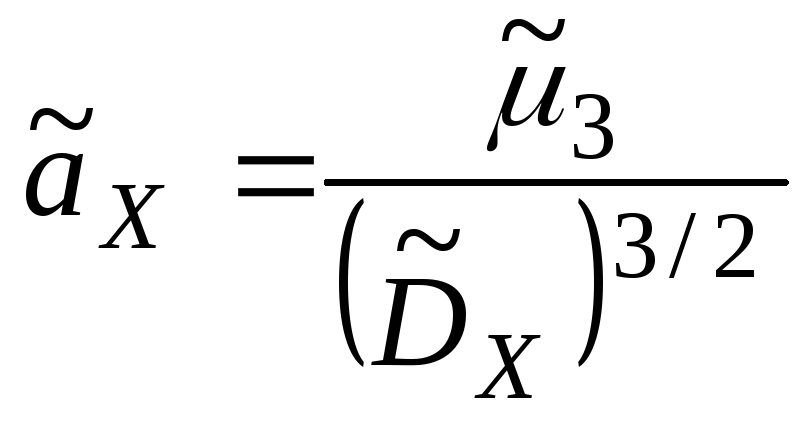
51. Выборочная
дисперсия
Докажем, что
выборочная дисперсия является
смещенной оценкой для дисперсии
генеральной совокупности.
Выполним следующие
преобразования
;
.
Найдем МО для
дисперсии:
.
.
МО не совпадает
с 2,
а отличается на –2/n
– смещение. Таким образом эта оценка
занимает в среднем истинное значение
дисперсии на величину 2/n,
правда это смещение сходит на нет при
n
.
Чтобы устранить
это смещение надо «исправить»
дисперсию.
;
;
.
Можно доказать,
что статистика S2
является и состоятельной оценкой для
дисперсии генеральной совокупности.Замечание.
К сожалению, на практике при оценке
параметров не всегда оказывается
возможным одновременное выполнение
требований: несмещенности, эффективности
и состоятельности.
54. Доверительный
интервал для оценки МО при НЕизвестной
дисперсии
2)Доверительный
интервал для оценки МО при неизвестной
дисперсии нормально распределенной
генеральной совокупности. Пусть
– выборочный вектор n–наблюдений
СВ
.
В качестве оценки для m
возьмем
.
Если дисперсия генеральной совокупности
неизвестна, то по выборке определяем
статистику
.
Доверительный интервал для m
в этом случае находится с помощью
статистики
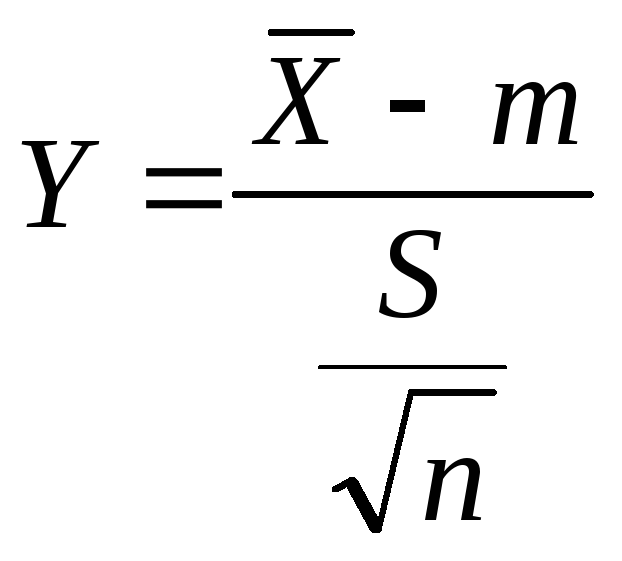
В
литературе по статистике показано,
что Y
имеет распределение Стьюдента с n–1
степенью свободы
.
По
заданной доверительной вероятности
,
используя таблицы распределения
Стьюдента с n–1
степенью свободы, находим
.
.
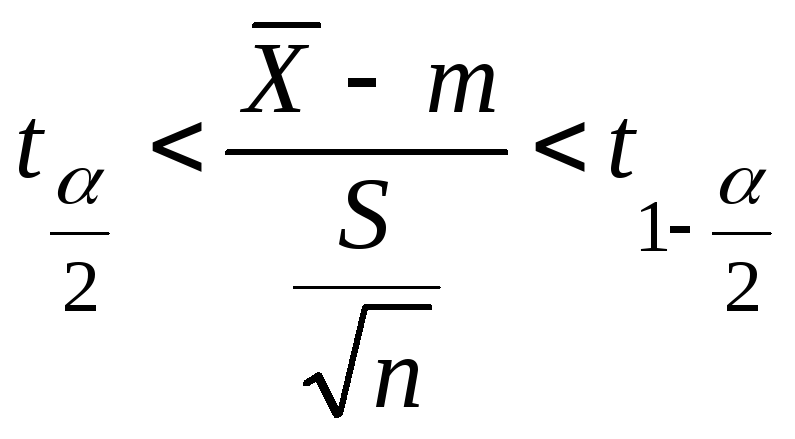
.
56.
Проверка статистических гипотез
Пусть
Х
– наблюдаемая СВ. Она может быть
дискретной, а может и непрерывной.
Опр.
Статистической
гипотезой Н называется предположение
относительно параметров или вида
распределения СВ Х. Гипотеза Н
называется простой, если она однозначно
определяет распределение СВ Х,
иначе Н называется сложной.
Если распределение
СВ Х известно и по выборке наблюдений
необходимо проверить предположение
о значении параметров этого
распределения, то такие гипотезы
называются параметрическими. А
гипотезы о виде распределения –
непараметрические.
Проверяемая
гипотеза называется нулевой гипотезой
и обозначается Н0.
Обязательно на ряду с Н0
рассматривают одну из альтернативных
гипотез Н1.
При
этом имеются различные ситуации для
Н1.
;
;
;
.
Выбор
альтернативной гипотезы Н1
определяется конкретной формулировкой
задачи.
Опр.Правило,
по которому принимается решение
принять или отклонить гипотезу Н0,
называется критерием К.
Так как решение принимается на основе
выборки наблюдений СВ Х,
то необходимо выбрать подходящую
статистику, которую мы будем называть
статистикой Z
критерия К.Замечание.
При проверке
простой параметрической гипотезы
Н0:
=0
в качестве статистики критерия
выбирают ту же статистику, что и для
оценки параметра ,
т.е..Основной
принцип при проверке статистической
гипотезы:
Маловероятные события считаются
невозможными, а события, имеющие
большую вероятность, считаются
достоверными. Реализация этого
принципа на практике. Перед анализом
выборки фиксируется некоторая малая
вероятность ,
называемая уровнем значимости. Пусть
V
множества значений статистики Z,
VK
– подмножество множества значений
статистики Z
(VK
V).
Это такое подмножество, что при условии
истинности гипотезы Н0,
имеем вероятность того, что P{ZVkH0}=.
Обозначим через zв
– выборочное значение статистики Z,
которое вычитается по конкретной
выборке. Критерии К
формулируется следующим образом.
Отклонить
гипотезу Н0,
если zвVk.
Отклонить гипотезу Н0,
если zвV
Vk.
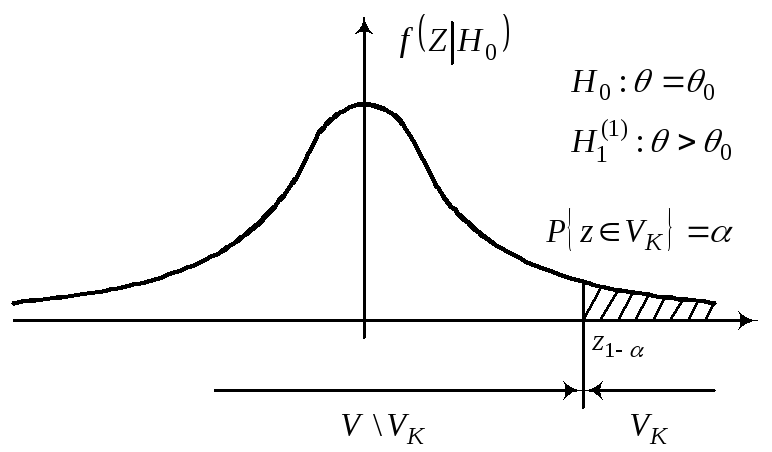
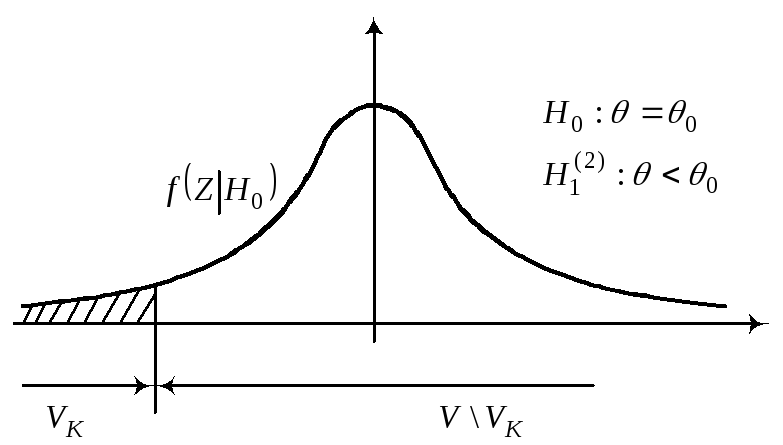
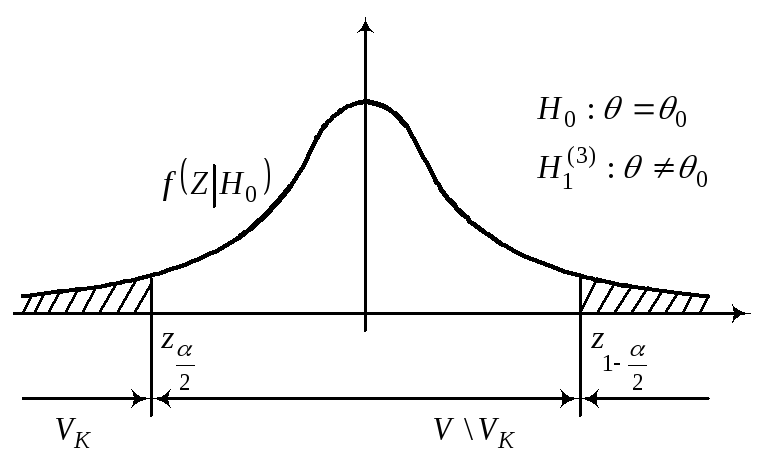
Уровень значимости
определяет размер критической области,
а ее положение зависит от альтернативной
гипотезы Н1.
Z1––квантиль
распределения Z
при условии, что верна гипотеза Н0.
Z–
квантиль распределения Z
при условии, что верна гипотеза Н0.
Проверку
параметрической гипотезы при помощи
критерия значимости можно разбить
на следующие этапы:1)сформулировать
Н0
и Н1;2)назначить
;3)выбрать
статистику Z
для проверки Н0;4)определить
выборочное распределение Z
при условии, что верна Н0;5)определить
VK
(она зависит от Н1);6)получить
выборку и вычислить zb
;7)принять статистическое решение:
zвVk
– отклонить Н0;
zвV
Vk
– принять Н0.
Статистическое решение может быть
ошибочным. При этом различают ошибки
I-го
и II-го
родов.Опр.
Ошибкой первого рода называется
ошибка, состоящая в том, что гипотеза
Н0
отклоняется, когда Н0
– верна. Вероятность P{ZVkH0}=..ОпрОшибкой
второго рода называется ошибка,
состоящая в том, что принимается
гипотеза Н0,
но в действительности верна
альтернативная гипотеза Н1.
Вероятность ошибки второго рода при
условии, что гипотеза Н1
– простая, P{ZVVkH1}=.Проверка
статистических гипотез и доверительных
интервалов.Проверка гипотез с
использованием критерия значимости
может быть проведена на основе
доверительных интервалов. При этом
одностороннему критерию значимости
будет соответствовать односторонний
доверительный интервал, а двустороннему
критерию значимости будет соответствовать,
двусторонний доверительный интервал.
Гипотеза Н0
– принимается, если значение 0
накрывается доверительным интервалом,
иначе отклоняется.
2.Вероятностное
пространство.Вероятность,ее
свойства.Теорема сложения.Тройка
(,
A,
P),
где
– это пространство элементарных
событий;A
– -алгебра
подмножеств ,
называемых событиями;P
– числовая
функция, определенная на событиях и
называемая вероятностью.P
называется вероятностным
пространством,
если выполнены следующие аксиомы:1)P(A)
0,AA.2)P()
= 1 (нормированность P).3)P(A+B)=P(A)
+ P(B),
если AB=
(аддитивность).4)Для любой убывающей
последовательности A1
A2
…
An…событий
из A
такой, что,
Имеет место равенство
(непрерывность
P).Замечания:
Аксиомы
3, 4 можно заменить одной аксиомой
-адди-тивности:
3*. Если события An
в последовательности A1,
A2,
… попарно
несовместны,
то
Из этих аксиом
вытекают Свойства
вероятностей:
1)Если
A
B,
то вероятность P(B–A)
= P(B)
– P(A).
Доказательство:
Разобьем событие
B
в сумму несовместных событий
B=A+(B-A),
A(B-A)=,
P(B)
= P(A+(B-A))=P(A)+P(B-A)
(по
аксиоме
3)
P(B—A)=P(B)
— P(A)
.
2)Если
A
B,
то P(A)
P(B)Доказательство:
Доказательство
следует из 1 свойства и аксиомы 1.
P(A)
+ P(B—A)
= P(B)
P(B—A)
0, следовательно
P(A)
P(B)
.
3)A
A
0
P(A)
1 Доказательство:
A
P(A)
P(),
P()
= 1(по
аксиоме
2)
P(A)
0, A
A(по
аксиоме
1) .
4)P(Ā)
= 1 — P(A)
Доказательство: A+
Ā =
,
A
Ā =
Тогда по аксиоме
3 и аксиоме 2 получаем
P(A+
Ā)
= P(),
P(A)
+ P(Ā)
= P(),
P(A)
+P(Ā)
=
1
P(Ā)
= 1 — P(A)
.
5) P()
= 0Доказательство:
+
=
Тогда по аксиоме 3 и 2 получаем, P()
+ P()
= P()
P()
+ 1 = 1, P()
= 0 .
6)Теорема
сложения
A,
B
A
: P(A+B)
= P(A)
+ P(B)
– P(AB)
Доказательство:
A
+ B
= A
+ (B
— AB),
A(B
— AB)
=
P(A+B)
= P(A)
+ P(B
— AB),
но AB
B
следовательно по первому свойству
(вероятность от разности равна разности
вероятностей).
P(A+B)
= P(A)
+ P(B)
– P(AB)
.
4.Основные
правила комбиноторики:«правило суммы»
и «правило произведения» Комбинаторика
– это наука о том, сколько различных
комбинаций удовлетворяющих условиям
можно составить на элементах конечного
множества. Комбинаторные схемы:
Правило
суммы: X
– конечное множество
X=n
– количество элементов.
Объект
x
из X
может быть выбран n-способами.
Пусть X1,…,Xk
попарно непересекающиеся множества,
то есть XiXj=,
ij
тогда очевидно выполняется равенство.
– правило
суммы
Правило
произведения:Если
объект x
может быть выбран m-способами
и после каждого из таких выборов
объект y
может быть выбран n-способами.
Тогда выбор упорядоченной пары (x,y)
может быть осуществлен – mn
способами. Доказательство: Воспользуемся
правилом суммы. {a1,…,am}–
множество элементов, из которых
выбирается объект x.i=1,..,m,рассмотрим
множество Xi={(ai
,y)},
тогда первая компонента совпадает с
ai.
Множества Xi
попарно не пересекаются. Xi=n.
Множество
пар Xi—это
объед.
В
общем случае правило произведения
формируется следующим образом: Если
объект x1
может
быть выбран n1
– способами, после чего объект x2
может быть выбран n2
способами и i,
где i=1,..,m-1
(2
i
m-1)
после выбора объектов x1,…,xi
объект xi+1
может быть выбран ni+1-способами,
то выбор упорядоченной последовательности
x1,…,xm
может быть осуществлен n1,…,nm
способами. Доказательство проводится
методом математической индукции.
10.Формулы
Байеса Теорема.Если
A1,…,An
– разбиение
и все
,
тогда имеет место следующая формула:
Доказательство:
По теореме
умножения:
Формулы Байеса
можно интерпретировать следующим
образом: назовём Ai
– гипотезой, а B
– результат некоторого эксперимента,
a
P(Ai)
– априорные вероятности, а условные
вероятности–апостериорные
вероятности (послеопытные
вероятности).Формулы Байеса позволяют
по априорным и условным вероятностям
вычислить апостериорные вероятности
гипотез. Пример:Детали,
изготовленные цехом завода, попадают
к одному из двух контролёров для
проверки на стандартность. Вероятность
того, что деталь попадёт к первому
контролёру – 0,6; ко второму контролёру,
соответственно, – 0,4. Вероятность
того, что годная деталь будет признана
стандартной, для первого контролёра
– 0,9; для второго – 0,98. Годная деталь
была признана стандартной. Найти
вероятность того, что её проверил
первый контролёр. Решение.
A1={деталь
проверил первый}
A2={деталь
проверил второй}
A1A2=,
A1+A2=
B={годная
деталь признана стандартной}
11. Независимость
событий Если
события A
и B
таковы, что P(B)>0
P(AB)
Определение.
Событие A
не зависит от события B,
если P(AB)
= P(A)
Если потребовать условия P(A)>0,
то
Понятие того,
что одно событие зависит от другого,
симметрично. Замечание
Из теоремы
умножения: P(AB)=P(B)
P(AB)
P(AB)=P(B)
P(A)
Это приводит к определению.
ОпределениеСобытия
A
и B
называются
независимыми,
если вероятность произведения событий
равна произведению вероятностей
событий (P(AB)=P(A)P(B)).
Если событие A
не зависит от события B,
то они являются просто независимыми.
Если P(AB)=P(A)P(B)
не
выполняется, то события являются
зависимыми.
P(AB)=P(A)P(B)–теоретико-вероятностная
(статистическая) независимость; её
следует отличать от причинной
независимости реальных явлений.
Причинная независимость реальных
явлений не устанавливается с помощью
этого равенства, а постулируется на
основе других внешних соображений.
Определение
(Независимость событий в совокупности)
События A1,…,An
называются независимыми, если
индексов 1i1<
i2<…<
imn,
где 2mn,
то выполняется:
В противном
случае — события зависимы. Замечание.Из
определения независимости событий
в совокупности следует, что события
любого подмножества
множества A1,…,An
будут независимы в совокупности.
Пример.
Имеются 4 числа: 2, 3, 5, 30. Наудачу
выбирается одно число. Вероятность
этого события – 0,25. Ak={выбранное
число делится на k}.
Решение.P(A2)=1/2;
P(A3)=1/2
; P(A5)=1/2;
P(A30)=1/2
P(A2A3)=1/4;P(A2A5)=1/4;P(A3A5)=1/4;P(A2A3A5)=1/4
P(A2A3)=P(A2)P(A3)
P(A2A5)=P(A2)P(A5)
— попарно
независимы
P(A3A5)=P(A3)P(A5)
P(A2)P(A3)
P(A5)=0.5*0.5*0.5=1/8
P(A2A3
A5)=1/4
(в совокупности
зависимы).
Совокупная
независимость более сильное свойство,
нежели попарная независимость.
Теорема.Если
события A1,…,An
являются
независимыми, индексы i1,…,in
, j1,…,jk
– все различны, вероятность
,
тогда:
14. Непрерывная
СВ. Плотность распределения.
Опр.Функция
есть плотность распределения СВ X,
если
(***)
Из определения
(***) следуют свойства плотности
распределения.
Свойства
1.
Замечание.
Для
СВ X
имеющей функции. Плотности из свойства
1 и теоремы из курса математического
анализа (о непрерывности интеграла
с переменным верхним пределом)
что
непрерывна.
2.
в точках непрерывности
.
3.
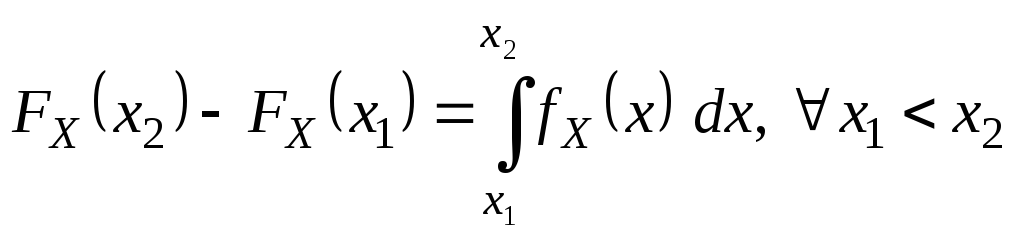
4.
,
т.к.
неубывающая функция, то
.
5.
Условия нормировки:
.
Опр.
СВ X
называется СВНТ,
если ее распределение имеет функцию
плотности
.
Через
плотность
можно выразить любую вероятность
17.Мода, медиана
и квантили
МО не единственная
характеристика положения, применяемая
в теории вероятностей.
Опр.
Модой
СВДТ Х
называется такое возможное значение
xm,
для которого
=xm.
Модой
СВНТ Х
называется действительное число dX,
являющееся точкой максимума функции
плотности вероятностей (fX
(x))
Пример.
X
0 1 2 3 4
P
0,05 0,3 0,25 0,2 0,2
dX=1
Замечание.
Мода может не
существовать, иметь единственное
значение, такие распределения
называются унимодальное, или иметь
множества значений – полимодальное
распределение.
Наличие более
чем одной моды, часто указывает на
разнородность статистического
материала, который положен в основу
исследований.
Опр.Медианой
СВ Х
называется действительное число hX,
удовлетворяющее условию:
,
то есть это корень уравнения FX
(x)=1/2.
Эта
характеристика применяется, как
правило, только для СВНТ и геометрически
медиана, это абсцисса той точки на
оси ОХ, для которой площади под графиком
fX
(x)лежащие
слева и справа от нее одинаковы и
равны 1/2
Замечание.
В случае
симметричного распределения (имеющего
моду) три характеристики: 1) МО ; 2) мода;
3) медиана совпадают.
Замечание.
Уравнение
Fx(x)=1/2
может иметь множество корней, поэтому
медиана может определяться неоднозначно.
Опр.
Квантильлью
порядка р распределения
СВНТ Х
называется действительное число tp,
удовлетворяющее уравнению P{X<tp}=p
Замечание.
Медиана
hx=t0,5
– квантиль порядка 0,5.
22.Локальная
предельная теорема Муавра-Лапласа.
Биномиальное
распределение имеет МО равное np
.
Пусть
p
– не близко к 0 и 1.
Теорема.
Если
в схеме независимых испытаний
,
то для любого C>0
равномерно по всем
вида
,
где m
– неотрицательные целые числа
Замечание.
Эти
таблицы даются, только для x>0.
18.Целочисленные
СВ и их производящие функции
В ряде случаев
при определении важнейших числовых
характеристик дискретных СВ может
помочь аппарат производящих функций.
Опр.
Дискретную
СВ Х,
принимающую только целые, неотрицательные
значения называют целочисленной
СВ.
Закон
распределения целочисленной СВ
определяется
.
Закон распределения
целочисленной СВ удобно изучать с
помощью производящей функции, которая
определяется, как
.
В
соответствии с определением МО:
.
Этот
ряд сходится абсолютно при
.
Поскольку
,
то между законом распределения
и производящими функциями
устанавливается взаимноодноз-начное
соответствие.
Замечание
– вероятностная производящая функция.
В математике
рассматриваются произвольные
производящие функции.
a0,
a1
,a2…
a0
+Sa1
+S2a2
+… –
производящая функция, если она имеет
не нулевой радиус сходимости.
Замечание
Возьмем
первую производную по S
от производящей функции.
,подставим
значение S
= 1.
.Возьмем
вторую производную по S
от производящей функции

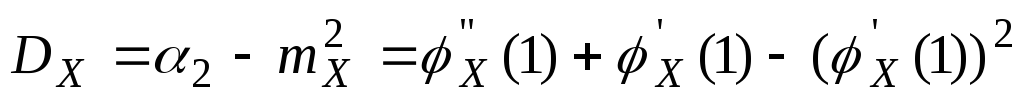
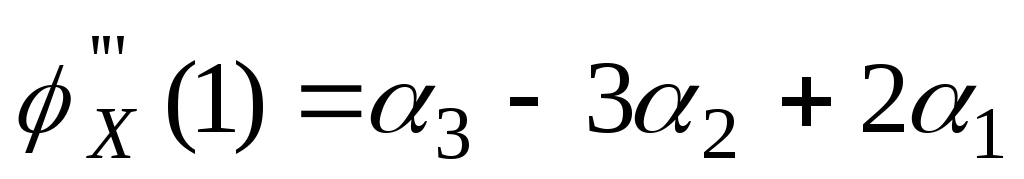
То есть можно
выразить начальные моменты более
высокого порядка, через начальные
моменты более низкого порядка.
23 Интегральная
предельная теорема Муавра-Лапласа
Теорема.
При
равномерно
по
Замечание.
– затабулирована.
Ее значения
приводятся только для 0
x3,5.
Ф(–x)=1–
Ф(x)
Пример.Вероятность
изделию некоторого производства
оказаться бракованным равна 0,005 (p
= 0,005).Чему
равна вероятность, что из n
= 10000 наудачу взятых изделий, бракованных
окажется не более 70 (m
= 70).
– ?
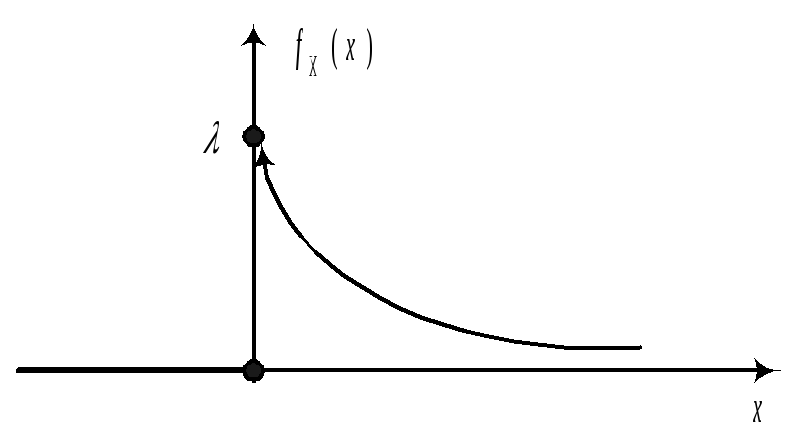
24.Геометрическое
распределение
Опр.СВДТ
Х имеет геометрическое распределение,
если ее возможные значения 0, 1, 2, …,
m,
…, а вероятности этих значений
Комментарий
Вероятности
Pm
для последовательных значений m
образуют геометрическую прогрессию
с первым членом p
и знаменателем q.На
практике геометрическое распределение
появляется в следующих условиях.
Пусть производится ряд независимых
испытаний (опытов) с целью получения
какого-то результата (“успеха”) А.
При каждом опыте “успех” достигается
с вероятностью p.
СВ Х
– это число безуспешных опытов до
первой попытки, в которой появляется
результат А.
Ряд распределения
имеет следующий вид.
X 0
1 2 … m ….
P p
qp q2p
… qmp
…
Найдем числовые
характеристики СВ Х
распределенной по геометрическому
закону.
;
mX=q/p
;
;
На практике чаще
приходится рассматривать не СВ Х,
имеющую геометрическое распределение,
а
Y=X+1
– это число попыток до первого успеха,
включая удавшуюся.Ряд распределения
Y
1 2 … m
….
P
p
qp
… qm–1p
…
–геометрическое
распределение,сдвинутое на 1
(геометрическое плюс1).
mY=M[X+1]=M[X]+1=q/p+1=1/p
DY=D[X+1]=D[X]=q/p2
25. Равномерное
распределение
Опр.
СВНТ Х
называется распределенной равномерно
на [a,b],
если fX(x)=0
(при x[a,b])
fX(x)=C
(при x[a,b]),
X~R(a,b).
Найдем
константу С.
;
;
C=1/(b–a).
Пример.Шкала
измерительного прибора проградуированных
в некоторых единицах. СВ Х – ошибка
при округлении отсчета до ближайшего
целого деления, то она будет иметь
равномерное распределение на (-1/2 ;
1/2).Найдем mX,
DX,
X
– ?
Решение.
Замечание.
Моды
равномерное распределение не имеет,
а медиана совпадает с МО. hX=mX
=(a+b)/2.
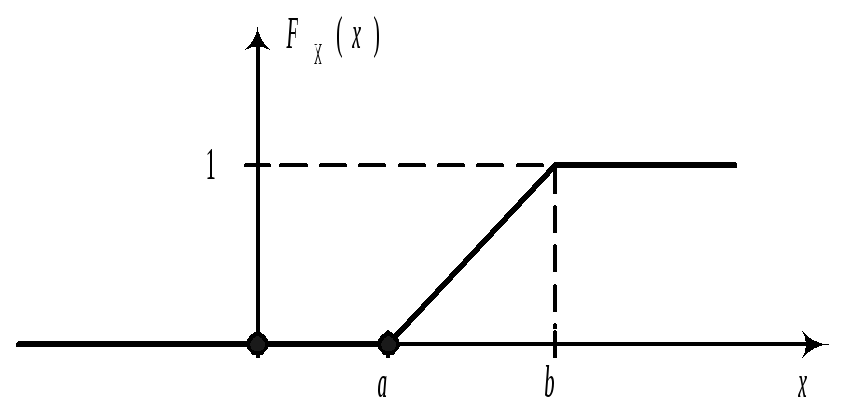
Найдем
функцию распределения и построим ее
график.
FX(x)=P{X<x}
1)Случай.
2)Случай
3)Случай
29.
Совместная
функция распределения
Пусть на одном
и том же вероятностном пространстве
(,A,P)
задано n
СВ,
,
совокупность
– называется многомерной (n-мерной)
СВ или случайным вектором.
Совместная
функция распределения:Рассмотрим
в одном и том же вероятностном
пространстве (,A,P)
набор СВ
.
Так как множество
,
таких пересечения
, поэтому существует вероятность
этого события, которая называется
многомерной функцией
распределения.Замечания:1.В
дальнейшем ограничимся случаем двух
случайных величин
.
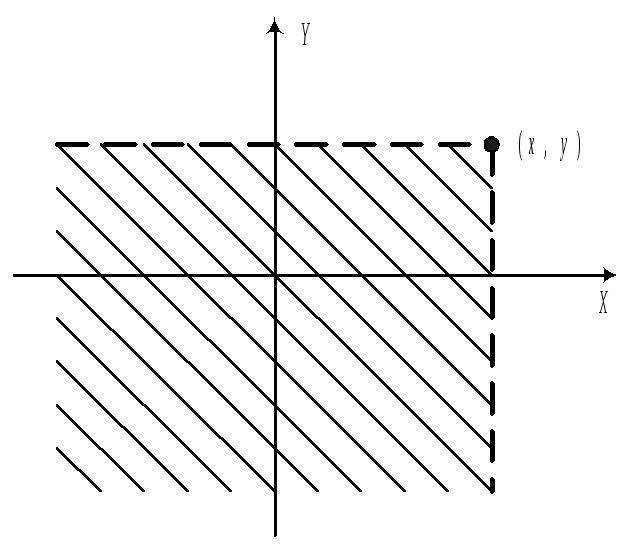
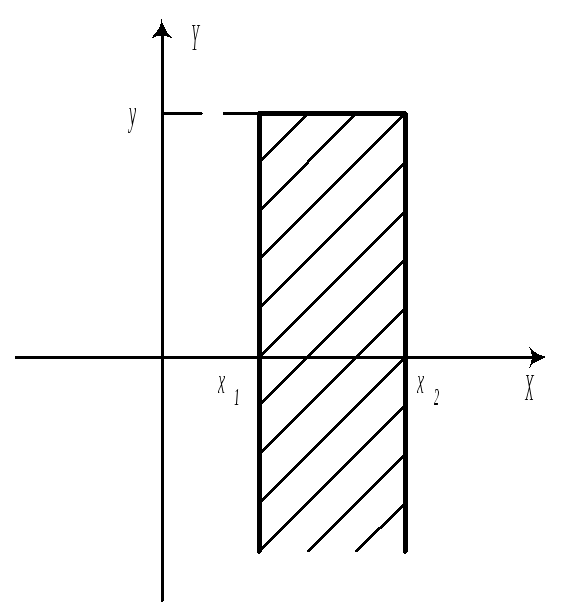
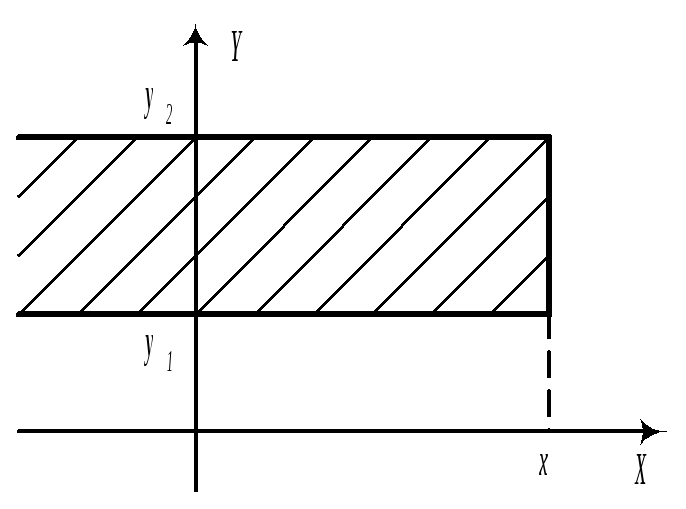
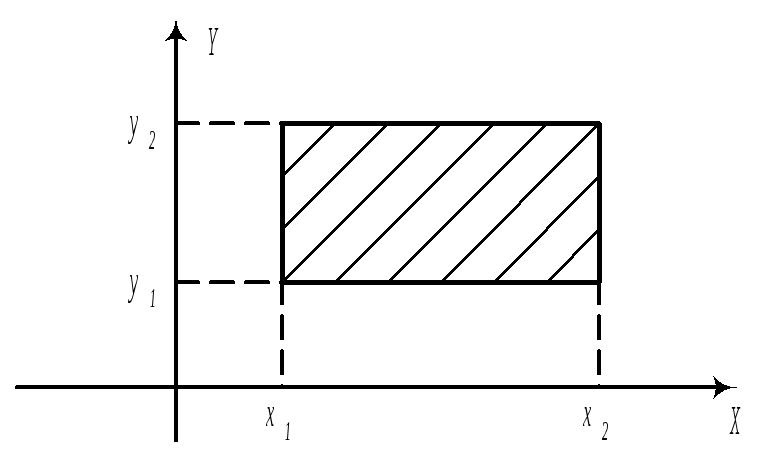
2.
Функция
– вероятность того, что случайная
точка
попадает в бесконечный квадрант с
вершиной в точке
.
С помощью F,
можно вычислить вероятность попадания
случайной точки в полуполосу или в
прямоугольник.
а)
б)
в)
Свойства.
1.
по каждому аргументу не
убывает и непрерывна
слева.
2.
.
3.
.
4. а) При
становится функцией распределения
компоненты x.
.
б) При
становится функцией распределения
компоненты y.
.
34.
Мультипликативные свойства
математических ожиданий, аддитивное
свойство дисперсии
Теорема.
Если СВ X
и Y
независимы,
то M[XY]=M[X]*M[Y].
Доказательство:
Ограничимся
случаем двух дискретных СВ принимающих
конечное множество значений, тогда
В силу аддитивности
МО,
Так как СВ
независимы, то
.
Следствие:
Если СВ
– независимы, то
(доказательство проводится методом
математической индукции).
Из
мультипликативного СВ МО
аддитивное свойство дисперсии.
Теорема. Если
СВ X
и Y
независимы, то D[X+Y]=D[X]+D[Y].
Доказательство:
D[X+Y]=M[((X+Y)–(mX
– mY))2]=
M[((X–
mX)+(
Y
– mY))2]=
M[(X–
mX)2+
2(X– mX)(
Y
–
mY)+
(Y
–
mY)2]=
DX+DY+2
M[(X– mX)(Y
–
mY)]
Так как X
и Y
независимы, то X–
mX
и Y
– mY
независимы
D[X+Y]=DX+DY+2
M[(X– mX)(Y
–
mY)],
где
X–
mX=MX
– mX=0
и MY
– mY=0
D[X+Y]=
DX+DY
.Следствие:
Если СВ X1,
X2
,..,Xn
– независимы, то
37.
Условное МО . Регрессия.
Опр.
Условным математическим ожиданием
одной из СВ входящих в систему (X;
Y)
называется ее МО вычисленное при
условии, что другая СВ приняла
определенное значение. Замечание.
То есть МО найденное на основе условного
закона распределения. Если СВ
дискретные, то
Если СВ X
и Y
непрерывные, то
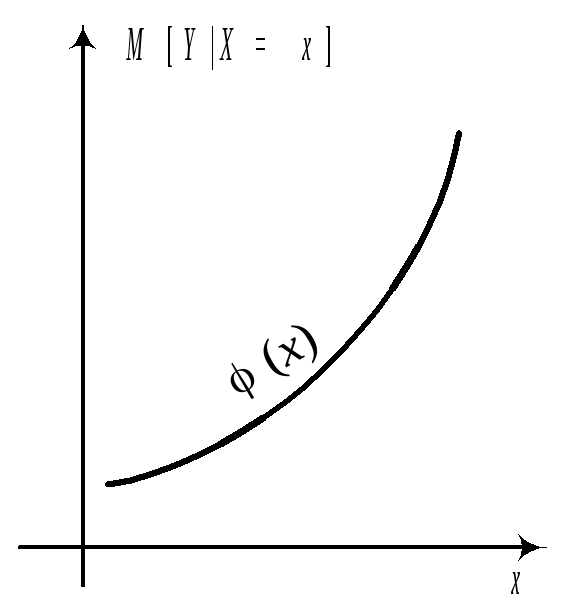
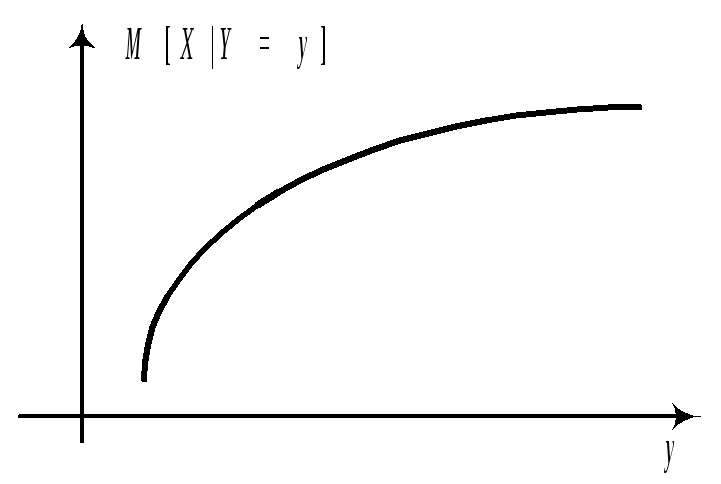
Опр
M[YX=x]=(x)
называется регрессией Y
на x.
M[XY=y]=(y)
называется
регрессией X
на y.
Графики этих
зависимостей от x
и от y
называются линиями регрессии или
кривыми регрессии.
Замечание.
Для независимых СВ линии регрессии
Y
на x
и X
на y
параллельны координатным осям так
как МО каждой из них не зависит от
того, какое значение приняла другая.
Линии регрессии
могут быть параллельны координатным
осям и для зависимых СВ, когда МО
каждой из них зависит от того, какое
значение приняла другая.
Так
как все моменты начальные и центральные
любых порядков представляют собой
МО, то можно говорить об условных
моментах. Например об условных
дисперсиях D[YX=x],
D[XY=y],.
38.Двумерные
нормальные распределения. Опр.Нормальным
законом распределения на плоскости
называется распределение вероятностей
двумерной СВ (X,
Y),
если
Итак,нормальный
закон на плоскости определяется 5-ю
параметрами: mX;
mY;
Y;
Y;
XY
. Убедимся
в том, что если компоненты X
и Y
не коррелированны, то они тогда и не
зависимы.
XY=0
Замечание:
Для нормально распределенных компонент
двумерной СВ понятие независимости
и некоррелированности равносильны.
Найдем
условные законы распределения СВ X
и Y
воспользовавшись формулами.
.
.
Как легко видеть,
каждый из условных законов распределения
является также нормальных с условным
МО и условной дисперсией вычисляемым
по формуле:
Замечание.
Из двух формул для условного МО видно,
что для системы нормально распределенных
X
и Y,
линии регрессии Y
на x
и X
на y
представляют собой прямые линии, то
есть регрессия всегда линейна.
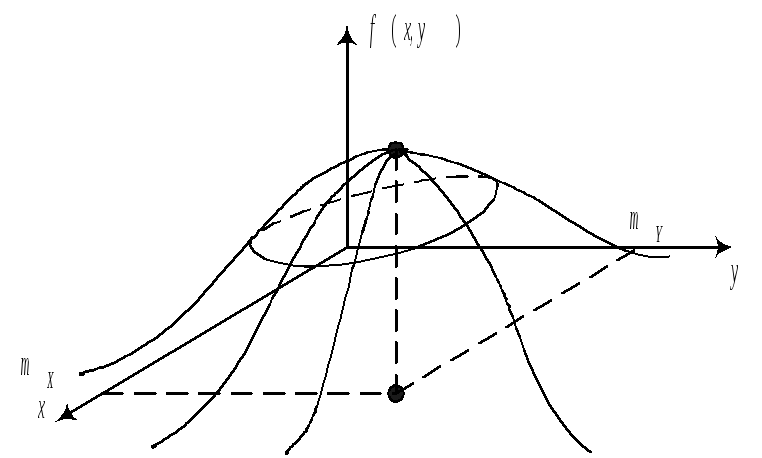
В геометрической
интерпретации график линейной формулы
плотности представляет собой
холмообразную поверхность.
.
Сечение
поверхности
плоскостями параллельными плоскости
XOY
представляют собой эллипсы.
41.Распределение
2.
(“хи-квадрат”).
Пусть
Zi
~N(0;1)
, i=1,2…k,
тогда
–называется
СВ распределенной по закону 2
с k
степенями свободны.
,
.
Распределение
2
определяется одним параметром числом
степеней свободы. С увеличением
степеней свободы распределение 2
медленно приближается к нормальному.
На практике при k
> 30 считают, что
,
где
.Для
СВ, имеющей 2
распределение существуют таблицы
квантилей.
43.
Распределение Фишера.Если
U
и V
независимые СВ, распределенные по
закону 2,
,
,
тогда
имеет распределение, которое называется
F–распределением
или распределением Фишера со степенями
свободы k1
и k2.
(
F–распределение
определяется двумя параметрами k1
и k2
и существует таблица квантилей..
44.
Неравенства Чебышева. Следующие
два неравенства называют неравенствами
Чебышева. Сформулируем их в виде
теорем. Теорема:
x>0
имеют место неравенства:.
Доказательство:
Разложим X
в сумму двух слагаемых
,
так как x
> 0, получаем
.
.
Замечание.
Очень часто второе неравенство
Чебышева дают в такой форме
.
Второе
неравенство Чебышева показывает, что
при малой дисперсии с вероятностью
близкой к 1 СВ Х
концентрируется около своего МО.
48.Статистическое
описание и вычисление оценок параметров
распределения системы двух СВ.
Пусть исход некоторого эксперимента
описывается двумя СВ (X;
Y).Предварительное
представление о зависимости между X
и Y
можно получить, нанося элементы
двумерной выборки (xi
,
yi
)
, i=1,..,n,
в виде точек на плоскость с выбранной
системой координат. Такое представление
называется диаграммой рассеяния.
Опр.
Распределением двумерной выборки
называется распределение двумерного
дискретного СВ случайного вектора,
принимающего значения (xi,,
yi)
с вероятностями 1/n.
Выборочные числовые характеристики
вычисляются как соответствующие
числовые характеристики двумерного
дискретного случайного вектора. Если
объем выборки небольшой, то тогда
вычисления проводятся в следующей
последовательности:
1.
.
Контроль
.
2. Суммы квадратов
отклонений от среднего и произведения
отклонений от среднего
.
3.
;
;
.
49.
Линии регрессии
Для СВ X
и Y.
Регрессией Y
на X
называется условное МО
.
используется
для предсказания значения СВ Y
по фиксированному значению СВ X.
Если
,
то говорят о линейной регрессии Y
на X.
– прямая регрессии.
Оценки параметров
линейной регрессии по выборке (xi
,
yi
)
, i=1,..,n
можно получить, используя МНК из
условия минимума суммы
.
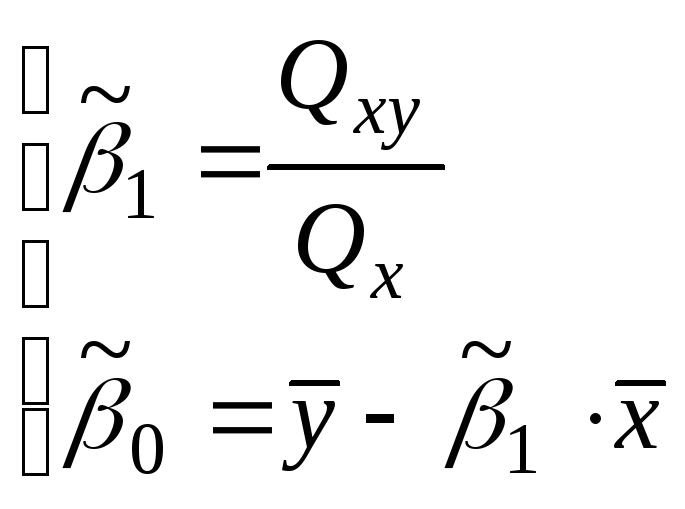
коэффициенты регрессии.
;
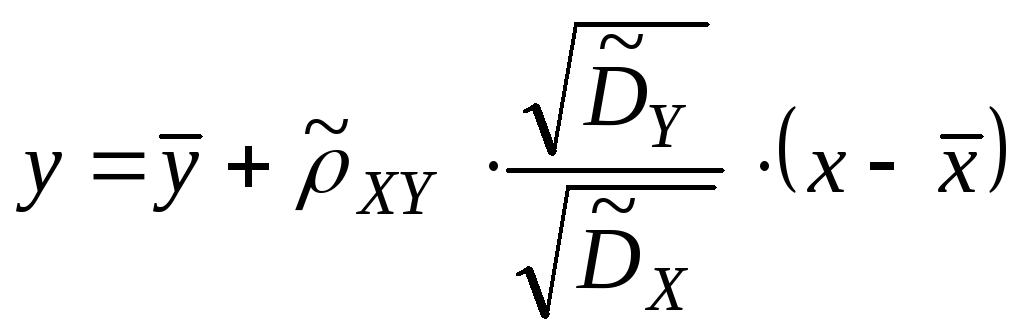
Выборочная
линейная регрессия Y
на X.
Аналогично рассматривается X
на Y.
;
;
.
Обе прямые
регрессий пересекаются в точке с
координатами
.
Угол между этими двумя прямыми
уменьшается при увеличении коэффициента
корреляции. При
обе прямые совпадают. Замечание
Прямые
и
должны быть различны.
52.
Интервальные
оценки. Доверительный интервал.
Доверительная вероятность.
В ряде задач
требуется не только найти для параметра
подходящую оценку
,
но и указать к каким ошибкам может
привести замена параметра
его оценкой
,
т.е. требуется оценить точность и
надежность оценки.
Для определения
точности оценки
в статистике пользуются доверительными
интервалами.
Для определения
надежности оценки
в статистике пользуются доверительной
вероятностью.
Опр.
Доверительным интервалом для параметра
называется интервал
,
содержащий истинное значение параметра
с заданной вероятностью
.
.
Опр.
Число
называется доверительной вероятностью,
а значение
– уровнем значимости.
Замечание.
Нижняя
и верхняя
граница доверительного интервала
определяется по результатам наблюдений
и следовательно является СВ. Поэтому
так и говорят, что доверительный
интервал «накрывает» оцениваемый
параметр с вероятностью
.
Выбор доверительной
вероятности каждый раз определяется
конкретной постановкой задачи. Обычно
р
= 0,9; р
= 0,95; р
= 0,99.
Часто применяют
односторонние доверительные интервалы
(левосторонний),
(правосторонний).
В
простейших случаях метод построения
доверительных интервалов состоит в
следующем
–оценка
,
.
Предположим, что существует непрерывная
и монотонная функция Y,
зависящая от
и
,
но такая, что ее распределение не
зависит от
и других параметров. Для нахождения
границ доверительного интервала
по заданной доверительной вероятности
.
В этом случае можно использовать
неравенство
,
где числа
,
определяются из условия
Рассмотрим
нахождение доверительного интервала
для среднего и дисперсии нормально
распределенной генеральной совокупности.
53. Доверительный
интервал для оценки МО при известной
дисперсии
1)
Доверительный
интервал для оценки МО при известной
дисперсии нормально распределенной
генеральной совокупности.
Пусть
– выборочный вектор n–наблюдений
СВ Х,
где
.
В качестве оценки для m
возьмем
.
Предположим, что
известна. Рассмотрим статистику
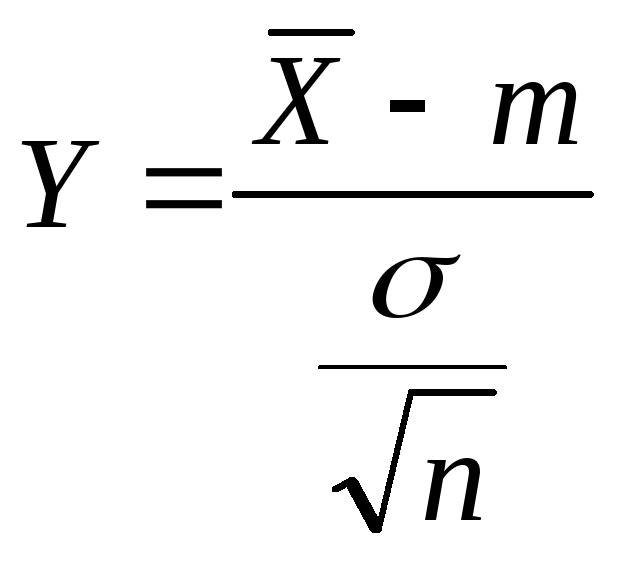
Статистика
.
По
таблице нормального распределения
найдем квантили
и
.
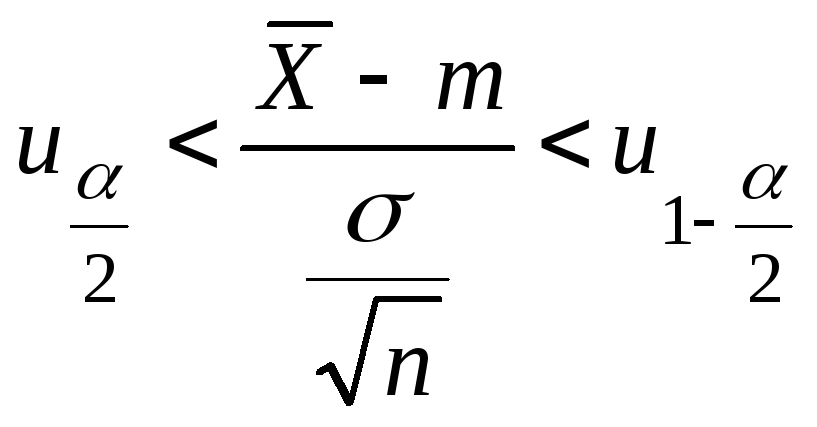
.
.
.
Учитывая,
что
получаем
.
57.
Критерий
и его применение.
Критерий
применяется в частности для проверки
гипотез о виде распределения генеральной
совокупности.
Процедура
применения критерия
для проверки гипотезы H0,
утверждающей, что СВ Х
имеет закон распределения
состоит из следующих этапов.
Этапы:
-
По
выборке найти оценки неизвестных
параметров предполагаемого закона
.
-
Если
Х–СВДТ – определить частоты
,
i
= 1, 2, …, r,
с которым каждое значение встречается
в выборке.
Если
Х–СВНТ – разбить множество значений
на r
– непересекающихся интервалов
и попавших в каждый из этих интервалов
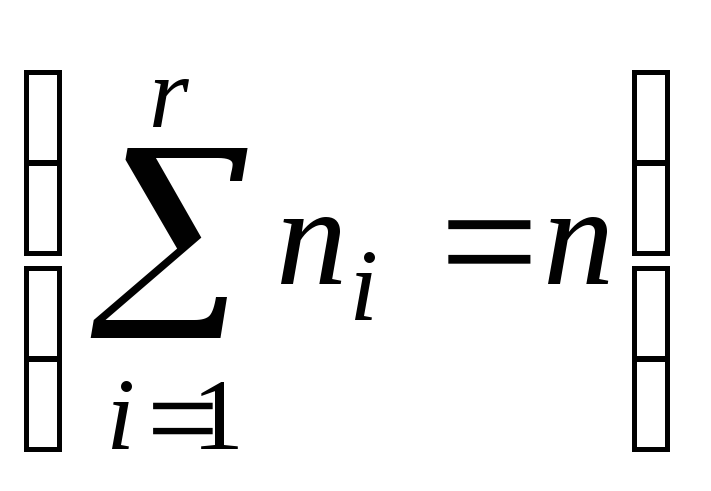
-
Х–СВДТ
вычислить
.
Х–СВНТ
вычислить
.
-
.
-
Принять
статистическое решение.
– гипотеза
Н0
– принимается.
– гипотеза
Н0
– отклоняется.
e
– количество оцениваемых параметров.
Малочисленные
частоты надо будет объединять.
Проверка гипотезы
о равномерном распределении генеральной
совокупности.
n
= 200
А;
|
№ |
(xi-1, |
ni |
|
|
1 |
2 – |
21 |
|
|
2 |
4 – |
16 |
|
|
3 |
6 – |
15 |
|
|
4 |
8 – |
26 |
|
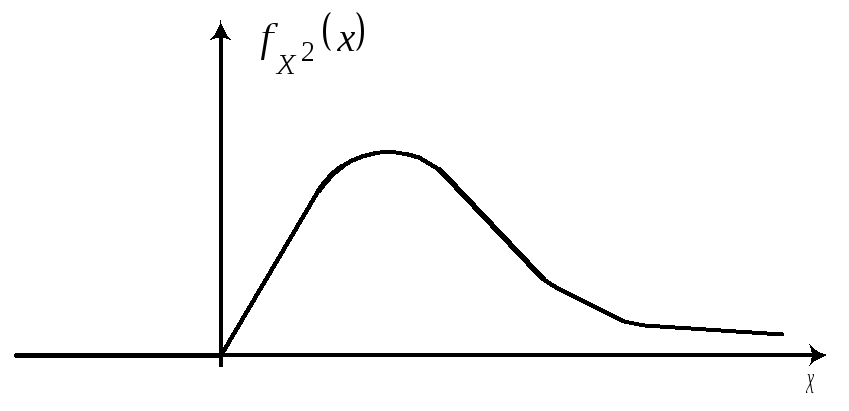
|
5 |
10 – |
22 |
|
|
6 |
12 – |
14 |
|
|
7 |
14 – |
21 |
|
|
8 |
16 – |
22 |
|
|
9 |
18 – |
18 |
|
|
10 |
20 – |
25 |
1.
2.
|
|
|
|
|
21 |
17,3 |
0,79 |
|
16 |
20 |
0,8 |
k
= 10 – 2 – 1 = 7
– нет
основания отвергать гипотезу о том,
что выборка взята из генеральной
совокупности и имеет равномерное
распределение.
5-6..Размещения
и сочетания
Набор
элементов xi1,
xi2,
…, xin
из множества X={x1,…,xn}
называется выборкой объема r
из n-элементов
<n,
r>-выборка.
Выборка называется упорядоченной,
если порядок следования элементов в
ней задан. Замечание:Две
упорядоченные выборки, различающиеся
лишь порядком следования элементов,
считаются различными. Если порядок
следования элементов не является
существенным, то выборка называется
неупорядоченной.
В выборках могут допускаться или не
допускаться повторения элементов.
Упорядоченная
<n,
r>-выборка,
в которой элементы могут повторяться,
называется<n,
r>-размещением
с повторениями. Упорядоченная<n,
r>-выборка
элементы, которой попарно различны,
называется <n,
r>размещением
без повторений (<n,
r>размещением).Замечание<n,n>-размещения
без повторений называются перестановками
множества X.Неупорядоченная<n,r>-выборка,
в которой элементы могут повторяться,
называется <n,
r>-сочетанием
с повторениями. Неупорядоченная
<n,
r>-выборка
элементы, которой попарно различны,
называется <n,
r>-сочетанием
без повторений (<n,
r>-сочетанием).Замечание:Любое
<n,
r>-сочетание
можно рассматривать, как r-элементное
подмножество n-элементного
множества.
Теорема
1:=
nr
Доказательство:
Каждое <n,r>-размещение
с повторениями является упорядоченной
последовательностью длины r.
Причем каждый элемент этой
последовательности может быть выбран
n-способами.
По правилу произведения получаем
=
nnn
.. n
=nr
.
Теорема
2:.
Доказательство:Каждое
<n,r>-размещение
без повторений является упорядоченной
последовательностью длины r.
По правилу произведения получаем
.
Теорема 3:
Доказательство:Каждое
<r,r>-сочетание
без повторений можно упорядочить
r!-способами.
Объединение получаемых таким образом
попарно непересекающихся множеств
<n,r>-размещений
без повторений для всевозможных
<n,r>-сочетаний
без повторений, даст все <n,r>-размещения
без повторений.
(суммирование
производится по всевозможным
<n,r>-сочетаниям
без повторений).
.
Теорема
4:=
7. Геометрические
вероятности .Задача Бюффона.Геометрические
вероятности –
класс моделей вероятностных пространств,
дающий геометрические вероятности.
Пусть Ω={ω} – ограниченное множество
n-мерного
евклидова пространства с конечным
n-мерным
объёмом. Событиями назовём подмножества
Ω, для которых можно определить
n-мерный
объём. Для любого A
A
положим P(A)=A/
Ω ,
где |V|-n-мерный
объем множества V
A.Это
вероятностное пространство служит
моделью задач, в которых частица
случайно бросается в область Ω.
Предполагается, что положение частицы
равномерно распределено на множестве
Ω, т. е. вероятность попадания частицы
в подмножество A
пропорциональна n-мерному
объёму этой области. Замечание:В
классе конечных вероятностных
пространств в систему A
входили все подмножества Ω. При
геометрическом определении вероятности
в качестве A
уже нельзя
взять все подмножества Ω, так как
некоторые из них не имеют n-мерного
объёма. Примеры:
1) Стержень
разламывается на две части в случайной
точке, равномерно распределённой по
длине стержня. Найти вероятность
того, что длина меньшего обломка
окажется не больше трети длины всего
стержня.
Обозначим
за x
расстояние от фиксированного конца
стержня до точки излома.

Задача
Бюффона:Плоскость
расчерчена па-раллельными прямыми,
расстояние между которыми равно a.
На плоскость наудачу брошена игла
длины l
(l<a).
Найти
вероятность того, что игла пересечет
какую-либо прямую. Решение:. Пусть y
– расстояние от центра иглы до
ближайшей прямой (0y
a/2),
а x
– ост-рый угол, составленный иглой с
этой прямой (0x
π2).
Пара чисел (x,
y)
задаёт положение иглы с точностью до
выбора конкретной прямой.
–игла
пересекает прямую.
12. Случайные
величины и законы их распределения
Пусть
(Ω, A,
P)–произвольное
вероятностное пространство. Определение:
Числовая функция X=X()
от элементарного события
называется случайной величиной (СВ),
еслиxR:
{X<x}={X()<x}
A
(*) Комментарий:
Смысл определения состоит в следующем:
поскольку не любое подмножество
пространства Ω
является
событием, и все события составляют
-алгебру
подмножества A,
то, естественно, рассматриваются
только такие функции X=X(),
для которых имеет смысл говорить о
вероятности попадания X=X()
в достаточно
большие числовые множества. Свойство
(*)
гарантирует, что для любого X
неравенство X<x
есть
событие, а, значит, имеет смысл говорить
о его вероятности. Замечание:
Если вероятностное пространство
(Ω,A,P)
является
конечным, то случайной величиной
называется любая числовая функция
от элементарного события.
Определение:
Множество возможных значений случайных
величин X
называется область значений числовой
функции X().
Если это множество является конечным
или счетным, то случайная величина
называется случайной величиной
дискретного типа (СВДТ). Если это
множество является несчетным, то
случайная величина называется
случайной величиной непрерывного
типа (СВНТ). Пример
1: СВДТ.
Опыт – бросание игральной кости. СВ
X
– число
выпавших очков. Множество значений
– {1, 2, 3, 4, 5, 6}.Пример
2: СВНТ.
Опыт – дважды измеряется емкость
конденсатора, с помощью точных
приборов. СВ X
– разность
между результатами первого и второго
измерений. Законом
распределения СВ
называется любое правило (таблица,
функция), позволяющее находить
вероятности всевозможных событий,
связанных со случайной величиной.Если
случайная величина X
имеет данный закон распределения, то
мы будем говорить, что она распределена
по этому закону (подчинена этому
закону распределения).Наиболее простую
форму можно придать закону распределения
СВДТ, обычно этот закон задается рядом
распределений.Рядом
распределений
СВДТ Х
называется
таблица
X
x1
x2
…
xn
P
p1
p2
… pn
pi=P{X=
xi
}, x1<x2<…<
xn<..
Так
как {X= x1
},{X= x2
},… –
попарно несовместны, и сумма этих
событий образует ..
С помощью этой
таблицы можно найти вероятности любых
событий.
Пример
X
1 3 5 7
P
0,1 0,3 0,2 0,4
P{-3X4}=0,1+0,3=0,4
Часто бывает
удобно иметь графическое изображение
ряда распределения, так называемый
многоугольник ряда распределения.
Часто удобной
бывает механическая интерпретация
СВДТ.
P1
+P2
+P3+P4=1
Аналитическое
задание СВДТ
15. Математическое
ожидание
Пусть
вероятность P
на конечном вероятностном пространстве
(,
A
, P)
определяется с помощью элементарных
вероятностей
.
Опр.
МО случайной величины
называется сумма
Замечание.
В литературе математическое ожидание
часто называют средним значением X.
Из определения
МО – вытекают следующие свойства
Свойства:
1.
.
Доказательство:
2.
Аддитивность:
.
Доказательство:
Замечание.
Из свойства 2 по
индукции выводится свойство конечной
аддитивности.
3.
.
Доказательство:
4.
Если
,
то
.
Доказательство:
По
свойствам 2 и 3
.
5. МО СВ X
выражается через ряд распределения
СВ X
с помощью формулы
Доказательство:
Так как СВ
,
тогда
.
Пусть
–
некоторая числовая функция, подставляя
вместо аргумента x
СВ Х,
получим новую СВ
– ?
1 способ. С помощью
закона распределения Y;
2 способ. С помощью
формулы
.
Докажем формулу
для
.
.
Все дальнейшие
выкладки повторяют свойство 5.
19.Биномиальное
распределение
Опр.СВДТ
Х
имеет биномиальное распределение,
если ее возможные значения 0,1,2,…,m,.,n,а
соответствующие вероятности
pm=P{X=m}=Cnm
pmqn–m
m=0,1,..,n
(0<p<1,q=1–p)
Это
распределение зависит от двух
параметров: n,
p.
В
литературе X~B(n,p).
Рассмотрим условия, при которых
возникает биномиальное распределение.
Пусть
производится n
независимых опытов (испытаний), в
каждом из которых событие А
(“успех”) появляется с вероятностью
p,
СВ Х
– это число успехов при n-опытах.
Коментарии:
Опыты называются независимыми, если
вероятность какого-либо исхода каждого
из них не зависит от того, какие исходы
имели другие опыты. Покажем, что СВ Х
имеет биномиальное распределение.B={x=m}
– это количество успехов в n
опытах , равно m.
Событие B
распадается
на ряд вариантов, в каждом варианте
успех достигается m
раз, а неуспех n–m
раз.
Если
успех ставим в соответствие 1. Если
неуспех ставим в соответствие 0.
0,1,1,…,0,1 – всего n
чисел
m
штук – “1” ; n–m
штук – “0”. Так как опыты независимы,
то каждый такой вариант имеет
вероятность P=pm(1–p)n–m
(по теореме умножения), а всего таких
вариантов Cnm
штук, причем все такие варианты
несовместны, то по теореме сложения
вероятностей несовместных событий
следует. P(B)=P{X=m}=
Cnm
pm(1–p)n–m
Найдем
важнейшие числовые характеристики
X~B(n,p).
Воспользуемся производящей функцией
Возьмем
производную по S.
;
;
20.Распределение
Пуассона.
Опр.
СВДТ Х
имеет распределение Пуассона, если
ее возможные значения 0, 1, 2, …, m,
… (счетное множество значений), а
соответствующие вероятности выражаются
формулой
Pm=P{X=m}=(am/m!)e—a.
Замечание.Закон
Пуассона зависит только от a,
смысл этого параметра состоит в
следующем, он одновременно является
МО и дисперсией СВ Х.
;
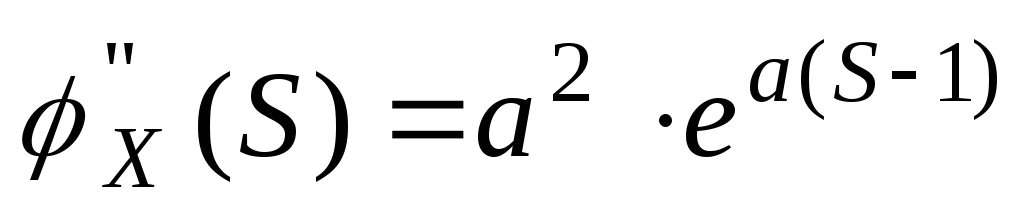
DX=a2+a–
a2=a;
X=a
Рассмотрим
условия, при которых возникает
Пуассоновское распределение. Покажем,
что оно является предельным, для
биноминального распределения при
n
и одновременно р0,
но nра
(а~0,1–10).
Теорема
(Пуассона).
Если n,
р0,
но npа,
то
фиксированного значения m,
где m=0,1,…
.
Доказательство.
фиксированного
значения m.
.
Комментарии:Так
как n-велико,
а вероятность p
— очень мала, то в каждом отдельном
опыте “успех” приходит редко.Поэтому
закон Пуассона в литературе называется
законом редких явлений.Пример:Завод
отправил на базу n=5000
доброкачественных изделий. Вероятность
того, что в пути изделие повредится
p=0,0002.
Найти вероятность того, что на базу
прибудут 3 негодных изделия.Решение.
n=5000.
p=0,0002.
np=1=a
Имеются
специальные таблицы, спомощью которых
можно найти P{X=m}.
26. Показательное
(экспоненциальное) распределение.
Опр.
СВНТ Х
называется распределенной по
показательному (экспоненциальному)
закону с параметром >0
, если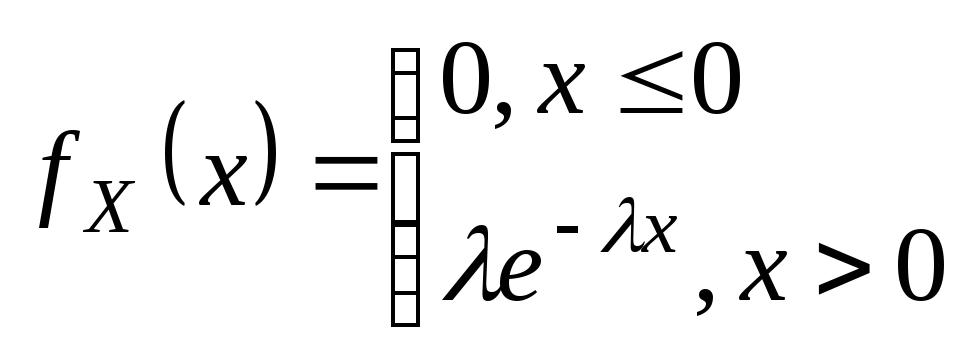
Найдем
mX,
DX,
X
– ?
DX=1/2
X
=1/
Замечание.
Среднее
квадратическое отклонение для
экспоненциального распределения
совпадает с МО.
mX
=X
=1/
Найдем
FX(x)
и построим ее график
I
Случай
.
II
Случай
X
=ln2/
Показательное
распределение тесно связано с
простейшим стационарным Пуассоновским
потоком событий.
Покажем,
что интервал времени Т между двумя
соседними событиями в простейшем
потоке, имеет показательное распределение
с параметром
равным интенсивности потока.
Найдем
.
Для
того, чтобы подсчитать эту вероятность
нужно, чтобы хотя
бы одно
событие потока попало на участок
длины t.
Продифференцировав
,
получим
Показательное
распределение играет большую роль в
Марковских случайных процессах,
теории массового обслуживания и
теории надежности.
31.Непрерывные
двумерные СВ
Пусть A
– -алгебра
множеств двумерного пространства
R2,
порожденная всевозможными
прямоугольниками вида
.
Опр.Двумерной
плотностью распределения
называется такая функция, что
вероятность
, где
.
Из определения
следуют ее свойства.
Свойства.
I.
.
II.
(условие нормировки).
III.
.
IV.
.
Опр.
Двумерная
СВ (X;
Y)
называется непрерывной, если ее
распределение имеет f(x,y)
Пример:(двумерное
равномерное распределение)
Плотность
равномерного распределения на области
конечной двумерной площади
.
Замечание.
По последней
формуле вычисляются так называемые
геометрические вероятности.
Пусть
известна
.
Найдем плотности распределения каждой
из компонент X
и Y.
Решение.
(*)
Продифференцируем
обе части равенства (*) по Х,
получим
32.Зависимые
и независимые СВ,
В
двух предыдущих параграфах было
показано, как зная закон распределения
системы двух (дискретных или непрерывных
СВ) найти законы распределения
отдельных компонент X
и Y.
Вопрос. Можно ли, зная законы
распределения отдельных СВ (X,
Y)
входящих в систему , найти закон
распределения всей системы? Нет, в
общем виде этого сделать нельзя –
это можно сделать только в одном
частном случае, когда СВ X
и Y
образующие эту систему—независимы.
Опр.Две
СВ X
и Y
называются независимыми, если
независимы все связанные с ними
события {X<xi}{Y<yi}{X=xi}{Y=yi}
Замечание.
Так как
зависимость и независимость событий
всегда взаимны, то зависимость и
независимость СВ, также всегда взаимна:
если X
не зависит от Y,
то Y
не зависит от X.
В терминах законов распределения,
независимость СВ можно определить
так: две СВ называются независимыми,
если закон распределения каждой из
них не зависит от того какое значение
приняла другая.Если компоненты X
и Y
двумерного вектора (X,
Y)
независимы, то функция распределения
F(x,y)
выражается, через функции распределения
отдельных компонент. F(x,y)=P{X<x
,Y<y
}
{X<x}и
{Y<y}–
независимы.
F(x,y)=P{X<x
,Y<y }= P{X<x}* P{Y<y }=
FX(x)*
FY(y)
Это правило
является необходимым и достаточным
условием независимости для любого
типа СВ.
1.
Если X
и Y
независимые дискретные СВ с матрицей
распределения
.
2.
Непрерывные СВ.
Если СВ образующие
систему зависимы, то для нахождения
закона распределения системы не
достаточно знать законы распределения
отдельных величин, входящих в систему,
требуется знать так называемый
условный закон распределения одной
из них.
35.Числовые
характеристики системы двух СВ:
Моменты начальные и центральные,
ковариация.
Опр.
Начальным моментом k+S
порядка системы двух СВ (X;Y)
называется K,S=M[XkYS].
Если система для двух дискретных СВ,
то
.
Если (X;Y)
система двух
непрерывных СВ, то
.
Опр.Центральным
моментом порядка k+S
системы двух СВ (X;Y)
называется
.
а) Если (X;Y)
система
двух дискретных СВ, то
б) Если (X;Y)
система
двух непрерывных СВ, то
На практике чаще
всего встречаются моменты I-го
и II-го
порядка.
Точка с координатами
на плоскости OXY
представляет собой характеристику
положения, точек X,
Y,
а их разброс рассеивания происходит
вокруг точек
.
.
Рассмотрим
отдельно.
– ковариация СВ
.
Механическая
интерпретация.
Когда распределение
вероятностей на плоскости ХOY трактуется,
как распределение единичной массы
на этой плоскости, точка
– центр масс распределения, дисперсии
и
– моменты инерции распределения или
относительно точки
в направлении осей OX
и OY
соответственно, а ковариация –
центральный момент инерции распределения
масс.
Теорема:
Если СВ X
и Y
независимы, то
Доказательство:
Для независимых
СВ
,
т.к. X
и Y
независимы.
.
Замечание
Попутно
доказано, что в общем случае
вычисляется по следующей формуле:,
Замечание.
характеризует не только степень
зависимости СВ, но также их рассеявание
вокруг точки центра масс, но к сожалению
размерность
равна произведению размерностей X
и Y.
Чтобы получить безразмерную величину,
характеризующую только зависимость,
а не разброс ковариацию делят на
произведение
.
39. Закон
распределения функции одного случайного
аргумента.
для
СВДТ:
|
X |
x1 |
x2 |
… |
xn |
|
P |
p1 |
p2 |
… |
pn |
Y=(X)
|
Y |
y1 |
… |
ym |
|||
|
P |
|
… |
|
|||
|
1 |
X |
–2 |
–1 |
0 |
1 |
2 |
|
P |
0,1 |
0,15 |
0,3 |
0,05 |
0,4 |
|
Y |
–8 |
–1 |
0 |
1 |
8 |
|
|
P |
0,1 |
0,15 |
0,3 |
0,05 |
0,4 |
|
|
2 |
X |
–2 |
–1 |
0 |
1 |
2 |
|
P |
0,1 |
0,15 |
0,3 |
0,05 |
0,4 |
-
Y
0
1
4
P
0,3
0,2
0,5
Пусть
теперь СВ X
– непрерывна и функция
– функция плотности. Y=(X)
Найдем
закон распределения СВ Y,
но при этом ограничимся случаем, когда
функция (X)
строго монотонна, непрерывна и
дифференцируема в интервале (a,
b)
всех возможных значений СВ X.
СВ
Y
будет определяться по формуле
.
монотонно
возрастает на (a,
b).
–
функция
обратная к функции
.
.
1)
– монотонно возрастает
2)
– монотонно убывает на (a;
b)
Дифференцируя
по y,
получим
45. Теореме
Чебышева. Теорема Бернулли. ЦПТ.
Теорема
(Чебышева):Если
– независимы
и существует С > 0, такая что
,
К = 1, 2, …, n,
тогда
:
Доказательство:
Рассмотрим
и применим к СВ
второе неравенство Чебышева.
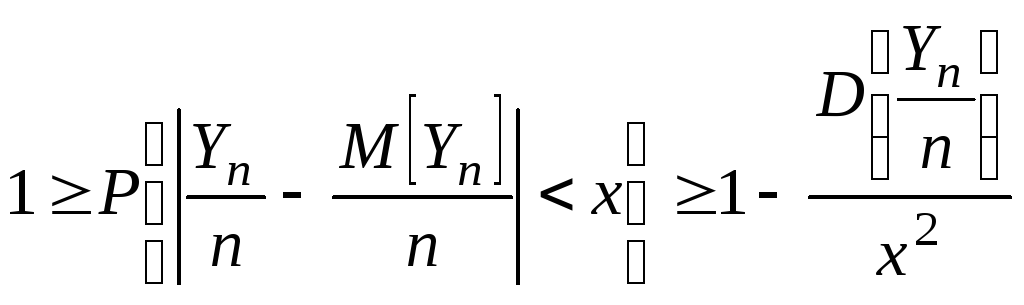
.
В силу аддитивного
свойства дисперсии, получаем
,
.
Следствие:
Если
– независимы
и одинаково распределены, т.е.
,
а
,
где k=
1, …, n,
тогда
.
Замечание.
Предельные утверждения, сформулированные
в теореме Чебышева и следствии к этой
теореме носят название закона больших
чисел (ЗБЧ). ЗБЧ утверждает, что с
вероятностью приближающейся при n
к 1, среднее арифметическое независимых
слагаемых при определенных условиях
становятся близким к константе.
Из утверждения
последнего следствия получаем ЗБЧ в
схеме Бернулли.
Теорема
(Бернулли): Пусть
– число успехов при n
независимых испытаниях с вероятностью
0 < p
< 1 в каждом испытании, тогда
:
.
Доказательство:
Представим
в виде суммы независимых СВ
,
где
,
или при i-ом
испытании произошел успех и
,
если при i-ом
испытании произошел неуспех.
.
Применяя следствие
к теореме Чебышева, получаем утверждение
к теореме Бернулли.
Понятие о теореме
Ляпунова. Формулировка центральной
предельной теоремы (ЦПТ).
Известно, что
нормально распределенные СВ широко
распространены на практике, объяснение
дал Ляпунов (ЦПТ).
Если
СВ Х
представляет собой сумму очень
большого числа взаимно независимых
СВ влияние каждой из которых на всю
сумму ничтожно мало, то СВ Х имеет
распределение близкое к нормальному.
Приведем
формулировку ЦПТ без доказательства.
Теорема(ЦПТ):Если
СВ в последовательности
,
n
= 1, 2, … независимы, одинаково распределены
и имеют конечные
,
, то
:
где
–
стандартизованное среднее арифметическое,
n-независимых
СВ в последовательности.
Замечание
Следствиями ЦПТ
являются локальная и интегральная
теоремы Муавра-Лапласса.
Общее:
и для 50 и для 51:
Пусть неизвестная
функция генеральной совокупности
зависит от некоторого параметра
.
Нужно по наблюдениям оценить параметр.
Для построения оценок используются
статистики – функции от выборочных
значений.
Примеры статистик..
Эта оценка
.
Будет рассматриваться,
как приближенное значение параметра
.Замечание.
Как правило, для оценки параметра
можно использовать несколько статистик,
получая при этом различные значения
параметра
.
Как измерить «близость» оценки
к истинному значению
?
Как определить качество оценки?
Комментарий:
Качество оценки определяется не по
одной конкретной выборке, а по всему
мыслимому набору конкретных выборок,
т.е. по случайному выборочному вектору
,
поэтому для установления качества
полученных оценок моментов
,
следует во всех этих формулах заменить
конкретные выборочные значения
на СВ Xi.
;
;
.
Качество оценки
устанавливают, проверяя, выполняются
ли следующие три свойства
(требования).Требования, предъявляемые
к точечным оценкам:
1. Несмещенность,
т.е.
.
Это свойство
желательно, но не обязательно. Часто
полученная оценка бывает существенной,
но ее можно поправить так, что она
станет несмещенной.
Иногда оценка
бывает смещенной, но асимптотически
несмещенной, т.е.
.
2. Состоятельность,
т.е.
.
Это свойство
является обязательным. Несостоятельные
оценки не используются.
3. Эффективность.
а) Если оценки
и
– несмещенные, то
и
.
Если
,
то оценка
более эффективна, чем
.
б) Если оценки
и
– смещенные, тогда
и
.
Если
,
то оценка
более эффективная, чем
.
Где
– средний квадрат отклонения оценки.
Рассмотрим
использование этих свойств на примерах
выбора оценок МО и дисперсии:
50. Выборочное
среднее:
является несмещенной и состоятельной
оценкой МО генеральной совокупности
(X1
,…,
Xn
),
причем каждое Xi
совпадает
с m
и 2.
а)
Несмещенность.
По определению выборочного вектора
,
причем Xi
– независимые
в совокупности СВ, тогда вычислим
M[Xсред]=M[(1/n)Xi]=(1/n)M[Xi]=
(1/n)M[Xi]=(1/n)nm
.
D[Xсред]=D[(1/n)Xi]=(1/n2)D[Xi]=
(1/n2)D[Xi]=(1/n)n2=2/n
б) Состоятельность
Воспользуемся
неравенством Чебышева:
Применим это
неравенство к
При n
,что
и доказывает состоятельность
.
55.Доверительный
интервал для оценки дисперсии при
неизвестном МО.
3)
Доверительный интервал для оценки
дисперсии при неизвестном МО нормально
распределенной генеральной совокупности.
Пусть
– выборочный вектор n–наблюдений
СВ
.
В этом случае в качестве оценки
дисперсии
используют
.
В
литературе по математической статистике
доказано, что
имеет распределение
.
По
таблице распределения
определяются квантили
и
.

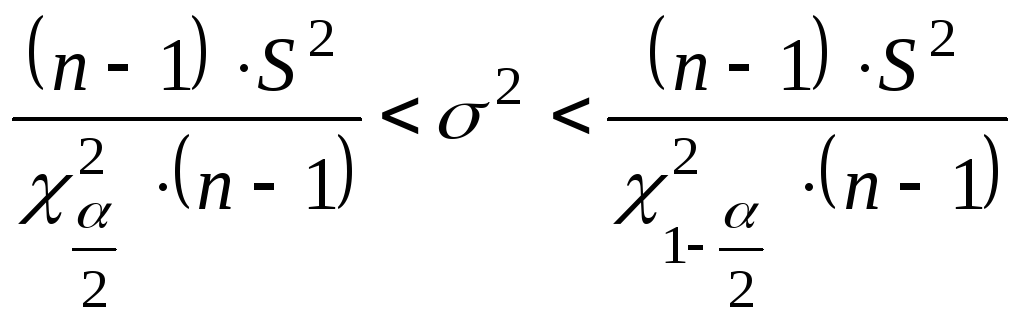
58. Марковская
зависимость испытаний.
Определение
цепи Маркова.
Непосредственным
обобщением схемы независимых испытаний
является схема цепей Маркова.
Пусть
производится последовательность
испытаний, в каждом из которых может
осуществляться одно и только одно из
k
несовместных
событий.
верхние индексы
обозначают номер испытания.
Опр.
Последовательность испытаний образует
простую цепь Маркова, если условная
вероятность в
испытании, где S=1,2,3,K
осуществится событию
,
зависит только от того, какое событие
произошло при S-ом
испытании и не изменяется от добавочных
сведений о том, какие события происходили
в более ранних испытаниях. Замечание.
Часто при изложении теории цепей
Маркова придерживаются иной терминологии
и говорят о некоторой физической
системе S,
которая в каждый момент времени может
находиться в одном из состояний A1
,A2
,K,Ak
и меняет
свое состояние только в моменты t1
,t2
,K,tn
,K
. Для цепей Маркова вероятность перейти
в какое-либо состояние
,
в момент времени tS
зависит только от самого
и того, в каком состоянии система
находилась в момент времени
и не изменяется оттого, что становятся
известными ее состояния в более ранние
моменты времени.
Пример
1. В модели
Бора атома водорода, электрон может
находиться на одной из допустимых
орбит. Обозначим, через
– электрон находится на i
орбите и предположим, что изменение
состояние атома может наступать
только в моменты
(в действительности эти моменты
представляют собой СВ), то тогда
вероятности перехода с i
орбиты на j
орбиту в
момент времени tS
зависит только от i
и j
и не зависит от того на каких орбитах
находился электрон в «прошлом».
Разность
(i–j)
зависит от количества энергии, на
которую изменился заряд атома в момент
времени tS.
Это пример цепи
Маркова с бесконечным числом состояний.
59.
Переходные вероятности.
Матрица
перехода.
Далее будем рассматривать только
однородные цепи Маркова, в которых
условная вероятность появления
события
при условии, что в предыдущем S-ом
испытании осуществилось
не зависит от номера испытания.
Назовем
эту вероятность – вероятностью
перехода и обозначим
.
Полную вероятностную
картину возможных изменений,
осуществляющихся при переходе от
одного испытания к следующему можно
задать с помощью матрицы
– матрица
перехода
Замечание.
-
Очевидно,
что
.
-
Из
того, что при переходе из состояния
система обязательно переходит в одно
из состояний
,
следовательно, в матрице перехода
.
Опр.
Любая квадратная матрица, элементы
которой удовлетворяют следующим
требованиям:
,
называется стохастической.
Одной из главных
задач в теории цепей Маркова является
задача определения вероятности
перехода
.
Рассмотрим
какое-нибудь промежуточное испытание
с номером (S+m).
В этом испытании осуществится
какое-либо одно из возможных событий
,
тогда вероятность перехода
,
а вероятность перехода
.
По формуле полной
вероятности получим
(*)
Обозначим через
Согласно формуле
(*) получаем, что
.
В частности,
когда n
= 2, получаем
n = 3
Отметим частный
случай формулы (*), когда m
= 1
.
Пример 2
Процесс блуждания с отражением.
Пусть частица,
находящаяся на прямой, движется по
этой прямой под влиянием случайных
толчков, происходящих в моменты
времени
Частица может находиться в точках с
целочисленными координатами
.
В точках a,
b
находятся отражающие стенки, каждый
толчок перемещает частицу вправо с
вероятностью
p,
а влево с вероятностью q,
если только частица не находится у
стенки. Если частица находится у
стенки, то любой толчок переводит ее
на 1 внутрь промежутка между стенками.
Получается
цепь Маркова с конечным числом
состояний.
Основные понятия теории вероятности.
Теория вероятности есть наука, изучающая закономерности случайных явлений.
Случайное явление – это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз по-разному.
В природе нет ни одного физического явления, в котором бы не присутствовали элементы случайностей. Факторы, влияющие на случайности, являются случайными и второстепенными.
Под событием в теории вероятности понимается всякий факт, который в результате опыта может произойти или не произойти. Если количественно сравнивать между собой события по степени их возможности, нужно с каждым событием связать число, которое тем больше, чем более возможно событие. Такое число называется вероятностью Р.
Для достоверного события Р=1, для невозможного события Р=0. Несколько событий в данном опыте называются равновозможными, если появление одного из них не более возможно, чем другого Непосредственный подсчет вероятности.
Для того, чтобы определить в опыте вероятность непосредственно из условий самого опыта, необходимо, чтобы различные исходы опыта обладали симметрией, и в силу этого были объективно одинаково возможны.
Несколько событий в одном опыте образуют полную группу событий, если в результате опыта непременно должно появиться хотя бы одно из них.
Несколько событий называются несовместными в данном опыте, если никакие 2 из них не могут появляться вместе.
Несколько событий в данном опыте называются равновозможными, если по условию симметрии есть основания считать, что ни одно из этих событий не является объективно более возможным, чем другие.
Существуют группы событий, обладающих всеми 3мя свойствами. Такие события называются случаями, и решение такой задачи называется схемой случаев или схемой урн. Классическая формула вероятности решает задачи, попадающие под схему урн.
Случайной величиной называется величина, которая в результате опыта может принимать то или иное значение, причем неизвестно заранее, какое именно.
Случайные величины, которые принимают только отдельные друг от друга значения, называются дискретными.
Случайные величины, всевозможные значения которых заполняют собой некоторый промежуток, называются непрерывными.
Суммой 2х событий А и В называют событие С, состоящее в выполнении или события А, или события В, или 2х одновременно.
Произведением 2х событий А и В называется событие С, состоящее в совместном появлении событий А и В.
Классическое определение вероятности.
Если n-общее число элементарных событий и все они равновозможные, то вероятность события А:
,
где mA— число исходов, благоприятствующих появлению события А.
Классическая формула вероятности решает задачи, попадающие под схему урн.
Частота или статистическая вероятность.
Частота – отношение числа появлений нужного события к общему числу опытов.
р=0 – для невозможных событий и р=1 для достоверных событий.
Частоту событий называют статистической вероятностью, и про нее говорят, что при увеличении количества опытов частота сходится по вероятности увеличения Р.
Геометрическая вероятность. Задача о встрече.
Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности — вероятности попадания точки в область (отрезок, часть плоскости и т. д.).
Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством
Р = Длина l / Длина L.
З а м е ч а н и е 1. Приведенные определения являются частными случаями общего определения геометрической вероятности. Если обозначить меру (длину, площадь, объем) области через mes, то вероятность попадания точки, брошенной наудачу (в указанном выше смысле) в область g — часть области G, равна
Р = mes g / mes G.
З а м е ч а н и е 2. В случае классического определения вероятность достоверного (невозможного) события равна единице (нулю): справедливы и обратные утверждения (например, если вероятность события равна нулю, то событие невозможно). В случае геометрического определения вероятности обратные утверждения не имеют места. Например, вероятность попадания брошенной точки в одну определенную точку области G равна нулю, однако это событие может произойти, и, следовательно, не является невозможным.
Задача о встрече:
Два лица и
условились встретиться в определенном месте между двумя и тремя часами дня. Пришедший первым ждет другого в течении 10 минут, после чего уходит. Чему равна вероятность встречи этих лиц, если каждый из них может прийти в любое время в течение указанного часа независимо от другого?
Решение. Будем считать интервал с 14 до 15 часов дня отрезком [0,1] длиной 1 час. Пусть («кси») и
(«эта») — моменты прихода
и
(точки отрезка [0,1]). Все возможные результаты эксперимента – множество точек квадрата со стороной 1:
.
Можно считать, что эксперимент сводится к бросанию точки наудачу в квадрат. При этом благоприятными исходами являются точки множества (10 минут = 1/6 часа). То есть попадание в множество
наудачу брошенной в квадрат точки означает, что
и
встретятся. Тогда вероятность встречи равна
Теоремы сложения вероятностей
Теорема: Вероятность суммы 2х несовместных событий равняется сумме их вероятностей.
Р(А+В)=Р(А)+Р(В)
Д-во:
Используем схему случаев, из которых m~A, k~B, P(A)=m/n, P(B)=k/n. Поскольку А и В несовместные, то получается, что
m+k=A+B
P(A+B)= (m+k)/n=m/n+k/n=P(A)+P(B )/
1. Если события А1…Аn образуют полную группу несовместных событий, то сумма их вероятностей = 1. Противоположными называются 2 несовместных события, которые образуют полную группу {0;P}
A=”0” – P
A=”P” – q
2. Сумма вероятностей события и его противоположности равняется 1
P(A)+P(-A)=1
p+q=1
3. Вероятность суммы 2х совместных событий А и В равняется сумме их вероятности без учета вероятности их совместного появления.
P(A+B)=P(A)+P(B)-P(AB)
Теоремы умножения вероятностей
Событие А называется независимым от события B, если вероятность события А не зависит от того, произошло событие В или нет.

События А и В называются независимыми тогда, когда Р(АВ) = Р(А)*Р(В)
Вероятность события А, вычисляемая при условии, что имело место другое событие В, называется условной вероятностью Р(А/В)=P(AB)/P(B).
Свойства условных вероятностей.
Свойства условных вероятностей аналогичны свойствам безусловных вероятностей.
1. 0 £ Р(А/В) £ 1, т.к. ; АВ Ì В, Р(АВ) £ Р(В)
2. Р(А/А)=1
3. ВÌА, è Р(А/В)=1
4.
5. Р[(A+C)/B] = Р(А/В) + Р(C/В) – Если события А и С несовместны
Р[(A+C)/B] = Р(А/В) + Р(C/В) — Р(АC/В) – Если события А и С совместны
Теорема. Вероятность произведения двух событий равна произведению вероятности одного события на условную вероятность другого.
Док—во:
P(AB)=l/n; P(A)=m/n; P(B/A)=l/m; l/n=m/n * l/m => P(AB)=P(A)*P(B/A)
Следствия:
1. Если событие А не зависит от события В, то и событие В не зависит от события А
2. Вероятность произведения 2х независимых событий равна произведению вероятностей этих событий.
P(AB)=P(A)*P(B)
Формула полной вероятности
Формула полной вероятности является следствием теории сложения и умножения. Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с событиями H1…Hn, образующих полную группу несовместных событий. Эти события называются гипотезами.
Докажем, что вероятность события А будет вычисляться по формуле:
Доказательство: Т.к. гипотезы Hi образуют полную группу, то событие А может появиться только в комбинации с какой-нибудь из гипотез. Т.к. гипотезы несовместны, то и комбинации будут несовместны, поэтому к ним можно применить теорему сложения:
А=Н1*А+Н2*А+…+Hn*A;
Формула Бейеса
Имеется полная группа несовместных гипотез H1…Hn. Вероятность этих гипотез до опыта известна. Произведен опыт, в результате которого произошло событие А.
Условные вероятности гипотез находятся по формуле:
P(A*Hi)=P(A)*P(Hi/A)=P(Hi)*P(A/Hi);

Повторение испытаний. Частная теорема о повторении опыта.
На практике часто прилагаются задачи, в которых один и тот же опыт повторяется неоднократно., причем нас интересует не отдельное, а общее число появлений события А в серии опытов. Предположим, что опыты являются независимыми величинами. Независимые опыты могут проводиться в одинаковых или разных условиях. При одинаковых условиях вероятность события А будет одинаковой и к нему относится частная теорема. Если опыты разные, то к нему относится общая теорема о повторении опытов.
Частная теорема:
Вероятность одного сложного события, состоящего в том, что в n испытаниях событие A наступит ровно k раз и не наступит n—k раз, по теореме умножения вероятностей независимых событий равна .Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по k элементов, т.е.
. Т.к. эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равно сумме вероятностей всех возможных сложных событий. Поскольку вероятности всех этих сложных событий одинаковы, то искомая вероятность равна вероятности одного сложного события, умноженной на их число:
. Эта формула называется формулой Бернулли.
Определение вероятностей по формуле Бернулли усложняется при больших значениях n и при малых p или q. В этом случае удобнее использовать приближенные асимптотические формулы. Если , а
, но
, то в этом случае
Эта формула определяется теоремой Пуассона. Если в схеме Бернулли количество опытов n достаточно велико , а вероятность р события А в каждом опыте постоянно, то вероятность
может определяться по приближенной формуле Муавра-Лапласа:
,
где ;
— локальная функция Лапласа, которая табулирована и приводится в справочниках. Данная формула отражает, так называемую, локальную теорему Муавра-Лапласа.
Вероятность появления события А не менее m раз при n опытах вычисляется по формуле:
Вероятность появления события А хотя бы один раз при n опытах
Наивероятнейшее число наступление события А в n опытах, в каждом из которых оно может наступить с вероятностью p (и не наступить с вероятностью q=1-p), определяется из двойного неравенства
Если событие А в каждом опыте может наступить с вероятностью p, то количество n опытов, которое необходимо произвести для того, чтобы с заданной вероятностью Рзад. можно было утверждать, что данное событие А произойдет по крайней мере один раз, находится по формуле:
Частная теорема о повторении опытов касается того случая, когда вероятность события А во всех опытах одна и та же.
Общая теорема о повторении опытов. Производящая функция.
Если производятся n независимых опытов в различных условиях, причем вероятность появления события А в i-м опыте равна то вероятность Р
того, что событие А в n опытах появится m раз, равна коэффициенту при Z
в разложении по степеням Z производящей функции
где
Функция распределения случайной величины.
Рассмотрим дискретную случайную величину Х со своими значениями, каждое из которых является возможным, но не равновозможным: p(x1)=p1 … p(xn)=pn. Сумма pi=1- критерий сходимости.
Законом распределения случайной величины называется всякое соотношение, которое связывает между собой значения всякой величины и ее вероятности.
|
X |
x1 |
x2 |
… |
xn |
|
P |
p1 |
p2 |
… |
pn |
Функция распределения:
Для непрерывной случайной величины невозможно составить закон распределения, поэтому для количественной характеристики удобно пользоваться не вероятностью отдельного события Х, а вероятностью события Х<x, где х – некоторая текущая переменная. Эти вероятности образуют некоторую функцию оси X.
F(x)=F(X<x)- интегральный закон распределения.
Свойства:
1. Функция F(x)-неубывающая функция.
Любой x2>x1 => F(x2)≥F(x1).
Д-во: Пусть х2>х1. Событие, состоящее в том, что Х примет значение, меньшее х2, можно подразделить на 2 несовместных события:
1) Х примет значение, меньшее х1, с вероятностью Р(Х<x1)
2) Х примет значение, удовлетворяющее неравенству x1≤X<x2, с вероятностью Р(x1≤X<x2).
По теореме сложения имеем
P(X<x2)=P(X<x1)+P( x1≤X<x2). Отсюда: P(X<x2)-P(X<x1)= P( x1≤X<x2) или F(x2)-F(x1)=P(x1≤X<x2). Так как любая вероятность есть число неотрицательное, то F(x2)-F(x1)≥0, или F(x2)≥F(x1), чтд.
2. F(-∞)=0
3. F(∞)=1
4. Значения функции распределения принадлежат отрезку [0;1]
0≤F(x)≤1
Д-во: Свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть неотрицательное число, не превышающее 1.
Функция распределения есть вероятность того, что случайная величина X, в результате нашего опыта попадает левее т. х.
Для дискретных случайных величин также можно составить функцию распределения:
F(x)=P(X<x)=.
Вероятность попадания случайной величины на заданный участок.
P(α≤x≤β)=F(β)-F(α).
Вероятность попадания для непрерывной случайной величины в любое отдельное значение =0.
Плотность распределения
Плотность распределения — производная абсолютно непрерывной функции распределения.
P(x<X<x+∆x)=F(x+∆x)-F(x)
P(α<x<β)=
F(x)=P(X<x)=P(-∞<X<x)
F(x)=
Основные свойства плотности распределения:
1. f(x)≥0
Д-во: Функция распределения – неубывающая функция, следовательно, ее производная – функция неотрицательная.
2. =1
Несобственный интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение, принадлежащее интервалу(-∞;∞). Очевидно, такое событие достоверно, следовательно, вероятность его равна 1.
Эти 2 свойства геометрически определяют то, что кривая распределения всегда лежит выше оси Ох и площадь под кривой равна 1.
Числовые характеристики случайных величин.
Числовые характеристики случайной величины – числа, суммарно описывающие случайную величину.
Математическое ожидание:
Для дискретной случ. величины – сумма произведений всех ее возможных значений на их вероятности.
M(x)=x1p1+x2p2+…+xnpn
Если дискретная случ. величина Х принимает счетное множество возможных значений, то
причем мат ожидание существует, если ряд в правой части сходится абсолютно.
Математическое ожидание числа появлений события в одном испытании равно вероятности этого события.
Вероятностный смысл : математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.
Математическое ожидание M(X) числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления событий в каждом испытании: M(X)=np.
Для непрерывной случ величины:
Отклонением называют разность между случ величиной и ее мат ожиданием.
Мат ожидание отклонения равно 0: M[X—M(X)]=0, т.к. M[X—M(X)]=M(X)-M[X(X)]=M(X)-M(X)=0.
Дисперсия:
Для дискретной случ величины — мат ожидание квадрата отклонения случ величины от ее мат ожидания: D(X)=M[X—M(X)]². Для тот, чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности
D(X)=M(X²)-[M(X)]²
Д-во: D(X)= M[X—M(X)]²=M[X²-2XM(X)+M²(X)]=M(X²)-2M(X)M(X)+M²(X)=M(X²)-M²(X).
Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность p появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D(X)=npq.
Для непрерывной случ величины:
Среднее квадратическое отклонение:
– для оценки рассеяния возможных значений случ величины вокруг ее среднего значения.
Начальный момент:
Центральный момент:
Мода случ величины – наиболее вероятное значение этой случ величины.
Медиана – это такое значение, для которого выполняется равенство p(x<Me)=P(x>Me). Геометрически это означает, что медиана является абсциссой точки, которой площадь, ограниченная кривой распределения, делится пополам.
Неравенство Чебышева
Пусть имеется случ величина Х, заданная mx и D(x). Неравенство Чебышева утверждает, что каково бы ни было положительное число α, вероятность того, что величина Х отклонится от своего мат ожидания не меньше, чем на α, ограничено сверху величиной:
Д-во:
Возьмем произвольное положительное число α>0 и вычислим вероятность того, что величина Х отклонится от своего mx не меньше чем на α.
Вероятность , т.е. надо просуммировать вероятности значений, которые не лежат на AB.
Т.к. не все члены суммы не отрицательны, то D(x) можно уменьшить , взяв не все значения xi:
что и требовалось доказать.
Теорема Чебышева
Среднее арифметическое (, my=mx, D(y)=D(x)/n) случ величины Х есть случ величина с очень маленькой дисперсией и при достаточно большом n ведет себя как не случ.
Теорема Чебышева:
При достаточно большом числе независимых опытов, среденее арифметическое наблюдаемых значений случ величины сходится по вероятности к ее mх.
P(|xn—a|<ε)>1-δ, ε, δ -> 0.
P(|(∑xi/n) — mx|1-δ
Д—во:
Y=∑xi/n, my=mx, Dy=Dx/n.
Применим к случ величине Y неравенство Чебышёва.
P(|y—my|≥ε)≤Dy/ε²=Dx/nε².
P(|(∑xi/n)-mx|≥ε)≤δ
P(|(∑xi/n)-mx|<ε)>1-δ
Обобщенная теорема Чебышева и теорема Маркова.
Обобщенная теорема Чебышёва:
Если х1…хn независимые случ величины, заданные своими мат ожиданиями и дисперсиями, и сами все дисперсии ограничены сверху одним и тем же числом L (D(x)<L), то при возрастании n ср. арифметическое наблюдаемых значений сходится к среднему арифметическому их мат ожиданий:
P(|(∑xi/n) – (∑mxi/n)|<ε)>1-δ;
Теорема Маркова:
Если имеются ЗАВИСИМЫЕ случ величины х1..хn и если при n->∞ выполняется условие , то среднее арифметическое наблюдаемых значений случ величины Х сходится к среднему арифметическому их мат ожидания.
Характеристические функции
Характеристической функцией случ величины Х называется функция , которая представляет собой мат ожидание некоторой комплексной величины
. Если х является дискретной случ величиной, заданной своим законом распределения, то ее характеристическая функция выглядит так:
Если х — непрерывная случ величина, то ее характеристическая функция:
Преобразование, которому надо подвергнуть f(x), чтобы получить g(x), является преобразование Фурье.
Свойства характеристических функций:
1. y=ax, gy(t)=gx(at)
2. y=∑Xk, gy(t)=∏gxk(t)
Центральная предельная теорема
Если x1…xn – независимые случ величины, имеющие один и тот же закон распределения, с мат ожиданием и дисперсией, то при неограниченном увеличении n, закон распределения Y неограниченно приближается к нормальному закону.
Yn=∑Xk
Д-во: согласно 2му свойству характеристической функции (все значения имеют одинаковый закон распределения, а значит и характеристическая функция у всех одинакова):
…
Следствие из теоремы Ляпунова-теоремы Лапласа.
Теорема Лапласа:
x1…xn – независимые случ величины, заданные своими мат ожиданиями и дисперсией. Предположим, что условия центральной предельной теоремы выполнены и число слагаемых достаточно для того, чтобы случ величина Y=∑Xi была распределена по нормальному закону. Тогда
Д-во: Пусть производится n независимых опытов, в каждом из которых событие А может появиться с вероятностью p. Согласно теореме Ляпунова следующие случ величины будут приближаться к нормальному закону распределения:
Локальная теорема Лапласа:
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события А равняется pn, наступит ровно k раз приблизительно равно:
Интегральная теорема Лапласа:
Вероятность того что в n независимых испытаниях, в каждом из которых вероятность появления события А=р, событие наступит не меньше к1 раз и не больше к2 раз, равна:
Pn(k1,k2)≈Ф(Xk2)-Ф(Xk1).
Xk1=(k1-np)/; Xk2=(k2-np)/
;
Свойства числовых характеристик(мат ожидание, дисперсия).
Мат ожидание:
1. Математическое ожидание постоянной величины равно самой постоянной:
M(C)=C
Д-во: Будем рассматривать постоянную С как дискретную случайную величину, которая имеет одно возможное значения С и принимает его с вероятностью р=1. М(С)=С*1=С.
2. Постоянный множитель можно выносить за знак математического ожидания: М(СХ)=СМ(Х)
Д-во: Пусть случайная величина Х задана законом распределения вероятностей:
|
Х |
x1 |
x2 |
… |
xn |
|
p |
p1 |
p2 |
… |
pn |
или
|
СХ |
Сx1 |
Сx2 |
… |
Сxn |
|
p |
p1 |
p2 |
… |
pn |
Математическое ожидание случ. величины СХ:
M(CX)=Cx1p1+Cx2p2+…Cxnpn=C(x1p1+x2p2+…xnpn)=CM(X) => M(CX)=CM(X).
3. Математическое ожидание произведения двух независимых случ. величин равно произведению их мат ожиданий. M(XY)=M(X)M(Y)
Д-во: Пусть независимы случайные величины Х и Y заданы своими законами распределения вероятностей:
|
X |
x1y1 |
Y |
y1y2 |
|
p |
p1p2 |
g |
g1g2 |
Составив все значения, которые может принимать случ. величина XY, напишем закон распределения XY.
|
ХY |
x1y1 |
x2y1 |
x1y2 |
x2y2 |
|
p |
p1g1 |
p2g1 |
p1g2 |
p2g2 |
Мат ожидание равно сумме произведений всех возможных значений на их вероятности:
M(XY)=x1y1*p1g1+x2y1*p2g1+x1y2*p1g2+x2y2*p2g2=y1g1(x1p1+x2p2)+y2g2(x1p1+x2p2)=
=(x1p1+x2p2)(y1g1+y2g2)=M(X)M(Y).
Следствие:
M(XYZ)=M(X)M(Z)M(Y)
4. Мат ожидание суммы двух случ величин равно сумме мат ожиданий слагаемых:
M(X+Y)=M(X)+M(Y)
Д-во: Пусть случ величины X и Y заданы следующими законами распределения:
|
X |
x1 |
x2 |
Y |
y1 |
y2 |
|
p |
p1 |
p2 |
g |
g1 |
g2 |
Составим все возможные значения величины X+Y: x1+y1; x2+y1; x1+y2; x2+y2. Обозначим их вероятности соответственно p11, p12, p21 и p22. Мат ожидание X+Y равно:
M(X+Y)=(x1+y1)p11+(x1+y2)p12+(x2+y1)p21+(x2+y2)p22=x1(p11+p12)+x2(p21+p22)+
+y1(p11+p21)+y2(p12+p22).
p11+p12=p, т.к. Событие «Х примет значение х1» влечет за собой событие «Х+Y примет значения x1+y1 или x1+y2», вероятность которого равно p11+p12. Следовательно, p11+p12=p1.
Аналогично: p21+p22=p2; p11+p21=g1 и p12+p22=g2. Получим:
M(X+Y)=(x1p1+x2p2)+(y1g1+y2g2)=M(X)+M(Y)
Следствие:M(X+Y+Z)=M(X)+M(Y)+M(Z)
Дисперсия:
1. D(C)=0;
Д-во: D(C)=M{[C—M(C)]²}=M[(C—C)²]=M(0)=0.
2. D(CX)=C²D(X)
Д—во: D(CX)=M{[CX-M(CX)]²}= M{[CX-CM(X)]²}=M{C²[X-M(X)]²}=C²M{[X-M(X)]²}=C²D(X).
3. D(X+Y) =D(X)+D(Y).
Д—во: D(X+Y) = M[(X+Y)²]-[M(X+Y)]²= M[X²+2XY++Y²]-[M(X)+M(Y)]²=M(X²)+2M(X)M(Y)+
+M(Y²)-M²(X)-2M(X)M(Y)-M²(Y)={ M(X²)-[M(X)]²}+{ M(Y²)-[M(Y)]²}=D(X)+D(Y).
Следствие 1: D(X+Y+Z)=D(X)+D(Y)+D(Z)
Следствие 2: D(C+X)=D(X)+D(C)=D(X)
4. D(X-Y)=D(X)+D(Y)
Д-во: D(X—Y)=D(X)+D(-Y)=D(X)+(-1)²D(Y)=D(X)+D(Y)
Нормальное распределение
Нормальным называют распределение вероятностей непрерывной случ величины, которое описывается плотностью:
где a-мат ожидание, а σ – среднее квадратическое отклонение Х.
1. D(f)=R
2.
3.
4.
Вероятность того, что Х примет значение, принадлежащее интервалу (α,β)
P(α<X<β)=Ф((β—a)/σ)-Ф((α—a)/σ), где – функция Лапласа.
1. Ф(-∞)=0
2. Ф(+∞)=1
3. Ф(-х)=1-Ф(х)
P(mx—l<x<mx+l)=Ф(l/σ)-Ф(-l/σ)=2Ф(l/σ)-1
Асимметрия, эксцесс, мода и медиана нормального распределения соответственно равны:
As=0, Ek=0, M0=a, Me=a, где a=M(x).
Правило «трех сигма».
Если случайная величина распределена нормально, то абсолютная величина ее отклонения от мат ожидания не превосходит утроенного среднего квадратического отклонения.
Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:
Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.
Это правило называется правилом трех сигм.
Равномерное распределение
На практике очень часто встречаются случ числа, про которые заранее известно, чтоих значения лежат в пределах некоторого интервала, и все значения случ величины одинаково вероятны.
О таких случ числах говорят, что они распределены равномерно. Плотность такого распределения сохраняет постоянное значение, а именно f(x)=1/(b—a). Вне этого интервала f(x)=0.
Вероятность попадания значения случ числа в заданный интервал (a;b), можно вычислить по формуле: .
График плотности равомерного распределения симметричен относительно прямой x=(a+b)/2, поэтому M(x)=(a+b)/2. Этот же результат можно получить по формуле .
. Подставив формулы, полученные выше, получим D(x)=(b—a)²/12. В таком случае среднее квадратическое отклонение случ числа равно
.
Закон Пуассона
Рассмотрим дискретную случ величину Х, которая может принимать целые неотрицательные значения. Говорят, что случ величина распределена по закону Пуассона, если вероятность того, что она примет значение m, выражена формулой: , где a – параметр Пуассона.
Доказательство:
x
/
/
.
Равенство мат ожидания и дисперсии параметру а используется на практике для решения вопроса правдоподобия гипотезы о том, что случ величина Х распределяется по закону Пуассона.
Пусть на оси абсцисс случ образом распределены точки. Допустим, что случ образом распределенные точки удовлетворяют следующим условиям:
1. Вероятность попадания того или иного числа точек на отрезок l зависит от их положения на оси абсцисс.
2. Точки распределяются по оси абсцисс независимо друг от друга.
3. Вероятность попадания на малый участок ∆х 2х и более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки.
Выделим отрезок длины l и рассмотрим дискретную случ величину Х числа точек, попадающих на этот отрезок.
Докажем, что случ величина Х подчиняется закону Пуассона и посчитаем вероятность того, что на этот отрезок попадет ровно m точек. Рассмотрим маленький участок этой прямой ∆х и вычислим вероятность того, что на этот участок попадет хотя бы одна точка.
Согласно 3му условию вероятность попадания на участок ∆х 2 и более точек ≈0, поэтому мат ожидание будет = вероятности попадания хотя бы одной точки на ∆х.
Для вычисления вероятности попадания на отрезок l ровно m точек, разделим этот участок на n частей: ∆х = l/n, p=λ∆x=λl/n, q=1-(λl/n).
По условию 2 вероятности попадания точек являются независимыми можно использовать частную теорему повторения опыта:
Параметр a определяется как ср. число точек, попадающих на нужный отрезок.
Функция одного случайного аргумента
Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента X: Y=φ(X).
Рассмотрим случай, когда X— дискретная случ величина с возможными значениями x1…xn, вероятности которых p1…pn. Тогда Yтоже является дискретной случ величиной со всевозможными случ событиями: y=f(x1)…y=f(xn).
Т.к. событие «величина X примет значение xi» влечет за собой событие «величина Y примет значение f(xi)», то вероятности всевозможных значений Y соответственно равны p1…pn.
Мат ожидание случ величины будет рассчитываться: M(y)=M(f(x))=∑f(xi)pi.
При записи закона распределения вероятности y руководствуются следующими правилами:
1. Если различным возможным значениям X соответствуют различные возможные значения Y, то вероятности соответствующих значений X и Y равны между собой: P(X=xi)=P(y=f(xi))=pi.
2. Если различным возможным значениям Х соответствуют значения Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений Y.
Рассмотрим непрерывную случ величину Х, которая задана своей плотностью, если у=f(x) дифференцируемая монотонная функция, обратная функция которой x=φ(y), то плотность распределения случ величины y определяется след функцией: g(y)=f[φ(y)|φ’(y)].
Соответствующее мат ожидание:
Если отыскание ф-ии g(y) является затрудненным, то можно исп. след формулу:
.
.
Функция двух случайных аргументов
Если каждой паре возможных значений случ величин X и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случ аргументов X и Y: Z=φ(X, Y).
1. Пусть X и Y – дискретные независимые случ величины. Для того, чтобы составить закон распределения функции Z=X+Y, надо найти все возможные значения Z и их вероятности. Т.к. X и Y независимые случ величины, то zi=xi+yi, pz=px*py. Если zi=zj, то их вероятности складываются.
2. Пусть X и Y – непрерывные случ величины. Доказано: если X и Y независимы, то плотность распределения g(z) суммы Z=X+Y (при условии, что плотность хотя бы одного из аргументов задана на интервале(-∞;∞) одной формулой) может быть найдена с помощью формулы:
, где f1, f2 – плотности распределения аргументов.
Если возможные значения аргументов неотрицательны, то g(z) находят по формуле:
Плотность распределения суммы независимых случ величин называют композицией, а закон распределения вероятностей называют устойчивым, если композиция таких законов есть тот же закон. M(z)=M(x)+M(y); D(z)=D(x)+D(y).
Закон распределения двумерной случайной величины
Законом распределения дискретной двумерной случ величины называют перечень возможных значений этой величины, т.е. пар чисел (xi, yj) и их вероятностей P(xi, yj).
|
y/x |
x1 |
x2 |
… |
xn |
|
y1 |
p(x1, y1) |
p(x2, y1) |
… |
p(xn, y1) |
|
y2 |
p(x1, y2) |
p(x2, y2) |
… |
p(xn, y2) |
|
… |
… |
… |
… |
… |
|
ym |
p(x1, ym) |
p(x2, ym) |
… |
p(xn, ym) |
Зная закон распределения двумерной дискретной случ величины, можно найти законы распределения каждой из составляющих. Например: События (X=x1, Y=y1)…(X=x1, Y=Ym) – несовместны, поэтому вероятность P(x1) того, что Х примет значение х1, по теореме сложения такова: P(x1)=p(x1, y1)+…+p(x1, ym). Т.о. вероятность того, что Х примет значение xi, равна сумме вероятностей «столбца хi». Аналогично, сложив «строки Yj», получим вероятность P(Y=yj).
Статистическое распределение выборки. Эмпирическая функция распределения. Полигон и гистограмма.
Пусть для изучения количественного признака Х из генеральной совокупности извлечена выборка x1…xk объема n. Наблюдавшиеся значения xi признака X называют вариантами, а последовательность вариант, записанных в возрастающем порядке, — вариационным рядом.
Статистическим распределением выборки называют перечень вариант xi вариационного ряда и соответствующих им частот ni (сумма всех частот равна n) или относительных частот wi(сумма = 1).
Статистическое распределение выборки можно задать также в виде последовательности интервалов и соответствующих им частот.
Эмпирической функцией распределения – называют функцию F*(x), определяющую для каждого значения х относительную частоту события X<x: F*(x)=nx/n, где nx – число вариант, меньших х, n— объем выборки. Эмпирическая функция обладает следующими свойствами:
1. Значения эмпирической функции принадлежат отрезку [0;1].
2. F*(x) – неубывающая функция.
3. Если x1 – наименьшая варианта, а xk – наибольшая, то F*(x)=0 при x≤x1 и F*(x)=1 при x≥xk.
А. Дискретное распределение признака X. Полигоном частот называют ломанную, отрезки которой соединяют точки (x1,n1)…(xk,nk), где xi – варианты выборки и ni – соответствующие им частоты.
Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (xk,wk), где xk – варианты выборки, а wk— соответствующие им относительные частоты.
Б. Непрерывное распределение признака X. При непрерывном распределении признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на ряд частичных интервалов длины h, и находят ni – сумму частот вариант, попавших в i-тый интервал. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны соотношению ni/h. Площадь прямоугольника равна h(ni/h)=ni – сумме частот вариант, попавших в интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны соотношению wi/h. Площадь прямоугольника равна соответствующей относительной частоте, а площадь гистограммы = 1.
Числовые характеристики статистического распределения
Критерии согласия(критерии Пирсона).
Допустим, что данное статистическое распределение выровнено с помощью некоторой теоретической кривой. Как бы хорошо ни была подобрана теоретическая кривая, между ней и мтатистич. распределением неизбежны некоторые расхождения. Критерий согласия отвечает на вопрос, объясняются ли эти расхождения ошибками измерения или расхождение явл. существенным и подобранная нами кривая плохо выравнивает статистическое распределение.
Выдвигается гипотеза Н, состоящая в том, что случ величина X подчиняется данному закону распределения. Для того, чтобы принять или опровергнуть гипотезу Н, рассматривают некоторую величину Н, характеризующую степень расхождения теоретического и статистического распределений.
В зависимости от выбора величины Н существует несколько критериев согласия. Используем для доказательства критерий χ² или критерий Пирсона.
Предположим, что произведено m независимых опытов, в каждом из которых случ величина Х приняла некоторое значение. Результаты записываются в виде статистического ряда. Для теоретического значения распределения можно найти теоретическую вероятность попадания случ величины в каждый интервал. Проверим согласованность теоретического и статистического распределений: выберем в качестве меры расхождения сумму квадратов отклонения, взятых с некоторым коэффициентом Сi.
Коэффициент Сi вводится, потому что в общем случае отклонения, относящиеся к различным разрядам нельзя считать равноправными.
Пирсон полагает, что если в качестве веса взятьCi=n/pi, то при больших значениях n распределение величины U обладает следующими свойствами: оно практически не зависит от ф-ии распределения, а зависит только от числа разрядов.
Распределение χ² зависит от параметра r, называемым числом степеней свободы, с увеличением которого распределение медленно приближается к нормальному.
После расчета χ² для статистического распределения по расчетным таблицам находим значение χ-критическое. Если χ² -критическое > χ² -наблюдаемого – нет оснований опровергать гипотезуH.
Функция распределения системы двух случайных величин
Систему случ чисел величин X и Y изображают случ точкой на плоскости с координатами (X,Y), тогда вместо т. используется понятие случ вектора. Функция распределения системы 2х случ величин называется вероятностью совместного выполнения двух неравенств:
P(x,y)=P(X<x)P(Y<y). Геометрически это означает, что функция распределения есть вероятность попадания случ точки в бесконечный квадрат с вершиной в точке (X,Y), лежащий ниже и левее этой точки.
Свойства функции распределения:
1. x2>x1, F(x2,y)≥F(x1,y)
y2>y1, F(x,y2)≥F(x, y1)
2. F(x,-∞)=F(-∞,y)=F(-∞,-∞)=0
3. F(∞,∞)=1
4. F(x, ∞)=F(x); F(∞,y)=F(y);
Плотность распределения системы двух случайных величин.
Плотностью распределения системы 2х случ величин называется вторая смешанная частная производная от функции распределения:
P((x,y)cP∆)=F(x+∆x, y+∆y)-F(x+∆x, y)-F(x, y+∆y)+F(x,y)
Плотность распределения системы случ величин представляет собой плотность распределения массы в точке с координатами x,y.
f(x,y)dxdy
Элем. вероятность f(x,y)dxdy есть вероятность попадания в элемент. прямоугольник со сторонами dx, dy. Эта вероятность равна объему параллелепипеда, ограниченного сверху поверхностью f(x,y) и отражающегося на элементарный участок dxdy.
Свойства плотности:
1. f(x,y)≥0
2. — полный объем тела, ограниченного поверхностью распределения с плоскостью xOy = 1.
Условные законы распределения.
Зная совместный закон распределения можно легко найти законы распределения каждой случайной величины, входящей в систему. Однако, на практике чаще стоит обратная задача – по известным законам распределения случайных величин найти их совместный закон распределения. В общем случае эта задача является неразрешимой, т.к. закон распределения случайной величины ничего не говорит о связи этой величины с другими случайными величинами. Кроме того, если случайные величины зависимы между собой, то закон распределения не может быть выражен через законы распределения составляющих, т.к. должен устанавливать связь между составляющими. Все это приводит к необходимости рассмотрения условных законов распределения.
Определение. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина приняла определенное значение, называется условным законом распределения. Условный закон распределения можно задавать как функцией распределения, так и плотностью распределения.
Условная плотность распределения вычисляется по формулам:
Условная плотность распределения обладает всеми свойствами плотности распределения одной случайной величины.
Зависимые и независимые случайные величины.
2 случ величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.
Следовательно, условные распределения независимых величин равны их безусловным распределениям.
Теорема: Для того, чтобы случайные величины X и Y были независимыми, необходимо и достаточно, чтобы функция распределения системы (X, Y) была равна произведению функций распределения составляющих:
F(x, y)=F1(x)F2(y)
Доказательство: а) необходимость. Пусть X, Y –независимы, тогда X<x, Y<y тоже независимы и P(X<x, Y<y)=P(X<x)P(Y<y); F(x,y)=F1(x)F2(y).
б) Достаточность: Пусть F(x, y)=F1(x)F2(y) => P(X<x, Y<y)=P(X<x)P(Y<y) => X, Y— независимы.
Следствие: Для того, чтобы непрерывные случайные величины X и Y были независимыми, необходимо и достаточно, чтобы плотность совместного распределения системы (X, Y) была равна произведению плотностей распределения составляющих:
f(x, y)=f1(x)f2(y)
Доказательство: а) необходимость. Пусть X и Y – независимые непрерывные случайные величины. Тогда F(x,y)=F1(x)F2(y). Дифференцируя это равенство по x, затем по y, имеем:
или f(x, y)=f1(x)f2(y).
б) достаточность: Пусть f(x, y)=f1(x)f2(y). Интегрируя по х, затем по у, получим
или F(x,y)=F1(x)F2(y). => X, Y – независимы.
Метод наименьших квадратов.
Метод наименьших квадратов (МНК) — метод оценки параметров модели на основании экспериментальных данных, содержащих случайные ошибки. В основе метода лежат следующие рассуждения: при замене точного (неизвестного) параметра модели приблизительным значением необходимо минимизировать разницу между экспериментальными данными и теоретическими (вычисленными при помощи предложенной модели). Это позволяет рассчитать параметры модели с помощью МНК с минимальной погрешностью.
Мерой разницы в методе наименьших квадратов служит сумма квадратов отклонений действительных (экспериментальных) значений от теоретических. Выбираются такие значения параметров модели, при которых сумма квадратов разностей будет наименьшей – отсюда название метода:
= min
где Y – теоретическое значение измеряемой величины, y – экспериментальное.
При этом полученные с помощью МНК параметры модели являются наиболее вероятными.
Метод наименьших квадратов, а также его различные модификации (нелинейный МНК, взвешенный МНК и т.д.) широко используется в аналитической химии, в частности, при построении градуировочной модели. Как правило, предполагается линейная зависимость (параметры которой требуется установить) между аналитическим сигналом и содержанием определяемого вещества. В этом случае метод наименьших квадратов позволяет оптимизировать параметры градуировки (и получить наименьшую погрешность анализа), а сумма квадратов разностей теоретического и экспериментального значения аналитического сигнала является мерой погрешности градуировки и линейно связана с так называемой остаточной дисперсией (дисперсией адекватности модели)
![Шпаргалка по теории вероятностей и математической статистике [04.10.08]](https://studrb.ru/files/works_screen/21/9.png)
Тема: Шпаргалка по теории вероятностей и математической статистике
Раздел: Бесплатные рефераты по теории вероятностей и математической статистике
Тип: Шпаргалка | Размер: 434.63K | Скачано: 1742 | Добавлен 04.10.08 в 15:24 | Рейтинг: +126 | Еще Шпаргалки
Вопросы к экзаменационному зачету:
1. Классификация случайных событий. Классическое определение вероятности. Свойства вероятности события, непосредственный подсчет вероятности. Примеры.
2. Статистическое определение вероятности события и условия его применимости. Пример.
3. Несовместимые и совместимые события. Сумма событий. Теорема сложения вероятностей с доказательством. Пример.
4. Полная группа событий. Противоположные события. Соотношения между вероятностями
противоположных событий (с выводом). Пример.
5. Зависимые и независимые события. Произведение событий. Понятие условной вер-ти. Теорема умножения вер-тей с док-вом. Пример.
6. Формулы полной вер-ти и Байеса с док-вом. Примеры.
7. Повторные независимые испытания. Формула Бернулли с выводом. Примеры.
8. Локальная теорема Муавра-Лапласа, условия её применимости. Св-ва ф-ии f(x). Пример.
9. Асимптотическая ф-ла Пуассона и условия её применимости. Пример.
10. Интегральная теорема Муавра-Лапласа и условия её применимости. Функция Лапласа f(x) и её свойства. Пример.
11. Следствия из интегральной теоремы Муавра-Лапласа с выводом. Примеры.
12. Понятие случайной величины и её описание. Дискретная слв и её закон (ряд) распределения. Независимые слв. Примеры.
13. Математ. операции над дискретными слвелечинами. Приведите пример построения закона распределения слвел Z=X+Y или Z=XY по заданным распределениям X и Y.
14. Математическое ожидание дискретной случвел и его свойства с выводом. Примеры.
15. Дисперсия дискретной случвел и её свойства с выводом. Примеры.
16. Математическое ожидание и дисперсия числа m и частности mn наступлений события в n-повторных независимых испытаниях, с выводом.
17. Случайная величина, распределённая по биномиальному закону, её математическое ожидание и дисперсия. Закон распределения Пуассона.
18. Функция и распределения случайной величины, её определение, свойства и график.
19. Непрерывная случайная величина (НСВ). Вероятность отдельного взятого значения НСВ. Математическое ожидание и дисперсия НСВ. (+Функция распределения НСВ.)
20. Плотность вероятности Непрерывных СВ, её определение, свойства. Кривая распределения. Связь между функцией распределения и плотностью вероятности НСВ. Математическое ожидание и дисперсия НСВ.
21. Определение нормального закона распределения. Теорико-вероятный смысл его параметров. Нормальная кривая и зависимость её положения и формы от параметров.
22. Функция распределения нормальной распределённой слвеличины и её выражение через функцию Лапласа.
23. Формулы для определения вероятности: а)попадания нормально распределённой слвел в заданный интервал; б) её отклонения от математического ожидания. Правило «трёх сигм».
24. Центральная предельная теорема. Понятия о теореме Ляпунова и её значение. Пример.
25. Понятие двумерной (n-мерной) слвел. Примеры. Таблица её распределения. Условные распределения и их нахождение по таблице распределения.
26. Ковариация и коэффициент корреляции (КК) слвеличин. Связь между некоррелированностью и независимостью слвеличин.
27. Понятие о двумерном нормальном законе распределения. Условные математические ожидания и дисперсии.
28. Неравенство Маркова (лемма Чебышева) с док-вом для дискретной слвеличины. Пример.
29. Неравенство Чебышева для средней арифметической слвеличин. Теорема Чебышева с док-м и её значение и пример.
30. Теорема Чебышева с выводом и его частные случаи для слв, распределённой по биномиальному закону, и для частности события.
31. Закон больших чисел. Теорема Бернулли с док-м и её значение. Пример.
32. Вариационный ряд, его разновидности. Средняя арифметическая и дисперсия ряда. Упрощённый способ их расчёта.
33. Генеральная и выборочные совокупности. Принцип образования выборки. Собственно-случайная выборка с повторным и бесповторным отбором членов. Репрезентативная выборка. Основная задача выборочного метода.
34. Понятие об оценке параметров генеральной совокупности. Свойства оценок: несмещенность, состоятельность, эффективность.
35. Оценка генеральной доли по собственно – случайной выборке. Несмещённость и состоятельность выборочной доли.
36. Оценка генеральной средней по собственно – случайной выборке. Несмещённость и состоятельность выборочной средней.
37. Оценка генеральной дисперсии по собственно – случайной выборке. Смещённость выборочной дисперсии (без вывода).
38. Понятие об интервальном оценивании. Доверительная вероятность и доверительный интервал. Предельная ошибка выборки. Ошибки репрезентативности выборки (случайные и систематические).
39. Формула доверительной вер-ти при оценке генеральной доли признака. Средняя квадратическая ошибка повторной и бесповторной выборок и построение доверительного интервала для генеральной доли признака.
40. Формула доверительной вер-ти при оценке генеральной средней. Средняя квадратическая ошибка повторной и бесповторной выборок и построение доверительного интервала для генеральной средней.
41. Определение необходимого объёма повторной и бесповторной выборок при оценке генеральной средней и доли.
42. Статистическая гипотеза и статистический критерий. Ошибки 1 и 2 ряда. Уровень значимости и мощности критерия. Принцип практической уверенности.
43. Построение теоретического закона распределения по опытным данным. Понятие о критериях согласия.
44. Критерий согласия x – Пирсона и схема его применения.
45. Функциональная, статистическая и корреляционная зависимости. Различия между ними. Основные задачи теории корреляции.
46. Линейная парная регрессия. Система нормальных уравнений для определения параметров прямых регрессии. Выборочная ковариация. Формулы для расчета коэффициентов регрессии.
47. Оценка тесноты связи. Коэффициент корреляции (выборочный), его свойства и оценка достоверности.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Бесплатная оценка
+126
04.10.08 в 15:24
Автор:nastyav
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Шпаргалки на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Шпаргалки для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Добавить работу
Если Шпаргалка, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
Похожие работы
- Шпоры по теории вероятностей и математической статистике
- Шпаргалка по теории вероятностей и математической статистике
- Шпаргалки по теории вероятностей и математической статистике
- Ответы на вопросы по теории вероятностей к экзамену
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Подборка по базе: Кукоба И.А._КТМ-02-22. Культура и её функции. Понятие культуры , ОСНОВЫ ПОЛИТОЛОГИИ И ТЕОРИИ ГОСУДАРСТВА.doc, Практические задания по предмету.docx, работа письменная по предмету Реглам. и нормир..docx, Понятие стати теории.docx, Лекция. Математическая грамотность. Понятие, подходы к развитию , 3. Лысенко Особенности развития познават.УУД у мл. школьн .Свя, Программа по предмету ОБЖ 1 курс ФГОС3+ТМ 107.doc, Курсовая Основные теории происхождения государства.docx, Практическая работа 5. Практикум по разработке учебных заданий д
1. Предмет теории вероятностей. Понятие случайного события.
2. Основные типы событий, алгебра событий.
События, которые могут произойти в результате опыта, можно подразделить на три вида:
а) достоверное событие – событие, которое всегда происходит при проведении опыта;
б) невозможное событие – событие, которое в результате опыта произойти не может;
в) случайное событие – событие, которое может либо произойти, либо не произойти.
Алгебра событий.
Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В.
Суммой нескольких событий, соответственно, называется событие, заключающееся в том, что произошло хотя бы одно из этих событий.
Назовем все возможные результаты данного опыта его исходами и предположим, что множество этих исходов, при которых происходит событие А (исходов, благоприятных событию А), можно представить в виде некоторой области на плоскости. Тогда множество исходов, при которых произойдет событие А+В, является объединением множеств исходов, благоприятных событиям А или В (рис. 1).
Произведением АВ событий А и В называется событие, состоящее в том, что произошло и событие А, и событие В. Аналогично произведением нескольких событий называется событие, заключающееся в том, что произошли все эти события.
Разностью АB событий А и В называется событие, состоящее в том, что А произошло, а В – нет.
Введем еще несколько категорий событий.
События А и В называются совместными, если они могут произойти оба в результате одного опыта. В противном случае (то есть если они не могут произойти одновременно) события называются несовместными.
Говорят, что события А1, А2,…,Ап образуют полную группу, если в результате опыта обязательно произойдет хотя бы одно из событий этой группы.
В частности, если события, образующие полную группу, попарно несовместны, то в результате опыта произойдет одно и только одно из них. Такие события называют элементарными событиями.
События называются равновозможными, если нет оснований считать, что одно из них является более возможным, чем другое.
3.Понятие вероятности события. Классическое, статистическое и геометрическое определение вероятности. Свойства вероятностей.
При изучении случайных событий возникает необходимость количественно сравнивать возможность их появления в результате опыта. Поэтому с каждым таким событием связывают по определенному правилу некоторое число, которое тем больше, чем более возможно событие. Это число называется вероятностью события.
Если все события, которые могут произойти в результате данного опыта,
а) попарно несовместны;
б) равновозможны;
в) образуют полную группу,
то говорят, что имеет место схема случаев.
Можно считать, что случаи представляют собой все множество исходов опыта. Пусть их число равно п ( число возможных исходов), а при т из них происходит некоторое событие А (число благоприятных исходов). Вероятностью события А называется отношение числа исходов опыта, благоприятных этому событию, к числу возможных исходов:
— (1.1)
1. классическое определение вероятности.
Свойство 1. Вероятность достоверного события равна единице.
Свойство 2. Вероятность невозможного события равна нулю.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Если требуется определять вероятность события иным образом, то введем вначале понятие относительной частоты W(A) события A как отношения числа опытов, в которых наблюдалось событие А, к общему количеству проведенных испытаний:
(1.2)
где N – общее число опытов, М – число появлений события А.
2. Статистической вероятностью события считают его относительную частоту или число, близкое к ней.
Из формулы (1.2) следует, что свойства вероятности, доказанные для ее классического определения, справедливы и для статистического определения вероятности.
Для существования статистической вероятности события А требуется:
возможность производить неограниченное число испытаний;
устойчивость относительных частот появления А в различных сериях достаточно большого числа опытов.
Недостатком статистического определения является неоднозначность статистической вероятности.
3. геометрическая вероятность.
Пусть на отрезок L наудачу брошена точка. Это означает, что точка обязательно попадет на отрезок L и с равной возможностью может совпасть с любой точкой этого отрезка. При этом вероятность попадания точки на любую часть отрезка L не зависит от расположения этой части на отрезке и пропорциональна его длине. Тогда вероятность того, что брошенная точка попадет на отрезок l, являющийся частью отрезка L, вычисляется по формуле:
где l – длина отрезка l, а L – длина отрезка L. Можно дать аналогичную постановку задачи для точки, брошенной на плоскую область S и вероятности того, что она попадет на часть этой области s:
где s – площадь части области, а S – площадь всей области. В трехмерном случае вероятность того, что точка, случайным образом расположенная в теле V, попадет в его часть v, задается формулой:
где v – объем части тела, а V – объем всего тела.
4. Элементы комбинаторики. Схемы выбора без возвращения и с возвращением.
Определим основные комбинации.
Перестановки – это комбинации, составленные из всех п элементов данного множества и отличающиеся только порядком их расположения. Число всех возможных перестановок
Рп = п!
Размещения – комбинации из т элементов множества, содержащего п различных элементов, отличающиеся либо составом элементов, либо их порядком. Число всех возможных размещений
(1.4)
Сочетания – неупорядоченные наборы из т элементов множества, содержащего п различных элементов (то есть наборы, отличающиеся только составом элементов). Число сочетаний
Схема выбора без возвращения. 
4 .


5. Теорема сложения вероятностей.
7. Зависимые и независимые события. Теорема умножения вероятностей.
Теорема умножения вероятностей.
Теорема 2.3 (теорема умножения). Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:
р (АВ) = р (А) · р (В/А). (2.6)
Доказательство.
Воспользуемся обозначениями теоремы 2.1. Тогда для вычисления р(В/А) множеством возможных исходов нужно считать тА (так как А произошло), а множеством благоприятных исходов – те, при которых произошли и А, и В ( тАВ ). Следовательно,
откуда следует утверждение теоремы.
Следствие. Если подобным образом вычислить вероятность события ВА, совпадающего с событием АВ, то получим, что р (ВА) = р (В) · р (А/В). Следовательно,
р (А) · р (В/А) = р (В) · р (А/В). (2.7)
Событие В называется независимым от события А, если появление события А не изменяет вероятности В, то есть р (В/А) = р (В).
Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий, в противном случае события называют зависимыми.
Если событие В не зависит от А, то и А не зависит от В. Действительно, из (2.7) следует при этом, что р (А) · р (В) = р (В) · р (А/В), откуда р (А/В) = р (А). Значит, свойство независимости событий взаимно.
Теорема умножения для независимых событий имеет вид:
р (АВ) = р (А) · р (В) , (2.8)
то есть вероятность произведения независимых событий равна произведению их вероятностей.
При решении задач теоремы сложения и умножения обычно применяются вместе.
6. Сумма и произведение совместных событий и их геометрическая интерпретация.
Суммой двух событий А и В называется событие С, состоящее в появлении или события А или события В или их вместе.
хотя бы одно из событий А или В. С=А+В Геометрическая интерпретация
u – множество исходов некоторого опыта.
Произведением двух событий А и В называется событие С, состоящее в одновременном появлении события А и В. С=А*В
Разностью событий А и В называется событие С, состоящее в появлении события А и не появлении события В С=АВ .
Два случайных события называются противоположными, если одно из них происходит в том и только в том случае, когда не происходит другое. . А+
=U A*
=V –невозможно.
8.Формула полной вероятности.
Определение 3.1. Пусть событие А может произойти только совместно с одним из событий Н1, Н2,…, Нп, образующих полную группу несовместных событий. Тогда события Н1, Н2,…, Нп называются гипотезами.
Теорема 3.1. Вероятность события А, наступающего совместно с гипотезами Н1, Н2,…, Нп, равна:
(3.1)
где p(Hi) – вероятность i- й гипотезы, а p(A/Hi) – вероятность события А при условии реализации этой гипотезы. Формула (3.1) носит название формулы полной вероятности.
Доказательство.
Можно считать событие А суммой попарно несовместных событий АН1, АН2,…, АНп. Тогда из теорем сложения и умножения следует, что
что и требовалось доказать.
9. Формула Бейеса.
Пусть известен результат опыта, а именно то, что произошло событие А. Этот факт может изменить априорные (то есть известные до опыта) вероятности гипотез. Например, в предыдущем примере извлечение из урны белого шара говорит о том, что этой урной не могла быть третья, в которой нет белых шаров, то есть р (Н3/А) = 0. Для переоценки вероятностей гипотез при известном результате опыта используется формула Байеса:
(3.2)
11. Предельные теоремы в схеме Бернулли. Формула Пуассона и условия её применимости.

10. Формула (схема) Бернулли.
Рассмотрим серию из п испытаний, в каждом из которых событие А появляется с одной и той же вероятностью р, причем результат каждого испытания не зависит от результатов остальных. Подобная постановка задачи называется схемой повторения испытаний. Найдем вероятность того, что в такой серии событие А произойдет ровно к раз (неважно, в какой последовательности). Интересующее нас событие представляет собой сумму равно-вероятных несовместных событий, заключающихся в том, что А произошло в некоторых к испытаниях и не произошло в остальных п – к испытаниях. Число таких событий равно числу сочетаний из п по к, то есть , а вероятность каждого из них: pkqn-k, где q = 1 – p – вероятность того, что в данном опыте А не произошло. Применяя теорему сложения для несовместных событий, получим формулу Бернулли:
,
14. Закон распределения дискретной случайно величины. Многоугольник распределения.
Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.
Закон распределения может быть задан аналитически, в виде таблицы или графически.
Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.
Законом распределения случайной дискретной величины (X) называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины (x1,x2,…xn) и соответствующими им вероятностями (p1,p2,… ,pn). При этом события (x1,x2,…xn) образуют полную группу (т.е. появление одного из них является достоверным событием), что означает
(1)
Про случайную величину X в таком случае говорят, что она подчинена данному закону распределения.
Простейшей формой задания этого закона является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:
| Возможное значение X | X1 | Х2 | … | Хn |
| Вероятность | Р1 | Р2 | … | Рn |
Такая таблица называется таблицей распределения (вероятностей) случайной величины X.
Графически закон распределения дискретной случайной величины можно представить в виде многоугольника распределения – ломаной, соединяющей точки плоскости с координатами (xi, pi).
x1 x2 x3 x4 x5
Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.