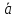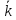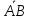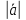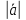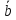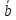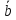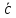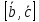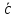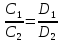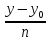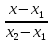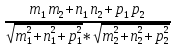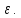Математический анализ. Шпаргалка для студента №11
Автор:
Михаль Ю.О.
Размер:
1,58 мб
Формат:
djvu
16964

Формулы по интегралам, производным и тригонометрическим функциям
Размер:
8 кб
Формат:
doc
9811

Шпаргалки по высшей математике
Размер:
178 кб
Формат:
doc
20413

Шпаргалка по высшей математике за 2 курс 3 семестр
Размер:
111 кб
Формат:
doc
21342

Шпаргалка по дискретной математике и булевой алгебре. Множества, логика, комбинаторика.
Размер:
196 кб
Формат:
doc
10235

Таблица интегралов шпаргалка
Размер:
42 кб
Формат:
rtf
21356

Шпаргалки по линейной и векторной алгебре
Автор:
Орлов Н.Г.
Размер:
104 кб
Формат:
doc
12477
Здесь представлены шпаргалки по математике, которые можно скачать бесплатно.
1.
Матрица
Это
прямоугольная таблица, состоящая из
m×n
элементов и содержащая m
строк и n
столбцов.
Числовая
матрица
– все элементы матрицы числа.
Квадратная
матрица
– m=n.
Операции
над матрицами
Сложение
– складываются все элементы, стоящие
на одинаковых местах (только у
равноразмерных).
Произведение
– каждый элемент матрицы умножается
на число (с).
2
Транспонирование
Транспонированная
матрица – это матрица, полученная из
матрицы А заменой строк столбцами.
Умножение
матриц
Вводится
только для согласованных матриц (число
столбцов м-цы А должно совпадать со
строками м-цы В).
При
умножении матриц появляется новая
матрица, элементы которой вычисляются
по формуле: c11=a11b11+a12b21+…(1
элемент 1 строки умножаем на 1 э-т 1
столбца + 2 э-т 1 с-ки на 2 э-т 2 с-ца, и т.д.)
3.
Определители
2 и 3 порядков
Определители
вводятся только для квадратных матриц.
Определителем (Δ) или детерминалом
матрицы А называется число det
A.
Для
2-го порядка Δ вычисляется по формуле:
a11a22-a12a21
(крест накрест).
Для
3-го порядка по правилу треугольников.
Свойства:
1)
Δ
единичной матрицы =1. 2) Δ треугольной
матрицы = произведению элементов,
стоящих на главной диагонали. 3)
det(A*B)=detA*detB.
4) если строка или столбец = 0, то Δ=0.
4.Определитель
n-го порядка
Определитель
n-го
порядка находится либо разложением по
элементам строки (столбца), либо
приведением определителя к треугольному
виду.
Миноры
и алгебраические дополнения
Минор
матрицы А соответствующей элементу
Aij
– это Δ
(n-1)
порядка, получаемый путём вычёркивания
i-ой
строки или j-го
столбца. Aij=(-1)i+jMij
называется алгебраическим дополнением
к элементу aij.
Разложение
определителя
Δ
раскладывается по элементам i-ой
строки или j-го
столбца по формуле:
Δ = ai1Ai1+
ai2Ai2+…+
ainAin
5.
Обратная
матрица. Теорема о существовании
обратной матрицы
Обратная
матрица существует только для квадратных
матриц.
Если
обратная матрица существует, то она
единственна.
Матрица
А-1
обратная
А,
если выполняется условие: А-1А=А
А-1=Е
(единичная матрица).
Для
того чтобы матрица А была обратной,
необходимо чтобы она была невырожденной
(Δ не должен =0).
Матрица,
состоящая из алгебр. дополнений,
полученная путём транспонирования
называется союзной
(Ас).
Вычисление
обратной матрицы: 1) Находим Δ
2) Вычислем алгебр. доп., 3) Строим Ас
и
вычисляем:
А-1=
Ас
, 4) Делаем проверку А-1А=Е
6.
Ранг
матрицы
Ранг
матрицы
– это максимальный порядок минора,
отличный от нуля. Способы вычисления:
1)Если существует минор Mk
(k
— какой-то порядок минора) и все Mk+1=0,
то ранг М=k.
2) Метод элементарных преобразований
(матрицу приводят к треугольной и
трапециевидной форме).
Элементарные
преобразования
1)
сложение 2-х любых строк матрицы. 2)
Умножение элементов строки на число.
Теорема
о базисном миноре
Базисный
минор – это минор, не равный 0, порядок
которого равен рангу матрицы.
7.
СЛАУ
(система линейных алгебраических
уравнений)
Если
эта система имеет хотя бы одно решение,
то она называется совместной, в противном
случае несовместной. (b1,
b2,
b3)
– столбец свободных членов. (x1,
x2,
x3)
– решение системы, если при подстановке
их в систему получаются верные равенства.
Решение
систем по формулам Крамера
Сначала
находим Δ
и убеждаемся, что он не равен 0. Затем
по формулам Крамера находим определители
уже как бы новых матриц с заменой
определённого столбца на столбец
свободных членов. Находим переменные
(x,
y,
z)
по формулам Δx
Δ
и
т.д. Делаем проверку.
8.
СЛАУ
(система линейных алгебраических
уравнений)
Если
эта система имеет хотя бы одно решение,
то она называется совместной, в противном
случае несовместной. (b1,
b2,
b3)
– столбец свободных членов. (x1,
x2,
x3)
– решение системы, если при подстановке
их в систему получаются верные равенства.
Матричный
метод
Сначала
находим Δ
и убеждаемся, что он не равен 0. Находим
союзную матрицу, а затем обратную по
формуле А-1=
Ас.
Затем находим переменные (x,
y,
z)
и делаем проверку.
9.
Решение
произвольных СЛАУ
Берём
обычную систему уравнений, где А –
матрица системы, а добавление к матрице
А столбец свободных членов даёт нам
расширенную матрицу

Теорема
Кренекера-Капелли
Для
того, чтобы система уравнений была
совместна, необходимо чтобы ранг А =
рангу

Если:
1) rA=
то система имеет единственное решение.
n
– последний член элемента (a1n)
2)
rA=
то система имеет бесконечное кол-во
решений.
10.
Векторы
в пространстве
Вектор
– это направленный отрезок.
– свободный;
– имеющий точку приложения. Длина
вектора – модуль.
Линейные
операции над векторами
1)
сложение (по правилу треугольника и
параллелограмма). Суммой 2 векторов
и
явл.
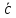
начало которого совпадает с началом 1
вектора (
а конец — с концом 2 вектора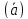
2)
вычитание (
Разностью
и
явл.

конец которого совпадает с концом

а начало — с концом
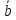
3)
умножение на число (Условия: 1) существует

2)
и
направлены одинаково если с
11.
Координаты
вектора в пространстве.
3
вектора (
образую
базис в пространстве если они взаимно
⊥
и имеют единичную длину.


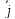
=
(x2—x1,
y2—y1,
z2—z1).

– длина
вектора
Направляющие
косинусы вектора
ax
= ПрOx
=

= ПрOy
=
cosβ;
az
= ПрOz
=
cosγ;
cosα=
Проекции
вектора на ось
образованный
с помощью осей Ox,
Oy,
Oz,
образует углы
α,
β, γ.
12.
Скалярное
произведение 2 векторов
Это
число, равное произведению длин этих
векторов на cos
угла между ними.
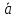
=
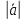

Свойство:
1)

=

2)
(
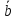
=



3)
Скалярное произведение на число =
произведение числа на один из векторов
и * на 2 вектор.
4)

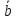
если
вектора
и
явл. Ортогональными (
⊥

13.
Векторное
произведение 2 векторов

произведением 2 векторов
и
явл.
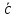
который удовлетворяет условиям: 1)
⊥


2)


– правая тройка векторов. 3)
=


(модуль произв. 2 векторов – площадь
параллелограмма)
Свойство:
1)

—

2)
=

3)

0 если
//
14.
Смешанное
произведение 3 векторов
Это
число = скалярному произведению 3-го
вектора на векторное произведение 2-х
первых векторов.
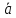

= (
—
объём параллелепипеда.
Свойство:
1)
От перемены мест множителей произведение
не меняется.
=
=
2)
Если умножить на число, то оно умножается
с одним из членов произведения.
3)
(α-
β)(
= α(
β (
15.
Базис
в пространстве
Компланарные
векторы лежат в одной плоскости.
3
любых некомпланарных вектора образуют
базис в пространстве.
Разложение
вектора по базису
Любой
вектор можно разложить по базису таким
способом: допустим B
(

– базис, а (α,
β, γ)
координаты определённого вектора,
например

Тогда разложение
по базису имеет вид:
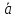
α
β
γ
16.
Прямая
на плоскости
Вектором
нормали
называется вектор перпендикулярный
плоскости. Пусть вектор
= (𝐴,
𝐵)
является вектором нормали к прямой 𝑙.
Произвольная точка плоскости 𝑀(𝑥,
𝑦)
принадлежит прямой 𝑙
тогда и только тогда, когда
⊥
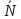
т.е. скалярное произведение этих векторов


0
Её
уравнения
1)
Уравнение прямой, проходящей через
заданную точку и имеющей заданный
вектор нормали 𝐴(𝑥–𝑥0)+𝐵(𝑦−𝑦0)=0
2)
Общее уравнение прямой: 𝐴𝑥
+ 𝐵𝑦
+ 𝐶
= 0
17.
Различные
уравнения плоскости
а)
Общее уравнение плоскости: Ax
+ By + Cz + D = 0
б)
Уравнение проходящее через точку
M0(x0,y0,z0)
и ⊥
вектору нормали

A(x—x0)
+ B(y—y0)
+C(z—z0)=0
в)
Уравнение плоскости, проходящей через
3 заданные точки.
г)
Уравнение плоскости в отрезках:
18.
Угол
между плоскостями
Допустим,
мы имеем 2 уравнения плоскости (α: A1x
+ B1y
+ C1z
+ D1
= 0
и β: A2x
+ B2y
+ C2z
+ D2
= 0)
и нам нужно вычислить угол между 2
плоскостями – двугранный
угол.
Он вычисляется по формуле: cos
(отношение произведения


к произведению модулей векторов
нормали).
Взаимное
расположение плоскостей
Две
плоскости в пространстве либо
параллельны, либо пересекаются.
α1//α2
– коллинеарные ⇒


– условие
параллельности.
α1⊥α2
⇒

⇒

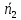

– условие
⊥.
19.
Прямая
в пространстве.
Различные
уравнения прямой в пространстве
1)
Параметрическое уравнение: x=x0+mt,
y=y0+nt,
z=z0+pt
(m,n,p)
– направляющий вектор прямой (l),
который параллелен этой прямой. M0(x0,
y0,
z0)
∈l.
2)
Каноническое уравнение:
=
=
3)
Уравнение прямой проходящей через 2
точки:
=
=
4)
Общее уравнение прямой в пространстве:
20.
Угол
между прямыми и их взаимное расположение
Допустим,
мы имеем 2 (канонических) уравнения
прямых, а также их направляющие векторы

и

Тогда угол между 2 прямыми
можно найти по формуле: cos
Условие
//-ти:

//
⇒


Условие
⊥—ти:
Расстояние
от точки до прямой в пространстве
У
нас есть уравнение прямой
=
=

её направляющий вектор
(m,n,p)
и точка не принадлежащая этой прямой
M(x1,y1,z1).
Расстояние от точки до прямой определяется
по формуле:
21.
Угол
между прямой и плоскостью.
Допустим,
у нас есть каноническое уравнение
прямой
=
=
и уравнение плоскости Ax
+ By
+ Cz
+ D
= 0.
Тогда угол между прямой и плоскостью
можно найти по формуле: Sin
=
22.
Взаимное
расположение прямой и плоскости
Условие
//-ти:
Am+Bn+Cp
= 0
Условие
⊥—ти:
Плоскости
могут совпадать, быть параллельными
или пересекаться по прямой.
23.
Эллипс
Эллипс
– это геометрическое место точек
плоскости, расстоянием от которых до
2 заданных точек называется фокусами
есть величина постоянная.
Вывод
канонического уравнения

= 1
Геометрические
свойства
1)
Эллипс является кривой 2-го порядка.
2)
Является ограниченной фигурой.
3)
Является симметричной фигурой, оси
симметрии Ox,
Oy.
4)
a – большая ось; b
– малая ось; Вершины: А1(а,0);
А2(-а,0);
В1(0,
b);
В2(0,
—b);
5)
=
– эксцентриситет эллипса; 0
1.
6)
Прямые
x
=
– директриса эллипса. При
=1 ⇒
а=с; а=b
– уравнение окружности.


24.
Гипербола
Гипербола
– геометрическое место точек на
плоскости, модуль разности расстояний
для 2 заданных точек называется фокусами
есть величина постоянная.
Вывод
канонического уравнения
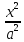
= 1
Геометрические
свойства
1)
Является кривой 2-го порядка.
2)
Является неограниченной кривой.
3)
Является симметричной фигурой.
4)
Пересекает Ox
в 2 точках, не пересекает ось Oy.
a – действительная полуось; b
– мнимая полуось;
5)
=
– эксцентриситет эллипса;

6)
x
=
– директриса.
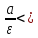
7)
y
=

– асимптоты
25.
Парабола
Парабола
– геометрическое место точек плоскости,
расстояние каждой из которых до заданной
точки называется фокусом и до определённой
прямой L,
называемой директрисой. (F∉L)
Вывод
канонического уравнения
p-
(параметр) расстояние от F
до L.
F(
– фокус параболы. x=
Уравнение: y2=2px
Геометрические
свойства
1)
Является кривой 2-го порядка.
2)
Симметричная фигура, ось симметрии –
Ox.
3)
Неограниченная фигура
4)
= 1
– эксцентриситет
26.
Числовая
последовательность
Если
каждому натуральному числу из множества
N
поставлено в соответствие некоторое
число или величина, то множество
последних образует последовательность.
xn
– числовая последовательность.
Предел
Число
a
называется пределом числовой
последовательности, если для любого
положительного числа существует
N-число,
такое, что для всех номеров N
последующий больше, чем это число по
модулю.
Теорема
о сходимости
Если
xn
имеет
предел, то он единственный. xn
наз.
ограниченной, если существует n
и все члены удовлетворяют

n
27.
Предел
функции
Если
к каждому числу из множества x
поставлено в соответствие одно число
и множество y,
то на множестве x
задана функция y=f(x)
Число
b
называется пределом функции f(x)
при x→a,
если для любого положительного
существует положительная дельта,
зависящая от
Теорема
о существовании предела функции
Для
того, чтобы f(x)
имела предел в точке a,
необходимо чтобы левый и правый пределы
были равны.
28.
Односторонние
пределы функции
Левый
и правый пределы называют односторонними
пределами.
1)
Число b
называется правым пределом функции
при x→a
справа если для всех

существует дельта от
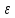
такой что 0
модуль f(x)-b

следовательно x
2)
Число b
называется левым пределом функции при
x→a
слева если для всех

существует дельта от

такой что —b
следовательно модуль f(x)-b
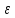
следовательно x
Теорема
о существовании предела функции
Для
того, чтобы f(x)
имела предел в точке a,
необходимо чтобы левый и правый пределы
были равны.
29.
Бесконечно-малые
и их свойства.
Бесконечно
малая функция
– это функция, предел которой в
данной точке равен нулю. Функция
α(x)
– бесконечно-малая при x→a,
если lim
α(x)
= 0.
При
x→a
lim
=
предел не существует.
Основные
свойства
1°
Сумма конечного числа б.м функций
является функцией б.м.
3°
Произведение двух б.м функций есть
функция б.м.
4°
Произведение б.м функции на константу
является б.м функцией.
5°
Частное от деления б.м функции на
функцию, предел которой
не равен нулю, есть функция б.м.
6°
Функция 
обратная
к б.м функции α(x)
0,
есть функция бесконечно большая. Верно
и обратное.
30.
Бесконечно-большие
функции.
Бесконечно
большая функция
– это функция, предел которой
стремится к
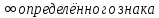
Теорема
о связи бесконечно-большой и
бесконечно-малой функции
Теорема.
Функция обратная бесконечно малой,
является бесконечно большой и наоборот.
Доказательство: Пусть предел функции
равен 0, а сама функция не = 0, при x→a,
т.е. задаём бесконечно-малую функцию

Тогда для любого числа 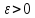
такое число дельта

что для всех x,
удовлетворяющих неравенству

выполняется неравенство 
т.е.

А из этого следует, что функция 
бесконечно большая.
1.
Матрица
Это
прямоугольная таблица, состоящая из
m×n
элементов и содержащая m
строк и n
столбцов.
Числовая
матрица
– все элементы матрицы числа.
Квадратная
матрица
– m=n.
Операции
над матрицами
Сложение
– складываются все элементы, стоящие
на одинаковых местах (только у
равноразмерных).
Произведение
– каждый элемент матрицы умножается
на число (с).
2
Транспонирование
Транспонированная
матрица – это матрица, полученная из
матрицы А заменой строк столбцами.
Умножение
матриц
Вводится
только для согласованных матриц (число
столбцов м-цы А должно совпадать со
строками м-цы В).
При
умножении матриц появляется новая
матрица, элементы которой вычисляются
по формуле: c11=a11b11+a12b21+…(1
элемент 1 строки умножаем на 1 э-т 1
столбца + 2 э-т 1 с-ки на 2 э-т 2 с-ца, и т.д.)
3.
Определители
2 и 3 порядков
Определители
вводятся только для квадратных матриц.
Определителем (Δ) или детерминалом
матрицы А называется число det
A.
Для
2-го порядка Δ вычисляется по формуле:
a11a22—a12a21
(крест накрест).
Для
3-го порядка по правилу треугольников.
Свойства:
1)
Δ
единичной матрицы =1. 2) Δ треугольной
матрицы = произведению элементов,
стоящих на главной диагонали. 3)
det(A*B)=detA*detB.
4) если строка или столбец = 0, то Δ=0.
4.Определитель
n-го порядка
Определитель
n-го
порядка находится либо разложением по
элементам строки (столбца), либо
приведением определителя к треугольному
виду.
Миноры
и алгебраические дополнения
Минор
матрицы А соответствующей элементу
Aij
– это Δ
(n-1)
порядка, получаемый путём вычёркивания
i-ой
строки или j-го
столбца. Aij=(-1)i+jMij
называется алгебраическим дополнением
к элементу aij.
Разложение
определителя
Δ
раскладывается по элементам i-ой
строки или j-го
столбца по формуле:
Δ = ai1Ai1+
ai2Ai2+…+
ainAin
5.
Обратная
матрица. Теорема о существовании
обратной матрицы
Обратная
матрица существует только для квадратных
матриц.
Если
обратная матрица существует, то она
единственна.
Матрица
А-1
обратная
А,
если выполняется условие: А-1А=А
А-1=Е
(единичная матрица).
Для
того чтобы матрица А была обратной,
необходимо чтобы она была невырожденной
(Δ не должен =0).
Матрица,
состоящая из алгебр. дополнений,
полученная путём транспонирования
называется союзной
(Ас).
Вычисление
обратной матрицы: 1) Находим Δ0,
2) Вычислем алгебр. доп., 3) Строим Ас
и
вычисляем:
А-1=*
Ас
, 4) Делаем проверку А-1А=Е
6.
Ранг
матрицы
Ранг
матрицы
– это максимальный порядок минора,
отличный от нуля. Способы вычисления:
1)Если существует минор Mk0
(k
— какой-то порядок минора) и все Mk+1=0,
то ранг М=k.
2) Метод элементарных преобразований
(матрицу приводят к треугольной и
трапециевидной форме).
Элементарные
преобразования
1)
сложение 2-х любых строк матрицы. 2)
Умножение элементов строки на число.
Теорема
о базисном миноре
Базисный
минор – это минор, не равный 0, порядок
которого равен рангу матрицы.
7.
СЛАУ
(система линейных алгебраических
уравнений)
Если
эта система имеет хотя бы одно решение,
то она называется совместной, в противном
случае несовместной. (b1,
b2,
b3)
– столбец свободных членов. (x1,
x2,
x3)
– решение системы, если при подстановке
их в систему получаются верные равенства.
Решение
систем по формулам Крамера
Сначала
находим Δ
и убеждаемся, что он не равен 0. Затем
по формулам Крамера находим определители
уже как бы новых матриц с заменой
определённого столбца на столбец
свободных членов. Находим переменные
(x,
y,
z)
по формулам Δx
Δ
и
т.д. Делаем проверку.
8.
СЛАУ
(система линейных алгебраических
уравнений)
Если
эта система имеет хотя бы одно решение,
то она называется совместной, в противном
случае несовместной. (b1,
b2,
b3)
– столбец свободных членов. (x1,
x2,
x3)
– решение системы, если при подстановке
их в систему получаются верные равенства.
Матричный
метод
Сначала
находим Δ
и убеждаемся, что он не равен 0. Находим
союзную матрицу, а затем обратную по
формуле А-1=*
Ас.
Затем находим переменные (x,
y,
z)
и делаем проверку.
9.
Решение
произвольных СЛАУ
Берём
обычную систему уравнений, где А –
матрица системы, а добавление к матрице
А столбец свободных членов даёт нам
расширенную матрицу
.
Теорема
Кренекера-Капелли
Для
того, чтобы система уравнений была
совместна, необходимо чтобы ранг А =
рангу
.
Если:
1) rA==n,
то система имеет единственное решение.
n
– последний член элемента (a1n)
2)
rA=,
то система имеет бесконечное кол-во
решений.
10.
Векторы
в пространстве
Вектор
– это направленный отрезок.
– свободный;
– имеющий точку приложения. Длина
вектора – модуль.
Линейные
операции над векторами
1)
сложение (по правилу треугольника и
параллелограмма). Суммой 2 векторов
и
явл.
,
начало которого совпадает с началом 1
вектора (),
а конец — с концом 2 вектора.
2)
вычитание (.
Разностью
и
явл.
,
конец которого совпадает с концом
,
а начало — с концом
.
3)
умножение на число (Условия: 1) существует
;
2)
и
направлены одинаково если с0.
11.
Координаты
вектора в пространстве.
3
вектора ()
образую
базис в пространстве если они взаимно
⊥
и имеют единичную длину.
=ax
+ay
+az
=
(x2—x1,
y2—y1,
z2—z1).
=
– длина
вектора
Направляющие
косинусы вектора
ax
= ПрOx
=
*cosα; ay
= ПрOy
=
cosβ;
az
= ПрOz
=
cosγ;
cosα=
Проекции
вектора на ось
образованный
с помощью осей Ox,
Oy,
Oz,
образует углы
α,
β, γ.
12.
Скалярное
произведение 2 векторов
Это
число, равное произведению длин этих
векторов на cos
угла между ними.
*
=
*
cosφ
Свойство:
1)
*
=
*
2)
(*
)
=
*
*
)
3)
Скалярное произведение на число =
произведение числа на один из векторов
и * на 2 вектор.
4)
*
=0,
если
вектора
и
явл. Ортогональными (
⊥
).
13.
Векторное
произведение 2 векторов
Векторным
произведением 2 векторов
и
явл.
,
который удовлетворяет условиям: 1)
⊥
,
;
2)
,
,
– правая тройка векторов. 3)
=
*
sinφ
(модуль произв. 2 векторов – площадь
параллелограмма)
Свойство:
1)
=
—
2)
=
+
3)
=
0 если
//
14.
Смешанное
произведение 3 векторов
Это
число = скалярному произведению 3-го
вектора на векторное произведение 2-х
первых векторов.
*
*
= ()
—
объём параллелепипеда.
Свойство:
1)
От перемены мест множителей произведение
не меняется.
=
=
2)
Если умножить на число, то оно умножается
с одним из членов произведения.
3)
(α-
β)(
= α(+
β (
15.
Базис
в пространстве
Компланарные
векторы лежат в одной плоскости.
3
любых некомпланарных вектора образуют
базис в пространстве.
Разложение
вектора по базису
Любой
вектор можно разложить по базису таким
способом: допустим B
(,
)
– базис, а (α,
β, γ)
координаты определённого вектора,
например
.
Тогда разложение
по базису имеет вид:
=
α+
β+
γ
16.
Прямая
на плоскости
Вектором
нормали
называется вектор перпендикулярный
плоскости. Пусть вектор
= (????,
????)
является вектором нормали к прямой ????.
Произвольная точка плоскости ????(????,
????)
принадлежит прямой ????
тогда и только тогда, когда
⊥
,
т.е. скалярное произведение этих векторов
*
=
0
Её
уравнения
1)
Уравнение прямой, проходящей через
заданную точку и имеющей заданный
вектор нормали ????(????–????0)+????(????−????0)=0
2)
Общее уравнение прямой: ????????
+ ????????
+ ????
= 0
17.
Различные
уравнения плоскости
а)
Общее уравнение плоскости: Ax
+ By + Cz + D = 0
б)
Уравнение проходящее через точку
M0(x0,y0,z0)
и ⊥
вектору нормали
(A,B,C):
A(x—x0)
+ B(y—y0)
+C(z—z0)=0
в)
Уравнение плоскости, проходящей через
3 заданные точки.
г)
Уравнение плоскости в отрезках:
18.
Угол
между плоскостями
Допустим,
мы имеем 2 уравнения плоскости (α: A1x
+ B1y
+ C1z
+ D1
= 0
и β: A2x
+ B2y
+ C2z
+ D2
= 0)
и нам нужно вычислить угол между 2
плоскостями – двугранный
угол.
Он вычисляется по формуле: cos=
(отношение произведения
1*
2
к произведению модулей векторов
нормали).
Взаимное
расположение плоскостей
Две
плоскости в пространстве либо
параллельны, либо пересекаются.
α1//α2
– коллинеарные ⇒
=
=
– условие
параллельности.
α1⊥α2
⇒
⊥
⇒
*
=0.
=0
– условие
⊥.
19.
Прямая
в пространстве.
Различные
уравнения прямой в пространстве
1)
Параметрическое уравнение: x=x0+mt,
y=y0+nt,
z=z0+pt
(m,n,p)
– направляющий вектор прямой (l),
который параллелен этой прямой. M0(x0,
y0,
z0)
∈l.
2)
Каноническое уравнение:
=
=
3)
Уравнение прямой проходящей через 2
точки:
=
=
4)
Общее уравнение прямой в пространстве:
20.
Угол
между прямыми и их взаимное расположение
Допустим,
мы имеем 2 (канонических) уравнения
прямых, а также их направляющие векторы
1
и
2.
Тогда угол между 2 прямыми
можно найти по формуле: cos=
Условие
//-ти:
1
//2
⇒
=
=
Условие
⊥—ти:
Расстояние
от точки до прямой в пространстве
У
нас есть уравнение прямой
=
=
,
её направляющий вектор
(m,n,p)
и точка не принадлежащая этой прямой
M(x1,y1,z1).
Расстояние от точки до прямой определяется
по формуле:
21.
Угол
между прямой и плоскостью.
Допустим,
у нас есть каноническое уравнение
прямой
=
=
и уравнение плоскости Ax
+ By
+ Cz
+ D
= 0.
Тогда угол между прямой и плоскостью
можно найти по формуле: Sin
=
22.
Взаимное
расположение прямой и плоскости
Условие
//-ти:
Am+Bn+Cp
= 0
Условие
⊥—ти:
Плоскости
могут совпадать, быть параллельными
или пересекаться по прямой.
23.
Эллипс
Эллипс
– это геометрическое место точек
плоскости, расстоянием от которых до
2 заданных точек называется фокусами
есть величина постоянная.
Вывод
канонического уравнения
+
= 1
Геометрические
свойства
1)
Эллипс является кривой 2-го порядка.
2)
Является ограниченной фигурой.
3)
Является симметричной фигурой, оси
симметрии Ox,
Oy.
4)
a – большая ось; b
– малая ось; Вершины: А1(а,0);
А2(-а,0);
В1(0,
b);
В2(0,
—b);
5)
=
– эксцентриситет эллипса; 0
1.
6)
Прямые
x
=
– директриса эллипса. При
=1 ⇒
а=с; а=b
– уравнение окружности.
+
=
24.
Гипербола
Гипербола
– геометрическое место точек на
плоскости, модуль разности расстояний
для 2 заданных точек называется фокусами
есть величина постоянная.
Вывод
канонического уравнения
—
= 1
Геометрические
свойства
1)
Является кривой 2-го порядка.
2)
Является неограниченной кривой.
3)
Является симметричной фигурой.
4)
Пересекает Ox
в 2 точках, не пересекает ось Oy.
a – действительная полуось; b
– мнимая полуось;
5)
=
– эксцентриситет эллипса;
1.
6)
x
=
– директриса.
1
7)
y
=
x
– асимптоты
25.
Парабола
Парабола
– геометрическое место точек плоскости,
расстояние каждой из которых до заданной
точки называется фокусом и до определённой
прямой L,
называемой директрисой. (F∉L)
Вывод
канонического уравнения
p—
(параметр) расстояние от F
до L.
F(;0)
– фокус параболы. x=.
Уравнение: y2=2px
Геометрические
свойства
1)
Является кривой 2-го порядка.
2)
Симметричная фигура, ось симметрии –
Ox.
3)
Неограниченная фигура
4)
= 1
– эксцентриситет
26.
Числовая
последовательность
Если
каждому натуральному числу из множества
N
поставлено в соответствие некоторое
число или величина, то множество
последних образует последовательность.
xn
– числовая последовательность.
Предел
Число
a
называется пределом числовой
последовательности, если для любого
положительного числа существует
N-число,
такое, что для всех номеров N
последующий больше, чем это число по
модулю.
Теорема
о сходимости
Если
xn
имеет
предел, то он единственный. xn
наз.
ограниченной, если существует n
и все члены удовлетворяют
M,
nN
27.
Предел
функции
Если
к каждому числу из множества x
поставлено в соответствие одно число
и множество y,
то на множестве x
задана функция y=f(x)
Число
b
называется пределом функции f(x)
при x→a,
если для любого положительного
существует положительная дельта,
зависящая от
Теорема
о существовании предела функции
Для
того, чтобы f(x)
имела предел в точке a,
необходимо чтобы левый и правый пределы
были равны.
28.
Односторонние
пределы функции
Левый
и правый пределы называют односторонними
пределами.
1)
Число b
называется правым пределом функции
при x→a
справа если для всех
0
существует дельта от
,
такой что 0следовательно
модуль f(x)-b
,
следовательно x
2)
Число b
называется левым пределом функции при
x→a
слева если для всех
0
существует дельта от
,
такой что —b
следовательно модуль f(x)-b
,
следовательно x
Теорема
о существовании предела функции
Для
того, чтобы f(x)
имела предел в точке a,
необходимо чтобы левый и правый пределы
были равны.
29.
Бесконечно-малые
и их свойства.
Бесконечно
малая функция
– это функция, предел которой в
данной точке равен нулю. Функция
α(x)
– бесконечно-малая при x→a,
если lim
α(x)
= 0.
При
x→a
lim
=
предел не существует.
Основные
свойства
1°
Сумма конечного числа б.м функций
является функцией б.м.
3°
Произведение двух б.м функций есть
функция б.м.
4°
Произведение б.м функции на константу
является б.м функцией.
5°
Частное от деления б.м функции на
функцию, предел которой
не равен нулю, есть функция б.м.
6°
Функция ,
обратная
к б.м функции α(x)
0,
есть функция бесконечно большая. Верно
и обратное.
30.
Бесконечно-большие
функции.
Бесконечно
большая функция
– это функция, предел которой
стремится к
.
Теорема
о связи бесконечно-большой и
бесконечно-малой функции
Теорема.
Функция обратная бесконечно малой,
является бесконечно большой и наоборот.
Доказательство: Пусть предел функции
равен 0, а сама функция не = 0, при x→a,
т.е. задаём бесконечно-малую функцию
.
Тогда для любого числа существует
такое число дельта
,
что для всех x,
удовлетворяющих неравенству
,
выполняется неравенство ,
т.е.
.
А из этого следует, что функция —
бесконечно большая.
31.
Бесконечно-малые
функции.
Бесконечно
малая функция
– это функция, предел которой в
данной точке равен нулю.
Функция
α(x)
– бесконечно-малая при x→a,
если lim
α(x)
= 0.
Терема
об отношении 2 бесконечно-малых функций
Предел
отношения 2 бесконечно-малых функций
= пределу отношения 2 других бесконечно-малых
функций, соотв. им пропорционально.
α1(x)
α2(x)
и β
1(x)
β
2(x)
=
32.
Замечательные
пределы.
1)
=1
2)
Раскрытие
неопределённостей
,
можно раскрыть используя правило
Лапиталя; разделяя каждый элемент на
x
в большей степени.
)
можно раскрыть используя 2 замечательный
предел.
(
сначала при помощи различных преобразований
приводим к
,
,
и раскрываем.
33.
Непрерывность
функции в точке
Функция называется
непрерывной
в точке, если: функция определена
в точке и ее окрестности; существует
конечный предел функции в точке;
этот предел равен значению функции
в точке.
Свойства
непрерывных функций
Точка,
в которой функция не является непрерывной,
называется точкой разрыва.
Если функция непрерывна
и справа и слева, то она непрерывна в
этой точке.
Если
функция y=f(x)
находится на отрезке
непрерывна в точке a
справа.
Если
функция y=f(x)
находится на отрезке
непрерывна в точке a
слева.
34.
Непрерывность фун. на интервале
Функция называется
непрерывной в интервале, если она
непрерывна в каждой точке этого интервала.
Основные
теоремы непрерывных функций
1)
Пусть заданы две функции f(x) и g(x) ,
непрерывные на некотором множестве X.
Сумма, произведение и частное (при
условии, что g(x) )
является также непрерывной функцией
на рассматриваемом множестве.
2)
Каждая элементарная функция, заданная
в окрестности некоторой точки, непрерывна
в этой точке.
3)
Пусть функция z=(x)
непрерывна
в точке x0,
а функция y=f(x)
непрерывна в точке z0,
где z0=(x0),
тогда сложная функция y=f((x))
является непрерывной в точке x0.
35.
Производная
функции
Это
предел отношения приращения функции
к приращению аргумента, когда приращение
аргумента стремится к нулю. Если функция
имеет производную в точке x0,
то в этой точке она непрерывна. Производная
в точке 0 не существует.
Геометрический
и механический смысл производной
1)
Геометрический смысл: производная
представляет собой угловой коэффициент
касательной к графику функции y=f(x) в
точке x0.
2)
Механический смысл: скорость – это
производная координаты по времени:
36.
Основные
правила дифференцирования
1)
Пусть u(x)
и v(x)
– дифференциальные функции в точке x,
тогда их произведение и частное также
дифференцируемы в точке x.
2)
Пусть сложная функция y=f(z),
где z=(x)
дифф-мы в точке z,
тогда y=f((x))
дифф-ма в точке x.
3)
Постоянный
множитель c можно выносить за знак
производной.
4)
Производная от суммы (разности) функции
= сумме (разности) производных.
37.
Производная
сложной и обратной функции
1)
Пусть сложная функция y=f(z),
где z=(x)
дифф-мы в точке z,
тогда y=f((x))
дифф-ма в точке x.
Производную сложной функции можно
найти по формуле: y‘=y‘z*z‘x.
2)
Если функции y=f(x)
и x=g(y)
— пара взаимно обратных функций, и
функция y=f(x) имеет производную f'(x),
то производная обратной функции
находится по формуле: g'(x)=1/f
‘(x).
38.
Дифференцирование
неявных функций и функций, заданных
параметрически
1)
Чтобы найти производную функции,
заданной неявно (когда слева и справа
есть переменная y)
каким-либо уравнением необходимо взять
производную из обоих частей уравнения,
затем переносим все y‘
влево и подставляем вместо y
исходное выражение.
2)
Пусть y=y(x)
задана параметрически:
,
тогда чтобы продифференцировать эту
функцию необходимо воспользоваться
формулой:
y‘x=
39.
Дифференциал
функции и её геометрический смысл
1)
Пусть функция y=f(x) дифференцируема в
точке x0,
тогда превращение можно представить
в виде
y=f
‘(x0)*x+0(
x)
y
f
‘(x0)*x
при
x→0
f
‘(x0)*x
в разложении
y
называется главной линейной относительно
х
частью превращения функции.
Главная
линейная относительно
х
функция наз. дифф-ой функцией и
обозначается dy.
dy=y‘*dx. y‘=
2)
Дифференциал функции y=f(x) в
точке x
равен приращению ординаты касательной
к графику функции в этой точке, когда x
получит приращение
х.
40.
Производные
высших порядков
Производная
от производной 1-го порядка называется
производной 2-го порядка. y‘=f
‘(x);
y»=(y’)’; yn=(yn-1)’
Дифференцируемость
функции
Пусть
функция y=f(x) дифф-ма в точке x0,
тогда превращение можно представить
в виде
y=f
‘(x0)*x+0(
x)
y
f
‘(x0)*x
при
x→0
f
‘(x0)*x
в разложении
y
называется главной линейной относительно
х
частью превращения функции.
Главная
линейная относительно
х
функция наз. дифф-ой функцией и
обозначается dy.
1
порядка)
dy=y‘*dx. y‘=
высших
порядков) d2y=y»dx2;
d3y=y»’dx3
41.
Теорема
Ролля и Лагранжа
1)
Пусть f(x)
удовлетворяет условиям: определена и
непрерывна на отрезке [a,b];
дифф-ма на (a,b,);
Значения функции на концах отрезков
совпадают f(a)=f(b).
Тогда существует точка c=(a,b)
такая что f‘(x)=0
2)
Пусть f(x)
удовлетворяет условиям: определена и
непрерывна на отрезке [a,b];
дифф-ма на (a,b,).
Тогда существует точка c
такая, что
=f
‘(c)
Правило
Лопиталя
Правило
Лопиталя используется при вычислении
предела функции и относится только для
раскрытия неопределённостей:
,
Такие пределы вычисляются по формуле:
=
42.
Условие
монотонности функции.
Пусть
f(x)
определена и непрерывна на отрезке
[a,b],
тогда если: 1) f(x)0,
для всех x
принадлежащих (a,b),
то f(x)
– не убывает; 2) f(x)0,
для всех x
принадлежащих (a,b),
то f(x)
– не возрастает;
Следовательно:
если f(x)0,
для всех x
принадлежащих (a,b),
то f(x)
– возрастает; а f(x)0
—
убывает
Необходимое
условие экстремума
Пусть
x0
– точка локального экстремума функции
f(x),
тогда f
‘(x)
обращается в 0 или не существует.
Критические
точки
— те, которые не входят в обл. определения
(чаще всего это точки разрыва).
Стационарные-точки
в которых значение производной равно
нулю (точки экстремума)
43.
Экстремум
фун. одной переменной
Пусть
у нас есть функция y=f(x)
и точка x0
– точка локального max
(min)
если существует x
принадлежащий дельта-окрестности x0,
то f(x0)f(x)
max;
f(x0)f(x)
min
Локальные
max
и min
– локальные экстремумы. x0
– точка локального максимума если
f(x0)=
максимальному
значению f(x).
Достаточные
условия экстремума
1) Пусть
функция f(x)
непрерывна в точке x0 и
имеет конечную производную f‘(x).
Если же при переходе через точку x0
производная не меняет знак, то в
точке x0 нет
экстремума.
2) Пусть
функция f(x)
дважды дифференцируема в точке x0,
причем
df(x0)
= 0, а d2f(x0)
> 0
(d2f(x0)
< 0 ).
Тогда
точка x0 есть
точка локального минимума (локального
максимума) функции f(x).
3)
Пусть
функция f(x)
имеет в точке х0 производные
f
‘(x0)
и f»(x0),
причем f‘(x0)
= 0, а f»(x0)
> 0
(f»(x0)
< 0 ).
Тогда
точка x0 есть
точка локального минимума (локального
максимума) функции f(x).
44.
Выпуклость
и вогнутость графика функции. Точки
перегиба
График
функции y=f(x)
называется вогнутым
на (a,b)
если он расположен ниже касательной,
проведённой к графику функции.
График
функции y=f(x)
называется выпуклым
на (a,b)
если он расположен выше касательной,
проведённой к графику функции.
Точка
перегиба функции
– это точка, в которой функция непрерывна
и её график имеет касательную (которая
может быть параллельна оси) и при
переходе через (x)
функция меняет направление выпуклости.
45.
Асимптоты
графика функции.
Асимптота
– значение, к которому стремится
функция. Различают вертикальные,
горизонтальные и наклонные асимптоты.
Прямая
называется вертикальной
асимптотой, если 1 из односторонних
пределов в этой точке =
.
Прямая
называется горизонтальной
асимптотой функции, если предел этой
функции при x→
= числу.
Прямая
y=kx+b
называется наклонной
асимптотой, если существуют конечные
пределы.
Схема
исследования функции
1)
Находим область определения функции.
2)
Определяем чётностьнечётность функции
и её периодичность.
3)
Находим точки пересечения с осями Ox
и Oy
(приравниваем x=0
и y=0)
4)
Исследуем функцию на наличие асимптот
5)
Определяем y‘
и её критические точки (y‘=0)
6)
Находим y»
и её критические точки.
7)
Результаты заносим в таблицу.

С помощью таблицы строим график функции.
Шпаргалка по высшей математике для студентов технических вузов, Учебное пособие, Попов М.Л., 2007.
Пособие содержит справочные материалы по всему курсу высшей математики для физико- математических и технических специальностей, в полном соответствии с Государственным образовательным стандартом. Материал пособия охватывает следующие разделы программы: элементы линейной алгебры и аналитической геометрии; введение в математический анализ; дифференциальное исчисление функции одной и нескольких переменных; интегральное исчисление функции одной переменной; числовые и функциональные ряды; гармонический анализ; дифференциальные уравнения и элементы качественной теории диф. уравнений; кратные, криволинейные и поверхностные интегралы; теория поля; теория функций комплексной переменной; операционное исчисление; уравнения математической физики; теория вероятностей; математическая статистика; основы дискретной математики; методы оптимизации; численные методы. В каждом разделе приведены основные определения, теоремы с доказательствами, формулы с полным выводом, графики, рисунки. Пособие будет полезно студентам физико-математических и технических специальностей вузов и других образовательных заведений для успешной сдачи экзаменов по высшей математике.
Шпаргалка.
Для простого и эффективного использования «Шпаргалки» разрежьте каждую страницу на четыре части по пунктирной линии. Сложите полученные листы по порядку> номеров — верхний левый, верхний правый, нижний левый, нижний правый. Для удобства использования можно скрепить получившуюся стопку степлером или скрепкой в верхнем левом углу.
Содержание.
Линейная алгебра и аналитическая геометрия.
Введение в математический анализ.
Дифференциальное исчисление функций одной переменной.
Дифференциальное исчисление функций нескольких переменных.
Интегральное исчисление функций одной переменной.
Числовые и функциональные ряды.
Гармонический анализ.
Обыкновенные дифференциальные уравнения.
Операционное исчисление.
Элементы качественной теории дифференциальных уравнений.
Кратные, криволинейные и поверхностные интегралы.
Теория функций комплексной переменной.
Теория поля.
Теория вероятностей.
Уравнения математической физики.
Математическая статистика.
Методы оптимизации.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Шпаргалка по высшей математике для студентов технических вузов, Учебное пособие, Попов М.Л., 2007 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать
— pdf — Яндекс.Диск.
Дата публикации: 07.08.2019 13:32 UTC
Теги:
шпаргалка по математике :: математика :: высшая математика :: шпаргалка :: Попов
Следующие учебники и книги:
- Сборник математических задач, Основы финансовой грамотности, 10-11 классы, Том 3, Моторо Н.П., Новожилова Н.В., Шалашова М.М., 2019
- Методические рекомендации к сборнику математических задач, Основы финансовой грамотности, 10-11 классы, Методические рекомендации, Том 3, Моторо Н.П., Новожилова Н.В., Шалашова М.М., 2019
- Методические рекомендации к сборнику математических задач, Основы финансовой грамотности, 5-9 классы, Том 2, Моторо Н.П., Новожилова Н.В., Шалашова М.М., 2019
- Сборник конкурсных задач по математике с решениями, Кущенко В.С., 1969
Предыдущие статьи:
- Математика, Решение упражнений к учебнику математики Моро М.И. и др.
- Дидактические карточки-задания по математике, 2 класс, Истомина Н.Б., Шмырева Г.Г., 2002
- Математика, Сборник упражнений, 4 класс, Шклярова Т.В., 2006
- Математика, Сборник упражнений, 3 класс, Шклярова Т.В.
- Раздел: Математика → Высшая математика (основы)
Сочи — 2010, СГУТ и КД.
Уравнения, системы уравнений.
Линейные уравнения.
Квадратные уравнения.
Уравнение третей степени.
Уравнения высших степеней сводящиеся к квадратным.
Системы уравнений.
Система трех уравнений с тремя переменными.
График функции.
Пределы.
Производные.
Интегральное исчисление.
- №1
- 128,69 КБ
- дата добавления неизвестна
- описание отредактировано 01.05.2011 00:39
- Раздел: Математика → Высшая математика (основы)
Основные понятия математики в экономике. Экономико-математические модели, их классификация. Задачи распределения. Понятие о задаче линейного программирования. Транспортные задачи. Задачи о назначениях. Теория графов.
- №2
- 159,94 КБ
- дата добавления неизвестна
- описание отредактировано 23.11.2010 11:18
- Раздел: Математика → Высшая математика (основы)
Линейная и векторная алгебра, аналитическая геометрия, дифференциальное исчисление функции одной переменной. Подходит для студентов БНТУ (Минск) 1 курс.
- №3
- 443,89 КБ
- дата добавления неизвестна
- описание отредактировано 10.02.2010 00:37
- Раздел: Математика → Высшая математика (основы)
61 вопрос. Векторы. Действия над векторами. Декартова прямоугольная система координат. Базис. Действия над векторами. Скалярное произведение векторов и его свойства. Векторное произведение 2-х векторов. Смешанное произведение векторов и его свойства. Уравнение линии и поверхности. Плоскость в пространстве. Общее уравнение плоскости. Взаимное расположение плоскостей….
- №4
- 349,24 КБ
- дата добавления неизвестна
- описание отредактировано 19.10.2016 23:13
- Раздел: Математика → Высшая математика (основы)
2011 г. Содержание: Основы дифференциального исчисления. Понятие производной. Геометрический смысл производной. Физический смысл производной. Связь между непрерывной и дифференцируемой функцией. Правила дифференцирования Доказательство 2-го правила. Теорема о производной сложной функции. Теорема о производной обратной функции. Таблица производных Дифференциал функции. Теорема…
- №5
- 293,17 КБ
- добавлен 02.11.2011 22:37
- описание отредактировано 07.11.2011 06:54
- Раздел: Математика → Высшая математика (основы)
Для студентов БГУИР (Минск, Беларусь)
Содержание:
Многочлены. Рациональные дроби.
Неопределенный интеграл.
Определенный интеграл
Функции нескольких переменных.
Кратные, криволинейные и поверхностные интегралы.
Элементы теории поля
- №6
- 534,36 КБ
- дата добавления неизвестна
- описание отредактировано 11.12.2009 00:57
- Раздел: Математика → Высшая математика (основы)
1-й семестр: теория множеств, предел функции, производная, теорема Тейлора, исследование функции
2-й семестр: автономные системы, Вычислене площадей, Вычисление объема, Дифференциальные уравнения, Изоклины, Интегралы, невыраж. через элементарные функции, Интегральная сумма, Интегрирование по частям, Интегрирование правильных дробей, Интегрирование произведения тригонометрических…
- №7
- 872,04 КБ
- дата добавления неизвестна
- описание отредактировано 19.11.2016 02:18
- Раздел: Математика → Высшая математика (основы)
Векторы на плоскости и в пространстве, Расстояние м/у двумя точками. Площадь треугольника, Системы линейных уравнений с n-переменными,Правило Крамера, Деление отрезка в данном отношении, Полярная система координат, Уравнение прямой с угловым коэффициентом, Уравнение прямой , проходящей через данную точку в заданном направлении. Уравнение прямой, проходящей через две данные точки,…
- №8
- 220,21 КБ
- дата добавления неизвестна
- описание отредактировано 02.07.2011 19:26
- Раздел: Математика → Высшая математика (основы)
Определители (детерминанты).
Операции с квадратными матрицами.
Операции с прямоугольными матрицами.
Ранг матрицы. Расширенная матрица системы уравнений. Частные определители.
Обратные матрицы.
Системы линейных алгебраических уравнений.
Операции с векторами на плоскости.
Операции с векторами в пространстве.
Векторное и смешанное произведение векторов.
Прямые и окружности…
- №9
- 17,95 МБ
- дата добавления неизвестна
- описание отредактировано 29.06.2011 23:48
- Раздел: Математика → Высшая математика (основы)
Собрание для подготовки к экзамену или зачету. Содержит аналитическую геометрию, линейную и векторную алгебру, математический анализ (производная сложной функции, дифференциал функции, формула Тейлора, Ролля, Коши, правило Лопиталя), метод Гаусса, формула Крамера, теорема Кронекера-Капелли, комплексные числа и др. Удобные в использовании Содержание: Матрицы. Линейные операции…
- №10
- 218,42 КБ
- добавлен 09.09.2011 13:14
- описание отредактировано 20.10.2016 00:10
- Раздел: Математика → Высшая математика (основы)
Россия, Пермь, ПНИПУ, 2008 г. 1 курс. 1 семестр.
Дисциплина: Высшая математика Специальность: Разработка и эксплуатация нефтяных и газовых месторождений (РНГМ). Преподаватель: Федотова Л.А.
Определители и их свойства. Понятие минора и алгебраического дополнения.
Системы линейных алгебраических уравнений и методы их решения (Крамера, Гаусса, матричный).
Матрицы и действия над…
- №11
- 626,40 КБ
- добавлен 20.09.2013 13:40
- описание отредактировано 20.10.2016 01:47
- Раздел: Математика → Высшая математика (основы)
Вопросы для самопроверки по дисциплине Математический анализ и линейная алгебра.
Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами: умножение на число, сложение, умножение матриц.
Определители 2, 3 и n-го порядков (определения и их свойства). Теорема Лапласа о разложении определителя по элементам строки или столбца….
- №12
- 1,25 МБ
- дата добавления неизвестна
- описание отредактировано 20.10.2016 02:00
- Раздел: Математика → Высшая математика (основы)
Ответы на вопросы к государственному экзамену на кафедре МОИС в ОГУ. Список вопросов Основные алгебраические структуры. Подструктуры. Множества. Наибольший общий делитель в кольце главных идеалов. Алгоритм Евклида. Простые элементы евклидова кольца, основная теорема арифметики. Кольцо многочленов над числовым полем Р. Теорема Безу. Схема Горнера. Формула Тейлора. Формулы Виета….
- №13
- 22,49 МБ
- добавлен 13.03.2012 12:26
- описание отредактировано 20.10.2016 22:07
- Раздел: Математика → Высшая математика (основы)
Экзамен. Республика Беларусь / г. Гомель, ГГТУ им. П. О. Сухого, 2010-2011 год. 50 вопросов.
Множества, операции над множествами, их свойства.
Комплексные числа, формы представления, основные операции.
Алгебраические уравнения высших степеней, теорема Безу, основная теорема алгебры.
Элементы линейной алгебры.
Определители, их свойства.
Матрицы, основные операции, их…
- №14
- 567,78 КБ
- добавлен 06.01.2012 23:39
- описание отредактировано 09.01.2012 00:55
- Раздел: Математика → Высшая математика (основы)
Бурдаков В.М. 68 билетов, шпоры сделаны по лекциям преподавателя. 1 семестр. ИНЭК. Вопросы: Асимптоты. Построение графиков функций. Бесконечно малые последовательности. Их свойства. Векторное произведение векторов. Его свойства. Векторное пространство. Базис векторного пространства. Выпуклость и вогнутость кривой. Точка перегиба. Необходимые условия точки перегиба. Вычисление…
- №15
- 579,93 КБ
- дата добавления неизвестна
- описание отредактировано 10.12.2010 21:31
- Раздел: Математика → Высшая математика (основы)
Ряды: определение сходимости ряда; необходимый признак сходимости (доказательство); признаки сравнения рядов (формулировка); признак Даламбера (доказательство); признак Коши (доказательство); интегральный признак (доказательство); знакопеременные ряды, условная и абсолютная сходимости ряда (формулировка); признак Лейбница (доказательство); функциональные ряды, область…
- №16
- 1,09 МБ
- дата добавления неизвестна
- описание отредактировано 24.01.2010 15:07
- Раздел: Математика → Высшая математика (основы)
Математика. Выверенные ответы на тесты. МЭСИ. Специальность Юриспруденция. 2012 г. Вопросы в алфавитном порядке. … — значение признака, при котором одна половина значений признака меньше ее, а другая половина больше … — наука о вычислении вероятностей случайных событий … анализ устанавливает форму зависимости между случайной величиной и значениями переменной величины, причем,…
- №17
- 1,06 МБ
- добавлен 23.07.2012 09:12
- описание отредактировано 25.07.2012 10:23
- Раздел: Математика → Высшая математика (основы)
Вашему вниманию предлагается учебное пособие по дисциплине «Математика» (часть 2). В нем изложены основные понятия геометрии, принципы дифференциального исчисления, а также идеи математического анализа, интегрального исчисления.
- №18
- 218,49 КБ
- добавлен 12.10.2013 22:54
- описание отредактировано 20.10.2016 18:30
- Раздел: Математика → Высшая математика (основы)
Линейные пространства, элементы теории множеств, матрица, система линейных алгебраических уравнений, метод Гаусса, векторы, уравнения прямой, уравнения плоскости, канонические поверхности 2-го порядка, числовая последовательность, функции, замечательные пределы, производные функций, производные и дифференциалы выс. порядков, теорема Ролля, криволинейный интеграл.
- №19
- 1,77 МБ
- дата добавления неизвестна
- описание отредактировано 20.10.2016 18:30
- Раздел: Математика → Высшая математика (основы)
DOC файл каждый вопрос на отдельной страницы (по возможности) удобно печатать 1 А4 на 8ст
Определение производной. Необходимые условия существования производной, Производная обратной функции, Раскрытие не определенности, Многочлен, разложение на множители, Интегрирование по частям, Интегрирование простых рациональных дробей, Интегрирование тригонометрических функций,…
- №20
- 284,75 КБ
- дата добавления неизвестна
- описание отредактировано 22.06.2011 10:30
- Раздел: Математика → Высшая математика (основы)
DOC файл каждый вопрос на отдельной страницы (по возможности) удобно печатать 1 А4 на 8ст
Понятие дифференцируемой функции. дифференциал. необходимое условие. Основные теоремы дифференциального исчисления. Теорема Ролля. Исследование функции. Комплексные числа. Производная суммы, производная частного. Производная сложения. Общий вид первообразных. Первообразная функция….
- №21
- 363,73 КБ
- дата добавления неизвестна
- описание отредактировано 20.10.2016 21:36
- Раздел: Математика → Высшая математика (основы)
Только следующие вопросы: основные типы уравнения 2-го порядка в частных производных, уравнение колебания струны, уравнение колебания струны закрепленной на концах методом Фурье, уравнение теплопроводности, задача Коши для неограниченного стержня, уравнение теплопроводности для стационарного случая, задача Дирихле для круга, уравнение теплопроводности методом конечных разностей,…
- №22
- 15,03 КБ
- дата добавления неизвестна
- описание отредактировано 11.12.2008 12:18
- Раздел: Математика → Высшая математика (основы)
Ответы по теории вероятностей и математической статистике к защите ДЗ для студентов II курса СФ, 218, 221-223, 215, 217 гр. Лектор — В.А. Кажан. МГУП( Природообустройства) 2012г. Вопросы:
1.Числовой ряд.
2. Признаки сходимости рядов.
- №23
- 1,10 МБ
- добавлен 03.10.2013 14:36
- описание отредактировано 09.10.2013 20:41
- Раздел: Математика → Высшая математика (основы)
Основные понятия теории множеств. Способы задания множест. Понятие множества. Отношения между множествами, их представление с помощью диаграмм Эйлера-Венна. Понятие множества. Основные операции над множествами. Изображение их результатов с помощью диаграмм Эйлера-Венна. Основные понятия математической логики (простые и составные высказывания, их логические значения). Логические…
- №24
- 53,16 КБ
- дата добавления неизвестна
- описание отредактировано 13.05.2009 17:12
- Раздел: Математика → Высшая математика (основы)
Функции комплексного переменного.
Основные элементарные функции комплексного переменного.
Аналитическая функция.
Производная ф-ции комплексного переменного.
Дифференцируемость функции. Условие Коши-Римана.
Связь между аналитическими и гармоническими функциями.
интегрирование функции комплексного переменного.
интегральная теорема Коши.
Формула ньютона-Лейбница.
Ряды…
- №25
- 14,01 КБ
- дата добавления неизвестна
- описание отредактировано 20.01.2009 02:34
- Раздел: Математика → Высшая математика (основы)
Экзамен. Россия, 2012 год, 37 вопросов: Дифференциальные исчисления, функция одной переменной. Таблица производных. Примеры. Уравнение касательной и нормали к кривой. Дифференциал функции, его геометрический смысл. Применение дифференциала в приближённых вычислениях.Производные сложных функций. Производная дифференциалов высших порядков. Производная от неявных функций. Производная…
- №26
- 558,15 КБ
- добавлен 14.06.2012 01:52
- описание отредактировано 16.06.2012 14:56
- Раздел: Математика → Высшая математика (основы)
Учебно пособие, Технически университет — София, Икономов Н. , 2011, 92 стр.
На Български език.
Съдържание:
Съдържа решени задачи, давани на изпит в Технически университет- София по следните раздели на математиката:
Числови редове;
Развитие на функции в ред на Фурие;
Екстремуми на функции;
Диференциални уравнения;
Линейни диференциални уравнения;
Двойни и тройни…
- №27
- 1,88 МБ
- добавлен 30.08.2012 01:42
- описание отредактировано 01.09.2012 10:14
- Раздел: Математика → Высшая математика (основы)
Ответы на зачет (экзамен)
Чем отличаются поверхностные интегралы 1-го и 2-го рода?
Выражение для grad φ rotА в декартовых координатах?
Формула Остроградского-Гаусса в инвариантной форме?
Разложение в ряд Фурье 2п-периодической функции (теорема Дирихле)?
Разложение в ряд Фурье четных и нечетных функций?
Алгебраическая, тригонометрическая и показательная формы записи…
- №28
- 2,17 МБ
- дата добавления неизвестна
- описание отредактировано 21.10.2016 01:41
- Раздел: Математика → Высшая математика (основы)
Здесь собраны 65 вопросов по вышке. коротко и содержательно описывается каждый вопрос. в отдельном файле каждый вопрос фонт 14, оформлено почти одинаково. Легко ориентироваться в ответе. Можно уменьшить шрифт и сделать реальную шпору.
- №29
- 1,21 МБ
- дата добавления неизвестна
- описание отредактировано 26.01.2011 19:01
- Раздел: Математика → Высшая математика (основы)
Шпаргалка до екзамену з вищої математики, Львів, Україна, 2014 рік, 26 сторінок Описано такі запитання: Означення еліпса, гіперболи. Канонічні рівняння еліпса, гіперболи. Загальне рівняння прямої на площині. Види рівняння прямої на площині. Навести приклади. Поняття матриці. Операції над матрицями (додавання; множення на число; транспонування). Навести приклади. Визначники…
- №30
- 277,22 КБ
- добавлен 26.12.2014 20:21
- описание отредактировано 27.12.2014 02:50
- Раздел: Математика → Высшая математика (основы)
Случайные события и их виды, понятие вероятности. Классическая формула подсчета вероятностей. Комбинаторика. Понятие геометрической и статистической вероятностей. Пространство элементарных событий, операции над событиями. Аксиоматическое определение вероятности. Теорема сложения вероятностей. Условная вероятность. Теорема умножения вероятностей. Формула полной вероятности….
- №31
- 110,92 КБ
- дата добавления неизвестна
- описание отредактировано 26.05.2010 22:34
- Раздел: Математика → Высшая математика (основы)
БрГУ, 2012г бизнес-администрирование 2 курс Вопросы: Понятие последовательности. Ограниченные последовательности. Предел последовательности. Единственность предела последовательности. Предел функции. Единственность предела функции. Критерий существования у функции конечного предела. Бесконечно малые функции и их свойства Бесконечно большие функции и их связь с бесконечно…
- №32
- 447,69 КБ
- добавлен 22.01.2012 21:04
- описание отредактировано 23.01.2012 05:25
- Раздел: Математика → Высшая математика (основы)
Шпаргалка по высшей математике. СПГГИ им. Плеханова. 2003 — 5с.
Включает в себя основные формулы и определения по следующим разделам «вышки»:
Линейная алгебра (матрицы), векторная алгебра, аналитическая геометрия, теория пределов.
- №33
- 94,30 КБ
- добавлен 06.06.2013 01:12
- описание отредактировано 09.06.2013 13:33
- Раздел: Математика → Высшая математика (основы)
Экзамен. — БГУИР, Беларусь, Пастушенко В.А., 2012. 1 семестр, 46 вопросов. Матрицы, определение, операции над матрицами. Определители, вычисление определителей, Теорема Лапласа. Свойства определителей. Обратная матрица. Условие наличие у матрицы обратной. Ранг матрицы. Определения, свойства. Теорема об элементарных преобразованиях матрицы. Линейная зависимость и независимость…
- №34
- 640,26 КБ
- добавлен 29.01.2014 00:16
- описание отредактировано 01.02.2014 15:30
- Раздел: Математика → Высшая математика (основы)
Новосибирск: Сибирское университетское издательство, Норматика, 2017. — 119 c. — 978-5-4374-0806-3 В пособии даны ответы на все основные экзаменационные вопросы по данной дисциплине, предусмотренные Государственным образовательным стандартом высшего профессионального образования. Кратко и понятно изложено самое главное, что необходимо знать студенту для успешной сдачи экзамена….
- №35
- 56,46 МБ
- добавлен 10.12.2017 00:49
- описание отредактировано 10.12.2017 03:10
- Раздел: Математика → Высшая математика (основы)
Операции над матрицами, Определители, Общее уравнение плоскости. Различные виды уравнения плоскости, Взаимное расположение двух прямых в пространстве, Цилиндрические поверхности, Предел числовой последовательности и его свойства, Непрерывность функции в точке, Связь между дифференцируемостью и непрерывностью функции, Правило Лопиталя, Точки экстремума и экстремумы функций и т.д.
- №36
- 5,10 МБ
- дата добавления неизвестна
- описание отредактировано 10.01.2011 21:28
- Раздел: Математика → Высшая математика (основы)
Действия над векторами, Расстояние от точки до прямой на плоскости и до плоскости в пространстве, Св-ва непрерывных ф-ций, Дифференцирование обратной ф-ции, Производные степенных и тригонометрических функций, Необходимые и достаточные признаки монотонности ф-ции, Правило Лопиталя, Теорема Лагранжа, Бнту, Лавренчик Е. Л.
- №37
- 212,33 КБ
- дата добавления неизвестна
- описание отредактировано 12.01.2011 04:58
- Раздел: Математика → Высшая математика (основы)
2008 г. Готовая удобная шпаргалка по математике с графиками. Основы дифференциального исчисления. Понятие производной Правила дифференцирования Таблица производных: Производная высших порядков. Основные теоремы математического анализа. Правила Лопиталя. Правила дифференцирования. Аналитические признаки поведения функции. Поиск наибольшего и наименьшего значения непрерывных…
- №38
- 154,29 КБ
- дата добавления неизвестна
- описание отредактировано 28.01.2011 16:38
- Раздел: Математика → Высшая математика (основы)
Шпаргалка подходит для сдачи экзамена не только в лицеях и техникумах, но и в университетах, и содержит следующие разделы: свойства степеней, основные формулы тригонометрии, тригонометрия, аргументы функции, логарифмы, правила дифференцирования, формулы сокращенного умножения, квадратное уравнение, обратные тригонометрические функции, интеграл, таблица интегралов, формулы…
- №39
- 275,38 КБ
- дата добавления неизвестна
- описание отредактировано 03.02.2010 20:00
- Раздел: Математика → Высшая математика (основы)
Шпаргалка по высшей математике и мат анализу. содержит: свойства степеней, корней, логарифмов, производные, интегралы, значение тригонометрических функций, свойства тригонометрических функций, формулы нахождения площади и объема фигуры
- №40
- 18,91 КБ
- добавлен 18.03.2013 14:27
- описание отредактировано 20.03.2013 23:47
- Раздел: Математика → Высшая математика (основы)
Содержание:
Определители. Основные определения. Вычисление определителей третьего порядка.
Свойства определителей.
Минор.
Алгебраическое дополнение.
Вычисление определителей любого порядка. Понятие определителя n-ого порядка.
Матрицы. Основные определения.
Операции над матрицами.
Понятие обратной матрицы и алгоритм её вычисления. Ранг матрицы. Элементарные преобразования….
- №41
- 45,33 КБ
- дата добавления неизвестна
- описание отредактировано 19.12.2010 21:08
- Раздел: Математика → Высшая математика (основы)
Материал взят из конспекта лекций по высшей математике Письменный Д. Т. Ряды: определение сходимости ряда; необходимый признак сходимости (доказательство); признаки сравнения рядов (формулировка); признак Даламбера (доказательство); признак Коши (доказательство); интегральный признак (доказательство); знакопеременные ряды, условная и абсолютная сходимости ряда (формулировка);…
- №42
- 17,02 МБ
- дата добавления неизвестна
- описание отредактировано 29.05.2011 23:51
- Раздел: Математика → Высшая математика (основы)
13 стр. 2008 г. пределы, интегралы, производные, дифференциальные уравнения, однородные уравнения первого порядка, Вероятность случайного события, Теоремы сложения и умножен вероятностей, Условная вероятность, Повторение испытаний.
- №43
- 63,72 КБ
- дата добавления неизвестна
- описание отредактировано 27.03.2010 13:28
- Раздел: Математика → Высшая математика (основы)
АУЭС, Алматы/Казахстан, 2016 Функции нескольких переменных. Частные производные. Смешанные производные Касательная плоскость и нормаль поверхности Полный дифференциал для функции нескольких переменных и его связь с частными производными. Экстремум функции двух переменных. Необходимые и достаточные условия экстремума Двойные интегралы, их свойства Тройные интегралы, их свойства…
- №44
- 212,60 КБ
- добавлен 04.12.2016 11:42
- описание отредактировано 04.12.2016 21:58
- Раздел: Математика → Высшая математика (основы)
В этой шпаргалке собраны все темы высшей математике, которую проходят в первом семестре технического института.
Всего она охватывает 42 темы, и они довольно хорошо описываются.
Объем 2 листа А4, 4 шрифтом, можно уменьшить еще больше.
- №45
- 79,14 КБ
- дата добавления неизвестна
- описание отредактировано 15.01.2011 02:36
- Раздел: Математика → Высшая математика (основы)
КПИ ИПСА.
Шпаргалки к гос экзаменам.
Ответы на вопросы по мат анализу, линейной алгебре, теории вероятностей, статистике.
Все ответы на украинском языке.
Формула та ряд Тейлора.
Рівномірна збіжність функціональних рядів.
Невласні інтеграли. Інтеграли, що залежать від параметру. Ейлерові інтеграли.
Умовний екстремум функцій кількох змінних. Метод множників Лагранжа….
- №46
- 770,29 КБ
- дата добавления неизвестна
- описание отредактировано 23.02.2010 02:11
- Раздел: Математика → Высшая математика (основы)
Понятие множества. Операции над множествами. Свойство числовых множеств и последовательностей. Евклидово пространство. Понятие окрестности точки. Функциональная зависимость. Графики и свойства основных элементарных функций. Предел числовой последовательности. Предел функции. Основные теоремы о пределах. Первый и второй замечательные пределы. Раскрытие неопределенностей, правило…
- №47
- 56,17 КБ
- добавлен 09.12.2011 00:27
- описание отредактировано 31.01.2020 02:06
- Раздел: Математика → Высшая математика (основы)
Учебно пособие,Технически университет — София, Икономов Н.,2011 г., 134 стр.
На Български език.
Съдържание:
Съдържа решени задачи, давани на изпит в Технически университет- София по следните раздели на математиката:
Линейна алгебра- полиноми, матрици, комплексни числа;
Математически анализ- граници, функции, неопределени интеграли, определени и специални интеграли….
- №48
- 1,62 МБ
- добавлен 30.08.2012 01:37
- описание отредактировано 01.09.2012 10:13
- Раздел: Математика → Высшая математика (основы)
Учебно пособие,Технически университет — София,Икономов Н., 2011 г., 74 стр.
На Български език.
Съдържание:
Съдържа решени задачи, давани на изпит в Технически университет- София по следните раздели на математиката:
Теория на вероятностите- условна вероятност, дискретна и непрекъсната случайна величина;
Комплексен анализ- хармонично спрегнати функции, резидиуми;
Операционно…
- №49
- 626,15 КБ
- добавлен 30.08.2012 01:50
- описание отредактировано 01.09.2012 10:14
- Раздел: Математика → Высшая математика (основы)
Сборник /учебно пособие/, издателство: Висше транспортно училище «Тодор Каблешков» — София, България,Михалев Д.Й., 2008 г.,58 с. На български език. Съдържа 190 решени задачи по Висша математика от следните раздели: диференциално смятане — производна, граница на функция, екстремум, изследване на функция, интегрално смятане -неопределен и определен интеграл, диференциални…
- №50
- 584,59 КБ
- добавлен 02.10.2012 16:10
- описание отредактировано 06.02.2013 02:51
- Раздел: Математика → Высшая математика (основы)
ННГУ, ФНФ, 1 курс. Комплексное число. Тригонометрическая форма комплексного числа. Операции над комплексными числами. Числовая последовательность. Предел числовой последовательности. Методы расчета пределов числовых последовательностей. Предел функции в точке и при неограниченном изменении аргумента. Основные теоремы о пределах функций одной переменной. Методы расчета пределов…
- №51
- 5,55 МБ
- дата добавления неизвестна
- описание отредактировано 26.01.2011 23:36
- Раздел: Математика → Высшая математика (основы)
Шпаргалки к экзамену, более 50 вопросов.
Пределы функции.
Производная и дифференциал функции.
Первообразная.
Неопределенный интеграл.
Определенный интеграл. Свойства определенного интеграла.
Теорема Ферма.
Теорема Ролля.
Теорема Лагранжа.
Теорема Коши.
Правило Лопиталя.
Формула Ньютона — Лейбница.
- №52
- 90,59 КБ
- дата добавления неизвестна
- описание отредактировано 13.02.2011 20:03
- Раздел: Математика → Высшая математика (основы)
Шпаргалки на вопросы к государственному экзамену на кафедре МОИС в ОГУ. Список вопросов Основные алгебраические структуры. Подструктуры. Множества. Наибольший общий делитель в кольце главных идеалов. Алгоритм Евклида. Простые элементы евклидова кольца, основная теорема арифметики. Кольцо многочленов над числовым полем Р. Теорема Безу. Схема Горнера. Формула Тейлора. Формулы…
- №53
- 3,86 МБ
- добавлен 13.03.2012 12:39
- описание отредактировано 14.06.2012 18:17
- Раздел: Математика → Высшая математика (основы)
ИБМТ БГУ 1 курс Определители и их свойства. Миноры, алгебраические дополнения. Методы вычисления определителей. Обратная матрица. Теорема о существовании обратной матрицы. Элементарные преобразования матрицы. Ранг матрицы. Правило вычисления ранга матрицы. Системы n линейных алгебраических уравнений с n неизвестными. Правило Крамера. Решение произвольных систем линейных…
- №54
- 464,41 КБ
- добавлен 21.09.2012 01:13
- описание отредактировано 25.09.2012 16:13
- Раздел: Математика → Высшая математика (основы)
Векторная алгебра.
плоскость в пространстве.
элементы линейной алгебры.
матрицы.
решение однородных систем линейных уравнений.
теорема о базисном миноре.
линейное пространство.
смешанное произведение.
канонические уравнения.
математический анализ.
пределы.
бесконечно малые функции.
производная.
логарифмическое дифференцирование.
Теорема Коши.
форма Лагранжа….
- №55
- 225,94 КБ
- дата добавления неизвестна
- описание отредактировано 21.01.2016 21:44
- Раздел: Математика → Высшая математика (основы)
Шпаргалки по математике, ответы на вопросы, некоторые с доказательствами и рисунками. Темы: Двойные, повторные интегралы Криволинейные интегралы Дифуры Ряды Мат. статистика ПГТУ, 1 курс, 2 сем., ускоренное обучение
- №56
- 1021,30 КБ
- дата добавления неизвестна
- описание отредактировано 21.01.2023 22:40
- Раздел: Математика → Высшая математика (основы)
НГУ, Днепропетровск, 2008 г. , 4 с. Формулы будут полезны для первокурсников, которые только приступают к изучению высшей математики. Тригонометрические формулы. Тригонометрический уравнения и неравенства. Квадратные уравнения. Прогрессии. Формулы сокр. умножения и разложения на множители. Показательные уравнения. Степени и корни. Логарифмы. Логарифмические неравенства….
- №57
- 243,70 КБ
- добавлен 25.07.2012 21:45
- описание отредактировано 28.07.2012 15:28
- Раздел: Математика → Высшая математика (основы)
Матрицы и операции над ними.
Определители, их свойства и вычисление.
Основные методы вычисления определителей.
Обратная матрица. Ранг матрицы.
Системы линейных уравнений.
Векторы в пространстве: линейные операции над векторами в геометрической форме, проекция вектора на ось.
Скалярное произведение.
Линейная зависимость векторов. Действия над векторами в координатной форме….
- №58
- 447,94 КБ
- дата добавления неизвестна
- описание отредактировано 03.05.2011 20:25
- Раздел: Математика → Высшая математика (основы)
Сфу 1 курс Алгебраическая структура группа, её свойства. Алгебраическая структура кольцо, её свойства. Алгебраическая структура поле, её свойства. Линейная зависимость векторов. Базис векторного пространства. Разложение вектора по базису. Замена базиса векторного пространства. Евклидово пространство. Ортонормированный и ортогональный базисы. Линейные преобразования и их свойства….
- №59
- 13,99 КБ
- дата добавления неизвестна
- описание отредактировано 29.01.2010 06:56
- Раздел: Математика → Высшая математика (основы)
Вопросы к экзамену по предмету «Математика»
Матрица. Операции над матрицами.
Система линейных уравнений. Ранг системы. Решение систем линейных уравнений. Формулы Крамера.
Определители и их свойства.
Вычисление определителей. Теорема Лапласа.
Решение систем линейных уравнений. Метод Гаусса.
Понятие вектора. Операции над векторами на плоскости. Координаты вектора.
Длина…
- №60
- 1,13 МБ
- добавлен 03.06.2013 22:35
- описание отредактировано 05.06.2013 23:33
- Раздел: Математика → Высшая математика (основы)
АГиЛА:векторы, определители, матрицы, системы линейных уравнений, прямая на плоскости, плоскость в пространстве, прямая в пространстве, кривые 2-го порядка, полярная система коородинат, поверхности 2-го порядка.
Матан: числовые последовательности (Бином Ньютона, пределы и т.д.), дифференцирование, формулы Тейлора, Маклорена и т.д.
- №61
- 4,23 МБ
- дата добавления неизвестна
- описание отредактировано 08.07.2011 04:28
- Раздел: Математика → Высшая математика (основы)
Угату Кривые 2 порядка. Парабола. Предел функции. Расстояние от точки до прямой. Правило Лопиталя. Параболоиды. Определение производной. Поверхности 2 порядка (перечисление и рисунки). Производная от функции многих переменных, заданной неявно и параметрически. Определители, миноры, алгебраические дополнения. Предел числовой последовательности. Эллипсоиды. Таблица основных…
- №62
- 486,63 КБ
- дата добавления неизвестна
- описание отредактировано 13.01.2010 15:33
- Раздел: Математика → Высшая математика (основы)
Линейная алгебра задачи и решения, уравнение стороны, уравнение высоты, проведенной из вершины, длина высоты, проведенной из вершины, величина угла (в радианах), длина ребра, угол между ребрами, площадь грани, объем пирамиды, длина высоты пирамиды, проведенной из вершины, метод Крамера, метод Гаусса, комплексные числа, пределы
- №63
- 99,30 КБ
- дата добавления неизвестна
- описание отредактировано 01.05.2010 10:17
- Раздел: Математика → Высшая математика (основы)
Интегрирование.
Неопределенный интеграл.
Основные св-ва.
Таблица неопределенных интегралов.
Методы интегрирования.
Полезные правила.
Определенный интеграл.
Замена переменной в определенном интеграле.
Вычисление площади фигуры с помощью определенного интеграла.
Алгоритм.
Функция нескольких переменных.
Частной производной первого порядка.
Частной производной высшего…
- №64
- 51,74 КБ
- дата добавления неизвестна
- описание отредактировано 10.05.2011 15:29
- Раздел: Математика → Высшая математика (основы)
Академія митної служби України Вища математика Питання: Означення функції. Основні елементарні функції. Способи задання функції. Означення обмеженої функції. Означення монотонних функцій. Неявне задані функції. Обернені функції. Параметрично задані функції. Поняття числової послідовності. Границя числової послідовності. Геометричний зміст. Границя змінної величини. Геометричний…
- №65
- 4,48 МБ
- дата добавления неизвестна
- описание отредактировано 27.03.2011 23:12
- Раздел: Математика → Высшая математика (основы)
(укр.яз) Формулы и теория Основные понятия Грани числовых множеств Числовые последовательности Неправильные функции на практике Сходящиеся и расходящиеся последовательности Свойства сходящихся последовательностей Теорема «Об единственности пределов» Экспонента или число е Функции одной переменной Обратные функции Предел функции в точке Свойства предела функции в точке…
- №66
- 335,18 КБ
- дата добавления неизвестна
- описание отредактировано 17.09.2009 13:34
- Раздел: Математика → Высшая математика (основы)
Технически университет-София, България,Икономов Н., 2011 г., 34 стр. на български език. Начертани са графики на функции и повърхнини. Основно съдържание: — Функции -тригонометрични и обратни тригонометрични; -хиперболични и обратни хиперболични; -още графики на функции; -производни на функции; -анализиране на функции; -Криви линии от втора степен — елипса, хипербола, парабола….
- №67
- 1,37 МБ
- добавлен 30.08.2012 03:13
- описание отредактировано 04.09.2012 09:36
- Раздел: Математика → Высшая математика (основы)
Собраны все формулы по высшей математике для подготовки к экзамену или зачету: n — ые производные, формулы Маклорена 1, формулы Маклорена 2, производные, интегралы, координаты центра тяжести, масса кривой d, признаки сходимости числовых рядов Коши, признаки сходимости произвольных числовых рядов Лейбница, Дирихле, Абеля и др.
- №68
- 122,15 КБ
- дата добавления неизвестна
- описание отредактировано 28.12.2010 22:34
- Раздел: Математика → Высшая математика (основы)
Шпаргалки подходят для студентов РГСУ ДТИ
краткое содержание:
экстремум,
первообразная,
неопределенный интеграл,
определенный интеграл.
- №69
- 157,26 КБ
- дата добавления неизвестна
- описание отредактировано 14.06.2010 21:06
- Раздел: Математика → Высшая математика (основы)
Интегрирование тригонометрических функций Дифференциальное ур-ние 1-ого порядка. Задача Коши. Теорема существования и единственности решения задачи Коши Диф-ные у-ния с разделяющимися переменными Диф-ные у-ния с однородными функциями Линейные диф-ные у-ния первого порядка. У-ние Бернулли Дифф-ные у-ния высших порядков. Задача Коши. Понятие о краевых задачах Условия, допускающие…
- №70
- 40,68 КБ
- дата добавления неизвестна
- описание отредактировано 07.06.2011 14:01
- Раздел: Математика → Высшая математика (основы)
Вычисление двойного интеграла.
Вычисление поверхностного интеграла 2 рода.
Гармоническое поле.
Геометрический и физический смысл двойного интеграла.
Двойные интегралы.
Дивергенция векторного поля.
Свойства двойного интеграла.
Физические свойства ротора и т. д.
- №71
- 114,35 МБ
- дата добавления неизвестна
- описание отредактировано 16.01.2011 14:52
- Раздел: Математика → Высшая математика (основы)
Интегралы, дифференциалы, дифференциальные уравнения
Интегрирование простейших иррациональностей.
Комплексные числа. Определение, геометрическая интерпретация, алгебраическая, тригонометрическая и показательная формы. Модуль и аргумент комплексного числа.
Первообразная функция и неопределённый интеграл, его свойства.
Интегрирование подстановкой и по частям.
Теорема Безу….
- №72
- 12,79 МБ
- дата добавления неизвестна
- описание отредактировано 12.12.2010 20:30
- Раздел: Математика → Высшая математика (основы)
Академия труда и социальных отношений
Волгоградский филиал
Заочное отделение Специальность Менеджмент1 курс преподаватель Кочергин В. И.
Перечень вопросов к экзаменам по дисциплине
Радел 1
Предмет математики и основные этапы её развития.
Понятие множества. Операции над множествами.
Понятие матрицы. Матрицы специальных размеров.
Основные действия с матрицами, схема Фалька….
- №73
- 758,74 КБ
- дата добавления неизвестна
- описание отредактировано 11.03.2011 19:31
- Раздел: Математика → Высшая математика (основы)
Сибирский федеральный университет, 1 курс, 23 билета Матрицы. Сложение и вычитание матриц. Умножение матриц на число. Свойства этих действий над матрицами. Произведение матриц. Свойства, связывающие сложение и умножение матриц. Транспонирование матриц. Транспонирование суммы и произведения матриц. Определители 2-го и 3-го порядка и их свойства. Определители N-го порядка….
- №74
- 98,14 КБ
- дата добавления неизвестна
- описание отредактировано 17.03.2011 20:44
- Раздел: Математика → Высшая математика (основы)
Список вопросов: Векторы в пространстве, их свойства. Линейные операции над векторами. Линейная зависимость и линейная независимость векторов. Базис. Представление векторов в базисе. Скалярное произведение двух векторов, его свойства. Вычисление в декартовой системе координат. Векторное произведение двух векторов, его свойства, Вычисление в декартовой системе координат….
- №75
- 235,40 КБ
- дата добавления неизвестна
- описание отредактировано 21.10.2016 18:46
- Раздел: Математика → Высшая математика (основы)
КФ УГАТУ, АП, 4 семестр, Загидуллина. Вопросы: Бином Ньютона и треугольник Паскаля. Близость кривых в смысле нулевого порядка. Расстояние между кривыми. Вариационные задачи в параметрической форме. Вероятность попадания в заданный интервал нормальной случайной величины. Вторая вариация функционала. Экстремум функционала. Необходимое условие экстремума. Высказывания, логические…
- №76
- 1,78 МБ
- дата добавления неизвестна
- описание отредактировано 21.10.2016 20:26
- Раздел: Математика → Высшая математика (основы)
УГАТУ, 2005 год.
Определение высказывания
Логическое следование
Осн. Правила. Вывода
Формулы логики предикатов и т. д.
- №77
- 24,12 КБ
- дата добавления неизвестна
- описание отредактировано 14.04.2010 20:04
- Раздел: Математика → Высшая математика (основы)
Декартова прямоугольная система координат. Базис. Уравнение прямой в пространстве, проходящей через две заданные точки. Гипербола и ее свойства. Действия над векторами. Смешанное произведение векторов и его свойства. Каноническое уравнение прямой на плоскости. Уравнение прямой, проходящей через две точки. Уравнение с угловым коэффициентом. Бесконечно малые величины и их свойства….
- №78
- 116,88 КБ
- дата добавления неизвестна
- описание отредактировано 21.01.2009 05:29
- Раздел: Математика → Высшая математика (основы)
Определители. Основные определения. Вычисление определителей третьего порядка.Алгебраическое дополнение.Понятие обратной матрицы и алгоритм её вычисления.Теорема Кронекера-Капелли.Скалярные и векторные величины. Основные определения.Базис в пространстве. Разложение вектора по базису R.Векторное произведение.Смешанное произведение векторов. Свойства смешанного произведения….
- №79
- 35,46 КБ
- дата добавления неизвестна
- описание отредактировано 21.01.2009 05:52
- Раздел: Математика → Высшая математика (основы)
Математический анализ функции одной переменной.
Понятие функции.
Основные характеристики функций.
Классификация функций.
Предел последовательности.
Бесконечнобольшие (б.б.) и бесконечномалые (б.м.) последовательности.
Основные свойства бесконечно малых/больших последовательностей.
Предел функции.
Основные определения.
Односторонние пределы.
Бесконечно большие (б.б.) и…
- №80
- 110,32 КБ
- дата добавления неизвестна
- описание отредактировано 21.10.2016 23:18
- Раздел: Математика → Высшая математика (основы)
ИНЭКА, 190701 Линии второго порядка. Окружность, Эллипс, Гипербола, Парабола, эллиптический цилиндр, параболический цилиндр, гиперболический цилиндр, эллипсоид, однополостный гиперболоид, двухполостный гиперболоид, эллиптический параболоид, гиперболический параболоид, конус второго порядка-Рисунки и формулы к ним
- №81
- 5,29 МБ
- дата добавления неизвестна
- описание отредактировано 10.05.2009 00:56
- Раздел: Математика → Высшая математика (основы)
1 курс ВУЗа УГТУ-УПИ.
Матрицы, пределы, интегралы, графики, ряды, кратные интегралы, аналитическая геометрия, линейная алгебра
- №82
- 630,38 КБ
- дата добавления неизвестна
- описание отредактировано 14.12.2008 14:23
- Раздел: Математика → Высшая математика (основы)
Система линейных уравнений. Определитель решения системы. Исследование линейной системы 2-ух уравнений с 2-мя неизвестными.
Определитель квадратной матрицы второго порядка. Формулы Крамера.
Определитель третьего порядка. Алгебраические дополнения, теорема о разложении определителя третьего порядка.
Матричное решение системы уравнений.
Исследование систем линейных уравнений….
- №83
- 916,78 КБ
- дата добавления неизвестна
- описание отредактировано 12.01.2009 23:15
- Раздел: Математика → Высшая математика (основы)
КазНТУ им. Сатпаева Горный институт специальность 050707 — горное дело, сборник шпаргалок за 4 семестра высшей математики (т. е. практический полный курс высшей математики): Линейная алгебра с элементами аналитической геометрии, Дифференциальное исчисление, Введение в анализ, Ряды, теория вероятностей, и т. д.
- №84
- 730,83 КБ
- дата добавления неизвестна
- описание отредактировано 22.12.2009 12:33
- Раздел: Математика → Высшая математика (основы)
Двойные интегралы.
Определение определенного интеграла.
Правило вычисления двойного интеграла.
Вычисление объемов тел с помощью двойного интеграла.
Вычисление площадей поверхностей фигур с помощью двойного интеграла.
Тройные интегралы.
Дифференциальные уравнения.
Дифференциальные уравнения второго порядка.
Три случая понижения порядка.
Линейные однородные дифференциальные…
- №85
- 110,37 КБ
- дата добавления неизвестна
- описание отредактировано 26.06.2009 18:26
- Раздел: Математика → Высшая математика (основы)
Формула Ньютона-Лейбница, Теорема Барроу, Свойства определенного интеграла, Определенный интеграл, Интегрирование по частям:, Определение обыкновенного дифференциального уравнения (ОДУ) и его решения,
Однородные дифференциальные уравнения первого порядка.
- №86
- 46,88 КБ
- дата добавления неизвестна
- описание отредактировано 15.06.2009 00:18
- Раздел: Математика → Высшая математика (основы)
Сборник лекций 1 курса 2 семестра, лектор: Миронов. РГРТУ. Список изложеных тем. Определение, простейшие свойства, вычисление неопределенного интеграла «по определению». Первообразные элементарных функций и стандартная таблица первообразных. Замена переменных в неопределенном интеграле. Интегрирование по частям. Интегрирование рациональных функций. Элементарные рациональные…
- №87
- 740,83 КБ
- дата добавления неизвестна
- описание отредактировано 07.08.2009 02:07
- Раздел: Математика → Высшая математика (основы)
Минск, БГЭУ. Основные понятия: Дифференциальное исчисление функции одной переменной: монотонность функции, точка минимума (максимума), локальный и глобальный экстремумы функции, выпуклость (вогнутость) графика функции, точка перегиба, асимптоты графика функции (вертикальные, наклонные, горизонтальные). Интегральное исчисление: первообразная, неопределённый интеграл, формулы…
- №88
- 232,43 КБ
- добавлен 10.02.2013 23:48
- описание отредактировано 13.02.2013 00:26
- Раздел: Математика → Высшая математика (основы)
МИТСО, г.Витебск, 2012г., «Менеджмент»- 2 курс (преподаватель В.А.) элементы теории множеств метод математической индукции матрицы. Операции над матрицами, их свойства определители, основные свойства определителей. Методы вычисления определителей обратная матрица, ее свойства Системы m линейных уравнений с n неизвестными Решение матричным методом системы линейн уравнений…
- №89
- 538,39 КБ
- добавлен 09.12.2012 23:18
- описание отредактировано 11.12.2012 23:21
- Раздел: Математика → Высшая математика (основы)
Введение в математический анализ (один из трех разделов части I).
Здесь есть терминология и ее значение, теоремы, формулы. Материал описан на доступном языке, оформлен наглядно. Размер одной страницы шпаргалки 10,5х14,8см.
Содержание .
Множества, операции над ними.
Числовые множества, их границы.
Операции над символами бесконечности.
Понятие функции.
Частные классы…
- №90
- 173,15 КБ
- добавлен 10.10.2011 22:54
- описание отредактировано 21.10.2016 23:18
- Раздел: Математика → Высшая математика (основы)
УГАТУ, 2010, Васильева Л.И., Коллоквиум 1 семестр
Матрицы. Действия над матрицами.
Определители 2-го и 3-го порядков. Свойства.
Определители произвольного порядка n. Теорема о разложении определителя по строке или столбцу.
Обратная матрица. Критерий существования обратной матрицы.
Системы n линейных уравнений. Правило Крамера.
Ранг матрицы. Элементарные преобразования…
- №91
- 45,60 КБ
- добавлен 13.11.2011 19:41
- описание отредактировано 14.11.2011 23:19
- Раздел: Математика → Высшая математика (основы)
Коллоквиум 2семестр, УГАТУ, Васильева Л.И.
Условный экстремум функции многих переменных.
Производная по направлению. Градиент.
Понятие неопределенного интеграла. Основные свойства.
Основные свойства и правила вычисления неопределенного интеграла.
Замена переменной в неопределенном интеграле. Примеры.
Неопределенный интеграл. Интегрирование по частям.
Интегрирование…
- №92
- 265,77 КБ
- добавлен 13.11.2011 19:46
- описание отредактировано 14.11.2011 23:18
- Раздел: Математика → Высшая математика (основы)
МЭСИ, Ижевск, 2012. …анализ устанавливает форму зависимости между случайной величиной и значениями переменной величины, причем, значения считаются точно заданными. …графика функции – прямая линия, к которой неограниченно приближается график, когда точка неограниченно удаляется от начала координат. Две выборки называются …, если числовые значения одного и того же признака…
- №93
- 191,71 КБ
- добавлен 12.02.2012 21:31
- описание отредактировано 17.02.2012 12:15
- Раздел: Математика → Высшая математика (основы)
Экзамен. ВГКС, Минск, Теслюк В.Н, 2011 Матрицы и линейные операции над ними. Транспонирование матриц. След матрицы. Определители n-го порядка и их свойства. Определитель произведения матриц. Обратная матрица.Свойства обратных матриц. Системы линейных алгебраических уравнений.Формулы Крамера, метод Гаусса. Ранг матрицы и его вычисление. Теорема о базисном миноре. Произвольные…
- №94
- 50,43 КБ
- добавлен 09.01.2012 17:46
- описание отредактировано 18.01.2012 01:29
- Раздел: Математика → Высшая математика (основы)
Экзамен. ВГКС, Минск, Теслюк В.Н, 2011.
Дифференциальные уравнения.
Матрицы.
Ряды.
Комплексные переменные.
Операционное исчисление.
- №95
- 63,22 КБ
- добавлен 09.01.2012 17:51
- описание отредактировано 18.01.2012 01:29
- Раздел: Математика → Высшая математика (основы)
11 файлов.
Собран материал по полному курсу высшей математики за 4 семестра, включая теорию вероятности (все 4 семестра), читаемого в БНТУ, БГУИР и БГУ.
Добавлены все необходимые формулы в компактном виде по каждой теме.
Перечень тем:
Алгебраические операции над матрицами. Определители второго, третьего и n — го порядков.
Обратная матрица. Ранг матрицы.
Системы линейных…
- №96
- 1020,89 КБ
- добавлен 18.03.2014 17:05
- описание отредактировано 14.04.2014 02:30
- Раздел: Математика → Высшая математика (основы)
Экзамен БГПУ им.М.Танка, Минск, Малиновский Е.А., 2015 Множество и его подмножества. Элементы множества. Пустое множество. Конечные и бесконечные множества. Обозначения и примеры. Операции над множествами: объединение, пересечение, разность. Свойства операций. Обозначения и примеры. Перестановки элементов множества. Число перестановок. Примеры вычисления. Размещения элементов…
- №97
- 67,33 КБ
- добавлен 19.06.2015 15:40
- описание отредактировано 22.06.2015 13:29
- Раздел: Математика → Высшая математика (основы)
Экзамен. КГЭУ (Казанский Государственный Энергетический Университет). 4 семестр. Преподаватель — Липачева Е.В. 2012г. Вопросы: Комплексные числа. Область, окрестность, предел последовательности. Функции комплексного переменного. Предел функции комплексного переменного. Дифференцируемость функции. Аналитичность функции. Теорема о дифференцируемости функции. Теометрический смысл…
- №98
- 142,05 КБ
- добавлен 20.07.2013 04:17
- описание отредактировано 27.08.2017 03:49
- Раздел: Математика → Высшая математика (основы)
Содержание: Декартова и полярная системы координат. Расстояние между двумя точками на плоскости. Деление отрезка в данном отношении. Уравнение прямой, проходящей через данную точку. Уравнение прямой, проходящей через две точки. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Общее уравнение прямой на плоскости. Уравнение прямой в отрезках по…
- №99
- 2,37 МБ
- добавлен 14.06.2013 12:25
- описание отредактировано 21.10.2016 17:45
- Раздел: Математика → Высшая математика (основы)
Кривые 2 порядка. Парабола. Предел функции. Расстояние от точки до прямой. Правило Лопиталя. Параболоиды. Определение производной. Поверхности 2 порядка (перечисление и рисунки). Производная от функции многих переменных, заданной неявно и параметрически. Определители, миноры, алгебраические дополнения. Предел числовой последовательности. Эллипсоиды. Таблица основных…
- №100
- 1006,09 КБ
- дата добавления неизвестна
- описание отредактировано 17.01.2009 11:46
- Раздел: Математика → Высшая математика (основы)
Предел. Односторонний предел.
Гипербола.
Общее уравнение прямой.
Уравнения плоскости.
Смешанное произведение векторов, св-ва.
Расстояние от точки до прямой на плоскости и до плоскости в пространстве.
Первый замечательный предел.
Парабола.
Матрицы, действия с ними.
Второй замеч. предел.
Непрерывность функций. (в точке).
Свойства операций над матрицами.
Обратная матрица:…
- №101
- 190,92 КБ
- дата добавления неизвестна
- описание отредактировано 18.01.2010 22:20
- Раздел: Математика → Высшая математика (основы)
85 ответов на вопросы матрицы, определители, элементы теории множеств, пучок прямых на плоскости, ранг матрицы и многое другое
- №102
- 427,96 КБ
- дата добавления неизвестна
- описание отредактировано 15.06.2011 23:25
- Раздел: Математика → Высшая математика (основы)
Выходные данные не указаны. — 2 с. Содержание комплекта Определение функции нескольких переменных. Функции 2-х переменных. Предел функции 2-х переменных. Частное производной. Нахождение частных производных. Полный дифференциал ф-ции 2-х переменных Полный дифференциал для функций нескольких переменных. Применение полного дифференциала для приближенных вычислений….
- №103
- 13,63 КБ
- добавлен 26.02.2018 20:10
- описание отредактировано 27.02.2018 02:57
- Раздел: Математика → Высшая математика (основы)
ОмГТУ,1 курс 2 семестр, содержит 47 вопросов: Дать опр. Обл., предела и непрерывности функции двух переменных. Пр. Дать опр. Дифференцируемости и полного дифференциала функции двух переменных. Пр. Дать опр. Частных производных функций двух переменных. Пр. Вывести формулы дифференцирования сложной функции двух переменных и формулу полной производной. Пр. Дать опр. Неявной…
- №104
- 572,71 КБ
- дата добавления неизвестна
- описание отредактировано 17.06.2009 11:12
- Раздел: Математика → Высшая математика (основы)
Экстремумы функций,
Формула Тейлора с остаточным членом в форме Лагранжа,
Формула Тейлора с остаточным членом в форме Пеано,
Теорема Ролля,
Теорема Лагранжа,
Теорема Коши,
Таблица производных,
Производная функции,
Производная сложной функции,
Производная обратной функции,
Правило Лопиталя,
Ответы к матану,
Непрерывность дифференцируемой функции,
Задание функций в…
- №105
- 3,65 МБ
- дата добавления неизвестна
- описание отредактировано 03.12.2015 21:00
- Раздел: Математика → Высшая математика (основы)
Экзамен. КГЭУ (Казанский Государственный Энергетический Университет), 2 семестр. Преподаватель — Липачева Е.В., 2011. Комплексные числа. Действия над комплексными числами в алгебраической форме. Различные формы комплексных чисел. Теорема об умножении и делении комплексных чисел в тригонометрической форме (с доказательством). Формула Муавра, формула Эйлера (с выводом)….
- №106
- 203,03 КБ
- добавлен 20.07.2013 03:38
- описание отредактировано 09.10.2017 07:51
- Раздел: Математика → Высшая математика (основы)
Экзамен. КГЭУ (Казанский Государственный Энергетический Университет). 3 семестр. Преподаватель — Липачева Е.В. 2011г. Вопросы: Числовые ряды, сумма ряда. Свойства сходящихся рядов. Геометрическая прогрессия. Критерий Коши и необходимое условие сходимости ряда. Гармонический ряд (доказательство расходимости). Признаки сравнения сходимости рядов с положительными членами, простой…
- №107
- 177,77 КБ
- добавлен 20.07.2013 03:44
- описание отредактировано 22.07.2013 10:15
- Раздел: Математика → Высшая математика (основы)
Специальность Бух.учет анализ и аудит 4семестр 2 курс БашГУ
Комбинаторика. Теоремы сложения и умножения.
Перестановки, размещения, сочетания. Примеры.
Классическое и статистическое определение вероятности. Геометрическая вероятность.
Теоремы сложения и умножения вероятностей.
Вероятность появления хотя бы одного события. Пример. Формула Бейеса.
Формула Бернулли. Примеры….
- №108
- 1,78 МБ
- добавлен 13.06.2012 15:43
- описание отредактировано 18.06.2012 17:07
- Раздел: Математика → Высшая математика (основы)
Шпоры по математике Экзамен. СГУТиКД, Россия, 2008 г. Матрицы. Линейные операции над ними и их свойства. Умножение матриц. Транспонирование. Свойства. Определители матриц. Свойства определителей. Миноры и алгебраические дополнения. Разложение определителя по элементам ряда. Теорема замещения. Обратная матрица. Достаточное условие существования обратной матрицы. Элементарные…
- №109
- 218,51 КБ
- добавлен 25.10.2011 00:00
- описание отредактировано 18.11.2011 14:01
- Раздел: Математика → Высшая математика (основы)
КФ УГАТУ, 3 семестр, Загидуллина, 50 вопросов, 20 страниц, шрифт — 6.
Примерные темы: уравнения матем физики, методы Даламбера и Фурье, решение задачи Коши, вычеты, ряды, сходимость и расходимость рядов и многое другое
- №110
- 1,88 МБ
- дата добавления неизвестна
- описание отредактировано 19.01.2010 20:07
- Раздел: Математика → Высшая математика (основы)
3 стр 2008 г. Элементы комбинаторики. Сочетания, размещения, перестановки. Предмет теории вероятности. Случайное событие. Основные понятия теории вероятности. Понятие о статистической и геометрической вероятности Алгебра событий. Сумма событий, противоположные события, сумма нескольких событий, произведение событий Условная вероятность. Зависимые и независимые события. Теорема…
- №111
- 12,33 КБ
- дата добавления неизвестна
- описание отредактировано 25.03.2010 20:00
- Раздел: Математика → Высшая математика (основы)
Список вопросов: Многочлены. Рациональные дроби. Понятие первообразной ф-ции и неопределенного интеграла. Замена переменной в неопределенном интеграле. Интегрирование по частям в неопределённом интеграле. Интегрирование рациональных функций. Интегрирование тригонометрических функций. Интегрирование иррациональных функций. Понятие определенного интеграла и его геометрический…
- №112
- 378,48 КБ
- дата добавления неизвестна
- описание отредактировано 21.10.2016 17:49
- Раздел: Математика → Высшая математика (основы)
Список вопросов: Комплексные числа. Многочлены. Понятие первообразной ф-ции и неопределенного интеграла. Замена переменной в неопределенном интеграле. Внесение множителя под знак дифференциала. Интегрирование по частям в неопределённом интеграле. Интегрирование тригонометрических функций. Интегрирование иррациональных функций. Понятие определенного интеграла и его…
- №113
- 364,71 КБ
- дата добавления неизвестна
- описание отредактировано 21.10.2016 18:35
- Раздел: Математика → Высшая математика (основы)
МЭСИ(филиал г. Сергиев Посад), 2009г.
Определители 2 и3 порядка. Вычисление определителей. Теорема Крамера.
Векторы Операции с векторами.
Скалярное произведение векторов.
Векторное произведение векторов.
Прямая на плоскости.
Различные виды уравнения прямой на плоскости.
Плоскость в пространстве.
Линии второго порядка.
- №114
- 51,96 КБ
- дата добавления неизвестна
- описание отредактировано 20.02.2011 21:54
- Раздел: Математика → Высшая математика (основы)
Ответы на вопросы по математике, преподаватель Бурдаков, 81 билетов, шпоры сделаны по лекциям преподавателя. 2 семестр. ИНЭК. Вопросы: Абсолютная и равномерная сходимость ф-ых рядов Абсолютно непрерывные распределения. Плотность распределения абсолютно непрерывной случайной величины Аксиоматическое построение теории вероятности Биноминальное распределение. Формула Бернулли…
- №115
- 472,04 КБ
- дата добавления неизвестна
- описание отредактировано 21.01.2023 22:40
- Раздел: Математика → Высшая математика (основы)
ЧНУ,Украина ,2012, 3 стр В арихіві 4 документа . Кожен документ відповідає наступним темам : Матриця,Аналітична геометрія, Похідна і функція ,Інтерал і Вищі порядки.Розкривається зміст наступних питань: Поняття матриці. Види матриць. Операції над матрицями. Сума матриць, властивості суми матриць. Поняття матриці. Транспонування матриць. Добуток матриць. Властивості добутку…
- №116
- 84,55 КБ
- добавлен 22.12.2012 05:47
- описание отредактировано 26.12.2012 20:06
- Раздел: Математика → Высшая математика (основы)
Ф-ции и числовые последовательности
Предел
Непрерывность ф-ции
Классификация точек разрыва
Дифференциальное исчисление
Таблица производных осн. элементарн. ф-ции
Правила Лопиталя
Интегрирование
Асимптомы кривой
Экстремумы ф-ции нескольких переменных
- №117
- 257,25 КБ
- добавлен 14.10.2012 18:44
- описание отредактировано 14.10.2012 20:13
- Раздел: Математика → Высшая математика (основы)
Шпоры по математике МЭСИ 2011г. Тесты по математике МЭСИ 2011г. Ответы на 15 контрольных вопросов. Расстояние от точки до прямой. Событие называется …, если оно обязательно произойдет. Совокупность всех первообразных. Уравнение прямой, проходящей через две данные точки P(4; -2) и Q (1;3). Условия перпендикулярности двух прямых. Фигура ограниченная графиком функции y=f(x),…
- №118
- 1,10 МБ
- дата добавления неизвестна
- описание отредактировано 07.06.2011 17:46
- Раздел: Математика → Высшая математика (основы)
В этой шпаргалке собраны все темы высшей математике, которую проходят в первом и втором семестре технического института.
Всего она охватывает 59 тем, и они довольно хорошо описываются.
Объем 3 листа А4, 4 шрифтом, можно уменьшить еще больше.
- №119
- 202,58 КБ
- дата добавления неизвестна
- описание отредактировано 15.01.2011 02:32
- Раздел: Математика → Высшая математика (основы)
Пределы — 20 примеров.
Дифференцирование — 19 примеров.
Аналитическая геометрия — 14 примеров.
Линейная алгебра — 12 примеров.
- №120
- 358,21 КБ
- дата добавления неизвестна
- описание отредактировано 10.04.2011 11:39
- Раздел: Математика → Высшая математика (основы)
Понятие множества. Множество действительных чисел.
Абсолютная величина числа. Окрестность
Функции: понятие, способы задания, свойства.
Элементарные функции. Классификация функций.
Предел числовой последовательности.
Предел функции в бесконечности и в точке.
Бесконечно малые величины, свойства.
Бесконечно большие величины, свойства.
Основные свойства предела.
Предел….
- №121
- 201,23 КБ
- дата добавления неизвестна
- описание отредактировано 28.02.2011 17:00
- Раздел: Математика → Высшая математика (основы)
Числовые ряды. Сумма ряда. Простейшие свойства рядов. Положительные ряды. Признаки сходимости. Знакопеременные и знакочередующиеся ряды. Абсолютная и условная сходимость рядов. Знакочередующиеся ряды. Признак Лейбница. Степенные ряды. Радиус сходимости степенного ряда. Свойства степенных рядов. Разложение функций в степенные ряды. Разложение в ряд Тейлора некоторых функций (e x…
- №122
- 226,18 КБ
- добавлен 13.11.2011 19:51
- описание отредактировано 23.10.2016 03:23
В этом разделе нет файлов.