Анна Малкова
На этой странице – всё, что необходимо для отличного освоения планиметрии и решения задачи 16 Профильного ЕГЭ по математике. В том числе – уникальные авторские материалы.
New: Теорема Менелая, теорема Чевы – нужны на ЕГЭ или нет?
Знаете ли вы, что задание 16 Профильного ЕГЭ по математике в 2018 и 2019 годах было значительно проще, чем «параметры» или «экономическая» задача? Получается, те, кто не брался за планиметрию на ЕГЭ, добровольно отказались от трех первичных баллов, и кому-то не хватило их для поступления.
Да, мы знаем, что в школе планиметрией занимаются мало.
У нас даже статья есть о том, как там всё печально: Геометрия в школе: засада для абитуриента
Однако выучить геометрию и сдать ЕГЭ все равно надо. Как же это сделать: Вам поможет наша Программа по геометрии. Список необходимых фактов и теорем.
Учим определения, формулы и теоремы. Вспоминаем, что такое синус и что такое косинус острого угла в прямоугольном треугольнике. Учим определения и свойства биссектрисы, медианы и высоты треугольника. И 5 (да, 5) формул площади треугольника.
В общем, всё, что необходимо для решения задания №1 первой части Профильного ЕГЭ по математике. До второй части и задачи 16 мы тоже дойдем!
Кратко – в нашем Справочнике.
Подробно – здесь:
Геометрия. Формулы площадей фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Тригонометрический круг: вся тригонометрия на одном рисунке
Внешний угол треугольника. Синус и косинус внешнего угла
Высота в прямоугольном треугольнике
Сумма углов треугольника
Углы при параллельных прямых и секущей
Высоты, медианы, биссектрисы треугольника
Четырёхугольники
Параллелограмм
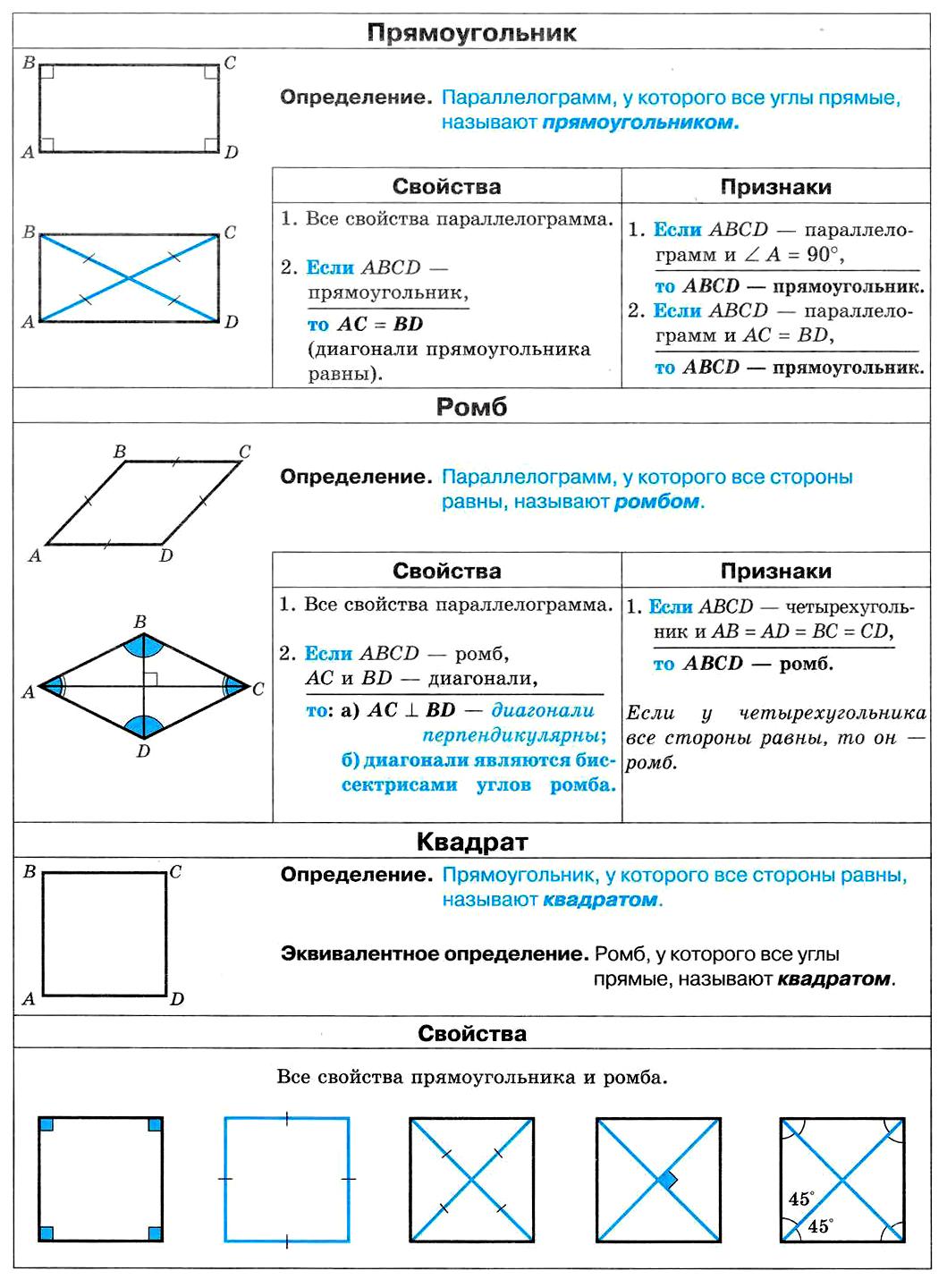
Прямоугольник
Ромб
Квадрат
Трапеция
Окружность. Центральный и вписанный угол
Касательная к окружности
Вписанные и описанные треугольники. Теорема синусов
Вписанные и описанные четырёхугольники
Правильный треугольник
Правильный шестиугольник
Обратите внимание на тему «Векторы»:
Векторы на ЕГЭ по математике
Задание 16 из второй части ЕГЭ состоит из пунктов (а) и (б). Пункт (а) — это доказательство. Как правило, доказать нужно не самый тривиальный факт, и нужно уметь это делать.
Вам помогут «домашние заготовки» — наши Полезные факты для решения задач по планиметрии (с доказательствами)
Докажите их все и проверьте, что у вас получилось. После этого вы сможете доказать любое утверждение, которое вам может встретиться на ЕГЭ в задаче 16.
Но это не всё. Знаете ли вы, что многие задачи 16 Профильного ЕГЭ строятся по одной из так называемых классических схем? И эти Классические схемы для решения задач по планиметрии (с доказательствами) надо знать.
А для тех, кому скучно на уроке, — два геометрических парадокса. Готовы ли вы поверить, что прямой угол равен тупому? И что катет равен гипотенузе? Попробуйте найти ошибку в этих «доказательствах».
Геометрический парадокс: Прямой угол равен тупому
Геометрический парадокс: Катет равен гипотенузе
Как оформить решение задачи №16 (планиметрия)? Смотри образец решения и оформления!
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 2, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 4, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 12, задача 16
Задача на доказательство. Планиметрия.
И несколько полезных советов:
1) Задачи ЕГЭ по планиметрии решаются без сложных формул. Все необходимые факты, определения и теоремы – на этой странице.
2) Часто пункт (а) задачи 16 Профильного ЕГЭ содержит подсказку для решения пункта (б).
3) Обратите внимание на теорему о секущей и касательной, а также на свойство биссектрисы. Их трудно найти в учебнике. А в задачах ЕГЭ они применяются постоянно.
4) Старшеклассники очень любят теорему Фалеса. Но на самом деле применяется она очень редко. Намного чаще применяются три признака подобия треугольников:
— по двум углам,
— по углу и двум прилежащим к нему сторонам,
— по трем пропорциональным сторонам.
5) Самое важное – правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Сначала – теория. Затем – доказательство полезных фактов и классических схем. И только после этого – задачи №16 Профильного ЕГЭ.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Планиметрия» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Теоремы и определения по Планиметрии
Теоремы и определения по Планиметрии. Справочник по геометрии для 7-11 классов, для подготовки к ОГЭ и ЕГЭ. Часть 1 «Планиметрия». Автор: Нелин Е.П. Использованы цитаты из пособия «Геометрия. 7-11 классы. Определения, свойства, методы решения задач в таблицах / М.: Илекса, 2018» из серии «Комплексная подготовка к ЕГЭ и ГИА (ОГЭ). Цитаты использованы в учебных целях.
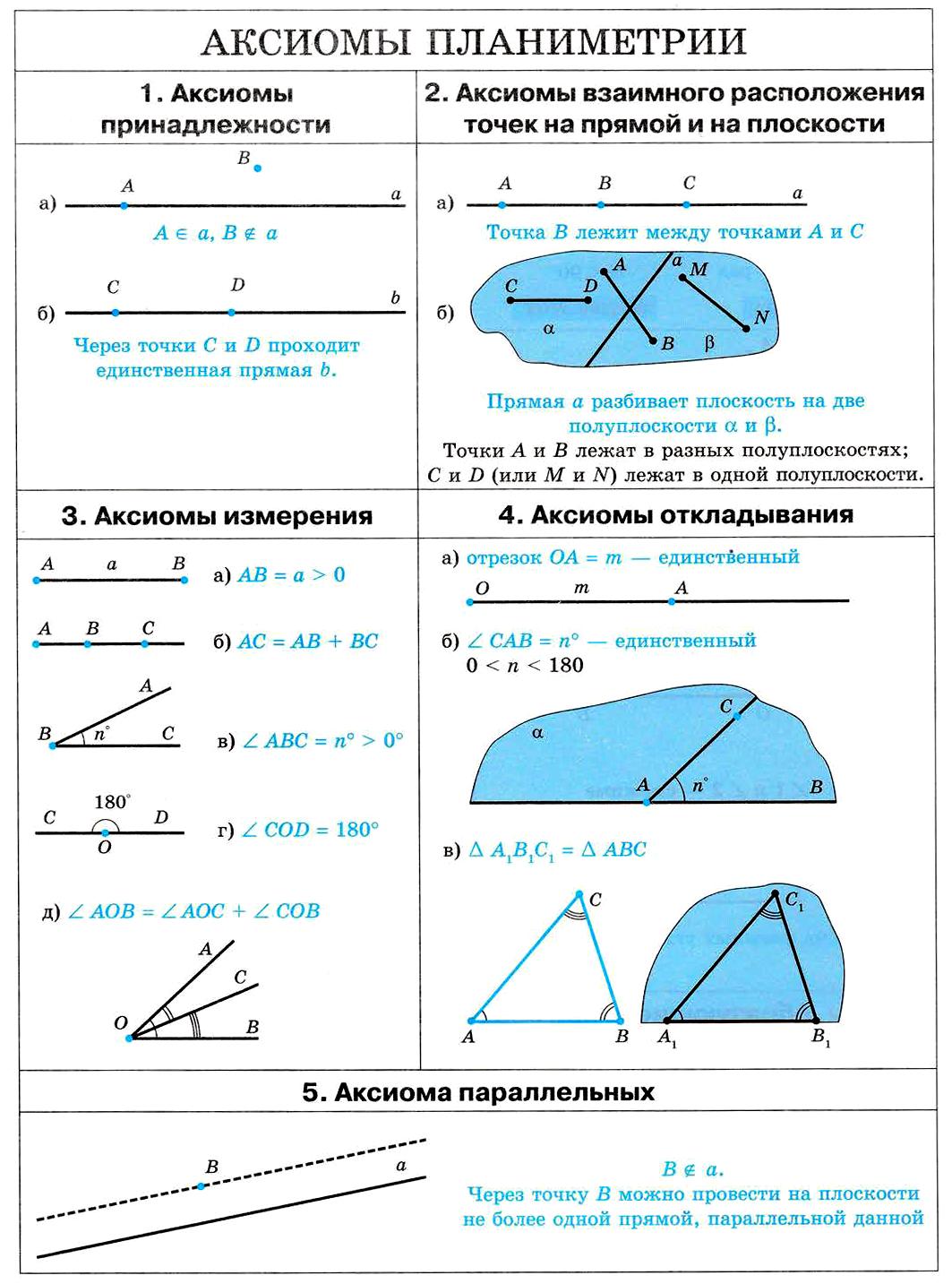
01. Аксиомы планиметрии.
Аксиомы принадлежности. Аксиомы взаимного расположения точек на прямой и плоскости. Аксиомы измерения. Аксиомы откладывания. Аксиома параллельных
02. Углы
Смежные углы. Вертикальные углы. Углы при пересечении
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
04. Свойства сторон и углов треугольника
Свойства сторон и углов треугольника. Внешний угол. Свойства. Неравенство треугольника. Равнобедренный треугольник
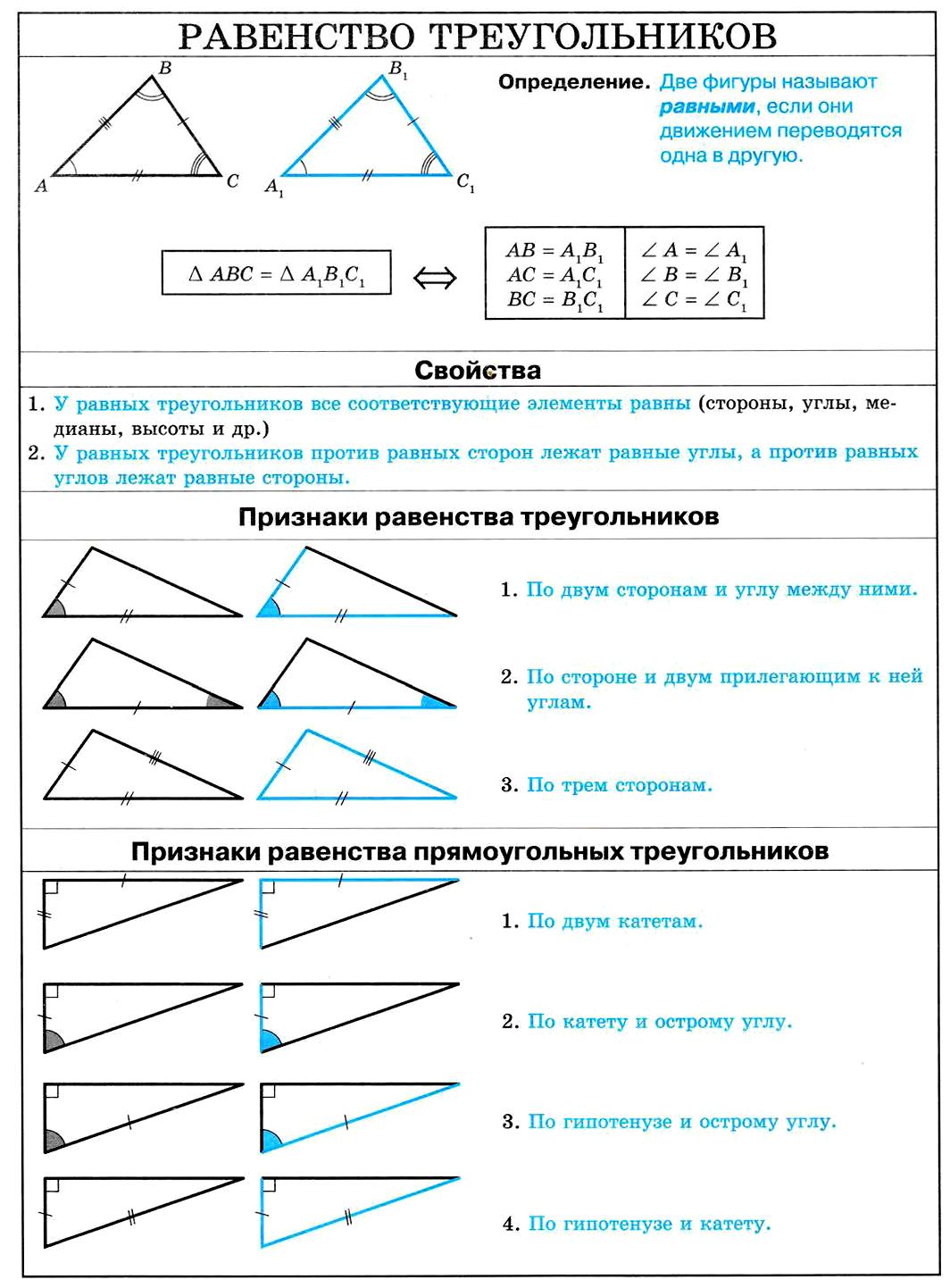
05. Равенство треугольников.
Равенство треугольников. Свойства. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников
06. Медиана треугольника.
Медиана треугольника. Свойства.
07. Биссектриса треугольника.
Биссектриса треугольника. Свойства
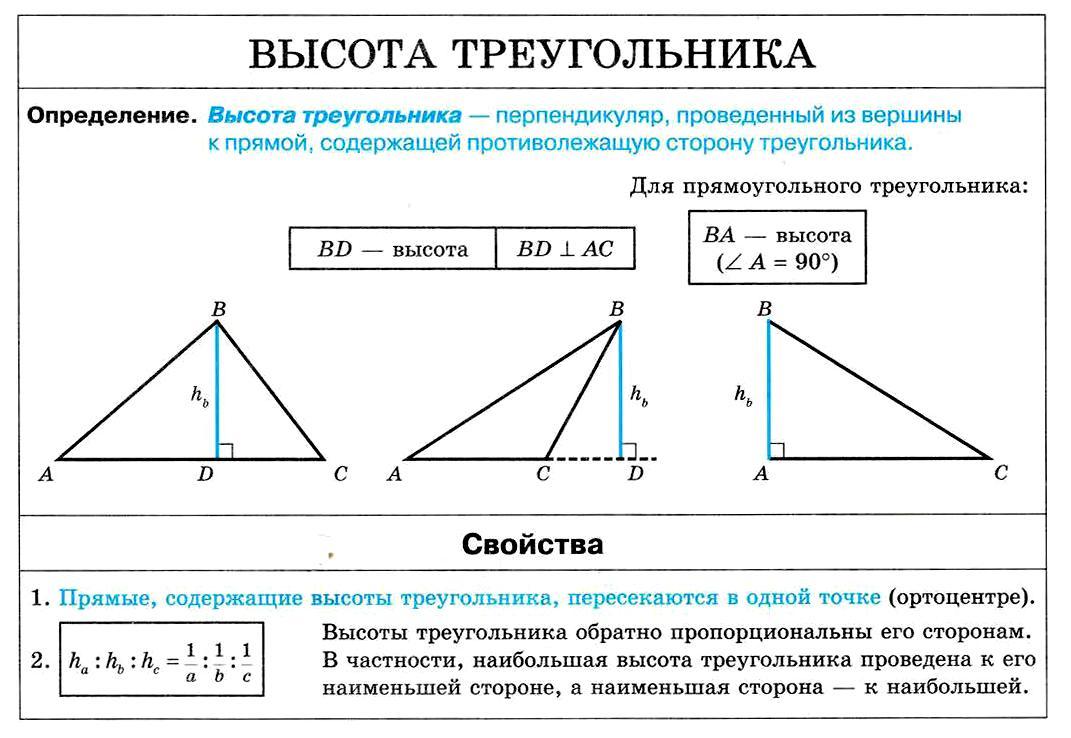
08. Высота треугольника
Высота треугольника. Свойства
09. Средняя линия треугольника
Средняя линия треугольника. Свойства
10. Соотношение между элементами прямоугольного треугольника
Соотношение между элементами прямоугольного треугольника
11. Соотношение между сторонами и углами в произвольном треугольнике
Соотношение между сторонами и углами в произвольном треугольнике
12. Преобразование фигур. Движение
Преобразование фигур. Движение. Симметрия относительно точки. Поворот. Симметрия относительно прямой. Параллельный перенос
13. Преобразование подобия
Преобразование подобия. Свойства. Гомотетия.
14. Подобие треугольников.
Подобие треугольников. Свойства. Признаки подобия треугольников
15. Параллелограмм и его виды.
Параллелограмм и его виды. Свойства. Признаки
Прямоугольник. Ромб. Квадрат.
16. Трапеция
Трапеция. Частные случаи трапеции. Средняя линия трапеции. Дополнительные построения для трапеции
17. Окружность, хорды и дуги
Окружность, хорды и дуги. Свойства
18. Окружность. Касательные и секущие.
Окружность. Касательные и секущие.
19. Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
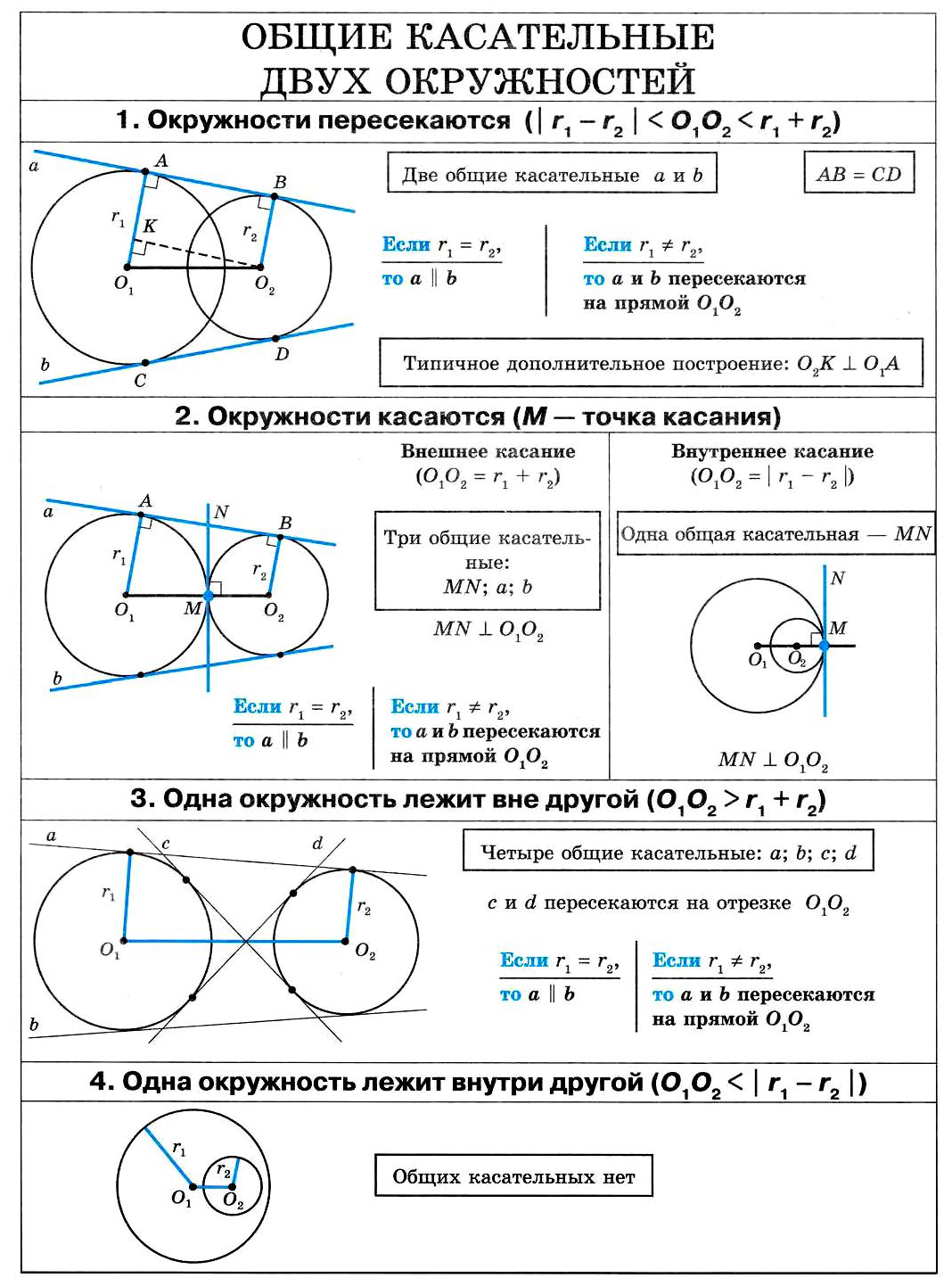
20. Общие касательные двух окружностей.
Общие касательные двух окружностей.
21. Углы в окружности.
Углы в окружности.
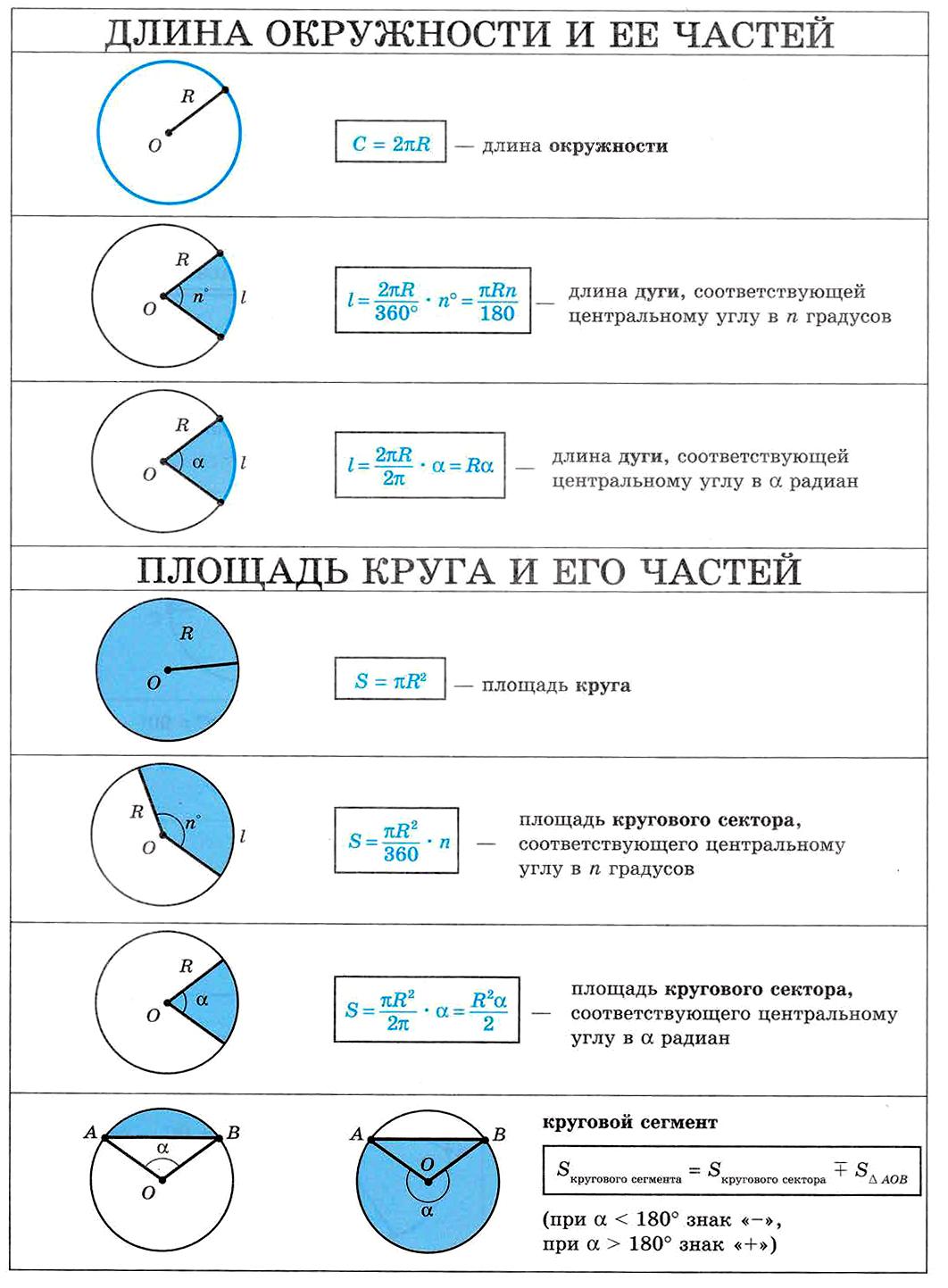
22. Длина окружности и её частей. Площадь круга и его частей
Длина окружности и её частей. Площадь круга и его частей
23. Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
24. Окружность, описанная около треугольника, и окружность, вписанная в треугольник.
25. Окружности, описанные и вписанные в правильные многоугольники
Окружности, описанные и вписанные в правильные многоугольники
26. Площади треугольников.
Площади треугольников.
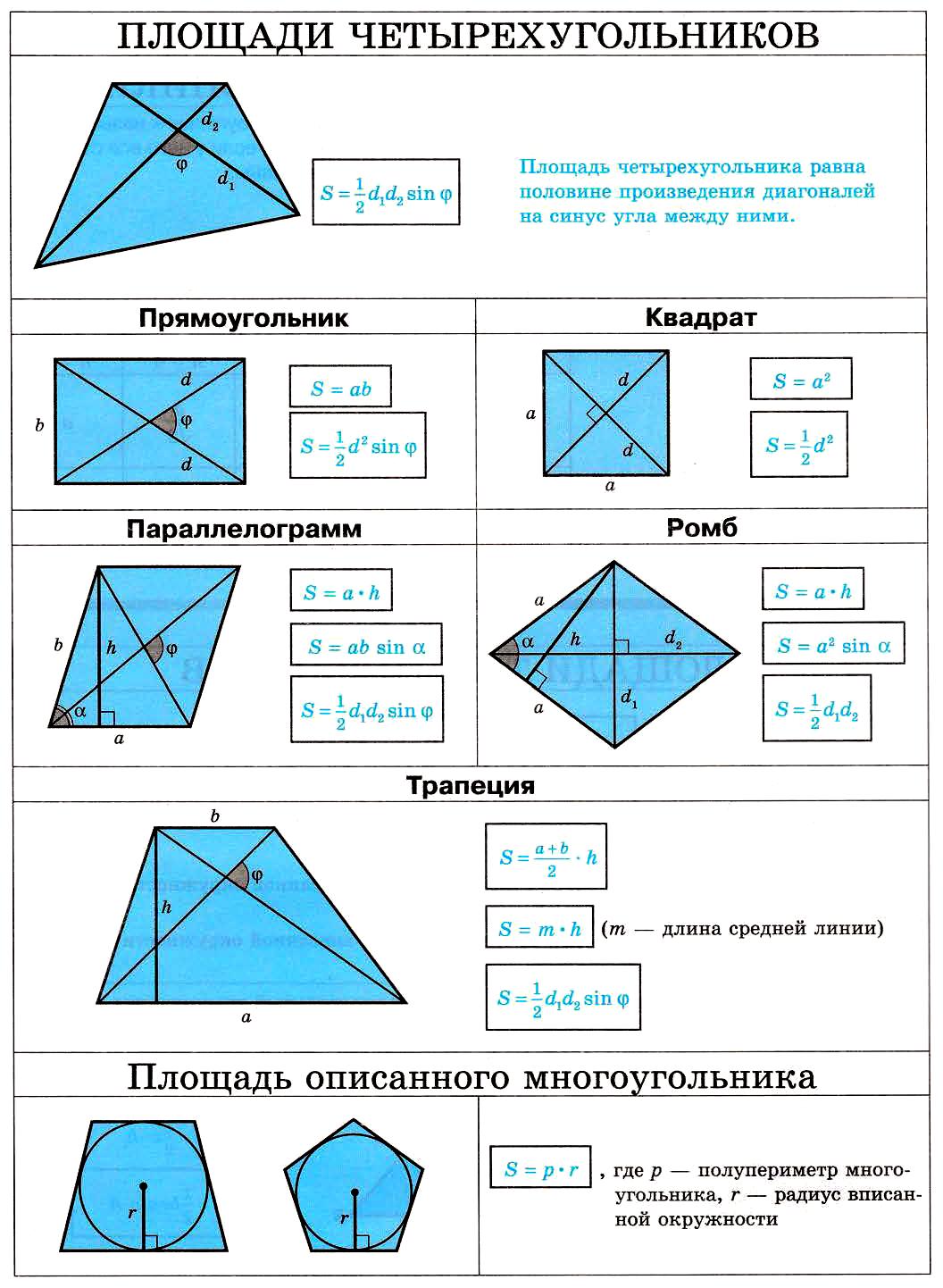
27. Площади четырехугольников.
Площади четырехугольников. Площадь описанного многоугольника
Вы смотрели справочник по геометрии для 7-11 классов «Теоремы и определения по Планиметрии».
Планиметрия
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Площади фигур
Площадь треугольника
- $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$
- $S={a·b·sinα}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$
- $S=p·r$, где $r$ — радиус вписанной окружности
- $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
- Для равностороннего треугольника $S={a^2 √3}/{4}$, где $а$ — длина стороны.
Площади четырехугольников
Прямоугольник
$S=a·b$, где $а$ и $b$ — смежные стороны.
Ромб
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
Трапеция
$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Квадрат
$S=a^2$, где $а$ — сторона квадрата.
Параллелограмм
$S=a·b·sinα$, где $а$ и $b$ — длины сторон параллелограмма, а $α$ — угол между этими сторонами.
Пропорциональные отрезки в прямоугольном треугольнике
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
$CD^2=DB·AD$
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
$CB^2=AB·DB$
$AC^2=AB·AD$
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
$AC·CB=AB·CD$
Метрические соотношения в окружности
1. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.
2. Если хорды $АС$ и $BD$ пересекаются в некоторой точке $N$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
$AN·NC=BN·ND$
Пример:
Хорды $АВ$ и $CD$ пересекаются в точке $Е$. Найдите $ЕD$, если $АЕ=16, ВЕ=9, СЕ=ED$.
Решение:
Если хорды $АВ$ и $СD$ пересекаются в некоторой точке $Е$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
$AЕ·ЕВ=СЕ·ЕD$
Так как $СЕ=ED$, данное выражение можно записать в виде:
$ЕD^2=AЕ·ЕВ$
Подставим числовые значения
$ЕD^2=16·9$
$ЕD=√{16·9}=4·3=12$
Ответ: $12$
3. Если из одной точки к одной окружности проведены две секущие, то произведение первой секущей на ее внешнюю часть равно произведению второй секущей на свою внешнюю часть.
$АС·ВС=EC·DC$
4. Если из одной точки к окружности проведены секущая и касательная, то произведение секущей на ее внешнюю часть равно квадрату длины касательной.
$BD·СB=AB^2$
Вписанные и описанные окружности для четырехугольников.
1. Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
$АВ+CD=BC+AD$
2. Если сумма противоположных углов четырехугольника равна $180°$, то только тогда около него можно описать окружность.
$∠В+∠D=180°$
$∠A+∠C=180°$
Вневписанные окружности
Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон и продолжений двух других.
Для каждого треугольника существует три вневписанных окружности, которые расположены вне треугольника, центрами вневписанных окружностей являются точки пересечения биссектрис внешних углов треугольника.
Точки $О_1, О_2$ и $О_3$ – центры вневписанных окружностей.
Связь площади треугольника с радиусами вневписанных окружностей.
Введем обозначения:
$S$ — площадь треугольника;
$p$ — полупериметр треугольника;
$a, b, c$ — стороны треугольника;
$r_a, r_b, r_c$ — радиусы вневписанных окружностей касающиеся соответственно сторон $a, b$ и $c$;
Для данных обозначений справедливы равенства:
$r_a={S}/{p-a};$
$r_b={S}/{p-b};$
$r_c={S}/{p-c}.$
Пример:
В прямоугольном треугольнике $АВС$ угол $С=90°, АС=6, ВС=8$. Найдите радиус вневписанной окружности, касающейся гипотенузы.
Решение:
Радиус вневписанной окружности, касающейся стороны $АВ$ равен:
$r_{АВ}={S}/{p-АВ}$, где $S$ — площадь треугольника, $р$ — полупериметр треугольника.
Чтобы подставить в формулу данные, найдем сначала площадь треугольника и его полупериметр.
Площадь прямоугольного треугольника равна половине произведения катетов:
$S={АС·АВ}/{2}={6·8}/{2}=24$
Нам неизвестна гипотенуза, найдем ее по теореме Пифагора:
$АВ=√{АС^2+СВ^2}=√{6^2+8^2}=√{100}=10$
Зная все стороны, вычислим полупериметр:
$р={6+8+10}/{2}=12$
Теперь можем все данные подставить в формулу нахождения радиуса вневписанной окружности:
$r_{АВ}={S}/{p-АВ}={24}/{12-10}={24}/{2}=12$
Ответ: $12$
Биссектриса
Биссектриса – это линия, которая делит угол пополам.
Свойства биссектрисы:
1. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
2. Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
$AD=DC$
3. Три биссектрисы в треугольнике пересекаются в одной точке, эта точка является центром вписанной в треугольник окружности.
4. Биссектриса угла в параллелограмме отсекает равнобедренный треугольник.
5. Биссектрисы смежных углов перпендикулярны.
6. В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.
${AB}/{AC}={BA_1}/{A_1C}$
7. Для нахождения длины биссектрисы справедлива формула:
$АА_1=√{АВ·АС-ВА_1·А_1 С}$
Медиана
Медиана — это линия, проведенная из вершины треугольника к середине противоположной стороны.
Свойства медиан:
1. Медиана делит треугольник на два равновеликих треугольника, т.е. на два треугольника, у которых площади равны.
$S_1=S_2$
2. Медианы пересекаются в одной точке и этой точкой делятся в отношении два к одному, считая от вершины.
3. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы и радиусу описанной около этого треугольника окружности.
4. Для нахождения длины медианы, проведенной к стороне «с», справедлива формула:
$М_с={√{2(а^2+b^2)-c^2}}/{2}$
Высота
Высота в треугольнике — это линия, проведенная из вершины треугольника к противоположной стороне под углом в 90 градусов.
$BB_1$ — высота
Свойства высот:
1. Три высоты (или их продолжения) пересекаются в одной точке.
2. При пересечении двух высот получаются подобные треугольники:
$∆АА_1 В~∆СС_1В;$
$∆АС_1 М~∆СМА1$
3. Угол между высотами в остроугольном треугольнике равен углу между сторонами, к которым эти высоты проведены.
4. Высоты треугольника обратно пропорциональны его сторонам:
$h_a:h_b:h_c={1}/{a}:{1}/{b}:{1}/{c}$
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ} ={c}/{sinγ} =2R$, где $R$ — радиус описанной около треугольника окружности.
Пример:
В треугольнике $АВС ВС=16, sin∠A={4}/{5}$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Решение:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
${ВС}/{sinA} =2R$
Далее подставим числовые данные и найдем $R$
${16·5}/{4}=2R$
$R={16·5}/{4·2}=10$
Ответ: $10$
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα.$
Справочный материал по планиметрии


Подборка по базе: Тактическая подготовка.docx, Огневая подготовка 2.docx, 02.03.2023г. Подготовка ГДЗС Организация работы ПБ.doc, Пожарно-тактическая подготовка 18.docx, физ. подготовка упражнения на перекладине 06,07,08,09 марта 2023, тест огневая подготовка.doc, ФИЗИЧЕСКАЯ ПОДГОТОВКА. Упражнение на перекладине 15,16,17,18 сен, Норматив 9.2 Подготовка ГАСИ к работе.docx, проект Мобильный наставнник Подготовка к проф конкурсам-1.pptx, тест подготовка педагога ч5.docx
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
1
Справочный материал по геометрии.
I. Параллельные прямые.
Признаки параллельности прямых:
1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны
3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180º, то прямые параллельны.
II. Некоторые аксиомы планиметрии.
1. Через любые две различные точки проходит прямая, и при этом только одна.
2. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
2
III. Углы.
IV. Треугольник.
В треугольнике ABC:
a, b и с — длины сторон BC, AC и AB соответственно.
A, B, C — величины углов ВАС, АВС и ВСА соответственно.
p =
— полупериметр треугольника ABC.
h a
, h b
, h c
— длины высот AA
2
, BB
2
, CC
2
треугольника ABC соответственно.
R — радиус окружности, описанной около треугольника ABC.
r — радиус окружности, вписанной в треугольник ABC;
S
ABC
— площадь треугольника ABC.
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
3
Имеют место следующие соотношения:
=
(теорема синусов); c
2
=a
2
+ b
2
-2abcosC (теорема косинусов);
Площадь треугольника ABC можно найти следующими способами:
S
ABC
=
ah a
;
S
ABC
=
absinC;
S
ABC
=
;
S
ABC
=pr;
S
ABC
=
(формула Герона)
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
4
Признаки равенства треугольников
Признаки подобия треугольников
По двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
1По двум углам.
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
По стороне и двум прилежащим углам.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
По двум сходственным сторонам и углу между ними.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
5
По трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
По трем сходственным сторонам
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Что еще вы должны знать про треугольник?
В любом треугольнике можно провести замечательные линии.
1. Высота — перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону.
2 Медиана — отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Основные свойства медианы: а) Медиана разбивает треугольник на два треугольника одинаковой площади. б) Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины.
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
6 3. Биссектриса — отрезок, который соединяет вершину с противоположной стороной и делит соответствующий угол пополам.
Какие формулы вам пригодятся:
Если в задаче дана медиана
Если в задаче дана биссектриса
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
7
IV.I. Прямоугольный треугольник и начало тригонометрии.
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
8
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
9
V. Четырехугольники.
II. Четырехугольники.
Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.
Свойства параллелограмма:
1. Противолежащие стороны равны;
2. Противоположные углы равны;
3. Диагонали точкой пересечения делятся пополам;
4. Сумма углов, прилежащих к одной стороне, равна 180°;
5. Сумма квадратов диагоналей равна сумме квадратов всех сторон:
Признаки параллелограмма:
Четырехугольник является параллелограммом, если хотя бы одно из условий выполняется:
1. Две его противоположные стороны равны и параллельны.
2. Противоположные стороны попарно равны.
3. Противоположные углы попарно равны.
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
10
Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойства прямоугольника:
1. Все свойства параллелограмма;
2. Диагонали равны.
Признаки прямоугольника:
Параллелограмм является прямоугольником, если хотя бы одно из условий выполняется:
1. Один из его углов прямой.
2. Его диагонали равны.
Ромбом называется параллелограмм, все стороны которого равны.
Свойства ромба:
1. Все свойства параллелограмма;
+
2. диагонали перпендикулярны;
3. диагонали являются биссектрисами его углов.
Признаки ромба:
Параллелограмм является ромбом, если хотя бы одно из условий выполняется:
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
11 1. Две его смежные стороны равны.
2. Его диагонали перпендикулярны.
3. Одна из диагоналей является биссектрисой его угла.
Квадратом называется прямоугольник, все стороны которого равны.
Из определения следует, что квадрат является ромбом, следовательно, он обладает всеми свойствами прямоугольника и ромба.
Еще свойства квадрата:
1. Все углы квадрата прямые;
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Признаки квадрата:
Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.
Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны.
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
12
Свойства трапеции:
1. Ее средняя линия параллельна основаниям и равна их полусумме;
2. Если трапеция равнобокая, то ее диагонали равны и углы при основании равны;
3. Если трапеция равнобокая, то около нее можно описать окружность;
4. Если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.
Признаки трапеции:
Четырехугольник является трапецией, если его параллельные стороны не равны
Друзья, для более наглядного понимания, вам будет удобно зарисовать
себе в тетрадь такую табличку:
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
13
Выпишите в тетрадь следующие формулы:
Для параллелограмма:
Для частных случаев параллелограмма (прямоугольник, ромб, квадрат):
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
14
И для трапеции:
MN — средняя линия.
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
15
VI. Окружность и круг.
Соотношения между элементами окружности и круга.
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
16
Свойства окружности и ее элементов:
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
17
Теперь самое главное:
Вписанная окружность.
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
18
И описанная окружность:
80-ballov.ru – подготовка к ЕГЭ и ОГЭ на 80+ баллов
19
VII. Правильные многоугольники.
Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
По теме: методические разработки, презентации и конспекты
Основные формулы и соотношения в 8 классе.
Основные формулыисоотношения. в 8 классе 2011-2012 г.Учитель: Удодова Л.В. Календарно-тематическое планирование Занятий дополнительного образованияпо математике в 8 классе (1…
Тема урока: Линзы. Основные формулы тонкой линзы.(8класс)
Тема урока: Линзы. Основные формулы тонкой линзы.Подготовила и провела учитель физики Широкова Людмила Николаевна Цель урока: дать знания о линзах, их физических свойствах и хар…
Виды четырёхугольников и основные формулы для вычисления их площадей
Данный наглядный материал может быть использован для повторения геометрии в конце учебного года при подготовке к ГИА и ЕГЭ….
Контроль знаний основных формул по алгебре и началам анализа учащихся 10 класса при подготовке к ЕГЭ.
Материал служит для контроля знаний тригонометрических формул при подготовке к ЕГЭ….
Основные формулы по тригонометрии
Приведены основные формулы по тригонометрии для 10 класса….
Шпаргалка ученику : Основные формулы планиметрии.
Основные формулы планиметрии….
Основные формулы планиметрии
Основные формулы планиметрии…