Шпора по стереометрии егэ

8 декабря 2019

В закладки

Обсудить

Жалоба

Шпаргалка по стереометрии

Краткие пояснения и алгоритмы по стереометрии.

В 8 и 14 заданиях проверяют знания стереометрии: умение разбираться с геометрическими фигурами, координатами и векторами.

Многие не решают это задание из-за того, что пугает его сложность. Но на самом деле это одно из простых заданий, на которых можно получить 14 баллов. Достаточно знать последовательность действий.

shpargalka_po_stereometrii.pdf

Источник: vk.com/hsege

Алгебра — ЕГЭ                Тригонометрия — ЕГЭ                Геометрия — ЕГЭ                Стереометрия — ЕГЭ                Алгебра — ОГЭ                Геометрия — ОГЭ

Шпаргалка по стереометрии для ЕГЭ

Формулы по стереометрии для ЕГЭ

Советская шпора по стереометрии

Площадь поверхности, объем, радиусы вписанной и описанной сфер

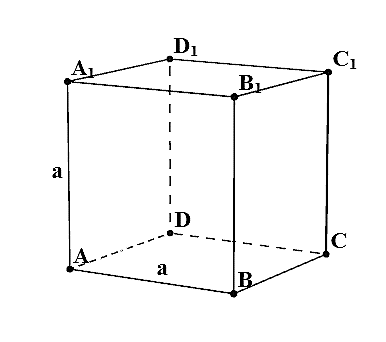
Формулы для многогранников

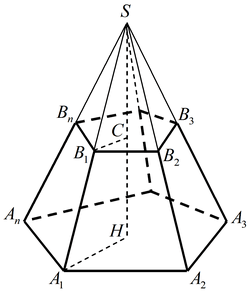
Формулы для пирамиды

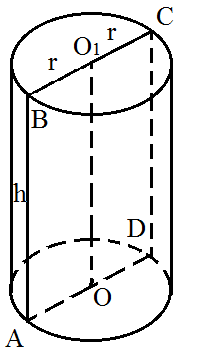
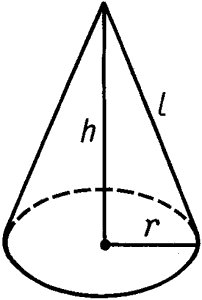
Формулы для тел вращения

Формулы стереометрии. Общий обзор!

Категория: Формулы Теория | ЕГЭ-№2Формулы

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

1.Ве­ро­ят­ность того, что в слу­чай­ный мо­мент вре­ме­ни тем­пе­ра­ту­ра тела здо­ро­во­го че­ло­ве­ка ока­жет­ся ниже чем 36,8 °С, равна 0,81. Най­ди­те ве­ро­ят­ность того, что в слу­чай­ный мо­мент вре­ме­ни у здо­ро­во­го че­ло­ве­ка тем­пе­ра­ту­ра ока­жет­ся 36,8 °С или выше.

1 − 0,81 = 0,19.

2.Ве­ро­ят­ность того, что новый элек­три­че­ский чай­ник про­слу­жит боль­ше года, равна 0,97. Ве­ро­ят­ность того, что он про­слу­жит боль­ше двух лет, равна 0,89. Най­ди­те ве­ро­ят­ность того, что он про­слу­жит мень­ше двух лет, но боль­ше года.

P(A) = 0,97 − 0,89 = 0,08.

3.По­ме­ще­ние осве­ща­ет­ся фонарём с двумя лам­па­ми. Ве­ро­ят­ность пе­ре­го­ра­ния лампы в те­че­ние года равна 0,3. Най­ди­те ве­ро­ят­ность того, что в те­че­ние года хотя бы одна лампа не пе­ре­го­рит.

0,3·0,3 = 0,09. 1 − 0,09 = 0,91.

4.В тор­го­вом цен­тре два оди­на­ко­вых ав­то­ма­та про­да­ют кофе. Ве­ро­ят­ность того, что к концу дня в ав­то­ма­те за­кон­чит­ся кофе, равна 0,3. Ве­ро­ят­ность того, что кофе за­кон­чит­ся в обоих ав­то­ма­тах, равна 0,12. Най­ди­те ве­ро­ят­ность того, что к концу дня кофе оста­нет­ся в обоих ав­то­ма­тах.

0,3 + 0,3 − 0,12 = 0,48. 1 − 0,48 = 0,52.

5.При ар­тил­ле­рий­ской стрель­бе ав­то­ма­ти­че­ская си­сте­ма де­ла­ет вы­стрел по цели. Если цель не уни­что­же­на, то си­сте­ма де­ла­ет по­втор­ный вы­стрел. Вы­стре­лы по­вто­ря­ют­ся до тех пор, пока цель не будет уни­что­же­на. Ве­ро­ят­ность уни­что­же­ния не­ко­то­рой цели при пер­вом вы­стре­ле равна 0,4, а при каж­дом по­сле­ду­ю­щем — 0,6. Сколь­ко вы­стре­лов по­тре­бу­ет­ся для того, чтобы ве­ро­ят­ность уни­что­же­ния цели была не менее 0,98?

Р(1) = 0,6. Р(2) = Р(1)·0,4 = 0,24.

Р(3) = Р(2)·0,4 = 0,096. Р(4) = Р(3)·0,4 = 0,0384;

Р(5) = Р(4)·0,4 = 0,01536.  

По­след­няя ве­ро­ят­ность мень­ше 0,02, по­это­му до­ста­точ­но пяти вы­стре­лов по ми­ше­ни.

6.Две фаб­ри­ки вы­пус­ка­ют оди­на­ко­вые стек­ла для ав­то­мо­биль­ных фар. Пер­вая фаб­ри­ка вы­пус­ка­ет 45% этих сте­кол, вто­рая — 55%. Пер­вая фаб­ри­ка вы­пус­ка­ет 3% бра­ко­ван­ных сте­кол, а вто­рая — 1%. Най­ди­те ве­ро­ят­ность того, что слу­чай­но куп­лен­ное в ма­га­зи­не стек­ло ока­жет­ся бра­ко­ван­ным.

0,45 · 0,03 = 0,0135. 0,55 · 0,01 = 0,0055.

0,0135 + 0,0055 = 0,019.

 7. В клас­се 26 че­ло­век, среди них два близ­не­ца — Ан­дрей и Сер­гей. Класс слу­чай­ным об­ра­зом делят на две груп­пы по 13 че­ло­век в каж­дой. Най­ди­те ве­ро­ят­ность того, что Ан­дрей и Сер­гей ока­жут­ся в одной груп­пе. Пусть один из близ­не­цов на­хо­дит­ся в не­ко­то­рой груп­пе. Вме­сте с ним в груп­пе ока­жут­ся 12 че­ло­век из 25 остав­ших­ся од­но­класс­ни­ков 12 : 25 = 0,48.

8.В Вол­шеб­ной стра­не бы­ва­ет два типа по­го­ды: хо­ро­шая и от­лич­ная, причём по­го­да, уста­но­вив­шись утром, дер­жит­ся не­из­мен­ной весь день. Из­вест­но, что с ве­ро­ят­но­стью 0,8 по­го­да зав­тра будет такой же, как и се­год­ня. Се­год­ня 3 июля, по­го­да в Вол­шеб­ной стра­не хо­ро­шая. Най­ди­те ве­ро­ят­ность того, что 6 июля в Вол­шеб­ной стра­не будет от­лич­ная по­го­да.

Ре­ше­ние.

Для по­го­ды на 4, 5 и 6 июля есть 4 ва­ри­ан­та: ХХО, ХОО, ОХО, ООО 

P(XXO) = 0,8·0,8·0,2 = 0,128;

P(XOO) = 0,8·0,2·0,8 = 0,128;

P(OXO) = 0,2·0,2·0,2 = 0,008;

P(OOO) = 0,2·0,8·0,8 = 0,128.

 P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392.

9.Ков­бой Джон по­па­да­ет в муху на стене с ве­ро­ят­но­стью 0,9, если стре­ля­ет из при­стре­лян­но­го ре­воль­ве­ра. Если Джон стре­ля­ет из не­при­стре­лян­но­го ре­воль­ве­ра, то он по­па­да­ет в муху с ве­ро­ят­но­стью 0,2. На столе лежит 10 ре­воль­ве­ров, из них толь­ко 4 при­стре­лян­ные. Ков­бой Джон видит на стене муху, на­уда­чу хва­та­ет пер­вый по­пав­ший­ся ре­воль­вер и стре­ля­ет в муху. Най­ди­те ве­ро­ят­ность того, что Джон про­махнётся.

Ре­ше­ние.

0,4·(1 − 0,9) = 0,04 и 0,6·(1 − 0,2) = 0,48. Эти со­бы­тия не­сов­мест­ны, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий: 0,04 + 0,48 = 0,52.

10.Аг­ро­фир­ма за­ку­па­ет ку­ри­ные яйца в двух до­маш­них хо­зяй­ствах. 40% яиц из пер­во­го хо­зяй­ства — яйца выс­шей ка­те­го­рии, а из вто­ро­го хо­зяй­ства — 20% яиц выс­шей ка­те­го­рии. Всего выс­шую ка­те­го­рию по­лу­ча­ет 35% яиц. Най­ди­те ве­ро­ят­ность того, что яйцо, куп­лен­ное у этой аг­ро­фир­мы, ока­жет­ся из пер­во­го хо­зяй­ства.

Ответ 0,75

11. Стре­лок стре­ля­ет по ми­ше­ни один раз. В слу­чае про­ма­ха стре­лок де­ла­ет вто­рой вы­стрел по той же ми­ше­ни. Ве­ро­ят­ность по­пасть в ми­шень при одном вы­стре­ле равна 0,7. Най­ди­те ве­ро­ят­ность того, что ми­шень будет по­ра­же­на (либо пер­вым, либо вто­рым вы­стре­лом).

0,7+(1-0,7) ·0,7=0,91

12.Чтобы по­сту­пить в ин­сти­тут на спе­ци­аль­ность «Линг­ви­сти­ка», аби­ту­ри­ент дол­жен на­брать на ЕГЭ не менее 70 бал­лов по каж­до­му из трёх пред­ме­тов — ма­те­ма­ти­ка, рус­ский язык и ино­стран­ный язык. Чтобы по­сту­пить на спе­ци­аль­ность «Ком­мер­ция», нужно на­брать не менее 70 бал­лов по каж­до­му из трёх пред­ме­тов — ма­те­ма­ти­ка, рус­ский язык и об­ще­ст­во­зна­ние.

Ве­ро­ят­ность того, что аби­ту­ри­ент З. по­лу­чит не менее 70 бал­лов по ма­те­ма­ти­ке, равна 0,6, по рус­ско­му языку — 0,8, по ино­стран­но­му языку — 0,7 и по об­ще­ст­во­зна­нию — 0,5.

Най­ди­те ве­ро­ят­ность того, что З. смо­жет по­сту­пить хотя бы на одну из двух упо­мя­ну­тых спе­ци­аль­но­стей.

0,6·0,8·(1 –(1-0,7)(1-0,5)) =0,48·(1-0,3·0,5)=0,408

13. На фаб­ри­ке ке­ра­ми­че­ской по­су­ды 10% про­из­ведённых та­ре­лок имеют де­фект. При кон­тро­ле ка­че­ства про­дук­ции вы­яв­ля­ет­ся 80% де­фект­ных та­ре­лок. Осталь­ные та­рел­ки по­сту­па­ют в про­да­жу. Най­ди­те ве­ро­ят­ность того, что слу­чай­но вы­бран­ная при по­куп­ке та­рел­ка не имеет де­фек­тов. Ре­зуль­тат округ­ли­те до сотых.

0,1·0,8=0,08, 1-0,08=0,92 0,9 : 0,92=0,98

14.Всем па­ци­ен­там с по­до­зре­ни­ем на ге­па­тит де­ла­ют ана­лиз крови. Если ана­лиз вы­яв­ля­ет ге­па­тит, то ре­зуль­тат ана­ли­за на­зы­ва­ет­ся по­ло­жи­тель­ным. У боль­ных ге­па­ти­том па­ци­ен­тов ана­лиз даёт по­ло­жи­тель­ный ре­зуль­тат с ве­ро­ят­но­стью 0,9. Если па­ци­ент не болен ге­па­ти­том, то ана­лиз может дать лож­ный по­ло­жи­тель­ный ре­зуль­тат с ве­ро­ят­но­стью 0,01. Из­вест­но, что 5% па­ци­ен­тов, по­сту­па­ю­щих с по­до­зре­ни­ем на ге­па­тит, дей­стви­тель­но боль­ны ге­па­ти­том. Най­ди­те ве­ро­ят­ность того, что ре­зуль­тат ана­ли­за у па­ци­ен­та, по­сту­пив­ше­го в кли­ни­ку с по­до­зре­ни­ем на ге­па­тит, будет по­ло­жи­тель­ным.

0,05·0,9+0,95·0,01 =0,0545

15. У Вити в ко­пил­ке лежит 12 рублёвых, 6 двух­рублёвых, 4 пя­ти­рублёвых и 3 де­ся­ти­рублёвых мо­не­ты. Витя на­у­гад достаёт из ко­пил­ки одну мо­не­ту. Най­ди­те ве­ро­ят­ность того, что остав­ша­я­ся в ко­пил­ке сумма со­ста­вит более 70 руб­лей.

Ре­ше­ние.

У Вити в ко­пил­ке лежит 12 + 6 + 4 + 3 = 25 монет на сумму 12 + 12 + 20 + 30 = 74 рубля. Боль­ше 70 руб­лей оста­нет­ся, если до­стать из ко­пил­ки либо рублёвую, либо двух­рублёвую мо­не­ту. Ис­ко­мая ве­ро­ят­ность равна 18 : 25 = 0,72.

16.В кар­ма­не у Пети было 2 мо­не­ты по 5 руб­лей и 4 мо­не­ты по 10 руб­лей. Петя, не глядя, пе­ре­ло­жил какие-то 3 мо­не­ты в дру­гой кар­ман. Най­ди­те ве­ро­ят­ность того, что пя­ти­руб­ле­вые мо­не­ты лежат те­перь в раз­ных кар­ма­нах. Всего 6 монет. Ве­ро­ят­ность того, что Петя взял пя­ти­руб­ле­вую мо­не­ту, затем де­ся­ти­руб­ле­вую, и затем еще одну де­ся­ти­руб­ле­вую (в ука­зан­ном по­ряд­ке) равна 2/6·4/5·3/4=0,2  По­сколь­ку Петя мог до­стать пя­ти­руб­ле­вую мо­не­ту не толь­ко пер­вой, но и вто­рой или тре­тьей, ве­ро­ят­ность до­стать набор из одной пя­ти­руб­ле­вой и двух де­ся­ти­руб­ле­вых монет в 3 раза боль­ше. Тем самым, она равна 0,6.

17. За круг­лый стол на 101 сту­л в слу­чай­ном по­ряд­ке рас­са­жи­ва­ют­ся 99 маль­чи­ков и 2 де­воч­ки. Най­ди­те ве­ро­ят­ность того, что между двумя де­воч­ка­ми будет си­деть один маль­чик.

Ре­ше­ние.

Пусть пер­вой за стол сядет де­воч­ка, тогда для каж­до­го из остав­ших­ся ребят (в том числе и для вто­рой де­воч­ки ) ве­ро­ят­ность ока­зать­ся на любом из остав­ших­ся сту­льев равна 0,01 . А мест, удо­вле­тво­ря­ю­щих усло­вию за­да­чи, толь­ко два. Таким об­ра­зом ве­ро­ят­ность, что между двумя де­воч­ка­ми будет си­деть один маль­чик равна 2·0,01 = 0,02

18. За круг­лый стол на 17 сту­льев в слу­чай­ном по­ряд­ке рас­са­жи­ва­ют­ся 15 маль­чи­ков и 2 де­воч­ки. Най­ди­те ве­ро­ят­ность того, что обе де­воч­ки будут си­деть рядом. 

Ре­ше­ние.

Пусть пер­вой за стол сядет де­воч­ка, тогда рядом с ней есть два места, на каж­дое из ко­то­рых пре­тен­ду­ет 16 че­ло­ве­ка, из ко­то­рых толь­ко одна де­воч­ка. Таким об­ра­зом, ве­ро­ят­ность, что де­воч­ки будут си­деть рядом равна 2·1/16 =1/8 =0,125

Не будут сидеть рядом 1-0,125=0,875

19. Про паука.

Произвольная призма

• S_бок =P_сеч*l;
• V = S_осн*H;
• V=S_сеч*l;
• S_полн= S_сеч + 2* S_осн;

Прямая призма

• S_бок =P*H;
• V = S_осн*H;
• S_полн=S_сеч + 2*S_осн;

Прямоугольный параллелепипед

• S_бок =P*H=2(a + b)c;
• V = abc;
• S_полн =2(ab + bc +ac);
• d² = a² + b² + c²;

Произвольная пирамида

• S_полн =S_бок+S_осн;
• V = frac{1}{3}V=31​ S_осн * H

Правильная пирамида

• S_бок =frac{1}{2}P*h; 21​ P∗ h;
• S_бок = S_осн : cos α;
• S_полн = S_бок + S_осн ;
• V = frac{1}{3}Sосн * HV=31​ Sосн∗ H

Произвольная усеченная пирамида

• V=frac{H}{3}(S_1 + S_2 + sqrt{S_1S_2})V=3H​ (S1​ +S2​ +S1​ S2​ ​ )

Правильная усеченная пирамида

• S_бок = frac{1}{2}(P_1 + P_2)21​ (P1​ +P2​ ), где P₁ и Р₂ — периметры оснований
• S_полн = S_бок + S₁ + S₂, где S₁ и S₂ — площади оснований

Цилиндр

• S_бок= 2 pi RH; 2π RH;
• S_полн = S_бок + 2S_осн;
• S_полн =2 pi R(R+H); 2π R(R+H);
• V=pi R^{2}HV=π R2H

Куб

• Если а — ребро куба, то V = a³;
• S_полн =6a^2; d = asqrt{3}; =6a2; d=a3​;

Конус

• S_бок= pi Rl; π Rl;
• S_полн = S_бок + S_осн;
• S_полн =pi R(R+l); π R(R+l);
• V=frac{1}{3} pi R^{2}HV=31​ π R2H

Усеченный конус

• S_бок=pi l(R+ r); π l(R+r);
• S_полн = S_бок+ S_1 + S_2; +S1​ +S2​;
• S_1 = pi R^2; S1​ =π R2;
• S_2 = pi r^2; S2​ =π r2;
• V = frac{pi H}{3}(R^2 + Rr + r^2)V=3π H​ (R2+Rr+r2)

Шаровая (или сферическая) поверхность

• S_шара = 4pi R^2 = pi D^24π R2=π D2
• V_шара= frac{4}{3}pi R^3 = frac{1}{6}pi D^334​ π R3=61​ π D3

Параллельность в пространстве

• Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.
• Если две прямые на плоскости перпендикулярны к третьей прямой, то они параллельны.
• Если две прямые в трехмерном пространстве перпендикулярны к одной плоскости, то они параллельны.
• Если прямая a, не лежащая в плоскости $α$, параллельна некоторой прямой $b$, которая лежит в плоскости $α$, то прямая a параллельна плоскости $α$.
• Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.

Перпендикулярность в пространстве

• Две прямые называются перпендикулярными, если угол между ними равен $90°$.
• Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
• Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то заданные плоскости перпендикулярны.
• Теорема о трех перпендикулярах: если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и самой наклонной.
• Если из одной точки проведены к плоскости перпендикуляр и наклонные, то:

1. Перпендикуляр короче наклонных.
2. Равные наклонные имеют равные проекции на плоскости.
3. Большей наклонной соответствует большая проекция на плоскости.

Скрещивающиеся прямые

• Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.
• Через две скрещивающиеся прямые проходит единственная пара параллельных плоскостей.
• Расстояние между скрещивающимися прямыми – это расстояние от некоторой точки одной из скрещивающихся прямых до плоскости, проходящей через другую прямую параллельно первой прямой.
• Угол между скрещивающимися прямыми – это острый угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым.

Многогранники

Введем общие обозначения

$P_{осн}$ — периметр основания;

$S_{осн}$ — площадь основания;

$S_{бок}$ — площадь боковой поверхности;

$S_{п.п}$ — площадь полной поверхности;

$V$ — объем фигуры.

Название	Определение и свойства фигуры	Обозначения и формулы объема, площади
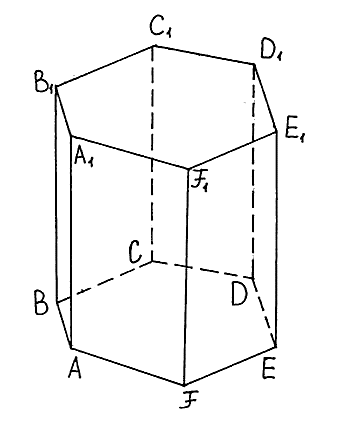
Прямоугольный параллелепипед	1. Все двугранные углы прямоугольного параллелепипеда – прямые. 2. Противоположные грани попарно равны и параллельны. 3. Диагонали прямоугольного параллелепипеда равны. 4. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты). $B_1D^2=AD^2+DC^2+C_1C^2$	$V=a·b·c$, где $a, b$ и $с$ – длина, ширина и высота. $S_{бок}=P_{осн}·c=2(a+b)·c$ $S_{п.п}=2(ab+bc+ac)$.
Куб	1. Противоположные грани попарно параллельны. 2. Все двугранные углы куба – прямые. 3. Диагональ куба в $√3$ раз больше его ребра. $B_1 D=АВ√3$ 4. Диагональ грани куба в $√2$ раза больше длины ребра. $DС1=DC√2$	Пусть $а$ — длина ребра куба, $d$ — диагональ куба, тогда справедливы формулы: $V=a^3={d^3}/{3√3}$. $S_{п.п}=6а^2=2d^2$ $R={a√3}/{2}$, где $R$ — радиус сферы, описанной около куба. $r={a}/{2}$, где $r$ — радиус сферы, вписанной в куб.
Призма	Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов. Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру. Прямая призма называется правильной, если ее основания – правильные многоугольники. В правильной четырехугольной призме диагонали точкой пересечения делятся пополам.	$S_{бок}=P_{осн}·h$ $S_{п.п}=S_{бок}+2S_{осн}$ $V=S_{осн}·h$
Пирамида	У треугольной пирамиды есть еще одно название – тетраэдр (четырехгранник). Пирамида называется правильной, если в ее основании лежит правильный многоугольник, а ее высота приходит в центр основания (в центр описанной окружности). Все боковые ребра правильной пирамиды равны, следовательно, все боковые грани являются равнобедренными треугольниками.	Формулы вычисления объема и площади поверхности правильной пирамиды. $h_a$ — высота боковой грани (апофема) $S_{бок}={P_{осн}·h_a}/{2}$ $S_{п.п}=S_{бок}+S_{осн}$ $V={1}/{3} S_{осн}·h$
Усеченная пирамида	Усеченной пирамидой называется многогранник, заключенный между пирамидой и секущей плоскостью, параллельной. Правильная усечённая пирамида получается при сечении правильной пирамиды плоскостью, параллельной основанию. У правильной усеченной пирамиды апофемы равны	$V={h(F+f+√{Ff})}/{3}$ Где $F,f$ — площади оснований; $h$ — высота (расстояние между основаниями); Для правильной ус. пирамиды $S_{бок}={(P+p)·a}/{2}$, где $P$ и $p$ – периметры оснований; $а$ – апофема.
Цилиндр	Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра. Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра. Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра. Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра. $R_{сферы}=R_{цилиндра}={h_{цилиндра}}/{2}$	$S_{бок.пов.}=2πR·h$ $S_{полной.пов.}=2πR(R+h)$ $V=πR^2·h$
Конус	Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса. Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$. Если радиус или диаметр конуса увеличить в $n$ раз, то его объем увеличится в $n^2$ раз. Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.	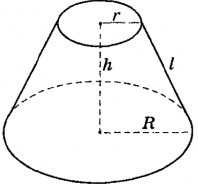$S_{бок.пов.}=πR·l$ $S_{полной.пов.}=πR^2+πR·l=πR(R+l)$ $V={πR^2·h}/{3}$
Усеченный конус	Усеченным конусом называется часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию. Осевым сечением усеченного конуса является равнобедренная трапеция.	$S_{бок}=πl(R+r)$ $S_{п.п.}=π(R^2+r^2+l(R+r))$ $V={πH(R^2+r^2+Rr)}/{3}$ Где $R$ и $r$ – радиусы оснований; $Н$ — высота усеченного конуса.
Сфера, шар	Тело, ограниченное сферой, называется шаром. Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара. Если радиус или диаметр шара увеличить в $n$ раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.	$S_{п.п}=4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ — радиус шара, $d$ — диаметр шара.

Тетраэдр

Радиус описанной сферы тетраэдра.

Вокруг тетраэдра можно описать сферу, радиус которой находим по формуле, где $R$ — радиус описанной сферы, $a$ — ребро тетраэдра.

$R={a√6}/{4}$

Радиус вписанной в тетраэдр сферы.

В тетраэдр можно вписать сферу, радиус вписанной сферы находим по формуле, приведенной ниже.

Где $r$ — радиус вписанной в тетраэдр сферы,

$a$ — ребро тетраэдра.

$r={a√6}/{12}$

Составные многогранники

Задачи на нахождение объема составного многогранника:

1. Разделить составной многогранник на несколько параллелепипедов.
2. Найти объем каждого параллелепипеда.
3. Сложить объемы.

Задачи на нахождение площади поверхности составного многогранника.

— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:

$S_{полн.пов.}=P_{осн}·h+2S_{осн}$

Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.

— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

Задачи на нахождение расстояния между точками составного многогранника.

В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.

Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Связь между сторонами правильного n-угольника и радиусами описанной и вписанной окружностей

$АВ=a_n$ — сторона правильного многоугольника

$R$ — радиус описанной окружности

$r$ — радиус вписанной окружности

$n$ — количество сторон и углов

$a_n=2·R·sin{180°}/{n}$;

$r=R·cos{180°}/{n}$;

$a_n=2·r·tg{180°}/{n}$.

Формула нахождения градусной меры угла в правильном многоугольнике:

$α={(n-2)·180°}/{n}$

Формулы площадей треугольников и многоугольников, которые могут находиться в основании многогранников

В основании лежит треугольник

1. $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне а

2. $S={a·b·sin⁡α}/{2}$, где $a, b$ — соседние стороны, $α$ — угол между этими соседними сторонами.

3. $S=p·r$, где $r$ — радиус вписанной окружности

4. $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности

5. Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.

В основании лежит четырехугольник

Прямоугольник

$S=a·b$, где $а$ и $b$ — смежные стороны.

Ромб

$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба

$S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.

Трапеция

$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.

Площади правильных многоугольников:

1. Для равностороннего треугольника $S={a^{2}√3}/{4}$, где $а$ — длина стороны.

2. Квадрат

$S=a^2$, где $а$ — сторона квадрата.

3. Правильный шестиугольник

Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:

$S=6·S_{треугольника}={6·a^{2}√3}/{4}={3·a^{2}√3}/{2}$, где $а$ — сторона правильного шестиугольника.

База 11

1). Плоскость, проходящая через три точки A, B и C,
разбивает куб на два многогранника. Сколько граней у многогранника, у
которого больше граней?     Ответ. 7.            

2). Плоскость, проходящая через три точки A, B и C,
разбивает куб на два многогранника. Сколько ребер у многогранника, у
которого больше?   Ответ. 15.

3). Плоскость, проходящая через три точки A, B и C,
разбивает куб на два многогранника. Сколько вершин у многогранника, у
которого больше?   Ответ. 10.

4). Плоскость, проходящая через три точки A, B и C,
разбивает куб на два многогранника. Сколько граней у многогранника, у
которого меньше граней?    Ответ. 5.

5). Плоскость, проходящая через три точки A, B и C,
разбивает куб на два многогранника. Сколько ребер у многогранника, у
которого меньше?   Ответ. 9.

6). Плоскость, проходящая через три точки A, B и C,
разбивает куб на два многогранника. Сколько вершин у многогранника, у
которого меньше?   Ответ. 6.

7). Плоскость, проходящая через три точки A, B и С,
разбивает правильную треугольную призму на два многогранника. Сколько рёбер
у многогранника, у которого больше вершин?  Ответ. 12.     

8). Плоскость, проходящая через три точки A, B и С,
разбивает правильную треугольную призму на два многогранника. Сколько граней
у многогранника, у которого больше ?  Ответ. 6.

9). Плоскость, проходящая через три точки A, B и С,
разбивает правильную треугольную призму на два многогранника. Сколько вершин
у многогранника, у которого больше?  Ответ. 8.

10). Плоскость, проходящая через три точки A, B и С,
разбивает правильную треугольную призму на два многогранника. Сколько рёбер
у многогранника, у которого меньше?  Ответ. 9.

11). Плоскость, проходящая через три точки A, B и С,
разбивает правильную треугольную призму на два многогранника. Сколько граней
у многогранника, у которого меньше?  Ответ. 5.

12). Плоскость, проходящая через три точки A, B и С,
разбивает правильную треугольную призму на два многогранника. Сколько вершин
у многогранника, у которого меньше?  Ответ. 6.

13). Плоскость, проходящая через точки A, B и C (см.
рис.), разбивает тетраэдр на два многогранника. Сколько рёбер у
получившегося многогранника с большим числом вершин?   Ответ. 9.    

14). Плоскость, проходящая через точки A, B и C (см.
рис.), разбивает тетраэдр на два многогранника. Сколько вершин у
получившегося многогранника с большим?   Ответ. 6.

15). Плоскость, проходящая через точки A, B и C (см.
рис.), разбивает тетраэдр на два многогранника. Сколько граней у
получившегося многогранника с большим?   Ответ. 5

16). Плоскость, проходящая через точки A, B и C (см.
рис.), разбивает тетраэдр на два многогранника. Сколько вершин у
получившегося многогранника с меньшим?   Ответ. 4.

17). Плоскость, проходящая через точки A, B и C (см.
рис.), разбивает тетраэдр на два многогранника. Сколько ребер у
получившегося многогранника с меньшим?   Ответ. 6.

18). Плоскость, проходящая через точки A, B и C (см.
рис.), разбивает тетраэдр на два многогранника. Сколько граней у
получившегося многогранника с меньшим?   Ответ. 4.

19). Пирамида Снофру имеет форму правильной четырёхугольной пирамиды,
сторона основания которой равна 220 м, а высота — 104 м. Сторона основания
точной музейной копии этой пирамиды равна 44 см. Найдите высоту
музейной копии. Ответ дайте в сантиметрах.

                220м = 22000см,   22000 : 44 = 500,   10400 : 500
= 20,8см.     Ответ. 20,8

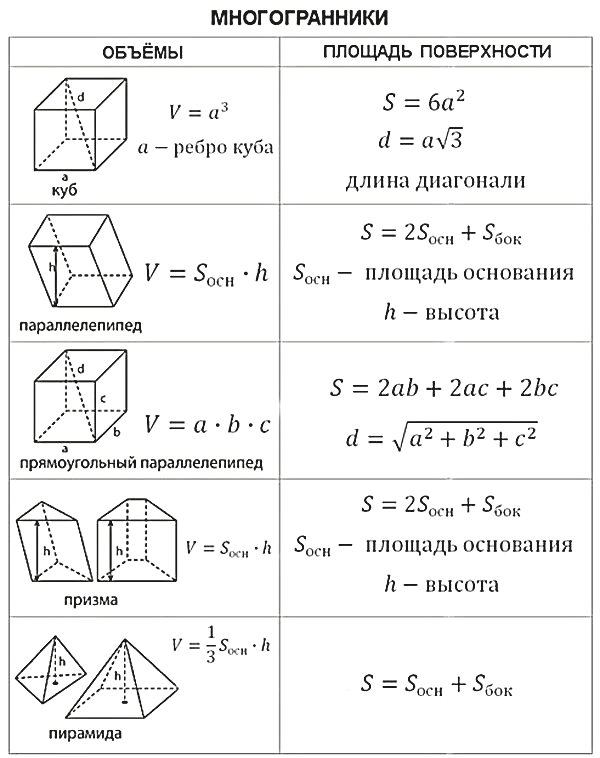
20). От деревянной правильной пятиугольной призмы отпилили все
её вершины (см. рис.). Сколько граней у получившегося многогранника
(невидимые рёбра на рисунке не изображены)? Ответ. 17.

21). От деревянной правильной пятиугольной призмы отпилили все
её вершины (см. рис.). Сколько ребер у получившегося многогранника
(невидимые рёбра на рисунке не изображены)? Ответ. 45.

22). От деревянной правильной пятиугольной призмы отпилили все
её вершины (см. рис.). Сколько вершин у получившегося многогранника
(невидимые рёбра на рисунке не изображены)? Ответ. 30.

23). От деревянного кубика отпилили все её вершины (см. рис.). Сколько
граней у получившегося многогранника (невидимые рёбра на рисунке не
изображены)? Ответ. 14.

24). От деревянного кубика отпилили все её вершины (см. рис.). Сколько
ребер у получившегося многогранника (невидимые рёбра на рисунке не
изображены)? Ответ. 36.

25). От деревянного кубика отпилили все её вершины (см. рис.). Сколько
вершин у получившегося многогранника (невидимые рёбра на рисунке не
изображены)? Ответ. 24.

26). От деревянной правильной треугольной призмы отпилили все
её вершины (см. рис.). Сколько граней у получившегося многогранника
(невидимые рёбра на рисунке не изображены)? Ответ. 11.

27). От деревянной правильной треугольной призмы отпилили все
её вершины (см. рис.). Сколько ребер у получившегося многогранника
(невидимые рёбра на рисунке не изображены)? Ответ. 27.

28). От деревянной правильной треугольной призмы отпилили все
её вершины (см. рис.). Сколько вершин у получившегося многогранника
(невидимые рёбра на рисунке не изображены)? Ответ. 18.

29). Двускатную крышу дома, имеющего в основании прямоугольник (см.
рис.), необходимо полностью покрыть рубероидом. Высота крыши равна 4 м, длины
стен дома равны 6 м и 8 м. Найдите, сколько рубероида.

  1) 6 : 2 = 3;   ;     3)     Ответ.80

30). К правильной треугольной призме со стороной основания 1
приклеили правильную треугольную пирамиду с ребром 1 так, что основания
совпали. Сколько граней у получившегося многогранника.Ответ.7.

31). К правильной треугольной призме со стороной основания 1
приклеили правильную треугольную пирамиду с ребром 1 так, что основания
совпали. Сколько ребер у получившегося многогранника?    Ответ. 12.

32). К правильной треугольной призме со стороной основания 1
приклеили правильную треугольную пирамиду с ребром 1 так, что основания
совпали. Сколько вершин у получившегося многогранника?      Ответ. 7.

33). К кубу с ребром 1 приклеили правильную четырёхугольную
пирамиду с ребром 1 так, что квадратные грани совпали. Сколько рёбер у
получившегося многогранника (невидимые рёбра на рисунке не изображены)? Ответ. 16.

34). К кубу с ребром 1 приклеили правильную четырёхугольную
пирамиду с ребром 1 так, что квадратные грани совпали. Сколько граней у
получившегося многогранника (невидимые рёбра на рисунке не изображены)? Ответ. 9.

35). К кубу с ребром 1 приклеили правильную четырёхугольную
пирамиду с ребром 1 так, что квадратные грани совпали. Сколько вершин у
получившегося многогранника (невидимые рёбра на рисунке )? Ответ. 9.

36). К правильной шестиугольной призме с ребром основания 1
приклеили правильную шестиугольную пирамиду с ребром основания 1 так, что
основания совпали. Сколько граней у получившегося многогранника?  Ответ.
13. 

37). К правильной шестиугольной призме с ребром основания 1
приклеили правильную шестиугольную пирамиду с ребром основания 1 так, что
основания совпали. Сколько ребер у получившегося многогранника ?  Ответ.
24.

38). К правильной шестиугольной призме с ребром основания 1
приклеили правильную шестиугольную пирамиду с ребром основания 1 так, что
основания совпали. Сколько вершин у получившегося многогранника ? 
Ответ. 13.

39). Ящик, имеющий форму куба с ребром 20 см без одной грани,
нужно покрасить со всех сторон снаружи. Найдите площадь поверхности,
которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.

                                                         Ответ. 2000

40). Аквариум имеет форму прямоугольного параллелепипеда  с
размерами 80 см × 30 см × 40 см. Сколько
литров составляет объём аквариума? В одном литре 1000 кубических
сантиметров.

     Ответ. 96.

41). В бак, имеющий форму правильной четырёхугольной призмы со
стороной основания, равной 40 см, налита жидкость. Чтобы
измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите
объём детали, если после её погружения уровень жидкости в баке поднялся на 10 см.

     Ответ. 16000.

42). В бак, имеющий форму прямой призмы, налито 5 л
воды. После полного погружения в воду детали уровень воды в баке
увеличился в 1,8 раза. Найдите объём детали. Ответ дайте в
кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.      Ответ. 4000.

43). Вода в сосуде, имеющем форму правильной четырёхугольной призмы,
находится на уровне h = 90 см. На каком уровне окажется вода,
если её перелить в другой сосуд, имеющий форму правильной четырёхугольной
призмы, у которого сторона основания втрое больше, чем у данного?               Ответ. 10.

44). Вода в сосуде, имеющем форму правильной четырёхугольной призмы,
находится на уровне h= 20 см. На каком уровне окажется вода,
если её перелить в другой сосуд, имеющий форму правильной четырёхугольной
призмы, у которого сторона основания вдвое меньше, чем у данного?            Ответ. 80.

45). Даны две коробки, имеющие форму правильной четырёхугольной призмы,
стоящей на основании. Первая коробка в полтора раза выше второй, а вторая
втрое шире первой. Во сколько раз объём первой коробки меньше
объёма второй?

46). Высота бака цилиндрической формы равна 40 см, а площадь
его основания равна 150 квадратным сантиметрам. Чему равен объём этого
бака (в литрах)? В одном литре 1000 кубических сантиметров.

     Ответ. 6.

47).  Даны две кружки цилиндрической формы. Первая кружка в четыре с
половиной раза выше второй, а вторая в полтора раза шире первой. Во сколько
раз объём второй кружки меньше объёма первой?     

   

48). Даны два конуса. Радиус основания и высота первого конуса равны
соответственно 4 и 9, а второго — 6 и 8. Во
сколько раз объём второго конуса больше объёма первого?

49). Однородный шар диаметром 3 см весит 162 грамма.
Сколько граммов весит шар диаметром 2 см, изготовленный из того же
материала?                        Ответ.   48.

50). Даны два шара с радиусами 8 и 2. Во сколько раз
объём большего шара больше объёма другого?

               Ответ.   64.

51). Даны два цилиндра. Радиус основания и высота первого цилиндра
равны соответственно 4 и 18, а второго — 2
и 3. Во сколько раз площадь боковой поверхности первого цилиндра
больше площади боковой поверхности второго?                                                                  Ответ.   12.

51). В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты.
Объём сосуда 1600 мл. Чему равен объём налитой жидкости?           .    Ответ. 200.

52). В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты.
Объём жидкости равен

30 мл. Найдите объём сосуда.                     ответ. 240.

53). В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты.
Объём жидкости равен 30 мл. Сколько миллилитров жидкости нужно
долить, чтобы наполнить сосуд доверху?

                                   ответ. 210.

54). Деталь имеет форму изображённого на рисунке многогранника (все
двугранные углы прямые). Числа на

рисунке обозначают длины рёбер в сантиметрах. Найдите объём
этой детали.

       ответ. 24.

55). Деталь имеет форму изображённого на рисунке многогранника (все
двугранные углы прямые). Числа на рисунке обозначают длины рёбер в
сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в
квадратных сантиметрах.

56). Найдите площадь поверхности многогранника, изображённого
на рисунке (все двугранные углы – прямые).                  

База 12

1).  На
прямой AB взята точка M. Луч MD — биссектриса
угла CMB. Известно, что ∠DMC=51°. Найдите величину угла CMA. Ответ дайте
в градусах.                 

2). На
прямой AB взята точка M. Луч MD — биссектриса
угла CMB. Известно, что ∠CMA=36°. Найдите угол DMB. Ответ дайте в
градусах.

3).  Прямые m и n параллельны
(см. рис.). Найдите  если  

4). В
треугольнике ABC проведена биссектриса AL,
угол ALC равен 145°, угол ABC равен 113°.
Найдите угол ACB. Ответ дайте в градусах.

5). В
треугольнике ABC сторона AC=56, 
BM — медиана, BH — высота, BC=BM. Найдите
длину отрезка AH.                                        

6).  В
прямоугольном треугольнике ABC внешний угол при вершине А равен 150 °. Катет BC=30. Найдите
длину гипотенузы AB.

7). В
треугольнике ABC внешние углы при
вершинах A и C равны 150°, AB=54. Найдите
длину биссектрисы BK.   

8).  В
треугольнике ABC угол B равен 120°.
Медиана BM делит угол B пополам и равна 27. Найдите
длину стороны AB.                                

9). В выпуклом
четырёхугольнике ABCD известно, что AB=BC, AD=CD, ∠B=61°, ∠D=151°. Найдите
угол A. Ответ дайте в градусах.                                         

10). Обе диагонали
параллелограмма равны 13. Одна из сторон параллелограмма равна 5.
Найдите сторону параллелограмма, соседнюю с данной.                         

11). В
трапеции ABCD известно, что AB=CD, ∠BDA=54° и ∠BDC=23°.
Найдите угол ABD. Ответ дайте в градусах.

12). Основания
трапеции равны 8 и 16, боковая сторона, равная 6, образует
с одним из оснований трапеции угол 150°. Найдите площадь
трапеции.

13). В
прямоугольной трапеции основания равны 3 и 5, а один из
углов равен 135°. Найдите меньшую боковую сторону.                

14). В
параллелограмме диагонали являются биссектрисами его углов и равны 16 и 30.
Найдите периметр параллелограмма. 

15). Сумма двух
углов ромба равна 120°, а его меньшая диагональ равна 8. Найдите
периметр  ромба   .

16). Сумма двух
углов ромба равна 120°, а его периметр равен 84. Найдите длину
меньшей диагонали ромба.

17). Стороны
параллелограмма равны 9 и 12. Высота, опущенная на меньшую
сторону, равна 8. Найдите высоту, опущенную на большую сторону параллелограмма.

18). Найдите
площадь ромба, если его высота равна 6, а острый угол равен 30°.

19). Ромб и
квадрат имеют равные стороны. Найдите площадь ромба, если его острый
угол равен 30°, а площадь квадрата равна 16.

20). В
треугольнике ABC  АВ = ВС =25   АС = 14 .Найдите
длину медианы ВМ.

21). В треугольнике
каждая из двух сторон равна 10, а третья сторона равна 12.Найдите
длину медианы, проведенной к третьей стороне.

22). Найдите
площадь прямоугольного треугольника, если его гипотенуза равна , а один из катетов равен 1.                                                                 

23). На
стороне BC прямоугольника ABCD, у которого AB=15 и AD=23,
отмечена точка E так, что треугольник ABE равнобедренный. Найдите ED.

24). Основания
равнобедренной трапеции равны 10 и 24, боковая сторона
равна 25. Найдите высоту трапеции.

25). В
треугольнике ABC известно, что AB=BC=13, AC=10.
Найдите площадь треугольника ABC.

26). В
равнобедренном треугольнике ABC основание AC равно 32,
площадь треугольника равна 192. Найдите длину боковой
стороны AB.           

27). В
треугольнике АВС АВ = ВС, медиана ВМ равна
6. Площадь треугольника АВС равна  .Найдите AB. 

28). В
параллелограмме АВСD отмечена точка M —середина
стороны ВС. Отрезки ВD и A M
пересекаются в точке K. Найдите длину отрезка ВK, если ВD=15.                     

 29).
Катет прямоугольного треугольника равен 24, одна из средних линий равна 3,5.
Найдите гипотенузу этого треугольника.  

30). В
равнобедренном треугольнике ABC медиана BK=16, боковая
сторона BC=34. Найдите длину отрезка MN, если известно,
что он соединяет середины боковых сторон.

31). В
равнобедренном треугольнике ABC с
основанием AC медиана BK=9, отрезок MN,
соединяющий середины боковых сторон, равен 40. Найдите боковую
сторону AB.

 32).
В треугольнике ABC угол C равен 90°, AB=12, AC=3. Найдите sinA.

 

33). В
треугольнике ABC угол C равен 90°, AB=25, AC=24.
Найдите  cosB.

  

34). В
треугольнике ABC угол C равен 90° АВ =  ,  ВС = 3.  Найдите 

35). В
равнобедренном треугольнике ABC боковые стороны AB=BC=20, АС=32.
Найдите синус угла ВАС.   

36). В
равнобедренном треугольнике ABC боковые стороны AB=BC=5,
медиана BM=3.Найдите cos∠BAC.

37). В
треугольнике ABC угол C равен 90°, AB=15, sinA=0,6.
Найдите AC.

38). В
треугольнике ABC угол C равен 90°, AB=39, . Найдите ВC.

39). В
треугольнике ABC угол C равен 90°, BС=32, тангенс
угла А равна . Найдите АВ.

40). В
прямоугольнике ABCD сторона ВС равна 48, тангенс угла CAD равна . Найдите площадь прямоугольника. 

41). В
равнобедренной трапеции одно из оснований равно 5,
а другое — 9. Высота трапеции равна 6. Найдите
тангенс острого угла трапеции.

42). В
равнобедренном треугольнике ABC медиана BM, проведённая к
основанию, равна 12, а tgA=12/5. Найдите длину боковой
стороны треугольника ABC.

43). В
треугольнике АВС известно, что АВ=ВС, АС=8, tg∠ВАС=√5/2. Найдите
длину стороны АВ.  

44). В
равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5.
Найдите площадь треугольника ABC. 

45). В
равнобедренном треугольнике ABC высота BM, проведённая к
основанию, равна 6, а tgA=0,3. Найдите площадь
треугольника ABC.

 46).
В равнобедренном треугольнике ABC боковая сторона AС=32, . Найдите площадь треугольника ABC.

47). Площадь
прямоугольника ABCD  равна 400, сторона АВ=14. Найдите тангенс угла CAD.

48). В окружности
с центром O отрезки AC и BD — диаметры.
Центральный угол AOD равен 124°. Найдите
угол ACB. Ответ дайте в градусах.  

49). На
окружности по разные стороны от диаметра AB отмечены
точки D и C. Известно, что ∠DBA=41°. Найдите
угол DCB. Ответ дайте в градусах.

50).
Четырёхугольник ABCD вписан в окружность.
Угол ABC равен 56°, угол CAD равен 42°.
Найдите угол ABD. Ответ дайте в градусах.    

51). На
окружности с центром O и диаметром AB отмечена
точка C так, что угол COB равен 120°, AC=34.
Найдите диаметр окружности.         

52). На окружности
радиуса 3 отмечена точка С. Отрезок АВ — диаметр
окружности,  AC=.   Найдите BC.  

 53).
На окружности радиуса 5 отмечена точка С. Отрезок АВ — диаметр
окружности,  AC=6.  Найдите cos∠BAC.    

54). На окружности
радиуса 5 отмечена точка С. Отрезок АВ — диаметр
окружности,  AC=8.  Найдите sin∠ABC.   

55). В
прямоугольной трапеции АВСD  с основаниями  ВС  и АD 
угол ВAD  прямой,  АВ=8,  ВС= CD=10.   Найдите
среднюю линию трапеции.    

56).  В
окружности с
центром O отрезки AC и BD — диаметры.
Вписанный угол ACB равен 36°. Найдите угол AOD.
Ответ дайте в градусах.          

57). Найдите
вписанный угол, опирающийся на дугу, длина которой равна 1/5 длины
окружности. Ответ дайте в градусах.    

58). В угол C,
равный 68°, вписана окружность с центром O, которая касается
сторон угла в точках A и B. Найдите угол AOB.
Ответ дайте в градусах.  

59). На
окружности отмечена точка С. Отрезок АВ — диаметр
окружности, AC=9, BC=12. Найдите радиус окружности.  

База 13

1). Два ребра прямоугольного параллелепипеда равны 8 и 5, а
объём параллелепипеда равен 280. Найдите площадь поверхности
этого параллелепипеда.        

2). В прямоугольном
параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и
диагональ DA1 боковой грани равны соответственно 3, 5 и .  Найдите объём параллелепипеда.

3). В основании прямой призмы лежит прямоугольный треугольник, катеты
которого равны 3 и 16. Найдите объём призмы, если её высота равна
3. 

4). В основании прямой призмы лежит прямоугольный треугольник, один из
катетов которого равен 3, а гипотенуза равна . Найдите объём призмы, если её высота равна 6.

5). Сторона основания правильной треугольной
призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4. Найдите объём призмы ABCA1B1C1.  

6). В треугольной
пирамиде ABCD рёбра AB, AC и AD взаимно
перпендикулярны. Найдите объём этой пирамиды, если AB=5, AC=24 и AD=3. 

7). В основании пирамиды SABCSABC лежит правильный
треугольник ABCABC со стороной 6, а боковое
ребро SASA перпендикулярно основанию и равно 6. Найдите объём пирамиды SABC.

8). Основанием четырёхугольной пирамиды является прямоугольник со
сторонами 9 и 4. Найдите высоту этой пирамиды, если её
объём равен 48.                            

9). Найдите объём правильной четырёхугольной пирамиды,
сторона основания которой равна 4, а боковое ребро равно .          

10). Сторона основания правильной треугольной пирамиды равна 3,
а высота пирамиды равна 4. Найдите объём этой пирамиды.              

11). Стороны основания правильной треугольной пирамиды равны 16,
а боковые рёбра равны 17. Найдите площадь боковой поверхности этой
пирамиды.           

12). Сторона основания правильной шестиугольной пирамиды равна 22,
боковое ребро равно 61. Найдите площадь боковой поверхности этой
пирамиды.

13). Даны два цилиндра. Радиус основания и высота первого цилиндра
равны соответственно 2 и 6, а второго — 6 и 4. Во
сколько раз объем второго цилиндра больше объема первого?  

14). Даны два цилиндра. Радиус основания и высота первого цилиндра
равны соответственно 4 и 18, а второго — 2 и 3. Во
сколько раз площадь боковой поверхности первого цилиндра больше площади боковой
поверхности второго?                

15). Радиус основания цилиндра равен 15, а его
образующая равна 19. Сечение, параллельное оси цилиндра,
удалено от неё на расстояние, равное 9. Найдите площадь сечения.

16). Объём конуса равен 32π, а его высота равна 6. Найдите
радиус основания конуса.

17). Объём конуса равен 16π, а радиус его основания равен 2.
Найдите высоту конуса. 

18). Даны два конуса. Радиус основания и высота первого конуса равны
соответственно 4 и 9, а второго  6 и 8. Во
сколько раз объём второго конуса больше объёма первого?

19). Даны два конуса. Радиус основания и образующая первого конуса
равны соответственно 5 и 6, а второго 

 2 и 3. Во сколько раз площадь боковой поверхности
первого конуса больше второго? 

20). Объём конуса равен 27. Через точку, делящую высоту конуса в
отношении 1:2, считая от вершины, проведена плоскость, параллельная
основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой
плоскостью.                         

21). Через точку, делящую высоту конуса в отношении 1:4,
считая от вершины, проведена плоскость, параллельная основанию. Найдите объём
этого конуса, если объём конуса, отсекаемого от данного конуса проведённой
плоскостью, равен 8.

22). Даны два шара с радиусами 8 и 2. Во сколько раз объём
большего шара больше объёма другого?

 

23). Даны два шара с радиусами 9 и 3. Во сколько раз площадь
поверхности большего шара больше объёма другого?

  

База 20

1). В сосуд, содержащий 5 литров 12−процентного водного
раствора некоторого вещества, добавили 7 литров воды. Сколько процентов
составляет концентрация получившегося раствора?

                    

2). Смешали некоторое количество 15−процентного раствора
некоторого вещества с таким же количеством 19−процентного раствора этого
вещества. Сколько процентов составляет концентрация получившегося раствора?  

3). Смешали 4 литра 15−процентного водного раствора
некоторого вещества с 6 литрами 25−процентного водного раствора
этого же вещества. Сколько процентов составляет концентрация получившегося
раствора?  

4). Имеется два сплава. Первый сплав содержит 10% меди, второй
− 30% меди. Из этих двух сплавов получили третий сплав, содержащий 25%
меди. Масса первого сплава равна 200кг. Найдите массу третьего?        

 

5). Имеется два сплава. Первый сплав содержит 15% меди, второй
− 35% меди. Из этих двух сплавов получили третий сплав, содержащий 30%
меди. Масса первого сплава равна 35кг. На сколько кг масса первого
сплава меньше массы второго? 

6). Из городов A и B, расстояние между
которыми равно 330 км, навстречу друг другу одновременно выехали два
автомобиля и встретились через 3 часа на расстоянии 180 км от
города  Найдите скорость автомобиля,
выехавшего из города    

7). Дорога между пунктами А и В состоит
из подъёма и спуска, а её длина равна 8 км. Турист прошёл путь из А в В за
5 часов. Время его движения на спуске составило 1 час. С какой
скоростью турист шёл на спуске, если скорость его движения на
подъёме меньше скорости движения на спуске на 3 км/ч?

 

8). Расстояние между городами A и B равно
470 км. Из города A в город B выехал
первый автомобиль, а через 3 часа после этого навстречу ему из
города B выехал со скоростью 60 км/ч второй автомобиль.
Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км
от города  

 

9). Расстояние между городами A и B равно
435 км. Из города A в город B со
скоростью 60 км/ч выехал первый автомобиль, а через час после
этого навстречу ему из города B выехал со скоростью 65 км/ч
второй автомобиль. На каком расстоянии от города A автомобили
встретятся? Ответ дайте в километрах.

 

 10). Два человека отправляются из одного и того же места
на прогулку до опушки леса, находящейся в 4,4 км от места отправления.
Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч.
Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком
расстоянии от точки отправления произойдёт их встреча?

 

11). Теплоход, скорость которого в неподвижной воде равна 25 км/ч,
проходит по течению реки и после стоянки возвращается в исходный пункт.
Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в
исходный пункт теплоход возвращается через 30 часов после отплытия из
него. Сколько километров прошел теплоход за весь рейс?              

12). Первые два часа автомобиль ехал со скоростью 50 км/ч,
следующий час — со скоростью 100 км/ч, а затем два часа —
со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении
всего пути.   

13). Первые 190 км автомобиль ехал со скоростью 50 км/ч,
следующие 180 км — со скоростью 90 км/ч, а затем 170 км —
со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на
протяжении всего пути.

14). Первую треть трассы автомобиль ехал со скоростью 60 км/ч,
вторую треть — со скоростью 120 км/ч, а последнюю — со скоростью 110 км/ч.
Найдите среднюю скорость автомобиля на протяжении всего пути.   

15). Путешественник переплыл море на яхте со средней скоростью 20 км/ч.
Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите
среднюю скорость путешественника на протяжении всего пути.            

16). Один мастер может выполнить заказ за 12 часов, а другой — за
6 часов. За сколько часов выполнят заказ оба мастера, работая вместе?  

17). Первый насос наполняет бак за 20 минут, второй — за 30
минут, а третий — за 1 час. За сколько минут наполнят бак три насоса,
работая одновременно?

18). Даша и Маша пропалывают грядку за 12 минут, а одна Маша —
за 20 минут. За сколько минут пропалывает грядку одна Даша?        

19). Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8
вопросов теста, а Ваня — на 9. Они одновременно начали отвечать на
вопросы теста, и Петя закончил свой тест позже Вани на 20 минут. Сколько
вопросов содержит тест?       

9). В понедельник акции компании подорожали на некоторое количество
процентов, а во вторник подешевели на то же самое количество процентов. В
результате они стали стоить на  дешевле, чем при открытии торгов в
понедельник. На сколько процентов подорожали акции компании в понедельник?

Дополнительные задачи.

10). Изюм получается в процессе сушки винограда. Сколько килограммов
винограда потребуется для получения 78 килограммов изюма, если виноград
содержит 82% воды, а изюм содержит 19% воды?

11). Девять одинаковых рубашек дешевле куртки на 10%. На сколько
процентов одиннадцать таких же рубашек дороже куртки?  

12). Семья состоит из мужа, жены и их дочери студентки. Если бы
зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы
стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на
4%. Сколько процентов от общего дохода семьи составляет зарплата жены? 

13). Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий
час — со скоростью 100 км/ч, а затем два часа — со скоростью 75 км/ч. Найдите
среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. 

17). Велосипедист выехал с постоянной скоростью из города А в город В,
расстояние между которыми равно 187 км. На следующий день он отправился
обратно в А со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку
на 6 часов. В результате велосипедист затратил на обратный путь столько же
времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из
А в В.          ответ.

18). Велосипедист выехал с постоянной скоростью из города А в город В,
расстояние между которыми равно 143 км. На следующий день он отправился
обратно в А со скоростью на 2 км/ч больше прежней. По дороге он сделал
остановку на 2 часов. В результате велосипедист затратил на обратный путь
столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на
пути из B в A.   

      ответ.

19). Два велосипедиста одновременно отправились в 240-километровый
пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и
прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста,
пришедшего к финишу первым.             ответ.

20). Два велосипедиста одновременно отправились в 88−километровый
пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и
прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста,
пришедшего к финишу вторым.                 ответ.

21). Из пункта А в пункт В, расстояние между которыми 30 км,
одновременно выехали автомобилист и велосипедист. За час автомобилист проезжает
на 70 км больше, чем велосипедист. Определите скорость велосипедиста,
если известно, что он прибыл в пункт В на 1 час 10 минут позже автомобилиста.                         

      ответ.

22). Расстояние между городами A и B равно 420 км. Из города A в
город B выехал автомобиль, а через 1 час следом за ним со скоростью
80 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул
обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите
расстояние от A до C. Ответ дайте в километрах.  

     ответ.

23). Из городов А и В навстречу друг другу одновременно выехали
мотоциклист и велосипедист. Мотоциклист приехал в город В на 12 часов раньше,
чем велосипедист приехал в город А, а встретились они через 2 часа 30 минут
после выезда. Сколько часов затратил на путь из города В в город А
велосипедист?

 

24). По двум параллельным железнодорожным путям друг навстречу другу
следуют скорый и пассажирский поезда, скорости которых равны соответственно
65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину
скорого поезда, если время, за которое он прошел мимо пассажирского поезда,
равно 36 секундам.

25). От пристани A к пристани B, расстояние между которыми равно
153 км, отправился с постоянной скоростью первый теплоход, а через 8 часов
после этого следом за ним со скоростью на 8 км/ч большей отправился второй.
Найдите скорость первого теплохода, если в пункт B оба теплохода прибыли
одновременно. Ответ дайте в км/ч.           ответ.

26). Пристани A и B расположены на
озере, расстояние между ними 390 км. Баржа отправилась с постоянной скоростью
из A в  На следующий день после прибытия она
отправилась обратно со скоростью на 3 км/ч больше прежней, сделав по пути
остановку на 9 часов. В результате она затратила на обратный путь столько же
времени, сколько на путь из A в  Найдите
скорость баржи на пути из A в  Ответ
дайте в км/ч.      ответ.

27). Теплоход, скорость которого в неподвижной воде равна 25 км/ч,
проходит по течению реки и после стоянки возвращается в исходный пункт.
Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт
теплоход возвращается через 30 часов после отплытия из него. Сколько километров
прошел теплоход за весь рейс?

28). Теплоход проходит по течению реки до пункта назначения
384 км и после стоянки возвращается в пункт отправления. Найдите
скорость теплохода в неподвижной воде, если скорость течения равна
4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход
возвращается через 48 часов.  

    ответ.

29). Теплоход проходит по течению реки до пункта назначения
468 км и после стоянки возвращается в пункт отправления. Найдите
скорость скорость течения, если скорость теплохода равна 22 км/ч,
стоянка длится 3 часа, а в пункт отправления теплоход возвращается через
47 часов.    ответ.

30). Моторная лодка прошла против течения реки 165 км и вернулась
в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость
лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ
дайте в км/ч.                ответ.

31). Моторная лодка прошла против течения реки 252 км и вернулась
в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость
течения, если скорость лодки в неподвижной воде равна 16 км/ч. Ответ
дайте в км/ч.      ответ.

32). Байдарка в 10 : 00 вышла из пункта А в пункт В,
расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, байдарка
отправилась назад и вернулась в пункт А в 16:00 того же дня.
Определите (в км/ч) собственную скорость байдарки, если известно, что
скорость течения реки равна 2 км/ч.

    ответ.

33). Баржа в 10:00 вышла из пункта А в пункт В,
расположенный в 30 км от А. Пробыв в пункте В 4 часа, баржа отправилась
назад и вернулась в пункт А в 22:00 того же дня. Определите (в
км/ч) скорость течения реки, если известно, что собственная скорость баржи
равна 8 км/ч.        ответ.

34). Расстояние между пристанями A и B равно 192 км. Из A в B по
течению реки отправился плот, а через 3 часа вслед за ним отправилась яхта,
которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому
времени плот проплыл 92 км. Найдите скорость яхты в неподвижной воде,
если скорость течения реки равна 4 км/ч.

      ответ.

35). Заказ на 140 деталей первый рабочий выполняет на 4 часа
быстрее, чем второй. Сколько деталей в час делает второй рабочий, если
известно, что первый за час делает на 4 детали больше?        ответ.

36). Заказ на 176 деталей первый рабочий выполняет на 5 часов быстрее,
чем второй. Сколько деталей в час делает первый рабочий, если
известно, что он за час делает на 5 деталей больше, чем второй?

    ответ.

37). На изготовление 720 деталей первый рабочий затрачивает на 6 часов
меньше, чем второй рабочий на изготовление 840 деталей. Известно, что первый
рабочий за час делает на 2 детали больше, чем второй. Сколько деталей в
час делает первый рабочий?    ответ.

38). На изготовление 696 деталей первый рабочий затрачивает на 5 часов
меньше, чем второй рабочий на изготовление 725 деталей. Известно, что первый
рабочий за час делает на 4 детали больше, чем второй. Сколько деталей в
час делает второй рабочий?       ответ.

39). Первая труба пропускает на 8 литров воды в минуту меньше, чем
вторая. Сколько литров воды в минуту пропускает первая
труба, если резервуар объёмом 180 литров она заполняет на 8 минут дольше, чем
вторая труба?      ответ.

40). Первая труба пропускает на 4 литров воды в минуту меньше, чем
вторая. Сколько литров воды в минуту пропускает вторая
труба, если резервуар объёмом 252 литров она заполняет на 4 минут быстрее, чем
первая труба?      ответ.

41). Первая труба наполняет резервуар на 13 минут дольше, чем
вторая. Обе трубы, работая одновременно, наполняют этот же
резервуар за 42 минуты. За сколько минут наполняет этот резервуар одна
вторая труба?   ?      ответ.

База 21

1). Кузнечик прыгает: данное число  плюс один.

2). В корзине лежат грибы: Сколько рыжиков в корзине?
Грузди минус один. Сколько груздей? Рыжик минус один.

3). Восемь столбов соединены: Перемножить данные два числа и
разделить на два.

4). Из десяти стран: Перемножить первые два числа, перемножаем
вторые два числа, складываем их и делим на два.

5). На поверхности глобуса: Параллель плюс один и умножаем на
меридиан.

6). В таблице три столбца и несколько строк. 119, 125, 133.
Больше 15, но меньше 18.

     Значит это числа 16 или 17. Складываем все три числа
119+125+133=377.Затем делим 377 на 16.    377:16=23.        

7). В конце четверти Петя:  Разлагаем данное число на простые
множители.    

                                                          (2+3+3+2+3):5=2,6.  Ответ. 3

8). Миша, Коля и Леша играют в теннис: Надо из большего числа
вычесть меньшее.

9). Из книги выпало несколько листов: 298.     289, 829,
892, 928, 982.

 289 не подходит, оно меньше 298. Из оставшихся чисел
выбираем нечетное число, это 829.   =265.

10).На ленте по разные стороны: Складываем данные
числа и делим на два.

11).  На палке отмечены поперечные линии: Складываем  все три
числа и вычитаем два.

12). На кольцевой дороге: Из первого числа вычитаем второе.

13). Про натуральные числа A, B  и   C известно, что каждое из них больше 4, но меньше 8.

Загадали натуральное число, затем его умножили А, потом прибавили B и вычли С. Получилось
165.  .  

А, B, С =5 или 6  или 7.   Ответ. 33

14). Если каждый множитель увеличить на 1, то их произведение
увеличилось бы на 3.

Каждый из них увеличится на 5. Решение:

 

 

15). Список заданий викторины: правильный ответ 7, а
неправильный 13. Набрал 56 очков.  .  Ответ. 21.

16). Клетки таблицы 4х5.   15 и 11.   

17). Прямоугольник разбить на четыре части. Найдите периметр.
14-12=2.  13-2=11.

  18). Прямоугольник разбить на четыре части. Найдите площадь.  
Ответ. 20.

19). Саша пригласил Петю в гости, сказав живет в 8 подъезде,
квартира №468, а этаж сказать забыл. Дом  двенадцатиэтажный. На каком
этаже живет Саша?

 

На каждом этаже по 5 квартир. 7 подъезд заканчивается
№420.   . Ответ. 10.

20). Во всех подъездах дома одинаковое число этажей: . Берем из них большее число. Ответ. 11.

21). Петя меняет маленькие фишки на большие за один обмен
получает 4 большие отдав 10 маленьких. Было 100 фишек, осталось 64.                Ответ.6

22). В доме всего 18 квартир с номерами от 1 до 18. В квартирах
с 1по 13 включительно живет 15 человек. А с 11 по 18 включительно живет 20
человек.               15+15 = 30. Ответ. 30

23). Маша и Медведь съели 51печенье…Медведь ест в четыре
раза быстрее.

       4² =16;    

24). В обменном пункте:  за 4 золотых получить 5 серебряных.

                                               За 8 серебряных получить 5
золотых.      45 медных.

  

25). Взяли несколько досок и распилили: Из большего вычесть
меньшее.

26). Среднее арифметическое 5 чисел равно 7.
Среднее арифметическое этих пяти чисел и шестого равно 8.    .                 Ответ. 13.

27). Хозяин договорился с рабочим: 4200; 1300; 11. 117700.

28). В магазине квас на разлив: 1л-36р; 2л-66р. Сколько 1,5?

29). Три луча разбивают на 3 разных угла. Наибольший угол в 2 раза
больше.

.  

                    90-72-1=17.    Ответ.17.