Шпора по тригонометрии на егэ

Алгебра — ЕГЭ                Тригонометрия — ЕГЭ                Геометрия — ЕГЭ                Стереометрия — ЕГЭ                Алгебра — ОГЭ                Геометрия — ОГЭ

Формулы по тригонометрии

Шпаргалка по тригонометрическим формулам

Таблица формул тригонометрии

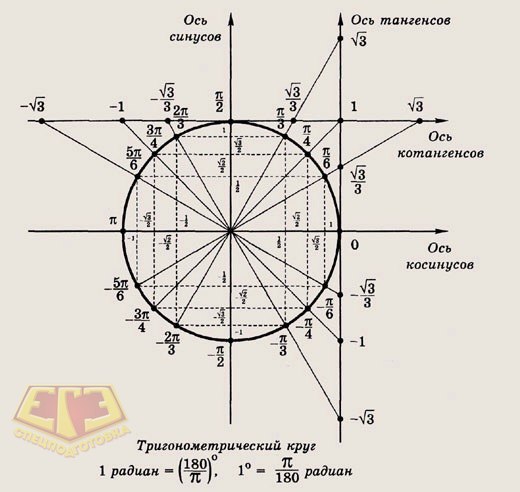
Единичный круг — тригонометрия

11 декабря 2020

В закладки

Обсудить

Жалоба

Шпаргалка по тригонометрии

Основные тригонометрические тождества и формулы.

shpargalka_po_trigonometrii.pdf

Содержание

Основные тригонометрические тождества.
Формулы приведения.
Формулы периодических углов.
Формулы суммы и разности углов.
Формулы двойного угла.
Формулы половинного угла (формулы понижения степени).
Формулы произведения тригонометрических функций.
Формулы суммы и разности тригонометрических функций.
Универсальная тригонометрическая подстановка (УТП).
Обратные тригонометрические функции (аркфункции).
Простые тригонометрические уравнения.

• Материалы для подготовки к ЕГЭ

•    

• Рубрики
  • 01 Геометрия (13)
  • 02 Стереометрия (9)
  • 03 Теория вероятностей ч.1 (1)
  • 04 Теория вероятностей ч.2 (1)
  • 05 Простейшие уравнения (5)
  • 06 Вычисления (5)
  • 07 Производная, ПО (4)
  • 08 «Прикладные» задачи (5)
  • 09 Текстовые задачи (7)
  • 10 Графики функций (7)
  • 11 Исследование функции (2)
  • 12 (С1) Уравнения (78)
  • 13 (С2) Стереометр. задачи (94)
  • 14 (С3) Неравенства (89)
  • 15 (С4) Практич. задачи (71)
  • 16 (С5) Планиметр. задачи (86)
  • 17 (С6) Параметры* (79)
  • 18 (С7) Числа, их свойства (38)
  • A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
  • A2 Читаем графики (нет в ЕГЭ-22) (1)
  • Видеоуроки (44)
  • ГИА (11)
    • II часть (11)
  • ЕГЭ (диагностич. работы) (70)
  • Иррациональные выражения, уравнения и неравенства (15)
  • Логарифмы (39)
  • МГУ (12)
  • Метод интервалов (4)
  • Метод рационализации (18)
  • Модуль (9)
  • Параметр (40)
  • Переменка (5)
  • Планиметрия (60)
  • Показательные выражения, уравнения и неравенства (8)
  • Разложение на множители (1)
  • Рациональные выражения, уравнения и неравенства (10)
  • Справочные материалы (92)
  • Стереометрия (52)
  • Т/P A. Ларина (443)
  • Текстовые задачи (12)
  • Теория чисел (2)
  • Тесты по темам (80)
  • Тригонометрические выражения, уравнения и неравенства (43)
  • Функции и графики (10)
• Дружественные сайты

  Сайт А. Ларина
  ЕгэТренер – О. Себедаш
  Математика?Легко!
  Егэ? Ок! – И. Фельдман
  

• Свежие записи
  • Тест «Гиперболы»
  • Тест. Графики функций. Комбинированные задачи
  • 10. Графики функций. Комбинированные задачи
  • Тест. Тригонометрические функции
  • 10. Тригонометрическая функция
  • Тест. Кусочно-линейная функция
  • 10. Кусочно-линейная функция
• Архивы Архивы

Предварительный просмотр:

• Мне нравится 

 

На странице вы найдете все формулы тригонометрии в удобном для использования оформлении. Формулы структурированы в блоки по количеству аргументов, степеням, арифметическим операциям над ними.

Все формулы тригонометрии

Основные тригонометрические тождества

tg alpha = dfrac {sin alpha}{ cos alpha} = dfrac{1}{ctg alpha}

---

ctg alpha = dfrac {cos alpha}{ sin alpha} = dfrac{1}{tg alpha}

---

sin ^2 alpha + cos ^2 alpha = 1

---

1+tg^2alpha=dfrac{1}{cos^2alpha}

---

1+ctg^2alpha=dfrac{1}{sin^2alpha}

---

tgalpha cdot ctgalpha=1

Формулы двойного угла (аргумента)

sin(2alpha)=2 cdot cos alpha cdot sin alpha

---

sin(2alpha)=dfrac{2 cdot tg alpha}{1+tg ^2 alpha}=dfrac{2 cdot ctg alpha}{1+ctg ^2 alpha}=dfrac{2}{tg alpha + ctg alpha}

---

cos(2alpha)=cos ^2 alpha- sin ^2 alpha = 2 cdot cos ^2 alpha- 1 = 1- 2 cdot sin ^2 alpha

---

cos(2alpha)=dfrac{1 -tg ^2 alpha}{1+tg ^2 alpha}=dfrac{ctg ^2 alpha- 1}{ctg ^2 alpha +1}=dfrac{ctg alpha-tg alpha}{ctg alpha + tg alpha}

---

tg(2alpha) = dfrac{2 cdot tg alpha}{1-tg ^2 alpha}=dfrac{2 cdot ctg alpha}{ctg ^2 alpha- 1}=dfrac{2}{ctg alpha- tg alpha}

---

ctg(2alpha) = dfrac{ctg ^2 alpha-1}{2 cdot ctg alpha}=dfrac{ctg alpha- tg alpha}{2}

Формулы тройного угла (аргумента)

sin(3alpha)=3 cdot sin alpha- 4 cdot sin ^3 alpha

---

cos(3alpha)= 4 cdot cos ^3 alpha- 3 cdot cos alpha

---

tg(3alpha)= dfrac{3 cdot tg alpha- tg ^3 alpha}{1-3 cdot tg ^2 alpha}

---

ctg(3alpha)= dfrac{ctg ^3 alpha- 3 cdot ctg alpha}{3 cdot ctg ^2 alpha -1}

Формулы понижения степени тригонометрических функций

Вторая степень

sin ^2 alpha = dfrac{1-cos(2alpha)}{2}

---

cos ^2 alpha = dfrac{1+cos(2alpha)}{2}

---

tg ^2 alpha = dfrac{1-cos(2alpha)}{1+cos(2alpha)}

---

ctg ^2 alpha = dfrac{1+cos(2alpha)}{1-cos(2alpha)}

---

(sin alpha- cos alpha)^2=1-sin(2 alpha)

---

(sin alpha+ cos alpha)^2=1+sin(2 alpha)

Третья степень

sin ^3 alpha = dfrac{3 cdot sin(alpha)-sin(3 alpha)}{4}

---

cos ^3 alpha = dfrac{3 cdot cos(alpha)+cos(3 alpha)}{4}

---

tg ^3 alpha = dfrac{3 cdot sin (alpha)-sin(3 alpha)}{3 cdot cos (alpha)+cos(3 alpha)}

---

ctg ^3 alpha = dfrac{3 cdot cos (alpha)+cos(3 alpha)}{3 cdot sin (alpha)-sin(3 alpha)}

Четвёртая степень

sin ^4 alpha = dfrac{3-4 cdot cos(2 alpha)+cos(4 alpha)}{8}

---

cos ^4 alpha = dfrac{3+4 cdot cos(2 alpha)+cos(4 alpha)}{8}

---

Пятая степень

sin ^5 alpha = dfrac{10 cdot sin(alpha)-5 cdot sin(3 alpha)+sin(5 alpha)}{16}

---

cos ^5 alpha = dfrac{10 cdot cos(alpha)+5 cdot cos(3 alpha)+cos(5 alpha)}{16}

Формулы половинного угла (аргумента)

sin Big( dfrac{alpha}{2} Big)=pm sqrt{dfrac{1-cos alpha}{2}}

---

cos Big( dfrac{alpha}{2} Big)=pm sqrt{dfrac{1+cos alpha}{2}}

---

tg Big( dfrac{alpha}{2} Big)= dfrac{1-cos alpha}{sin alpha}= dfrac{sin alpha}{1+cos alpha}

---

ctg Big( dfrac{alpha}{2} Big)= dfrac{1+cos alpha}{sin alpha}= dfrac{sin alpha}{1-cos alpha}

Формулы понижения степени половинного угла (аргумента)

sin ^2 Big( dfrac{alpha}{2} Big)=dfrac{1-cos alpha}{2}

---

cos ^2 Big( dfrac{alpha}{2} Big)=dfrac{1+cos alpha}{2}

---

tg ^2 Big( dfrac{alpha}{2} Big)=dfrac{1-cos alpha}{1+cos alpha}

---

ctg ^2 Big( dfrac{alpha}{2} Big)=dfrac{1+cos alpha}{1-cos alpha}

Формулы сложения аргументов

sin(alpha + beta)=sin alpha cdot cos beta + cos alpha cdot sin beta

---

cos(alpha + beta)=cos alpha cdot cos beta- sin alpha cdot sin beta

---

tg(alpha + beta)= dfrac{tg alpha + tg beta}{1-tg alpha cdot tg beta}

---

ctg(alpha + beta)= dfrac{ctg alpha cdot ctg beta-1}{ctg alpha + ctg beta}

Формулы вычитания аргументов

sin(alpha- beta)=sin alpha cdot cos beta- cos alpha cdot sin beta

---

cos(alpha- beta)=cos alpha cdot cos beta+ sin alpha cdot sin beta

---

tg(alpha- beta)= dfrac{tg alpha- tg beta}{1+tg alpha cdot tg beta}

---

ctg(alpha- beta)= dfrac{ctg alpha cdot ctg beta+1}{ctg beta — ctg alpha}

Формулы суммы тригонометрических функций

sin alpha+ sin beta=2 cdot sin big( dfrac{alpha + beta}{2} big) cdot cos big( dfrac{alpha- beta}{2} big)

---

cos alpha+ cos beta=2 cdot cos big( dfrac{alpha + beta}{2} big) cdot cos big( dfrac{alpha- beta}{2} big)

---

tg alpha + tg beta = dfrac{sin(alpha + beta)}{cos alpha cdot cos beta}

---

ctg alpha + ctg beta = dfrac{sin(alpha + beta)}{cos alpha cdot cos beta}

---

sin (alpha)+cos(alpha)=sqrt{2} cdot sin Big( alpha+ dfrac{pi}{4} Big)

Формулы разности тригонометрических функций

sin alpha- sin beta=2 cdot sin big( dfrac{alpha- beta}{2} big) cdot cos big( dfrac{alpha+ beta}{2} big)

---

cos alpha- cos beta=-2 cdot sin big( dfrac{alpha + beta}{2} big) cdot sin big( dfrac{alpha- beta}{2} big)

---

tg alpha- tg beta = dfrac{sin(alpha- beta)}{cos alpha cdot cos beta}

---

ctg alpha- ctg beta = dfrac{sin(alpha + beta)}{sin alpha cdot sin beta}

---

sin (alpha)-cos(alpha)=sqrt{2} cdot sin Big( alpha- dfrac{pi}{4} Big)

Формулы произведения тригонометрических функций

sin alpha cdot sin beta = dfrac{cos (alpha- beta)-cos(alpha + beta)}{2}

---

sin alpha cdot cos beta = dfrac{sin (alpha- beta)+sin(alpha + beta)}{2}

---

cos alpha cdot cos beta = dfrac{cos (alpha- beta)+cos(alpha + beta)}{2}

---

tg alpha cdot tg beta = dfrac{cos(alpha- beta)- cos(alpha+beta)}{cos(alpha- beta)+ cos(alpha+beta)}=dfrac{tg alpha + tg beta}{ctg alpha + ctg beta}

---

ctg alpha cdot ctg beta = dfrac{cos(alpha- beta)+ cos(alpha+beta)}{cos(alpha- beta)- cos(alpha+beta)}=dfrac{ctg alpha + ctg beta}{tg alpha + tg beta}

---

tg alpha cdot ctg beta = dfrac{sin(alpha- beta)+ sin(alpha+beta)}{sin(alpha+ beta)- sin(alpha-beta)}

Формулы произведения тригонометрических функций в степени

sin ^2 (alpha) cdot cos ^2 (alpha) = dfrac{1-cos(4 alpha)}{8}

---

sin ^3 (alpha) cdot cos ^3 (alpha) = dfrac{3 cdot sin(2 alpha)- sin(6 alpha)}{32}

---

sin ^4 (alpha) cdot cos ^4 (alpha) = dfrac{3-4 cdot cos(4 alpha)+ cos(8 alpha)}{128}

---

sin ^5 (alpha) cdot cos ^5 (alpha) = dfrac{10 cdot sin (2 alpha)-5 cdot sin(6 alpha)+sin (10 alpha)}{512}

Все формулы тригонометрии на одном листе

На этой картинке собраны все формулы тригонометрии для печати. Лист можно распечатать и использовать при решении задач ЕГЭ или вырезать таблицы и использовать как шпаргалку. Распечатанный лист можно применять как справочный материал при решении задач по тригонометрии в 10 и 11 классе.