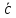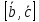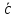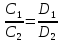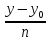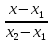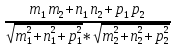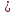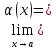Шпоры для экзамена по мат анализу

1.
Матрица

Это
прямоугольная таблица, состоящая из
m×n
элементов и содержащая m
строк и n
столбцов.

Числовая
матрица
– все элементы матрицы числа.

Квадратная
матрица
– m=n.

Операции
над матрицами

Сложение
– складываются все элементы, стоящие
на одинаковых местах (только у
равноразмерных).

Произведение
– каждый элемент матрицы умножается
на число (с).

2
Транспонирование

Транспонированная
матрица – это матрица, полученная из
матрицы А заменой строк столбцами.

Умножение
матриц

Вводится
только для согласованных матриц (число
столбцов м-цы А должно совпадать со
строками м-цы В).

При
умножении матриц появляется новая
матрица, элементы которой вычисляются
по формуле: c₁₁=a₁₁b₁₁+a₁₂b₂₁+…(1
элемент 1 строки умножаем на 1 э-т 1
столбца + 2 э-т 1 с-ки на 2 э-т 2 с-ца, и т.д.)

3.
Определители
2 и 3 порядков

Определители
вводятся только для квадратных матриц.
Определителем (Δ) или детерминалом
матрицы А называется число det
A.

Для
2-го порядка Δ вычисляется по формуле:
a₁₁a₂₂-a₁₂a₂₁
(крест накрест).

Для
3-го порядка по правилу треугольников.

Свойства:
1)
Δ
единичной матрицы =1. 2) Δ треугольной
матрицы = произведению элементов,
стоящих на главной диагонали. 3)
det(A*B)=detA*detB.
4) если строка или столбец = 0, то Δ=0.

4.Определитель
n-го порядка

Определитель
n-го
порядка находится либо разложением по
элементам строки (столбца), либо
приведением определителя к треугольному
виду.

Миноры
и алгебраические дополнения

Минор
матрицы А соответствующей элементу
A_ij
– это Δ
(n-1)
порядка, получаемый путём вычёркивания
i-ой
строки или j-го
столбца. A_ij=(-1)­^i+jM_ij
называется алгебраическим дополнением
к элементу a_ij.

Разложение
определителя

Δ
раскладывается по элементам i-ой
строки или j-го
столбца по формуле:
Δ = a_i1A_i1+
a_i2A_i2+…+
a_inA_in

5.
Обратная
матрица. Теорема о существовании
обратной матрицы

Обратная
матрица существует только для квадратных
матриц.

Если
обратная матрица существует, то она
единственна.

Матрица
А^-1
обратная
А,
если выполняется условие: А^-1А=А
А^-1=Е
(единичная матрица).

Для
того чтобы матрица А была обратной,
необходимо чтобы она была невырожденной
(Δ не должен =0).

Матрица,
состоящая из алгебр. дополнений,
полученная путём транспонирования
называется союзной
(А^с).

Вычисление
обратной матрицы: 1) Находим Δ0,
2) Вычислем алгебр. доп., 3) Строим А^с
и
вычисляем:

А^-1=*
А^с
, 4) Делаем проверку А^-1А=Е

6.
Ранг
матрицы

Ранг
матрицы
– это максимальный порядок минора,
отличный от нуля. Способы вычисления:
1)Если существует минор M_k0
(k
— какой-то порядок минора) и все M_k+1=0,
то ранг М=k.
2) Метод элементарных преобразований
(матрицу приводят к треугольной и
трапециевидной форме).

Элементарные
преобразования

1)
сложение 2-х любых строк матрицы. 2)
Умножение элементов строки на число.

Теорема
о базисном миноре

Базисный
минор – это минор, не равный 0, порядок
которого равен рангу матрицы.

7.
СЛАУ
(система линейных алгебраических
уравнений)

Если
эта система имеет хотя бы одно решение,
то она называется совместной, в противном
случае несовместной. (b₁,
b_2,
b₃)
– столбец свободных членов. (x₁,
x_2,
x₃)
– решение системы, если при подстановке
их в систему получаются верные равенства.

Решение
систем по формулам Крамера

Сначала
находим Δ
и убеждаемся, что он не равен 0. Затем
по формулам Крамера находим определители
уже как бы новых матриц с заменой
определённого столбца на столбец
свободных членов. Находим переменные
(x,
y,
z)
по формулам Δx
Δ
и
т.д. Делаем проверку.

8.
СЛАУ
(система линейных алгебраических
уравнений)

Если
эта система имеет хотя бы одно решение,
то она называется совместной, в противном
случае несовместной. (b₁,
b_2,
b₃)
– столбец свободных членов. (x₁,
x_2,
x₃)
– решение системы, если при подстановке
их в систему получаются верные равенства.

Матричный
метод

Сначала
находим Δ
и убеждаемся, что он не равен 0. Находим
союзную матрицу, а затем обратную по
формуле А^-1=*
А^с.
Затем находим переменные (x,
y,
z)
и делаем проверку.

9.
Решение
произвольных СЛАУ

Берём
обычную систему уравнений, где А –
матрица системы, а добавление к матрице
А столбец свободных членов даёт нам
расширенную матрицу
.

Теорема
Кренекера-Капелли

Для
того, чтобы система уравнений была
совместна, необходимо чтобы ранг А =
рангу
.

Если:
1) r_A==n,
то система имеет единственное решение.
n
– последний член элемента (a_1n)

2)
r_A=,
то система имеет бесконечное кол-во
решений.

10.
Векторы
в пространстве

Вектор
– это направленный отрезок.

– свободный;

– имеющий точку приложения. Длина
вектора – модуль.

Линейные
операции над векторами

1)
сложение (по правилу треугольника и
параллелограмма). Суммой 2 векторов

и

явл.
,
начало которого совпадает с началом 1
вектора (),
а конец — с концом 2 вектора.

2)
вычитание (.
Разностью

и

явл.
,
конец которого совпадает с концом
,
а начало — с концом
.

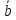
3)
умножение на число (Условия: 1) существует
;
2)

и

направлены одинаково если с0.

11.
Координаты
вектора в пространстве.

3
вектора ()
образую
базис в пространстве если они взаимно
⊥
и имеют единичную длину.
=a_x+a_y+a_z

=
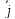
(x₂—x₁,
y₂—y₁,
z₂—z₁).

=
– длина
вектора

Направляющие
косинусы вектора

a_x
= Пр_Ox
=
*cosα; a_y
= Пр_Oy
=

cosβ;
a_z
= Пр_Oz
=

cosγ;
cosα=

Проекции
вектора на ось

образованный
с помощью осей Ox,
Oy,
Oz,
образует углы
α,
β, γ.

12.
Скалярное
произведение 2 векторов

Это
число, равное произведению длин этих
векторов на cos
угла между ними.
*
=
*cosφ

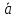
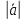
Свойство:
1)
*
=
*

2)
(*)
=
**)

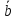
3)
Скалярное произведение на число =
произведение числа на один из векторов
и * на 2 вектор.

4)
*=0,
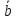
если
вектора

и

явл. Ортогональными (
⊥
).

13.
Векторное
произведение 2 векторов

Векторным
произведением 2 векторов

и

явл.
,
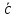
который удовлетворяет условиям: 1)

⊥
,
;

2)
,
,

– правая тройка векторов. 3)

=
*sinφ
(модуль произв. 2 векторов – площадь
параллелограмма)

Свойство:

1)
=
—

2)

=
+

3)
=
0 если


//

14.
Смешанное
произведение 3 векторов

Это
число = скалярному произведению 3-го
вектора на векторное произведение 2-х
первых векторов.

**
= ()

—
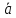
объём параллелепипеда.

Свойство:

1)
От перемены мест множителей произведение
не меняется.

=

=

2)
Если умножить на число, то оно умножается
с одним из членов произведения.

3)
(α-
β)(
= α(+
β (

15.
Базис
в пространстве

Компланарные
векторы лежат в одной плоскости.

3
любых некомпланарных вектора образуют
базис в пространстве.

Разложение
вектора по базису

Любой
вектор можно разложить по базису таким
способом: допустим B
(,)
– базис, а (α,
β, γ)
координаты определённого вектора,
например
.
Тогда разложение

по базису имеет вид:
=
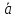
α+
β+
γ

16.
Прямая
на плоскости

Вектором
нормали
называется вектор перпендикулярный
плоскости. Пусть вектор

= (𝐴,
𝐵)
является вектором нормали к прямой 𝑙.
Произвольная точка плоскости 𝑀(𝑥,
𝑦)
принадлежит прямой 𝑙
тогда и только тогда, когда

⊥
,
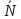
т.е. скалярное произведение этих векторов
*
=
0

Её
уравнения

1)
Уравнение прямой, проходящей через
заданную точку и имеющей заданный
вектор нормали 𝐴(𝑥–𝑥₀)+𝐵(𝑦−𝑦₀)=0

2)
Общее уравнение прямой: 𝐴𝑥
+ 𝐵𝑦
+ 𝐶
= 0

17.
Различные
уравнения плоскости

а)
Общее уравнение плоскости: Ax
+ By + Cz + D = 0

б)
Уравнение проходящее через точку
M₀(x₀,y₀,z₀)
и ⊥
вектору нормали
(A,B,C):
A(x—x₀)
+ B(y—y₀)
+C(z—z₀)=0

в)
Уравнение плоскости, проходящей через
3 заданные точки.

г)
Уравнение плоскости в отрезках:

18.
Угол
между плоскостями

Допустим,
мы имеем 2 уравнения плоскости (α: A₁x
+ B₁y
+ C₁z
+ D₁
= 0
и β: A₂x
+ B₂y
+ C₂z
+ D₂
= 0)
и нам нужно вычислить угол между 2
плоскостями – двугранный
угол.
Он вычисляется по формуле: cos=
(отношение произведения
₁*₂
к произведению модулей векторов
нормали).

Взаимное
расположение плоскостей

Две
плоскости в пространстве либо
параллельны, либо пересекаются.

α₁//α₂
– коллинеарные ⇒
==
– условие
параллельности.

α₁⊥α₂
⇒
⊥
⇒
*=0.
=0
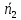
– условие
⊥.

19.
Прямая
в пространстве.
Различные
уравнения прямой в пространстве

1)
Параметрическое уравнение: x=x₀+mt,
y=y₀+nt,
z=z₀+pt

(m,n,p)
– направляющий вектор прямой (l),
который параллелен этой прямой. M₀(x₀,
y₀,
z₀)
∈l.

2)
Каноническое уравнение:

=

=

3)
Уравнение прямой проходящей через 2
точки:

=

=

4)
Общее уравнение прямой в пространстве:

20.
Угол
между прямыми и их взаимное расположение

Допустим,
мы имеем 2 (канонических) уравнения
прямых, а также их направляющие векторы
₁
и
₂.
Тогда угол между 2 прямыми

можно найти по формуле: cos=

Условие
//-ти:
₁
//₂
⇒

==

Условие
⊥—ти:

Расстояние
от точки до прямой в пространстве

У
нас есть уравнение прямой

=

=
,
её направляющий вектор

(m,n,p)
и точка не принадлежащая этой прямой
M(x₁,y₁,z₁).
Расстояние от точки до прямой определяется
по формуле:

21.
Угол
между прямой и плоскостью.

Допустим,
у нас есть каноническое уравнение
прямой

=

=

и уравнение плоскости Ax
+ By
+ Cz
+ D
= 0.
Тогда угол между прямой и плоскостью
можно найти по формуле: Sin
=

22.
Взаимное
расположение прямой и плоскости

Условие
//-ти:
Am+Bn+Cp
= 0

Условие
⊥—ти:

Плоскости
могут совпадать, быть параллельными
или пересекаться по прямой.

23.
Эллипс

Эллипс
– это геометрическое место точек
плоскости, расстоянием от которых до
2 заданных точек называется фокусами
есть величина постоянная.

Вывод
канонического уравнения

+

= 1

Геометрические
свойства

1)
Эллипс является кривой 2-го порядка.

2)
Является ограниченной фигурой.

3)
Является симметричной фигурой, оси
симметрии Ox,
Oy.

4)
a – большая ось; b
– малая ось; Вершины: А₁(а,0);
А₂(-а,0);
В₁(0,
b);
В₂(0,
—b);

5)

=

– эксцентриситет эллипса; 0
1.

6)
Прямые
x
=

– директриса эллипса. При

=1 ⇒
а=с; а=b
– уравнение окружности.
+=

24.
Гипербола

Гипербола
– геометрическое место точек на
плоскости, модуль разности расстояний
для 2 заданных точек называется фокусами
есть величина постоянная.

Вывод
канонического уравнения

—

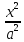
= 1

Геометрические
свойства

1)
Является кривой 2-го порядка.

2)
Является неограниченной кривой.

3)
Является симметричной фигурой.

4)
Пересекает Ox
в 2 точках, не пересекает ось Oy.
a – действительная полуось; b
– мнимая полуось;

5)

=

– эксцентриситет эллипса;

1.

6)
x
=

– директриса.
1

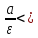
7)
y
=
x
– асимптоты

25.
Парабола

Парабола
– геометрическое место точек плоскости,
расстояние каждой из которых до заданной
точки называется фокусом и до определённой
прямой L,
называемой директрисой. (F∉L)

Вывод
канонического уравнения

p-
(параметр) расстояние от F
до L.
F(;0)
– фокус параболы. x=.
Уравнение: y²=2px

Геометрические
свойства

1)
Является кривой 2-го порядка.

2)
Симметричная фигура, ось симметрии –
Ox.

3)
Неограниченная фигура

4)

= 1
– эксцентриситет

26.
Числовая
последовательность

Если
каждому натуральному числу из множества
N
поставлено в соответствие некоторое
число или величина, то множество
последних образует последовательность.
xⁿ
– числовая последовательность.

Предел

Число
a
называется пределом числовой
последовательности, если для любого
положительного числа существует
N-число,
такое, что для всех номеров N
последующий больше, чем это число по
модулю.

Теорема
о сходимости

Если
xⁿ
имеет
предел, то он единственный. xⁿ
наз.
ограниченной, если существует n
и все члены удовлетворяют
M,
nN

27.
Предел
функции

Если
к каждому числу из множества x
поставлено в соответствие одно число
и множество y,
то на множестве x
задана функция y=f(x)

Число
b
называется пределом функции f(x)
при x→a,
если для любого положительного

существует положительная дельта,
зависящая от

Теорема
о существовании предела функции

Для
того, чтобы f(x)
имела предел в точке a,
необходимо чтобы левый и правый пределы
были равны.

28.
Односторонние
пределы функции

Левый
и правый пределы называют односторонними
пределами.

1)
Число b
называется правым пределом функции
при x→a
справа если для всех
0
существует дельта от
,
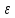
такой что 0следовательно
модуль f(x)-b
,
следовательно x

2)
Число b
называется левым пределом функции при
x→a
слева если для всех
0
существует дельта от
,
такой что —b
следовательно модуль f(x)-b
,
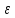
следовательно x

Теорема
о существовании предела функции

Для
того, чтобы f(x)
имела предел в точке a,
необходимо чтобы левый и правый пределы
были равны.

29.
Бесконечно-малые
и их свойства.

Бесконечно
малая функция
– это функция, предел которой в
данной точке равен нулю. Функция
α(x)
– бесконечно-малая при x→a,
если lim
α(x)
= 0.

При
x→a
lim

=
предел не существует.

Основные
свойства

1°  
Сумма конечного числа б.м функций
является функцией б.м.

3°  
Произведение двух б.м функций есть
функция б.м.

4°  
Произведение б.м функции на константу
является б.м функцией.

5°  
Частное от деления б.м функции на
функцию, предел которой
не равен нулю, есть функция б.м.

6°  
Функция ,
обратная
к б.м функции α(x)

0,
есть функция бесконечно большая. Верно
и обратное.

30.
Бесконечно-большие
функции.

Бесконечно
большая функция
– это функция, предел которой
стремится к
.

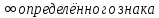
Теорема
о связи бесконечно-большой и
бесконечно-малой функции

Теорема.
Функция обратная бесконечно малой,
является бесконечно большой и наоборот.
Доказательство: Пусть предел функции
равен 0, а сама функция не = 0, при x→a,
т.е. задаём бесконечно-малую функцию
.
Тогда для любого числа 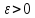 существует
такое число дельта
,
что для всех x,
удовлетворяющих неравенству
 ,
выполняется неравенство ,
т.е.
 .
А из этого следует, что функция  —
бесконечно большая.

Шпаргалка: Математический анализ

Определение функции нескольких
переменных.

Переменная u называется f(x,y,z,..,t), если для любой совокупности значений (x,y,z,..,t) ставится в соответствие вполне определенное значение
переменной u.

Множество совокупностей значение
переменной называют областью определения ф-ции.

G — совокупность (x,y,z,..,t)
— область определения .

Функции 2-х переменных.

Переменная z называется функцией 2х переменных f(x,y),
если для любой пары значений (x,y)
Î G
ставится в соответствие определенное значение переменной z.

Предел функции 2-х переменных.

Пусть задана функция z=f(x,y), р(х,у)-текущая точка, р0(х0,у0)- рассматриваемая точка.

Опр. Окрестностью точки р0
называется круг с центром в точке р0 и радиусом r. r = Ö(х-х0)2+(у-у0)2Ø

Число А называется пределом
функции |в точке р0, если для любого

Lim f(x,y)

pàp0

сколь угодно малого числа e можно указать такое число r (e)>0, что при всех значениях х и у, для
которых расстояние от т. р до р0 меньше r выполняется неравенство: ½f(x,y)
— А½<e, т.е. для всех точек р,
попадающих в окрестность точки р0, с радиусом r, значение функции отличается от А меньше
чем на e по
абсолютной величине. А это значит, что когда точка р  приблизится к точке р0 по
любому пути, значение функции неограниченно приближается к числу А.

Непрерывность функции.

Пусть задана функция z=f(x,y), р(х,у)-текущая точка, р0(х0,у0)- рассматриваемая точка.

Опр. Функция z=f(x,y) называется непрерывной в т. р0, если выполняются 3
условия:

1)функция определена в этой точке.
f(р0) = f(x,y);

2)ф-я имеет предел в этой точке.

Lim f(р) = b

pàp0

3)Предел равен значению функции в
этой точке:  b = f(x0,y0);

Lim f(x,y) = f(x0,y0);

pàp0

Если хотя бы 1 из условий
непрерывности нарушается, то точка р называется точкой разрыва. Для функций 2х
переменных могут существовать отдельные точки разрыва и целые линии разрыва.

Понятие предела и непрерывности
для функций большего числа переменных определяется аналогично.

Функцию трех переменных невозможно
изобразить графически, в отличие от функции 2х переменных.

Для функции 3х переменных могут
существовать точки разрыва, линии и поверхности разрыва.

Частное производной.

Рассморим функцию z=f(x,y), р(х,у)- рассматриваемая точка.

Дадим аргументу х приращение Dх;  х+Dх, получим точку р1(х+Dх,у), вычислим разность значений
функции в точке р:

Dхz
= f(p1)-f(p) = f(x+Dx,y)
— f(x,y) —
частное приращение функции соответствующее приращению аргумента х.

Опр. Частное производной функции z=f(x,y) по переменной х называется предел отношения частного
приращения этой функции по переменной х к этому приращению, когда последнее
стремится к нулю.

¶z = Lim      Dxz

¶x    Dx®0  Dx   

à ¶z = Lim     f(x+Dx,y) —
f(x,y)

    ¶x     Dx®0            Dx

Аналогично определяем частное
производной по переменной у.

Нахождение частных производных.

При определении частных
производных каждый раз изменяется только одна переменная, остальные переменные
рассматриваются как постоянные. В результате каждый раз мы рассматриваем
функцию только одной переменной и частная производной совпадает с обычной
производной этой функции одной переменной. Отсюда правило нахождения частных
производных: частноя производная по рассматриваемой переменной ищется как
обычная производнаяфункции одной этой переменной, остальные переменные
расстатриваются как постоянные величины. При этом оказываются справедливыми все
формулы дифференцирования функции одной переменной (производноя суммы,
произведения, частного).

(Лекция № 2)

Полный дифференциал ф-ции 2-х
переменных.

z=f(x,y) в области D.

p(x,y)
Î D —
рассматриваемая точка. Дадим х приращение Dх, у — Dу. Получим р1(х+Dх, у+Dу). Вычилим значение функции. Полным
приращение функции называется разность:

Dz = f(p1)-f(p)

Dz = f(x+Dx,y+Dy) — f(x,y)

Опр. Полным дифференциалом функции
z=f(x,y) называется главная линейная
часть приращения этой функции, если приращение можно преобразовать к виду:

Dz = ADx + BDy + a

А, В — не зависят от Dх, Dу;

a — зависит от Dх и Dу и при этом

Lim   a = 0

r®0 r

r — расстояние между точками р и р1

S = рр1 = ÖDх2 +Dу2Ø

a является бесконечно малой, более
высокого порядка, чем r

При ументшении Dх и Dу a®0 быстрее, чем r. Из определения следует, что полный дифференциал функции равен

z = ADx + BDy

При малых Dх и Dу имеет место равенство Dz » dz.

Опр. Если  функция  z=f(x,y) имеет полный дифференциал в точке р, то она называется
дифференцируемой в этой точке.

Теорема. Необходимые условия
дифференцируемости функции.

Если  функция  z=f(x,y) дифференцируема в точке р, то она имеет частные
производные в этой точке и при этом выражение поного дифференциала  А = ¶z/¶x  B
= ¶z/¶y, т.е. полный дифференциал может
быть записак в виде:

dz = ¶z/¶x Dx + ¶z/¶y  Dy

Док-во: По определению
дифференцируемости приращение функции может быть записано в виде:

Dz = ADx+BDy +a при
любом Dх и Dу.

Рассмотрим 2 частных случая

1)Dх¹0 Dу = 0

При этом Dz=ADx+a   /Dx и перейдем к пределу. Полное приращение функций
превращается в частное приращение.

Lim    Dxz/Dx  = Lim A+a/Dx

Dx®0                Dx®0

¶z/¶x= A+Lim(Dx®0)a/Dx =0 т.к. r=Dх

В результате получаем А=¶z/¶x

2)Dx=0 Dy¹0

При этом аналогичным образом получим,
что В=¶z/¶y

Теорема доказана. Как следствие à полный дифференциал
дифференцируемой функции определяется по формуле:

dz=¶z/¶x·Dx+¶z/¶y·Dy, если
при этом учесть, сто приращение независимых переменных х и у равны их
дифференциалам Dx=dx,
Dy=dy, то окончательно получим:

dz=¶z/¶x·dx+¶z/¶y·dy

Теорема 2.  Достаточное услови
дифференцируемости функции.

Если z=f(x,y) имеет в точке р(х,у) непрерывные частные производные, то
она дифференцируема в этой точке, т.е. она имеет полный дифференциал.

Полный дифференциал для функций
нескольких переменных.

Для функций многих переменный
полный дифференциал определяется аналогично, при этом:

u=f(x,y,z,…,t)

du=¶u/¶x·dx+¶u/¶y·dy+¶u/¶z·dz+…+¶u/¶t·dt

Применение полного дифференциала
для приближенных вычислений.

Пусть задана функция z=f(x,y) рассмотрим ее полное приращение.

Dz=f(x+Dx,y+Dy) — f(x,y)

При малых Dх и Dу à Dz»dz è

f(x+Dx,y+Dy) — f(x,y) » ¶z/x¶·Dx+¶z/¶y·dy®

f(x+Dx,y+Dy)» f(x,y)+¶z/¶x·dx+¶z/¶y·dy —
формула для приближенных вычислений.

Эта формула позволяет вычислять
приближенное значение функции в точке р1 по известному ее в точке р и значением
ее частных производных в точке р. Чем меньше Dх и Dу, тем меньше погрешность.

Дифференцирование сложных функций.

Опр. Переменная z=z(t)
— называется сложной функцией переменной t, если
она определяется равенством:

z=z(t)=f[x(t),y(t)] — сложная функция от t.

Теорема. Если функция z=f(x,y) дифференцируема в точке р(х, у), а функции x=x(t)
и y=y(t) дифференцируемы в ссответствующей точке t, то сложная функция z=z(t) также дифференцируема в точке t и ее производная определяется равенством:

dz/dt = ¶z/¶x·dx/dt+ ¶x/¶y·dy/dt  [**]

Док-во: Дадим переменной t приращение Dt, при
этом х=х(t) получит приращение Dх, а у=у(t) à Dу,
в результате переменная z=f(x,y) получит приращение Dz, т.к. z(х,у) — дифференцируемая функция,
то это приращение может быть представлено в виде:

Dz=¶z/¶x·Dx + ¶z/¶y·Dy + a

разделим на Dt и перейдем к пределу

Lim(Dt®0)Dz/Dt = ¶z/¶x·Lim(Dt®0)Dx/Dt +

+ ¶z/¶y·Lim(Dt®0)Dy/Dt + Lim(Dt®0)a/Dt

dz/dt = ¶z/¶x·dx/dt + ¶z/¶y·dy/dt + Lim(Dt®0) a/r·r/Dt  è 0

r=ÖDx2+Dy2Ø

Lim(Dt®0)a/r=0 — по
определению дифференциала.

Lim(Dt®0)r/Dt = Lim(Dt®0)Ö(Dx/Dt)2+(Dy/Dt)2Ø=

=Ö(dx/dt)2+(dy/dt)2ع¥

Формула [**] доказана.

Рассмотрим частный случай сложной
функции:

z= f[x,y(x)] = z(x)

в ф-ле [**] вместо tàх, получим

dz/dx= ¶z/¶x·dx/dx+ ¶z/¶y·dy/dx

dz/dx= ¶z/¶x+ ¶z/¶y·dy/dx  [***]

Формула [**] распространяется на
сложные функции большего числа переменных.

Пусть z=f(x,y), где x=x(r,s,..t),
y=y(r,s,..,t)
è z=z(r,s,..,t) — cложная
функция.

При этом формула [**] принимает
вид:

¶z/¶r=¶z/¶x·¶x/¶r+¶x/¶y·¶y/¶r

¶z/¶s=¶z/¶x·¶x/¶s+ ¶z/¶y·¶y/¶s    [****]

Лекция №3

Дифференцирование функций,
заданных неявно.

Опр.  Функция z=f(x,y) наз. Заданной неявно, если она определена равенством,
неразрешенным относительно z .

F(x,y,z)=0

x+y+z=ez — это равенство задаем некоторую функцию z=f(x,y), которую нельзя выразить в полном виде.

x2+y2+z2=0
— не задает никакой функции.

Теорема: Если ф-я F(x,y,z) —
непрерывна в т. р0(x0,y0,z0) и ее производная по z  Fz(x,y,z)¹0, то
равенство F(x,y,z)=0 однозначно определяет в
неявном виде функцию z=f(x,y), при этом эта функция
дифференцируема и ее производная находится по формулам:

¶z/¶x=— F¢x(x,y,z)/F¢z(x,y,z)

¶z/¶y=—F¢z (x,y,z)/F¢y(x,y,z)

Док-во: Найдем полный дифференциал
функции

dF(x,y,z)=¶F/¶x*dx+¶F/¶y*dy+¶F/¶x*dz

F(x0,y0,z0)=0èdF=0è

¶F/¶x*dx+¶F/¶y*dy+¶F/¶x*dz=0

dz=—(¶F/¶x)/(¶F/¶z)*dx—(¶F/¶y)/(¶F/¶z)*dy  (*)

С другой стороны:

z=f(x,y), dz=¶z/¶x*dx+¶z/¶y*dy  (**)

Сравнивая (*) и(**) è

¶z/¶x=— F¢x(x,y,z)/F¢z(x,y,z)

¶z/¶y=—F¢z (x,y,z)/F¢y(x,y,z)

Частные производные высшего
порядка.

Пусть задана функция 2х переменных
z=f(x,y),найдем ее частные производные.

¶z/¶x=f¢x(x,y)

¶z/¶y=f¢y(x,y)

В общем случае,  эти производные
также являются функциями 2х и можно искать их частные производные. При этом
получаем часные производные 2-ого и более порядков.Производные, в которых
дифференцирование производится по разным переменным, называются смешанными.

Теорема: О независимости часных
производных от порядка (последовательности) дифференцирования.

Две смешанные частные роизводные
одного порядка, отличающиеся только порядком диф-я равны.

¶2z/¶x¶y=¶2z/¶y¶x — в
следствии этого, при обозначении смешанных частных производных
последовательность диф-я не указывается.

¶nz/¶xn-2¶y2

Экстремумы функции 2ух переменных.

Рассмотрим функцию 2х переменных z=f(x,y) в области Д, пусть р0(x0,y0) — внутренняя точка этой области.

Опр. Точка р0 наз. Точкой max  функции, если в некоторой окресности этой точки
выполняется неравенство:

f(x,y)<
f(x0,y0)

min —
наоборот

Теорема: Необходимое условие
существования экстремума функции в точке р0.

Если ф-я z=f(x,y) диф-ма в точке р0 и имеет в этой точке экстремум, то
часные производные функции в этой точке равны нулю.

f¢x(x0,y0)=0

f¢y(x0,y0)=0

Пусть в точке р0  функция
достигает max. Рассмотрим часную производную
этой функции по у.

f¢y(x,y)=j¢(у)

При нахождении этой частной
производной мы имеем дело с функцией, зависящей только от х, при этом эта
функция в точке р0 достигает max, поэтому по теореме о
существовании экстремума функции одной переменной имеем:

j¢( y0)=0
® f¢y(x0,y0)=0, аналогично по х.

Опр. Точка р0 при этом наз.
стационарной точкой (в которой часные производные равны нулю).

Из этого следует, что экстремум
функция 2х переменных может достигать только в стационарных точках (если она
диф-ма ), но не во всякой стационарной точке функция достигает экстремума, т.к
это только необходимое условие, но недостаточное условие.

Теорема: Достаточное условие
существования экстремума ф-ции 2х переменных.

Пусть ф-я z=f(x,y) диф-ма в точке р0 и эта точка явл. стационарной точкой ,
найдем часные производные 2ого порядка этой  функции

r=¶2z/¶x2    s=¶2z/¶x¶y   t=¶2z/¶y2

Вычислим в точке р0 значение
выражения  (rt—s2)po, если это выражение >0, то в т. р0 сущ. экстремум.

При этом если r>0 р0 —min; r<0 р0 —max

Если rt—s2<0 — экстремума нет.

rt—s2=0 — экстремум возможен, требуются
дополнительные исследования.

Определение наибольшего и
наименьшего значения функции в замкнутой области.

Пусть задана ф-я z=f(x,y) в замкнутой области Д.

F(x,y)=0
— уравнение границы Д.

Требуется найти наибольшее и
наименьшее значения ф-ции в этой области.

Эти значения функция может
достигать либо в экстремальных точках внутри области, либо на границе области,
поэтому решение задачи делится на 2 этапа:

1.Сначала находим стационарные
точки внутри области. В этих тосках возможны экстремумы. Вычисляем зачение
заданной функции в этой точке.

2.Определяем наиб. и наим.
Значение функции на границе области.

3.Сравниваем полученное значение и
выбираем наиб. и наим. знач.

Нахождение наибольшего и наименьшего
значения на границе области Д.

Пусть граница области имеет
уравнение F(x,y)=0 è y=y(x) —
на гр. обл. Д

z=f(x,y) = f[x,y(x)]=z(x) —
является сложной функцией.

 Необходимо найти min и max z(x) на границе. Для этого надо найти экстремумы внутри
области (достаточно найти точки, где возможны экстремумы и вычислить значение
функции в этих точках).

Леция №4

Определение интеграла по фигуре.

Пусть дана фигура G , р — текущая точка на фигуре.

f(p) — заданная на фигуре  G

Выполним след. операции:

1.Разобьем G на куски: DG1, DG2,…, DGn, —
меры кусков.

2.Внутри каждого куска выберем по
1 точке р1, р2, р3…

3.Вычисляем значение функции в
выбранных точках

4.Составляем сумму произведений

f(p1)* DG1+ f(p2)* DG2+… +f(pn)* DGn=(n/i=1)åf(pi)*DGi —

эта сумма  называется интегральной
суммой функции f(p)
по фигуре G при разбиениии n

Опр. Интегралом по фигуре G функции f(p)
называется предел интегральных сумм этой функции, когда n®0

òGf(p)dG=Lim(n®¥)*(n/i=1)åf(Pi)*DGi

Если этот предел существует и
независит от способов разбиения при условии, что диаметры кусков при этом
стремятся к нулю.

Диаметром куска называется его
максимальный линейный размер.

Max dim DG ®0

Cвойства интеграла по фигуре.

1.Итеграл по фигуре от единичной функции
равен мере фигуры.

òGdG=G — мера фигуры

Док-во: по определению

òGdG=Lim(n®¥)*(n/i=1)å1*DG=G — как
сумма мер всех кусков.

¥¥¥¥¥¥¥¥¥¥òòòòòòòòåååååå